Identification of Denatured Biological Tissues Based on Time-Frequency Entropy and Refined Composite Multi-Scale Weighted Permutation Entropy during HIFU Treatment
Abstract
:1. Introduction
2. Methods
2.1. Time-Frequency Entropy Based on Generalized S-Transform (GST)
2.2. MPE
2.3. RCMWPE
2.4. Intra-Class Distance and Inter-Class Distance
3. Experimental Methods and Results
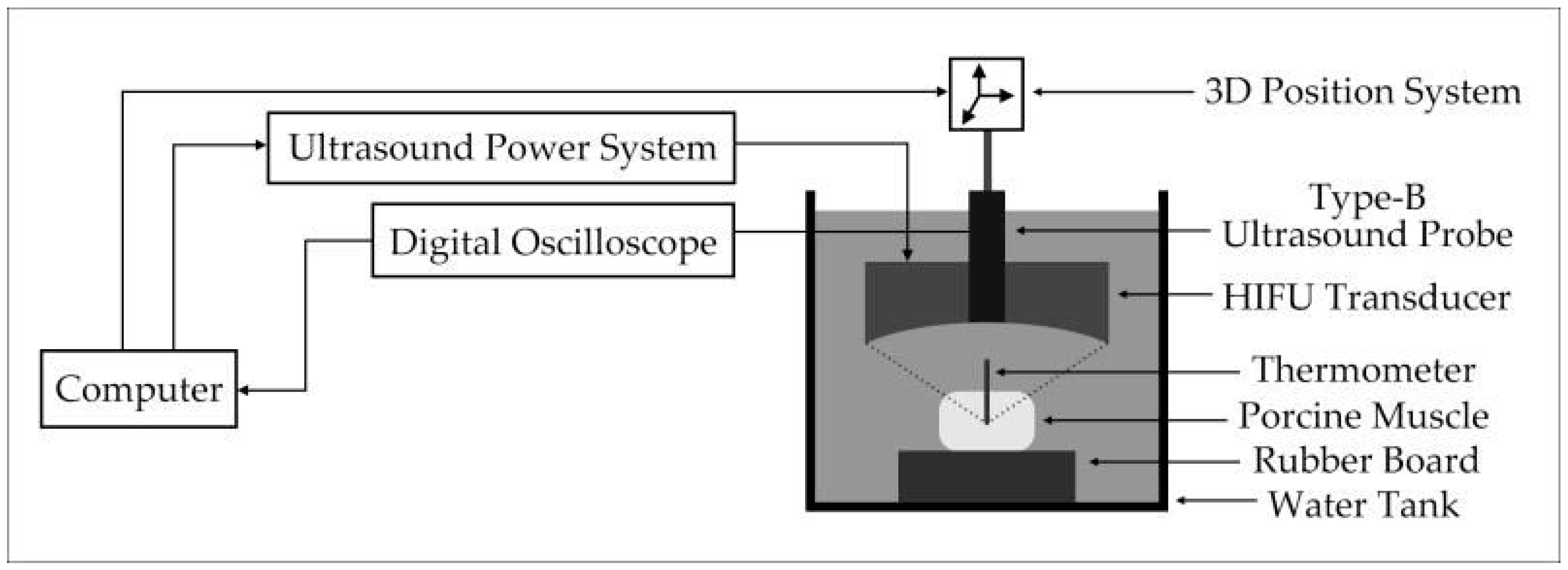
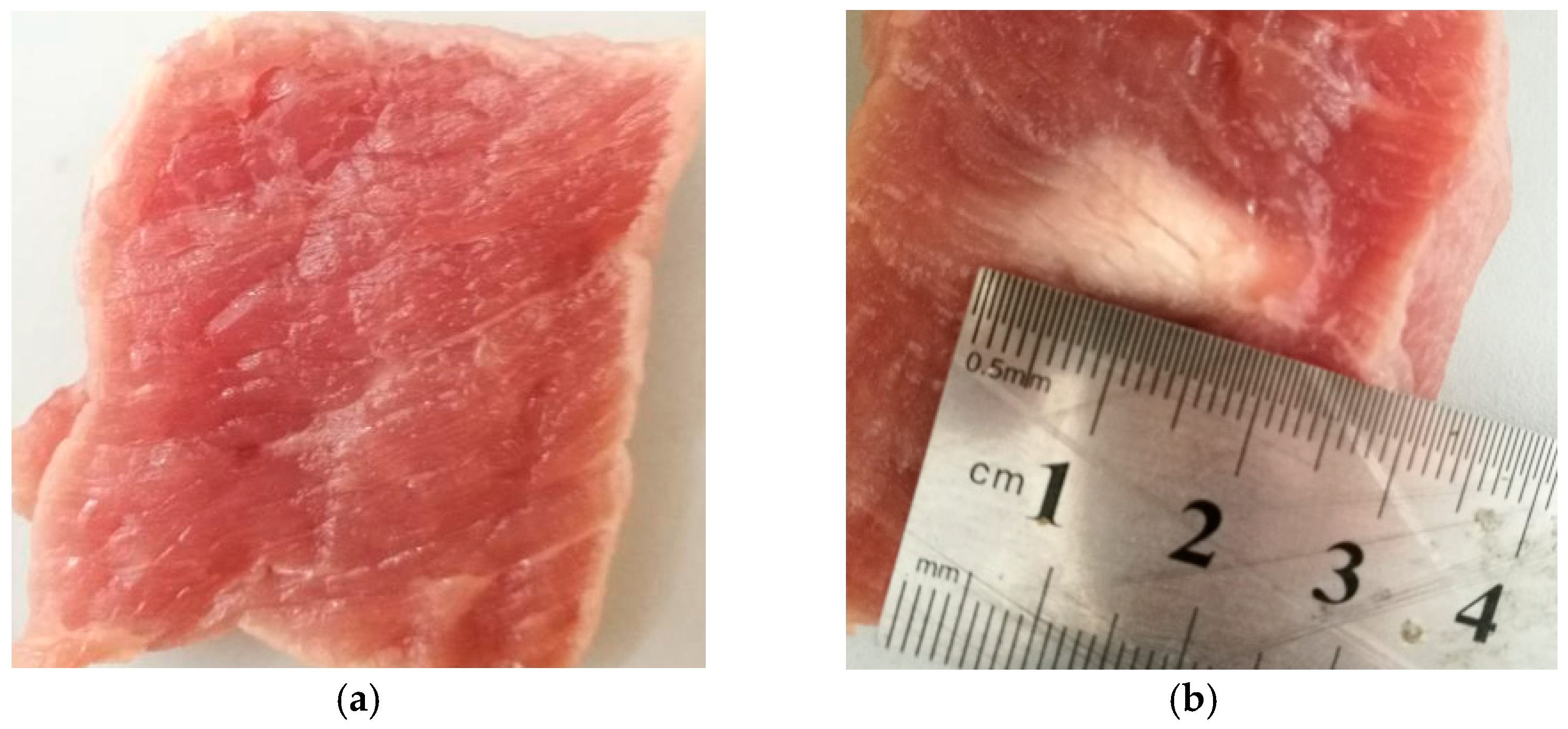
3.1. Experimental System
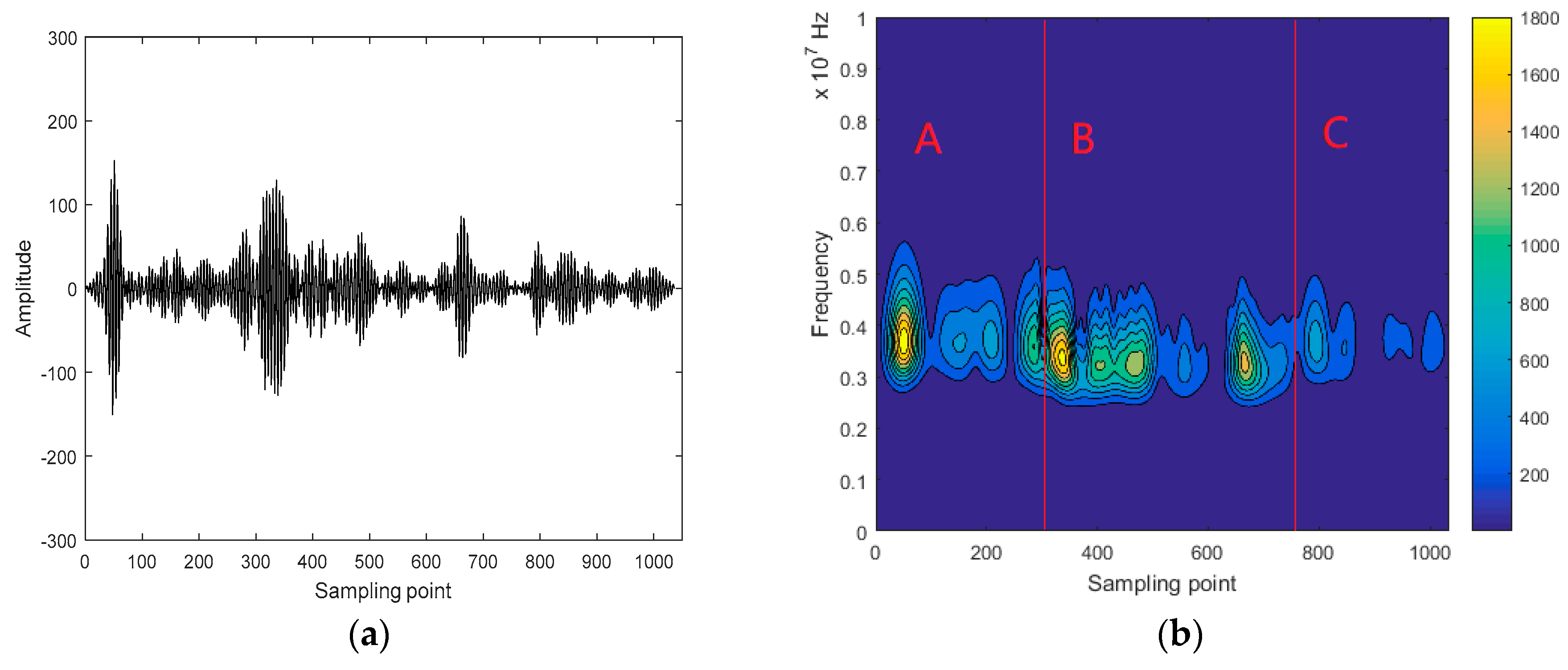
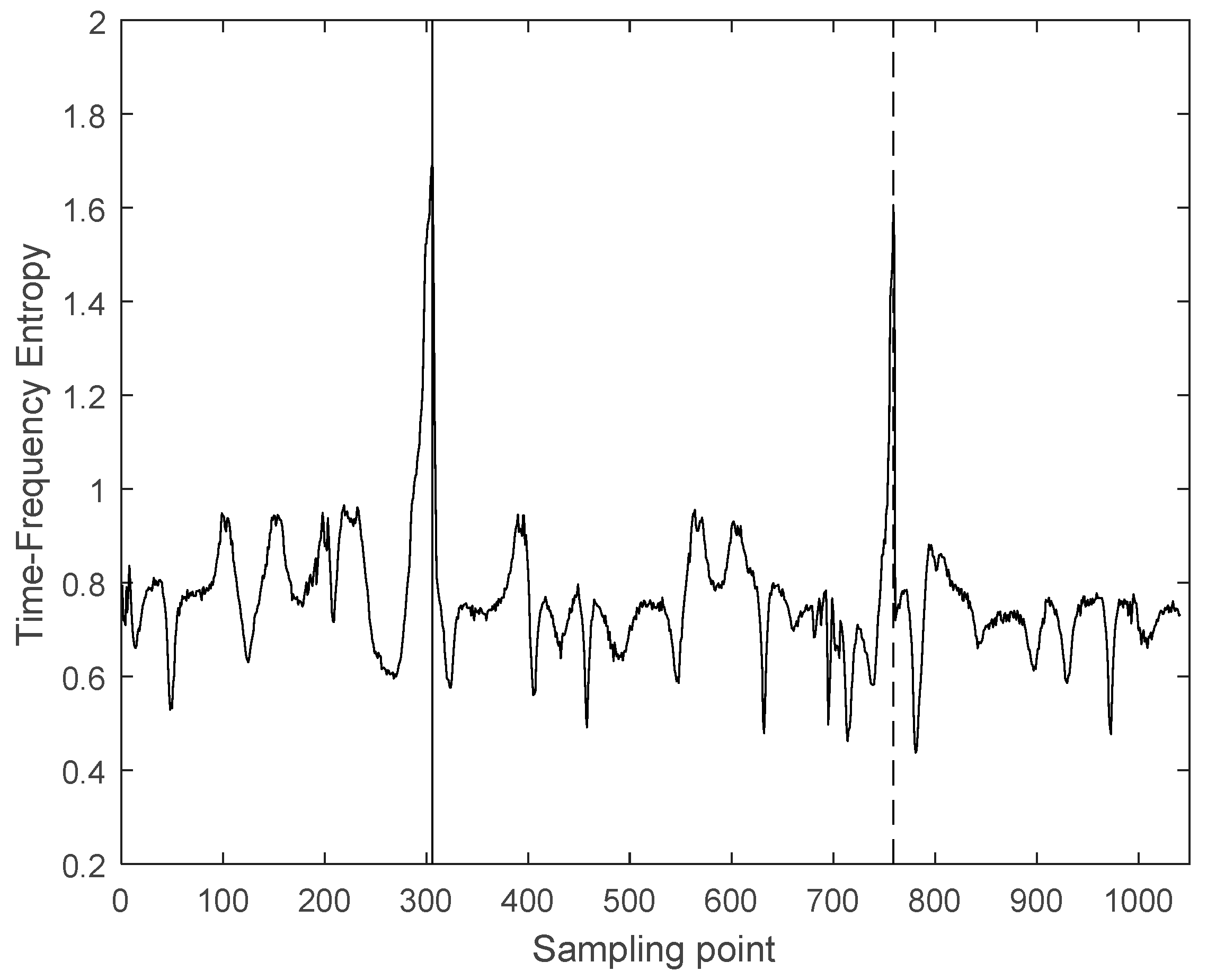
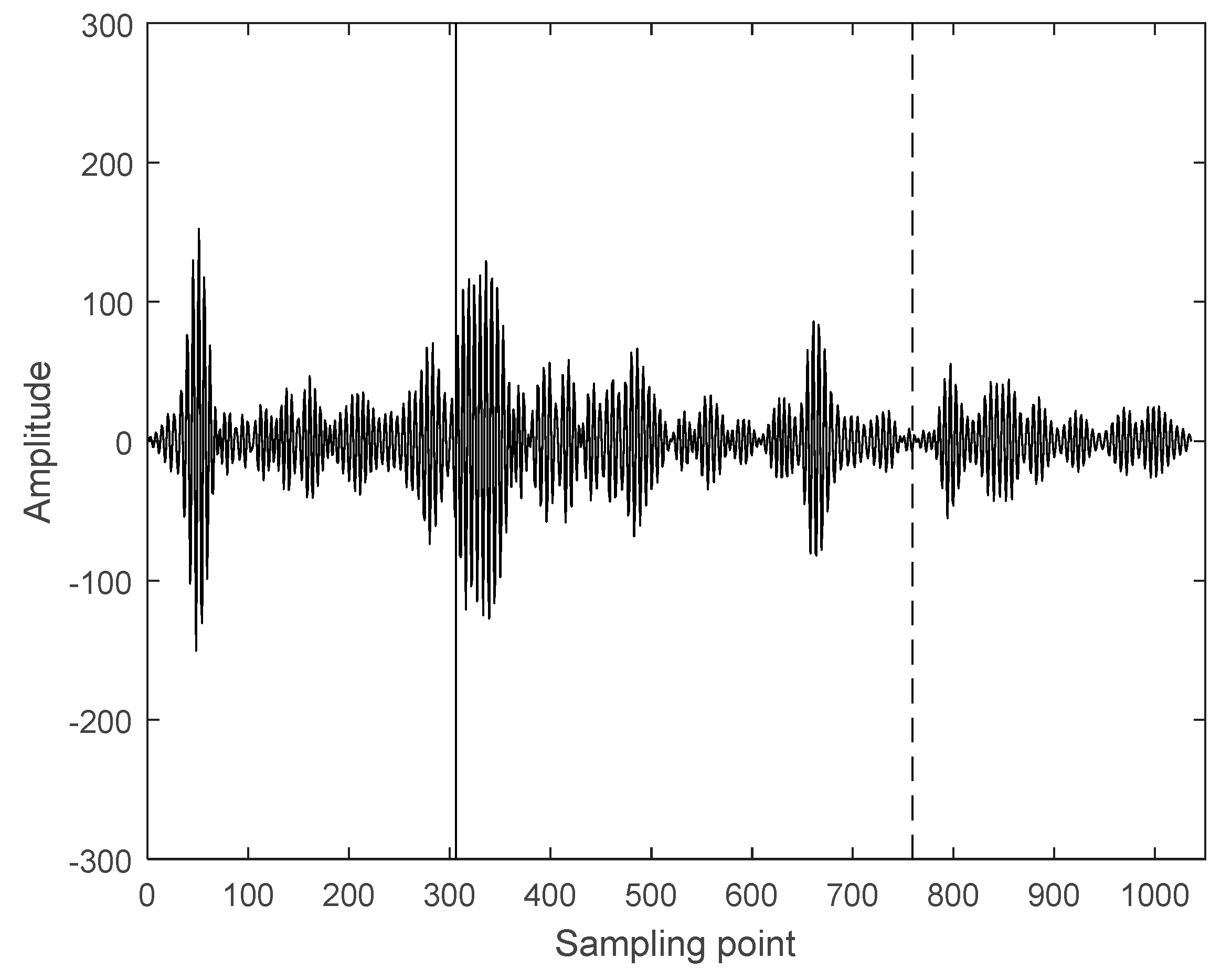
3.2. Interception of Ultrasonic Scattered Echo Signal Based on Time-Frequency Entropy
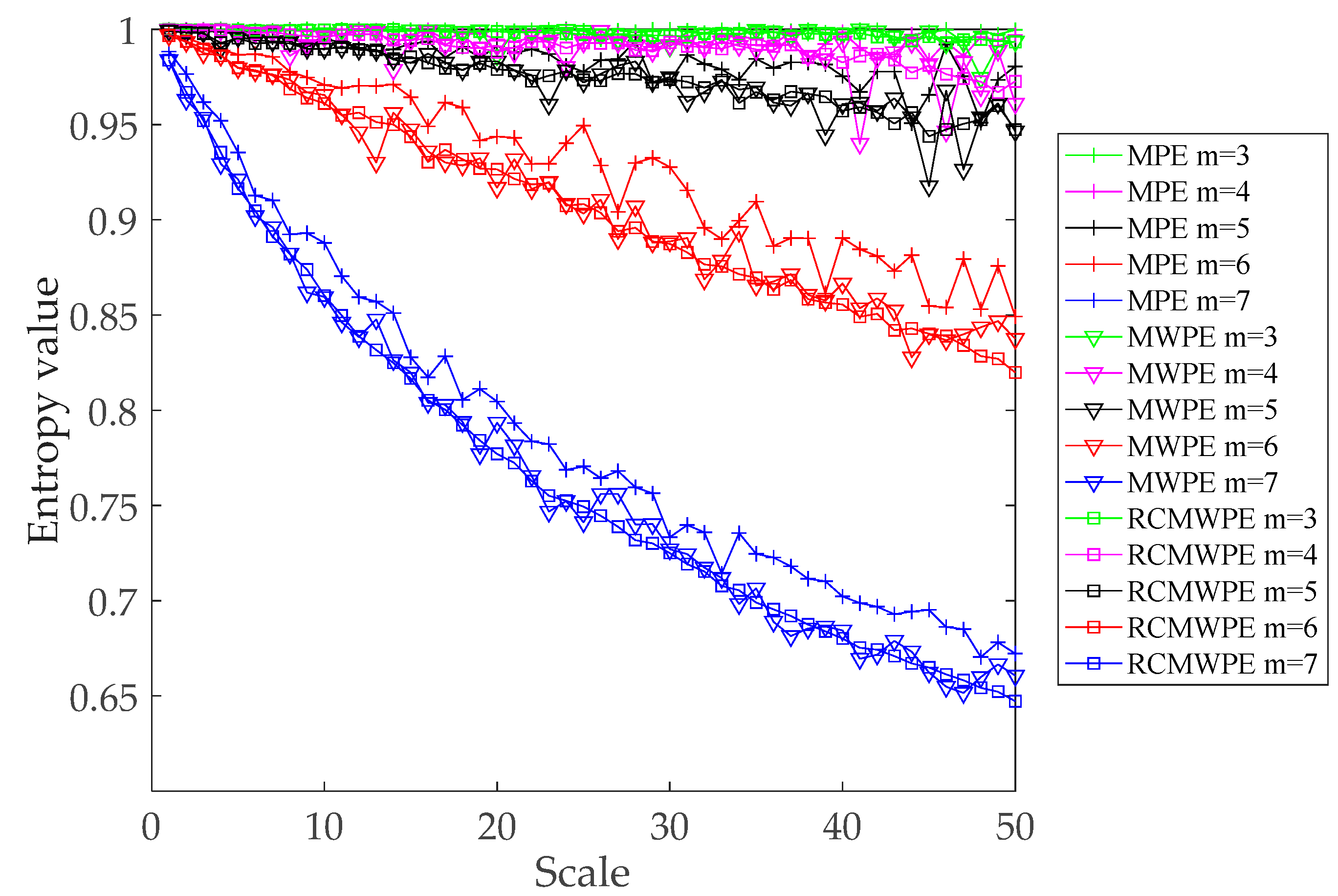
3.3. Comparison between Different Entropies of Simulated Signal
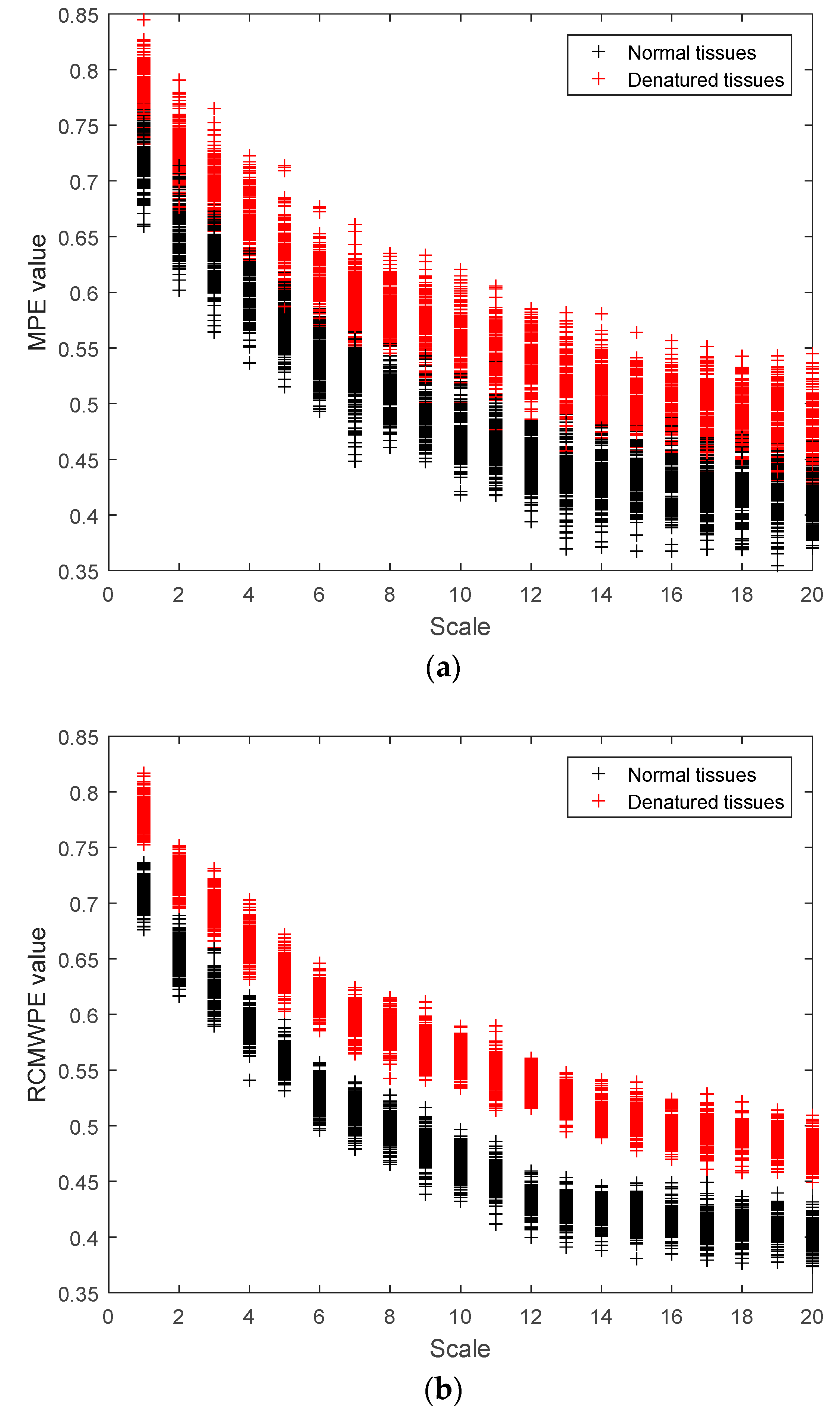
3.4. MPE and RCMWPE of Actual Ultrasonic Scattered Echo Signals
3.5. Intra-Class Distance and Inter-Class Distance of the MPE and RCMWPE
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cranston, D. A review of high intensity focused ultrasound in relation to the treatment of renal tumours and other malignancies. Ultrason. Son. 2015, 27, 654–658. [Google Scholar] [CrossRef] [PubMed]
- Ellens, N.; Hynynen, K. Frequency considerations for deep ablation with high-intensity focused ultrasound: A simulation study. Med. Phys. 2015, 42, 4896–4910. [Google Scholar] [CrossRef] [PubMed]
- Bailey, M.R.; Khokhlova, V.A.; Sapozhnikov, O.A.; Kargl, S.G.; Crum, L.A. Physical mechanisms of the therapeutic effect of ultrasound (a review). Acoust. Phys. 2003, 49, 369–388. [Google Scholar] [CrossRef]
- Yang, C.; Zhu, H.; Wu, S.C. Correlations between B-mode ultrasonic image texture features and tissue temperature in microwave ablation. J. Ultrasound Med. 2010, 29, 1787–1799. [Google Scholar] [CrossRef] [PubMed]
- Wust, P.; Cho, C.H.; Hildebrandt, B. Thermal monitoring: Invasive minimal-invasive and non-invasive approaches. Int. J. Hyperth. 2006, 22, 255–262. [Google Scholar] [CrossRef] [PubMed]
- Goldhaber, D.M.; Deli, M.; Mineyev, M.I.; Gronemeyer, D.H.W. Measurement of tissue temperature by MRI. In Proceedings of the 1993 IEEE Conference Record Nuclear Science Symposium and Medical Imaging Conference, San Francisco, CA, USA, 31 October–6 November 1993; Volume 3, pp. 1702–1705. [Google Scholar]
- Wilkins, T.; Tadkod, A.; Hepburn, I.; Schade, R.R. Nonalcoholic fatty liver disease: Diagnosis and management. Am. Fam. Phys. 2013, 88, 35–42. [Google Scholar]
- Seip, R.; Tavakkoli, J.; Carlson, R.F.; Wunderlich, A. High-intensity focused ultrasound(HIFU) multiple lesion imagine: Comparison of detection algorithms for real-time treatment control. In Proceedings of the 2002 IEEE Ultrasonics Symposium, Munich, Germany, 8–11 October 2002; pp. 1427–1430. [Google Scholar]
- Damianou, C.A.; Sanghvi, N.T.; Fry, F.J.; Maassmoreno, R. Dependence of ultrasonic attenuation and absorption in dog soft tissue on temperature and thermal dose. J. Acoust. Soc. Am. 1997, 102, 628–634. [Google Scholar] [CrossRef]
- Rahimian, S.; Tavakkoli, J. Estimating dynamic changes of tissue attenuation coefficient during high- intensity focused ultrasound treatment. J. Ther. Ultrasound 2013, 1, 1–22. [Google Scholar] [CrossRef]
- Ghoshal, G.; Oelze, M.L. Use of quantitative ultrasound to detect temperature variations in biological phantoms due to heating. In Proceedings of the 2009 IEEE International Ultrasonics Symposium (IUS), Rome, Italy, 20–23 September 2009. [Google Scholar]
- Seip, R.; Ebbini, E.S. Noninvasive estimation of tissue temperature response to heating fields using diagnostic ultrasound. IEEE Trans. Biomed. Eng. 1995, 42, 828–839. [Google Scholar] [CrossRef]
- Straube, W.L.; Arthur, R.M. Theoretical estimation of the temperature dependence of backscattered ultrasonic power for noninvasive thermometry. Ultrasound Med. Biol. 1994, 20, 915–922. [Google Scholar] [CrossRef]
- Huang, N.; Chen, H.; Zhang, S.; Cai, G.; Li, W.; Xu, D.; Fang, L. Mechanical Fault Diagnosis of High Voltage Circuit Breakers Based on Wavelet Time-Frequency Entropy and One-Class Support Vector Machine. Entropy 2016, 18, 7. [Google Scholar] [CrossRef]
- Cai, H.P.; He, Z.H.; Huang, D.J.; Li, R. Reservoir Distribution Detection based on Time-Frequency Entropy. J. Oil Gas Technol. 2010, 32, 66–68. [Google Scholar]
- Allen, J. Short term spectral analysis, synthesis, and modification by discrete Fourier transform. IEEE Trans. Acoust. Speech Signal Process. 2003, 25, 235–238. [Google Scholar] [CrossRef]
- Daubechies, I. Ten Lectures on Wavelets; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1992; p. 1671. [Google Scholar]
- Stockwell, R.G.; Mansinha, L.; Lowe, R.P. Localization of the Complex Spectrum: The S Transform. IEEE Trans. Signal Process. 1996, 44, 998–1001. [Google Scholar] [CrossRef]
- Sun, S.; Castagna, J.P.; Siegfried, R.W. Examples of wavelet transform time-frequency analysis in direct hydrocarbon detection. Seg. Tech. Program Expand. Abstr. 2002, 21, 2478. [Google Scholar]
- Gilles, J. Empirical Wavelet Transform. IEEE Trans. Signal Process. 2013, 61, 3999–4010. [Google Scholar] [CrossRef]
- Mandic, D.P.; Rehman, N.U.; Wu, Z.; Huang, N.E. Empirical Mode Decomposition-Based Time- Frequency Analysis of Multivariate Signals: The Power of Adaptive Data Analysis. Signal Process. Mag. IEEE 2013, 30, 74–86. [Google Scholar] [CrossRef]
- Gao, J.H.; Chen, W.C.; Youming, L.I.; Tian, F. Generalized S Transform and Seismic Response Analysis of Thin Interbedss Surrounding Regions by Gps. Chin. J. Geophys. 2003, 46, 759–768. [Google Scholar]
- Mobasheri, S.; Behnam, H.; Rangraz, P.; Tavakkoli, J. Radio Frequency Ultrasound Time Series Signal Analysis to Evaluate High-intensity Focused Ultrasound Lesion Formation Status in Tissue. J. Med. Signals Sens. 2016, 6, 91–98. [Google Scholar]
- Tsui, P.-H.; Wan, Y.-L. Effects of Fatty Infiltration of the Liver on the Shannon Entropy of Ultrasound Backscattered Signals. Entropy 2016, 18, 341. [Google Scholar] [CrossRef]
- Montirosso, R.; Riccardi, B.; Molteni, E.; Borgatti, R.; Reni, G. Infant’s emotional variability associated to interactive stressful situation: A novel analysis approach with Sample Entropy and Lempel–Ziv Complexity. Infant Behav. Dev. 2010, 33, 346–356. [Google Scholar] [CrossRef] [PubMed]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
- Tao, M.; Poskuviene, K.; Alkayem, N.; Cao, M.; Ragulskis, M. Permutation entropy Based on Non-Uniform Embedding. Entropy 2018, 20, 612. [Google Scholar] [CrossRef]
- Wu, S.D.; Wu, P.H.; Wu, C.W.; Ding, J.J.; Wang, C.C. Bearing Fault Diagnosis Based on Multiscale Permutation Entropy and Support Vector Machine. Entropy 2012, 14, 1343–1356. [Google Scholar] [CrossRef] [Green Version]
- Gao, Y.; Villecco, F.; Li, M.; Song, W. Multi-Scale permutation entropy based on improved LMD and HMM for rolling bearing diagnosis. Entropy 2017, 19, 176. [Google Scholar] [CrossRef]
- Liu, B.; Hu, W.P.; Zou, X.; Ding, Y.J.; Qian, S.Y. Recognition of denatured biological tissue based on variational mode decomposition and multi-scale permutation entropy. Acta. Phys. Sin. 2019, 68, 028702. [Google Scholar]
- Fadlallah, B.; Chen, B.; Keil, A.; Príncipe, J. Weighted-permutation entropy: A complexity measure for time series incorporating amplitude information. Phys. Rev. E 2013, 87, 022911. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, S.D.; Wu, C.W.; Lin, S.G.; Wang, C.C.; Lee, K.Y. Time Series Analysis Using Composite Multiscale. Entropy 2013, 15, 1069–1084. [Google Scholar] [CrossRef]
- Zheng, J.; Pan, H.; Cheng, J. Rolling bearing fault detection and diagnosis based on composite multiscale fuzzy entropy and ensemble support vector machines. Mech. Syst. Signal Process. 2017, 85, 746–759. [Google Scholar] [CrossRef]
- Wu, S.D.; Wu, C.W.; Lin, S.G.; Lee, K.Y.; Peng, C.K. Analysis of complex time series using refined composite multiscale entropy. Phys. Lett. A 2014, 378, 1369–1374. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, B.; Qian, S.; Hu, W. Identification of Denatured Biological Tissues Based on Time-Frequency Entropy and Refined Composite Multi-Scale Weighted Permutation Entropy during HIFU Treatment. Entropy 2019, 21, 666. https://doi.org/10.3390/e21070666
Liu B, Qian S, Hu W. Identification of Denatured Biological Tissues Based on Time-Frequency Entropy and Refined Composite Multi-Scale Weighted Permutation Entropy during HIFU Treatment. Entropy. 2019; 21(7):666. https://doi.org/10.3390/e21070666
Chicago/Turabian StyleLiu, Bei, Shengyou Qian, and Weipeng Hu. 2019. "Identification of Denatured Biological Tissues Based on Time-Frequency Entropy and Refined Composite Multi-Scale Weighted Permutation Entropy during HIFU Treatment" Entropy 21, no. 7: 666. https://doi.org/10.3390/e21070666
APA StyleLiu, B., Qian, S., & Hu, W. (2019). Identification of Denatured Biological Tissues Based on Time-Frequency Entropy and Refined Composite Multi-Scale Weighted Permutation Entropy during HIFU Treatment. Entropy, 21(7), 666. https://doi.org/10.3390/e21070666



