Entropy and Information within Intrinsically Disordered Protein Regions
Abstract
1. Information—Central to the Central Dogma
1.1. Information in IDRs—Problems for The Paradigm
1.2. Uniting Different Entropies and Extracting Information
2. Sequence Entropy Metrics Fail to Extract Information from IDRs
2.1. Sequence Entropy Can be Computed Horizontally and Vertically
2.2. Sequence Entropy in Biological Macromolecules: The “Positional Information Paradigm”
2.3. Evolutionary Origin of Positional Information in Sequence Alignments
2.4. Intrinsically Disordered Regions Contain Little Positional Information, but Still Encode Function
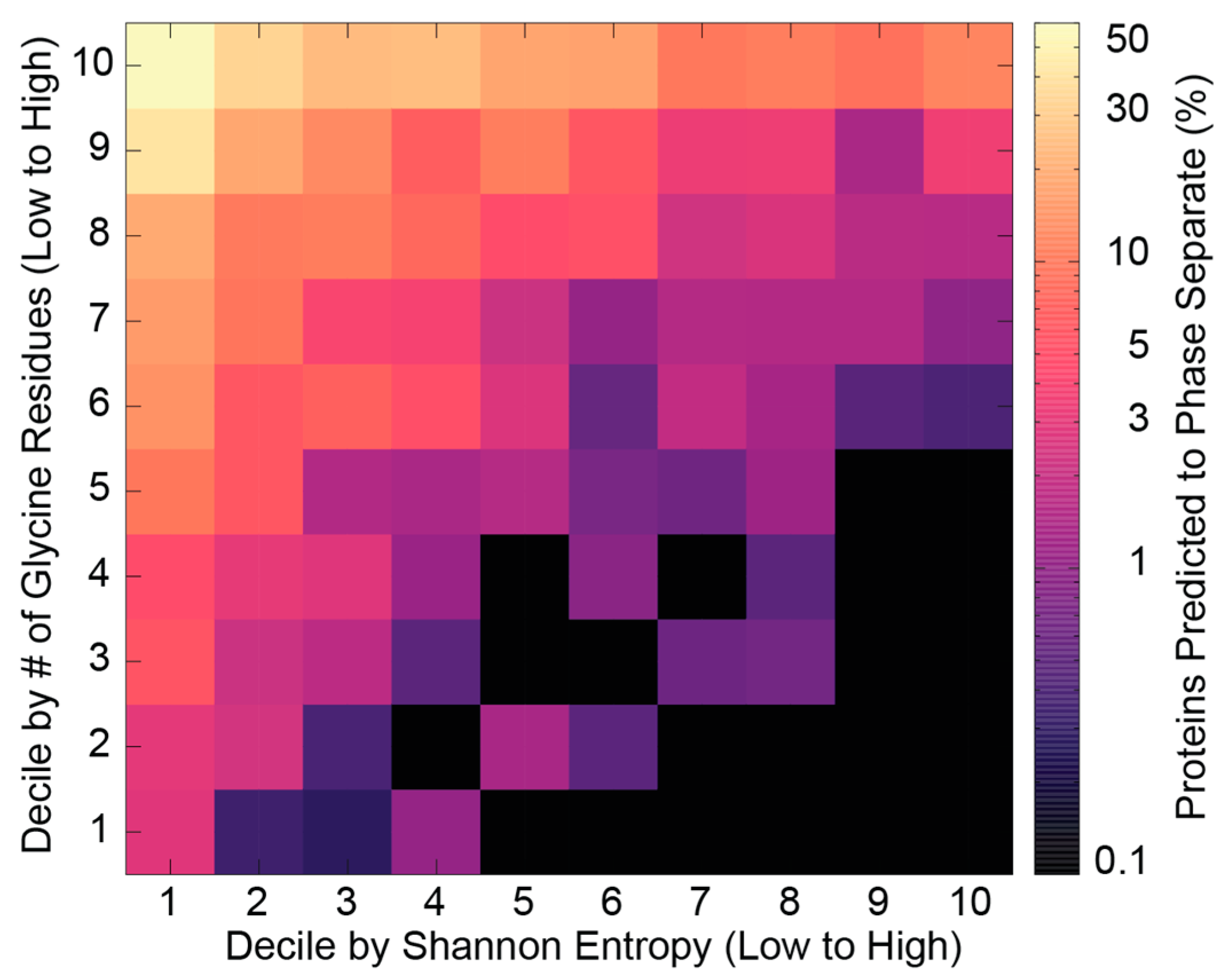
2.5. Information in Low-Complexity IDR Sequences
3. IDRs Feature High Conformational Entropy
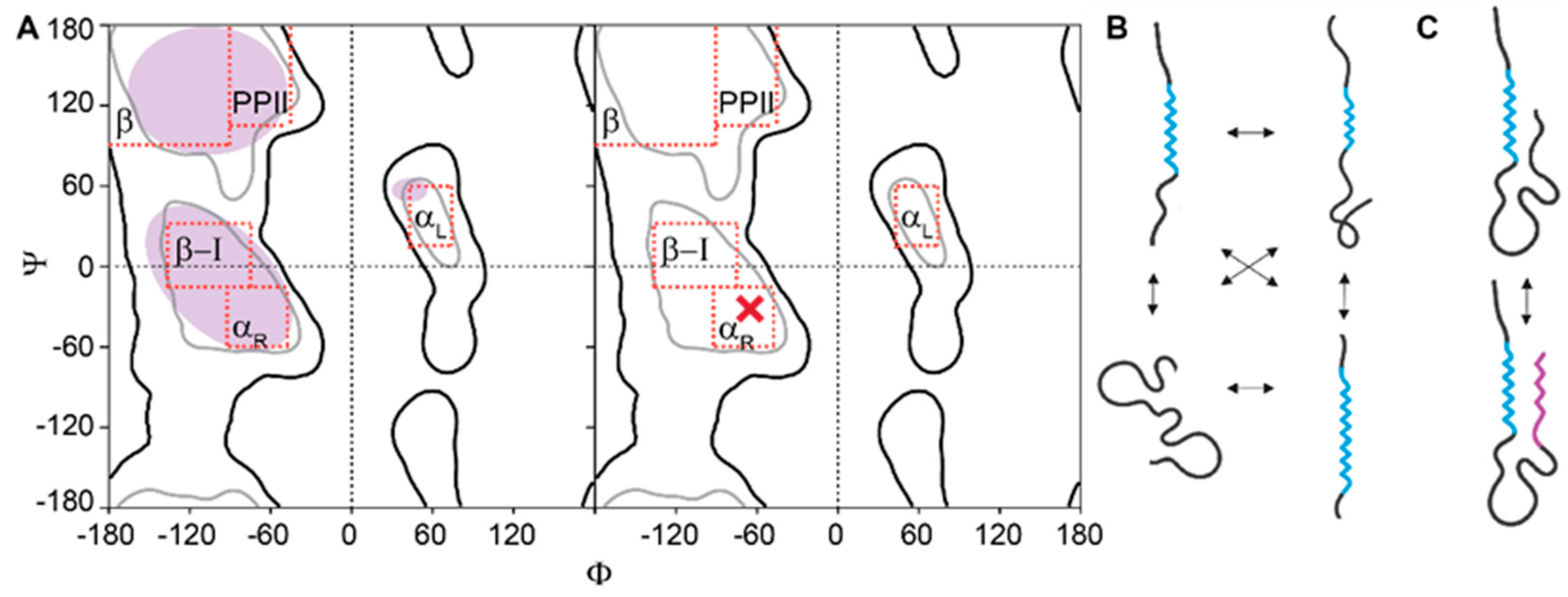
3.1. Conformational Entropy of IDRs is Difficult to Measure Precisely
3.2. Conformational Diversity and Information in Ensembles of IDRs
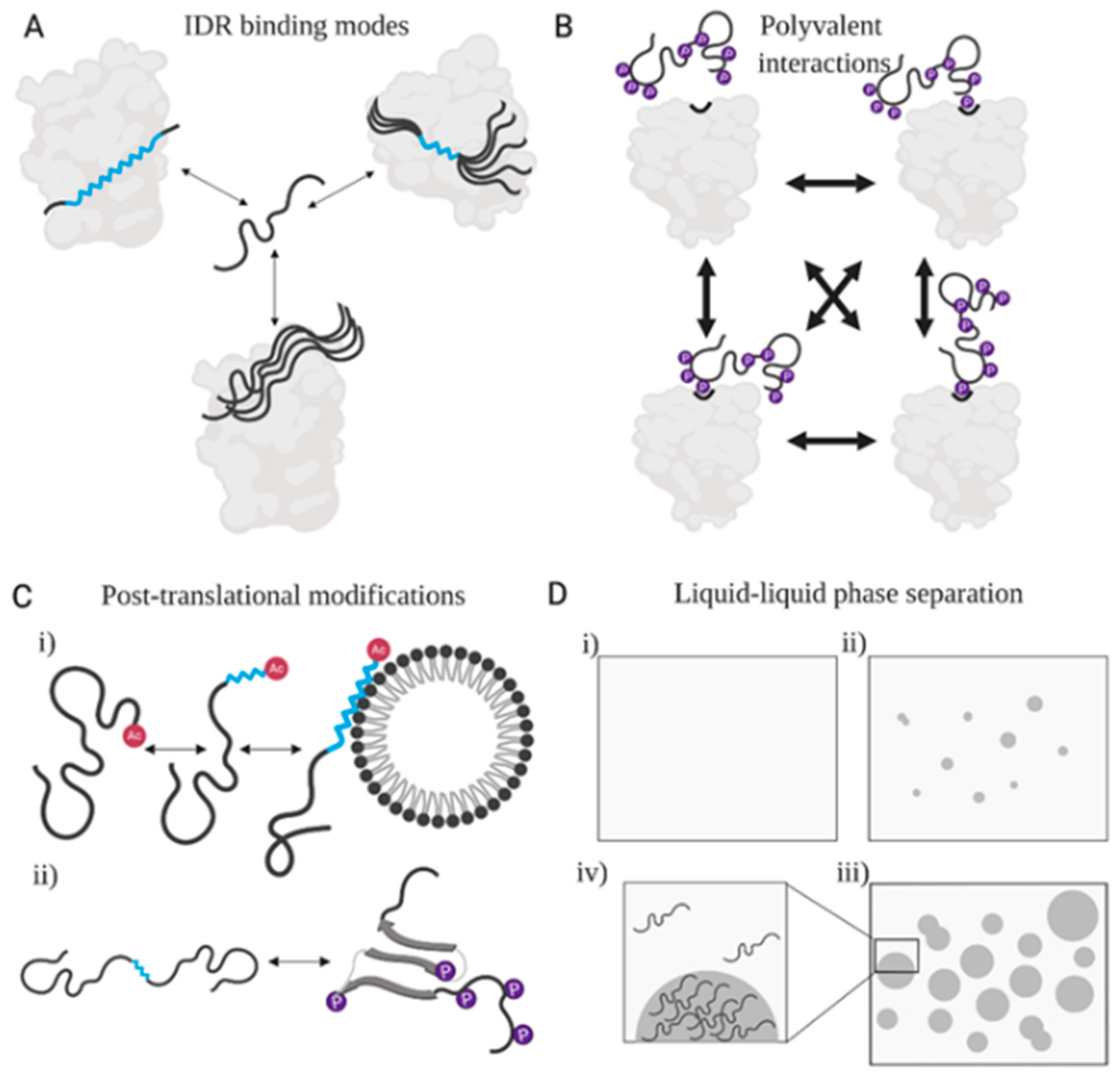
3.3. IDRs Can Retain High Conformational Entropy in Complexes
3.4. Post-Translationally Modified Sites in IDRs Transmit Biological Information
3.5. Functional Engagements of IDRs Alter Physical Entropy in All Directions
4. Conclusions and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Crick, F.H.C. On Protein Syntesis. Symp. Soc. Exp. Biol. XII 1958, 12, 139–163. [Google Scholar]
- Ebeling, W.; Volkenstein, M.V. Entropy and the evolution of biological information. Physica A 1990, 163, 398–402. [Google Scholar] [CrossRef]
- Anfinsen, C.B. Principles that govern the folding of protein chains. Science 1973, 181, 223–230. [Google Scholar] [CrossRef] [PubMed]
- Berman, H.M.; Westbrook, J.; Feng, Z.; Gilliland, G.; Bhat, T.N.; Weissig, H.; Shindyalov, I.N.; Bourne, P.E. The Protein Data Bank. Struct. Bioinform. 2000, 28, 235–242. [Google Scholar] [CrossRef] [PubMed]
- Śledź, P.; Caflisch, A. Protein structure-based drug design: From docking to molecular dynamics. Curr. Opin. Struct. Biol. 2018, 48, 93–102. [Google Scholar] [CrossRef] [PubMed]
- Dunker, A.K.; Babu, M.M.; Barbar, E.; Blackledge, M.; Bondos, S.E.; Dosztányi, Z.; Dyson, H.J.; Forman-Kay, J.; Fuxreiter, M.; Gsponer, J.; et al. What’s in a name? Why these proteins are intrinsically disordered. Intrinsically Disord. Proteins 2013, 1, e24157. [Google Scholar] [CrossRef]
- Walsh, I.; Giollo, M.; Di Domenico, T.; Ferrari, C.; Zimmermann, O.; Tosatto, S.C.E. Comprehensive large-scale assessment of intrinsic protein disorder. Bioinformatics 2015, 31, 201–208. [Google Scholar] [CrossRef]
- van der Lee, R.; Buljan, M.; Lang, B.; Weatheritt, R.J.; Daughdrill, G.W.; Dunker, A.K.; Fuxreiter, M.; Gough, J.; Gsponer, J.; Jones, D.T.; et al. Classification of Intrinsically Disordered Regions and Proteins. Chem. Rev. 2014, 114, 6589–6631. [Google Scholar] [CrossRef]
- Zarin, T.; Tsai, C.N.; Nguyen Ba, A.N.; Moses, A.M. Selection maintains signaling function of a highly diverged intrinsically disordered region. Proc. Natl. Acad. Sci. USA 2017, 114, E1450–E1459. [Google Scholar] [CrossRef]
- Zarin, T.; Strome, B.; Nguyen Ba, A.N.; Alberti, S.; Forman-Kay, J.D.; Moses, A.M. Proteome-wide signatures of function in highly diverged intrinsically disordered regions. bioRxiv 2019, 578716. [Google Scholar] [CrossRef]
- Milles, S.; Salvi, N.; Blackledge, M.; Jensen, M.R. Characterization of intrinsically disordered proteins and their dynamic complexes: From in vitro to cell-like environments. Prog. Nucl. Magn. Reson. Spectrosc. 2018, 109, 79–100. [Google Scholar] [CrossRef] [PubMed]
- Tompa, P.; Davey, N.E.; Gibson, T.J.; Babu, M.M. A Million peptide motifs for the molecular biologist. Mol. Cell 2014, 55, 161–169. [Google Scholar] [CrossRef] [PubMed]
- Beltrao, P.; Albanèse, V.; Kenner, L.R.; Swaney, D.L.; Burlingame, A.; Villén, J.; Lim, W.A.; Fraser, J.S.; Frydman, J.; Krogan, N.J. Systematic functional prioritization of protein posttranslational modifications. Cell 2012, 150, 413–425. [Google Scholar] [CrossRef] [PubMed]
- Chong, P.A.; Forman-Kay, J.D. Liquid–liquid phase separation in cellular signaling systems. Curr. Opin. Struct. Biol. 2016, 41, 180–186. [Google Scholar] [CrossRef] [PubMed]
- Forman-Kay, J.D.; Mittag, T. From sequence and forces to structure, function, and evolution of intrinsically disordered proteins. Structure 2013, 21, 1492–1499. [Google Scholar] [CrossRef] [PubMed]
- Forman-Kay, J.D.; Kriwacki, R.W.; Seydoux, G. Phase Separation in Biology and Disease. J. Mol. Biol. 2018, 430, 4603–4606. [Google Scholar] [CrossRef] [PubMed]
- Alberti, S.; Carra, S. Quality Control of Membraneless Organelles. J. Mol. Biol. 2018, 430, 4711–4729. [Google Scholar] [CrossRef]
- Babu, M.M. The contribution of intrinsically disordered regions to protein function, cellular complexity, and human disease. Biochem. Soc. Trans. 2016, 44, 1185–1200. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2005; ISBN 9780471241959. [Google Scholar]
- Ebeling, W. Physical Approaches to Biological Evolution; Springer: Berlin/Heidelberg, Germany, 2011; Volume 191, pp. 142–143. [Google Scholar]
- Müller, I. A History of Thermodynamics: The Doctrine of Energy and Entropy; Springer: Berlin/Heidelberg, Germany, 2007; ISBN 3540462260. [Google Scholar]
- Gibbs, J.W. Elementary Principles in Statistical Mechanics; Gale: New York, NY, USA, 1902; ISBN 1108017029. [Google Scholar]
- Boltzmann, L. Über die Beziehung eines allgemeinen mechanischen Satzes zum zweiten Hauptsatze der Wärmetheorie. In Kinetische Theorie II: Irreversible Prozesse Einführung und Originaltexte; Brush, S.G., Ed.; Vieweg + Teubner Verlag: Wiesbaden, Germany, 1970; pp. 240–247. ISBN 978-3-322-84986-1. (In German) [Google Scholar]
- Shannon, C.E. The Mathematical Theory of Communication; The University of Illinois Press: Champagne, IL, USA, 1964; Volume 14, pp. 306–317. [Google Scholar]
- Vinga, S. Information theory applications for biological sequence analysis. Brief. Bioinform. 2014, 15, 376–389. [Google Scholar] [CrossRef]
- Konorski, J.; Szpankowski, W. What is information? In Proceedings of the 2008 IEEE Information Theory Workshop, Porto, Portugal, 5–9 May 2008; Volume 374, pp. 269–270. [Google Scholar]
- Wootton, J.C.; Federhen, S. Statistics of local complexity in amino acid sequences and sequence databases. Comput. Chem. 1993, 17, 149–163. [Google Scholar] [CrossRef]
- Wootton, J.C.; Federhen, S. Analysis of compositionally biased regions in sequence databases. Methods Enzymol. 1996, 266, 554–571. [Google Scholar]
- Romero, P.; Obradovic, Z.; Li, X.; Garner, E.C.; Brown, C.J.; Dunker, A.K. Sequence complexity of disordered protein. Proteins Struct. Funct. Genet. 2001, 42, 38–48. [Google Scholar] [CrossRef]
- Adami, C. Information theory in molecular biology. Phys. Life Rev. 2004, 1, 3–22. [Google Scholar] [CrossRef]
- Adami, C. The use of information theory in evolutionary biology. Ann. N. Y. Acad. Sci. 2012, 1256, 49–65. [Google Scholar] [CrossRef]
- Durbin, R.; Eddy, S.R.; Mitchison, G.J. Biological Sequence Analysis, Probabilistic Models of Proteins and Nucleic Acids; Cambridge University Press: Cambridge, UK, 1998; ISBN 9780521629713. [Google Scholar]
- Schneider, T.D.; Stephens, R.M. Sequence logos: A new way to display consensus sequences. Nucleic Acids Res. 1990, 18, 6097–6100. [Google Scholar] [CrossRef] [PubMed]
- Crooks, G.E.; Hon, G.; Chandonia, J.M.; Brenner, S.E. WebLogo: A sequence logo generator. Genome Res. 2004, 14, 1188–1190. [Google Scholar] [CrossRef]
- Berg, O.G.; von Hippel, P.H. Selection of DNA binding sites by regulatory proteins. Trends Biochem. Sci. 1988, 13, 207–211. [Google Scholar] [CrossRef]
- Schneider, T.D.; Stormo, G.D.; Gold, L.; Ehrenfeucht, A. Information content of binding sites on nucleotide sequences. J. Mol. Biol. 1986, 188, 415–431. [Google Scholar] [CrossRef]
- Oliveira, L.; Paiva, P.B.; Paiva, A.C.M.; Vriend, G. Identification of functionally conserved residues with the use of entropy-variability plots. Proteins Struct. Funct. Genet. 2003, 52, 544–552. [Google Scholar] [CrossRef] [PubMed]
- Lawrence, C.E.; Altschul, S.F.; Boguski, M.S.; Liu, J.S.; Neuwald, A.F.; Wootton, J.C. Detecting subtle sequence signals: A gibbs sampling strategy for multiple alignment. Science 1993, 262, 208–214. [Google Scholar] [CrossRef]
- Dewey, T.G. Algorithmic complexity and thermodynamics of sequence-structure relationships in proteins. Phys. Rev. E 1997, 56, 4545–4552. [Google Scholar] [CrossRef]
- Atchley, W.R.; Wollenberg, K.R.; Fitch, W.M.; Terhalle, W.; Dress, A.W. Correlations among amino acid sites in bHLH protein domains: An information theoretic analysis. Mol. Biol. Evol. 2000, 17, 164–178. [Google Scholar] [CrossRef] [PubMed]
- Marks, D.S.; Colwell, L.J.; Sheridan, R.; Hopf, T.A.; Pagnani, A.; Zecchina, R.; Sander, C. Protein 3D structure computed from evolutionary sequence variation. PLoS ONE 2011, 6, e28766. [Google Scholar] [CrossRef] [PubMed]
- Martin, L.C.; Gloor, G.B.; Dunn, S.D.; Wahl, L.M. Using information theory to search for co-evolving residues in proteins. Bioinformatics 2005, 21, 4116–4124. [Google Scholar] [CrossRef] [PubMed]
- Dunn, S.D.; Wahl, L.M.; Gloor, G.B. Mutual information without the influence of phylogeny or entropy dramatically improves residue contact prediction. Bioinformatics 2008, 24, 333–340. [Google Scholar] [CrossRef]
- Capra, J.A.; Singh, M. Predicting functionally important residues from sequence conservation. Bioinformatics 2007, 23, 1875–1882. [Google Scholar] [CrossRef]
- Hopf, T.A.; Schärfe, C.P.I.; Rodrigues, J.P.G.L.M.; Green, A.G.; Kohlbacher, O.; Sander, C.; Bonvin, A.M.J.J.; Marks, D.S. Sequence co-evolution gives 3D contacts and structures of protein complexes. Elife 2014, 3, e03430. [Google Scholar] [CrossRef]
- Kimura, M. Natural selection as the process of accumulating genetic information in adaptive evolution. Genet. Res. 1961, 2, 127. [Google Scholar] [CrossRef]
- Moses, A.M.; Chiang, D.Y.; Kellis, M.; Lander, E.S.; Eisen, M.B. Position specific variation in the rate of evolution in transcription factor binding sites. BMC Evol. Biol. 2003, 3, 19. [Google Scholar] [CrossRef][Green Version]
- Moses, A.M.; Durbin, R. Inferring selection on amino acid preference in protein domains. Mol. Biol. Evol. 2009, 26, 527–536. [Google Scholar] [CrossRef]
- Koonin, E.V. The meaning of biological information. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 20150065. [Google Scholar] [CrossRef] [PubMed]
- Colak, R.; Kim, T.H.; Michaut, M.; Sun, M.; Irimia, M.; Bellay, J.; Myers, C.L.; Blencowe, B.J.; Kim, P.M. Distinct Types of Disorder in the Human Proteome: Functional Implications for Alternative Splicing. PLoS Comput. Biol. 2013, 9, e1003030. [Google Scholar] [CrossRef] [PubMed]
- Vacic, V.; Oldfield, C.J.; Mohan, A.; Radivojac, P.; Cortese, M.S.; Uversky, V.N.; Dunker, A.K. Characterization of molecular recognition features, MoRFs, and their binding partners. J. Proteome Res. 2007, 6, 2351–2366. [Google Scholar] [CrossRef] [PubMed]
- Cumberworth, A.; Lamour, G.; Babu, M.M.; Gsponer, J. Promiscuity as a functional trait: Intrinsically disordered regions as central players of interactomes. Biochem. J. 2013, 454, 361–369. [Google Scholar] [CrossRef] [PubMed]
- Davey, N.E.; Van Roey, K.; Weatheritt, R.J.; Toedt, G.; Uyar, B.; Altenberg, B.; Budd, A.; Diella, F.; Dinkel, H.; Gibson, T.J. Attributes of short linear motifs. Mol. Biosyst. 2012, 8, 268–281. [Google Scholar] [CrossRef] [PubMed]
- Nguyen Ba, A.N.; Yeh, B.J.; Van Dyk, D.; Davidson, A.R.; Andrews, B.J.; Weiss, E.L.; Moses, A.M. Proteome-wide discovery of evolutionary conserved sequences in disordered regions. Sci. Signal. 2012, 5, rs1. [Google Scholar] [CrossRef]
- Gouw, M.; Michael, S.; Sámano-Sánchez, H.; Kumar, M.; Zeke, A.; Lang, B.; Bely, B.; Chemes, L.B.; Davey, N.E.; Deng, Z.; et al. The eukaryotic linear motif resource—2018 update. Nucleic Acids Res. 2018, 46, D428–D434. [Google Scholar] [CrossRef]
- Lovell, S.C. Are non-functional, unfolded proteins (‘junk proteins’) common in the genome? FEBS Lett. 2003, 554, 237–239. [Google Scholar] [CrossRef]
- Good, M.C.; Zalatan, J.G.; Lim, W.A. Scaffold proteins: Hubs for controlling the flow of cellular information. Science 2011, 332, 680–686. [Google Scholar] [CrossRef]
- Ravarani, C.N.; Erkina, T.Y.; De Baets, G.; Dudman, D.C.; Erkine, A.M.; Babu, M.M. High-throughput discovery of functional disordered regions: Investigation of transactivation domains. Mol. Syst. Biol. 2018, 14, e8190. [Google Scholar] [CrossRef]
- Daughdrill, G.W.; Narayanaswami, P.; Gilmore, S.H.; Belczyk, A.; Brown, C.J. Dynamic behavior of an intrinsically unstructured linker domain is conserved in the face of negligible amino acid sequence conservation. J. Mol. Evol. 2007, 65, 277–288. [Google Scholar] [CrossRef] [PubMed]
- Lemas, D.; Lekkas, P.; Ballif, B.A.; Vigoreaux, J.O. Intrinsic disorder and multiple phosphorylations constrain the evolution of the flightin N-terminal region. J. Proteom. 2016, 135, 191–200. [Google Scholar] [CrossRef] [PubMed]
- Banani, S.F.; Lee, H.O.; Hyman, A.A.; Rosen, M.K. Biomolecular condensates: Organizers of cellular biochemistry. Nat. Rev. Mol. Cell Biol. 2017, 18, 285–298. [Google Scholar] [CrossRef] [PubMed]
- Protter, D.S.W.; Rao, B.S.; Van Treeck, B.; Lin, Y.; Mizoue, L.; Rosen, M.K.; Parker, R. Intrinsically Disordered Regions Can Contribute Promiscuous Interactions to RNP Granule Assembly. Cell Rep. 2018, 22, 1401–1412. [Google Scholar] [CrossRef] [PubMed]
- Mittag, T.; Parker, R. Multiple Modes of Protein–Protein Interactions Promote RNP Granule Assembly. J. Mol. Biol. 2018, 430, 4636–4649. [Google Scholar] [CrossRef] [PubMed]
- Boeynaems, S.; Alberti, S.; Fawzi, N.L.; Mittag, T.; Polymenidou, M.; Rousseau, F.; Schymkowitz, J.; Shorter, J.; Wolozin, B.; Van Den Bosch, L.; et al. Protein Phase Separation: A New Phase in Cell Biology. Trends Cell Biol. 2018, 28, 420–435. [Google Scholar] [CrossRef] [PubMed]
- Chong, P.A.; Vernon, R.M.; Forman-Kay, J.D. RGG/RG Motif Regions in RNA Binding and Phase Separation. J. Mol. Biol. 2018, 430, 4650–4665. [Google Scholar] [CrossRef]
- Martin, E.W.; Mittag, T. Relationship of Sequence and Phase Separation in Protein Low-Complexity Regions. Biochemistry 2018, 57, 2478–2487. [Google Scholar] [CrossRef]
- Uversky, V.N. Intrinsically disordered proteins in overcrowded milieu: Membrane-less organelles, phase separation, and intrinsic disorder. Curr. Opin. Struct. Biol. 2017, 44, 18–30. [Google Scholar] [CrossRef]
- Tsang, B.; Arsenault, J.; Vernon, R.M.; Lin, H.; Sonenberg, N.; Wang, L.Y.; Bah, A.; Forman-Kay, J.D. Phosphoregulated FMRP phase separation models activity-dependent translation through bidirectional control of mRNA granule formation. Proc. Natl. Acad. Sci. USA 2019, 116, 4218–4227. [Google Scholar] [CrossRef]
- Brady, J.P.; Farber, P.J.; Sekhar, A.; Lin, Y.-H.; Huang, R.; Bah, A.; Nott, T.J.; Chan, H.S.; Baldwin, A.J.; Forman-Kay, J.D.; et al. Structural and hydrodynamic properties of an intrinsically disordered region of a germ cell-specific protein on phase separation. Proc. Natl. Acad. Sci. USA 2017, 114, E8194–E8203. [Google Scholar] [CrossRef] [PubMed]
- Nott, T.J.; Petsalaki, E.; Farber, P.; Jervis, D.; Fussner, E.; Plochowietz, A.; Craggs, T.D.; Bazett-Jones, D.P.; Pawson, T.; Forman-Kay, J.D.; et al. Phase Transition of a Disordered Nuage Protein Generates Environmentally Responsive Membraneless Organelles. Mol. Cell 2015, 57, 936–947. [Google Scholar] [CrossRef] [PubMed]
- Conicella, A.E.; Zerze, G.H.; Mittal, J.; Fawzi, N.L. ALS Mutations Disrupt Phase Separation Mediated by α-Helical Structure in the TDP-43 Low-Complexity C-Terminal Domain. Structure 2016, 24, 1537–1549. [Google Scholar] [CrossRef] [PubMed]
- Ryan, V.H.; Dignon, G.L.; Zerze, G.H.; Chabata, C.V.; Silva, R.; Conicella, A.E.; Amaya, J.; Burke, K.A.; Mittal, J.; Fawzi, N.L. Mechanistic View of hnRNPA2 Low-Complexity Domain Structure, Interactions, and Phase Separation Altered by Mutation and Arginine Methylation. Mol. Cell 2018, 69, 465–479.e7. [Google Scholar] [CrossRef] [PubMed]
- Xiang, S.; Kato, M.; Wu, L.C.; Lin, Y.; Ding, M.; Zhang, Y.; Yu, Y.; McKnight, S.L. The LC Domain of hnRNPA2 Adopts Similar Conformations in Hydrogel Polymers, Liquid-like Droplets, and Nuclei. Cell 2015, 163, 829–839. [Google Scholar] [CrossRef] [PubMed]
- Banani, S.F.; Rice, A.M.; Peeples, W.B.; Lin, Y.; Jain, S.; Parker, R.; Rosen, M.K. Compositional Control of Phase-Separated Cellular Bodies. Cell 2016, 166, 651–663. [Google Scholar] [CrossRef] [PubMed]
- Burke, K.A.; Janke, A.M.; Rhine, C.L.; Fawzi, N.L. Residue-by-Residue View of In Vitro FUS Granules that Bind the C-Terminal Domain of RNA Polymerase II. Mol. Cell 2015, 60, 231–241. [Google Scholar] [CrossRef]
- Ambadipudi, S.; Biernat, J.; Riedel, D.; Mandelkow, E.; Zweckstetter, M. Liquid-liquid phase separation of the microtubule-binding repeats of the Alzheimer-related protein Tau. Nat. Commun. 2017, 8, 275. [Google Scholar] [CrossRef]
- Murray, D.T.; Kato, M.; Lin, Y.; Thurber, K.R.; Hung, I.; McKnight, S.L.; Tycko, R. Structure of FUS Protein Fibrils and Its Relevance to Self-Assembly and Phase Separation of Low-Complexity Domains. Cell 2017, 171, 615–627.e16. [Google Scholar] [CrossRef]
- Murakami, T.; Qamar, S.; Lin, J.Q.; Schierle, G.S.K.; Rees, E.; Miyashita, A.; Costa, A.R.; Dodd, R.B.; Chan, F.T.S.; Michel, C.H.; et al. ALS/FTD Mutation-Induced Phase Transition of FUS Liquid Droplets and Reversible Hydrogels into Irreversible Hydrogels Impairs RNP Granule Function. Neuron 2015, 88, 678–690. [Google Scholar] [CrossRef]
- Patel, A.; Lee, H.O.; Jawerth, L.; Maharana, S.; Jahnel, M.; Hein, M.Y.; Stoynov, S.; Mahamid, J.; Saha, S.; Franzmann, T.M.; et al. A Liquid-to-Solid Phase Transition of the ALS Protein FUS Accelerated by Disease Mutation. Cell 2015, 162, 1066–1077. [Google Scholar] [CrossRef] [PubMed]
- Mar Albà, M.; Santibáñez-Koref, M.F.; Hancock, J.M. Amino acid reiterations in yeast are overrepresented in particular classes of proteins and show evidence of a slippage-like mutational process. J. Mol. Evol. 1999, 49, 789–797. [Google Scholar] [CrossRef] [PubMed]
- Albà, M.; Tompa, P.; Veitia, R. Amino acid repeats and the structure and evolution of proteins. Genome Dyn. 2007, 3, 119–130. [Google Scholar] [PubMed]
- Morgulis, A.; Gertz, E.M.; Schäffer, A.A.; Agarwala, R. A Fast and Symmetric DUST Implementation to Mask Low-Complexity DNA Sequences. J. Comput. Biol. 2006, 13, 1028–1040. [Google Scholar] [CrossRef] [PubMed]
- Boratyn, G.M.; Camacho, C.; Cooper, P.S.; Coulouris, G.; Fong, A.; Ma, N.; Madden, T.L.; Matten, W.T.; McGinnis, S.D.; Merezhuk, Y.; et al. BLAST: A more efficient report with usability improvements. Nucleic Acids Res. 2013, 41, W29–W33. [Google Scholar] [CrossRef] [PubMed]
- Vernon, R.M.; Chong, P.A.; Tsang, B.; Kim, T.H.; Bah, A.; Farber, P.; Lin, H.; Forman-Kay, J.D. Pi-Pi contacts are an overlooked protein feature relevant to phase separation. Elife 2018, 7, e31486. [Google Scholar] [CrossRef] [PubMed]
- Kato, M.; McKnight, S.L. Cross-β polymerization of low complexity sequence domains. Cold Spring Harb. Perspect. Biol. 2017, 9, a023598. [Google Scholar] [CrossRef]
- Boeynaems, S.; Bogaert, E.; Van Damme, P.; Van Den Bosch, L. Inside out: The role of nucleocytoplasmic transport in ALS and FTLD. Acta Neuropathol. 2016, 132, 159–173. [Google Scholar] [CrossRef]
- Kato, M.; Han, T.W.; Xie, S.; Shi, K.; Du, X.; Wu, L.C.; Mirzaei, H.; Goldsmith, E.J.; Longgood, J.; Pei, J.; et al. Cell-free formation of RNA granules: Low complexity sequence domains form dynamic fibers within hydrogels. Cell 2012, 149, 753–767. [Google Scholar] [CrossRef]
- Hennig, S.; Kong, G.; Mannen, T.; Sadowska, A.; Kobelke, S.; Blythe, A.; Knott, G.J.; Iyer, S.S.; Ho, D.; Newcombe, E.A.; et al. Prion-like domains in RNA binding proteins are essential for building subnuclear paraspeckles. J. Cell Biol. 2015, 210, 529–539. [Google Scholar] [CrossRef]
- Franzmann, T.M.; Alberti, S. Prion-like low-complexity sequences: Key regulators of protein solubility and phase behavior. J. Biol. Chem. 2019, 294, 7128–7136. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Choi, J.M.; Holehouse, A.S.; Lee, H.O.; Zhang, X.; Jahnel, M.; Maharana, S.; Lemaitre, R.; Pozniakovsky, A.; Drechsel, D.; et al. A Molecular Grammar Governing the Driving Forces for Phase Separation of Prion-like RNA Binding Proteins. Cell 2018, 174, 688–699.e16. [Google Scholar] [CrossRef] [PubMed]
- Hughes, M.P.; Sawaya, M.R.; Boyer, D.R.; Goldschmidt, L.; Rodriguez, J.A.; Cascio, D.; Chong, L.; Gonen, T.; Eisenberg, D.S. Atomic structures of low-complexity protein segments reveal kinked b sheets that assemble networks. Science 2018, 359, 698–701. [Google Scholar] [CrossRef] [PubMed]
- Lancaster, A.K.; Nutter-Upham, A.; Lindquist, S.; King, O.D. PLAAC: A web and command-line application to identify proteins with prion-like amino acid composition. Bioinformatics 2014, 30, 2501–2502. [Google Scholar] [CrossRef] [PubMed]
- Bolognesi, B.; Gotor, N.L.; Dhar, R.; Cirillo, D.; Baldrighi, M.; Tartaglia, G.G.; Lehner, B. A concentration-dependent liquid phase separation can cause toxicity upon increased protein expression. Cell Rep. 2016, 16, 222–231. [Google Scholar] [CrossRef]
- Brangwynne, C.P.; Tompa, P.; Pappu, R.V. Polymer physics of intracellular phase transitions. Nat. Phys. 2015, 11, 899–904. [Google Scholar] [CrossRef]
- Lin, Y.H.; Forman-Kay, J.D.; Chan, H.S. Theories for Sequence-Dependent Phase Behaviors of Biomolecular Condensates. Biochemistry 2018, 57, 2499–2508. [Google Scholar] [CrossRef]
- Lin, Y.H.; Song, J.; Forman-Kay, J.D.; Chan, H.S. Random-phase-approximation theory for sequence-dependent, biologically functional liquid-liquid phase separation of intrinsically disordered proteins. J. Mol. Liq. 2017, 228, 176–193. [Google Scholar] [CrossRef]
- Garner, E.; Cannon, P.; Romero, P.; Obradovic, Z.; Dunker, A.K. Predicting Disordered Regions from Amino Acid Sequence: Common Themes Despite Differing Structural Characterization. Genome Inform. Ser. Workshop Genome Inform. 1998, 9, 201–213. [Google Scholar]
- Uversky, V.N. The alphabet of intrinsic disorder. Intrinsically Disord. Proteins 2013, 1, e24684. [Google Scholar] [CrossRef]
- Romero, P.; Obradovic, Z.; Kissinger, C.R.; Villafranca, J.E.; Garner, E.; Guilliot, S.; Dunker, A.K. Thousands of proteins likely to have long disordered regions. Pac. Symp. Biocomput. 1998, 437–448. [Google Scholar]
- Meng, F.; Uversky, V.N.; Kurgan, L. Comprehensive review of methods for prediction of intrinsic disorder and its molecular functions. Cell. Mol. Life Sci. 2017, 74, 3069–3090. [Google Scholar] [CrossRef] [PubMed]
- Flock, T.; Weatheritt, R.J.; Latysheva, N.S.; Babu, M.M. Controlling entropy to tune the functions of intrinsically disordered regions. Curr. Opin. Struct. Biol. 2014, 26, 62–72. [Google Scholar] [CrossRef] [PubMed]
- Latysheva, N.S.; Flock, T.; Weatheritt, R.J.; Chavali, S.; Babu, M.M. How do disordered regions achieve comparable functions to structured domains? Protein Sci. 2015, 24, 909–922. [Google Scholar] [CrossRef] [PubMed]
- Mittag, T.; Kay, L.E.; Forman-Kaya, J.D. Protein dynamics and conformational disorder in molecular recognition. J. Mol. Recognit. 2010, 23, 105–116. [Google Scholar] [CrossRef]
- Heller, G.T.; Sormanni, P.; Vendruscolo, M. Targeting disordered proteins with small molecules using entropy. Trends Biochem. Sci. 2015, 40, 491–496. [Google Scholar] [CrossRef]
- Mantsyzov, A.B.; Shen, Y.; Lee, J.H.; Hummer, G.; Bax, A. MERA: A webserver for evaluating backbone torsion angle distributions in dynamic and disordered proteins from NMR data. J. Biomol. NMR 2015, 63, 85–95. [Google Scholar] [CrossRef]
- Mantsyzov, A.B.; Maltsev, A.S.; Ying, J.; Shen, Y.; Hummer, G.; Bax, A. A maximum entropy approach to the study of residue-specific backbone angle distributions in α-synuclein, an intrinsically disordered protein. Protein Sci. 2014, 23, 1275–1290. [Google Scholar] [CrossRef]
- Schneider, R.; Maurin, D.; Communie, G.; Kragelj, J.; Hansen, D.F.; Ruigrok, R.W.H.; Jensen, M.R.; Blackledge, M. Visualizing the molecular recognition trajectory of an intrinsically disordered protein using multinuclear relaxation dispersion NMR. J. Am. Chem. Soc. 2015, 137, 1220–1229. [Google Scholar] [CrossRef]
- Iešmantavičius, V.; Jensen, M.R.; Ozenne, V.; Blackledge, M.; Poulsen, F.M.; Kjaergaard, M. Modulation of the intrinsic helix propensity of an intrinsically disordered protein reveals long-range helix-helix interactions. J. Am. Chem. Soc. 2013, 135, 10155–10163. [Google Scholar] [CrossRef]
- Huggins, M.L. Principles of Polymer Chemistry; Cornell University Press: Ithaca, NY, USA, 1953; Volume 76. [Google Scholar]
- Karplus, M.; Kushick, J.N. Method for Estimating the Configurational Entropy of Macromolecules. Macromolecules 1981, 14, 325–332. [Google Scholar] [CrossRef]
- Karplus, M.; Ichiye, T.; Pettitt, B.M. Configurational entropy of native proteins. Biophys. J. 1987, 52, 1083–1085. [Google Scholar] [CrossRef]
- Leavitt, S.; Freire, E. Direct measurement of protein binding energetics by isothermal titration calorimetry. Curr. Opin. Struct. Biol. 2001, 11, 560–566. [Google Scholar] [CrossRef]
- Wand, A.J.; Sharp, K.A. Measuring Entropy in Molecular Recognition by Proteins. Annu. Rev. Biophys. 2018, 47, 41–61. [Google Scholar] [CrossRef] [PubMed]
- Dyson, H.J.; Wright, P.E. Intrinsically unstructured proteins and their functions. Nat. Rev. Mol. Cell Biol. 2005, 6, 197–208. [Google Scholar] [CrossRef] [PubMed]
- Cordeiro, T.N.; Herranz-Trillo, F.; Urbanek, A.; Estaña, A.; Cortés, J.; Sibille, N.; Bernadó, P. Structural characterization of highly flexible proteins by small-angle scattering. In Advances in Experimental Medicine and Biology; Springer Nature: New York, NY, USA, 2017; Volume 1009, pp. 107–129. [Google Scholar]
- Schuler, B.; Soranno, A.; Hofmann, H.; Nettels, D. Single-Molecule FRET Spectroscopy and the Polymer Physics of Unfolded and Intrinsically Disordered Proteins. Annu. Rev. Biophys. 2016, 45, 207–231. [Google Scholar] [CrossRef] [PubMed]
- Le Breton, N.; Martinho, M.; Mileo, E.; Etienne, E.; Gerbaud, G.; Guigliarelli, B.; Belle, V. Exploring intrinsically disordered proteins using site-directed spin labeling electron paramagnetic resonance spectroscopy. Front. Mol. Biosci. 2015, 2, 21. [Google Scholar] [CrossRef] [PubMed]
- Allison, J.R. Using simulation to interpret experimental data in terms of protein conformational ensembles. Curr. Opin. Struct. Biol. 2017, 43, 79–87. [Google Scholar] [CrossRef]
- Best, R.B. Computational and theoretical advances in studies of intrinsically disordered proteins. Curr. Opin. Struct. Biol. 2017, 42, 147–154. [Google Scholar] [CrossRef]
- Boomsma, W.; Ferkinghoff-Borg, J.; Lindorff-Larsen, K. Combining Experiments and Simulations Using the Maximum Entropy Principle. PLoS Comput. Biol. 2014, 10, e1003406. [Google Scholar] [CrossRef]
- Sormanni, P.; Piovesan, D.; Heller, G.T.; Bonomi, M.; Kukic, P.; Camilloni, C.; Fuxreiter, M.; Dosztanyi, Z.; Pappu, R.V.; Babu, M.M.; et al. Simultaneous quantification of protein order and disorder. Nat. Chem. Biol. 2017, 13, 339–342. [Google Scholar] [CrossRef] [PubMed]
- Sekhar, A.; Kay, L.E. An NMR View of Protein Dynamics in Health and Disease. Annu. Rev. Biophys. 2019, 48, 297–319. [Google Scholar] [CrossRef] [PubMed]
- Schneider, R.; Blackledge, M.; Jensen, M.R. Elucidating binding mechanisms and dynamics of intrinsically disordered protein complexes using NMR spectroscopy. Curr. Opin. Struct. Biol. 2019, 54, 10–18. [Google Scholar] [CrossRef] [PubMed]
- Jensen, M.R.; Zweckstetter, M.; Huang, J.; Blackledge, M. Exploring Free-Energy Landscapes of Intrinsically Disordered Proteins at Atomic Resolution Using NMR Spectroscopy. Chem. Rev. 2014, 114, 6632–6660. [Google Scholar] [CrossRef] [PubMed]
- Jensen, M.R.; Ruigrok, R.W.H.; Blackledge, M. Describing intrinsically disordered proteins at atomic resolution by NMR. Curr. Opin. Struct. Biol. 2013, 23, 426–435. [Google Scholar] [CrossRef]
- Bhowmick, A.; Brookes, D.H.; Yost, S.R.; Dyson, H.J.; Forman-Kay, J.D.; Gunter, D.; Head-Gordon, M.; Hura, G.L.; Pande, V.S.; Wemmer, D.E.; et al. Finding Our Way in the Dark Proteome. J. Am. Chem. Soc. 2016, 138, 9730–9742. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, J.T.; Mulder, F.A.A. POTENCI: Prediction of temperature, neighbor and pH-corrected chemical shifts for intrinsically disordered proteins. J. Biomol. NMR 2018, 70, 141–165. [Google Scholar] [CrossRef]
- Krzeminski, M.; Marsh, J.A.; Neale, C.; Choy, W.Y.; Forman-Kay, J.D. Characterization of disordered proteins with ENSEMBLE. Bioinformatics 2013, 29, 398–399. [Google Scholar] [CrossRef]
- Nodet, G.; Salmon, L.; Ozenne, V.; Meier, S.; Jensen, M.R.; Blackledge, M. Quantitative description of backbone conformational sampling of unfolded proteins at amino acid resolution from NMR residual dipolar couplings. J. Am. Chem. Soc. 2009, 131, 17908–17918. [Google Scholar] [CrossRef]
- Salvi, N.; Abyzov, A.; Blackledge, M. Atomic resolution conformational dynamics of intrinsically disordered proteins from NMR spin relaxation. Prog. Nucl. Magn. Reson. Spectrosc. 2017, 102–103, 43–60. [Google Scholar] [CrossRef]
- Charlier, C.; Bouvignies, G.; Pelupessy, P.; Walrant, A.; Marquant, R.; Kozlov, M.; De Ioannes, P.; Bolik-Coulon, N.; Sagan, S.; Cortes, P.; et al. Structure and Dynamics of an Intrinsically Disordered Protein Region That Partially Folds upon Binding by Chemical-Exchange NMR. J. Am. Chem. Soc. 2017, 139, 12219–12227. [Google Scholar] [CrossRef] [PubMed]
- Bottaro, S.; Lindorff-Larsen, K. Biophysical experiments and biomolecular simulations: A perfect match? Science 2018, 361, 355–360. [Google Scholar] [CrossRef] [PubMed]
- Bah, A.; Vernon, R.M.; Siddiqui, Z.; Krzeminski, M.; Muhandiram, R.; Zhao, C.; Sonenberg, N.; Kay, L.E.; Forman-Kay, J.D. Folding of an intrinsically disordered protein by phosphorylation as a regulatory switch. Nature 2015, 519, 106–109. [Google Scholar] [CrossRef] [PubMed]
- Bah, A.; Forman-Kay, J.D. Modulation of intrinsically disordered protein function by post-translational modifications. J. Biol. Chem. 2016, 291, 6696–6705. [Google Scholar] [CrossRef] [PubMed]
- Heller, G.T.; Aprile, F.A.; Bonomi, M.; Camilloni, C.; De Simone, A.; Vendruscolo, M. Sequence Specificity in the Entropy-Driven Binding of a Small Molecule and a Disordered Peptide. J. Mol. Biol. 2017, 429, 2772–2779. [Google Scholar] [CrossRef] [PubMed]
- Heller, G.T.; Aprile, F.A.; Vendruscolo, M. Methods of probing the interactions between small molecules and disordered proteins. Cell. Mol. Life Sci. 2017, 74, 3225–3243. [Google Scholar] [CrossRef]
- Wright, P.E.; Dyson, H.J. Linking folding and binding. Curr. Opin. Struct. Biol. 2009, 19, 31–38. [Google Scholar] [CrossRef]
- Fuxreiter, M. Fuzziness in Protein Interactions—A Historical Perspective. J. Mol. Biol. 2018, 430, 2278–2287. [Google Scholar] [CrossRef]
- Mittag, T.; Orlicky, S.; Choy, W.-Y.; Tang, X.; Lin, H.; Sicheri, F.; Kay, L.E.; Tyers, M.; Forman-Kay, J.D. Dynamic equilibrium engagement of a polyvalent ligand with a single-site receptor. Proc. Natl. Acad. Sci. USA 2008, 105, 17772–17777. [Google Scholar] [CrossRef]
- Maltsev, A.S.; Ying, J.; Bax, A. Impact of N-terminal acetylation of α-synuclein on its random coil and lipid binding properties. Biochemistry 2012, 51, 5004–5013. [Google Scholar] [CrossRef]
- Marsh, J.A.; Singh, V.K.; Jia, Z.; Forman-Kay, J.D. Sensitivity of secondary structure propensities to sequence differences between α- and γ-synuclein: Implications for fibrillation. Protein Sci. 2006, 15, 2795–2804. [Google Scholar] [CrossRef] [PubMed]
- Camilloni, C.; De Simone, A.; Vranken, W.F.; Vendruscolo, M. Determination of secondary structure populations in disordered states of proteins using nuclear magnetic resonance chemical shifts. Biochemistry 2012, 51, 2224–2231. [Google Scholar] [CrossRef] [PubMed]
- Bernadó, P.; Bertoncini, C.W.; Griesinger, C.; Zweckstetter, M.; Blackledge, M. Defining long-range order and local disorder in native α-synuclein using residual dipolar couplings. J. Am. Chem. Soc. 2005, 127, 17968–17969. [Google Scholar] [CrossRef] [PubMed]
- Allison, J.R.; Varnai, P.; Dobson, C.M.; Vendruscolo, M. Determination of the free energy landscape of α-synuclein using spin label nuclear magnetic resonance measurements. J. Am. Chem. Soc. 2009, 131, 18314–18326. [Google Scholar] [CrossRef]
- Iešmantavičius, V.; Dogan, J.; Jemth, P.; Teilum, K.; Kjaergaard, M. Helical propensity in an intrinsically disordered protein accelerates ligand binding. Angew. Chemie Int. Ed. 2014, 53, 1548–1551. [Google Scholar] [CrossRef]
- Kim, D.-H.; Han, K.-H. Transient Secondary Structures as General Target-Binding Motifs in Intrinsically Disordered Proteins. Int. J. Mol. Sci. 2018, 19, 3614. [Google Scholar] [CrossRef]
- Marsh, J.A.; Dancheck, B.; Ragusa, M.J.; Allaire, M.; Forman-Kay, J.D.; Peti, W. Structural diversity in free and bound states of intrinsically disordered protein phosphatase 1 regulators. Structure 2010, 18, 1094–1103. [Google Scholar] [CrossRef]
- Borcherds, W.; Theillet, F.X.; Katzer, A.; Finzel, A.; Mishall, K.M.; Powell, A.T.; Wu, H.; Manieri, W.; Dieterich, C.; Selenko, P.; et al. Disorder and residual helicity alter p53-Mdm2 binding affinity and signaling in cells. Nat. Chem. Biol. 2014, 10, 1000–1002. [Google Scholar] [CrossRef]
- Krieger, J.M.; Fusco, G.; Lewitzky, M.; Simister, P.C.; Marchant, J.; Camilloni, C.; Feller, S.M.; De Simone, A. Conformational recognition of an intrinsically disordered protein. Biophys. J. 2014, 106, 1771–1779. [Google Scholar] [CrossRef]
- Arai, M.; Sugase, K.; Dyson, H.J.; Wright, P.E. Conformational propensities of intrinsically disordered proteins influence the mechanism of binding and folding. Proc. Natl. Acad. Sci. USA 2015, 112, 9614–9619. [Google Scholar] [CrossRef]
- Crabtree, M.D.; Borcherds, W.; Poosapati, A.; Shammas, S.L.; Daughdrill, G.W.; Clarke, J. Conserved Helix-Flanking Prolines Modulate Intrinsically Disordered Protein: Target Affinity by Altering the Lifetime of the Bound Complex. Biochemistry 2017, 56, 2379–2384. [Google Scholar] [CrossRef] [PubMed]
- Sugase, K.; Dyson, H.J.; Wright, P.E. Mechanism of coupled folding and binding of an intrinsically disordered protein. Nature 2007, 447, 1021–1025. [Google Scholar] [CrossRef] [PubMed]
- Sormanni, P.; Camilloni, C.; Fariselli, P.; Vendruscolo, M. The s2D method: Simultaneous sequence-based prediction of the statistical populations of ordered and disordered regions in proteins. J. Mol. Biol. 2015, 427, 982–996. [Google Scholar] [CrossRef] [PubMed]
- Uversky, V.N. Multitude of binding modes attainable by intrinsically disordered proteins: A portrait gallery of disorder-based complexes. Chem. Soc. Rev. 2011, 40, 1623–1634. [Google Scholar] [CrossRef] [PubMed]
- Dyson, H.J.; Wright, P.E. Coupling of folding and binding for unstructured proteins. Curr. Opin. Struct. Biol. 2002, 12, 54–60. [Google Scholar] [CrossRef]
- Gianni, S.; Dogan, J.; Jemth, P. Coupled binding and folding of intrinsically disordered proteins: What can we learn from kinetics? Curr. Opin. Struct. Biol. 2016, 36, 18–24. [Google Scholar] [CrossRef] [PubMed]
- Borgia, A.; Borgia, M.B.; Bugge, K.; Kissling, V.M.; Heidarsson, P.O.; Fernandes, C.B.; Sottini, A.; Soranno, A.; Buholzer, K.J.; Nettels, D.; et al. Extreme disorder in an ultrahigh-affinity protein complex. Nature 2018, 555, 61–66. [Google Scholar] [CrossRef] [PubMed]
- Delaforge, E.; Kragelj, J.; Tengo, L.; Palencia, A.; Milles, S.; Bouvignies, G.; Salvi, N.; Blackledge, M.; Jensen, M.R. Deciphering the Dynamic Interaction Profile of an Intrinsically Disordered Protein by NMR Exchange Spectroscopy. J. Am. Chem. Soc. 2018, 140, 1148–1158. [Google Scholar] [CrossRef] [PubMed]
- Lindström, I.; Dogan, J. Dynamics, Conformational Entropy, and Frustration in Protein-Protein Interactions Involving an Intrinsically Disordered Protein Domain. ACS Chem. Biol. 2018, 13, 1218–1227. [Google Scholar] [CrossRef] [PubMed]
- Yang, D.; Kay, L.E. Contributions to conformational entropy arising from bond vector fluctuations measured from NMR-derived order parameters: Application to protein folding. J. Mol. Biol. 1996, 263, 369–382. [Google Scholar] [CrossRef] [PubMed]
- Frederick, K.K.; Marlow, M.S.; Valentine, K.G.; Wand, A.J. Conformational entropy in molecular recognition by proteins. Nature 2007, 448, 325–329. [Google Scholar] [CrossRef] [PubMed]
- Tzeng, S.R.; Kalodimos, C.G. Protein activity regulation by conformational entropy. Nature 2012, 488, 236–240. [Google Scholar] [CrossRef] [PubMed]
- Alderson, T.R.; Lee, J.H.; Charlier, C.; Ying, J.; Bax, A. Propensity for cis-Proline Formation in Unfolded Proteins. ChemBioChem 2018, 19, 37–42. [Google Scholar] [CrossRef] [PubMed]
- Baker, J.M.R.; Hudson, R.P.; Kanelis, V.; Choy, W.Y.; Thibodeau, P.H.; Thomas, P.J.; Forman-Kay, J.D. CFTR regulatory region interacts with NBD1 predominantly via multiple transient helices. Nat. Struct. Mol. Biol. 2007, 14, 738–745. [Google Scholar] [CrossRef] [PubMed]
- Kragelj, J.; Palencia, A.; Nanao, M.H.; Maurin, D.; Bouvignies, G.; Blackledge, M.; Jensen, M.R. Structure and dynamics of the MKK7–JNK signaling complex. Proc. Natl. Acad. Sci. USA 2015, 112, 3409–3414. [Google Scholar] [CrossRef] [PubMed]
- Martinez, A.I.C.; Weinhäupl, K.; Lee, W.K.; Wolff, N.A.; Storch, B.; Zerko, S.; Konrat, R.; Kozminski, W.; Breuker, K.; Thévenod, F.; et al. Biochemical and structural characterization of the interaction between the siderocalin NGAL/LCN2 (Neutrophil Gelatinase-associated lipocalin/lipocalin 2) and the N-terminal domain of its endocytic receptor SLC22A17. J. Biol. Chem. 2016, 291, 2917–2930. [Google Scholar] [CrossRef]
- Ferreon, J.C.; Martinez-Yamout, M.A.; Dyson, H.J.; Wright, P.E. Structural basis for subversion of cellular control mechanisms by the adenoviral E1A oncoprotein. Proc. Natl. Acad. Sci. USA 2009, 106, 13260–13265. [Google Scholar] [CrossRef]
- Martin, E.W.; Holehouse, A.S.; Grace, C.R.; Hughes, A.; Pappu, R.V.; Mittag, T. Sequence Determinants of the Conformational Properties of an Intrinsically Disordered Protein Prior to and upon Multisite Phosphorylation. J. Am. Chem. Soc. 2016, 138, 15323–15335. [Google Scholar] [CrossRef]
- Oldfield, C.J.; Dunker, A.K. Intrinsically Disordered Proteins and Intrinsically Disordered Protein Regions. Annu. Rev. Biochem. 2014, 83, 553–584. [Google Scholar] [CrossRef]
- Iakoucheva, L.M.; Radivojac, P.; Brown, C.J.; O’Connor, T.R.; Sikes, J.G.; Obradovic, Z.; Dunker, A.K. The importance of intrinsic disorder for protein phosphorylation. Nucleic Acids Res. 2004, 32, 1037–1049. [Google Scholar] [CrossRef]
- Radivojac, P.; Vacic, V.; Haynes, C.; Cocklin, R.R.; Mohan, A.; Heyen, J.W.; Goebl, M.G.; Iakoucheva, L.M. Identification, analysis, and prediction of protein ubiquitination sites. Proteins Struct. Funct. Bioinforma. 2010, 78, 365–380. [Google Scholar] [CrossRef] [PubMed]
- Pejaver, V.; Hsu, W.L.; Xin, F.; Dunker, A.K.; Uversky, V.N.; Radivojac, P. The structural and functional signatures of proteins that undergo multiple events of post-translational modification. Protein Sci. 2014, 23, 1077–1093. [Google Scholar] [CrossRef] [PubMed]
- Kang, L.; Moriarty, G.M.; Woods, L.A.; Ashcroft, A.E.; Radford, S.E.; Baum, J. N-terminal acetylation of α-synuclein induces increased transient helical propensity and decreased aggregation rates in the intrinsically disordered monomer. Protein Sci. 2012, 21, 911–917. [Google Scholar] [CrossRef]
- Alderson, T.R.; Markley, J.L. Biophysical characterization of α-synuclein and its controversial structure. Intrinsically Disord. Proteins 2013, 1, 18–39. [Google Scholar] [CrossRef] [PubMed]
- Theillet, F.X.; Binolfi, A.; Bekei, B.; Martorana, A.; Rose, H.M.; Stuiver, M.; Verzini, S.; Lorenz, D.; Van Rossum, M.; Goldfarb, D.; et al. Structural disorder of monomeric α-synuclein persists in mammalian cells. Nature 2016, 530, 45–50. [Google Scholar] [CrossRef] [PubMed]
- Binolfi, A.; Limatola, A.; Verzini, S.; Kosten, J.; Theillet, F.X.; May Rose, H.; Bekei, B.; Stuiver, M.; Van Rossum, M.; Selenko, P. Intracellular repair of oxidation-damaged α-synuclein fails to target C-terminal modification sites. Nat. Commun. 2016, 7, 10251. [Google Scholar] [CrossRef] [PubMed]
- Arribas-Layton, M.; Dennis, J.; Bennett, E.J.; Damgaard, C.K.; Lykke-Andersen, J. The C-Terminal RGG Domain of Human Lsm4 Promotes Processing Body Formation Stimulated by Arginine Dimethylation. Mol. Cell. Biol. 2016, 36, 2226–2235. [Google Scholar] [CrossRef] [PubMed]
- Landry, C.R.; Freschi, L.; Zarin, T.; Moses, A.M. Turnover of protein phosphorylation evolving under stabilizing selection. Front. Genet. 2014, 5, 245. [Google Scholar] [CrossRef]
- Johnson, L.N.; Lewis, R.J. Structural basis for control by phosphorylation. Chem. Rev. 2001, 101, 2209–2242. [Google Scholar] [CrossRef]
- Darling, A.L.; Uversky, V.N. Intrinsic disorder and posttranslational modifications: The darker side of the biological dark matter. Front. Genet. 2018, 9, 158. [Google Scholar] [CrossRef]
- Alderson, T.R.; Roche, J.; Gastall, H.Y.; Dias, D.M.; Pritišanac, I.; Ying, J.; Bax, A.; Benesch, J.L.P.; Baldwin, A.J. Local unfolding of the HSP27 monomer regulates chaperone activity. Nat. Commun. 2019, 10, 1068. [Google Scholar] [CrossRef] [PubMed]
- Arbesú, M.; Iruela, G.; Fuentes, H.; Teixeira, J.M.C.; Pons, M. Intramolecular Fuzzy Interactions Involving Intrinsically Disordered Domains. Front. Mol. Biosci. 2018, 5, 39. [Google Scholar] [CrossRef] [PubMed]
- Tompa, P. Multisteric regulation by structural disorder in modular signaling proteins: An extension of the concept of allostery. Chem. Rev. 2014, 114, 6715–6732. [Google Scholar] [CrossRef] [PubMed]
- Hilser, V.J.; Thompson, E.B. Intrinsic disorder as a mechanism to optimize allosteric coupling in proteins. Proc. Natl. Acad. Sci. USA 2007, 104, 8311–8315. [Google Scholar] [CrossRef] [PubMed]
- Motlagh, H.N.; Hilser, V.J. Agonism/antagonism switching in allosteric ensembles. Proc. Natl. Acad. Sci. USA 2012, 109, 4134–4139. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Hilser, V.J. Assessing Allostery in Intrinsically Disordered Proteins with Ensemble Allosteric Model. Methods Enzymol. 2018, 611, 531–557. [Google Scholar] [PubMed]
- Zhang, L.; Li, M.; Liu, Z. A comprehensive ensemble model for comparing the allosteric effect of ordered and disordered proteins. PLoS Comput. Biol. 2018, 14, e1006393. [Google Scholar] [CrossRef] [PubMed]
- Follis, A.V.; Llambi, F.; Kalkavan, H.; Yao, Y.; Phillips, A.H.; Park, C.G.; Marassi, F.M.; Green, D.R.; Kriwacki, R.W. Regulation of apoptosis by an intrinsically disordered region of Bcl-xL. Nat. Chem. Biol. 2018, 14, 458–465. [Google Scholar] [CrossRef]
- Vacic, V.; Markwick, P.R.L.; Oldfield, C.J.; Zhao, X.; Haynes, C.; Uversky, V.N.; Iakoucheva, L.M. Disease-Associated Mutations Disrupt Functionally Important Regions of Intrinsic Protein Disorder. PLoS Comput. Biol. 2012, 8, e1002709. [Google Scholar] [CrossRef]
- Meyer, K.; Kirchner, M.; Uyar, B.; Cheng, J.Y.; Russo, G.; Hernandez-Miranda, L.R.; Szymborska, A.; Zauber, H.; Rudolph, I.M.; Willnow, T.E.; et al. Mutations in Disordered Regions Can Cause Disease by Creating Dileucine Motifs. Cell 2018, 175, 239–253.e17. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pritišanac, I.; Vernon, R.M.; Moses, A.M.; Forman Kay, J.D. Entropy and Information within Intrinsically Disordered Protein Regions. Entropy 2019, 21, 662. https://doi.org/10.3390/e21070662
Pritišanac I, Vernon RM, Moses AM, Forman Kay JD. Entropy and Information within Intrinsically Disordered Protein Regions. Entropy. 2019; 21(7):662. https://doi.org/10.3390/e21070662
Chicago/Turabian StylePritišanac, Iva, Robert M. Vernon, Alan M. Moses, and Julie D. Forman Kay. 2019. "Entropy and Information within Intrinsically Disordered Protein Regions" Entropy 21, no. 7: 662. https://doi.org/10.3390/e21070662
APA StylePritišanac, I., Vernon, R. M., Moses, A. M., & Forman Kay, J. D. (2019). Entropy and Information within Intrinsically Disordered Protein Regions. Entropy, 21(7), 662. https://doi.org/10.3390/e21070662





