Variability and Reproducibility of Directed and Undirected Functional MRI Connectomes in the Human Brain
Abstract
1. Introduction
2. Materials and Methods
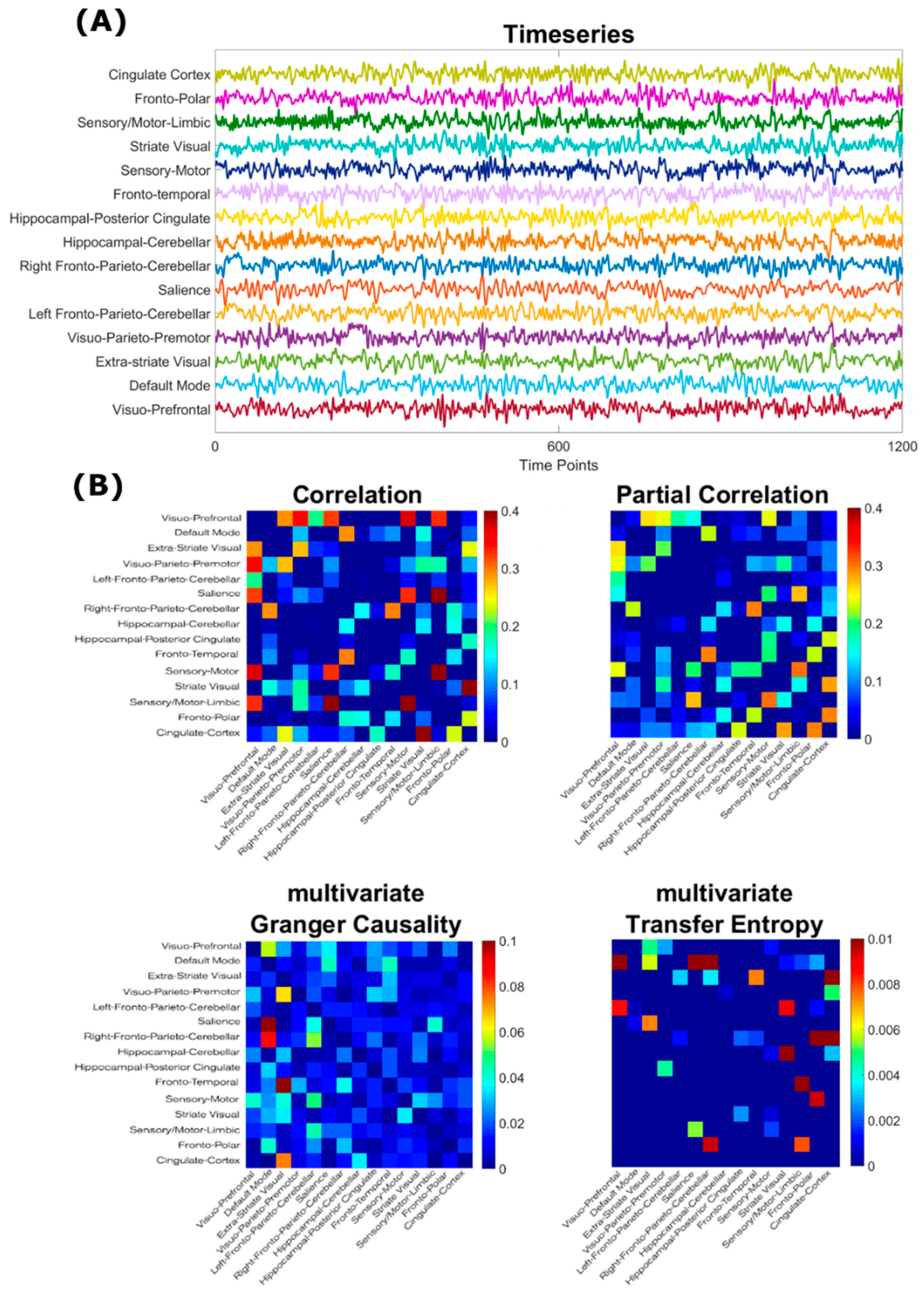
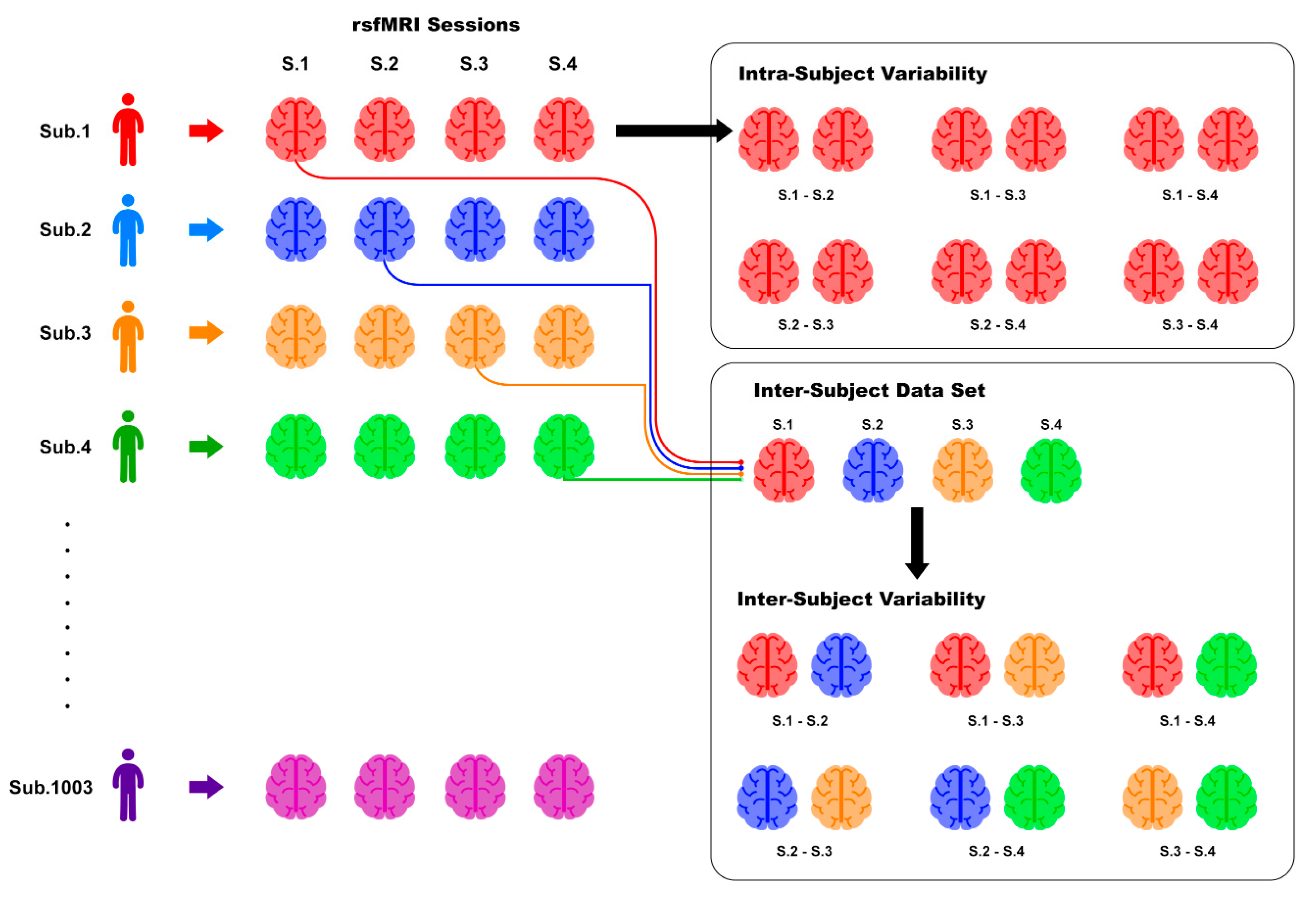
2.1. rsfMRI Data
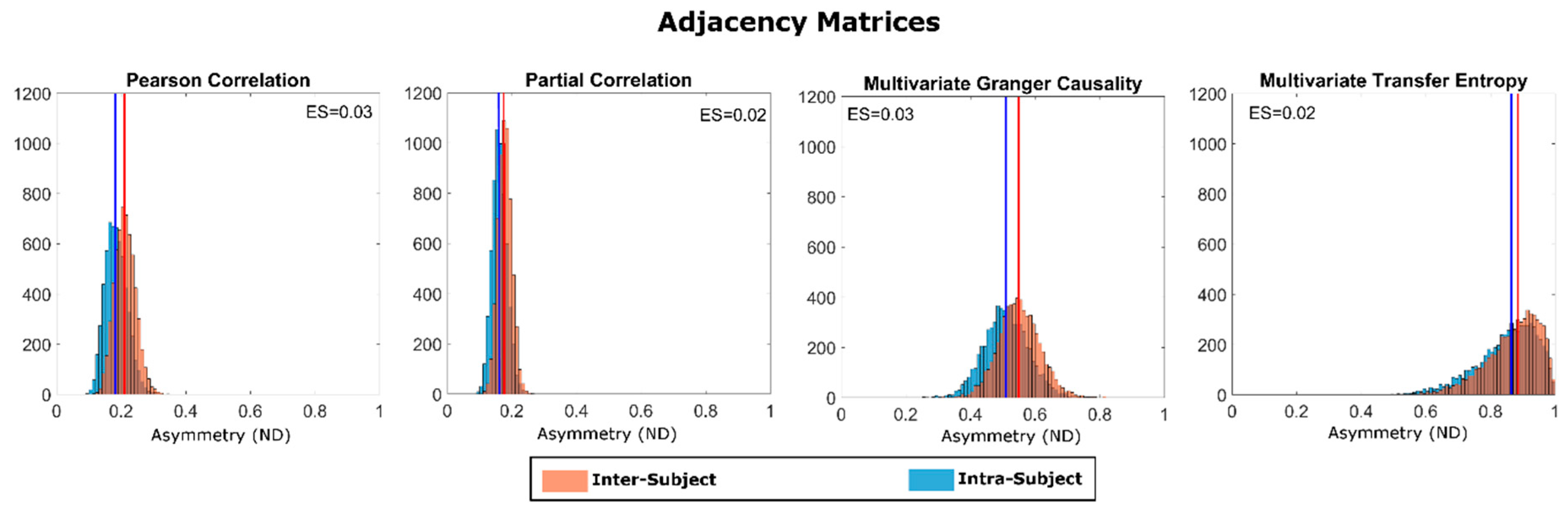
2.2. Estimation of Adjacency Matrices
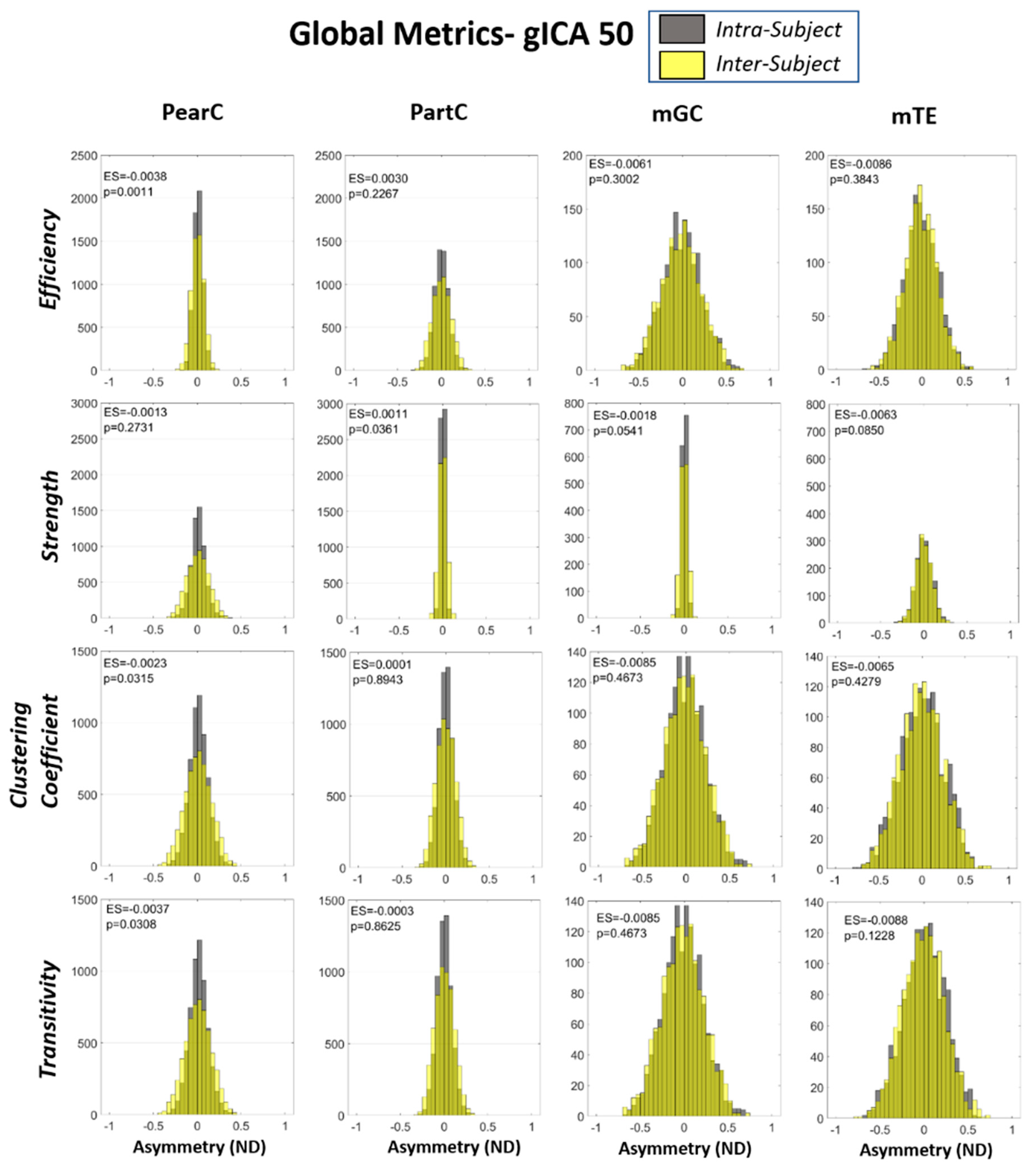
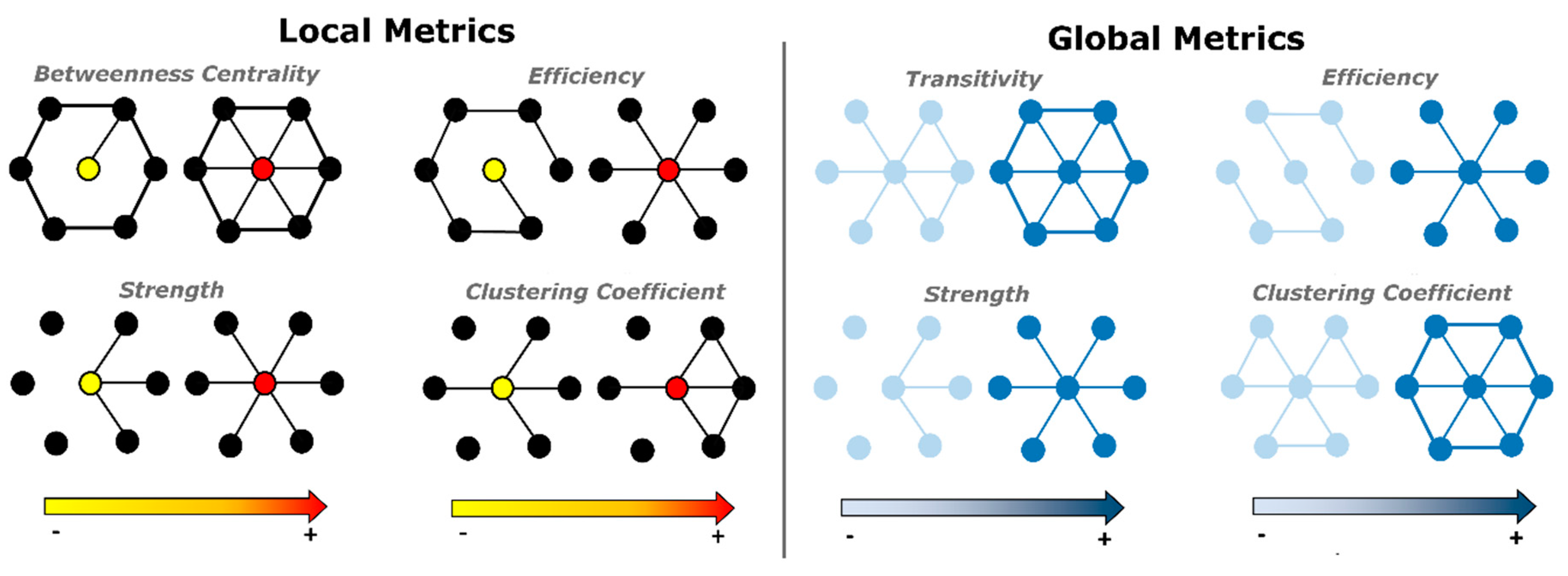
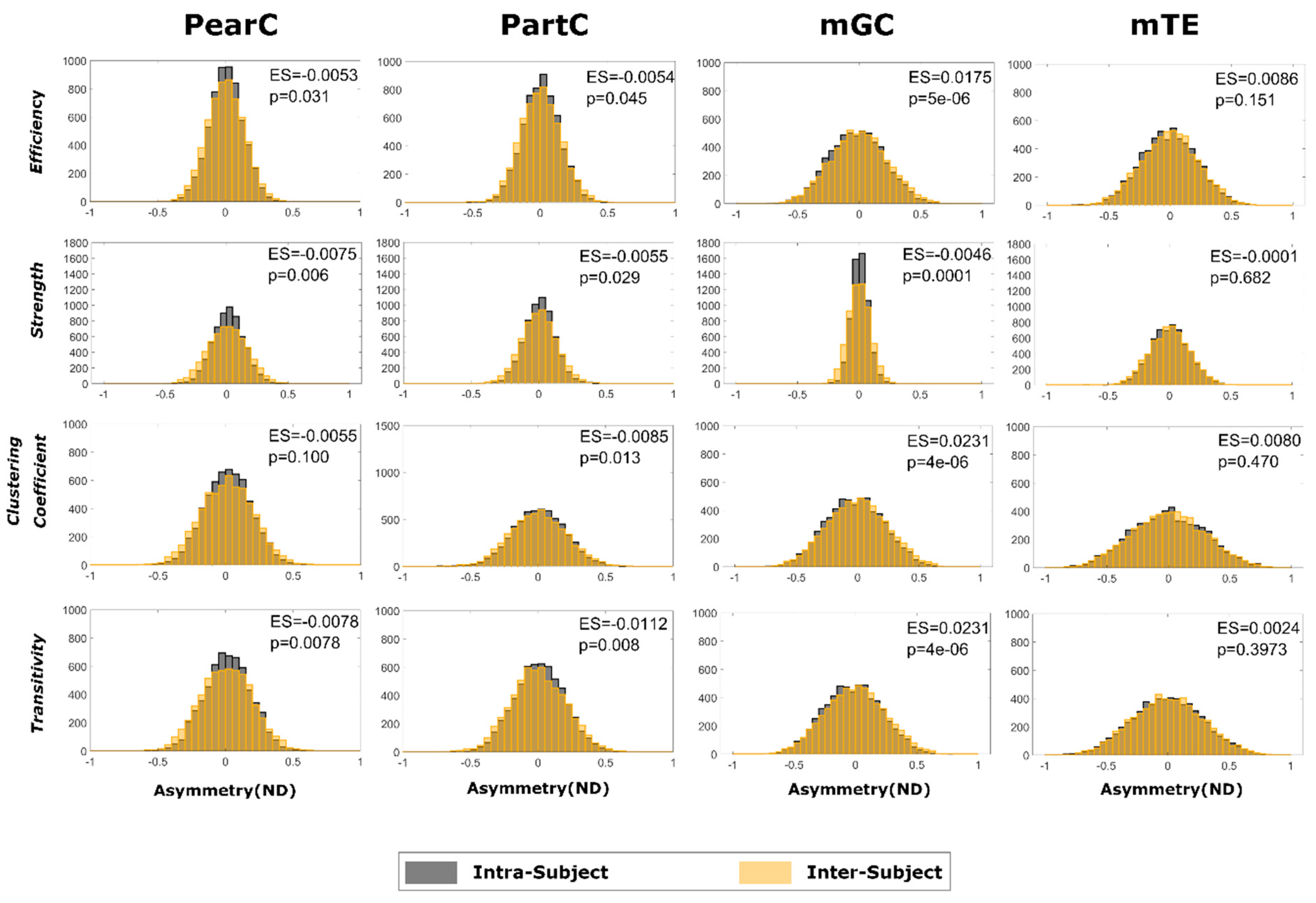
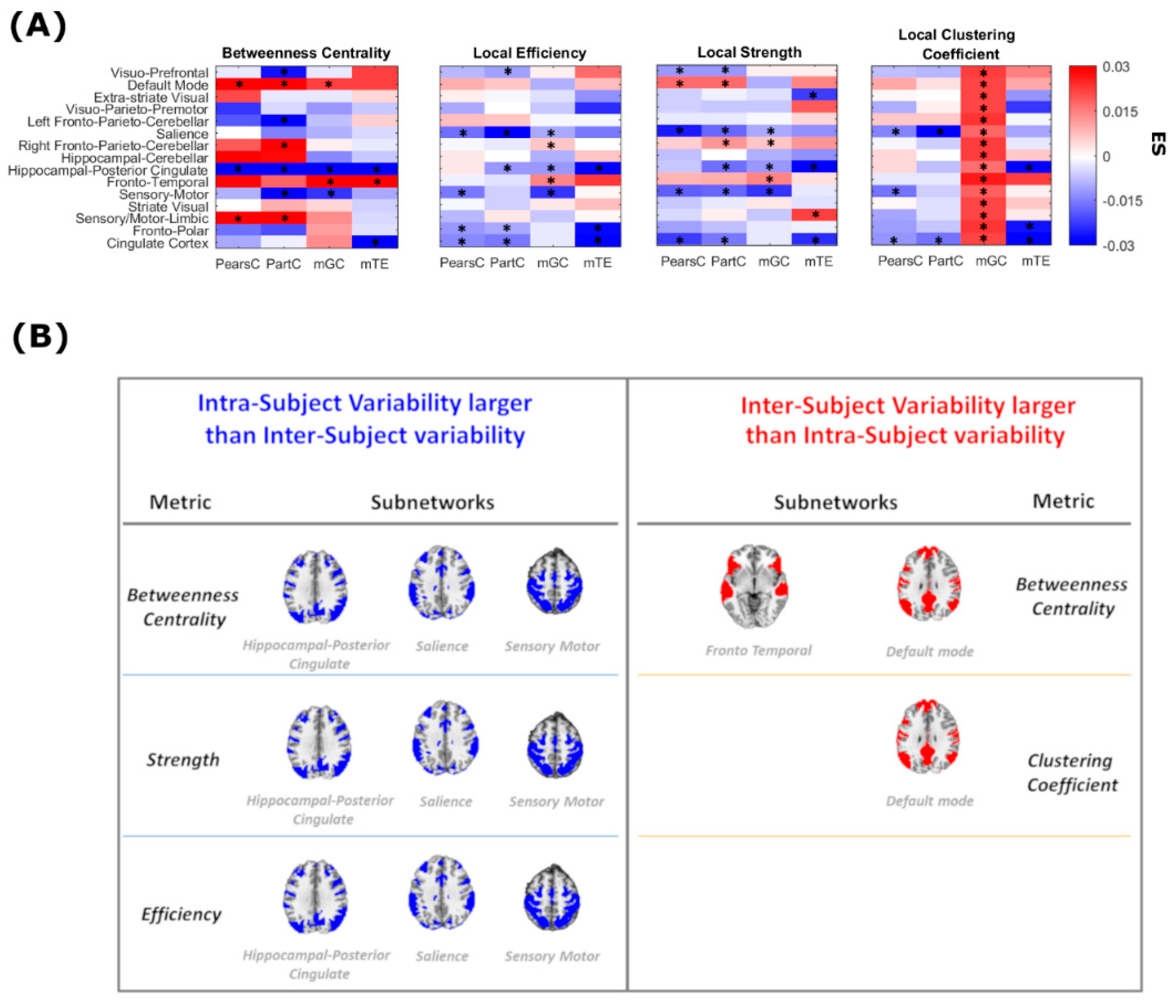
2.3. Global and Local Graph Metric Estimation
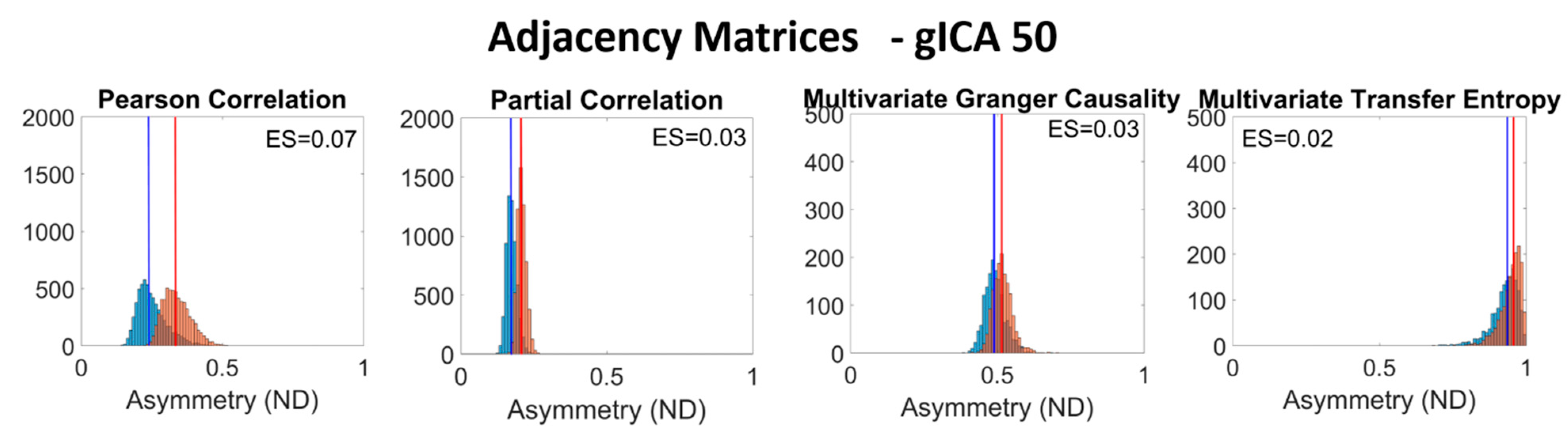
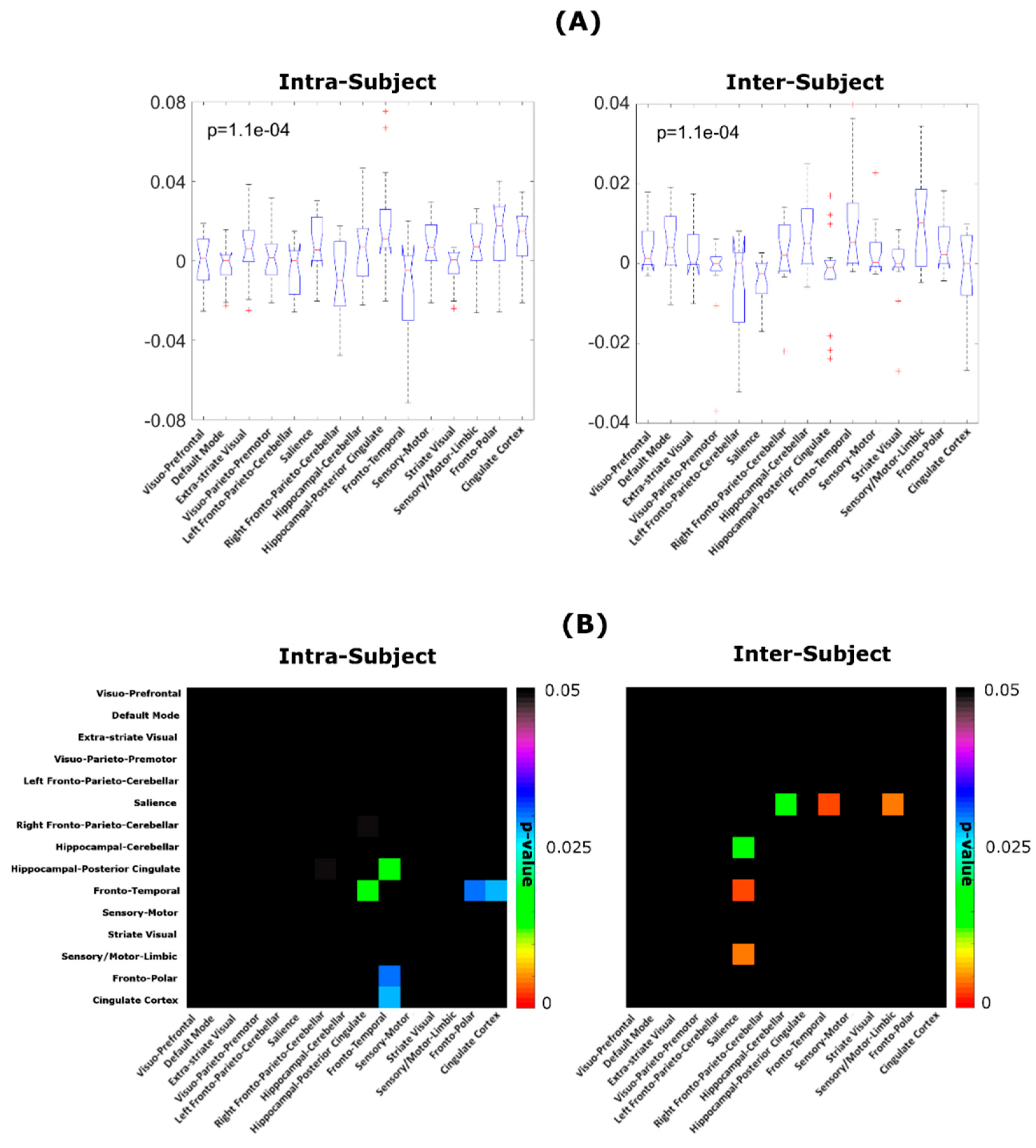
2.4. Inter- and Intra-Subject Variability Distributions
2.5. Statistical Analysis
3. Results
4. Discussion
Limitations and Future Perspectives
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Variability and Reproducibility of Directed and Undirected Functional MRI Connectomes in the Human Brain
References
- Wang, H.E.; Bénar, C.G.; Quilichini, P.P.; Friston, K.J.; Jirsa, V.K.; Bernard, C. A systematic framework for functional connectivity measures. Front. Mol. Neurosci. 2014, 8, 8. [Google Scholar] [CrossRef] [PubMed]
- Blinowska, K.J. Review of the methods of determination of directed connectivity from multichannel data. Med. Boil. Eng. 2011, 49, 521–529. [Google Scholar] [CrossRef] [PubMed]
- Bullmore, E.; Sporns, O.; Bullmore, E. The economy of brain network organization. Nat. Rev. Neurosci. 2012, 13, 336–349. [Google Scholar] [CrossRef] [PubMed]
- Fornito, A.; Zalesky, A.; Bullmore, E.T. (Eds.) Chapter 3—Connectivity Matrices and Brain Graphs. In Fundamentals of Brain Network Analysis; Academic Press: San Diego, CA, USA, 2016; pp. 89–113. [Google Scholar]
- Schmidt, C.; Pester, B.; Schmid-Hertel, N.; Witte, H.; Wismüller, A.; Leistritz, L. A Multivariate Granger Causality Concept towards Full Brain Functional Connectivity. PLoS ONE 2016, 11, 0153105. [Google Scholar] [CrossRef] [PubMed]
- Schoffelen, J.-M.; Hultén, A.; Lam, N.; Marquand, A.F.; Uddén, J.; Hagoort, P. Frequency-specific directed interactions in the human brain network for language. Proc. Natl. Acad. Sci. USA 2017, 114, 8083–8088. [Google Scholar] [CrossRef] [PubMed]
- Salvador, R.; Suckling, J.; Schwarzbauer, C.; Bullmore, E.; Bullmore, E. Undirected graphs of frequency-dependent functional connectivity in whole brain networks. Philos. Trans. R. Soc. B Boil. Sci. 2005, 360, 937–946. [Google Scholar] [CrossRef]
- Sporns, O. Graph theory methods: Applications in brain networks. Dialogues Clin. Neurosci. 2018, 20, 111–121. [Google Scholar]
- Duggento, A.; Passamonti, L.; Valenza, G.; Barbieri, R.; Guerrisi, M.; Toschi, N. Multivariate Granger causality unveils directed parietal to prefrontal cortex connectivity during task-free MRI. Sci. Rep. 2018, 8, 5571. [Google Scholar] [CrossRef]
- Toschi, N.; Riccelli, R.; Indovina, I.; Terracciano, A.; Passamonti, L. Functional connectome of the five-factor model of personality. Pers. Neurosci. 2018, 1, 1. [Google Scholar] [CrossRef]
- Vecchio, F.; Miraglia, F.; Rossini, P.M. Connectome: Graph theory application in functional brain network architecture. Clin. Neurophysiol. Pract. 2017, 2, 206–213. [Google Scholar] [CrossRef]
- Fornito, A.; Zalesky, A.; Bullmore, E.T. (Eds.) Chapter 1—An Introduction to Brain Networks. In Fundamentals of Brain Network Analysis; Academic Press: San Diego, CA, USA, 2016; pp. 1–35. [Google Scholar]
- Deshpande, G.; LaConte, S.; James, G.A.; Peltier, S.; Hu, X. Multivariate Granger causality analysis of fMRI data. Hum. Brain Mapp. 2009, 30, 1361–1373. [Google Scholar] [CrossRef] [PubMed]
- Baccala, L.A.; Sameshima, K. Partial directed coherence: A new concept in neural structure determination. Boil. Cybern. 2001, 84, 463–474. [Google Scholar] [CrossRef] [PubMed]
- Vicente, R.; Wibral, M.; Lindner, M.; Pipa, G. Transfer entropy—A model-free measure of effective connectivity for the neurosciences. J. Comput. Neurosci. 2011, 30, 45–67. [Google Scholar] [CrossRef] [PubMed]
- Zhang, N.; Wang, F.; Turner, G.H.; Gore, J.C.; Avison, M.J.; Chen, L.M. Intra- and inter-subject variability of high field fMRI digit maps in somatosensory area 3b of new world monkeys. Neuroscience 2010, 165, 252–264. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Smith, S.M.; Beckmann, C.F.; Ramnani, N.; Woolrich, M.W.; Bannister, P.R.; Jenkinson, M.; Matthews, P.M.; Mcgonigle, D.J. Variability in fMRI: A re-examination of inter-session differences. Hum. Brain Mapp. 2005, 24, 248–257. [Google Scholar] [CrossRef] [PubMed]
- Seghier, M.L.; Price, C.J. Interpreting and Utilising Intersubject Variability in Brain Function. Trends Cogn. Sci. 2018, 22, 517–530. [Google Scholar] [CrossRef]
- Vakorin, V.A.; Ross, B.; Krakovska, O.; Bardouille, T.; Cheyne, D.; McIntosh, A.R. Complexity analysis of source activity underlying the neuromagnetic somatosensory steady-state response. NeuroImage 2010, 51, 83–90. [Google Scholar] [CrossRef]
- Baig, M.Z.; Kavakli, M. Connectivity Analysis Using Functional Brain Networks to Evaluate Cognitive Activity during 3D Modelling. Brain Sci. 2019, 9, 24. [Google Scholar] [CrossRef]
- Shovon, M.H.; Nandagopal, N.; Vijayalakshmi, R.; Du, J.T.; Cocks, B. Directed Connectivity Analysis of Functional Brain Networks During Cognitive Activity Using Transfer Entropy. Neural Process. Lett. 2017, 45, 807–824. [Google Scholar] [CrossRef]
- Duggento, A.; Bianciardi, M.; Passamonti, L.; Wald, L.L.; Guerrisi, M.; Barbieri, R.; Toschi, N. Globally conditioned Granger causality in brain–brain and brain–heart interactions: A combined heart rate variability/ultra-high-field (7 T) functional magnetic resonance imaging study. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 20150185. [Google Scholar] [CrossRef]
- Marinazzo, D.; Liao, W.; Chen, H.; Stramaglia, S. Nonlinear connectivity by Granger causality. NeuroImage 2011, 58, 330–338. [Google Scholar] [CrossRef] [PubMed]
- Barnett, L.; Barrett, A.B.; Seth, A.K. Granger Causality and Transfer Entropy Are Equivalent for Gaussian Variables. Phys. Rev. Lett. 2009, 103, 238701. [Google Scholar] [CrossRef] [PubMed]
- Seth, A.K.; Barrett, A.B.; Barnett, L. Granger Causality Analysis in Neuroscience and Neuroimaging. J. Neurosci. 2015, 35, 3293–3297. [Google Scholar] [CrossRef] [PubMed]
- Van Essen, D.C.; Smith, S.M.; Barch, D.M.; Behrens, T.E.; Yacoub, E.; Ugurbil, K. WU-Minn HCP Consortium The WU-Minn Human Connectome Project: An overview. NeuroImage 2013, 80, 62–79. [Google Scholar] [CrossRef] [PubMed]
- Toschi, N.; Duggento, A.; Passamonti, L. Functional Connectivity in Amygdalar-Sensory/(Pre)Motor networks at rest: New evidence from the Human Connectome Project. Eur. J. Neurosci. 2017, 45, 1224–1229. [Google Scholar] [CrossRef] [PubMed]
- Deshpande, G.; Sathian, K.; Hu, X. Effect of hemodynamic variability on Granger causality analysis of fMRI. Neuroimage 2010, 52, 884–896. [Google Scholar] [CrossRef] [PubMed]
- Wu, G.-R.; Liao, W.; Stramaglia, S.; Ding, J.-R.; Chen, H.; Marinazzo, D. A blind deconvolution approach to recover effective connectivity brain networks from resting state fMRI data. Med. Image Anal. 2013, 17, 365–374. [Google Scholar] [CrossRef] [PubMed]
- Barnett, L.; Seth, A.K. Granger causality for state-space models. Phys. Rev. E 2015, 91, 040101. [Google Scholar] [CrossRef]
- Faes, L.; Nollo, G.; Stramaglia, S.; Marinazzo, D. Multiscale Granger causality. Phys. Rev. E 2017, 96, 042150. [Google Scholar] [CrossRef]
- Faes, L.; Nollo, G.; Porta, A. Information Domain Approach to the Investigation of Cardio-Vascular, Cardio-Pulmonary, and Vasculo-Pulmonary Causal Couplings. Front. Physiol. 2011, 2, 2. [Google Scholar] [CrossRef]
- Rubinov, M.; Sporns, O. Complex network measures of brain connectivity: Uses and interpretations. NeuroImage 2010, 52, 1059–1069. [Google Scholar] [CrossRef] [PubMed]
- Song, X.; Panych, L.P.; Chou, Y.-H.; Chen, N.-K. A Study of Long-Term fMRI Reproducibility Using Data-Driven Analysis Methods. Int. J. Imaging Syst. Technol. 2014, 24, 339–349. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Lu, B.; Yan, C.-G. Reproducibility of R-fMRI metrics on the impact of different strategies for multiple comparison correction and sample sizes. Hum. Brain Mapp. 2018, 39, 300–318. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Rangarajan, G.; Feng, J.; Ding, M. Analyzing multiple nonlinear time series with extended Granger causality. Phys. Lett. A 2004, 324, 26–35. [Google Scholar] [CrossRef]
- Benhmad, F. Modeling nonlinear Granger causality between the oil price and U.S. dollar: A wavelet based approach. Econ. Model. 2012, 29, 1505–1514. [Google Scholar] [CrossRef]
- Montalto, A.; Stramaglia, S.; Faes, L.; Tessitore, G.; Prevete, R.; Marinazzo, D. Neural networks with non-uniform embedding and explicit validation phase to assess Granger causality. Neural Netw. 2015, 71, 159–171. [Google Scholar] [CrossRef] [PubMed]
- Schreiber, T. Measuring Information Transfer. Phys. Rev. Lett. 2000, 85, 461–464. [Google Scholar] [CrossRef] [PubMed]
- Wibral, M.; Vicente, R.; Lizier, J.T. (Eds.) Directed Information Measures in Neuroscience; Understanding Complex Systems; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Wen, X.; Rangarajan, G.; Ding, M. Is Granger Causality a Viable Technique for Analyzing fMRI Data? PLoS ONE 2013, 8, e67428. [Google Scholar] [CrossRef] [PubMed]
- Ramsey, J.; Hanson, S.; Hanson, C.; Halchenko, Y.; Poldrack, R.; Glymour, C.; Halchenko, Y. Six problems for causal inference from fMRI. NeuroImage 2010, 49, 1545–1558. [Google Scholar] [CrossRef]
- Laumann, T.O.; Gordon, E.M.; Adeyemo, B.; Snyder, A.Z.; Joo, S.J.; Chen, M.-Y.; Gilmore, A.W.; McDermott, K.B.; Nelson, S.M.; Dosenbach, N.U.; et al. Functional system and areal organization of a highly sampled individual human brain. Neuron 2015, 87, 657–670. [Google Scholar] [CrossRef]
- Mueller, S.; Wang, D.; Fox, M.D.; Yeo, B.T.; Sepulcre, J.; Sabuncu, M.R.; Shafee, R.; Lu, J.; Liu, H. Individual Variability in Functional Connectivity Architecture of the Human Brain. Neuron 2013, 77, 586–595. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Xu, T.; Zhou, C.; Wang, L.; Yang, N.; Wang, Z.; Dong, H.-M.; Yang, Z.; Zang, Y.-F.; Zuo, X.-N.; et al. Individual Variability and Test-Retest Reliability Revealed by Ten Repeated Resting-State Brain Scans over One Month. PLoS ONE 2015, 10, e0144963. [Google Scholar] [CrossRef] [PubMed]
- Kong, R.; Li, J.; Sun, N.; Sabuncu, M.R.; Schaefer, A.; Zuo, X.-N.; Holmes, A.J.; Eickhoff, S.; Yeo, B.T.T. Controlling for Intra-Subject and Inter-Subject Variability in Individual-Specific Cortical Network Parcellations. bioRxiv 2017, 213041. [Google Scholar] [CrossRef]
- Hodkinson, D.J.; O’Daly, O.; A Zunszain, P.; Pariante, C.M.; Lazurenko, V.; O Zelaya, F.; A Howard, M.; Williams, S.C.R. Circadian and homeostatic modulation of functional connectivity and regional cerebral blood flow in humans under normal entrained conditions. Br. J. Pharmacol. 2014, 34, 1493–1499. [Google Scholar] [CrossRef] [PubMed]
- Shannon, B.J.; Dosenbach, R.A.; Su, Y.; Vlassenko, A.G.; Larson-Prior, L.J.; Nolan, T.S.; Snyder, A.Z.; Raichle, M.E. Morning-evening variation in human brain metabolism and memory circuits. J. Neurophysiol. 2013, 109, 1444–1456. [Google Scholar] [CrossRef] [PubMed]
- Gordon, E.M.; Breeden, A.L.; Bean, S.E.; Vaidya, C.J. Working memory-related changes in functional connectivity persist beyond task disengagement. Hum. Brain Mapp. 2014, 35, 1004–1017. [Google Scholar] [CrossRef] [PubMed]
- Lewis, C.M.; Baldassarre, A.; Committeri, G.; Romani, G.L.; Corbetta, M. Learning sculpts the spontaneous activity of the resting human brain. Proc. Natl. Acad. Sci. USA 2009, 106, 17558–17563. [Google Scholar] [CrossRef]
- Tambini, A.; Ketz, N.; Davachi, L. Enhanced Brain Correlations during Rest Are Related to Memory for Recent Experiences. Neuron 2010, 65, 280–290. [Google Scholar] [CrossRef]
- Yeo, B.T.; Tandi, J.; Chee, M.W. Functional connectivity during rested wakefulness predicts vulnerability to sleep deprivation. NeuroImage 2015, 111, 147–158. [Google Scholar] [CrossRef]
- Laumann, T.O.; Snyder, A.Z.; Mitra, A.; Gordon, E.M.; Gratton, C.; Adeyemo, B.; Gilmore, A.W.; Nelson, S.M.; Berg, J.J.; Greene, D.J.; et al. On the Stability of BOLD fMRI Correlations. Cereb. Cortex 2017, 27, 4719–4732. [Google Scholar] [CrossRef]
- Wang, C.; Ong, J.L.; Patanaik, A.; Zhou, J.; Chee, M.W.L. Spontaneous eyelid closures link vigilance fluctuation with fMRI dynamic connectivity states. Proc. Natl. Acad. Sci. USA 2016, 113, 9653–9658. [Google Scholar] [CrossRef] [PubMed]
- Shine, J.M.; Koyejo, O.; Poldrack, R.A. Temporal metastates are associated with differential patterns of time-resolved connectivity, network topology, and attention. Proc. Natl. Acad. Sci. USA 2016, 113, 9888–9891. [Google Scholar] [CrossRef] [PubMed]
- Vecchio, F.; Miraglia, F.; Marra, C.; Quaranta, D.; Vita, M.G.; Bramanti, P.; Rossini, P.M. Human brain networks in cognitive decline: A graph theoretical analysis of cortical connectivity from EEG data. J. Alzheimer’s Dis. 2014, 41, 113–127. [Google Scholar] [CrossRef] [PubMed]
- Anastasiadou, M.N.; Christodoulakis, M.; Papathanasiou, E.S.; Papacostas, S.S.; Hadjipapas, A.; Mitsis, G.D. Graph Theoretical Characteristics of EEG-Based Functional Brain Networks in Patients with Epilepsy: The Effect of Reference Choice and Volume Conduction. Front. Mol. Neurosci. 2019, 13, 221. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Wang, Y.; Lui, Y.W. Generalized Recurrent Neural Network accommodating Dynamic Causal Modeling for functional MRI analysis. NeuroImage 2018, 178, 385–402. [Google Scholar] [CrossRef] [PubMed]
- Gilson, M.; Zamora-Lopez, G.; Pallares, V.; Adhikari, M.H.; Senden, M.; Campo, A.T.; Mantini, D.; Corbetta, M.; Deco, G.; Insabato, A. MOU-EC: Model-based whole-brain effective connectivity to extract biomarkers for brain dynamics from fMRI data and study distributed cognition. bioRxiv 2019, 531830. [Google Scholar] [CrossRef]
- Preti, M.G.; Bolton, T.A.; Van De Ville, D. The dynamic functional connectome: State-of-the-art and perspectives. NeuroImage 2017, 160, 41–54. [Google Scholar] [CrossRef]

| Method | Betweenness Centrality | Local Efficiency | Strength | Clustering Coefficient | Mean(sd) % out of 15 |
|---|---|---|---|---|---|
| PearsC | 3(2/1) | 4(0/4) | 5(1/4) | 3(0/3) | 5%(6%) |
| PartC | 7(3/4) | 5(0/5) | 7(2/5) | 2(0/2) | 8%(9%) |
| mGC | 4(2/2) | 5(2/3) | 5(2/3) | 15(15/0) | 35%(38%) |
| mTE | 3(1/2) | 3(0/3) | 4(1/3) | 3(0/3) | 3%(3%) |
| Mean(sd) % out of 15 | 28%(13%) | 28%(6%) | 35%(8%) | 38%(41%) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Conti, A.; Duggento, A.; Guerrisi, M.; Passamonti, L.; Indovina, I.; Toschi, N. Variability and Reproducibility of Directed and Undirected Functional MRI Connectomes in the Human Brain. Entropy 2019, 21, 661. https://doi.org/10.3390/e21070661
Conti A, Duggento A, Guerrisi M, Passamonti L, Indovina I, Toschi N. Variability and Reproducibility of Directed and Undirected Functional MRI Connectomes in the Human Brain. Entropy. 2019; 21(7):661. https://doi.org/10.3390/e21070661
Chicago/Turabian StyleConti, Allegra, Andrea Duggento, Maria Guerrisi, Luca Passamonti, Iole Indovina, and Nicola Toschi. 2019. "Variability and Reproducibility of Directed and Undirected Functional MRI Connectomes in the Human Brain" Entropy 21, no. 7: 661. https://doi.org/10.3390/e21070661
APA StyleConti, A., Duggento, A., Guerrisi, M., Passamonti, L., Indovina, I., & Toschi, N. (2019). Variability and Reproducibility of Directed and Undirected Functional MRI Connectomes in the Human Brain. Entropy, 21(7), 661. https://doi.org/10.3390/e21070661








