An Image Encryption Scheme Based on Block Scrambling, Modified Zigzag Transformation and Key Generation Using Enhanced Logistic—Tent Map
Abstract
1. Introduction
2. Materials and Methods
2.1. Logistic Map
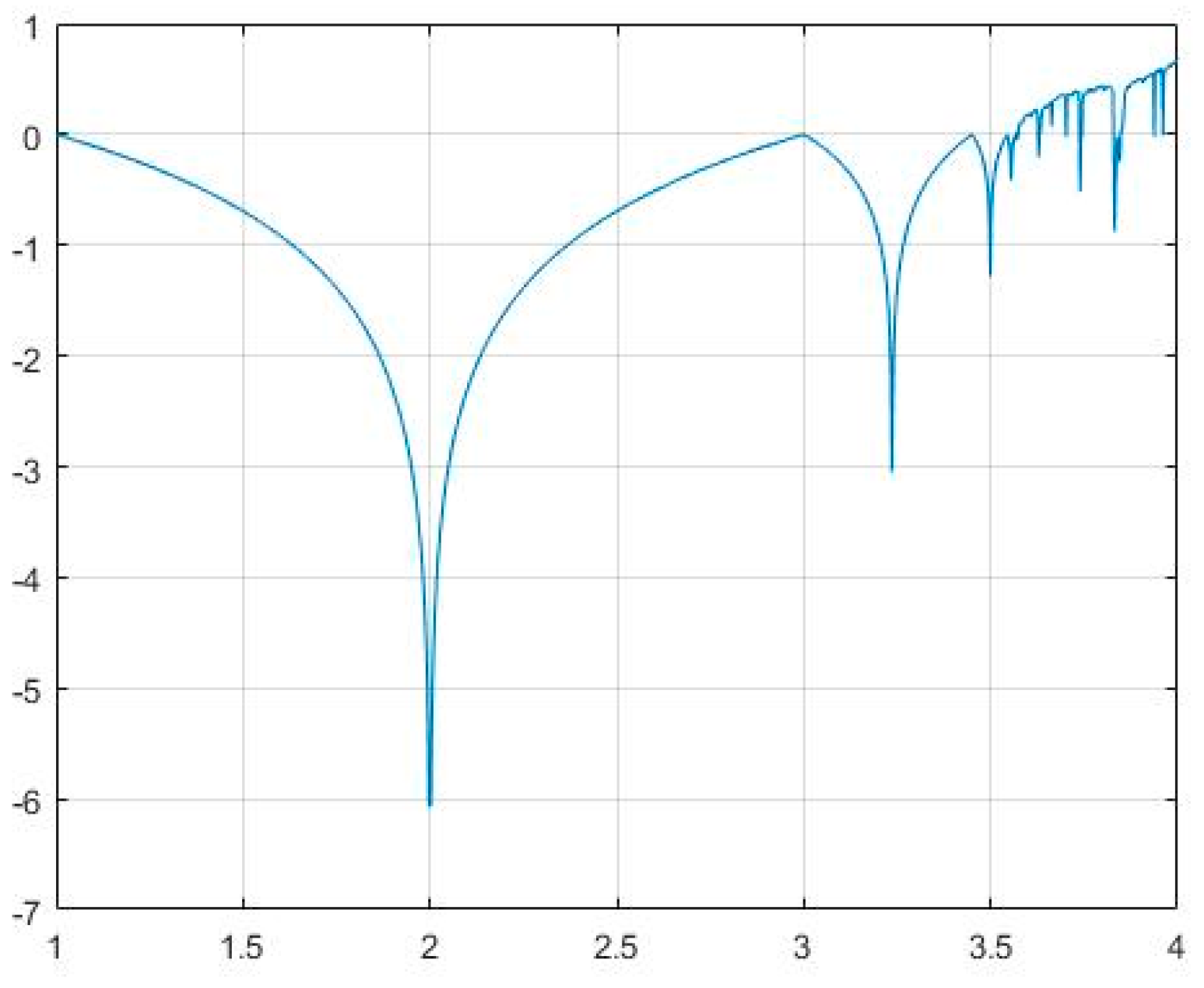
2.2. Skew Tent Map
2.3. Block Scrambling
2.4. Modified Zigzag Transformation
2.5. Enhanced Logistic Map (ELM)
2.6. Key Generation
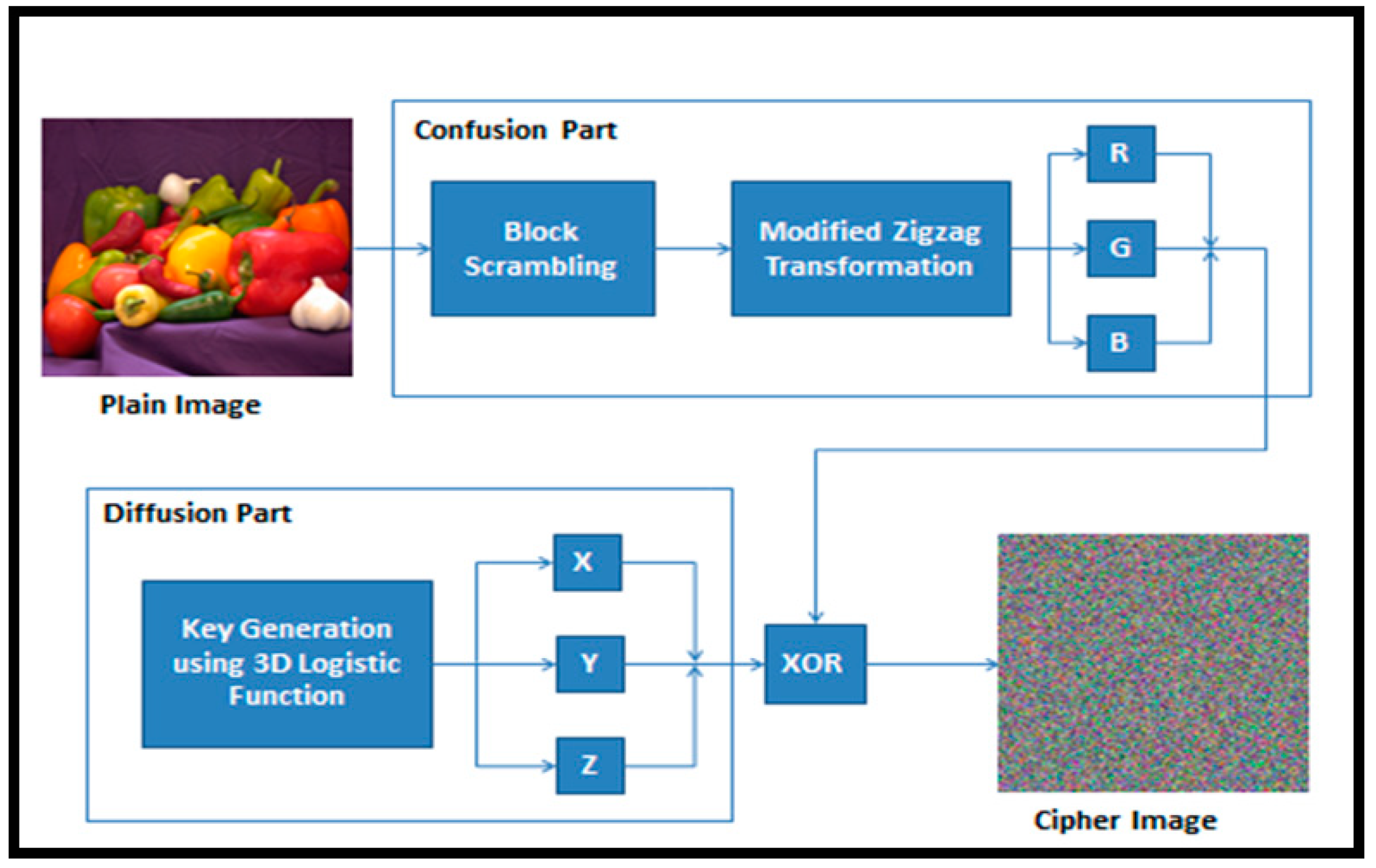
2.7. Encryption Algorithm
| Algorithm 1: Algorithm of the encryption process |
| Input: plain color image of size Output: cipher image Step 1: Block scrambling is applied on , which is split into 64 blocks each of size 32 × 32 represented as . Step 2: Modified zigzag transform (ZT) is performed on the scrambled blocks to obtain . Step 3: is split into RGB channels each of size . Step 4: Using ELM, the intermediate key is generated with initial values are taken as , respectively. Step 5: The final key is generated by applying the chosen values from image and external user as initial condition and parameters. Step 6: The secret key K is EX-OR-ed with the RGB channels received after modified ZT to obtain . |
2.8. Evaluation
2.8.1. Key Space Analysis
2.8.2. Key Sensitivity Analysis
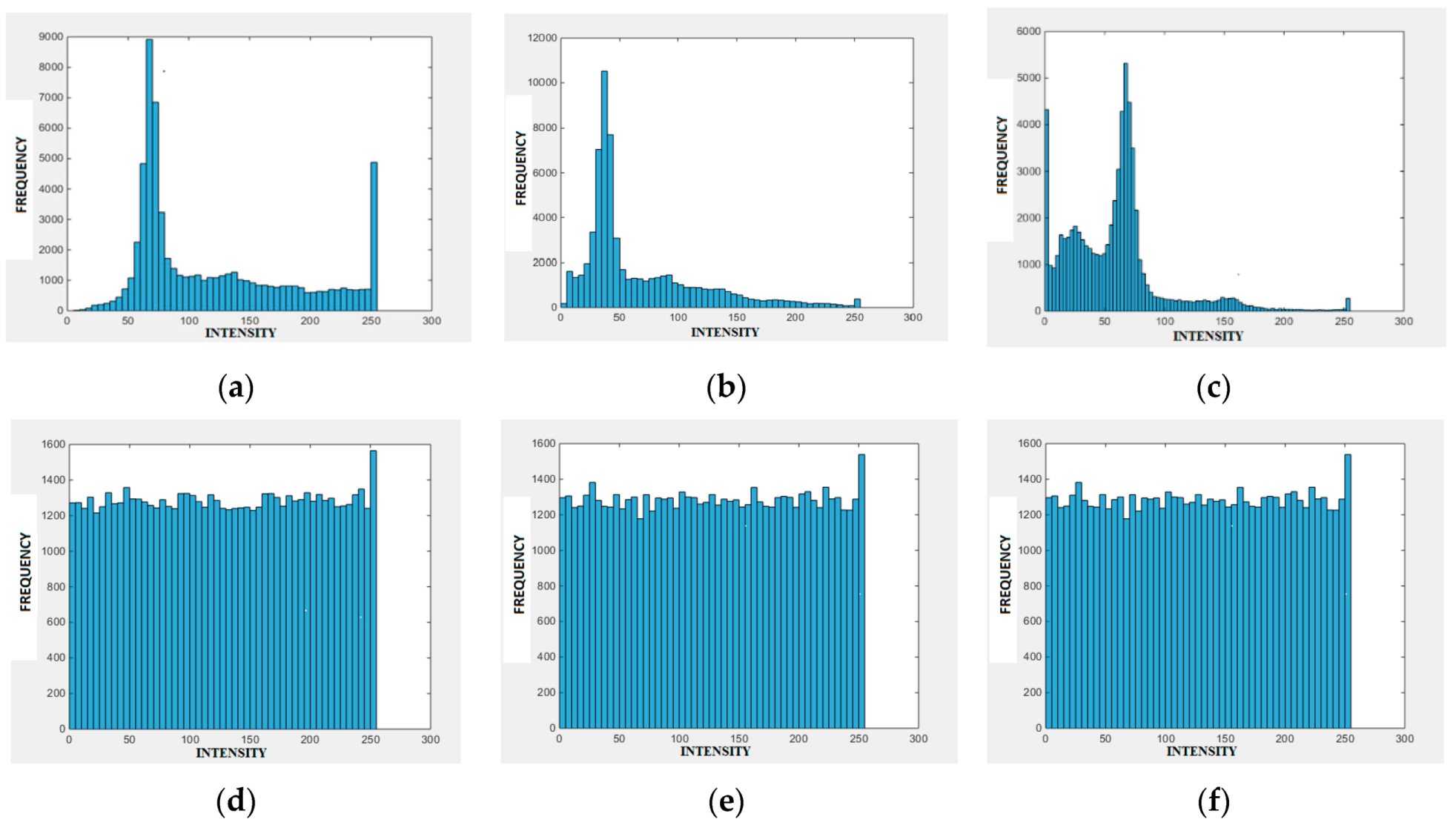
2.8.3. Histogram Analysis
2.8.4. Correlation Coefficient Analysis
2.8.5. NPCR and UACI Analysis
2.8.6. Information Entropy Analysis
2.8.7. PSNR Analysis
3. Results and Analysis
3.1. Settings
3.2. Results
4. Statistical Test Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kadhim, I.J.; Premaratne, P.; Vial, P.J.; Halloran, B. Comprehensive survey of image steganography: Techniques, evaluations, and trends in future research. Neurocomputing 2019, 335, 299–326. [Google Scholar] [CrossRef]
- Qasim, A.F.; Meziane, F.; Aspin, R. Digital watermarking: Applicability for developing trust in medical imaging workflows state of the art review. Comput. Sci. Rev. 2018, 27, 45–60. [Google Scholar] [CrossRef]
- Arul Murugan, C.; KarthigaiKumar, P. Survey on image encryption schemes, bio cryptography and efficient encryption algorithms. Mob. Netw. Appl. 2018, 1–6. [Google Scholar] [CrossRef]
- Kozioł, F.; Borowik, G.; Woźniak, M.; Chaczko, Z. Toward dynamic signal coding for safe communication technology. In Proceedings of the Asia-Pacific Conference on Computer-Aided System Engineering, APCASE, Washington, DC, USA, 14 July 2015; pp. 246–251. [Google Scholar] [CrossRef]
- Khalifa, N.; Filali, R.L.; Benrejeb, M. A Fast Selective Image Encryption Using Discrete Wavelet Transform and Chaotic Systems Synchronization. Inf. Technol. Control. 2016, 45, 235–242. [Google Scholar] [CrossRef]
- Askar, S.S.; Karawia, A.A.; Al-Khedhairi, A.; Al-Ammar, F.S. An Algorithm of Image Encryption Using Logistic and Two-Dimensional Chaotic Economic Maps. Entropy 2019, 21, 44. [Google Scholar] [CrossRef]
- Ballesteros, D.M.; Peña, J.; Renza, D. A Novel Image Encryption Scheme Based on Collatz Conjecture. Entropy 2018, 20, 901. [Google Scholar] [CrossRef]
- Fan, C.; Ding, Q. A Novel Image Encryption Scheme Based on Self-Synchronous Chaotic Stream Cipher and Wavelet Transform. Entropy 2018, 20, 445. [Google Scholar] [CrossRef]
- Hanis, S.; Amutha, R. Double image compression and encryption scheme using logistic mapped convolution and cellular automata. Multimed. Tools Appl. 2018, 77, 6897–6912. [Google Scholar] [CrossRef]
- Huang, L.; Cai, S.; Xiao, M.; Xiong, X. A Simple Chaotic Map-Based Image Encryption System Using Both Plaintext Related Permutation and Diffusion. Entropy 2018, 20, 535. [Google Scholar] [CrossRef]
- Liu, H.; Wen, F.; Kadir, A. Construction of a new 2D chebyshev-sine map and its application to color image encryption. Multimed. Tools Appl. 2019, 78, 15997–16010. [Google Scholar] [CrossRef]
- Huang, X.; Ye, G. An Image Encryption Algorithm Based on Time-Delay and Random Insertion. Entropy 2018, 20, 974. [Google Scholar] [CrossRef]
- Li, S.; Ding, W.; Yin, B.; Zhang, T.; Ma, Y. A Novel Delay Linear Coupling Logistics Map Model for Color Image Encryption. Entropy 2018, 20, 463. [Google Scholar] [CrossRef]
- Li, T.; Shi, J.; Li, X.; Wu, J.; Pan, F. Image Encryption Based on Pixel-Level Diffusion with Dynamic Filtering and DNA-Level Permutation with 3D Latin Cubes. Entropy 2019, 21, 319. [Google Scholar] [CrossRef]
- Liu, X.; Xiao, D.; Liu, C. Double Quantum Image Encryption Based on Arnold Transform and Qubit Random Rotation. Entropy 2018, 20, 867. [Google Scholar] [CrossRef]
- Mondal, B.; Kumar, P.; Singh, S. A chaotic permutation and diffusion based image encryption algorithm for secure communications. Multimed. Tools Appl. 2018, 77, 31177–31198. [Google Scholar] [CrossRef]
- Sreelaja, N.K.; Vijayalakshmi Pai, G.A. Stream cipher for binary image encryption using ant colony optimization based key generation. Appl. Soft Comput. J. 2012, 12, 2879–2895. [Google Scholar] [CrossRef]
- Stoyanov, B.; Kordov, K. Image Encryption Using Chebyshev Map and Rotation Equation. Entropy 2015, 17, 2117–2139. [Google Scholar] [CrossRef]
- Sun, Y.; Chen, L.; Xu, R.; Kong, R. An image encryption algorithm utilizing Julia sets and Hilbert curves. PLoS ONE 2014, 9, e84655. [Google Scholar] [CrossRef]
- Tong, X.; Liu, Y.; Zhang, M.; Xu, H.; Wang, Z. An Image Encryption Scheme Based on Hyper chaotic Rabinovich and Exponential Chaos Maps. Entropy 2015, 17, 181–196. [Google Scholar] [CrossRef]
- Wang, X.; Zhu, X.; Zhang, Y. An image encryption algorithm based on Josephus traversing and mixed chaotic map. IEEE Access 2018, 6, 23733–23746. [Google Scholar] [CrossRef]
- Zhu, H.; Zhao, Y.; Song, Y. 2D logistic-modulated-sine-coupling-logistic chaotic map for image encryption. IEEE Access 2019, 7, 14081–14098. [Google Scholar] [CrossRef]
- Huang, X. Image encryption algorithm using chaotic Chebyshev generator. Nonlinear Dyn. 2012, 67, 2411–2417. [Google Scholar] [CrossRef]
- Ye, G. Image scrambling encryption algorithm of pixel bit based on chaos map. Pattern Recognit. Lett. 2010, 31, 347–354. [Google Scholar] [CrossRef]
- Zhu, C.X. A novel image encryption scheme based on improved hyper-chaotic sequences. Opt. Commun. 2012, 285, 29–37. [Google Scholar] [CrossRef]
- Wang, X.-Y.; Yang, L.; Liu, R.; Kadir, A. A chaotic image encryption algorithm based on perceptron model. Nonlinear Dyn. 2010, 62, 615–621. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiao, D. An image encryption scheme based on rotationmatrix bit-level permutation and block diffusion. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 74–82. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiao, D. Double optical image encryption using discrete Chirikov standard map and chaos-based fractional random transform. Opt. Lasers Eng. 2013, 51, 472–480. [Google Scholar] [CrossRef]
- Li, C.; Luo, G.; Qin, K.; Li, C. An image encryption scheme based on chaotic tent map. Nonlinear Dyn. 2017, 87, 127–133. [Google Scholar] [CrossRef]
- Wu, X.; Zhu, B.; Hu, Y.; Ran, Y. A novel color image encryption scheme using rectangular transform-enhanced chaotic tent maps. IEEE Access 2017, 5, 6429–6436. [Google Scholar]
- Li, C.; Lin, D.; Lü, J. Cryptanalyzing an image-scrambling encryption algorithm of pixel bits. IEEE Multimed. 2017, 24, 64–71. [Google Scholar] [CrossRef]
- Li, C.; Liu, Y.; Xie, T.; Chen, M.Z.Q. Breaking a novel image encryption scheme based on improved hyperchaotic sequences. Nonlinear Dyn. 2013, 73, 2083–2089. [Google Scholar] [CrossRef]
- Guo, J.; Zhang, F. An equivalent key attack on an image cryptosystem. Acta Electron. Sin. 2010, 38, 781–785. [Google Scholar]
- Zhang, Y.-Q.; Wang, X.-Y. A new image encryption algorithm based on non-adjacent coupled map lattices. Appl. Soft. Comput. 2015, 26, 10–20. [Google Scholar] [CrossRef]
- Sam, I.S.; Devaraj, P.; Bhuvaneswaran, R.S. An intertwining chaotic maps based image encryption scheme. Nonlinear Dyn. 2012, 69, 1995–2007. [Google Scholar]
- Wang, X.; Luan, D.; Bao, X. Cryptanalysis of an image encryption algorithm using Chebyshev generator. Digit. Signal Process. 2014, 25, 244–247. [Google Scholar] [CrossRef]
- Wang, X.; Teng, L.; Qin, X. A novel colour image encryption algorithm based on chaos. Signal Process. 2012, 92, 1101–1108. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, Z.; Fu, C.; Zhang, L.; Zhang, Y. An efficient image encryption scheme using lookup table-based confusion and diffusion. Nonlinear Dyn. 2015, 81, 1151–1166. [Google Scholar] [CrossRef]
- Liu, R. New binary image encryption algorithm based on combination of confusion and diffusion. J. Chem. Pharm. Res. 2014, 6, 621–629. [Google Scholar]
- Murugan, B.; Nanjappa Gounder, A.G. Image encryption scheme based on block-based confusion and multiple levels of diffusion. IET Comput. Vis. 2016, 10, 593–602. [Google Scholar] [CrossRef]
- Praveenkumar, P.; Amirtharajan, R.; Thenmozhi, K.; Rayappan, J.B.B. Fusion of confusion and diffusion: A novel image encryption approach. Telecommun. Syst. 2017, 65, 65–78. [Google Scholar] [CrossRef]
- Sinha, R.K.; Sahu, S.S. Secure image encryption based on improved bat optimized piecewise linear chaotic map through integrated permutation-confusion and double diffusion. J. Intell. Fuzzy Syst. 2018, 35, 1567–1578. [Google Scholar] [CrossRef]
- Zhang, W.; Wong, K.; Yu, H.; Zhu, Z. An image encryption scheme using lightweight bit-level confusion and cascade cross circular diffusion. Opt. Commun. 2012, 285, 2343–2354. [Google Scholar] [CrossRef]
- Murillo-Escobar, M.A.; Cruz-Hernández, C.; Cardoza-Avendaño, L.; Méndez-Ramírez, R. A novel pseudorandom number generator based on pseudorandomly enhanced logistic map. Nonlinear Dyn. 2017, 87, 407–425. [Google Scholar] [CrossRef]
- Zhou, Y.; Bao, L.; Chen, C.P. A new 1D chaotic system for image encryption. Signal Process. 2014, 97, 172–182. [Google Scholar] [CrossRef]
- Arroyo, D.; Alvarez, G.; Fernandez, V. On the inadequacy of the logistic map for cryptographic applications. arXiv 2008, arXiv:0805.4355. [Google Scholar]
- Naseer, Y.; Shah, D.; Shah, T. A Novel Approach to improve multimedia security utilizing 3D Mixed Chaotic map. Microprocess. Microsyst. 2019, 65, 1–6. [Google Scholar] [CrossRef]
- Ye, G.; Huang, X. An efficient symmetric image encryption algorithm based on an intertwining logistic map. Neurocomputing 2017, 251, 45–53. [Google Scholar] [CrossRef]
- Kumar, M.; Kumar, S.; Budhiraja, R.; Das, M.K.; Singh, S. Intertwining logistic map and Cellular Automata based color image encryption model. In Proceedings of the International Conference on Computational Techniques in Information and Communication Technologies (ICCTICT), New Delhi, India, 13 March 2016; pp. 618–623. [Google Scholar]
- Li, Y.; Li, X.; Jin, X.; Zhao, G.; Ge, S.; Tian, Y.; Wang, Z. An Image Encryption Algorithm Based on Zigzag Transformation and 3-Dimension Chaotic Logistic Map. In Applications and Techniques in Information Security; Springer: Berlin/Heidelberg, Germany, 2015; pp. 3–13. [Google Scholar]
- Pareek, N.K.; Patidar, V.; Sud, K.K. Image encryption using chaotic logistic map. Image Vis. Comput. 2006, 24, 926–934. [Google Scholar] [CrossRef]
- Khade, P.N.; Narnaware, M. 3D chaotic functions for image encryption. Int. J. Comput. Sci. Issues 2012, 9, 323–328. [Google Scholar]
- Kadir, A.; Hamdulla, A.; Guo, W.Q. Color image encryption using skew tent map and hyper chaotic system of 6th-order CNN. Opt.-Int. J. Light Electron Opt. 2014, 125, 1671–1675. [Google Scholar] [CrossRef]
- Xu, X.; Feng, J. Research and Implementation of Image Encryption Algorithm Based on Zigzag Transformation and Inner Product Polarization Vector. In Proceedings of the 2010 IEEE International Conference on Granular Computing, San Jose, CA, USA, 16 August 2010; pp. 556–561. [Google Scholar] [CrossRef]
- Ahmad, J.; Larijani, H.; Emmanuel, R.; Mannion, M. Secure Occupancy Monitoring System for IoT Using Lightweight Intertwining Logistic Map. In Proceedings of the 2018 10th Computer Science and Electronic Engineering (CEEC), Essex, UK, 19 September 2018; pp. 208–213. [Google Scholar]
- Ahmad, J.; Hwang, S.O. A secure image encryption scheme based on chaotic maps and affine transformation. Multimed. Tools Appl. 2016, 75, 13951–13976. [Google Scholar] [CrossRef]
- Wu, Y.; Noonan, J.P.; Agaian, S. NPCR and UACI randomness tests for image encryption. J. Sel. Areas Telecommun. 2011, 1, 31–38. [Google Scholar]
- Xu, L.; Li, Z.; Li, J.; Hua, W. A novel bit-level image encryption algorithm based on chaotic maps. Opt. Lasers Eng. 2016, 78, 17–25. [Google Scholar] [CrossRef]
- Wang, X.Y.; Zhang, Y.Q.; Bao, X.M. A novel chaotic image encryption scheme using DNA sequence operations. Opt. Lasers Eng. 2015, 73, 53–61. [Google Scholar] [CrossRef]
- Liu, H.J.; Wang, X.Y. Color image encryption based on one-time keys and robust chaotic maps. Comput. Math. Appl. 2010, 59, 3320–3327. [Google Scholar] [CrossRef]
- Hussain, I.; Shah, T.; Gondal, M.A. Image encryption algorithm based on PGL (2, GF (28)) S-boxes and TD-ERCS chaotic sequence. Nonlinear Dyn. 2012, 70, 181–187. [Google Scholar] [CrossRef]
- Wang., X.Y.; Zhang, H.L. A color image encryption with heterogeneous bit-permutation and correlated chaos. Opt. Commun. 2015, 342, 51–60. [Google Scholar] [CrossRef]
- Askar, S.S.; Karawia, A.A.; Alammar, F.S. Cryptographic algorithm based on pixel shuffling and dynamical chaotic economic map. IET Image Process. 2018, 12, 158–167. [Google Scholar] [CrossRef]
- Tang, Z.; Song, J.; Zhang, X.; Sun, R. Multiple-image encryption with bit-plane decomposition and chaotic maps. Opt. Lasers Eng. 2016, 80, 1–11. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, X. Multiple-image encryption algorithm based on mixed image element and chaos. Comput. Electr. Eng. 2017, 62, 401–413. [Google Scholar] [CrossRef]
- Karawia, A. Encryption algorithm of multiple-image using mixed image elements and two dimensional chaotic economic map. Entropy 2018, 20, 801. [Google Scholar] [CrossRef]
- Rukhin, A.L.; Soto, J.; Nechvatal, J.; Smid, M.; Barker, E.; Leigh, S.; Levenson, M.; Vangel, M.; Banks, D.; Heckert, A.; et al. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Application; NIST Special Publication 800-22; Revision 1a (Revised: April 2010); Lawrence, E.B., III, Ed.; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2010. Available online: https://www.nist.gov/publications/statistical-test-suite-random-and-pseudorandom-number-generators-cryptographic (accessed on 2 July 2019).




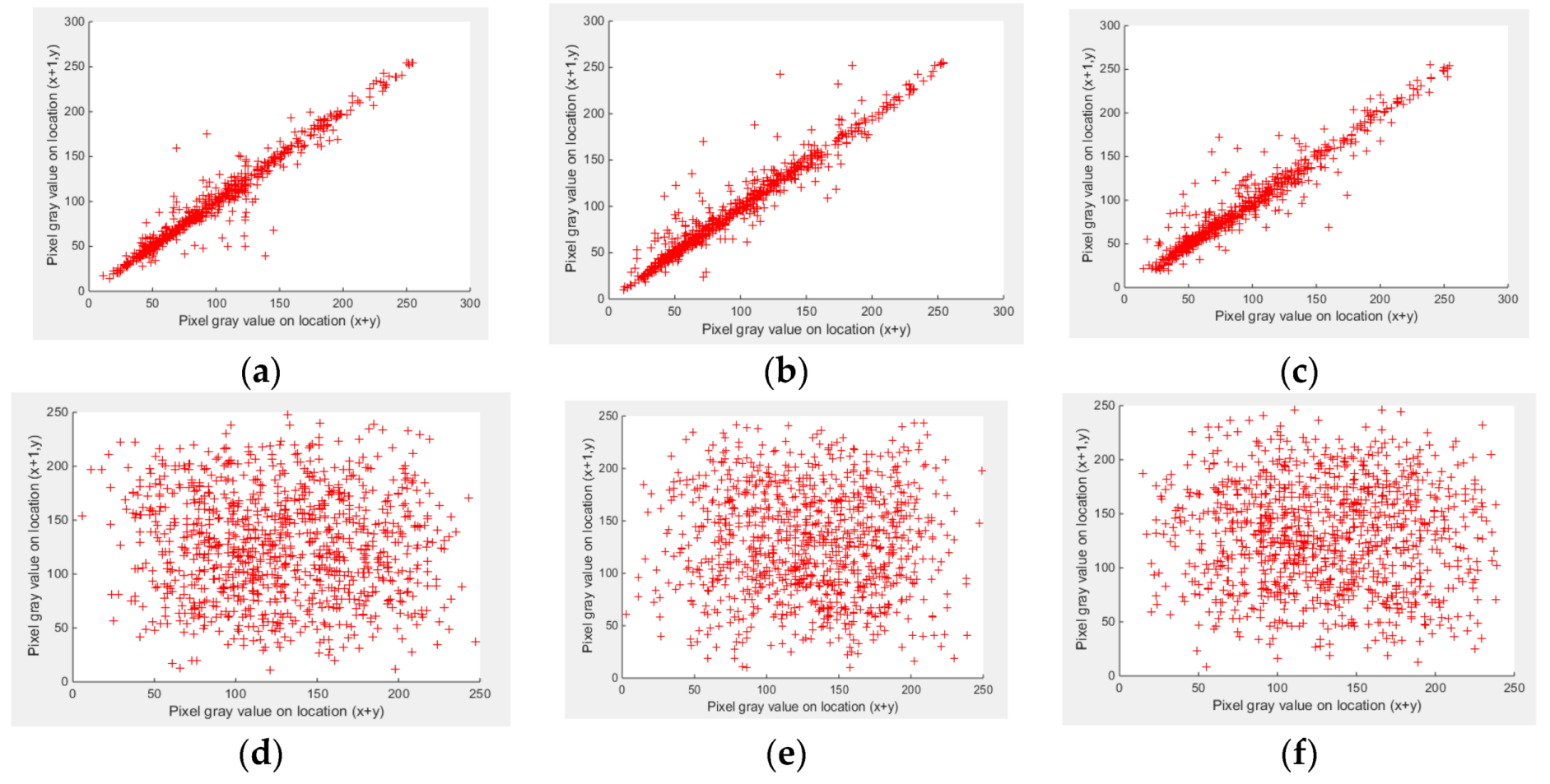


| Images | Horizontal | Vertical | Diagonal | |||
|---|---|---|---|---|---|---|
| Plain | Cipher | Plain | Cipher | Plain | Cipher | |
| Lena | 0.9505 | −0.0237 | 0.9745 | −0.0237 | 0.9668 | −0.0284 |
| Peppers | 0.9789 | −0.0727 | 0.9750 | −0.0225 | 0.9711 | −0.0242 |
| Barbara | 0.9444 | −0.0298 | 0.9555 | −0.0611 | 0.9225 | −0.0294 |
| Baboon | 0.9618 | −0.0261 | 0.9686 | −0.0572 | 0.9475 | −0.0356 |
| Images | NPCR (%) | UACI (%) | PSNR | Entropy Plain Image Cipher Image | |
|---|---|---|---|---|---|
| Baboon | 99.6017 | 33.2039 | 11.8337 | 7.2730 | 7.9993 |
| Barbara | 99.6073 | 33.5692 | 8.6936 | 7.6320 | 7.9990 |
| Lena | 99.6221 | 33.5887 | 6.7494 | 7.7329 | 7.9994 |
| Peppers | 99.5987 | 33.9060 | 9.8369 | 7.3785 | 7.9992 |
| Measure | [50] | [56] | [27] | [58] | [59] | [60] | [61] | [62] | Proposed |
|---|---|---|---|---|---|---|---|---|---|
| Horizontal correlation | 0.0327 | 0.9407 | 0.0018 | −0.0230 | 0.0020 | 0.0965 | −0.0067 | −0.0098 | −0.0237 |
| Vertical correlation | 0.0219 | −0.0273 | 0.0011 | 0.0019 | −0.0007 | −0.0318 | −0.0137 | −0.0050 | −0.0178 |
| Diagonal correlation | 0.0180 | −0.0140 | −0.0012 | −0.0034 | −0.0014 | 0.0362 | −0.0563 | −0.0013 | −0.0284 |
| Entropy | 7.9993 | n/a | 7.9994 | 7.9974 | 7.9970 | n/a | n/a | 7.9974 | 7.9995 |
| UACI | n/a | 15.38 | 33.4365 | 3.5100 | 27.97 | n/a | 33.4647 | 32.48 | 33.5887 |
| NPCR | n/a | 99.10 | 99.6166 | 99.6200 | 98.36 | n/a | 98.6810 | 93.21 | 99.6221 |
| Sample Images | Gaussian Mean = 0 & Variance = 0.001 | Salt & Pepper Density = 0.05 | ||
|---|---|---|---|---|
| MSE | PSNR | MSE | PSNR | |
| Baboon | 0.2698 | 53.8199 | 0.1711 | 58.7987 |
| Plane | 0.2711 | 53.7987 | 0.0793 | 59.1405 |
| Lena | 0.2013 | 54.1722 | 0.1022 | 58.0382 |
| Peppers | 0.2368 | 54.3872 | 0.0995 | 58.3375 |
| NIST Test | p-Value | Pass Rate |
|---|---|---|
| Frequency (monobit) | 0.576884 | 995/1000 |
| Block-frequency | 0.783572 | 996/1000 |
| Cumulative sums (Forward) | 0.541882 | 996/1000 |
| Cumulative sums (Reverse) | 0.914691 | 993/1000 |
| Runs | 0.843905 | 984/1000 |
| Longest run of Ones | 0.062147 | 986/1000 |
| Rank | 0.400721 | 991/1000 |
| FFT | 0.186524 | 993/1000 |
| Non-overlapping templates | 0.497492 | 993/1000 |
| Overlapping templates | 0.230513 | 990/1000 |
| Universal | 0.087607 | 986/1000 |
| Approximate entropy | 0.198766 | 994/1000 |
| Random-excursions | 0.689012 | 615/621 |
| Random-excursions Variant | 0.397213 | 618/621 |
| Serial 1 | 0.893692 | 992/1000 |
| Serial 2 | 0.699795 | 993/1000 |
| Linear complexity | 0.344217 | 992/1000 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramasamy, P.; Ranganathan, V.; Kadry, S.; Damaševičius, R.; Blažauskas, T. An Image Encryption Scheme Based on Block Scrambling, Modified Zigzag Transformation and Key Generation Using Enhanced Logistic—Tent Map. Entropy 2019, 21, 656. https://doi.org/10.3390/e21070656
Ramasamy P, Ranganathan V, Kadry S, Damaševičius R, Blažauskas T. An Image Encryption Scheme Based on Block Scrambling, Modified Zigzag Transformation and Key Generation Using Enhanced Logistic—Tent Map. Entropy. 2019; 21(7):656. https://doi.org/10.3390/e21070656
Chicago/Turabian StyleRamasamy, Priya, Vidhyapriya Ranganathan, Seifedine Kadry, Robertas Damaševičius, and Tomas Blažauskas. 2019. "An Image Encryption Scheme Based on Block Scrambling, Modified Zigzag Transformation and Key Generation Using Enhanced Logistic—Tent Map" Entropy 21, no. 7: 656. https://doi.org/10.3390/e21070656
APA StyleRamasamy, P., Ranganathan, V., Kadry, S., Damaševičius, R., & Blažauskas, T. (2019). An Image Encryption Scheme Based on Block Scrambling, Modified Zigzag Transformation and Key Generation Using Enhanced Logistic—Tent Map. Entropy, 21(7), 656. https://doi.org/10.3390/e21070656







