Multiobjective Optimization of a Plate Heat Exchanger in a Waste Heat Recovery Organic Rankine Cycle System for Natural Gas Engines
Abstract
:1. Introduction
2. Description and Model of the System
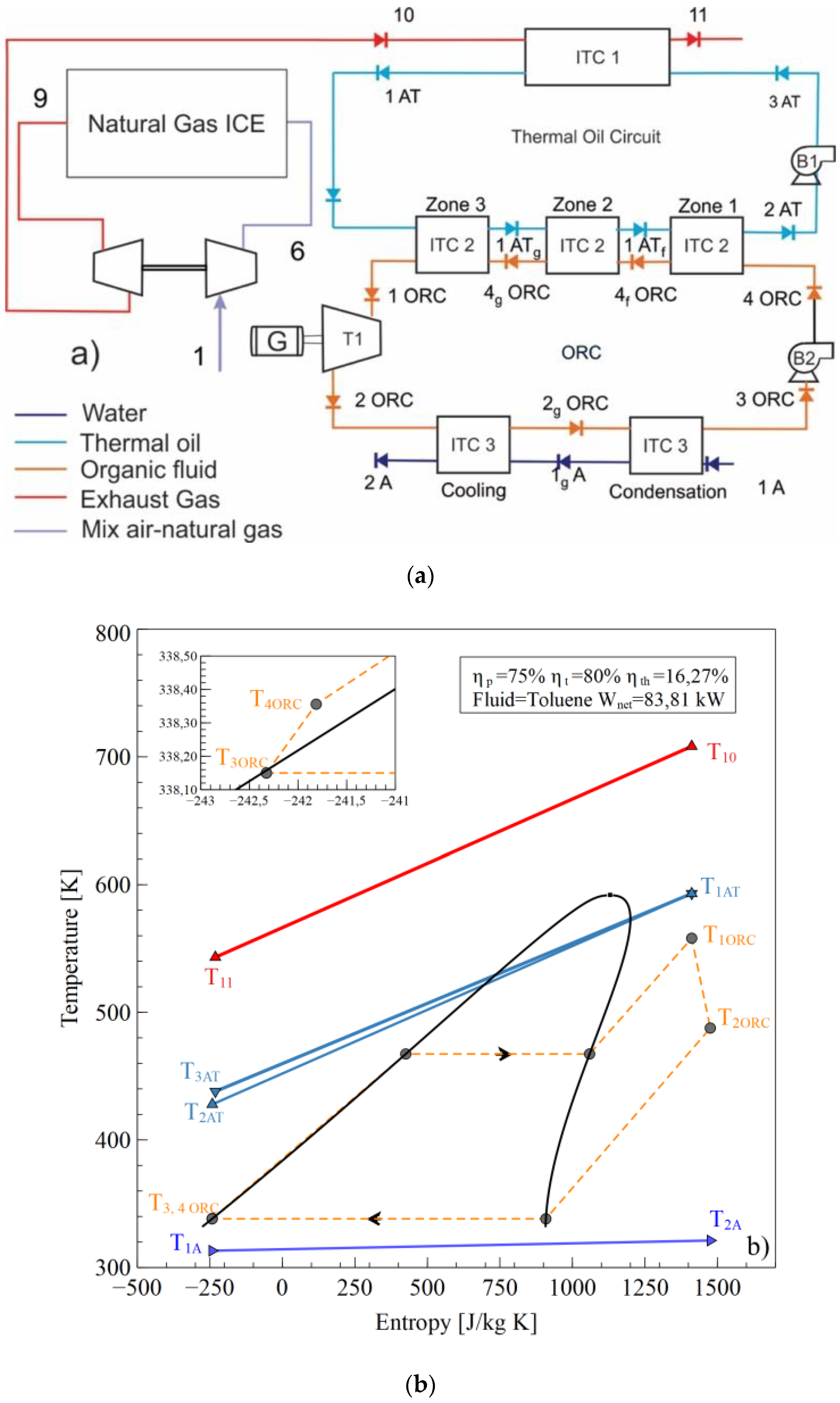
2.1. Description of The Waste Heat Recovery System
2.2. Energy Analysis
2.3. Exergy Analysis
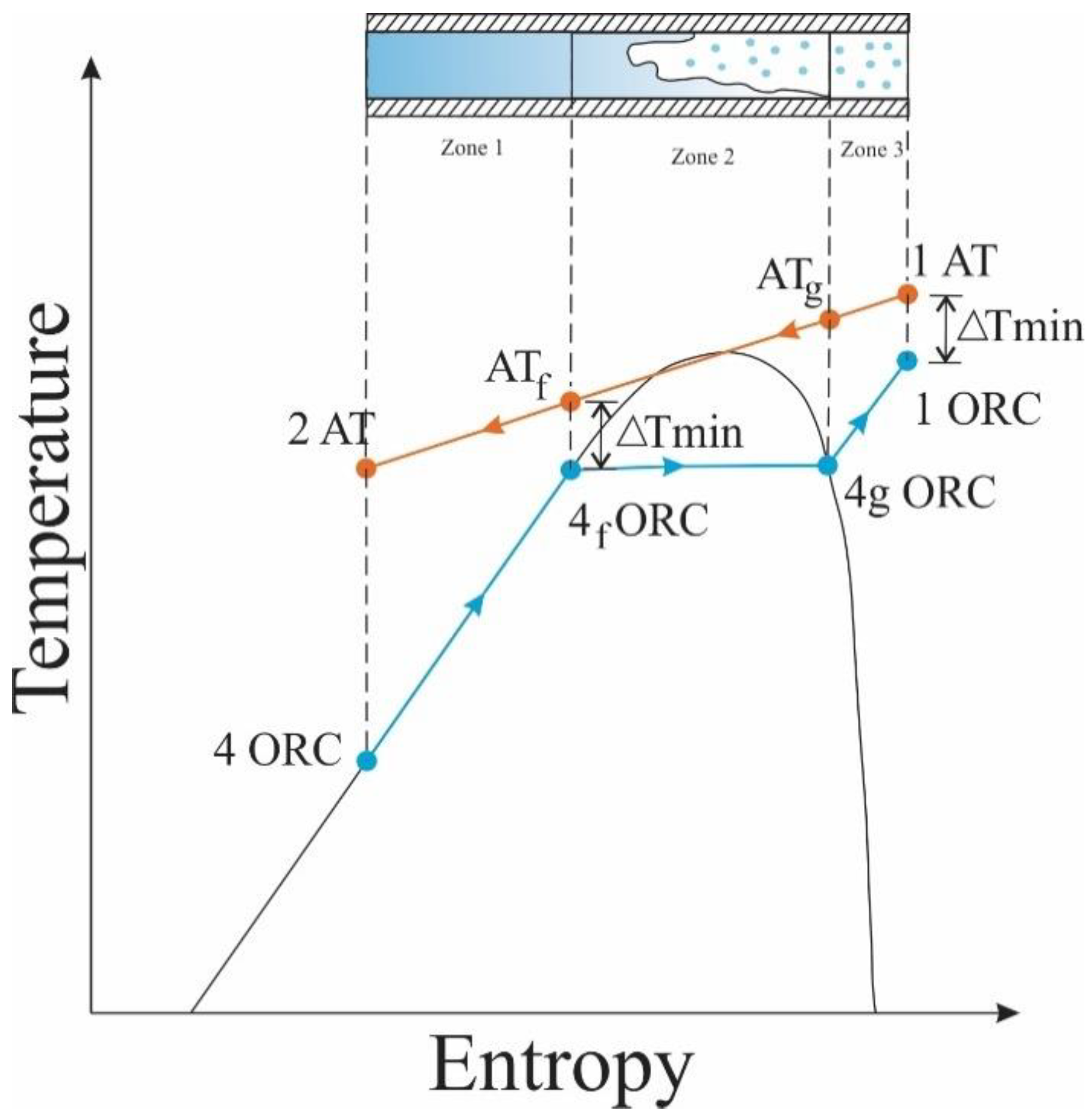
2.4. Modeling of The Plate Heat Exchanger
3. Multi-Objective Optimization
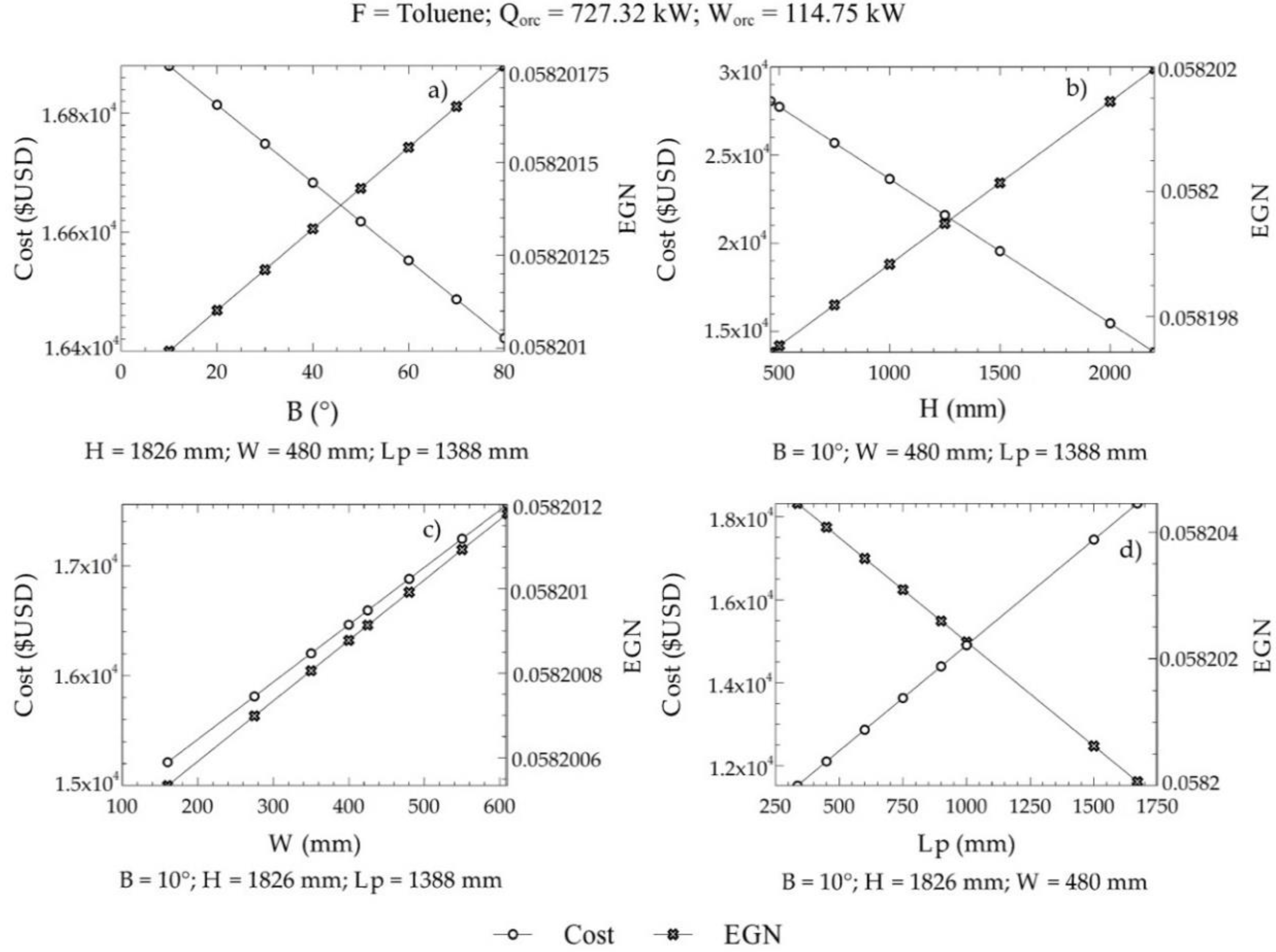
3.1. Methodology of Design
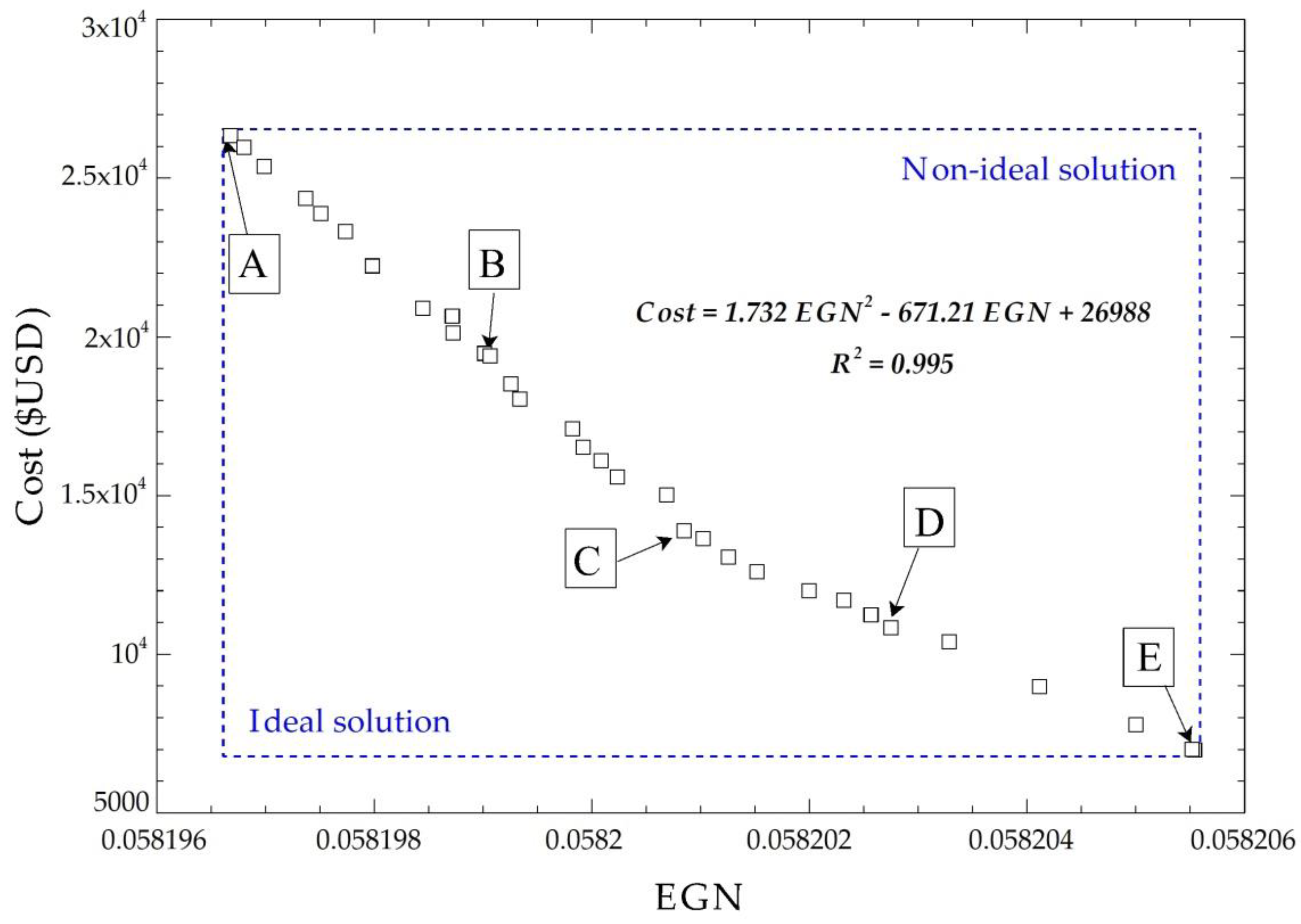
3.2. Multi-Criteria Decision
4. Results and Discussion
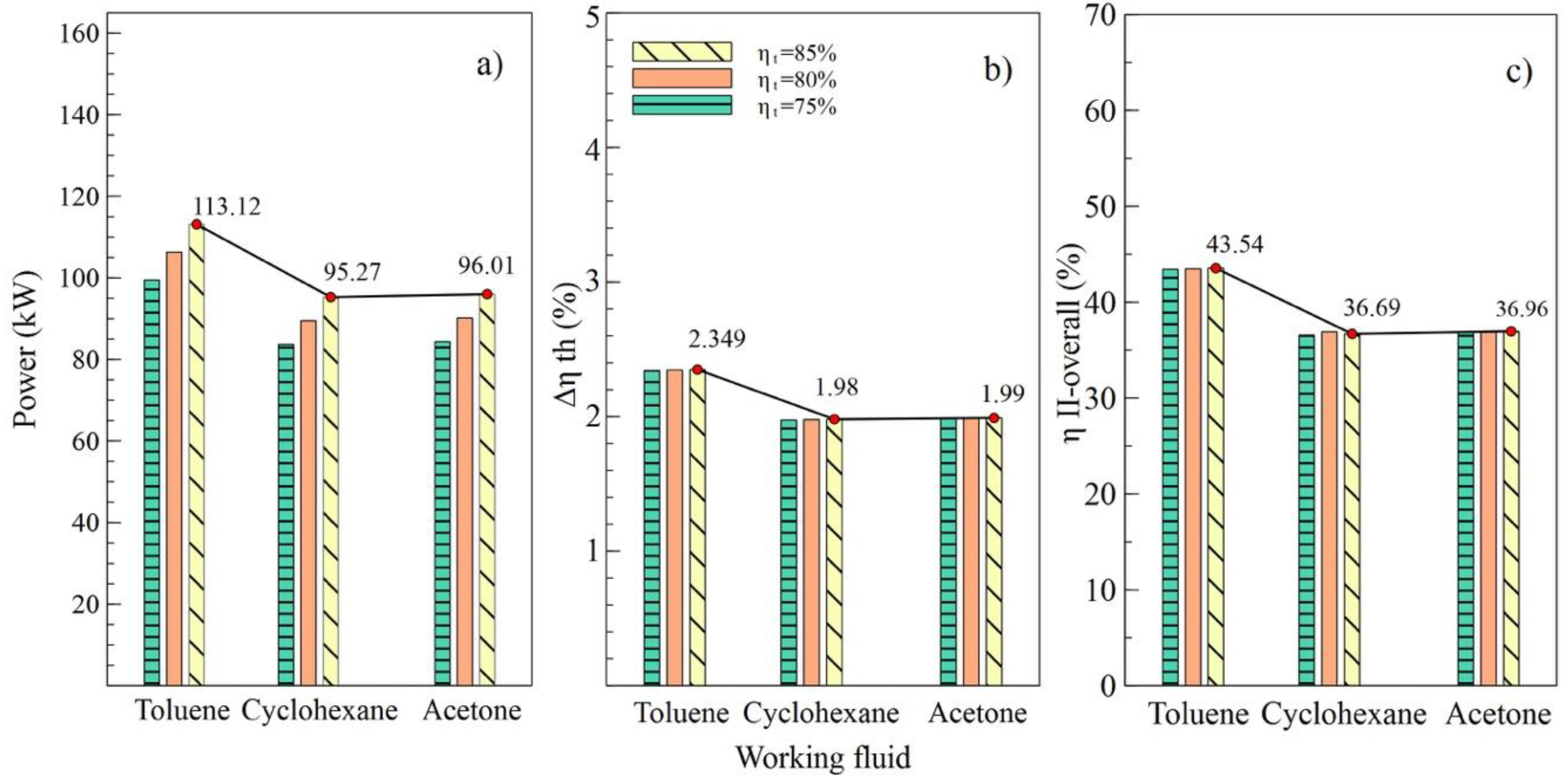
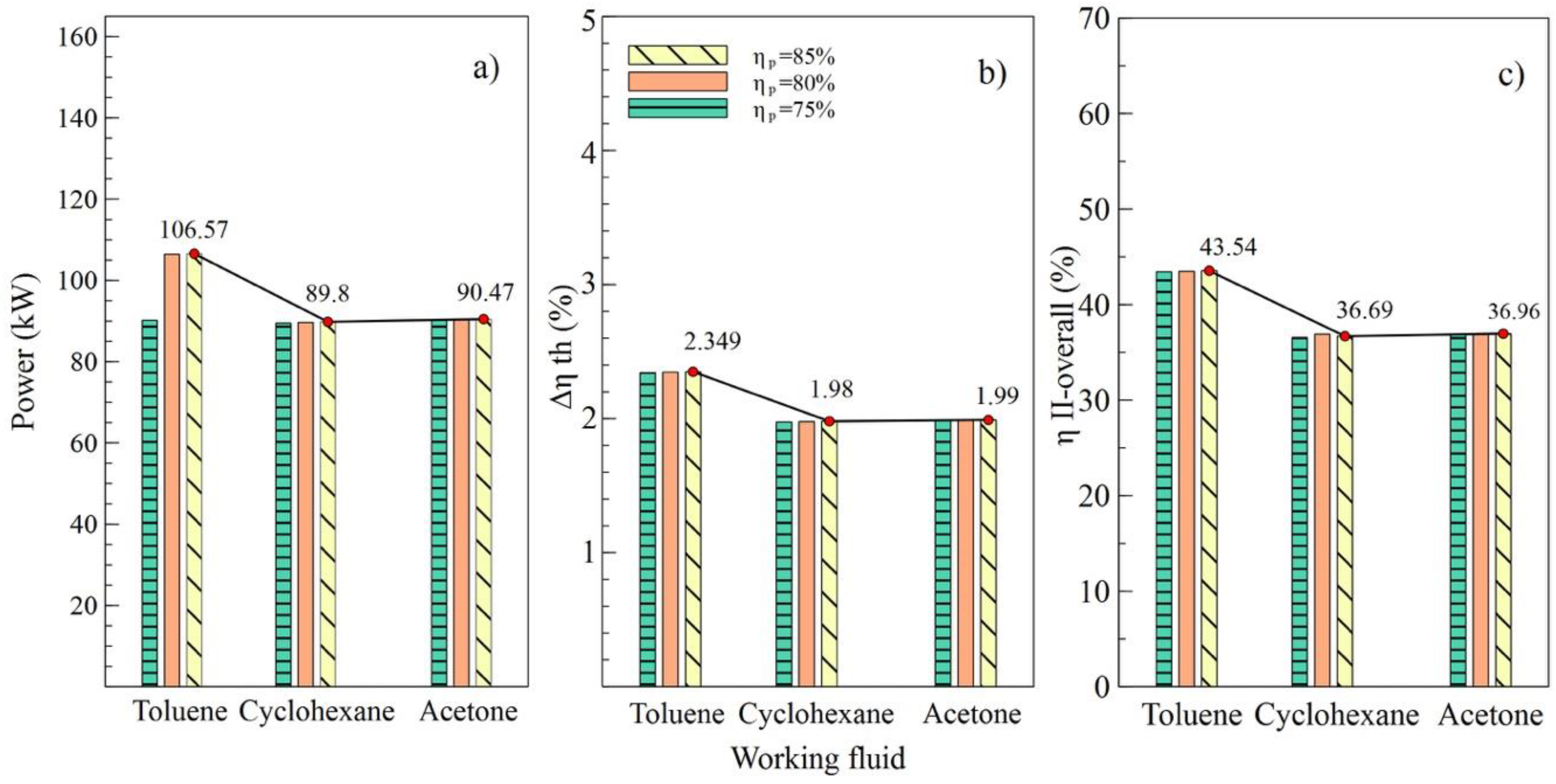
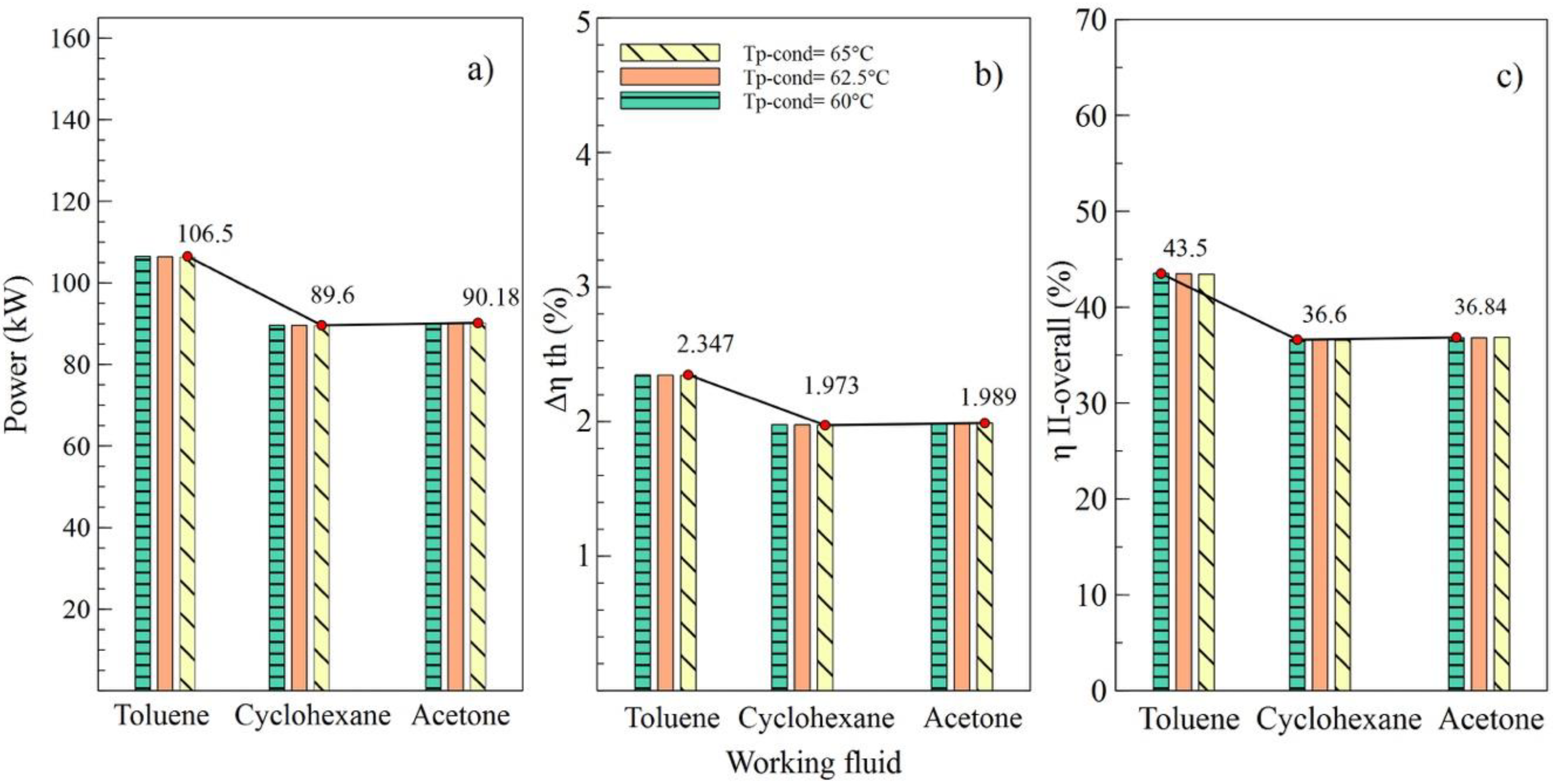
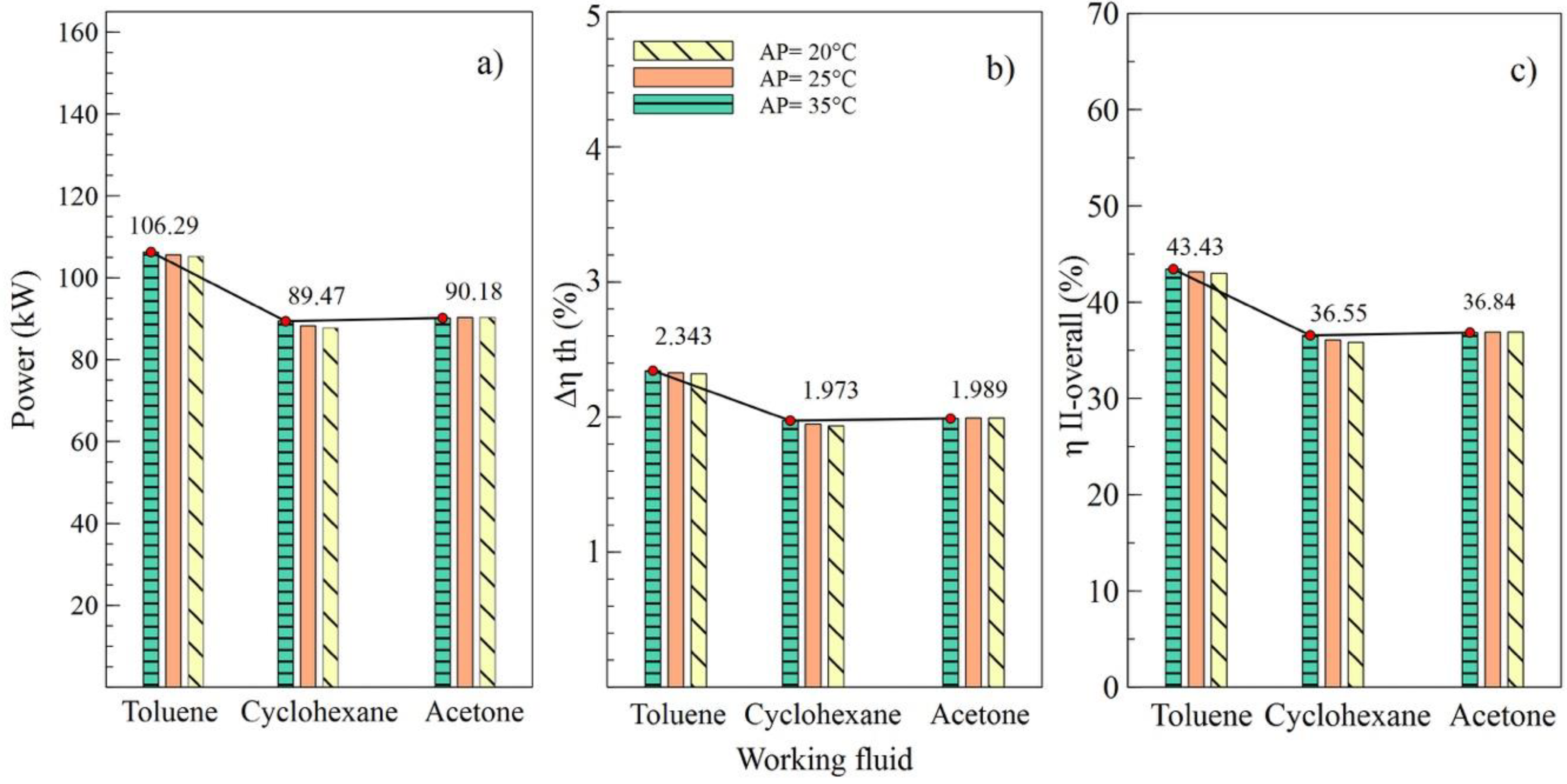
4.1. Working Fluid Selection
4.2. Parametric Study
4.3. Results of The Optimization
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| BSFC | Brake-Specific Fuel Consumption |
| EGN | Entropy Generation Number |
| ICE | Internal Combustion Engine |
| LMTD | Logarithmic Media Temperature Difference |
| ORC | Organic Rankine Cycle |
| WHR | Waste heat recovery |
| Nomenclature | |
| A | Area (m2) |
| Plate area (m2) | |
| Heat transfer area zone 1 (m2) | |
| Cp | Specific heat at constant pressure |
| D | Diameter (m) |
| Destroyed exergy (kW) | |
| E | Energy (J) |
| ex | Specific exergy (kJ/kg) |
| Chemical exergy of exhaust gases (kJ/kg) | |
| H | Plate height (mm) |
| Specific enthalpy | |
| jf | Heat transfer Colburn factor |
| K | Thermal conductivity (W/m·K) |
| L | Length (mm) |
| LHV | Lower heating value (kJ/kg) |
| Lp | Length between plates (mm) |
| m | Mass (kg) |
| Mass flow (kg/s) | |
| Number of plates | |
| Nu | Nusselt number |
| Pinch | Minimum temperature difference (°C) |
| Pr | Prandtl number |
| Heat transfer flow (kW) | |
| R | Universal gas constant |
| Re | Reynolds number |
| S | Entropy (kJ/K) |
| Generated entropy (kW) | |
| T | Temperature (K) |
| U | Overall heat transfer coefficient (W/m2K) |
| v | Velocity (m/s) |
| W | Plate width (mm) |
| ORC Power (mbar) | |
| Pressure drop on the tube side (mbar) | |
| Pressure drop on the shell side (mbar) | |
| Inlet pressure drop (mbar) | |
| Flow pressure drop (mbar) | |
| Molar gas fraction | |
| Greek Symbol | |
| Angle of inclination | |
| Density (kg/m3) | |
| Heat recovery efficiency | |
| Thermal efficiency of the cycle | |
| Absolute increase in thermal efficiency | |
| Overall energy conversion efficiency | |
| Overall exergetic efficiency | |
| Exergetic efficiency based on the second law of thermodynamics | |
| Kinematic viscosity (m2/s) | |
| Subscript | |
| 0 | Reference |
| AT | Thermal oil |
| EXT | External |
| G | Exhaust gases |
| TOT | Total |
| Z1 | Preheating zone in ITC2 |
| Z2 | Evaporation zone in ITC2 |
| Z3 | Overheating zone in ITC2 |
References
- Fadiran, G.; Adebusuyi, A.T.; Fadiran, D. Natural gas consumption, and economic growth: Evidence from selected natural gas vehicle markets in Europe. Energy 2019, 169, 467–477. [Google Scholar] [CrossRef]
- Feijoo, F.; Iyer, G.C.; Avraam, C.; Siddiqui, S.A.; Clarke, L.E.; Sankaranarayanan, S.; Binsted, M.T.; Patel, P.L.; Prates, N.C.; Torres-Alfaro, E.; et al. The future of natural gas infrastructure development in the United states. Appl. Energy 2018, 228, 149–166. [Google Scholar] [CrossRef]
- Wang, X.; Shu, G.; Tian, H.; Liu, P.; Jing, D.; Li, X. Dynamic analysis of the dual-loop organic rankine cycle for waste heat recovery of a natural gas engine. Energy Convers. Manag. 2017, 148, 724–736. [Google Scholar] [CrossRef]
- Nami, H.; Ertesvåg, I.S.; Agromayor, R.; Riboldi, L.; Nord, L.O. Gas turbine exhaust gas heat recovery by organic rankine cycles (ORC) for offshore combined heat and power applications—Energy and exergy analysis. Energy 2018, 165, 1060–1071. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; University of Michigan Press: Ann Arbor, MI, USA, 1975; ISBN 9780472084609. [Google Scholar]
- De Jong, K. An Analysis of the Behavior of a Class of Genetic Adaptive Systems; University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Martin, H. Economic optimization of compact heat exchangers. In Proceedings of the EF-Conference on Compact Heat Exchangers and Enhancement Technology for the Process Industries, Banff, AB, Canada, 18–23 July 1999; pp. 1–6. [Google Scholar]
- Reneaume, J.-M.; Niclout, N. MINLP optimization of Plate Fin Heat Exchangers. Chem. Biochem. Eng. Q. 2003, 17, 65–76. [Google Scholar]
- Selbaş, R.; Kızılkan, Ö.; Reppich, M. A new design approach for shell-and-tube heat exchangers using genetic algorithms from economic point of view. Chem. Eng. Process. Process Intensif. 2006, 45, 268–275. [Google Scholar] [CrossRef]
- Muralikrishna, K.; Shenoy, U.V. Heat exchanger design targets for minimum area and cost. Chem. Eng. Res. Des. 2000, 78, 161–167. [Google Scholar] [CrossRef]
- Ozkol, I.; Komurgoz, G. Determination of the optimum geometry of the heat exchanger body via a genetic algorithm. Numer. Heat Transf. Part A Appl. 2005, 48, 283–296. [Google Scholar] [CrossRef]
- Jarzebski, A.B.; Wardas-Koziel, E. Dimensioning of plate heat exchangers to give minimum annual operating costs. Chem. Eng. Res. Des. 1985, 63, 211–218. [Google Scholar]
- Zhu, J.; Zhang, W. Optimization design of plate heat exchangers (PHE) for geothermal district heating systems. Geothermics 2004, 33, 337–347. [Google Scholar] [CrossRef]
- Ahmadi, P.; Dincer, I.; Rosen, M.A. Thermodynamic modeling and multi-objective evolutionary-based optimization of a new multigeneration energy system. Energy Convers. Manag. 2013, 76, 282–300. [Google Scholar] [CrossRef]
- Ahmadi, P.; Dincer, I.; Rosen, M.A. Thermoeconomic multi-objective optimization of a novel biomass-based integrated energy system. Energy 2014, 68, 958–970. [Google Scholar] [CrossRef]
- Wang, J.; Wang, M.; Li, M.; Xia, J.; Dai, Y. Multi-objective optimization design of condenser in an organic Rankine cycle for low grade waste heat recovery using evolutionary algorithm. Int. Commun. Heat Mass Transf. 2013, 45, 47–54. [Google Scholar] [CrossRef]
- Aneke, M.; Agnew, B.; Underwood, C. Optimising thermal energy recovery, utilisation, and management in the process industries. Appl. Therm. Eng. 2012, 36, 171–180. [Google Scholar] [CrossRef]
- Valencia, G.; Fontalvo, A.; Cárdenas, Y.; Duarte, J.; Isaza, C. Energy and exergy analysis of different exhaust waste heat recovery systems for natural gas engine based on ORC. Energies 2019, 12, 2378. [Google Scholar] [CrossRef]
- Hou, G.; Bi, S.; Lin, M.; Zhang, J.; Xu, J. Minimum variance control of organic rankine cycle based waste heat recovery. Energy Convers. Manag. 2014, 86, 576–586. [Google Scholar] [CrossRef]
- Le, V.L.; Kheiri, A.; Feidt, M.; Pelloux-Prayer, S. Thermodynamic and economic optimizations of a waste heat to power plant driven by a subcritical ORC (Organic Rankine Cycle) using pure or zeotropic working fluid. Energy 2014, 78, 622–638. [Google Scholar] [CrossRef]
- Peris, B.; Navarro-Esbrí, J.; Molés, F. Bottoming organic rankine cycle configurations to increase internal combustion engines power output from cooling water waste heat recovery. Appl. Therm. Eng. 2013, 61, 364–371. [Google Scholar] [CrossRef]
- Xi, H.; Li, M.-J.; Xu, C.; He, Y.-L. Parametric optimization of regenerative organic rankine cycle (ORC) for low grade waste heat recovery using genetic algorithm. Energy 2013, 58, 473–482. [Google Scholar] [CrossRef]
- Quoilin, S.; Aumann, R.; Grill, A.; Schuster, A.; Lemort, V.; Spliethoff, H. Dynamic modeling and optimal control strategy of waste heat recovery organic rankine cycles. Appl. Energy 2011, 88, 2183–2190. [Google Scholar] [CrossRef]
- Wang, E.; Yu, Z.; Zhang, H.; Yang, F. A regenerative supercritical-subcritical dual-loop organic rankine cycle system for energy recovery from the waste heat of internal combustion engines. Appl. Energy 2017, 190, 574–590. [Google Scholar] [CrossRef]
- Wang, L.; Sundén, B. Optimal design of plate heat exchangers with and without pressure drop specifications. Appl. Therm. Eng. 2003, 23, 295–311. [Google Scholar] [CrossRef]
- Starace, G.; Fiorentino, M.; Longo, M.P.; Carluccio, E. A hybrid method for the cross flow compact heat exchangers design. Appl. Therm. Eng. 2017, 111, 1129–1142. [Google Scholar] [CrossRef]
- Starace, G.; Fiorentino, M.; Meleleo, B.; Risolo, C. The hybrid method applied to the plate-finned tube evaporator geometry. Int. J. Refrig. 2018, 88, 67–77. [Google Scholar] [CrossRef]
- Gullapalli, V.S. Modeling of brazed plate heat exchangers for ORC systems. Energy Procedia 2017, 129, 443–450. [Google Scholar] [CrossRef]
- Durmuş, A.; Benli, H.; Kurtbaş, İ.; Gül, H. Investigation of heat transfer and pressure drop in plate heat exchangers having different surface profiles. Int. J. Heat Mass Transf. 2009, 52, 1451–1457. [Google Scholar] [CrossRef]
- Kehlhofer, R.; Rukes, B.; Hannemann, F.; Stirnimann, F. Combined-Cycle Gas & Steam Turbine Power Plants; PennWell: Tulsa, OK, USA, 2009; ISBN 9781593701680. [Google Scholar]
- Gusew, S. Heat Transfer in Plate Heat Exchangers in the Transition Flow Regime. J. Enhanc. Heat Transf. 2015, 22, 441–455. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhu, L.; Yu, J.; Li, Y. Optimization of plate-fin heat exchangers by minimizing specific entropy generation rate. Int. J. Heat Mass Transf. 2014, 78, 942–946. [Google Scholar] [CrossRef]
- Genić, S.; Jaćimović, B.; Petrovic, A. A novel method for combined entropy generation and economic optimization of counter-current and co-current heat exchangers. Appl. Therm. Eng. 2018, 136, 327–334. [Google Scholar] [CrossRef]
- Ayadi, A.; Zanni-Merk, C.; de Beuvron, F.B.; Krichen, S. A multi-objective method for optimizing the transittability of complex biomolecular networks. Procedia Comput. Sci. 2018, 126, 507–516. [Google Scholar] [CrossRef]
- Zare, V. A comparative exergoeconomic analysis of different ORC configurations for binary geothermal power plants. Energy Convers. Manag. 2015, 105, 127–138. [Google Scholar] [CrossRef]
- Etghani, M.M.; Shojaeefard, M.H.; Khalkhali, A.; Akbari, M. A hybrid method of modified NSGA-II and TOPSIS to optimize performance and emissions of a diesel engine using biodiesel. Appl. Therm. Eng. 2013, 59, 309–315. [Google Scholar] [CrossRef]
- Chen, S.J.; Hwang, C.L. Fuzzy multiple attribute decision making methods. In Fuzzy Multiple Attribute Decision Making; Springer: Heidelberg, Germany, 1992; Volume 375, pp. 289–486. [Google Scholar]
- Valencia, G.; Benavides, A.; Cardenas, Y. Economic and environmental multi-objective optimization of a wind-solar-fuel cell hybrid energy system in the colombian caribbean region. Energies 2019, 12, 2119. [Google Scholar] [CrossRef]
- Feng, Y.; Zhang, Y.; Li, B.; Yang, J.; Shi, Y. Sensitivity analysis and thermoeconomic comparison of ORCs (organic Rankine cycles) for low temperature waste heat recovery. Energy 2015, 82, 664–677. [Google Scholar] [CrossRef]
- De Oliveira Neto, R.; Adolfo Rodriguez Sotomonte, C.; Coronado, C.J.R.; Nascimento, M. Technical and economic analyses of waste heat energy recovery from internal combustion engines by the Organic Rankine Cycle. Energy Convers. Manag. 2016, 129, 168–179. [Google Scholar] [CrossRef]
- Imran, M.; Pambudi, N.A.; Farooq, M. Thermal and hydraulic optimization of plate heat exchanger using multi objective genetic algorithm. Case Stud. Therm. Eng. 2017, 10, 570–578. [Google Scholar] [CrossRef]
- Imran, M.; Usman, M.; Park, B.-S.; Kim, H.-J.; Lee, D.-H. Multi-objective optimization of evaporator of organic rankine cycle (ORC) for low temperature geothermal heat source. Appl. Therm. Eng. 2015, 80, 1–9. [Google Scholar] [CrossRef]


| Fluid | BSFC | |||||||
|---|---|---|---|---|---|---|---|---|
| (kW) | (%) | (%) | (%) | (%) | (%) | (g/kWh) | (kW) | |
| Acetone | 100.47 | 40.80 | 2.21 | 19.51 | 7.96 | 41.05 | 169.63 | 114.97 |
| C6H12 | 84.94 | 40.46 | 1.87 | 16.50 | 6.73 | 34.71 | 169.50 | 127.95 |
| Toluene | 84.46 | 40.45 | 1.86 | 16.40 | 6.69 | 34.51 | 169.50 | 128.90 |
| n-heptane | 71.72 | 40.17 | 1.58 | 13.92 | 5.68 | 29.30 | 169.89 | 139.59 |
| n-octane | 65.33 | 40.03 | 1.44 | 12.69 | 5.17 | 26.69 | 169.24 | 145.43 |
| n-nonane | 59.74 | 39.91 | 1.32 | 11.60 | 4.73 | 24.41 | 169.29 | 150.59 |
| n-decane | 54.86 | 39.80 | 1.21 | 10.65 | 4.35 | 22.41 | 169.54 | 155.13 |
| MDM | 48.90 | 39.67 | 1.08 | 9.50 | 3.87 | 19.98 | 169.67 | 159.36 |
| D4 | 45.83 | 39.61 | 1.02 | 8.90 | 3.63 | 18.72 | 169.77 | 162.61 |
| MD2M | 41.24 | 39.50 | 0.91 | 8.01 | 3.27 | 16.85 | 169.87 | 166.35 |
| D5 | 39.02 | 39.46 | 0.87 | 7.58 | 3.09 | 15.94 | 169.89 | 168.38 |
| MD3M | 33.97 | 39.35 | 0.76 | 6.60 | 2.69 | 13.88 | 169.93 | 172.72 |
| D6 | 32.04 | 39.30 | 0.71 | 6.22 | 2.54 | 13.09 | 169.95 | 174.16 |
| MD4M | 30.84 | 39.28 | 0.69 | 5.99 | 2.44 | 12.60 | 169.96 | 175.82 |
| Variable Decision | Symbol | Unit | Minimum Value | Maximum Value | Criteria |
|---|---|---|---|---|---|
| Angle of inclination | ° | 10 | 80 | C1 | |
| Plate height | H | mm | 460 | 2200 | C2 |
| Plate width | W | mm | 160 | 610 | C3 |
| Plate spacing | Lp | mm | 336 | 1671 | C4 |
| Parameter of Design | Unit | Base State | Optimal Values | ||||
|---|---|---|---|---|---|---|---|
| A (min EGN) | B | C | D | E (min cost) | |||
| ° | 10 | 10.05 | 18.23 | 14.32 | 20.44 | 74.60 | |
| mm | 1826 | 658.29 | 1462.94 | 2112.66 | 2070.32 | 2198.65 | |
| mm | 480 | 201.09 | 203.87 | 204.79 | 205.16 | 212.52 | |
| mm | 1388 | 1652.38 | 1593.48 | 1500.74 | 800.49 | 400.14 | |
| m2 | 0.876 | 0.132 | 0.298 | 0.4325 | 0.424 | 0.467 | |
| - | 35 | 360 | 90 | 52 | 52 | 48 | |
| m2 | 30.6 | 47.52 | 26.82 | 22.49 | 22.04 | 22.42 | |
| kW | 693.87 | 693.87 | 693.87 | 693.87 | 693.87 | 693.87 | |
| kW | 114.75 | 114.75 | 114.75 | 114.75 | 114.75 | 114.75 | |
| - | 0.41 | 0.41 | 0.41 | 0.41 | 0.41 | 0.41 | |
| m/s | 0.146 | 0.0423 | 0.156 | 0.253 | 0.253 | 0.262 | |
| m/s | 1.509 | 0.437 | 1.613 | 2.615 | 2.612 | 2.705 | |
| - | 1029.03 | 245.62 | 969.11 | 1669.78 | 1668.07 | 1747.41 | |
| - | 12,017.13 | 2,868.33 | 11,317.45 | 19,499.90 | 19,479.93 | 20,406.45 | |
| 1596.7 | 946.47 | 1758.86 | 2172.31 | 2171.12 | 2196.62 | ||
| 996.95 | 696.24 | 1141.11 | 1309.68 | 1309.99 | 1313 | ||
| - | 0.0748 | 0.115 | 0.0762 | 0.0647 | 0.0647 | 0.0638 | |
| - | 4.698 | 17.05 | 4.823 | 2.985 | 2.95 | 4.38 | |
| mbar | 22.13 | 4.12 | 33.55 | 66.37 | 35.34 | 18.45 | |
| mbar | 845.8 | 371.92 | 129.28 | 1863.6 | 980.32 | 772.5 | |
| m/s | 4.024 | 4.024 | 4.024 | 4.024 | 4.024 | 4.024 | |
| m/s | 1527.42 | 1527.42 | 1527.42 | 1527.42 | 1527.42 | 1527.42 | |
| Cost | $ USD | 16,954.07 | 26,335.14 | 19,406.80 | 13,644.11 | 10,385.55 | 6,979.19 |
| EGN | - | 0.058219 | 0.058197 | 0.058199 | 0.058201 | 0.058203 | 0.058206 |
| Objective Function | Optimal Value | Value of The Decision Variables | |||
|---|---|---|---|---|---|
| C1 | C2 | C3 | C4 | ||
| Equipment cost ($ USD) | 10,385.55 | 20.44 | 2070.32 | 205.16 | 800.49 |
| EGN | 0.05820328 | ||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Valencia, G.; Núñez, J.; Duarte, J. Multiobjective Optimization of a Plate Heat Exchanger in a Waste Heat Recovery Organic Rankine Cycle System for Natural Gas Engines. Entropy 2019, 21, 655. https://doi.org/10.3390/e21070655
Valencia G, Núñez J, Duarte J. Multiobjective Optimization of a Plate Heat Exchanger in a Waste Heat Recovery Organic Rankine Cycle System for Natural Gas Engines. Entropy. 2019; 21(7):655. https://doi.org/10.3390/e21070655
Chicago/Turabian StyleValencia, Guillermo, José Núñez, and Jorge Duarte. 2019. "Multiobjective Optimization of a Plate Heat Exchanger in a Waste Heat Recovery Organic Rankine Cycle System for Natural Gas Engines" Entropy 21, no. 7: 655. https://doi.org/10.3390/e21070655
APA StyleValencia, G., Núñez, J., & Duarte, J. (2019). Multiobjective Optimization of a Plate Heat Exchanger in a Waste Heat Recovery Organic Rankine Cycle System for Natural Gas Engines. Entropy, 21(7), 655. https://doi.org/10.3390/e21070655







