1. Introduction
Shannon’s mutual information (MI) [
1] is a widely-used measure in various research domains. The MI between two random variables evaluates in bits the reduction of the uncertainty (entropy) of one of the variables given the other (i.e., averaged over all possible realizations of the other). This measure is non-parametric and hence can be used to describe complex interactions. Predictive information (PI) [
2] was proposed as a measure of MI between one time series’ past and another’s future (either the same one or a different time series). One example is the MI between different stocks’ prices over different time periods, as discussed next. If we limit the prediction to one step ahead, the PI is directly related to the known transfer entropy (TE) [
3,
4] that measures the conditional PI between input and output time series, given the past realizations of the output. For the past two decades, TE has been widely used for analyzing information flow between different time series and causality analysis (see a comprehensive review on TE and related measures at [
4,
5]). However, a difficulty arises when these measures need to be estimated from data. The number of possible sequences for which information contributions should be estimated is exponential in the number of time lags. In some cases, when most realized past sequences are uninformative about the future, false information contributors lead to overestimation of PI, hence associating predictive power with uninformative sequences. We call this condition sparse PI (SPI).
When dealing with real valued data, one can assume an AR-based model as in [
5,
6] to estimate PI with relatively low complexity and high accuracy. Nevertheless, this assumption often fails when the times lags between the series are not linearly correlated, or in the discrete data case. Methods that rely on non-parametric approaches are at risk of encountering a large estimation error under the SPI conditions. Such methods are based on commonly-used MI estimation methods ranging from naive binning to bias corrections and nearest neighbor methods (see for example the benchmark study in [
7]). When applied to time series, these methods resolve the time dimensionality challenge by keeping relevant time lags entirely, even if some of them contain few informative sequences, and so, positive bias occurs. Thus, these methods do not apply estimation correction at a realization level, which removes a significant share of uninformative sequences, yet enables an improved explainability at the realization level.
We provide a solution for estimating the PI in discrete data, which is based on an expansion of the lossy compression context tree (CT) algorithm [
8,
9,
10], which is called the input/output context tree (I/O CT) [
11,
12].
This algorithm parses the input time series into a tree of contexts (sequences), where in each node, the conditional probability of the output given the context is assigned. Only nodes with conditional probabilities that are significantly different from those of their parent nodes (this difference is often measured by the Kullback–Leibler distance) are kept, and the others are pruned. The pruning stage is governed by the pruning constant c [
9,
10]. In the SPI condition, c has a significant impact even for relatively small values, where most of the nodes are pruned. On the other hand, c should not be too high, to avoid pruning of informative nodes. Usually, c is determined heuristically or by cross-validation.
The CT (and I/O CT) algorithm, as well as other algorithms from the variable order Markov models family were proposed to overcome overfitting in learning tasks such as classification and prediction [
11]. Estimating the information between a time series’ past and future was usually not one of the tasks for which these algorithms were used.
In this paper, we show how to estimate PI between time series as the sum of the Kullback–Leibler divergence [
13] between the root node and the leaves of I/O CT. Furthermore, we utilize the dependency of PI on the pruning constant to determine the value of c that enables good separation among informative and uninformative contexts. This is done without the need for an additional run over the data as in, e.g., cross-validation procedures.
The proposed procedure is implemented by a new context-based predictive information (CBPI) algorithm: First, a full I/O CT is built (c = 0). Second, the PI is calculated for ascending values of c. Third, by identifying the threshold at which redundant information is removed, a value of c is chosen to return an estimation for the “filtered” PI and most of the informative sequences.
The CBPI algorithm is designated for discrete data. Nevertheless, it can be implemented also on real valued data by performing any type of binning, such as described in [
7]. In many cases, binning results in some loss of information [
7,
14], due to the compression procedure. Often the number of bins controls such loss, where a large number of bins leads to a closer distribution to the real valued data and vice versa. An important consideration is the relevancy of the binning to the domain from which data are sourced. The approach taken in this paper, following other works (e.g., [
15,
16,
17]), is that after removing the uninformative sequences, domain-relevant insights could be immediately drawn. We also note that methods that are applied directly on real valued data are limited when dealing with time series where non-linear sequential characteristics are important (as opposed to treating every time lag as a feature on its own), and in addition, they suffer from limited explainability capabilities.
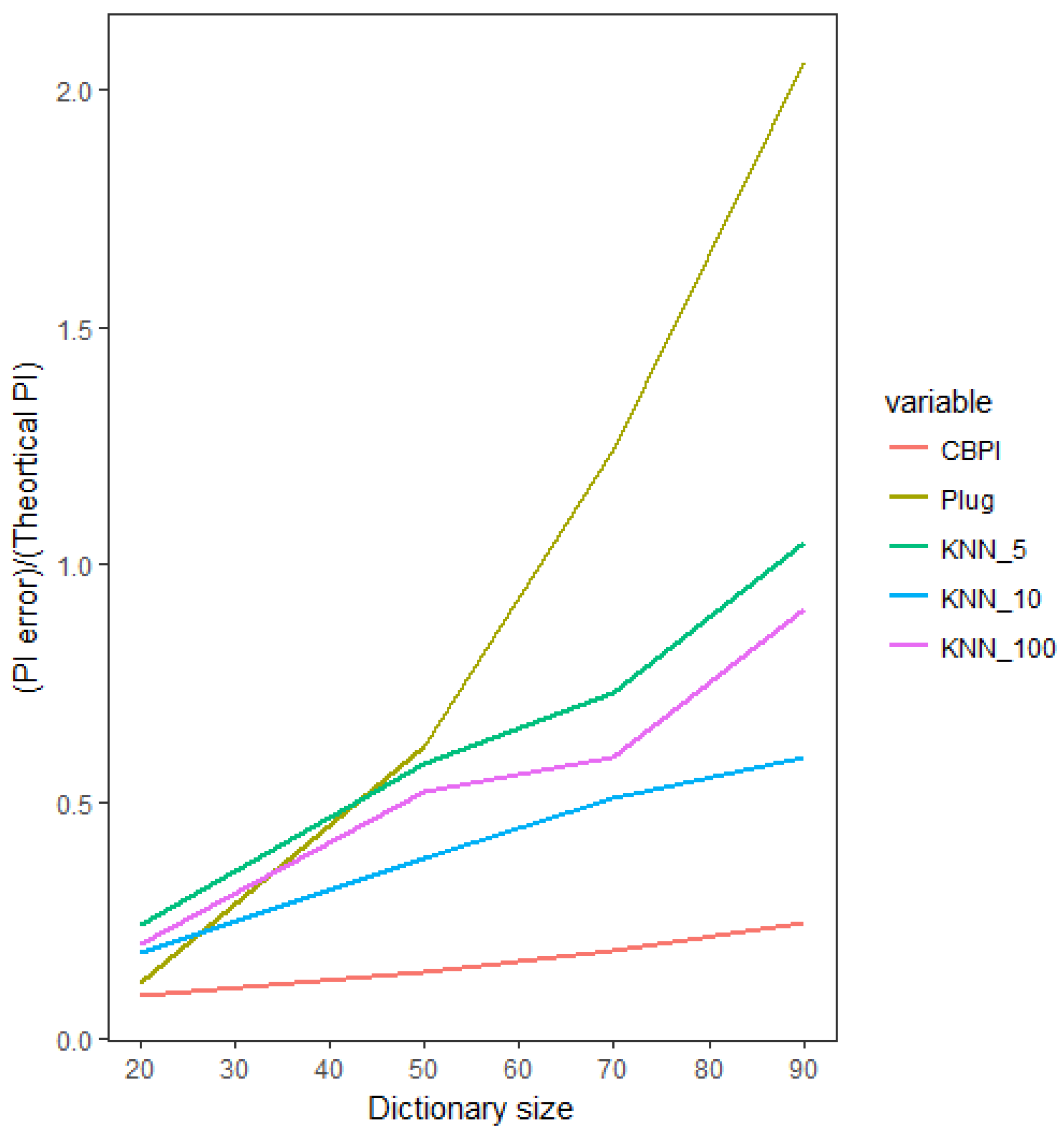
A relevant question to ask is whether SPI exists in practice. The generic answer is that it exists whenever compression of one time series with respect to another results in a significant reduction in data, while most important information is preserved. As an example, we can consider time series in a large stock market. Due to market efficiency, PI between time series of stock prices is expected to be small or equal to zero. In the case of a small PI, most of the past sequences are uninformative, and the SPI condition might occur (e.g., see [
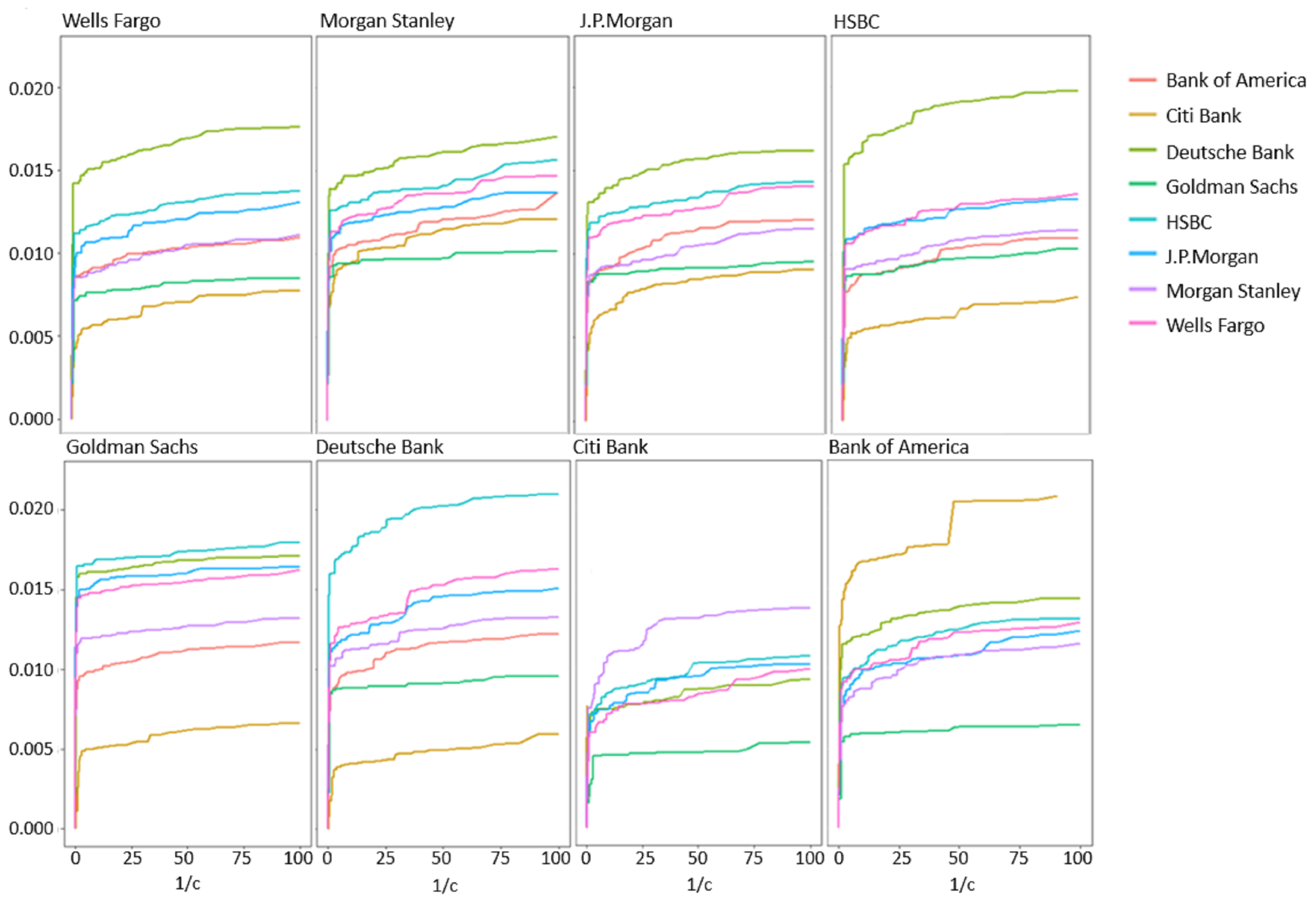
15] and the discussion therein). We discuss these types of scenarios in the Results Section and exemplify the CBPI algorithm’s contribution by implementing it on a simulated setup for benchmarking it relative to other methods, as well as on real stock market data of eight large banks in the U.S. In the latter example, we also demonstrate how the outcome of the CBPI algorithm can be exploited to gain important insights by performing a higher resolution analysis of the PI contributors.
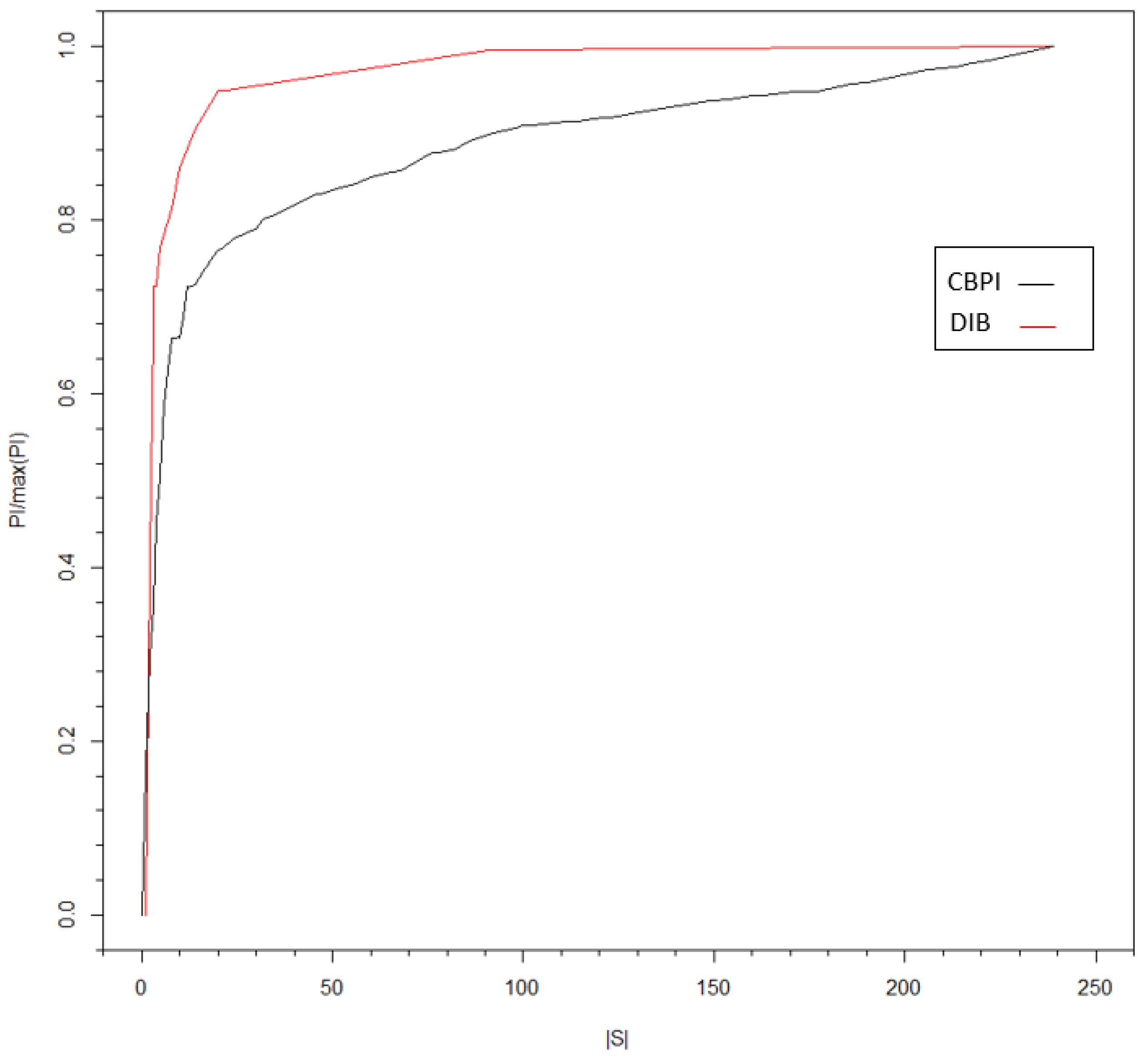
In the last part of this paper, we discuss an interesting observation about the connection between the CBPI algorithm and the deterministic information bottleneck (DIB) [
18]. The DIB is a variant of the well-known IB algorithm [
19] that enables deterministic compression of one variable with respect to another. We give an intuitive explanation of this connection and formalize an optimization problem inspired by DIB that relies on the I/O CT algorithm. With the extraction of PI, I/O CT can serve as a complement to DIB in deterministic compression tasks of one time series with respect to another.
To conclude, the first main contribution of this paper is demonstrating the extraction of PI from an I/O CT constructed from input and output time series. The second contribution is introducing a novel algorithm, called the CBPI, for PI estimation, while offering a new method of identifying the value of the pruning constant that governs the compression rate. The third contribution is showing how the CBPI algorithm can be used for in-depth analysis of interaction fundamentals. Finally, the linkage of the context tree algorithm and the deterministic information bottleneck method is discussed by formalizing an optimization problem that describes the I/O CT algorithm.
This paper is organized as follows. Related work is reviewed in
Section 2.
Section 3 discusses basic concepts and the mathematical background of the ideas presented in this work. In
Section 4, the extraction of PI from the I/O CT algorithm, the pruning constant’s identification, and the CBPI algorithm are described.
Section 5 shows the experimental results of implementing CPBI in both simulated and real data settings.
Section 6 discusses the general characteristics of the pruning constant and the relation between I/O CT and DIB. In
Section 7, we conclude this work.
2. Related Work
MI was originally introduced by Shannon and discussed widely in the literature, with [
1] being an extensively cited source. Many methods are used for MI estimation. The simplest and most straightforward one is the so-called plug-in method, where marginal and conditional probabilities are evaluated through counts [
1]. Other existing methods of MI estimation, such as [
20,
21,
22,
23,
24], use different corrections of probabilities due to the finite size of data. The K-nearest neighbors method proposed in [
22] is one of the most commonly used in recent years.
PI was formulated by Bialek, Nemenman, and Tishby in [
2]. There, the researchers discussed the theoretical attributes of PI and its connection to important aspects of model learning. Empirically measuring PI is important for the estimation of TE, which was initially proposed by [
3]. To calculate TE, one should estimate a conditional PI, although this is not stated directly in papers that discuss TE.
Researchers such as [
14,
25] used standard methods of MI estimation, mentioned in the beginning of this section, to estimate TE. Those studies proposed algorithms to avoid dimensionality explosion due to the time dimension by removing uninformative time lags. According to those methods, when a specific time lag is found to be informative in a specific realization, all its realizations, including uninformative ones, are included in the estimation. In sequential data, where the number of different realizations is potentially large, this drawback can be crucial by adding many uninformative sequences to the estimation.
To overcome this challenge, we utilize the CT algorithm, a lossy compression member of the family of variable order Markov models that were originally constructed for compression of a single time series and found to be well-suited to the prediction task of discrete time series [
9,
15,
26]. These works extend the basic Markov model by proposing an algorithm for data compression that extract important sequences (i.e., “contexts”) not necessarily of the same order, which contained significant information about the conditioned symbol. The CT algorithm constructs a universal source. This means that the model can asymptotically replace any source from the class of tree sources with optimal code length, hence approaching the sequence’s entropy with the optimal convergence rate [
9].
Variable order Markov models and their usage have been extensively explored, e.g., for prediction tasks [
15,
26,
27], time series classification [
28,
29], clustering [
30,
31], anomaly detection [
10,
32], and modeling DNA sequences [
11,
33]. Two works were found that incorporated variable order models and information or entropy. In [
21], the authors used several models from this family to estimate the entropy of a sequential source. In [
28], the goal was to construct a discriminative model (to perform the classification task) for time series, with each series belonging to one of
K classes. The MI between a symbol and a class
given the contexts was obtained from the prediction suffix tree algorithm to find discriminative contexts (that the researchers called features).
Ben-Gal et al. [
11] and later Brice et al. [
12] proposed an input/output formulation of the context tree algorithm (I/O CT), where the branches of the context tree belong to one time series and the leaves belong to another. In this way, the researchers could incorporate data from different time series for learning tasks, such as structure learning and anomaly detection within the CT framework.
The pruning constant c is the only hyper-parameter in the I/O CT algorithm. When properly tuned, it reduces the variance of the model while keeping a low bias. In [
9], c was suggested to be
, where
d is the alphabet size, without any clear theoretical justification. Model evaluation methods such as the AIC [
34,
35] were proposed in [
36,
37] in relation to pruning constant determination. They involve a brute force search for
c by calculating the log-likelihood over the training data for each value of c. A structured method that provides justification for c based on data characteristics is yet to be proposed.
A relevant practical fact when considering large datasets is that the I/O CT algorithm can be distributed to multiple machines similarly to other algorithms from the same family [
38,
39,
40]. In this paper, the key-value approach is utilized, where the keys are the contexts and the values are the counters of the output time series, similar to [
38,
40].
In the final part of this paper, we discuss the relation between I/O CT and the IB [
19]. IB and its implications for understanding learning mechanism have been extensively explored (for example see [
41]). In [
42,
43,
44], PI was incorporated theoretically in the IB framework.
The deterministic IB (DIB) [
18] is a variant of IB that leads to hard clustering, which we will refer to in the final part of this paper.
3. Preliminaries and Mathematical Background
Henceforth, unless stated otherwise, random variables are represented by uppercase letters, while their realizations are denoted by lowercase letters; multi-dimensional variables are denoted by bold letters and sets with calligraphic letters.
Mutual information [1]: Given two discrete random variables X and Y, the mutual information between them is defined as:
is a positive symmetrical measure. The
Kullback–Leibler divergence (
) between arbitrary probability functions
and
is given by:
Following Equation (
2),
can be written as:
where
is the expectation with respect to the subscript distribution.
Predictive information (PI) [44]: The MI between two random vectors, one representing the past
time lags,
, and another representing time series values from the future
time lags,
, can be measured by the PI. Following Equation (
3), PI can be defined by using
:
Context tree (CT) algorithm [9,10]: Given a sequence of length
N,
, generated from a tree source
X, the CT algorithm finds a finite set
of size |
| of contexts
.
satisfies the requirement that the conditional probability to obtain a symbol given the whole sequence preceding that symbol is close enough to the conditional probability of obtaining the symbol given a context, i.e.,
Given Equation (
5), when |
| sequences are informative, the number of conditional probability parameters needed to describe
equals |
, where
d is the alphabet size of
X.
To obtain
, the learning algorithm constructs a context tree where each node holds a set of ordered counters that represent the distribution of symbols that follow that context, which is defined by the path to that node [
10]. At the next step, a pruning procedure is performed to leave only those contexts in
(also called optimal contexts [
10]), with corresponding nodes in the tree that represent the conditional distribution of the output variable conditioned on the context, which is different from the distributions of the output variable conditioned only on part of the context. This difference between the conditioned distributions is measured by the
measure. The pruning phase is regulated by the pruning constant c, which is a tunable hyper-parameter. As proven by [
9], this procedure leads to the optimal description of the tree source, e.g., one with the minimal description length of the generating tree source. Descriptions of the main principles of the CT Algorithm, how to obtain
, and a numerical example appear in
Appendix A.
The I/O CT [
11,
12] algorithm is a generalization of the CT algorithm where the tree’s contexts are from the input sequence and the leaves represent counters of the output sequence, in contrast to Equation (
5), where the input and the output are from the same time series,
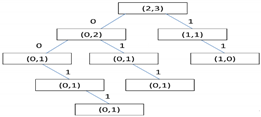
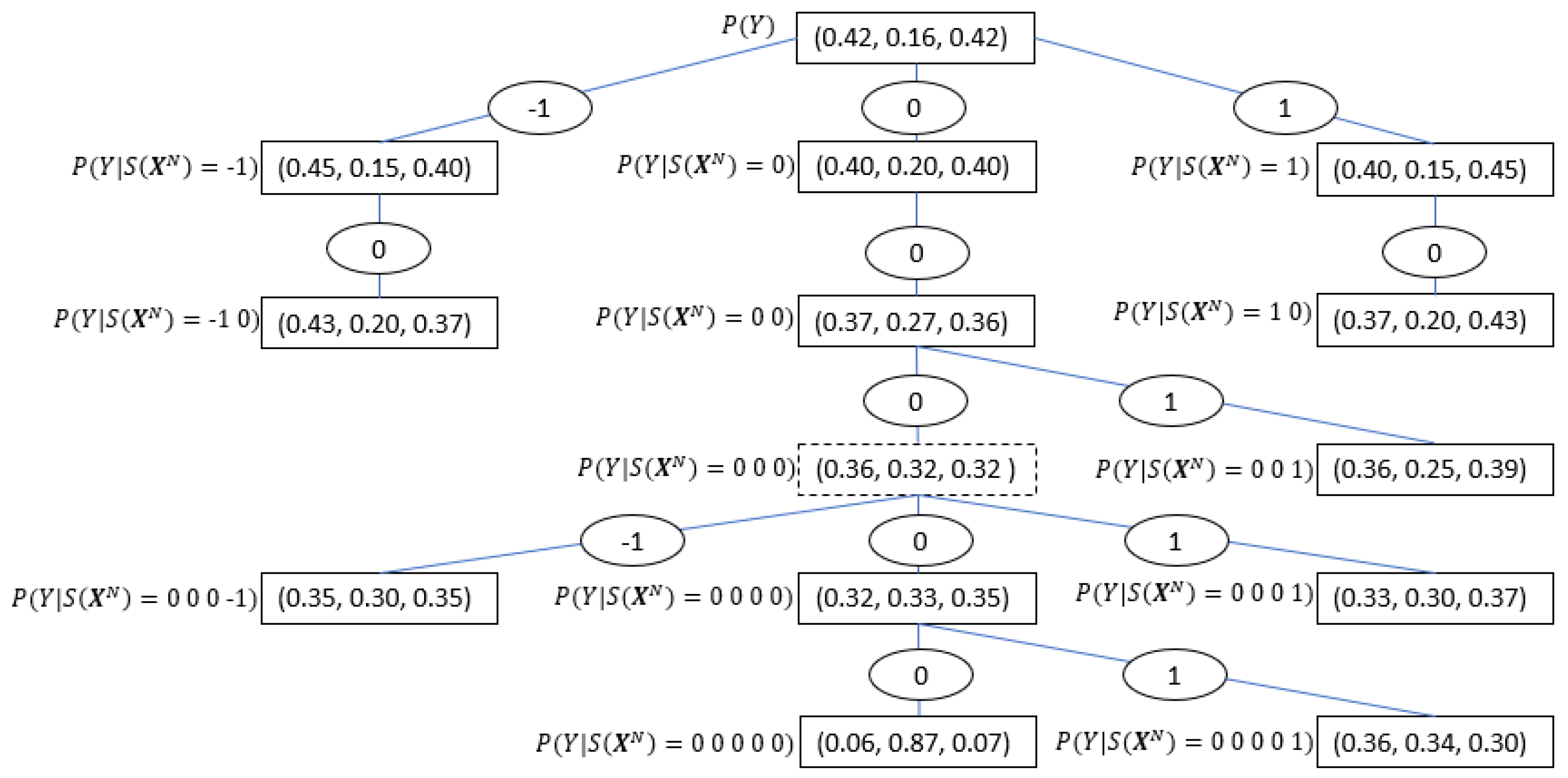
Figure 1 along with
Table 1, show an I/O CT example based on the results from the real data experiment discussed in
Section 5.2, where the symbols -1, 0, 1 denote negative, zero and positive change respectively in the financial time series. By investigating the tree structure, one can extract important characteristics of the considered time series interaction, such as the maximal memory of the process (represented by the tree depth, which in this case equals five), the significant sequences, and their conditioned probabilities, which in this case are relatively symmetric with respect to a zero change, etc. See further discussion in the Results Section.
4. The Context-Based Predictive Information Algorithm
Let
and
be the input and the output time series of length
N, respectively. The PI of the input about the output can be stated similarly to Equation (
4), where in this case, the past and the future trajectories belong to different time series.
represent the informative and uninformative contexts respectively from the input time series;
represents the sequences from the output time series; and
represent the estimated PI. We aim to remove
, for which the true
, although the estimated
, because this measure is positively biased due to the finite size of the data [
7]. This will be done while keeping the informative sequences. In the SPI condition (see
Section 1), where
, removing these contexts can significantly decrease the
estimation error. Namely, removing a large number of contexts with positively-biased information contribution that tend to zero when the data size is growing will reduce the total positive biased estimation error that comes from uninformative sequences.
To achieve this goal, we apply some of the principles implemented in [
28] to introduce a novel method for
estimation using the I/O CT. As shown in
Figure 1 and discussed in
Section 3, the root node of the I/O CT represents the marginal (unconditioned) distribution of
(the symbols’ frequency in
). The estimated PI between the input and the output time series is the sum of the
between the probability in the root node and the conditional probability distributions given the contexts in
, weighted by the probabilities of these contexts, following Equation (
4)
where
is the empirical PI obtained from the I/O CT algorithm with a pruning constant c and
is its corresponding optimal context set. To continue with the running example of banks’ data, we use
Table 1, which represents the tree in
Figure 1; using Equation (
7),
with c = 1 can be calculated as follows:
So far, the extraction of
from CT with a given c value has been described. A tuning method for finding the value of c that provides a good separation between informative and uninformative contexts is now proposed by utilizing the statistics gained by the first stage in the CT algorithm. Consider the vector
c of indexed pruning constant values
. The empirical second derivative of
with respect to
can be obtained by [
45]:
When the absolute value of (
9) reaches a greater value than a threshold
, the correspondent pruning constant is chosen. The second derivative is used to enable the detection of changes from higher than a linear order (e.g., curved-shaped changes) in the
. A linear decrease is expected to happen when uninformative contexts are removed. The reason for this behavior lies in the pruning threshold of the CT algorithm. This threshold equals to the probability of a context times a parent-child
measure. In the uninformative case, incrementally increasing the pruning constant will result in the pruning of all the leaves at the same tree level in the reverse order. Hence, in each incremental increase in the pruning constant c, the same size of
is subtracted. When one of the contexts contains a significant amount of information, its pruning will result in a higher order change in the empirical PI.
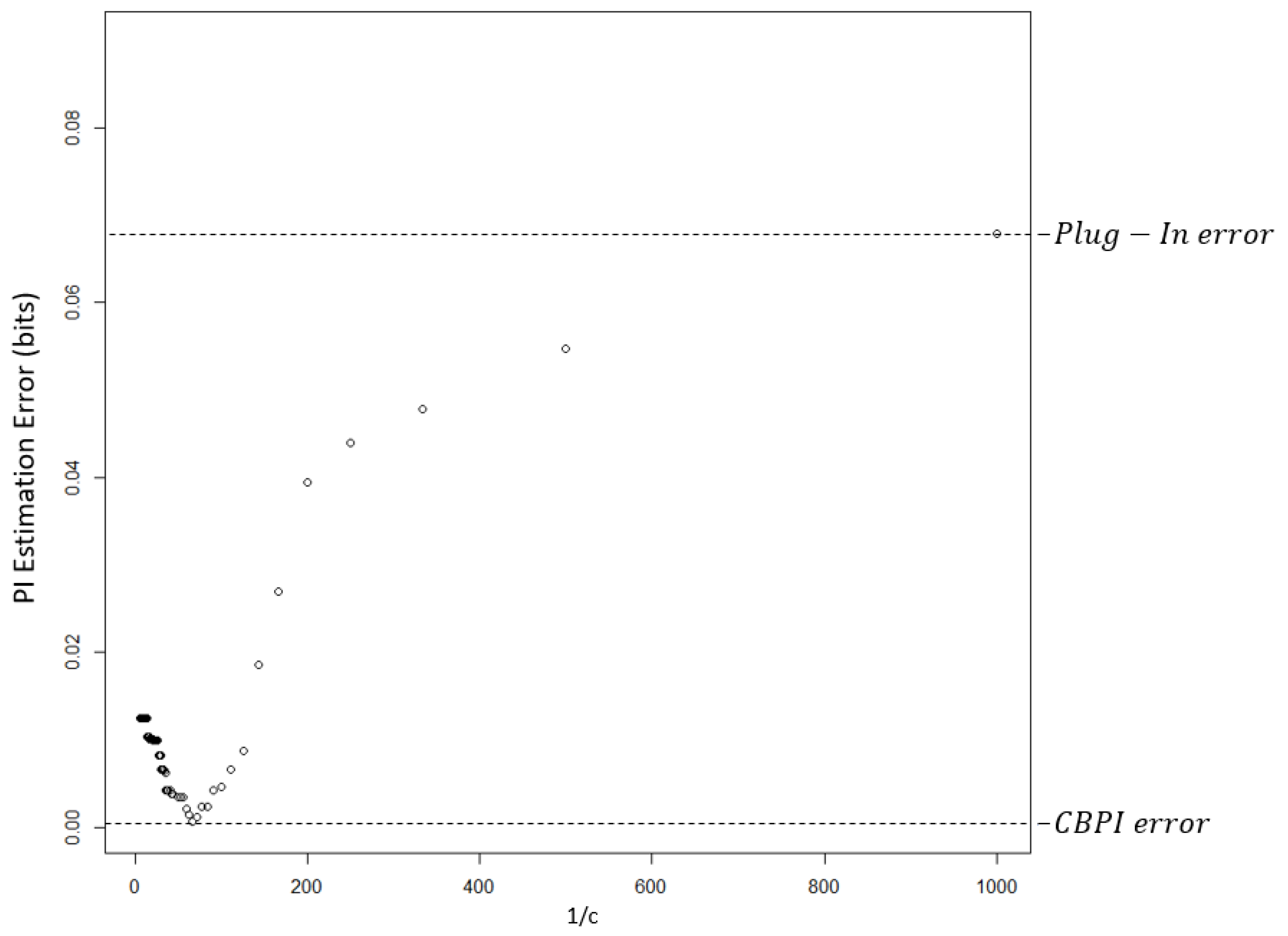
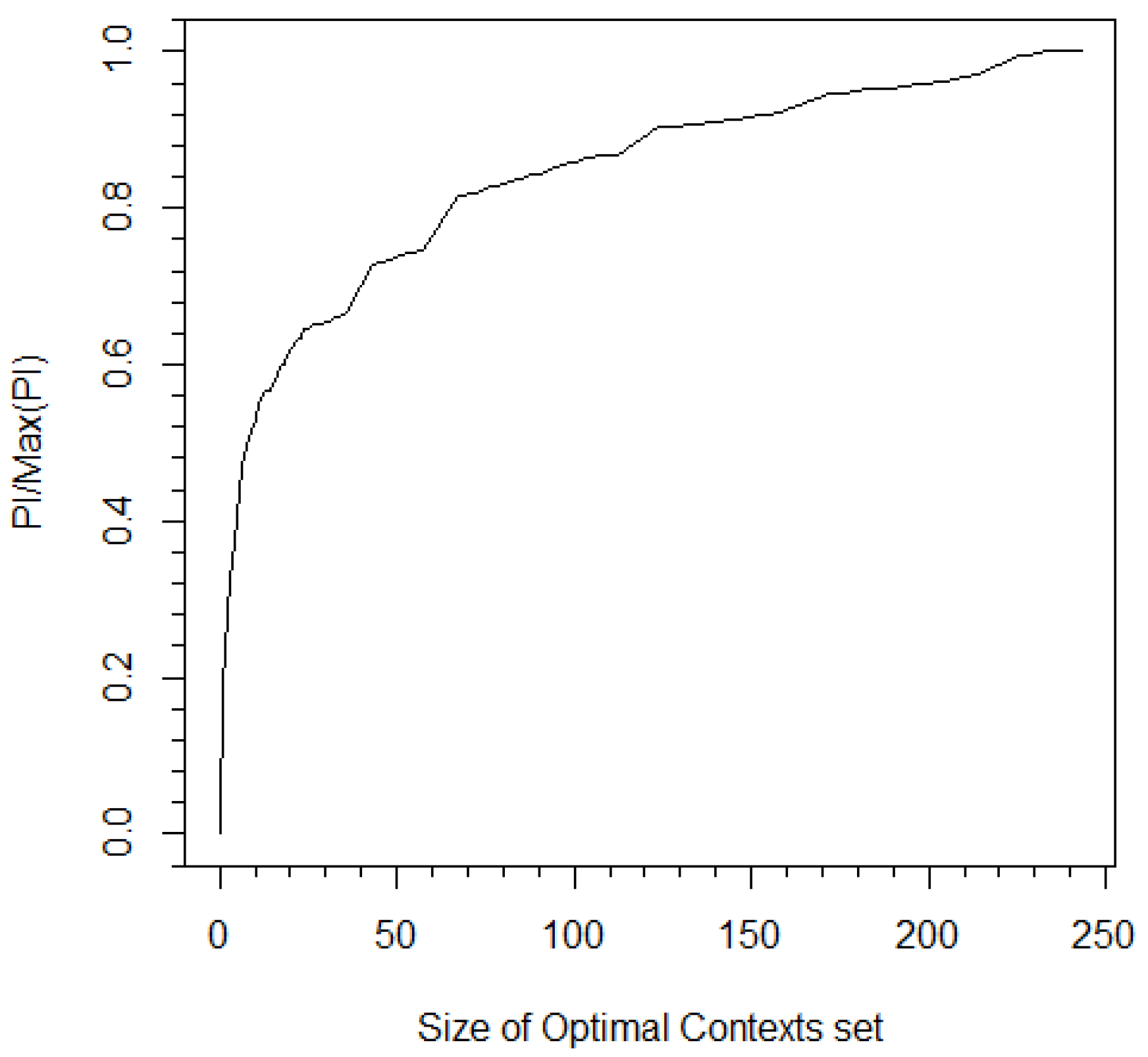
extraction and tuning of the pruning constant c constitute the CBPI algorithm. Let us summarize the CBPI algorithm, which is described in Algorithm 1: First, a full CT is constructed (by setting the pruning constant to c = 0). Then, for an increasing order of the pruning constant value with a fixed step, a CT is constructed for each pruning constant, and its estimated PI is calculated. This procedure repeats itself until the second derivative condition (which is exemplified by the curve in Figure 5) is satisfied and the algorithm stops and returns the values of the pruning constant c, as well as the PI of the last iteration.
Considering the
randomness, we need to reject the null hypothesis that
= 0, especially in the case of SPI condition. Here, we adopt the approach of [
46] by setting the stopping threshold
to be higher than the 95 percentile value of the
obtained by repeatedly reshuffling the time series and measuring the resulting
.
| Algorithm 1 Context-based predictive information: pseudocode. |
- 1:
Input: , , c, - 2:
Implement on , the first stage of the I/O CT algorithm to obtain a full I/O context tree - 3:
fori in 1 to do - 4:
Implement the following stages of the I/O CT algorithm - 5:
with , , , and obtain , , - 6:
Calculate - 7:
if || = || then - 8:
- 9:
else - 10:
- 11:
end if - 12:
if then - 13:
return , - 14:
end if - 15:
end for - 16:
return
|
Complexity Analysis
The complexity of the CBPI is comprised of two main parts: (i) the complexity of the context tree construction, which is constructed in the first part of the algorithm; and (ii) the calculation of the PI in every iterative step at the second stage of the algorithm. The construction of the full I/O CT has a complexity of
, where
N is the input sequence size [
47]. The complexity of the PI calculation depends linearly on the number of contexts in the tree, which is the sum of a geometric series of length
, the length of the longest context in the tree. In each one of
iterations, one needs at most
summation operations, where
d denotes the alphabet size. Accordingly, the full complexity of the CBPI algorithm is:
As mentioned in
Section 1, the left complexity term can be controlled by a distributed tree construction procedure via multiple processors, while the right complexity term can be controlled by limiting the depth of the full context tree, which makes sense since the probability for extracting significant sequences decreases with the sequence length.