1. Introduction
In the last two decades, there has been a substantial development of a well-founded risk measure theory, particularly propelled since the axiomatic approach introduced by [
1] in relation to the concept of coherency. While, to a large extent, the theory has been fundamentally inspired and motivated with financial risk assessment objectives in perspective, many other areas of application are currently or potentially benefited by the formal mathematical construction of the discipline.
The coherency axioms of monotonicity, translation invariance, positive homogeneity and sub-additivity lead to a representation for coherent risk measures of the form
where
X is a real-valued measurable function on the measurable space
representing benefit, and
is a certain set of probability measures on
. Since its introduction, such a formulation has been the matter of an important debate in the following years, mainly due to the restrictive conditions implied by the axiom of sub-additivity, which make coherent measures of risk unsuitable in certain applications. Relaxation of this axiom in terms of a weaker convexity condition, as was introduced by [
2,
3], provides a more flexible representation in the form
where
is a suitable set of probability measures on
, and
is a penalty function defined on
. The minimal penalty function for
is convex, being defined by
where
is the space of all Borel-measurable functions defined on
. With additional assumptions (see, for example, [
4]), there exists a one-to-one pairing between
and
via Legendre-Fenchel (LF) duality. The theories of convex and coherent risk measures have been increasingly and deeply developed as a central axis of the general theory of measures of risk, owing to the contributions by many researchers (e.g., [
4,
5,
6,
7,
8,
9,
10,
11,
12], etc; see also early work of [
13], among others). In the law-invariant case [
14], the value
only depends on the distribution of
under the assumption of a prefixed probability measure
P on
. Typical examples are value-at-risk (VaR), average value-at-risk (AVaR), tail value-at-risk (TVaR), the entropic risk measure, the
-divergence risk measure related to the optimized certainty equivalent (OCE), etc; the authors of [
15] comparatively study various generalized entropy-based forms of risk measures. The details on the VaR related family of risk measures can be found in the large range of the literature connected with duality. Here we just review some basic definitions focused on the entropic risk measure and
-divergence risk measure used in the examples of
Section 2.1.
In the decision theory under uncertainty, especially in the context of economics, the numerical representation of preferences shares a similar structure as the dual form of risk measures. In this context, it is postulated that an agent can evaluate the consequences of an alternative decision according to
where
u denotes the utility function and the penalty function
here is explained as the ambiguity attitude in this related strand of the literature. For more details on the ambiguity of variational preferences, we refer to the work by [
16], which also proves that the preference relation satisfies the axioms of preferences when there exists a non-constant affine utility function and demonstrates a new class of preferences, built on the
-divergence, for handling Ellsberg-type puzzles [
17]. This numerical form leads to the definition of a loss functional,
, satisfying
but we are interested in the risk measure, the payoff of the financial position, which is equivalent to the negative certainty equivalent
where
, named as the de-utility function. The (generalized) Donsker-Varadhan variational formula [
18,
19] plays a vital role in these connections, which recently also spread to the classical Gini index of income inequality [
20] through the linkage tool derived from [
21]. Some other efforts have been made to connect both of these research fields, such as in [
2,
7], and more recently [
22].
From the perspective of convex risk measures, intuitively, the dual representation of Equation (
2) can be regarded as a risk-measure generator obeying the axiomatic framework, i.e., we are able to produce a certain risk measure through selecting among different penalty functions. For instance, [
8] constructed a bridge between the expected utility framework and the
-divergence risk-measure framework (Lemma A2). On the one hand, any utility function satisfying certain suitable conditions can generate its related convex risk measure. Conversely, any
-divergence can provide a possibly analytic form of a risk measure useful for calculation in practice, such as the Tsallis divergence.
Thus, the penalty function plays a substantive role in the evaluation of risk, with its properties determining the behavior of the linked risk measure. Moreover, from our understanding, this viewpoint on the sensitivity is ignored in the dual theory of convex risk measures. Besides early work, as in [
23,
24], discussing the sensitivity concentrated on cases of VaR-type with respect to portfolio allocation, recently, the authors of [
25] have stated a framework for sensitivity analysis both on the measurement processes and the dataset through robust statistics and the estimation procedures, respectively. These sensitivity studies focus on trend identification (direction of change), which reveals how a shift of position affects the output risk measurements. In an extensive review, [
26] identify and comparatively discuss different sensitivity analysis strategies in the literature, with a clear distinction between local (deterministic) and global (probabilistic) approaches.
The contribution of this paper is twofold. First, after reviewing the literature on the ambiguity aversion (or loving) of preferences in
Section 2.2, we study the sensitivity of convex risk measures and examine the modified version of the
-divergence risk measure to declare this issue clearly and operationally presented in
Section 2.2 and
Section 3 in terms of the reference probability measure and the input financial position.
Moreover, there are some important measures of divergence that cannot be obtained as particular cases of the
-divergence; for instance, Rényi divergence. For this reason, the authors of [
27] worked with an extended formulation, the so-called
)-divergence, denoted by
, from which various well-known divergences can be obtained through the extra distortion
h. Our second contribution is, in a first step, straightforward: By replacing the penalty function to the
-divergence in the dual form of convex risk measure, we derive a new family of convex risk measures, the
-divergence risk measure
Recent study on risk measures has focused on the extension of the risk-neutral valuation. Under the probability measure
Q, the part
is equivalent to the neutral risk. One more general approach to evaluating
X consists in considering
, where a non-linear and convex
leads to a risk-averse evaluation by the so-called
-convex risk measures. Based on this extension, the authors of [
7] develop a subclass of the entropic risk measure and contribute the connections with variational preferences by assuring the de-utility function
as linear or exponential. The authors of [
9] extend to a more general form based on the utility theory, while the authors of [
28] develop the optimal expected utility (OEU) risk measure by modifying the OCE, which benefits from the easy application defined on optimizing in the real field.
Our article is organized as follows. In
Section 2, we briefly review the content of the dual representation for convex risk measures and the concept of ambiguity in the field of the preference in decision making theory. In
Section 3, we strengthen the analysis on the modified version of
-divergence risk measure and its sensitivity on the financial positions, and analyze the sensitivity on the probability measure. In
Section 4, we extend the penalty term to the
-divergence for defining the new family of convex risk measures, and derive relative OCE bounds. The case of Rényi divergence is addressed in particular. Some numerical studies by cases are shown in
Section 5. Conclusions and directions of continuing work are given in
Section 6.
4. -Divergence Risk Measure
Our new extended family of risk measures derives from
-divergence, the definition of which in [
27] is recalled below.
Definition 3. An extension of the ϕ-divergence, called -divergence, is defined byfor , where and, for , are nondecreasing and continuous functions with , are positive weights, and the functions satisfy the conditions for a ϕ-divergence risk measure. We denote by
the set of probability measures
Q on
which are absolutely continuous with respect to
P. For simplicity, here we consider the reduced form of the
-divergence for the case
, given by
The parameter in the modified -divergence risk measure can be interpreted as the simple case of a linear scale distortion on the -divergence, whereas the operator h is extendedly interpreted as a general case of a non-linear distortion on it.
Definition 4. Suppose that is convex. The -divergence risk measure is defined by By the definition of a convex measure of risk and the convexity of the penalty term in the dual form, it is clear to state that the
-divergence risk measure is a convex measure of risk. It retrieves to the modified
-divergence risk measure in Equation (
12) when
h is linear.
Observing the similar structure to the modified -divergence risk measure, the following property on the static sensitivity with respect to X still holds.
Proposition 5. Under the same assumptions and setting as in Proposition 4, and assuming that exists, The proof can also be derived from [
7,
16].
The following theorem shows that, under certain conditions, the -divergence risk measure can be bounded in terms of the OCE-type form provided by the corresponding -divergence risk measure.
Theorem 2. Under the convexity of , and assuming that satisfies the conditions for a ϕ-divergence, if h is concave,conversely, if h is convex,withwhere is the conjugate function of . Proof. We denote by
v the optimal value of the right hand side minimization problem of the above equation (the notations are presented in
Appendix A.1):
The Lagrangian dual is given by
If
is concave, denoted by
(e.g., log function), by using Jensen inequality and Lemma A1, it follows that
By applying Lemma A2, the equation is equal to the convex risk measure of the OCE-type form
where
is the conjugate of
. It completes the proof by verifying that the ‘constraint qualification’ stated in Theorem 4.2 of [
8] holds, which results in
. For convex
h, the proof is similar. □
Remark 4. If h is convex, the lower bound of any -divergence risk measure is its related ϕ-divergence risk measure. However, when h is concave, there may be a potential range of cases for meeting the demands from the industries since they prefer both convex and smaller measures.
Remark 5. As the -divergence risk measure extends from a general divergence, the degree of complexity of its sensitivity analysis increases, adapting to multi-parameter forms, such as, for instance, Sharma-Mittal divergence [41,42], rather than the one-parameter cases of Tsallis- or Rényi-divergence risk measures. To handle the sensitivity analysis in relation to the multiple parameters involved, with or without different units, we refer to the framework of the differential importance measure (see [43,44] and references therein for details). Rényi-divergence risk measure. Intuitively, the Rényi-divergence risk measure is derived as
where
with
and
, with
and
. When
, Rényi divergence (as well as Tsallis divergence) is equal to KL divergence.
Remark 6. The parameter α of or , as well as θ in , can be interpreted as calibrating parameters of the level of ambiguity aversion in the preferences. However, θ essentially states the balance between the expected risk and the ambiguity aversion, yet α determines the structural profile of ambiguity, which corresponds to the nature of the preferences in the decision-making agents. Their behaviors are shown in the design of the simulation in the next section. The Rényi-divergence risk measure, among others, is deeply discussed in the recent paper [45]. It is easy to check that Rényi divergence is a convex measure of risk when
. Then, the lower bound of the Rényi-divergence risk measure via the convexity of
h is
where
5. Simulated Examples
The aim of the simulations described in this section is to compare the performances for the different divergence-based risk measures. One comparison is given between Rényi-divergence risk measure and Tsallis-divergence risk measure when
. In both divergences, which constitute an important reference in information theory and its multiple applications [
46], the parameter
calibrates the structural deviations between two probability measures and hence, as mentioned before, the profile of ambiguity aversion by the agent in the context of preferences. The second comparison is addressed to assess the effect derived in Tsallis-divergence risk measure by the extra distortion of a non-linear or linear function
h. In this case, the parameter
is in
.
In the setting of the dual representation of convex measures of risk, it is difficult to perform numerical studies depending on the nature of the measure
P and the supremum of
Q without the quantified OCE-type expression. Therefore, it is natural to consider the simulation via the idea of perturbation in the compositional data analysis. We assume an initial discrete distribution
of the financial position
, and the optimized distribution
for
, where
n denotes the size of the sample space, such that
,
. In this case, our proposed risk measure can be rewritten by the form
The complexity of this form increases rapidly with the size of the sample space, so we simplify the setting that
n is 10 and
is from 0.1 to 1 in the numerical studies. Since the influence of the reference distribution
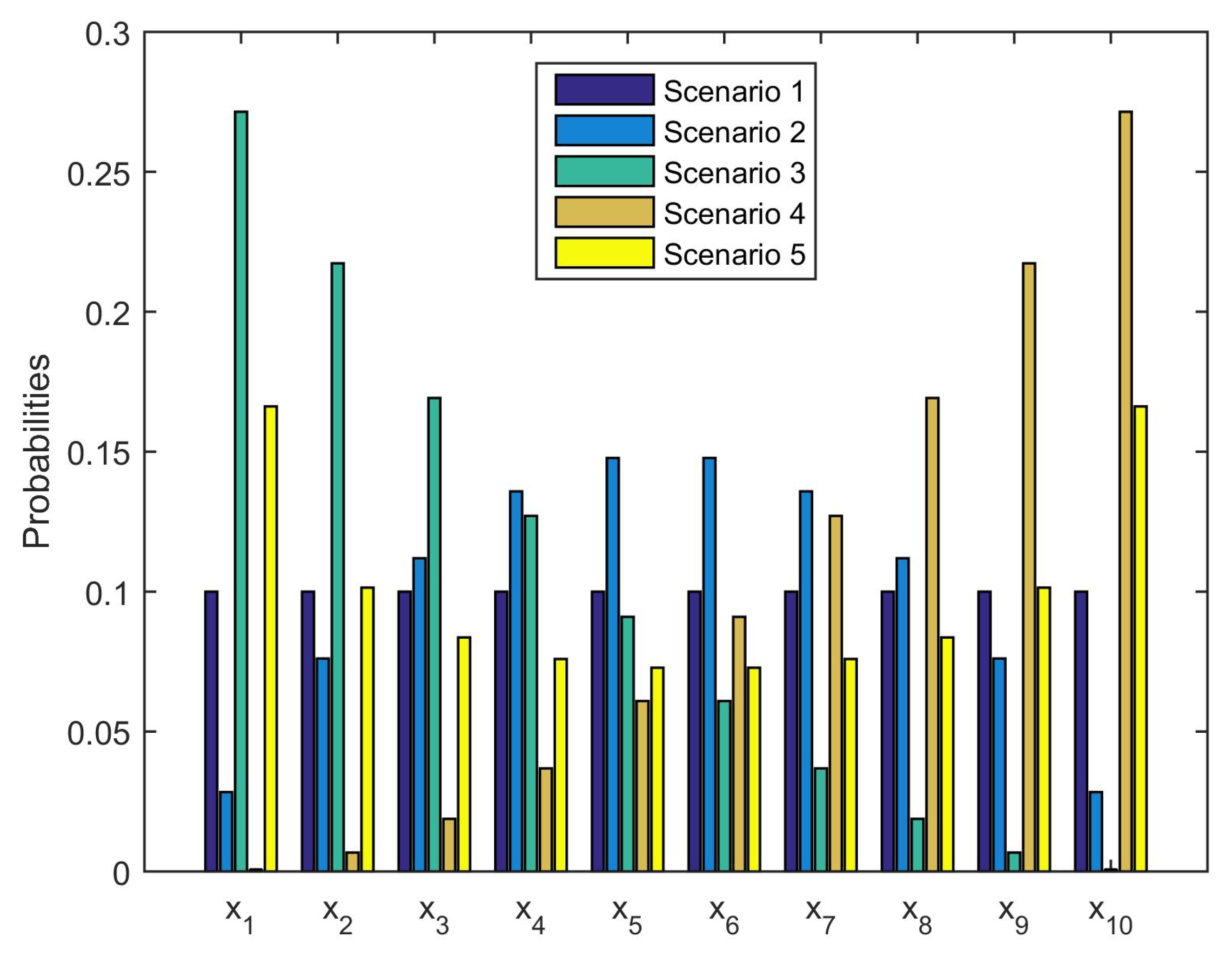
is obviously important to the value of risk measure, we took five scenarios on
with respect to
for consideration, see
Figure 1. Scenario 1 is chosen to be the equiprobability case,
; Scenario 2 consists in assigning the larger probability to the value of
in the middle range and the smaller probability to the small and large values of
; Scenario 3 is putting large probabilities on the small-value financial positions; Scenario 4 is the reverse of Scenario 3; Scenario 5 is the reverse of Scenario 2.
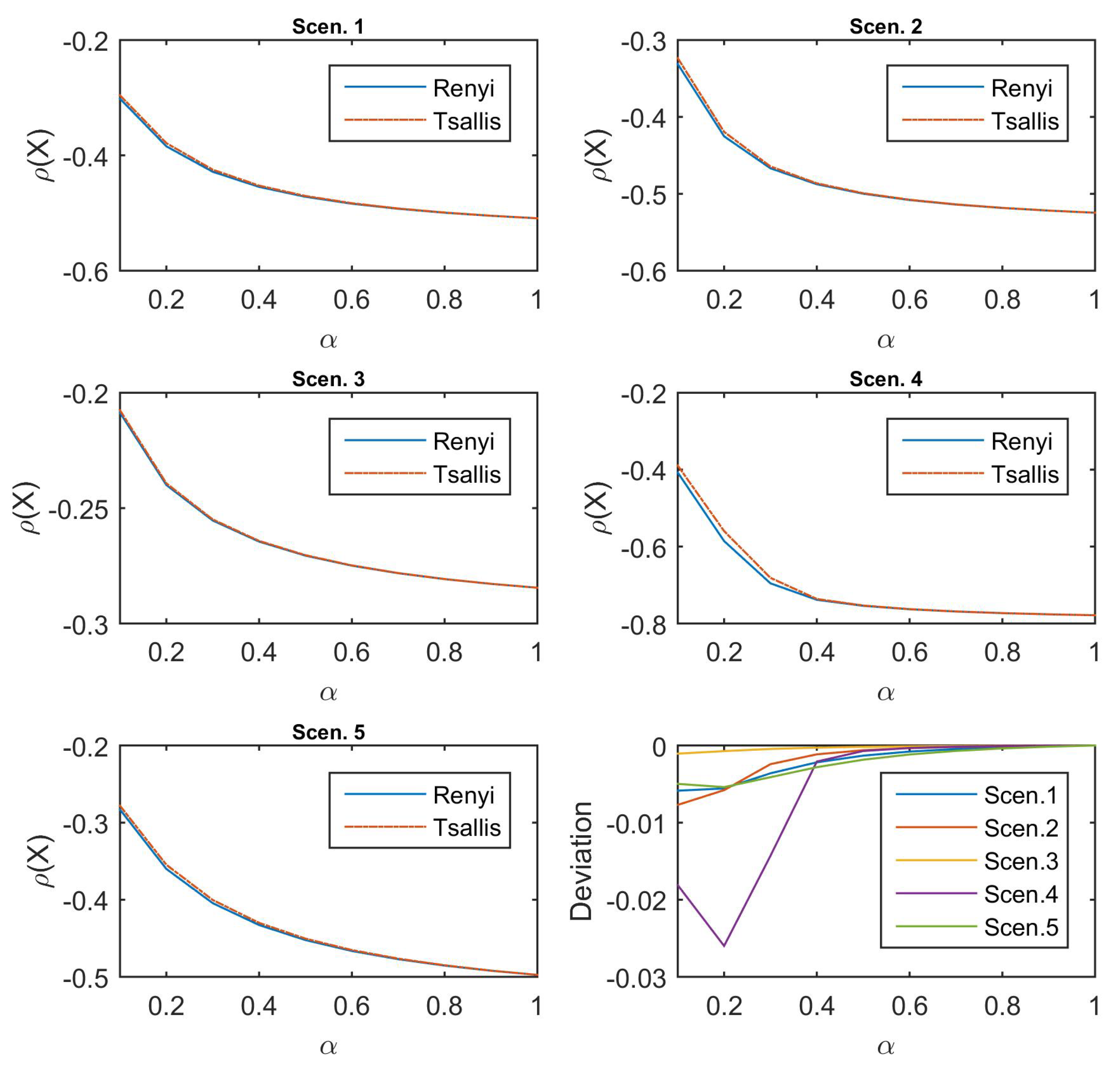
Figure 2 depicts the performance of Rényi-divergence risk measure (the solid line in blue) and Tsallis-divergence risk measure (the solid line in red) under the five scenarios considered, with
. All the five subfigures show the same declining shape of the values for these two risk measures for increasing
, hence the structures of the two penalties do not change that much in the measure of risk according to the same
; the value of Rényi-divergence risk measure is slightly smaller than that of Tsallis-divergence in the last subfigure of
Figure 2. In addition, the deviation in Scenario 4, which puts the larger probabilities on the larger values, is smaller than in other scenarios when
is small, whereas Scenario 3, which is the reverse of Scenario 4, shows almost no deviation of both measures of risk.
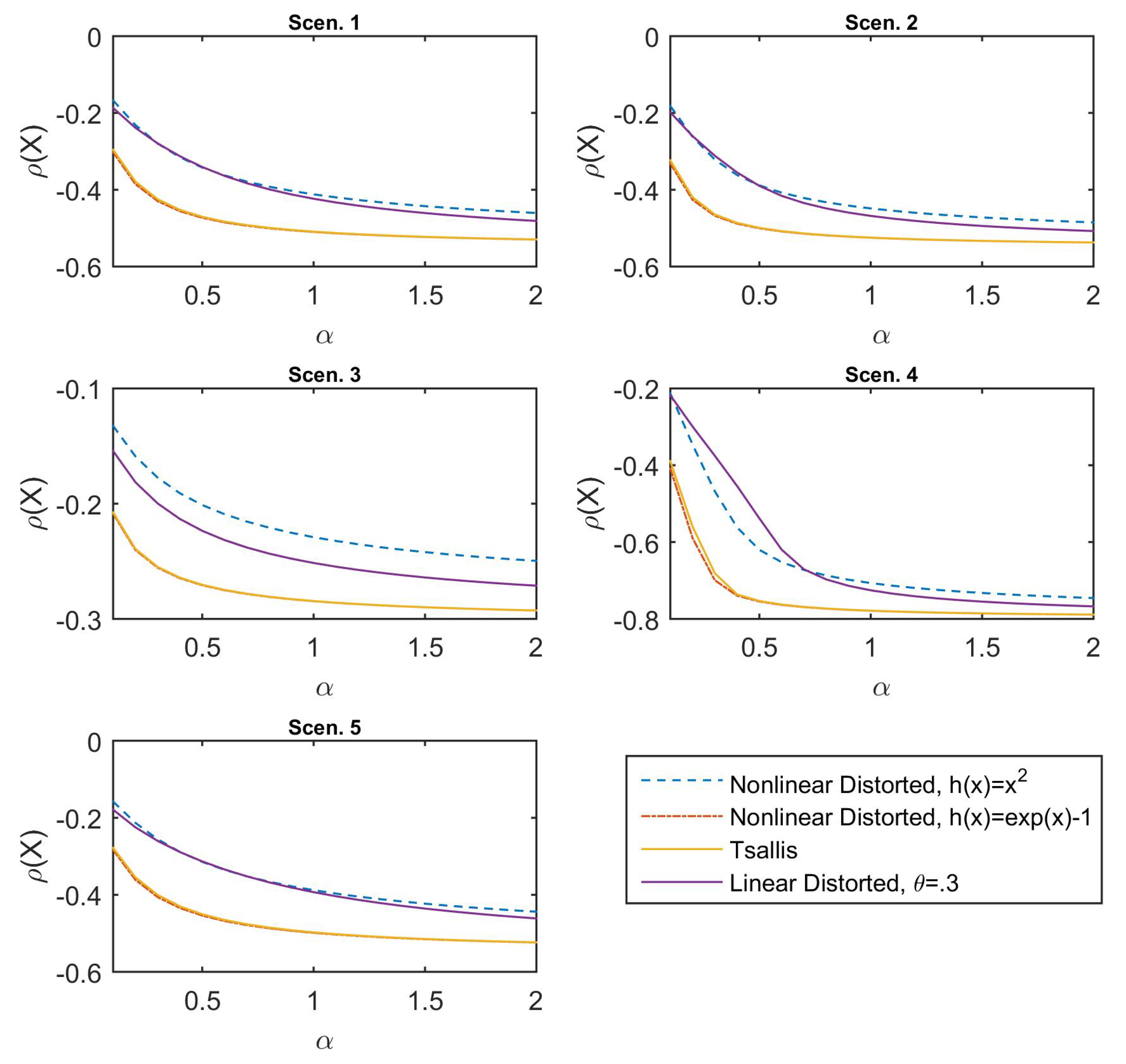
For the second comparison, we consider these three non-linear and linear deformations on Tsallis divergence: (1) Second-order polynomial
; (2) exponential
; and (3) linear case
. The results are presented in
Figure 3. It can be observed that the Tsallis-family risk measures exhibit the same behavior on the declining shapes, the values of which are decreasing for increasing
. In particular, the value of the second-order polynomial (the dash line in blue) is apparently larger but declines more gently than that of the original Tsallis-divergence risk measure (the solid line in yellow), and it also leads to a much stronger distortion on the scale than that of the exponential deformation (the dash–dot line in red), the value of which is slightly smaller than the Tsallis-divergence risk measure. Moreover, even for the linear function (the solid line in purple) operating on Tsallis divergence, the risk measure reveals non-linear variations. Shortly, all the figures verify the fact that the divergence-based risk measure remains sensitive on the reference distribution of the financial positions.
6. Conclusions
A basic and straightforward approach to the analysis of the sensitivity of the modified -divergence convex risk measure based on Gâteaux differentiability is proposed, and further, by non-linearly distorting the divergence, a wider range of the divergence family of convex risk measures is explored. In particular, interest is focused on the deviations of the risk measure derived from slight modifications of both the input financial position in and the probability measure in , benefiting from the preference and robust-statistics area shared with the relative formation and frame, respectively. The extension introduced, called (h,)-divergence risk measure, which is inspired by the dual representation of convex risk measures and covers a larger variety of divergences as penalty functionals, also nurtures the divergence preference on expanding the class of the ambiguity attitudes. A lower bound for the (h,)-divergence risk measure is established in the case where h is a convex function, in terms of the related -divergence risk measure.
Several directions for study on the (
h,
)-divergence risk measure are open and are beyond the sensitivity and boundedness properties discussed in this paper. First, the relationship with the certainty equivalent, in a similar way to the general Donsker-Varadhan formula or the relation between
-divergence risk measure and OCE, would be useful in order to efficiently implement the quantification of risk in practical applications. In this case, the sensitivity property of the (
h,
)-divergence risk measure, with respect to the reference probability, can also be studied through the relation. Furthermore, as shown in [
39,
40], the framework of risk measures on Orlicz space introduced by [
47], applying merely to the law-invariant convex risk measures, is useful for studying their qualitative robustness through Kusuoka representations. Exploring the specific type and comparative degree of robustness for general convex risk measures defined through the dual representation, such as the
-divergence or
-divergence risk measures, also constitutes an important challenge of interest for continuing research.