Stationary-State Statistics of a Binary Neural Network Model with Quenched Disorder
Abstract
1. Introduction
2. Materials and Methods
2.1. The Network Model
2.2. Statistical Properties of the Network Model
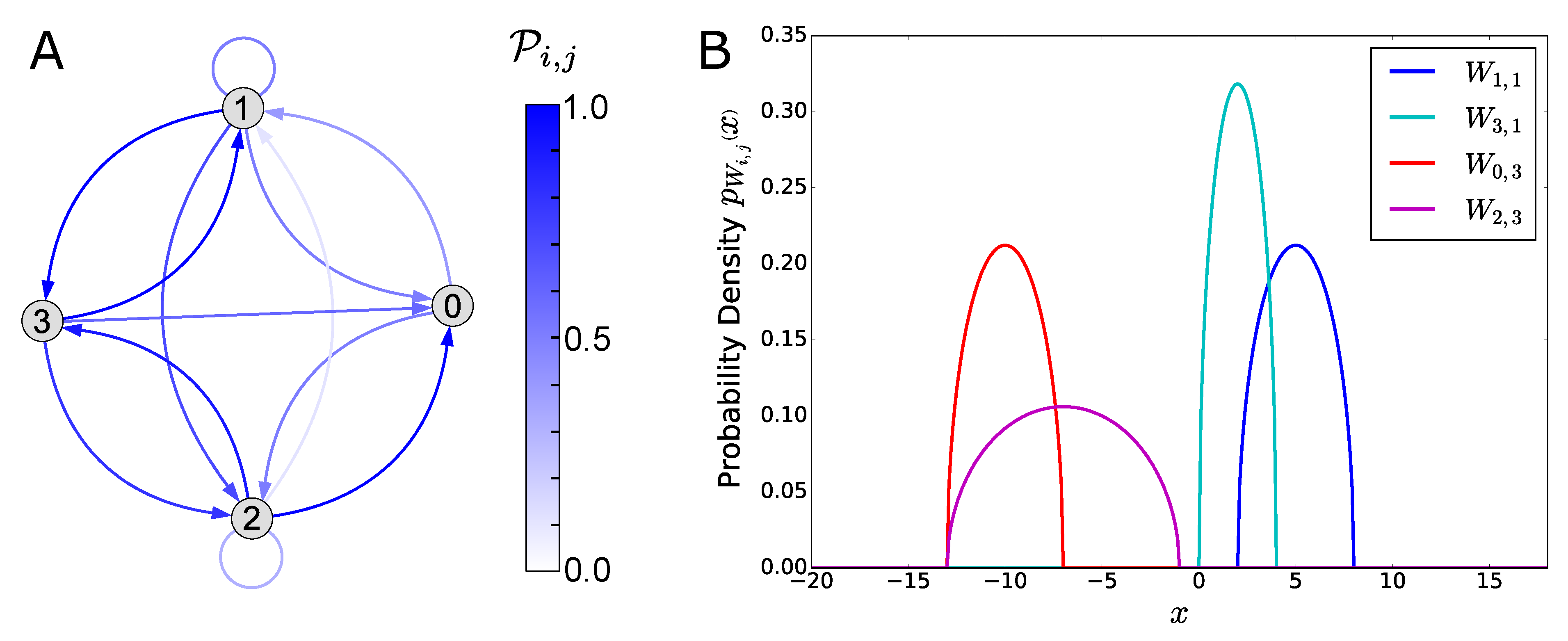
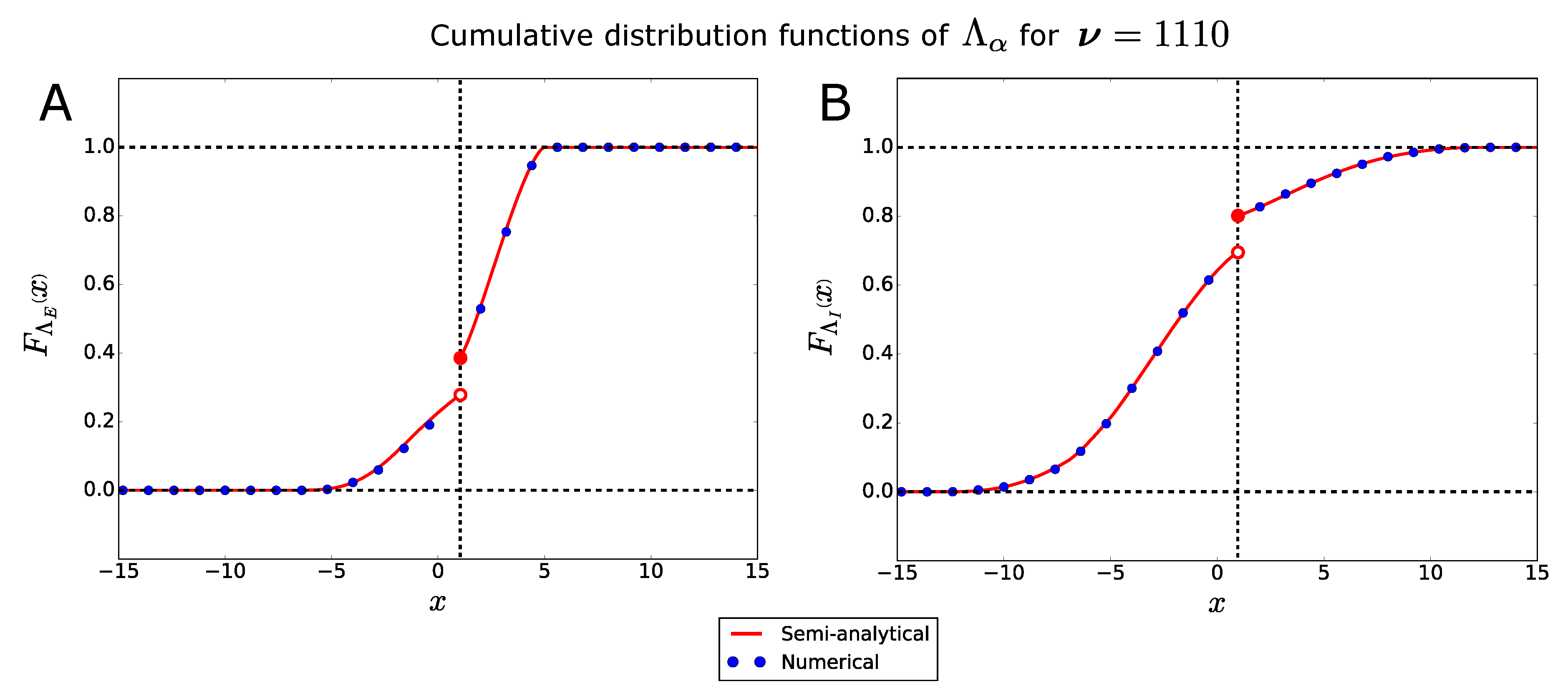
2.2.1. Probability Distribution of the Bifurcation Points
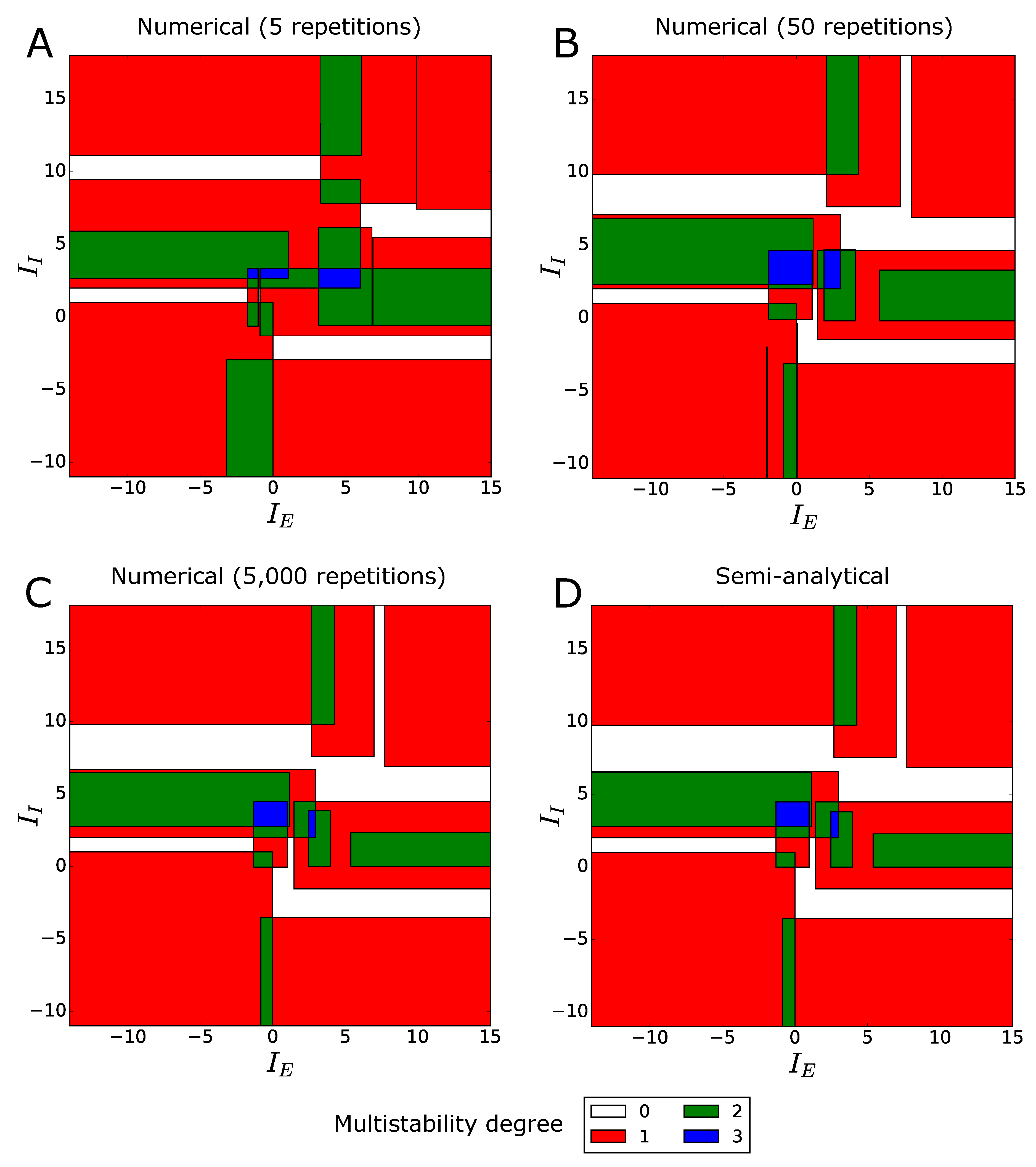
2.2.2. Mean Multistability Diagram
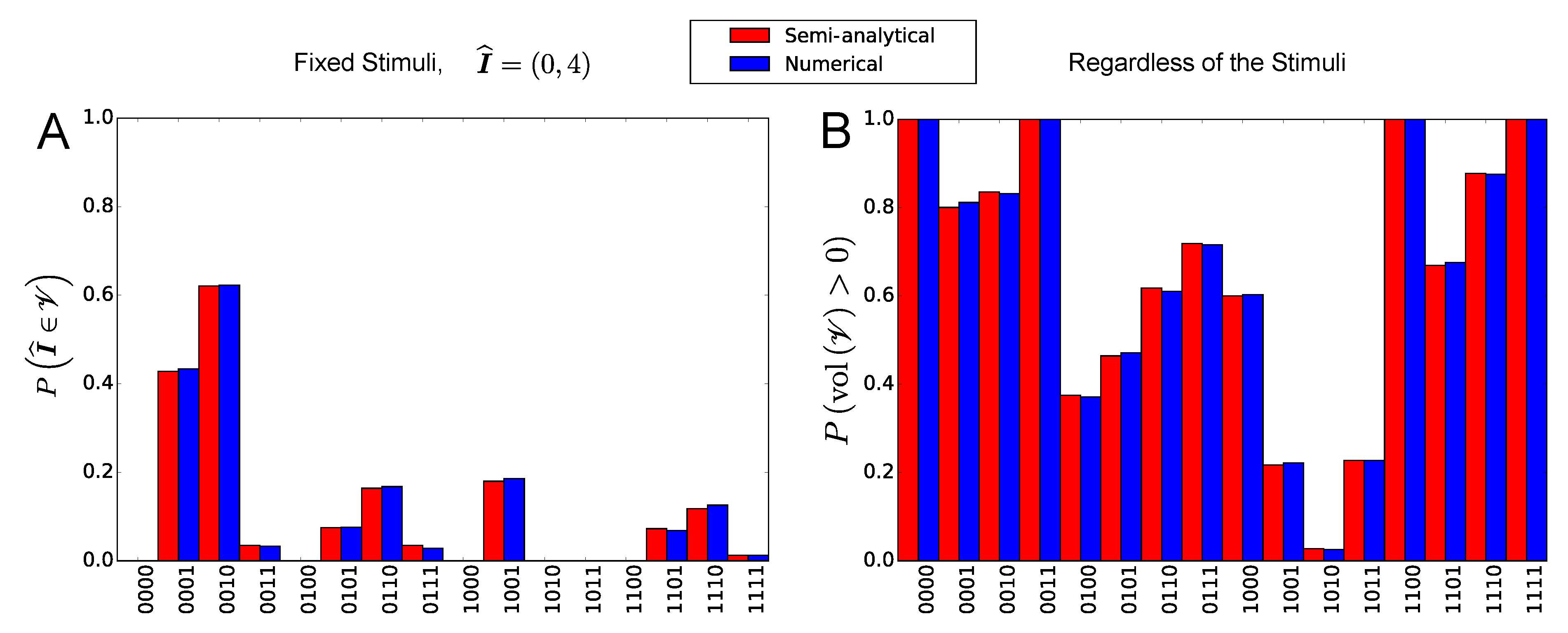
2.2.3. Occurrence Probability of the Stationary States for a Given Combination of Stimuli
2.2.4. Occurrence Probability of the Stationary States Regardless of the Stimuli
2.3. The Special Case of Multi-Population Networks Composed of Statistically Homogeneous Populations
2.4. Large-Network Limit
2.5. Numerical Simulations
3. Results
4. Discussion
4.1. Progress with Respect to Previous Work on Bifurcation Analysis
4.2. Limitations of Our Approach
4.3. Directions for Future Work on the Statistical Mechanics of Networks with Quenched Disorder
4.4. Possible Implications of This Work for Circuit Neuroscience
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Marder, E.; Goaillard, J.M. Variability, compensation and homeostasis in neuron and network function. Nat. Rev. Neurosci. 2006, 7, 563–574. [Google Scholar] [CrossRef] [PubMed]
- Dobrunz, L.E.; Stevens, C.F. Heterogeneity of release probability, facilitation, and depletion at central synapses. Neuron 1997, 18, 995–1008. [Google Scholar] [CrossRef]
- Waters, J.; Smith, S.J. Vesicle pool partitioning influences presynaptic diversity and weighting in rat hippocampal synapses. J. Physiol. 2002, 541, 811–823. [Google Scholar] [CrossRef] [PubMed]
- Parker, D. Variable properties in a single class of excitatory spinal synapse. J. Neurosci. 2003, 23, 3154–3163. [Google Scholar] [CrossRef] [PubMed]
- Branco, T.; Staras, K. The probability of neurotransmitter release: Variability and feedback control at single synapses. Nat. Rev. Neurosci. 2009, 10, 373–383. [Google Scholar] [CrossRef] [PubMed]
- Santhakumar, V.; Soltesz, I. Plasticity of interneuronal species diversity and parameter variance in neurological diseases. Trends Neurosci. 2004, 27, 504–510. [Google Scholar] [CrossRef] [PubMed]
- Sherrington, D.; Kirkpatrick, S. Solvable model of a spin-glass. Phys. Rev. Lett. 1976, 35, 1792–1796. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Sherrington, D. Infinite-ranged models of spin-glasses. Phys. Rev. B 1978, 17, 4384–4403. [Google Scholar] [CrossRef]
- De Almeida, J.R.L.; Thouless, D.J. Stability of the Sherrington-Kirkpatrick solution of a spin glass model. J. Phys. A Math. Gen. 1978, 11, 983–990. [Google Scholar] [CrossRef]
- Mézard, M.; Sourlas, N.; Toulouse, G.; Virasoro, M. Replica symmetry breaking and the nature of the spin glass phase. J. Phys. 1984, 45, 843–854. [Google Scholar] [CrossRef]
- Mézard, M.; Parisi, G.; Virasoro, M. Spin Glass Theory and Beyond: An Introduction to the Replica Method and Its Applications; World Scientific Singapore: Singapore, 1986. [Google Scholar]
- Sherrington, D. Spin glasses. In Physics of Novel Materials; Das, M.P., Ed.; World Scientific Singapore: Singapore, 1999; Chapter 4; pp. 146–204. [Google Scholar] [CrossRef]
- Litwin-Kumar, A.; Doiron, B. Slow dynamics and high variability in balanced cortical networks with clustered connections. Nat. Neurosci. 2012, 15, 1498–1505. [Google Scholar] [CrossRef] [PubMed]
- Doiron, B.; Litwin-Kumar, A. Balanced neural architecture and the idling brain. Front. Comput. Neurosci. 2014, 8, 56. [Google Scholar] [CrossRef] [PubMed]
- Rosenbaum, R.; Doiron, B. Balanced networks of spiking neurons with spatially dependent recurrent connections. Phys. Rev. X 2014, 4, 021039. [Google Scholar] [CrossRef]
- Sompolinsky, H.; Crisanti, A.; Sommers, H.J. Chaos in random neural networks. Phys. Rev. Lett. 1988, 61, 259–262. [Google Scholar] [CrossRef] [PubMed]
- Cessac, B. Increase in complexity in random neural networks. J. Phys. I France 1995, 5, 409–432. [Google Scholar] [CrossRef]
- Faugeras, O.; Touboul, J.; Cessac, B. A constructive mean-field analysis of multi-population neural networks with random synaptic weights and stochastic inputs. Front. Comput. Neurosci. 2009, 3, 1. [Google Scholar] [CrossRef] [PubMed]
- Hermann, G.; Touboul, J. Heterogeneous connections induce oscillations in large-scale networks. Phys. Rev. Lett. 2012, 109, 018702. [Google Scholar] [CrossRef] [PubMed]
- Cabana, T.; Touboul, J. Large deviations, dynamics and phase transitions in large stochastic and disordered neural networks. J. Stat. Phys. 2013, 153, 211–269. [Google Scholar] [CrossRef]
- Coolen, A.C.C.; Sherrington, D. Dynamics of fully connected attractor neural networks near saturation. Phys. Rev. Lett. 1993, 71, 3886–3889. [Google Scholar] [CrossRef]
- Williams, R.W.; Herrup, K. The control of neuron number. Ann. Rev. Neurosci. 1988, 11, 423–453. [Google Scholar] [CrossRef]
- Mountcastle, V.B. The columnar organization of the neocortex. Brain 1997, 120, 701–722. [Google Scholar] [CrossRef] [PubMed]
- Helmstaedter, M.; de Kock, C.P.; Feldmeyer, D.; Bruno, R.M.; Sakmann, B. Reconstruction of an average cortical column in silico. Brain Res. Rev. 2007, 55, 193–203. [Google Scholar] [CrossRef] [PubMed]
- Meyer, H.S.; Wimmer, V.C.; Oberlaender, M.; de Kock, C.P.; Sakmann, B.; Helmstaedter, M. Number and laminar distribution of neurons in a thalamocortical projection column of rat vibrissal cortex. Cereb. Cortex 2010, 20, 2277–2286. [Google Scholar] [CrossRef] [PubMed]
- De Luca, M.; Beckmann, C.F.; de Stefano, N.; Matthews, P.M.; Smith, S.M. fMRI resting state networks define distinct modes of long-distance interactions in the human brain. NeuroImage 2006, 29, 1359–1367. [Google Scholar] [CrossRef] [PubMed]
- Mantini, D.; Perrucci, M.G.; Del Gratta, C.; Romani, G.L.; Corbetta, M. Electrophysiological signatures of resting state networks in the human brain. Proc. Natl. Acad. Sci. USA 2007, 104, 13170–13175. [Google Scholar] [CrossRef] [PubMed]
- Fasoli, D.; Panzeri, S. Optimized brute-force algorithms for the bifurcation analysis of a binary neural network model. Phys. Rev. E 2019, 99, 012316. [Google Scholar] [CrossRef]
- Kuznetsov, Y.A. Elements of Applied Bifurcation Theory; Springer: New York, NY, USA, 1998; Volume 112. [Google Scholar]
- Hopfield, J.J. Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. USA 1982, 79, 2554–2558. [Google Scholar] [CrossRef]
- Coolen, A.C.C. Statistical mechanics of recurrent neural networks I—Statics. In Handbook of Biological Physics; Elsevier: Amsterdam, The Netherlands, 2001; Volume 4, pp. 553–618. [Google Scholar]
- Glauber, R.J. Time dependent statistics of the Ising model. J. Math. Phys. 1963, 4, 294–307. [Google Scholar] [CrossRef]
- De Haan, L.; Ferreira, A. Extreme Value Theory: An Introduction; Springer: New York, NY, USA, 2006. [Google Scholar]
- Vaughan, R.J.; Venables, W.N. Permanent expressions for order statistic densities. J. R. Stat. Soc. Ser. B 1972, 34, 308–310. [Google Scholar] [CrossRef]
- Bapat, R.B.; Beg, M.I. Order statistics for nonidentically distributed variables and permanents. Sankhyā Ser. A 1989, 51, 79–93. [Google Scholar]
- Bapat, R.B. Permanents in probability and statistics. Linear Algebra Appl. 1990, 127, 3–25. [Google Scholar] [CrossRef]
- Hande, S. A note on order statistics for nondentically distributed variables. Sankhyā Ser. A 1994, 56, 365–368. [Google Scholar]
- Valiant, L.G. The complexity of computing the permanent. Theor. Comput. Sci. 1979, 8, 189–201. [Google Scholar] [CrossRef]
- Balasubramanian, K. Combinatorics and Diagonals of Matrices. Ph.D. Thesis, Indian Statistical Institute, Calcutta, India, 1980. [Google Scholar]
- Bax, E.; Franklin, J. A Finite-Difference Sieve to Compute the Permanent; Technical Report CalTech-CS-TR-96-04; CalTech: Pasadena, CA, USA, 1996. [Google Scholar]
- Bax, E. Finite-Difference Algorithms for Counting Problems. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 1998. [Google Scholar]
- Glynn, D.G. The permanent of a square matrix. Eur. J. Combin. 2010, 31, 1887–1891. [Google Scholar] [CrossRef]
- Billingsley, P. Probability and Measure; John Wiley & Sons: New York, NY, USA, 1995. [Google Scholar]
- Sompolinsky, H.; Zippelius, A. Dynamic theory of the spin-glass phase. Phys. Rev. Lett. 1981, 47, 359–362. [Google Scholar] [CrossRef]
- Ben-Arous, G.; Dembo, A.; Guionnet, A. Aging of spherical spin glasses. Probab. Theory Relat. Fields 2001, 120, 1–67. [Google Scholar] [CrossRef]
- Yilmaz, E.; Ozer, M.; Baysal, V.; Perc, M. Autapse-induced multiple coherence resonance in single neurons and neuronal networks. Sci. Rep. 2016, 6. [Google Scholar] [CrossRef] [PubMed]
- Fisher, R.A.; Tippett, L.H.C. Limiting forms of the frequency distribution of the largest or smallest member of a sample. Math. Proc. Camb. Philos. Soc. 1928, 24, 180–190. [Google Scholar] [CrossRef]
- Gnedenko, B. Sur la distribution limite du terme maximum d’une série aléatoire. Ann. Math. 1943, 44, 423–453. [Google Scholar] [CrossRef]
- Gumbel, E.J. Statistics of Extremes; Columbia University Press: New York, NY, USA, 1958. [Google Scholar]
- Vivo, P. Large deviations of the maximum of independent and identically distributed random variables. Eur. J. Phys. 2015, 36, 055037. [Google Scholar] [CrossRef]
- Strata, P.; Harvey, R. Dale’s principle. Brain Res. Bull. 1999, 50, 349–350. [Google Scholar] [CrossRef]
- Fasoli, D.; Cattani, A.; Panzeri, S. Pattern storage, bifurcations and groupwise correlation structure of an exactly solvable asymmetric neural network model. Neural Comput. 2018, 30, 1258–1295. [Google Scholar] [CrossRef] [PubMed]
- Borisyuk, R.M.; Kirillov, A.B. Bifurcation analysis of a neural network model. Biol. Cybern. 1992, 66, 319–325. [Google Scholar] [CrossRef] [PubMed]
- Beer, R.D. On the dynamics of small continuous-time recurrent neural networks. Adapt. Behav. 1995, 3, 469–509. [Google Scholar] [CrossRef]
- Pasemann, F. Complex dynamics and the structure of small neural networks. Netw.-Comp. Neural 2002, 13, 195–216. [Google Scholar] [CrossRef]
- Haschke, R.; Steil, J.J. Input space bifurcation manifolds of recurrent neural networks. Neurocomputing 2005, 64, 25–38. [Google Scholar] [CrossRef]
- Leine, R.I.; van Campen, D.H.; van de Vrande, B.L. Bifurcations in nonlinear discontinuous systems. Nonlinear Dyn. 2000, 23, 105–164. [Google Scholar] [CrossRef]
- Awrejcewicz, J.; Lamarque, C.H. Bifurcation and Chaos in Nonsmooth Mechanical Systems; World Scientific: Singapore, 2003. [Google Scholar]
- Leine, R.I.; van Campen, D.H. Bifurcation phenomena in non-smooth dynamical systems. Eur. J. Mech. A-Solid 2006, 25, 595–616. [Google Scholar] [CrossRef]
- Makarenkov, O.; Lamb, J.S.W. Dynamics and bifurcations of nonsmooth systems: A survey. Phys. D 2012, 241, 1826–1844. [Google Scholar] [CrossRef]
- Harris, J.; Ermentrout, B. Bifurcations in the Wilson–Cowan equations with nonsmooth firing rate. SIAM J. Appl. Dyn. Syst. 2015, 14, 43–72. [Google Scholar] [CrossRef]
- Parui, S.; Banerjee, S. Border collision bifurcations at the change of state-space dimension. Chaos 2002, 12, 1054–1069. [Google Scholar] [CrossRef] [PubMed]
- Avrutin, V.; Schanz, M.; Banerjee, S. Multi-parametric bifurcations in a piecewise-linear discontinuous map. Nonlinearity 2006, 19, 1875–1906. [Google Scholar] [CrossRef]
- Mézard, M.; Parisi, G. The cavity method at zero temperature. J. Stat. Phys. 2003, 111, 1–34. [Google Scholar] [CrossRef]
- Kreinovich, V.; Nguyen, H.T.; Sriboonchitta, S.; Kosheleva, O. Modeling extremal events is not easy: Why the extreme value theorem cannot be as general as the central limit theorem. In Uncertainty Modeling; Kreinovich, V., Ed.; Springer International Publishing: New York, NY, USA, 2017; Chapter 8; pp. 123–133. [Google Scholar] [CrossRef]
- Faugeras, O.; MacLaurin, J. Asymptotic description of neural networks with correlated synaptic weights. Entropy 2015, 17, 4701–4743. [Google Scholar] [CrossRef]
- Bao, G.; Zeng, Z. Analysis and design of associative memories based on recurrent neural network with discontinuous activation functions. Neurocomputing 2012, 77, 101–107. [Google Scholar] [CrossRef]
- Treves, A.; Rolls, E.T. What determines the capacity of autoassociative memories in the brain? Netw. Comput. Neural Syst. 1991, 2, 371–397. [Google Scholar] [CrossRef]
- Brunel, N.; Wang, X.J. What determines the frequency of fast network oscillations with irregular neural discharges? I. Synaptic dynamics and excitation-inhibition balance. J. Neurophysiol. 2003, 90, 415–430. [Google Scholar] [CrossRef] [PubMed]
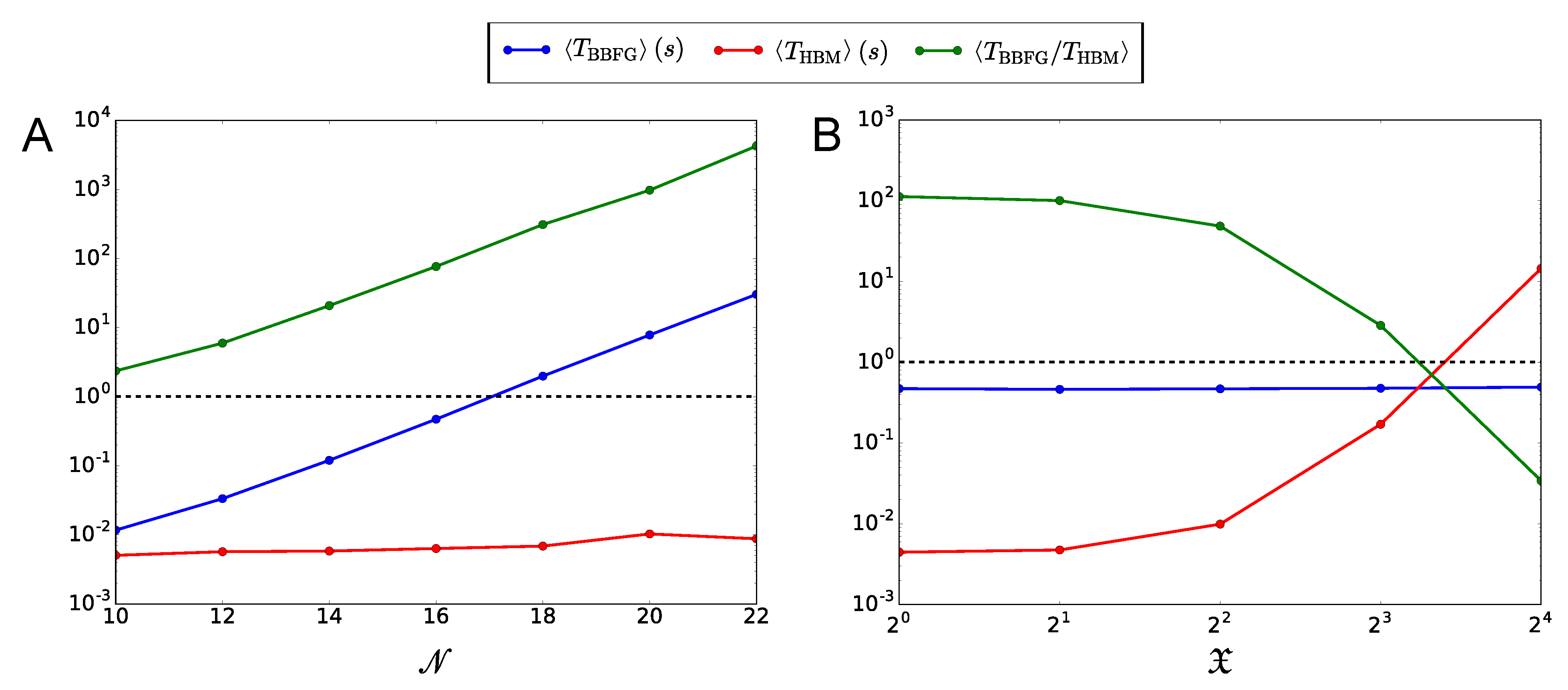
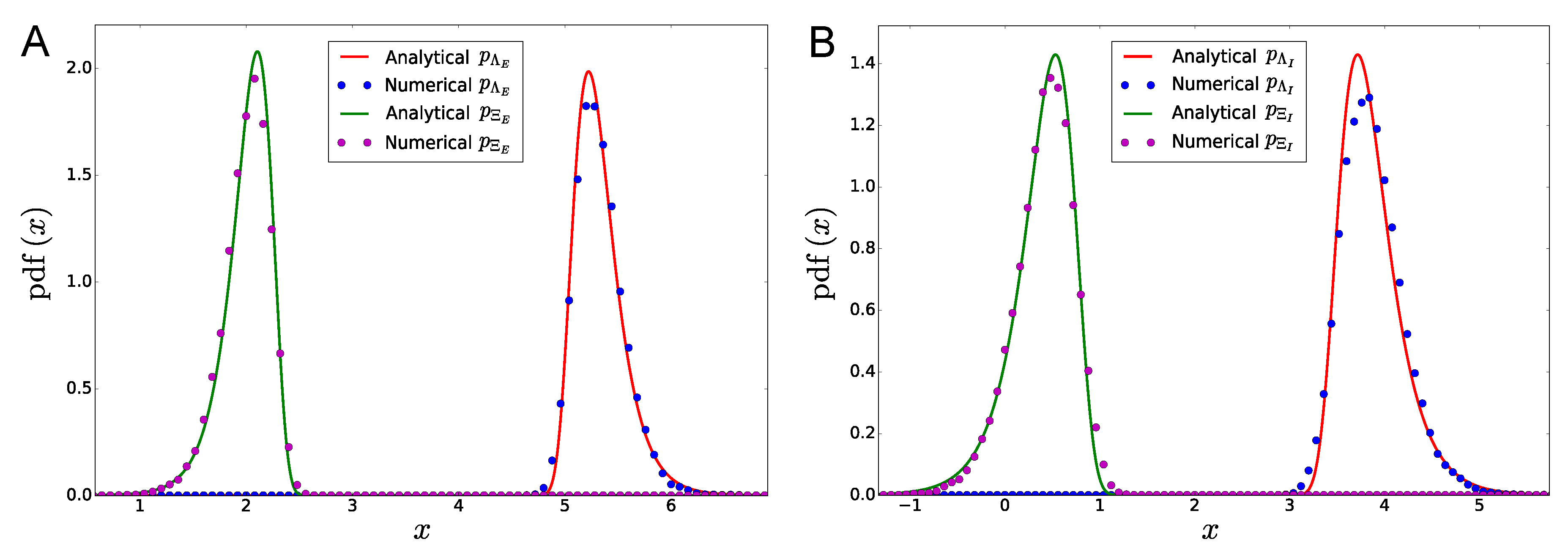
| Panel A | |||
|---|---|---|---|
| Panel B | |||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fasoli, D.; Panzeri, S. Stationary-State Statistics of a Binary Neural Network Model with Quenched Disorder. Entropy 2019, 21, 630. https://doi.org/10.3390/e21070630
Fasoli D, Panzeri S. Stationary-State Statistics of a Binary Neural Network Model with Quenched Disorder. Entropy. 2019; 21(7):630. https://doi.org/10.3390/e21070630
Chicago/Turabian StyleFasoli, Diego, and Stefano Panzeri. 2019. "Stationary-State Statistics of a Binary Neural Network Model with Quenched Disorder" Entropy 21, no. 7: 630. https://doi.org/10.3390/e21070630
APA StyleFasoli, D., & Panzeri, S. (2019). Stationary-State Statistics of a Binary Neural Network Model with Quenched Disorder. Entropy, 21(7), 630. https://doi.org/10.3390/e21070630






