Experimental Investigation of a 300 kW Organic Rankine Cycle Unit with Radial Turbine for Low-Grade Waste Heat Recovery
Abstract
1. Introduction
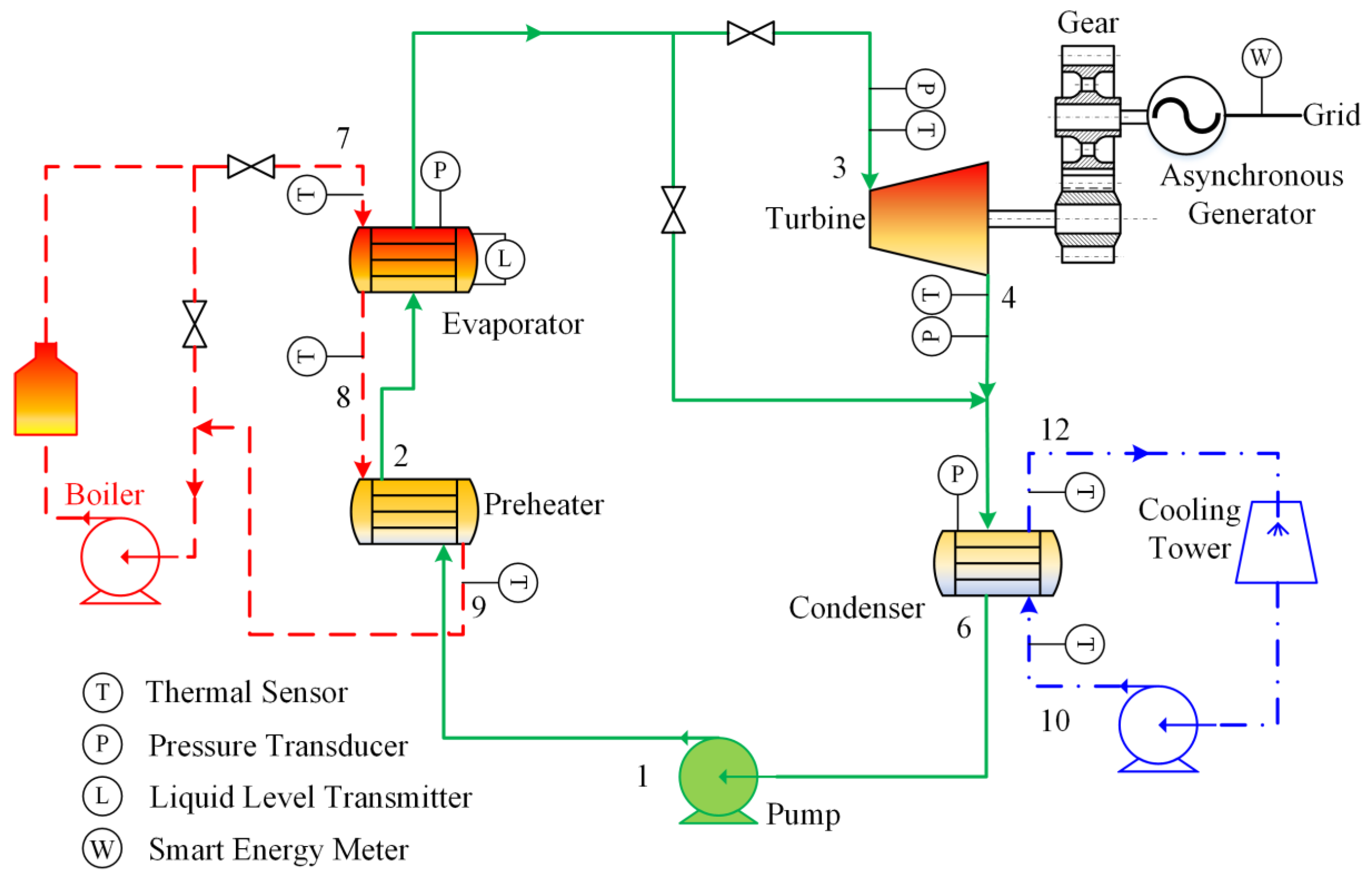
2. Experimental Apparatus and Equipment
2.1. Heating Source Loop
2.2. ORC Loop
2.3. Cooling Source Loop
2.4. Measurement Instruments and Uncertainty Analysis
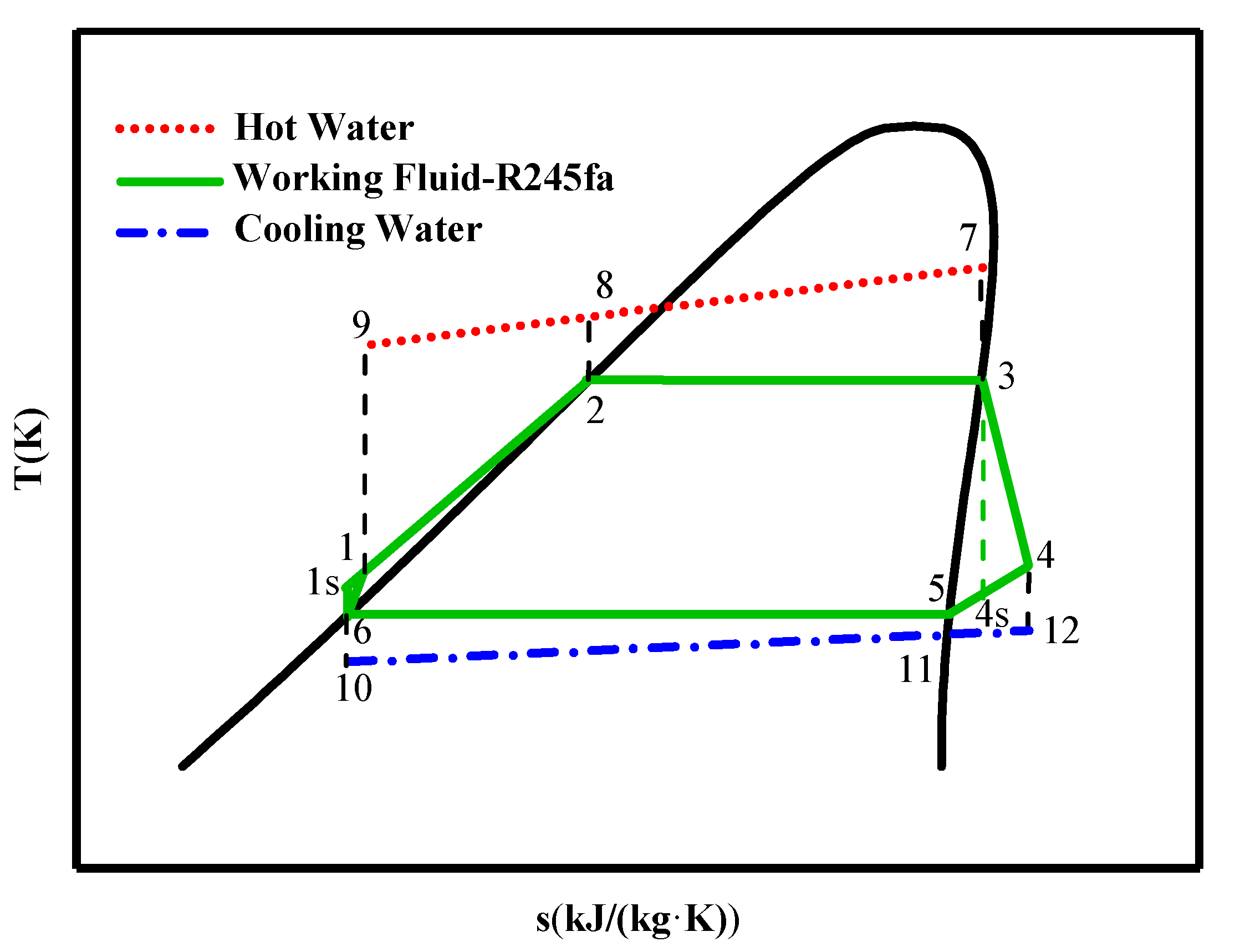
3. Thermodynamic Analysis
4. Experimental Results and Discussion
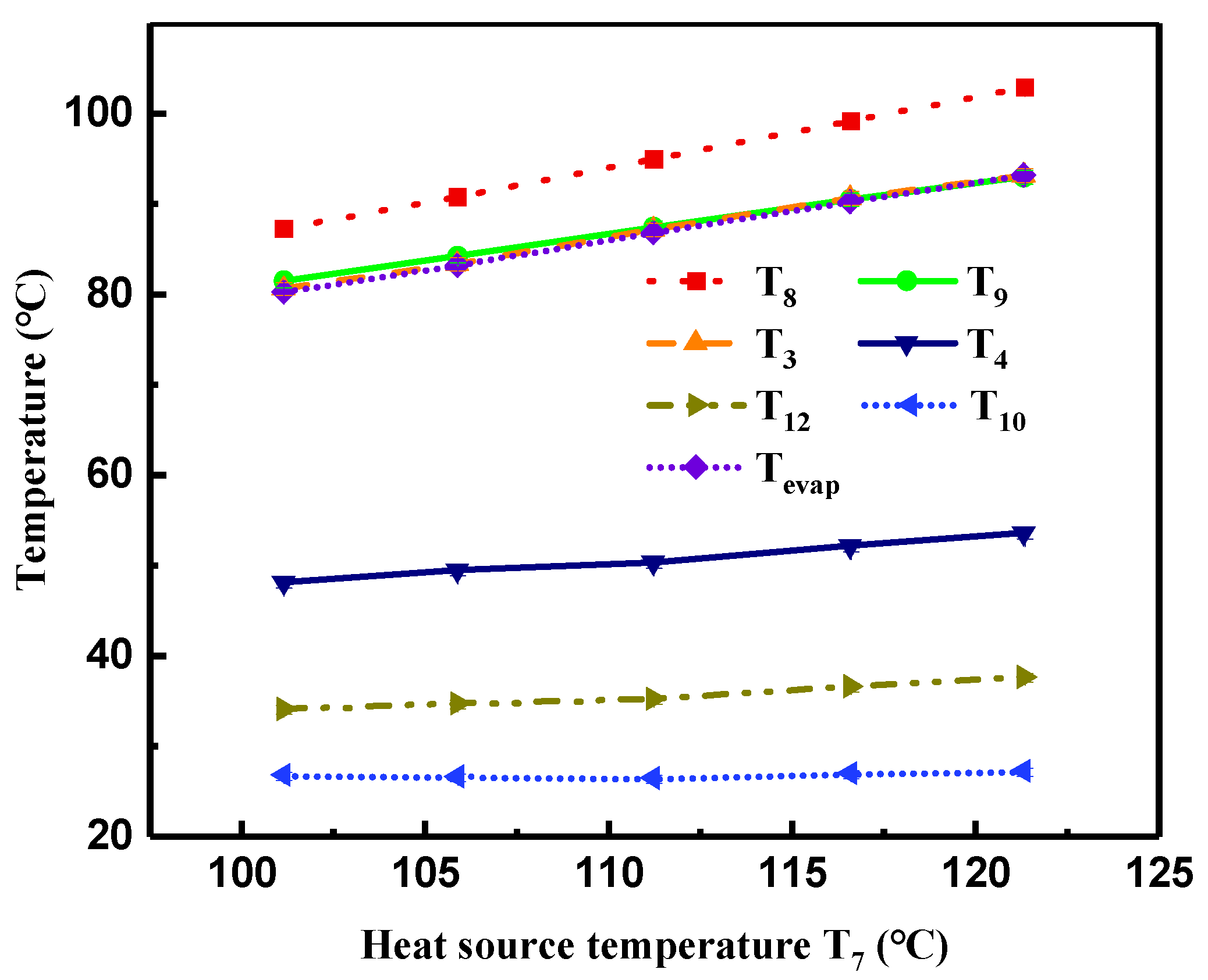
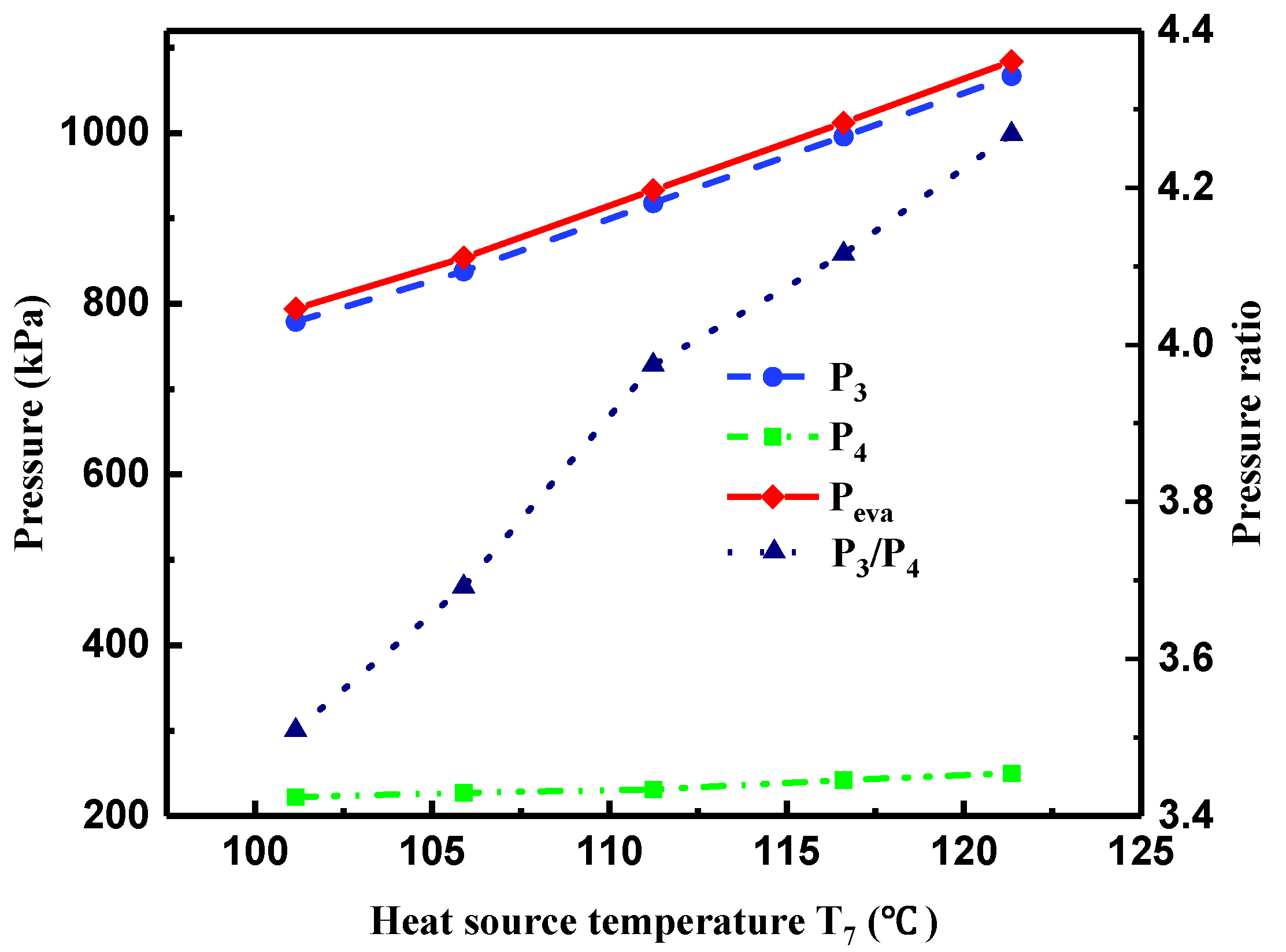
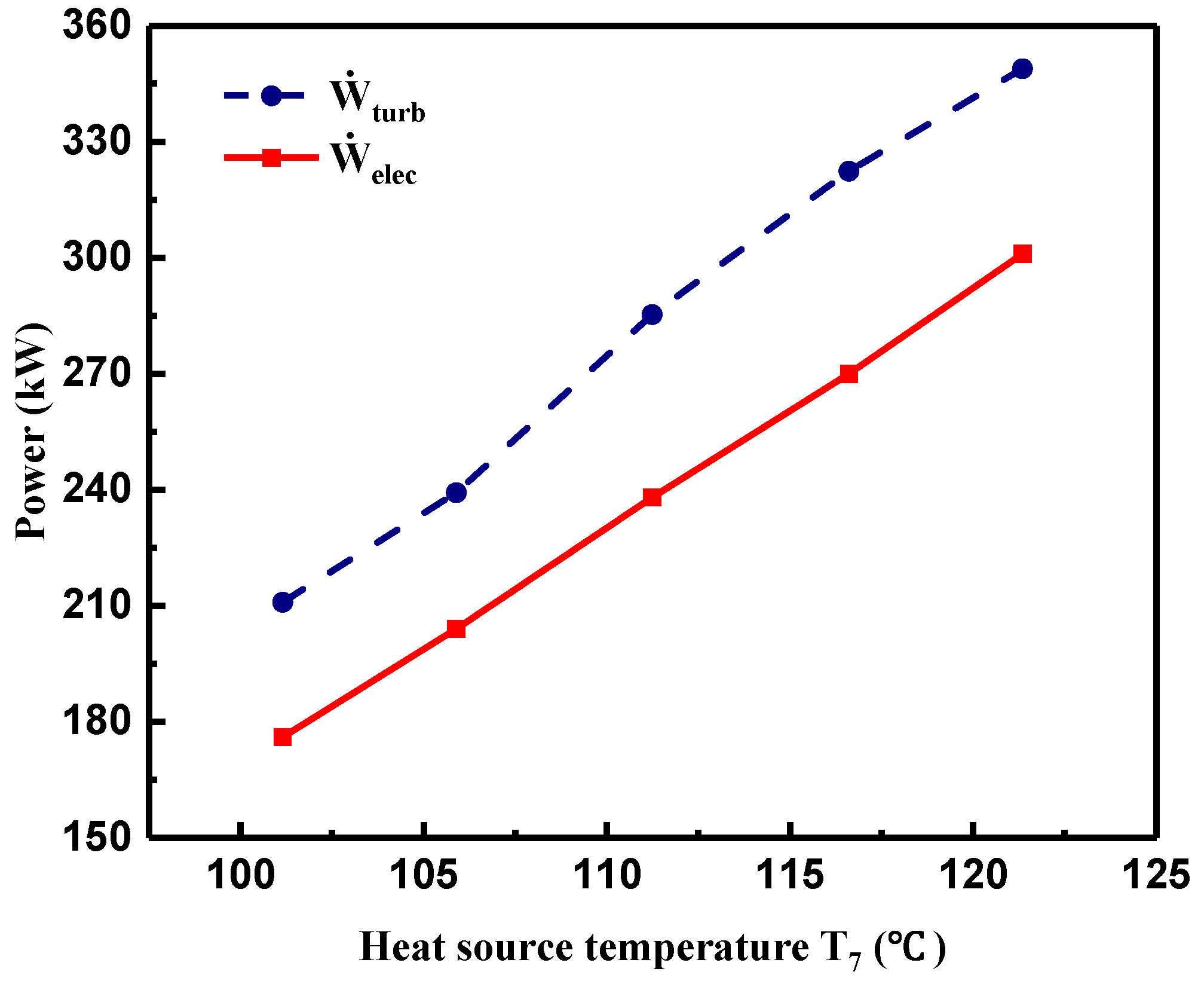
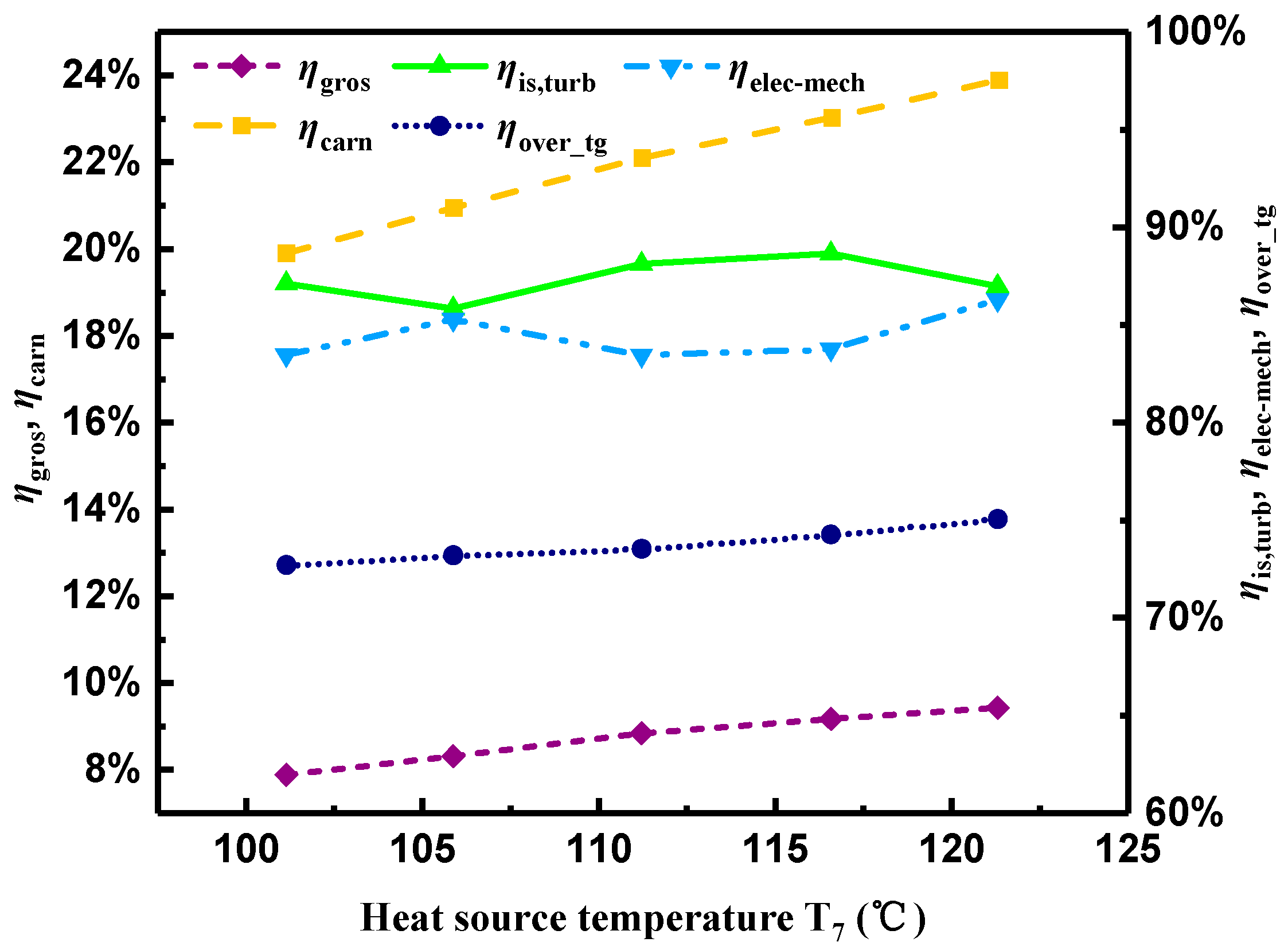
4.1. Effect of Heat Source Temperature on System Performance
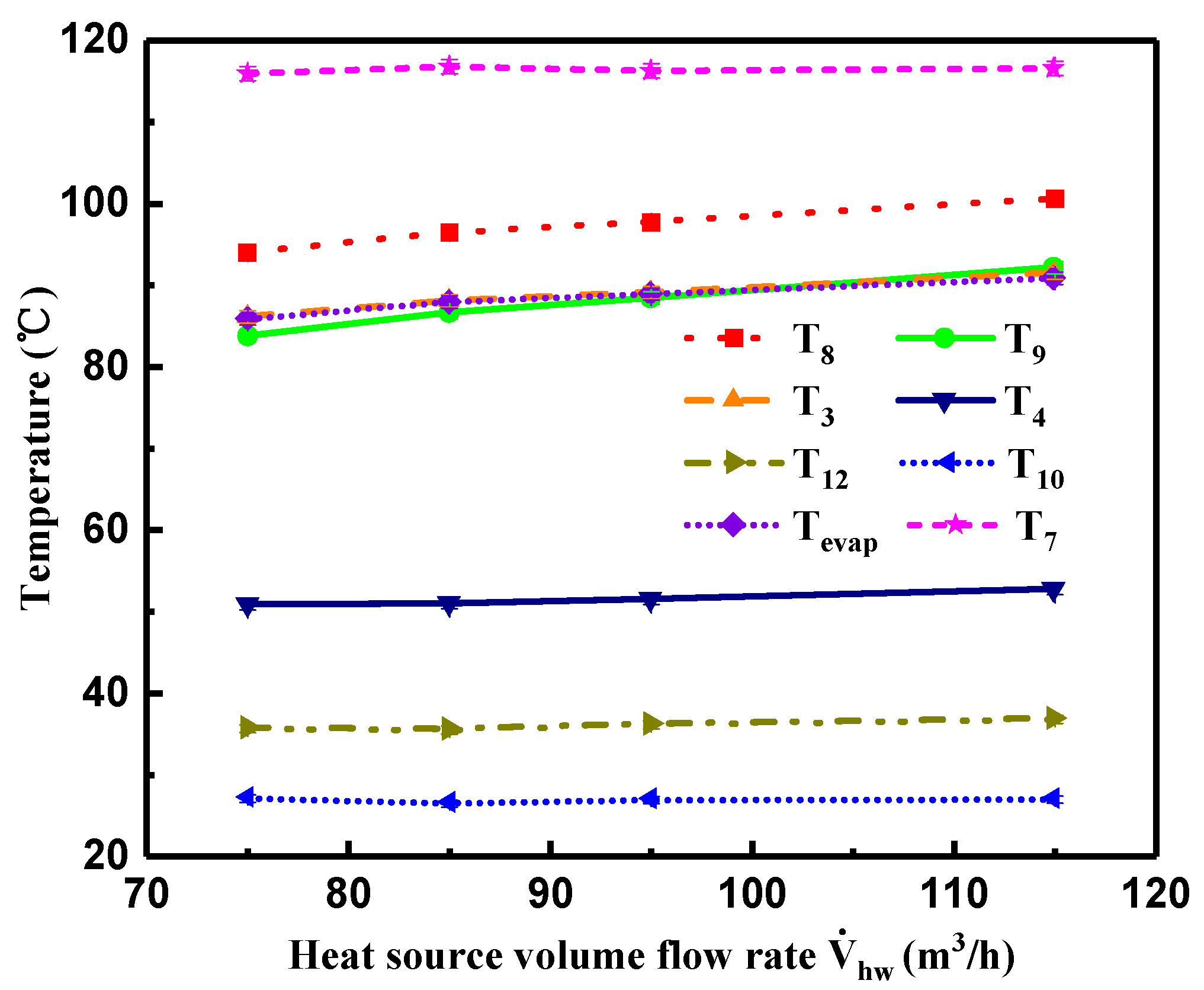
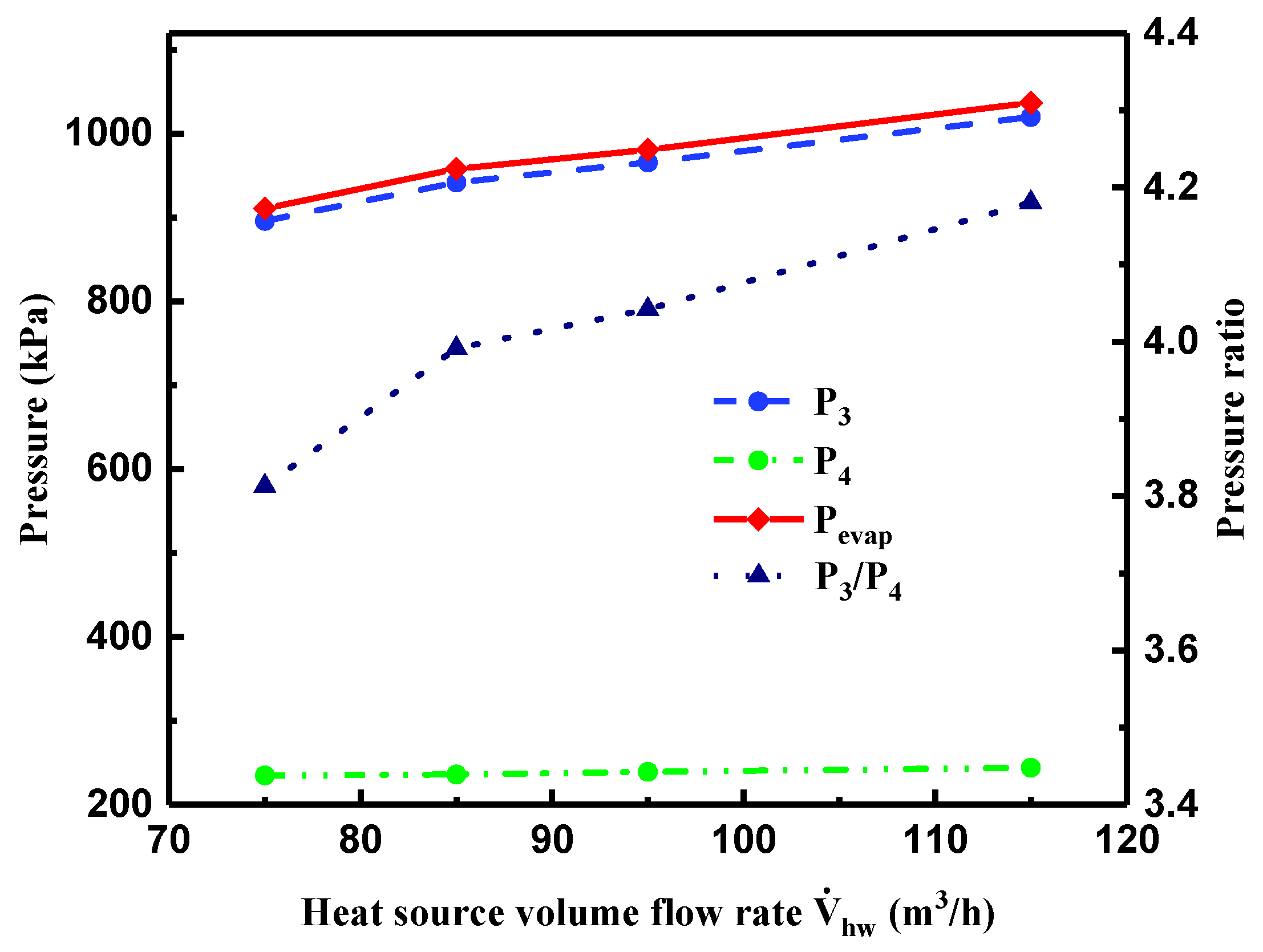
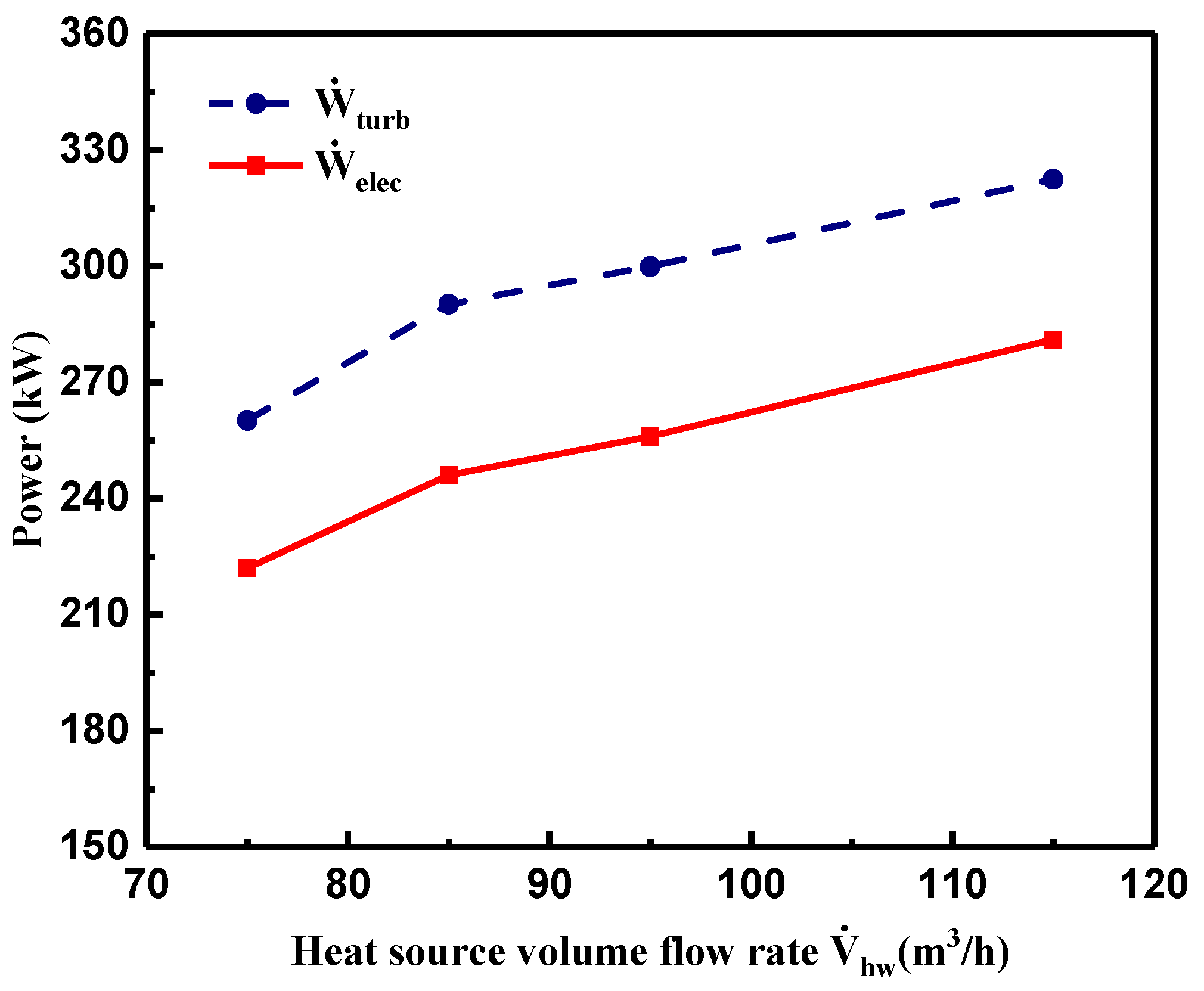
4.2. Effect of Heat Source Volume Flow Rate on System Performance
5. Conclusions
- As the heat transfer rates in the evaporator and preheater increased with the increasing heat source temperature or volume flow rate, the heat source temperature at the evaporator and preheater outlet, the temperature of R245fa at the turbine inlet and outlet, and the evaporation temperature of R245fa increased to some extent. However, the cooling water temperature at the condenser outlet showed a relatively slight variation due to the approximately constant operating condition of the cooling source.
- The evaporation pressure and the pressure of R245fa at the turbine inlet exhibited a noticeable increment with higher heat transfer rate in the evaporator, while the pressure of R245fa at the turbine outlet presented a gradual increasing tendency, resulting in the increased electric power output and gross generating efficiency. The highest electric power output and gross generating efficiency were 301 kW and 9.4%, respectively. Higher electric power output yielded higher gross generating efficiency.
- The maximum Carnot efficiency, the theoretical thermodynamic limit of ORC, was 23.9%, which indicates that it is a technology with intrinsic low efficiency. The gross generating efficiency of the ORC in the current experiment accounted for about 40.5% of the Carnot efficiency, which was higher than the average value obtained by statistics. The turbine isentropic efficiency was above 85%. As for improving the system efficiency, regenerative ORC or regenerative extraction ORC could be employed. Furthermore, an economic evaluation would be indispensable when improving the ORC performance.
- Both the turbine isentropic efficiency and electromechanical efficiency of the generator had slight variations with diverse heat source temperature and volume flow rate, but the trends were contrary. The maximum isentropic efficiency of 88.6% and electromechanical efficiency of 87.1% were obtained.
- The overall efficiency of the integrated turbine and generator exhibited a gentle variation, which indicated that it was in a stable operating condition in the experiments.
Author Contributions
Acknowledgments
Conflicts of Interest
Nomenclature
| heat transfer rate, kW | |
| power, kW | |
| temperature, °C | |
| volume flow rate, m3/h | |
| mass flow rate, kg/s | |
| enthalpy, kJ/kg | |
| Greek symbols | |
| isentropic efficiency of turbine | |
| gross generating efficiency of ORC system | |
| electromechanical efficiency of generator unit | |
| overall efficiency of integrated turbine and generator unit | |
| Carnot efficiency | |
| Subscripts | |
| 1–12 | state points |
| hw | hot water |
| wf | working fluid |
| cw | cooling water |
| preh | preheater |
| evap | evaporator |
| turb | turbine |
| cond | condenser |
| pump | pump |
References
- BP Statistical Review of World Energy in 2018. Available online: https://www.bp.com/zh_cn/china/reports-and-publications/_bp_2018-_.html (accessed on 30 July 2018).
- Yamamoto, T.; Furuhata, T.; Arai, N.; Mori, K. Design and testing of the Organic Rankine Cycle. Energy 2001, 26, 239–251. [Google Scholar] [CrossRef]
- Hung, T.C.; Shai, T.Y.; Wang, S.K. A Review of organic rankine cycles (ORCs) for the recovery of low-grade waste heat. Energy 1997, 22, 661–667. [Google Scholar] [CrossRef]
- Chen, H.; Goswami, D.Y.; Stefanakos, E.K. A review of thermodynamic cycles and working fluids for the conversion of low-grade heat. Renew. Sust. Energy Rev. 2010, 14, 3059–3067. [Google Scholar] [CrossRef]
- Bao, J.; Zhao, L. A review of working fluid and expander selections for organic Rankine cycle. Renew. Sust. Energy Rev. 2013, 24, 325–342. [Google Scholar] [CrossRef]
- Imran, M.; Haglind, F.; Asim, M.; Zeb Alvi, J. Recent research trends in organic Rankine cycle technology: A bibliometric approach. Renew. Sust. Energy Rev. 2018, 81, 552–562. [Google Scholar] [CrossRef]
- Quoilin, S.; Lemort, V. Technological and Economical Survey of Organic Rankine Cycle Systems. Available online: https://orbi.uliege.be/handle/2268/14609 (accessed on 23 June 2019).
- Piero, C.; Emiliano, C.; Carsten, T.; Tiemo, M.; Jaakko, L.; Turunen-Saaresti, T.; Uusitalo, A. Organic Rankine Cycle Power Systems- From the Concept to Current Technology, Applications, and an Outlook to the Future. J. Eng. Gas Turb. Power 2015, 137. [Google Scholar] [CrossRef]
- Hung, T.C. Waste heat recovery of organic Rankine cycle using dry fluids. Energy Convers. Manag. 2001, 42, 539–553. [Google Scholar] [CrossRef]
- Liu, B.-T.; Chien, K.-H.; Wang, C.-C. Effect of working fluids on organic Rankine cycle for waste heat recovery. Energy 2004, 29, 1207–1217. [Google Scholar] [CrossRef]
- Modi, A.; Haglind, F. A review of recent research on the use of zeotropic mixtures in power generation systems. Energy Convers. Manag. 2017, 138, 603–626. [Google Scholar] [CrossRef]
- Feng, Y.-Q.; Luo, Q.-H.; Wang, Q.; Wang, S.; He, Z.-X.; Zhang, W.; Wang, X.; An, Q.-S. Entropy and Entransy Dissipation Analysis of a Basic Organic Rankine Cycles (ORCs) to Recover Low-Grade Waste Heat Using Mixture Working Fluids. Entropy 2018, 20, 818. [Google Scholar] [CrossRef]
- Kosmadakis, G.; Landelle, A.; Lazova, M.; Manolakos, D.; Kaya, A.; Huisseune, H.; Karavas, C.-S.; Tauveron, N.; Revellin, R.; Haberschill, P.; et al. Experimental testing of a low-temperature organic Rankine cycle (ORC) engine coupled with concentrating PV/thermal collectors: Laboratory and field tests. Energy 2016, 117, 222–236. [Google Scholar] [CrossRef]
- Lemort, V.; Quoilin, S.; Cuevas, C.; Lebrun, J. Testing and modeling a scroll expander integrated into an Organic Rankine Cycle. Appl. Therm. Eng. 2009, 29, 3094–3102. [Google Scholar] [CrossRef]
- Imran, M.; Usman, M.; Park, B.S.; Lee, D.H. Volumetric expanders for low grade heat and waste heat recovery applications. Renew. Sust. Energy Rev. 2016, 57, 1090–1109. [Google Scholar] [CrossRef]
- Song, P.; Wei, M.; Shi, L.; Danish, S.N.; Ma, C. A review of scroll expanders for organic Rankine cycle systems. Appl. Therm. Eng. 2015, 75, 54–64. [Google Scholar] [CrossRef]
- Rahbar, K.; Mahmoud, S.; Al-Dadah, R.K.; Moazami, N.; Mirhadizadeh, S.A. Review of organic Rankine cycle for small-scale applications. Energy Convers. Manag. 2017, 134, 135–155. [Google Scholar] [CrossRef]
- Park, B.-S.; Usman, M.; Imran, M.; Pesyridis, A. Review of Organic Rankine Cycle experimental data trends. Energy Convers. Manag. 2018, 173, 679–691. [Google Scholar] [CrossRef]
- Nguyen, V.M.; Doherty, P.S.; Riffat, S.B. Development of a prototype low-temperature Rankine cycle electricity generation system. Appl. Therm. Eng. 2001, 21, 169–181. [Google Scholar] [CrossRef]
- Quoilin, S.; Lemort, V.; Lebrun, J. Experimental study and modeling of an Organic Rankine Cycle using scroll expander. Appl. Energy 2010, 87, 1260–1268. [Google Scholar] [CrossRef]
- Pei, G.; Li, J.; Li, Y.; Wang, D.; Ji, J. Construction and dynamic test of a small-scale organic rankine cycle. Energy 2011, 36, 3215–3223. [Google Scholar] [CrossRef]
- Kang, S.H. Design and experimental study of ORC (organic Rankine cycle) and radial turbine using R245fa working fluid. Energy 2012, 41, 514–524. [Google Scholar] [CrossRef]
- Zheng, N.; Zhao, L.; Wang, X.D.; Tan, Y.T. Experimental verification of a rolling-piston expander that applied for low-temperature Organic Rankine Cycle. Appl. Energy 2013, 112, 1265–1274. [Google Scholar] [CrossRef]
- Han, S.; Seo, J.; Choi, B.-S. Development of a 200 kW ORC radial turbine for waste heat recovery. J. Mech. Sci. Technol. 2014, 28, 5231–5241. [Google Scholar] [CrossRef]
- Hsu, S.-W.; Chiang, H.-W.; Yen, C.-W. Experimental Investigation of the Performance of a Hermetic Screw-Expander Organic Rankine Cycle. Energies 2014, 7, 6172–6185. [Google Scholar] [CrossRef]
- Minea, V. Power generation with ORC machines using low-grade waste heat or renewable energy. Appl.Therm. Eng. 2014, 69, 143–154. [Google Scholar] [CrossRef]
- Bamorovat Abadi, G.; Yun, E.; Kim, K.C. Experimental study of a 1 kw organic Rankine cycle with a zeotropic mixture of R245fa/R134a. Energy 2015, 93, 2363–2373. [Google Scholar] [CrossRef]
- Fu, B.-R.; Lee, Y.-R.; Hsieh, J.-C. Design, construction, and preliminary results of a 250-kW organic Rankine cycle system. Appl. Therm. Eng. 2015, 80, 339–346. [Google Scholar] [CrossRef]
- Galloni, E.; Fontana, G.; Staccone, S. Design and experimental analysis of a mini ORC (organic Rankine cycle) power plant based on R245fa working fluid. Energy 2015, 90, 768–775. [Google Scholar] [CrossRef]
- Miao, Z.; Xu, J.; Yang, X.; Zou, J. Operation and performance of a low temperature organic Rankine cycle. Appl. Therm. Eng. 2015, 75, 1065–1075. [Google Scholar] [CrossRef]
- Muhammad, U.; Imran, M.; Lee, D.H.; Park, B.S. Design and experimental investigation of a 1kW organic Rankine cycle system using R245fa as working fluid for low-grade waste heat recovery from steam. Energy Convers. Manag. 2015, 103, 1089–1100. [Google Scholar] [CrossRef]
- Peris, B.; Navarro-Esbrí, J.; Molés, F.; González, M.; Mota-Babiloni, A. Experimental characterization of an ORC (organic Rankine cycle) for power and CHP (combined heat and power) applications from low grade heat sources. Energy 2015, 82, 269–276. [Google Scholar] [CrossRef]
- Yun, E.; Kim, D.; Yoon, S.Y.; Kim, K.C. Experimental investigation of an organic Rankine cycle with multiple expanders used in parallel. Appl. Energy 2015, 145, 246–254. [Google Scholar] [CrossRef]
- Pu, W.; Yue, C.; Han, D.; He, W.; Liu, X.; Zhang, Q.; Chen, Y. Experimental study on Organic Rankine cycle for low grade thermal energy recovery. Appl. Therm. Eng. 2016, 94, 221–227. [Google Scholar] [CrossRef]
- Sung, T.; Yun, E.; Kim, H.D.; Yoon, S.Y.; Choi, B.S.; Kim, K.; Kim, J.; Jung, Y.B.; Kim, K.C. Performance characteristics of a 200-kW organic Rankine cycle system in a steel processing plant. Appl. Energy 2016, 183, 623–635. [Google Scholar] [CrossRef]
- Feng, Y.-Q.; Hung, T.-C.; Wu, S.-L.; Lin, C.-H.; Li, B.-X.; Huang, K.-C.; Qin, J. Operation characteristic of a R123-based organic Rankine cycle depending on working fluid mass flow rates and heat source temperatures. Energy Convers. Manag. 2017, 131, 55–68. [Google Scholar] [CrossRef]
- Shao, L.; Zhu, J.; Meng, X.; Wei, X.; Ma, X. Experimental study of an organic Rankine cycle system with radial inflow turbine and R123. Appl. Therm. Eng. 2017, 124, 940–947. [Google Scholar] [CrossRef]
- Ziviani, D.; James, N.A.; Accorsi, F.A.; Braun, J.E.; Groll, E.A. Experimental and numerical analyses of a 5 kWe oil-free open-drive scroll expander for small-scale organic Rankine cycle (ORC) applications. Appl. Energy 2018, 230, 1140–1156. [Google Scholar] [CrossRef]
- Moffat, R.J. Describing the uncertainties in experimental results. Exp. Therm. Fluid Sci. 1988, 1, 3–17. [Google Scholar] [CrossRef]
- Li, L.; Ge, Y.T.; Luo, X.; Tassou, S.A. Experimental investigations into power generation with low grade waste heat and R245fa Organic Rankine Cycles (ORCs). Appl. Thermal Eng. 2017, 115, 815–824. [Google Scholar] [CrossRef]



| Classification | Heat Source Temperature (°C) | Classification | Power Capacity (kW) |
|---|---|---|---|
| Low | <150 | Micro | <3 |
| Medium | 150–250 | Mini | 3–50 |
| High | >250 | Small | 50–500 |
| Medium | 500–5000 | ||
| Large | >5000 |
| Authors | Heat Source | Temperature | Heat Source Capacity | Working Fluid | Expander Type | Power Output | Cycle Efficiency | Isentropic Efficiency |
|---|---|---|---|---|---|---|---|---|
| Nguyen et al. [19] | Hot water | 93 °C | 60 kW | n-pentane | Radial turbine | 1.44 kW | 4.3% | 49.8% |
| Yamamoto et al. [2] | Electric heater | 50–80 °C | 20 kW | R123 | Radial turbine | 150 W | 1.25% | 47.8% |
| Quoilin et al. [20] | Hot air | 101–163 °C | – | R123 | Scroll expander | 1.8 kW | 7.4% | 68% |
| Pei et al. [21] | Hot oil | 105 °C | 18.3 kW | R123 | Radial turbine | 1 kW | 6.8% | 65% |
| Kang [22] | Steam | 77–83 °C | 700 kW | R245fa | Radial turbine | 32.7 kW | 5.22% | 78.7% |
| Zheng et al. [23] | Hot water | 40–90 °C | 36 kW | R245fa | Piston expander | 0.35 kW | 5% | 43.3% |
| Han et al. [24] | Hot water | 140 °C 150 °C | 2 MW | R245fa | Radial turbine | 201 kW | – | 72.4% |
| Hsu et al. [25] | Hot Water | 80–125 °C | 1050 kW | R245fa | Screw expander | 50 kW | 10.5% | 72.5% |
| Minea [26] | Hot water | 85–116 °C | 700 kW | R245fa | Screw expander | 39.9 kW | 7.57% | – |
| Abadi et al. [27] | Hot water | 80–120 °C | 110 kW | R245fa/R134a | Scroll expander | 1.2 kW | 6% | 65% |
| Fu et al. [28] | Hot water | 119.2 °C | 3788 kW | R245fa | Turbine | 225 kW | 7.94% | 63.7% |
| Galloni et al. [29] | Hot water | 75–95 °C | 11 kW | R245fa | Scroll expander | 1.2 kW | 9.28% | 84.9% |
| Miao et al. [30] | Hot oil | 140 °C 160 °C | 100 kW | R123 | Scroll expander | 2.35 kW 3.25 kW | 6.39% 5.12% | 81% |
| Muhammad et al. [31] | Steam | 100–140 °C | 17.4 kW | R245fa | Scroll expander | 1.02 kW | 5.75% | 77.74% |
| Peris et al. [32] | Hot oil | 90–150 °C | 390 kW | R245fa | Volumetric expander | 36.6 kW | 9.4% | 70% |
| Yun et al. [33] | Hot water | 120 °C | 45 kW | R245fa | Scroll expander | 3.4 kW | 7.5% | 61.4% |
| Pu et al. [34] | Hot water | <100 °C | – | HFE7100 R245fa | Axial turbine | 1.03 kW 1.98 kW | 4.01% 4.17% | 59.7% 62% |
| Sung et al. [35] | Hot water | 140 °C | 2200 kW | R245fa | Radial turbine | 177 kW | 9.6% | 68.1% |
| Feng et al. [36] | Hot oil | 110–140 °C | 80 kW | R123 | Scroll expander | 2.01 kW | 3.25% | 85.17% |
| Shao et al. [37] | Hot oil | 110–140 °C | 55 kW | R123 | Radial turbine | 1.88 kW | 5.7% | 83.6% |
| Ziviani et al. [38] | Hot water | 85 °C 110 °C | 100 kW | R245fa | Scroll expander | 3.75 kW | – | 58% |
| Working Fluid | Molecular Weight (g/mol) | Tnb 1 (K) | Tcr 2 (K) | Pcr 3 (kPa) | ODP 4 | GWP 5 | ASHRAE 6 Safety Group |
|---|---|---|---|---|---|---|---|
| R245fa | 134.05 | 15.14 | 154.01 | 3651 | 0 | 858 | B1 |
| R123 | 152.93 | 27.82 | 183.68 | 3662 | 0.012 | 120 | B1 |
| Parameter | Instrument | Measurement Range | Uncertainty |
|---|---|---|---|
| Temperature | WZPK2 | −200 to 600 °C | ±(0.3 + 0.5% |t|) °C |
| Pressure | dTRANS | 0–25 bar | ±0.2% |
| Electric power | Smart energy meter | N/A | ±0.5% |
| ±8.27% | |||
| P3/P4 | ±0.29% | ||
| ηcarn | ±0.95% | ||
| ηgros | ±6.1% | ||
| ηis,turb | ±6.4% | ||
| ηelec–mech | ±8.3% | ||
| ηover_tg | ±10.5% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, R.; Kuang, G.; Zhu, L.; Wang, S.; Zhao, J. Experimental Investigation of a 300 kW Organic Rankine Cycle Unit with Radial Turbine for Low-Grade Waste Heat Recovery. Entropy 2019, 21, 619. https://doi.org/10.3390/e21060619
Wang R, Kuang G, Zhu L, Wang S, Zhao J. Experimental Investigation of a 300 kW Organic Rankine Cycle Unit with Radial Turbine for Low-Grade Waste Heat Recovery. Entropy. 2019; 21(6):619. https://doi.org/10.3390/e21060619
Chicago/Turabian StyleWang, Ruijie, Guohua Kuang, Lei Zhu, Shucheng Wang, and Jingquan Zhao. 2019. "Experimental Investigation of a 300 kW Organic Rankine Cycle Unit with Radial Turbine for Low-Grade Waste Heat Recovery" Entropy 21, no. 6: 619. https://doi.org/10.3390/e21060619
APA StyleWang, R., Kuang, G., Zhu, L., Wang, S., & Zhao, J. (2019). Experimental Investigation of a 300 kW Organic Rankine Cycle Unit with Radial Turbine for Low-Grade Waste Heat Recovery. Entropy, 21(6), 619. https://doi.org/10.3390/e21060619





