Structural Characteristics of Two-Sender Index Coding
Abstract
1. Introduction
- Macro-cell networks with caching helpers [14]—cellular networks deploying dedicated nodes, called helpers, with large storage capacity instead of femto-cell access points to reduce backhaul loads,
- cooperative data exchange [15]—peer-to-peer networks with data exchange within a group of closely-located wireless nodes, and
- distributed storage—storage networks where data are distributed over multiple storage devices/locations.
1.1. Prior Works
1.2. Our Work and Contributions
- Proposing a new coloring concept for confusion graphs in TSUIC, called two-sender graph coloring (Definition 8, Section 4.3): For SSUIC, the chromatic number of its confusion graph gives the optimal broadcast rate and the corresponding index code (for a specific message size). However, for TSUIC, as the two senders (encoders) contain some messages in common, the standard method of graph coloring of the confusion graph may not lead us to an index code. In this regard, we need a different kind of coloring function in TSUIC, and thus, in this paper, we propose a novel coloring technique to color the confusion graphs in TSUIC, and its optimization gives the optimal broadcast rate and optimal index code.
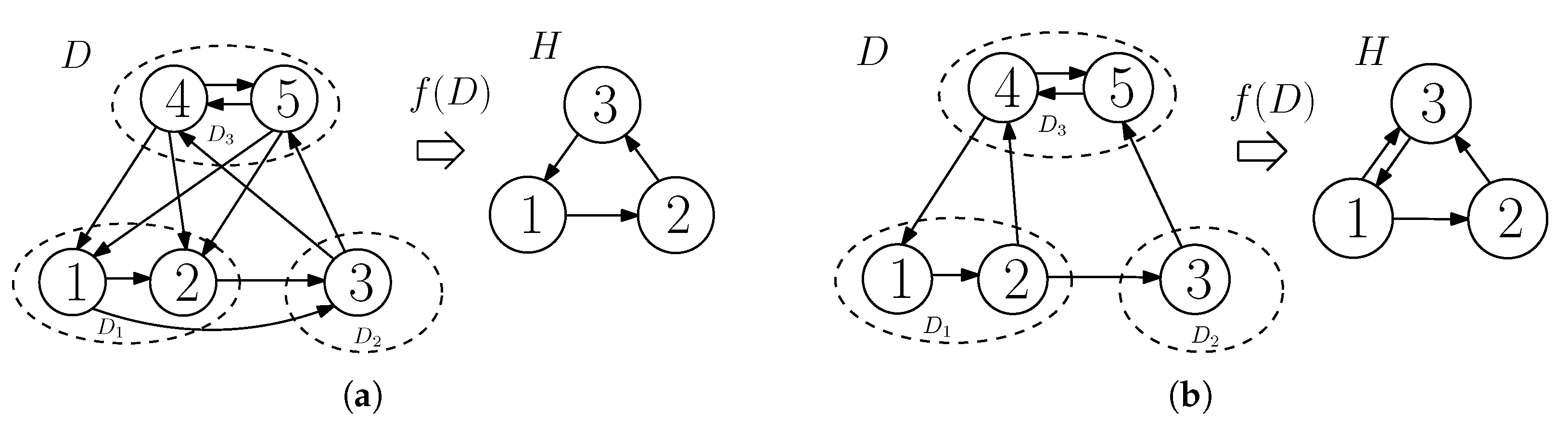
- Presenting a way of grouping the vertices of confusion graphs in TSUIC (Appendix B): By exploiting the symmetry of the confusion graph, we propose a way of grouping its vertices for analysis purposes mainly in its two-sender graph coloring. In particular, this grouping helps us to analyze the number of colors used in two-sender graph coloring of a confusion graph.
- Deriving the optimal broadcast rates of TSUIC problems as a function of the optimal broadcast rates of its sub-problems (Theorems 4–8): We divide a TSUIC problem into three independent sub-problems based on the requested messages by receivers, specifically whether the messages are present in only one of the senders or in both senders. Now in TSUIC, considering the interactions (defined by side-information available at the receivers) between these three independent sub-problems, we derive the optimal broadcast rate (in both asymptotic and non-asymptotic regimes in the message size) of the problem as a function of the optimal broadcast rates of its sub-problems. Moreover, we bound the optimal broadcast rate, and show that the bounds are tight for several classes of TSUIC instances (sometimes with conditions). Furthermore, we find a class of TSUIC instances where a TSUIC scheme can achieve the same optimal broadcast rate as the same instances when the two senders form a single sender having all messages.
- Characterizing a class of TSUIC instances where a certain type of side-information is not critical (Corollary 1): For a class of TSUIC instances, we prove that certain interactions between the three independent sub-problems can be removed without affecting the optimal broadcast rate (in the asymptotic regime). This means that those interactions are not critical.
- Generalizing the results of some classes of TSUIC problems to multiple senders (Section 6): For some classes of TSUIC problems, we generalize the two-sender graph coloring of confusion graphs and the proposed grouping of their vertices. Then, we compute the optimal broadcast rates of those problems as a function of the optimal broadcast rates of their sub-problems.
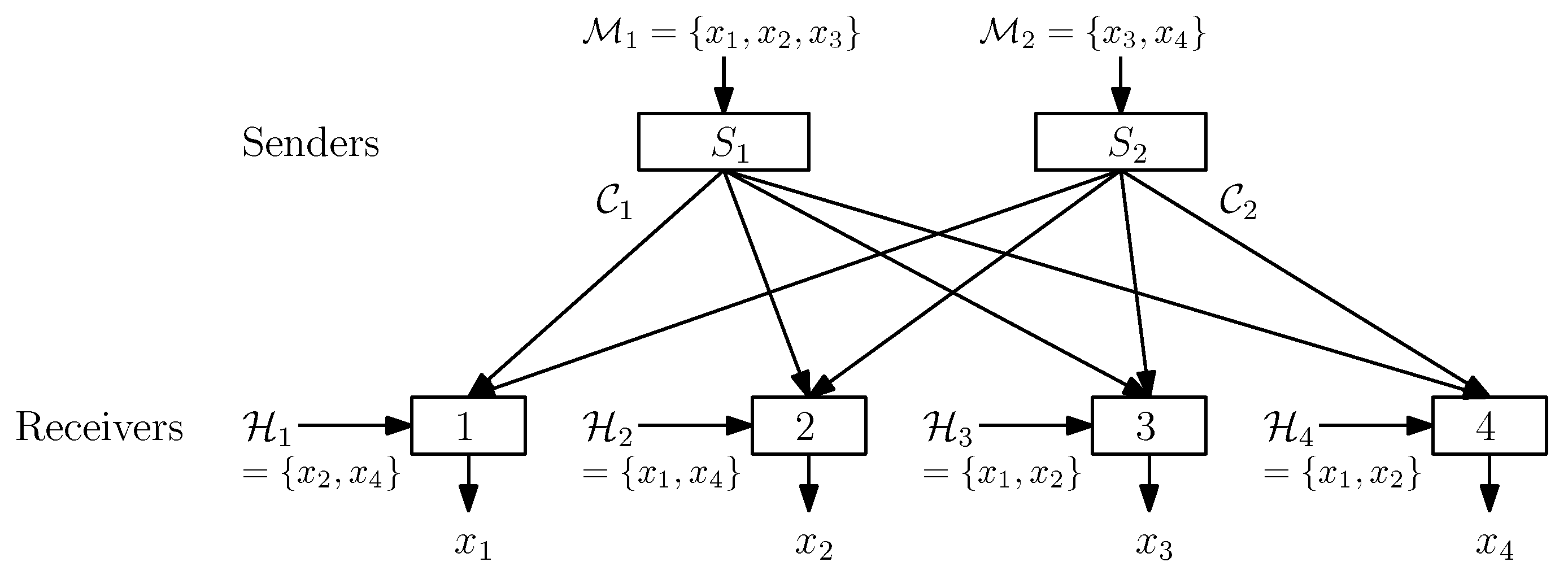
2. Problem Definitions and Graphical Representation
2.1. Problem Setup
- (i)
- an encoding function for each sender , such that , and
- (ii)
- a decoding function for every receiver r, such that .
2.2. Representation of the Receivers’ Side-Information and the Senders’ Message Setting in TSUIC Problems
3. A New Way of Classifying TSUIC Problems and Main Results
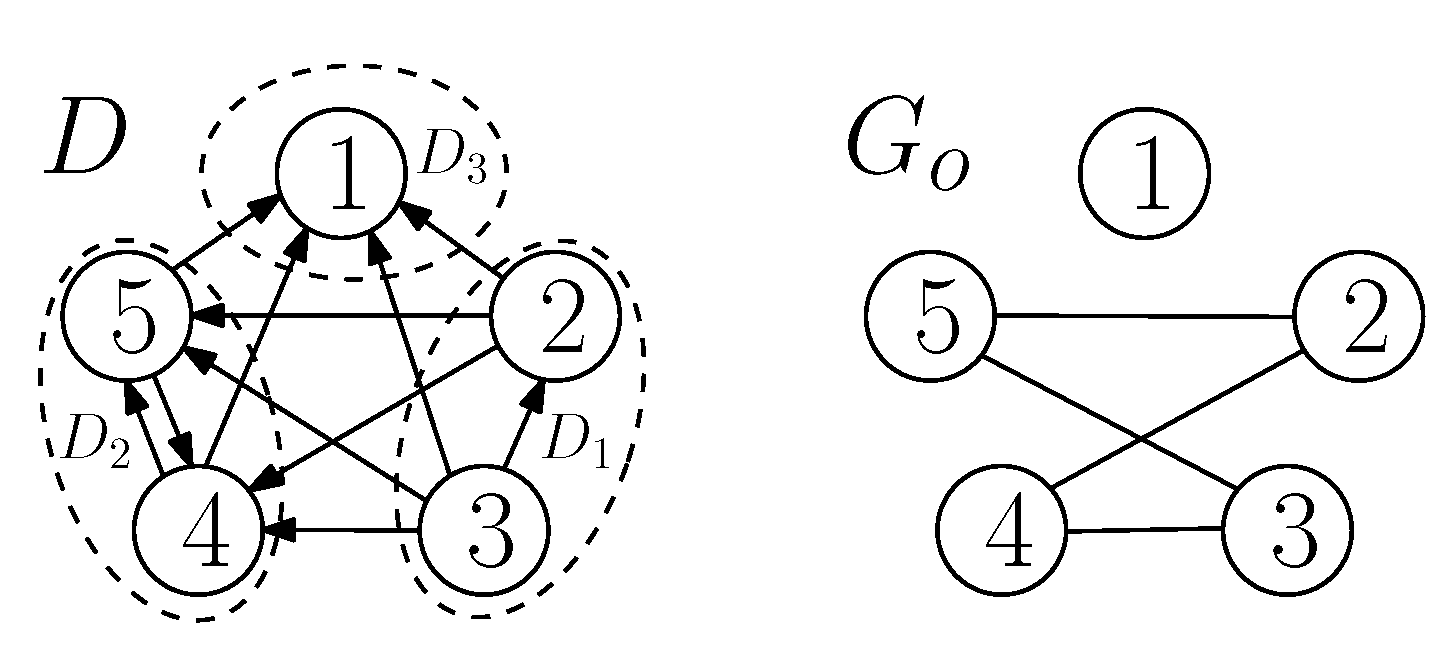
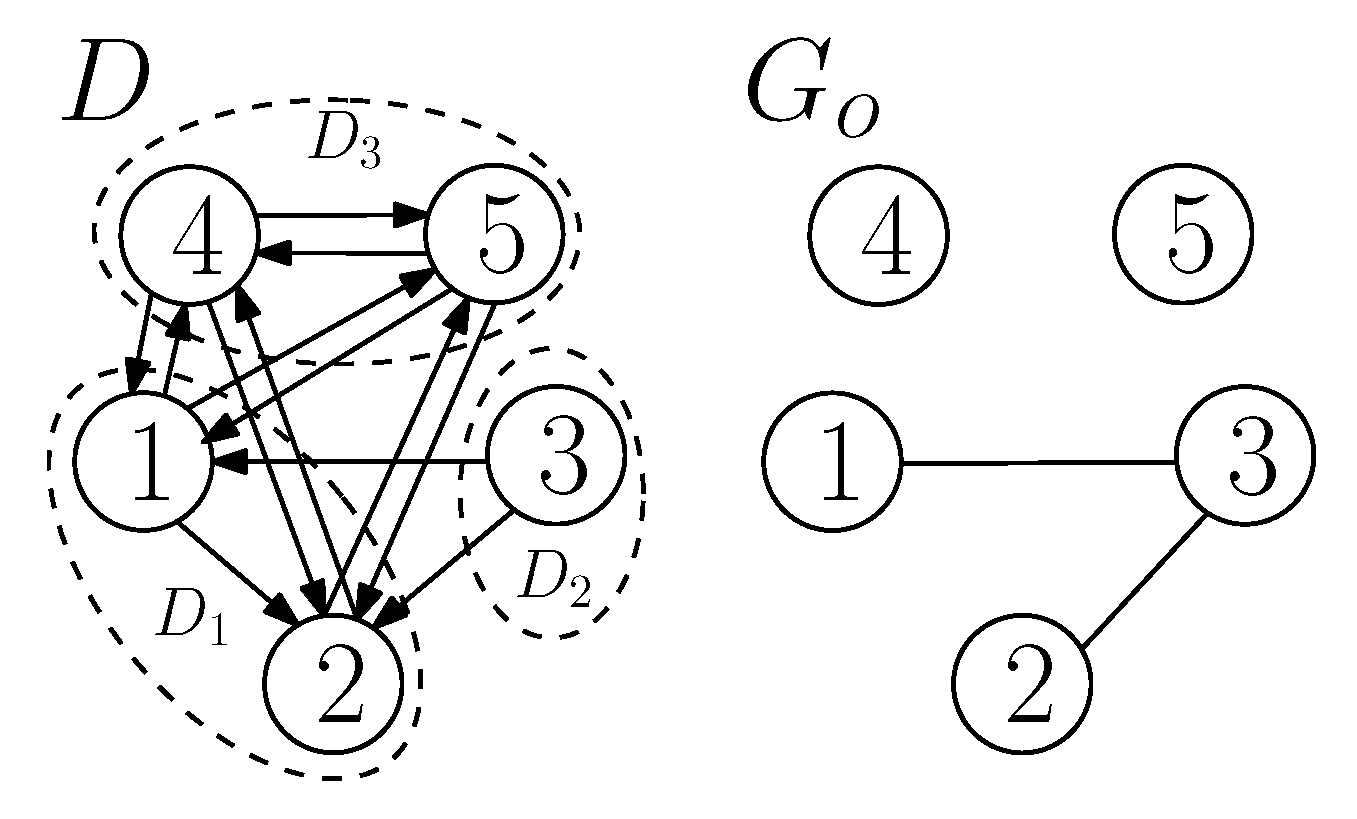
3.1. Interactions between , and
3.2. A Compact Representation of Interactions
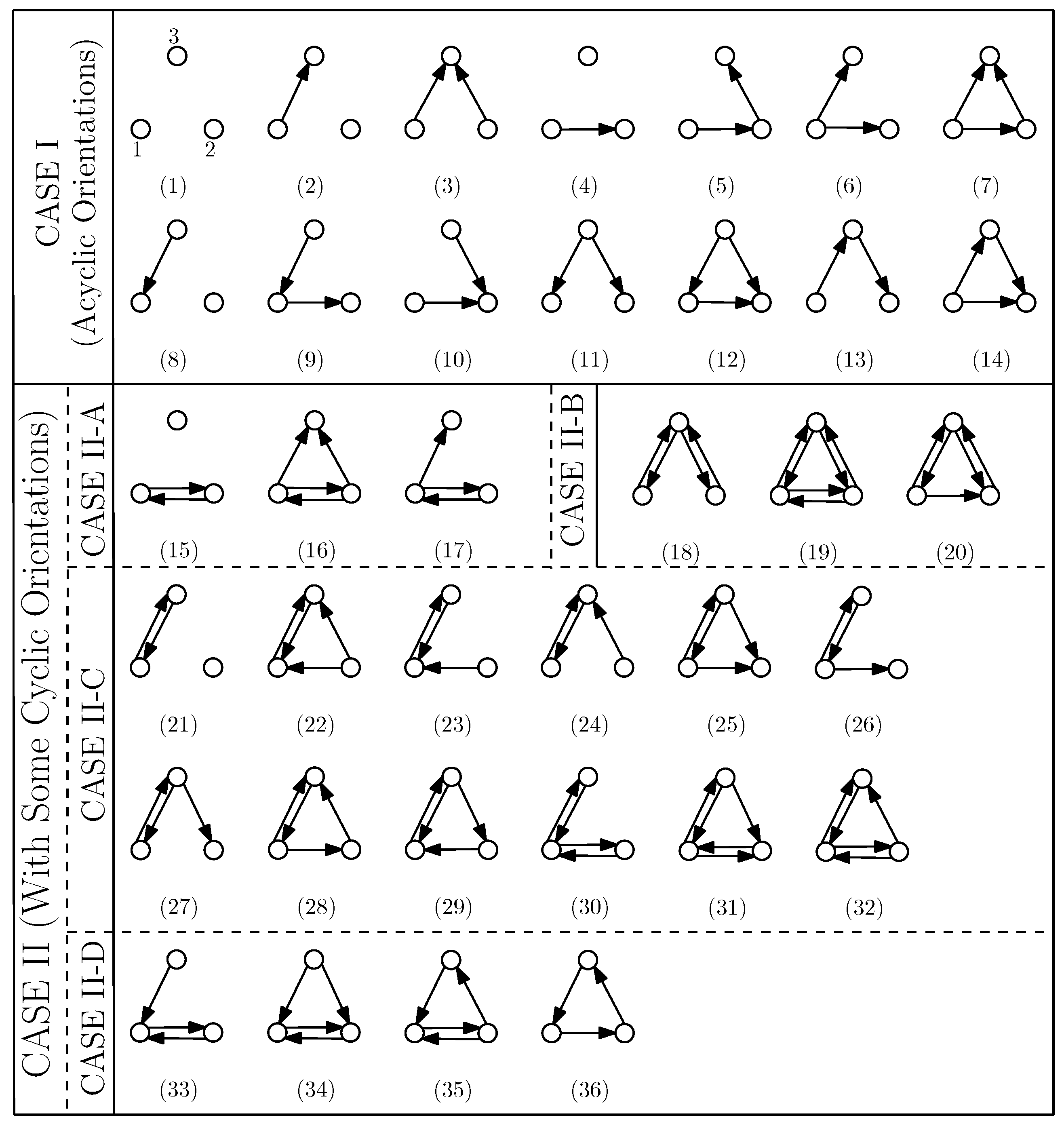
3.3. A Classification of the Interactions
3.4. Main Results
4. Confusion Graphs and Their Coloring
4.1. Confusion Graphs
- (i)
- , and
- (ii)
- .
4.2. A Review of Confusion Graph Coloring for SSUIC
4.3. Proposed Confusion Graph Coloring for TSUIC
- Without loss of generality, we assume to be the messages requested by vertices in , the messages requested by vertices in , and the messages requested by vertices in with .
- Indices , and are used in the representation of possible realizations of words of , and bits, respectively. For convenience, we use three indices (e.g., ) for the same set of numbers, where the first index (e.g., i) is used for a general case, and the remaining two indices (e.g., and ) are used to indicate any two words within the group of words.
- We group the bits associated with the messages requested by vertices of , . Within each group, each realization of the bits, i.e., each member in is represented by a unique label , . Figure A1a in Appendix A outlines each tuple for . Each message tuple realization can then be uniquely written as for some .
4.4. A Few Lemmas for the TSUIC Confusion Graph Coloring
5. The Optimal Broadcast Rate for TSUIC
5.1. Lower Bounds
- (i)
- if there is (i) no interaction between and (i.e., no and ), or (ii) a one-way interaction (either partially or fully participated) between and , i.e., either or , but not both and
- (ii)
- if there is a fully participated both way interaction between and (i.e., fully participated ).
5.2. Optimal Broadcast Rates for CASE I and CASE II-A: The Arcs between , and Are Not Critical in Asymptotic Regime in the Message Size
5.3. Optimal Broadcast Rates for CASE II-B
5.4. Optimal Broadcast Rates for CASE II-C: An Upper Bound, and Special Cases Where the Upper Bound Is Tight
- (i)
- ,
- (ii)
- if ,
- (iii)
- , and
- (iv)
- if .
- (i)
- if , then ,
- (ii)
- if , then
- (a)
- if , then , with a strict inequality if is non-empty, and
- (b)
- if , then for a non-empty .
- (i)
- from Proposition 2, Theorem 3, Corollarys 3 and 4, and Lemma 5. This implies .
- (ii)
- from Proposition 2, Theorem 3, Corollarys 3 and 4, and Lemma 5. This implies .
5.5. Optimal Broadcast Rates for CASE II-D
- (i)
- ,
- (ii)
- if ,
- (iii)
- , and
- (iv)
- if .
6. Generalizing the Results of Some Classes of TSUIC Problems to Multiple Senders
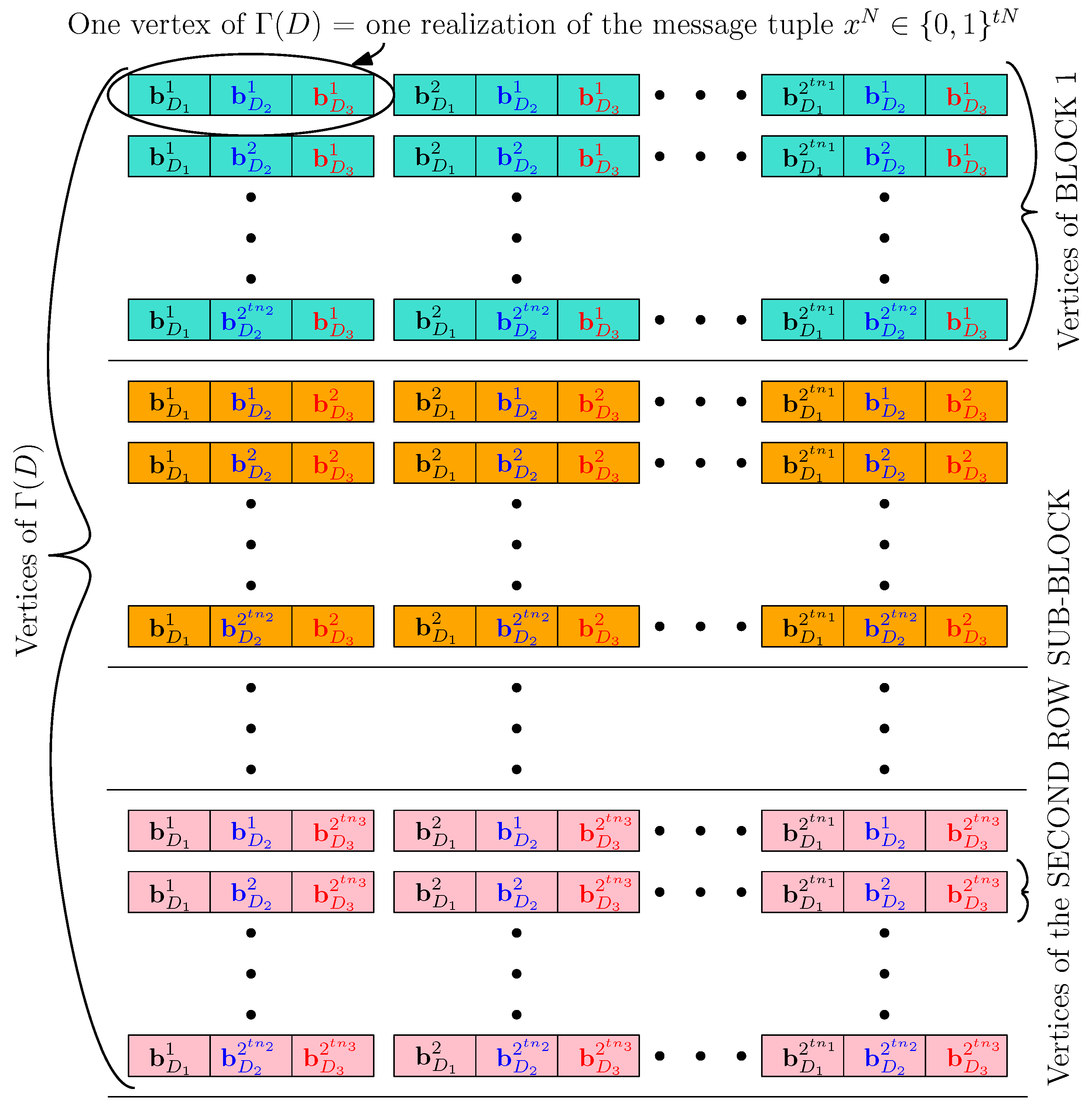
- Vertices labeled by all , , and , with the same sub-label,
- any row sub-block consists of vertices labeled by all , , , with the same sub-labels, and
- any -th column sub-block consists of vertices labeled by all , , , with the same and sub-labels. Moreover, in contrast to SSUIC, there are multiple sub-labels other than and in MSUIC, so we arrange the vertices of any -th column sub-block as dictated by Figure A2 in Appendix A. Clearly, a block has column sub-blocks and row sub-blocks.
7. Discussion
- The role of side-information of the vertices in (vertices requesting the common messages) about the messages requested by vertices in (vertices requesting the private messages) in TSUIC: It is proved in SSUIC that, if the interaction between , and is acyclic, i.e., belongs to one of the digraphs in CASE I, then (by using Theorem 3). This means that the arcs contributing acyclic interactions between the sub-digraphs of D can be removed without affecting the optimal broadcast rate of D; in other words, those are non-critical arcs. In this paper, we have proved that this result is also true in TSUIC (by Theorem 5). Moreover, in TSUIC, we have proved that, for D, if the vertices in have no side-information about the messages requested by vertices in , i.e., , then by Theorem 5, we have (behaves like having acyclic interactions between , and ). Under this condition, any arc that is contributing any interaction between , and is non-critical.
- Non-critical arcs in SSUIC are not necessarily non-critical in TSUIC: We illustrate this with an example. Consider the TSUIC problem stated in Example 1 (whose ). In SSUIC, we know that the optimal broadcast rate . This problem has an arc that is non-critical in SSUIC (its removal does not change the optimal broadcast rate), but it is critical in TSUIC. This can be understood from the following: In SSUIC, we can remove the arc , and still form a valid index code that achieves . This infers that removing the arc does not affect the optimal broadcast rate in SSUIC. However, in TSUIC, if we remove the arc , then the new problem, say , has (applying Theorem 5), whereas we get a valid two-sender index code of codelength two if we consider . Now, it is evident that there exist cases in TSUIC where some side-information (e.g., and ) cannot be exploited directly during encoding by senders because of the constraint due to the two senders. However, that side-information can be utilized during decoding process at receivers’ end due to the presence of other helping side-information (e.g., ). Thus, this helping side-information can be critical in TSUIC. This observation was also made by Sadeghi et al. [20] for MSUIC under a different performance metric (rate region with fixed capacity links).
8. Concluding Remarks and Open Problems
- Study of the critical edges in the TSUIC problems: It is observed that the non-critical arcs in SSUIC can be critical arcs in TSUIC. This requires further study.
- Study of a general distributed index coding: As our study is a step towards understanding multi-sender index coding, it is left as a future work to extend the approaches implemented and the results obtained in this paper to more general setups.
- Finding the optimal broadcast rates of TSUIC problems with cyclic-partially-participated interactions: The analysis of D with partially-participated interactions between its sub-digraphs , and is left as a future work.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| MSUIC | Multi-sender unicast index coding |
| SMSUIC | Special multi-sender unicast index coding |
| SSUIC | Single-sender unicast index coding |
| TSUIC | Two-sender unicast index coding |
| UIC | Unicast index coding |
Appendix A
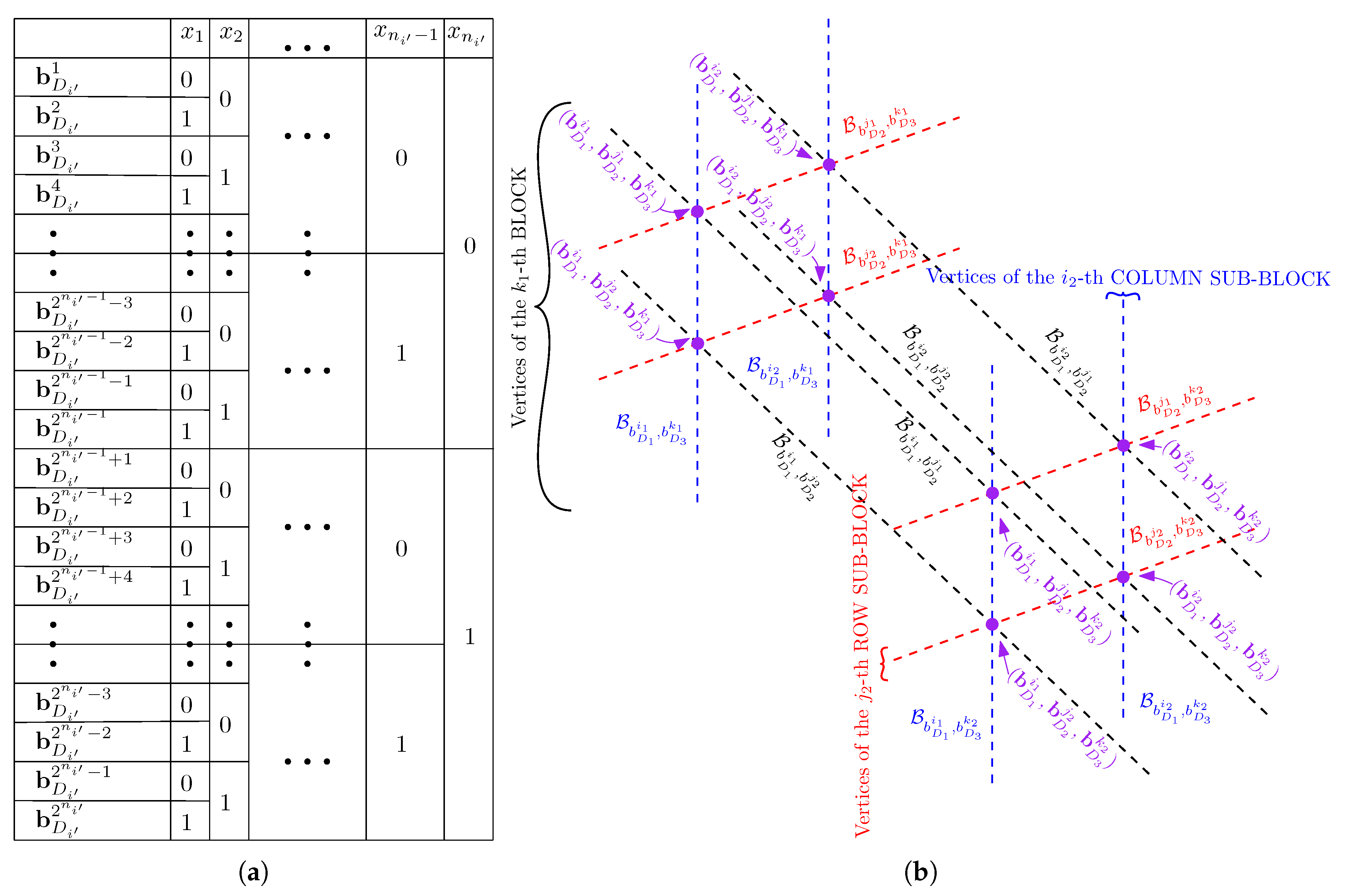
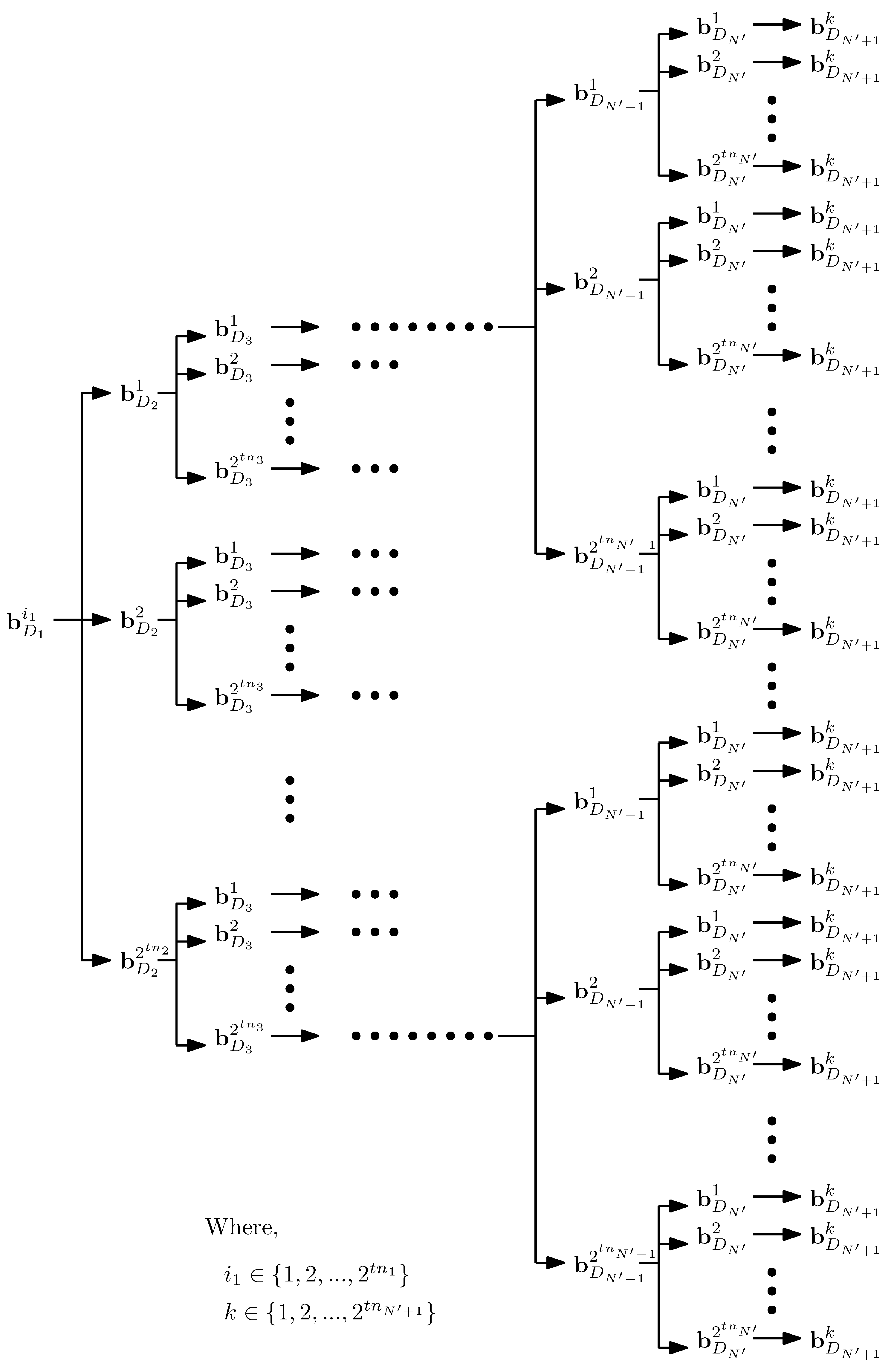
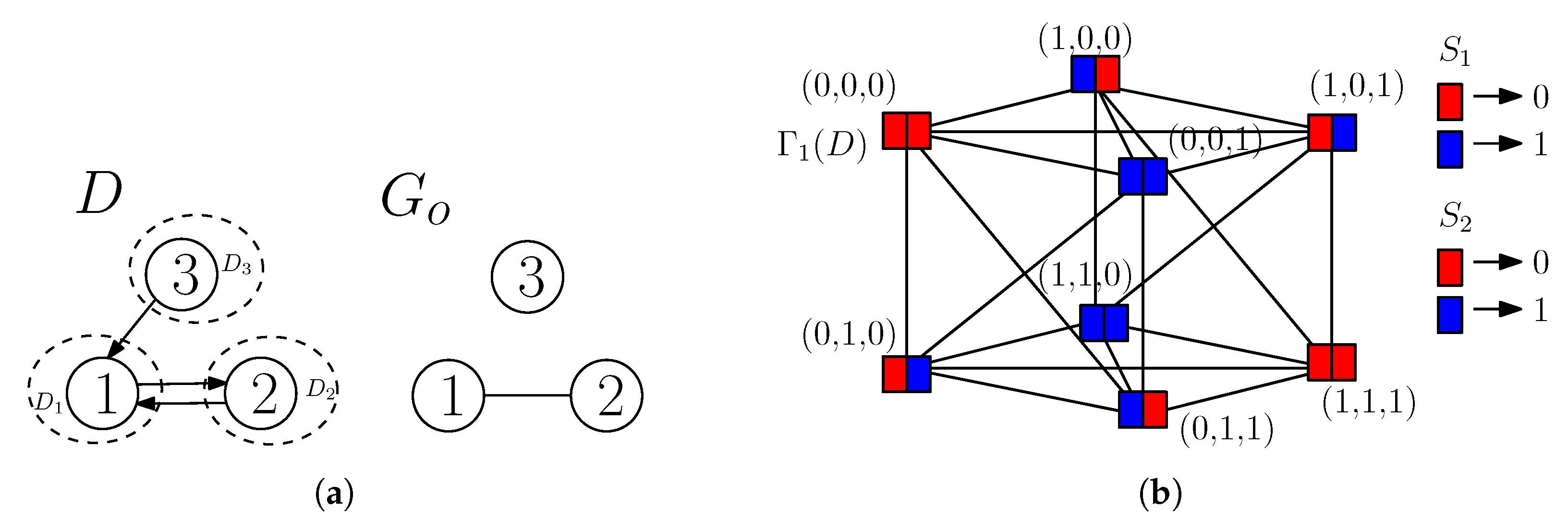
Appendix B. Proposed Grouping of the Vertices of and Its Characteristics
Some Lemmas
Appendix C. Proof of Proposition 1
Appendix C.1. An Example
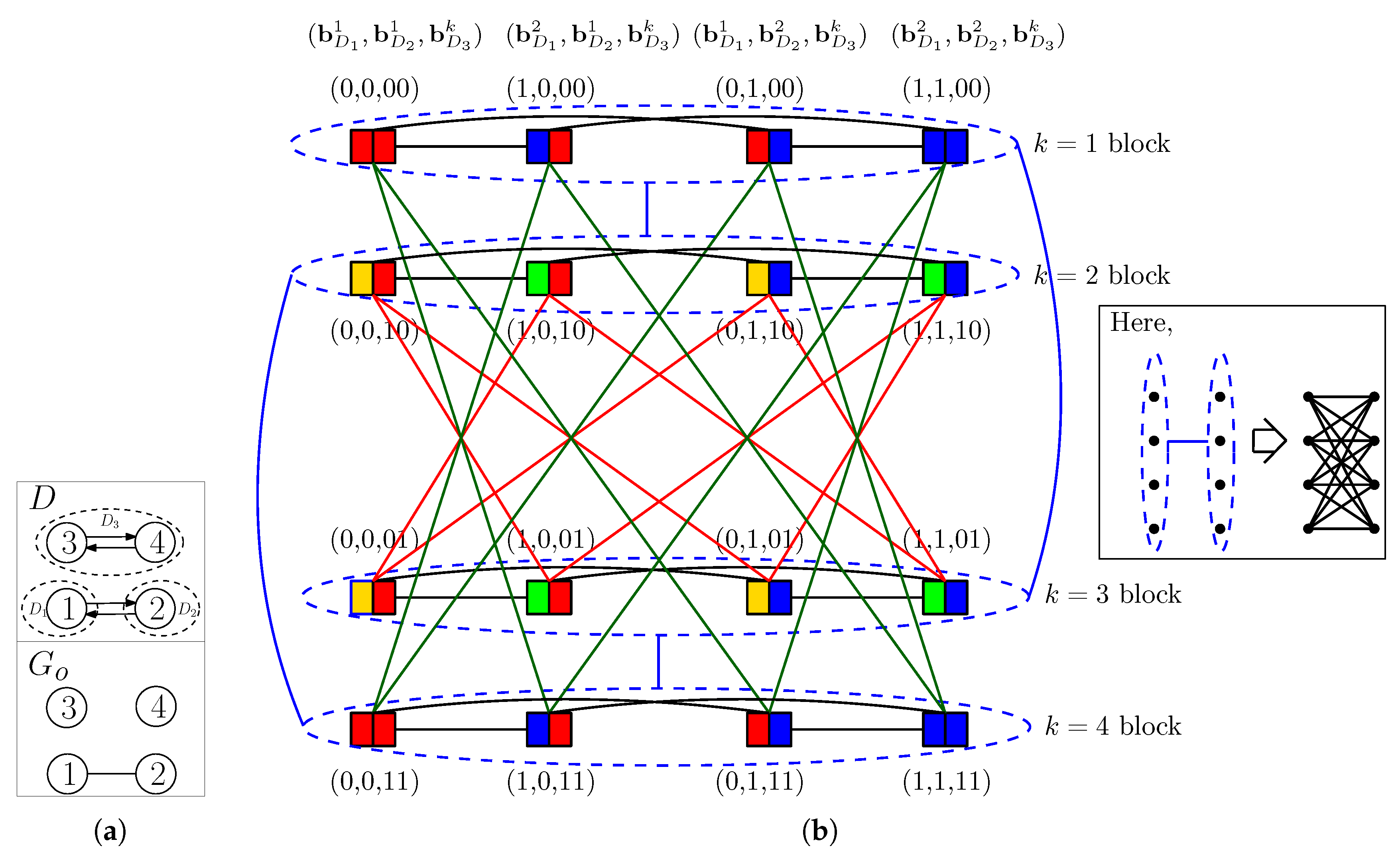
Appendix C.1.1. Intra-Block Coloring
Appendix C.1.2. Inter-Block Coloring
Appendix C.2. Ingredients for the Proof
Appendix C.3. Proof of Proposition 1
Appendix C.3.1. Construction and Coloring of Γt (D16)
- (i)
- Edges in due to the confusion at some vertices in : The confusion at any vertex in contributes to only intra-edges due to Lemma A8.
- (ii)
- Edges in due to the confusion at some vertices in : The confusion at any vertex in contributes to only intra-edges due to Lemma A8.
- (iii)
- Edges in due to the confusion at some vertices in : If there exists an edge due to the confusion at some vertices in between any vertex pair , then each of the vertices in the -th block has edges with all the vertices in the -th block. This is because any vertex in has no message requested by any vertex in as its side-information. This results in no effect due to a change in bits of or sub-label once we have an edge due to confusion at some receivers in , which corresponds to the change in bits of the sub-label.
Appendix C.3.2. Construction and Coloring of Γt (D1)
Appendix D. Proof of Theorem 6
- Let be an index code (linear or nonlinear,) having a codeword length of bits, for a given t (message bits) that achieves . For convenience, we represent by such that .
- Let the sequence of bits in be , where , .
- Let and with be two parts of the sequence of bits of a codeword of such that with .
- For any two codes and with codeword lengths of and bits, respectively, refers to the bit-wise XOR of bits of and with zero padding if . This means contains bits. For example, if and , then .
Appendix E. Proof of Theorem 7
Appendix F. Proof of Theorem 8
Appendix G. Proof of Proposition 4
References
- Birk, Y.; Kol, T. Informed-source coding-on-demand (ISCOD) over broadcast channels. Proc. IEEE INFOCOM 1998, 3, 1257–1264. [Google Scholar]
- Birk, Y.; Kol, T. Coding on demand by an informed source (ISCOD) for efficient broadcast of different supplemental data to caching clients. IEEE Trans. Inf. Theory 2006, 52, 2825–2830. [Google Scholar] [CrossRef]
- Bar-Yossef, Z.; Birk, Y.; Jayram, T.S.; Kol, T. Index Coding With Side Information. IEEE Trans. Inf. Theory 2011, 57, 1479–1494. [Google Scholar] [CrossRef]
- Blasiak, A.; Kleinberg, R.; Lubetzky, E. Broadcasting With Side Information: Bounding and Approximating the Broadcast Rate. IEEE Trans. Inf. Theory 2013, 59, 5811–5823. [Google Scholar] [CrossRef]
- Rouayheb, S.E.; Sprintson, A.; Georghiades, C. On the index coding problem and its relation to network coding and matroid theory. IEEE Trans. Inf. Theory 2010, 56, 3187–3195. [Google Scholar] [CrossRef]
- Maleki, H.; Cadambe, V.R.; Jafar, S.A. Index Coding—An Interference Alignment Perspective. IEEE Trans. Inf. Theory 2014, 60, 5402–5432. [Google Scholar] [CrossRef]
- Arbabjolfaei, F.; Bandemer, B.; Kim, Y.H.; Sasoglu, E.; Wang, L. On the capacity region for index coding. In Proceedings of the 2013 IEEE International Symposium on Information Theory (ISIT), Istanbul, Turkey, 7–12 July 2013; pp. 962–966. [Google Scholar]
- Arbabjolfaei, F.; Kim, Y.H. Structural properties of index coding capacity using fractional graph theory. In Proceedings of the 2015 IEEE International Symposium on Information Theory (ISIT), Hong Kong, China, 14–19 June 2015; pp. 1034–1038. [Google Scholar]
- Tahmasbi, M.; Shahrasbi, A.; Gohari, A. Critical Graphs in Index Coding. IEEE J. Sel. Areas Commun. 2015, 33, 225–235. [Google Scholar] [CrossRef]
- Shanmugam, K.; Dimakis, A.G.; Langberg, M. Local graph coloring and index coding. Proc. IEEE Int. Symp. Inf. Theory (ISIT) 2013, 1152–1156. [Google Scholar] [CrossRef]
- Ong, L. Optimal Finite-Length and Asymptotic Index Codes for Five or Fewer Receivers. IEEE Trans. Inf. Theory 2017, 63, 7116–7130. [Google Scholar] [CrossRef]
- Thapa, C.; Ong, L.; Johnson, S.J. Interlinked Cycles for Index Coding: Generalizing Cycles and Cliques. IEEE Trans. Inf. Theory 2017, 63, 3692–3711. [Google Scholar] [CrossRef]
- Thapa, C.; Ong, L.; Johnson, S.J. Corrections to Interlinked Cycles for Index Coding: Generalizing Cycles and Cliques. IEEE Trans. Inf. Theory 2018, 64, 6460. [Google Scholar] [CrossRef]
- Shanmugam, K.; Golrezaei, N.; Dimakis, A.G.; Molisch, A.F.; Caire, G. FemtoCaching: Wireless Content Delivery Through Distributed Caching Helpers. IEEE Trans. Inf. Theory 2013, 59, 8402–8413. [Google Scholar] [CrossRef]
- Rouayheb, S.E.; Sprintson, A.; Sadeghi, P. On coding for cooperative data exchange. Proc. IEEE Inf. Theory Workshop (ITW) 2010, 1–5. [Google Scholar] [CrossRef]
- Ong, L.; Ho, C.K.; Lim, F. The Single-Uniprior Index-Coding Problem: The Single-Sender Case and the Multi-Sender Extension. IEEE Trans. Inf. Theory 2016, 62, 3165–3182. [Google Scholar] [CrossRef]
- Thapa, C.; Ong, L.; Johnson, S.J. Graph-Theoretic Approaches to Two-Sender Index Coding. Proc. IEEE Globecom Workshops 2016, 1–6. [Google Scholar] [CrossRef]
- Chaudhry, M.A.R.; Asad, Z.; Sprintson, A.; Langberg, M. On the complementary Index Coding problem. Proc. IEEE Int. Symp. Inf. Theory (ISIT) 2011, 224–248. [Google Scholar] [CrossRef]
- Neely, M.J.; Tehrani, A.S.; Zhang, Z. Dynamic Index Coding for Wireless Broadcast Networks. IEEE Trans. Inf. Theory 2013, 59, 7525–7540. [Google Scholar] [CrossRef]
- Sadeghi, P.; Arbabjolfaei, F.; Kim, Y.H. Distributed Index Coding. Proc. IEEE Inf. Theory Workshop (ITW) 2016, 330–334. [Google Scholar] [CrossRef]
- Liu, Y.; Sadeghi, P.; Arbabjolfaei, F.; Kim, Y.H. On the Capacity for Distributed Index Coding. Proc. IEEE Int. Symp. Inf. Theory (ISIT) 2017, 3055–3059. [Google Scholar] [CrossRef]
- Li, M.; Ong, L.; Johnson, S.J. Improved Bounds for Multi-Sender Index Coding. Proc. IEEE Int. Symp. Inf. Theory (ISIT) 2017, 3060–3064. [Google Scholar] [CrossRef]
- Li, M.; Ong, L.; Johnson, S.J. Cooperative Multi-Sender Index Coding. IEEE Trans. Inf. Theory 2019, 65, 1725–1739. [Google Scholar] [CrossRef]
- Li, M.; Ong, L.; Johnson, S.J. Multi-Sender Index Coding for Collaborative Broadcasting: A Rank-Minimization Approach. IEEE Trans. on Comm. 2019, 67, 1452–1466. [Google Scholar] [CrossRef]
- Wan, K.; Tuninetti, D.; Ji, M.; Caire, G.; Piantanida, P. Fundamental Limits of Decentralized Data Shuffling. 2019. Available online: https://arxiv.org/pdf/1807.00056.pdf (accessed on 7 June 2019).
- Porter, A.; Wootters, M. Embedded Index Coding. 2019. Available online: https://arxiv.org/pdf/1904.02179.pdf (accessed on 7 June 2019).
- Arbabjolfaei, F. Index Coding: Fundamental Limits, Coding Schemes, and Structural Properties. Ph.D. Dissertation, University of California, San Diego, CA, USA, 2017. [Google Scholar]
- Alon, N.; Hassidim, A.; Lubetzky, E.; Stav, U.; Weinstein, A. Broadcasting with side information. In Proceedings of the 2008 49th Annual IEEE Symposium on Foundations of Computer Science, Philadelphia, PA, USA, 25–28 October 2008; pp. 823–832. [Google Scholar]
- Thapa, C.; Ong, L.; Johnson, S.J. Structural Characteristics of Two-Sender Index Coding. 2017. Available online: https://arxiv.org/pdf/1711.08150v1.pdf (accessed on 8 February 2019).
- Arunachala, C.; Rajan, B.S. Optimal Scalar Linear Index Codes for Three Classes of Two-Sender Unicast Index Coding Problem. 2018. Available online: https://arxiv.org/pdf/1804.03823.pdf (accessed on 18 January 2019).
- Arunachala, C.; Aggarwal, V.; Rajan, B.S. Optimal Linear Broadcast Rates of the Two-Sender Unicast Index Coding Problem with Fully-Participated Interactions. 2018. Available online: https://arxiv.org/pdf/1808.09775.pdf (accessed on 18 January 2019).
- Arunachala, C.; Aggarwal, V.; Rajan, B.S. On the Optimal Broadcast Rate of the Two-Sender Unicast Index Coding Problem with Fully-Participated Interactions. 2018. Available online: https://arxiv.org/pdf/1809.08116.pdf (accessed on 18 January 2019).
- Fekete, M. Uber die Verteilung der Wurzeln bei gewissen algebraischen Gleichungen mit ganzzahligen Koeffizienten. Math. Z. 1923, 17, 228–249. [Google Scholar] [CrossRef]
- Arbabjolfaei, F.; Kim, Y.H. On Critical Index Coding Problems. In Proceedings of the 2015 IEEE Information Theory Workshop - Fall (ITW), Jeju Island, Korea, 11–15 October 2015; pp. 9–13. [Google Scholar]
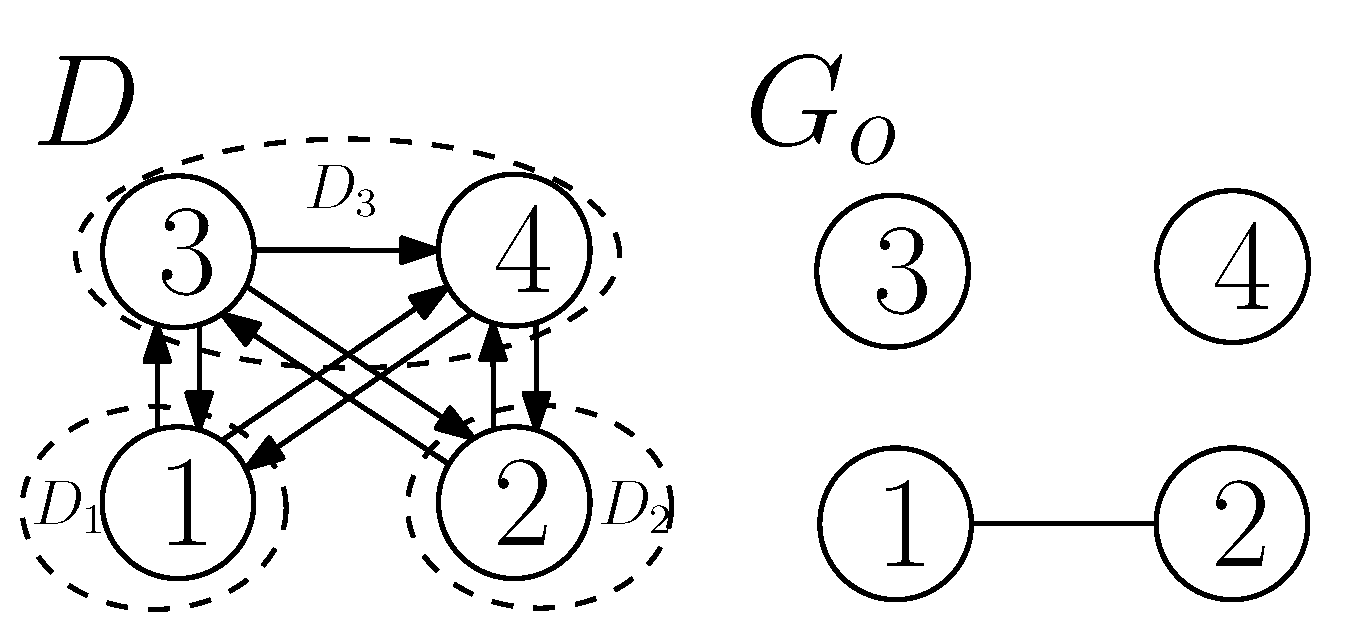

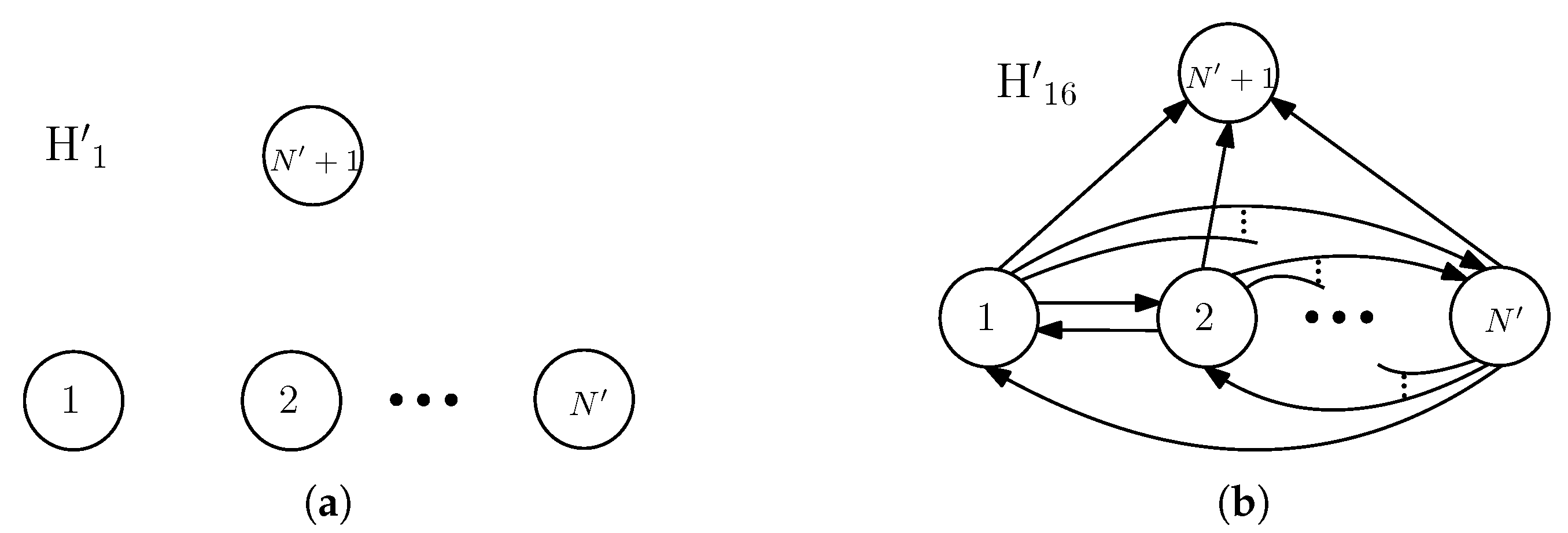

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thapa, C.; Ong, L.; Johnson, S.J.; Li, M. Structural Characteristics of Two-Sender Index Coding. Entropy 2019, 21, 615. https://doi.org/10.3390/e21060615
Thapa C, Ong L, Johnson SJ, Li M. Structural Characteristics of Two-Sender Index Coding. Entropy. 2019; 21(6):615. https://doi.org/10.3390/e21060615
Chicago/Turabian StyleThapa, Chandra, Lawrence Ong, Sarah J. Johnson, and Min Li. 2019. "Structural Characteristics of Two-Sender Index Coding" Entropy 21, no. 6: 615. https://doi.org/10.3390/e21060615
APA StyleThapa, C., Ong, L., Johnson, S. J., & Li, M. (2019). Structural Characteristics of Two-Sender Index Coding. Entropy, 21(6), 615. https://doi.org/10.3390/e21060615






