Abstract
In this paper, we show that the presence of nonlinear coupling between time series may be detected using kernel feature space representations while dispensing with the need to go back to solve the pre-image problem to gauge model adequacy. This is done by showing that the kernelized auto/cross sequences in can be computed from the model rather than from prediction residuals in the original data space . Furthermore, this allows for reducing the connectivity inference problem to that of fitting a consistent linear model in that works even in the case of nonlinear interactions in the -space which ordinary linear models may fail to capture. We further illustrate the fact that the resulting -space parameter asymptotics provide reliable means of space model diagnostics in this space, and provide straightforward Granger connectivity inference tools even for relatively short time series records as opposed to other kernel based methods available in the literature.
1. Introduction
Describing ‘connectivity’ has become of paramount interest in many areas of investigation that involve interacting systems. Physiology, climatology, and economics are three good examples where dynamical evolution modelling is often hindered as system manipulation may be difficult or unethical. Consequently, interaction inference is frequently constrained to using time observations alone.
A number of investigation approaches have been put forward [1,2,3,4,5]. However, the most popular and traditional one still is the nonparametric computation of cross-correlation (CC) between pairs of time series, and variants thereof, like coherence analysis [6], even despite their many shortcomings [7].
When it comes to connectivity analysis, recent times have seen the rise of Granger Causality (GC) as a unifying concept. This is mostly due to GC’s unreciprocal character [8] (as opposed to CC) which allows for establishing the direction of information flow between component subsystems.
Most GC approaches rest on fitting parametric models to time series data and, again as opposed to CC, under appropriate conceptualization, also holds for more than just pairs of time series, giving rise to the ideas of (a) Granger connectivity and (b) Granger influentiability [9].
GC inferential methodology is dominated by the use of linear multivariate time series models [10]. This is so because linear models have statistical properties (and shortcomings) that are well understood besides having the advantage of sufficing when the data are Gaussian. As an added advantage GC characterization allows immediate frequency domain connectivity characterization via concepts like ‘directed coherence’ (DC) and ‘partial directed coherence’ (PDC) [11].
It is often the case, however that data Gaussianity does not hold. Whereas nonparametric approaches do exist [1,4,5], parametric nonlinear modelling offers little relief from the need for long observation data sets for reliable estimation in sharp contrast to linear models that perform well under the typical scenario of fairly short datasets over which natural phenomena can be considered stable. A case in point is neural data where animal behaviour changes are associated with relatively short-lived episodic signal modifications.
The motivation for the present development is that reproducing kernel transformations applied to data, as in the support vector machine learning classification case [12], can effectively produce estimates that inherit many of the good convergence properties of linear methods. Because these properties carry over under proper kernelization, it is possible to show that nonlinear links between subsystems can be rigorously detected.
Before proceeding, it is important to have in mind that the present developments focus on addressing the connectivity detection issue exclusively, in which we clearly show that solving the so-called pre-image reconstruction problem is unnecessary as has been until now assumed essential. This leads to a considerably simpler approach.
2. Problem Formulation
The most popular approach to investigating GC connectivity is through modeling multivariate time series via linear vector autoregressive models [10], where the central idea is to compare prediction effectiveness for a time series when the past of other time series is taken into account in addition to its own past. Namely,
Under mild conditions, Equation (1) constitutes a valid representation of a linear stationary stochastic process where the evolution of is obtained by filtering suitable purely stochastic innovation processes, i.e., where and are independent provided [13]. If are jointly Gaussian, so are and the problem of characterizing connectivity reduces to well known procedures to estimate the parameters in Equation (1) via least squares, which is the applicable maximum likelihood procedure. Nongaussian translate into nongaussian even if some actual (1) linear generation mechanism holds. Linearity among nongaussian time series may be tested with help of cross-polyspectra [14,15], which, if unrejected, still allows for a representation like (1) whose optimal estimation requires a suitable likelihood function to accommodate the observed non-Gaussianity.
If linearity is rejected, non-Gaussianity is a sign of nonlinear mechanisms of generation modelled by
which generalizes (1) where stands for ’s past under some suitable dynamical law .
The distinction between (a) nonlinear that are nonetheless linearly coupled as in (1) under nongaussian and (b) fully nonlinearly coupled processes is often overlooked. In the former case, linear methods suffice for connectivity detection [16] but fail in the latter case [17] calling for the adoption of alternative approaches. In some cases, however, linear approximations are inadequate in so far as to preclude connectivity detection [17].
In the present context, the solution to the connectivity problem entails a suitable data driven approximation of whilst singling out the and of interest. To do so, we examine the employment of kernel methods [18] where functional characterization is carried out with the help of a high dimensional space representation
for ), where is a mapping from the input space into the feature space whose role is to properly unwrap the data and yet ensure that the inner product can be written as a simple function of and dispensing with the need for computations in . This possibility is granted by chosing to satisfy the so-called Mercer condition [19].
A simple example of (3) is the mapping
for and using Dirac’s bra-ket notation. In this case, the Mercer kernel is given by
which is the simplest example of a polynomial kernel [18].
In the multivariate time series case, we consider
where, for simplicity, we adopt the same transformation for each time series component so that the
is a matrix whose elements are given by . In the development below, we follow the standard practice of denoting the quantities as in view of the assumed stationarity of the processes under study.
Rather than go straight into the statement of the general theory, a simple example is more enlightening. In this sense, consider a bivariate stationary time series
where are nonlinear functions and only the previous instant is relevant in producing the present behaviour. An additional feature, thru (9), is that is connected to (Granger causes) but not conversely. Application of the kernel transformation leads to
However, if one assumes the possibility of a linear approximation in , one may write
where stands for approximation errors in the form of innovations. Mercer kernel theory allows for taking the external product with respect to on both sides of (12) leading to
after taking expectations on both sides where
and
since for given that plays a zero mean innovations role.
It is easy to obtain from sample kernel estimates. Furthermore, it is clear that (8) holds if and only if .
To (13), which plays the role of Yule–Walker equations and which can be written more simply as
and one may add the following equation to compute the innovations covariance
where only reference to the difference is explicitly denoted assuming signal stationarity so that (17) simplifies to
This formulation is easy to generalize to model orders and to more time series via
where
which is assumed as due to filtering appropriately modelled innovations . For the present formulation, one must also consider the associated ‘ket’-vector
that when applied to (19) for after taking expectations under the zero mean innovations nature of leads to
where and ’s elements are given by so that (22) constitutes a generalization of the Yule–Walker equations. By making one may reframe (22) in matrix form as
where is block Toeplitz matrix containing p Toeplitz blocks. Equation (23) provides equations for the same number of unknown parameters in .
The high model order counterpart to (17) is given by
It is not difficult to see that the more usual Yule–Walker complete equation form becomes
There are a variety of ways for solving for the parameters. A simple one is to define leading to
Even though one may employ least-squares solution methods to solve either (26) or (23), a Total-Least-Squares (TLS) approach [20] has proven a better solution since both members of the equations are affected by estimation inaccuracies that are better dealt with using TLS.
Likewise, (24) can be used in conjunction with generalizations of model order criteria of Akaike’s AIC type
where stands for the number of available time observations. In generalizing Akaike’s criterion to the multivariate case , whereas for the Hannan–Quinn criterion, our choice in this paper.
Thus far, we have described procedures for choosing model order in the space. In ordinary time series analysis, in addition to model order identification, one must also perform proper model diagnostics. This entails checking for residual whiteness among other things. This is usually done by checking the residual auto/crosscorrelation functions for their conformity to a white noise hypothesis.
In the present formulation because, we do not explicitly compute the space series, we must resort to means other than computing the latter correlation functions from the residual data as usual. However, using the same ideas for computing (24), one may obtain estimates of the innovation cross-correlation in the feature space at various lags as
by replacing by their estimates and using obtained by solving (22) for between a minimum to a maximum lag. The usefulness of (28) is to provide means to test model accuracy and quality as a function of choice under the best model order provided by the model order criterion.
By defining a suitable normalized estimated lagged kernel correlation function (KCF)
which, given the inner product nature of kernel definition, satisfies the condition
as easily proved using the Cauchy–Schwarz inequality.
The notion of applies not only to the original kernels but also in connection with the residual kernel values given by (28) where, for explicitness, we write it as
where are the matrix entries in (28).
In the numerical illustrations that follow, we have assumed that asymptotically under the white residual hypothesis
This choice turned out to be reasonably consistent in practice. Along the same line of reasoning, other familiar tests over residuals, such as the Portmanteau test [10] were also carried out and consistently allowed verifying residual nonwhiteness.
One may say that the present theory follows closely the developments of ordinary second order moment theory with the added advantage that now nonlinear connections can be effectively captured by replacing second order moments by their respective lagged kernel estimates.
2.1. Estimation and Asymptotic Considerations
The essential problem then becomes that of estimating the entries of , entries. They can be obtained by averaging kernel values computed over the available data
for nonzero terms in the range.
Under these conditions, for an appropriately defined kernel function, the feature space becomes linearized and, following [21], it is fair to assume that the estimated vector stacked representation of the model coefficient matrices
is asymptotically Gaussian, i.e.,
where is the feature space residual matrix given by (28) and where
for the ‘bra’-vector
and the ‘ket’-vector
which are used to construct the kernel scalar products. It is immediate to note that (36) is a Toeplitz matrix composed of suitably displaced blocks.
An immediate consequence of (35) is that one may test for model coefficient nullity and thereby provide a kernel Granger Causality test. This is equivalent to testing for so that the statistic
where is a contrast matrix (or structure selection matrix) so that the null hypothesis becomes
Hence, under (35),
where corresponds to the number of the explicitly imposed constraints on .
Data Workflow
Given , analysis proceeds by
- If analysis does not suggest feature space model residual whiteness, p is increased by 1, and the procedure from step 1 is repeated until feature space model residual whiteness is obtained and attains its first local minimum meaning that the ideal model order has been reached;
- Once the best model is attained, one employs the (39) to infer connectivity.
These steps closely mirror those of ordinary time series model fitting and analysis.
3. Numerical Illustrations
The following examples consist of nonlinearly coupled systems that are simulated with the help of zero mean unit variance normal uncorrelated innovations . All simulations (10,000 realizations each) were preceded by an initial a burn-in period of 10,000 data points to avoid transient phenomena. Estimation results are examined as a function of with significance.
For brevity, Example 1 is carried out in full detail, whereas approach performance for the other ones is gauged mostly through the computation of observed detection rates except for Examples 4 and 5 which also portray model order choice criterion behaviour.
Simulation results are displayed in terms of how true and false detection rates depend on realization length .
3.1. Example 1
Consider the simplest possible system whose connectivity cannot be captured by linear methods [17] as there is a unidirectional quadratic coupling from to
with , and .
An interesting aspect of this simple system is the possibility of easily relating its coefficients a, b and c to those in (14) that describe its space evolution. This may be carried out explicitly after substituting (42) into the computed kernels of Equation (13). After a little algebra, this leads to
where and depend on the computed kernel values. From (43), it immediately follows for example that and more importantly that as expected. Vindication of the observation of these theoretically determined values also gives the means for testing estimation accuracy.
For illustrations’ sake, we write the kernel Yule–Walker Equations (22) with their respective solutions () for one given (typical) realization
for the quadratic kernels () and
for the quartic kernels (). Superscripts point to kernel order. One may readily notice approximate compliance to the expected coefficients.
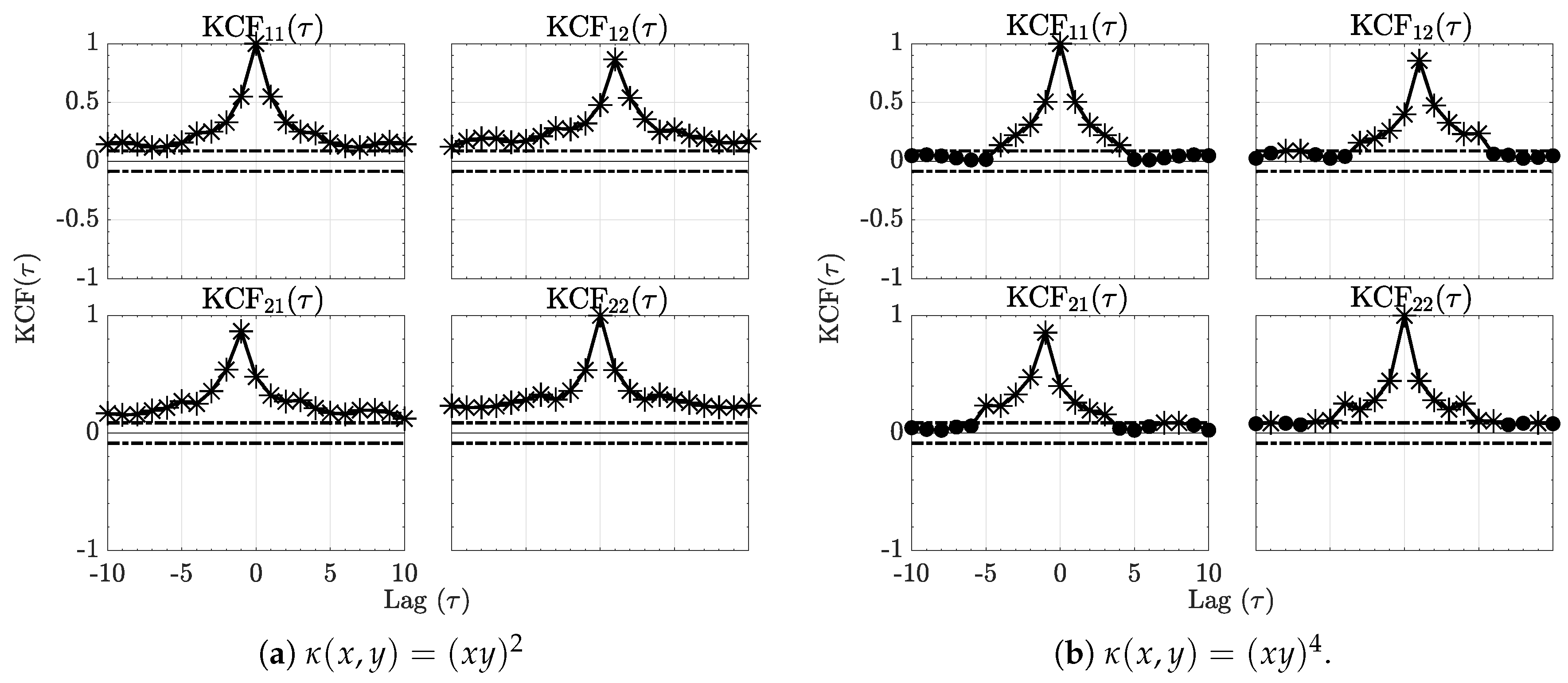
Further appreciation of this example may be obtained via a plot of the normalized estimated (29) shown in Figure 1.
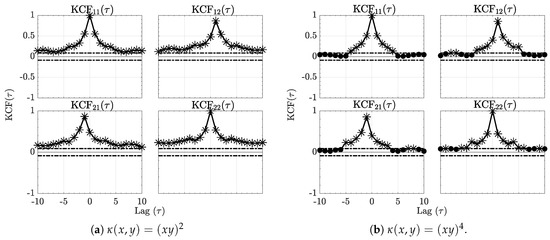
Figure 1.
The sequence kernel correlation functions (KCF) respectively for the quadratic and quartic kernels are contained in Figure 1a,b for Example 1. Horizontal dashed lines represent significance threshold interval out of which the null hypothesis of no correlation is rejected. Asterisks (*) further stress signficant values.
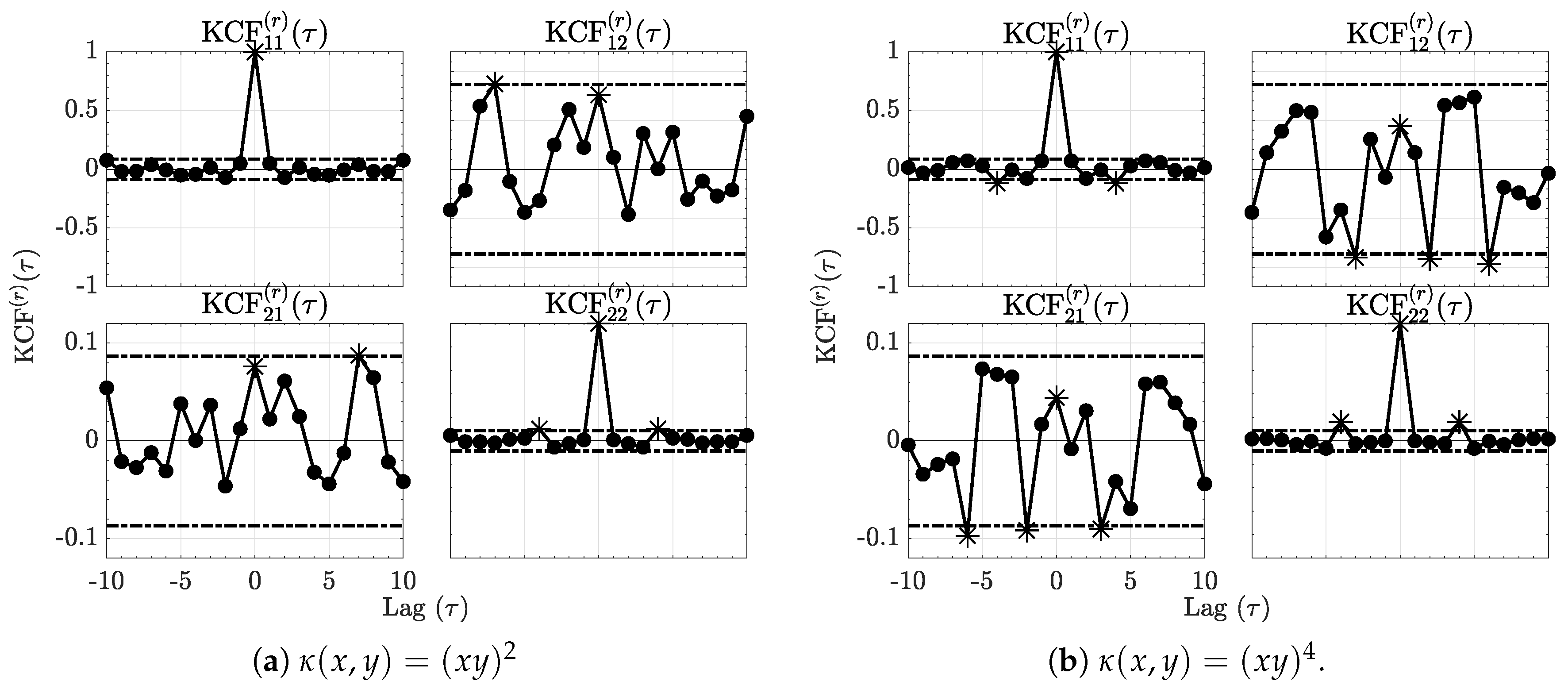
The residual normalized kernel sequences (31) computed using (28) are depicted in Figure 2 for each kernel and show effective decrease below the null hypothesis decision threshold line vindicating adequate modelling.
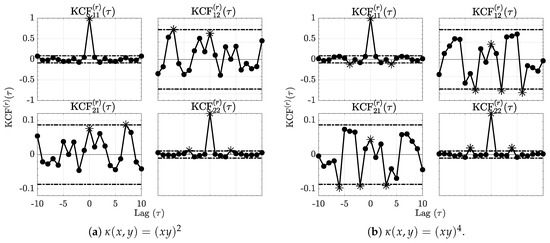
Figure 2.
The residue kernel correlation functions (KCF) respectively for the quadratic and quartic kernels are shown in Figure 2a,b for Example 1. Comparing them to Figure 1, it is clear that the kernel correlations are reduced after modelling as it is now impossible to reject KCF nullity at as no more than of the values lie outside the dashed interval around zero. Asterisks (*) further stress significant values.
Moreover, for this realization, one may show that the Hannan–Quinn Information Criterion (27) points to the correct order of . In addition, Portmanteau tests do not reject whiteness in the space for either kernel further confirming successful modelling in both cases.
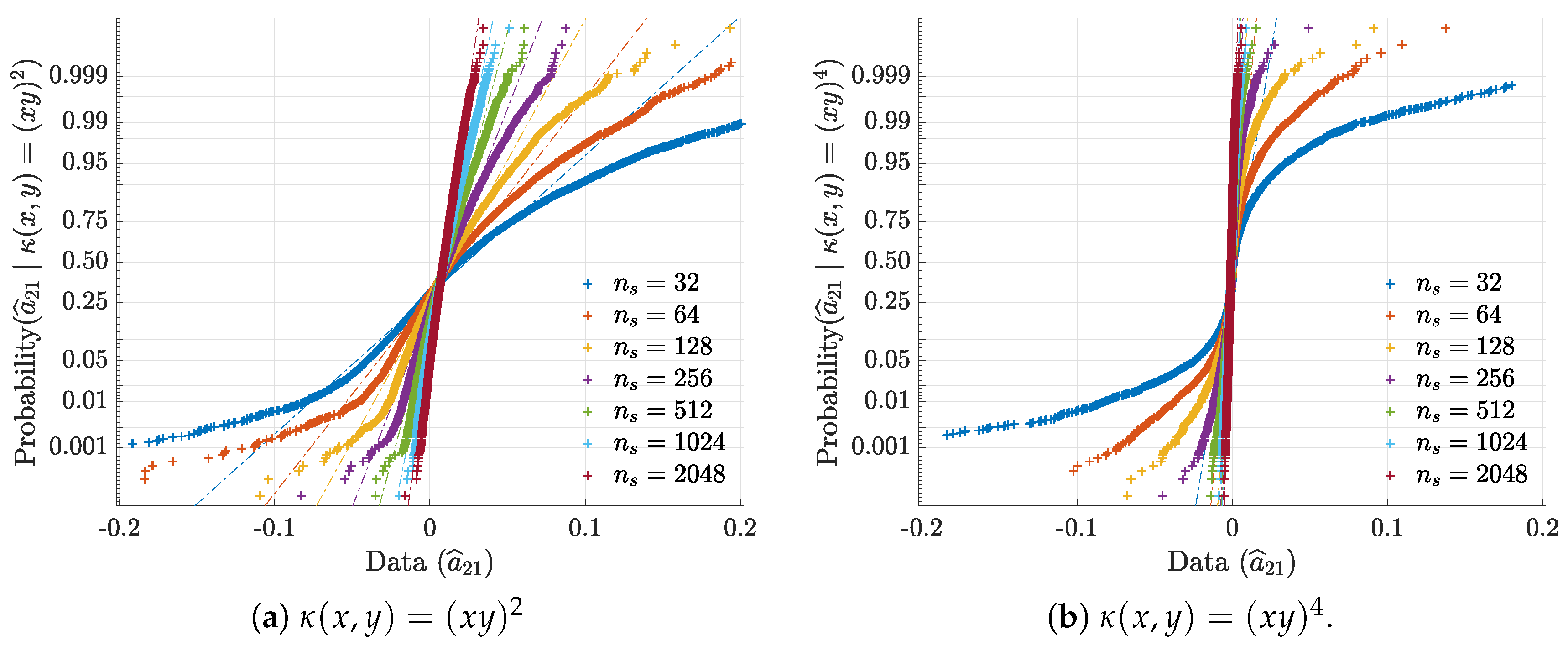
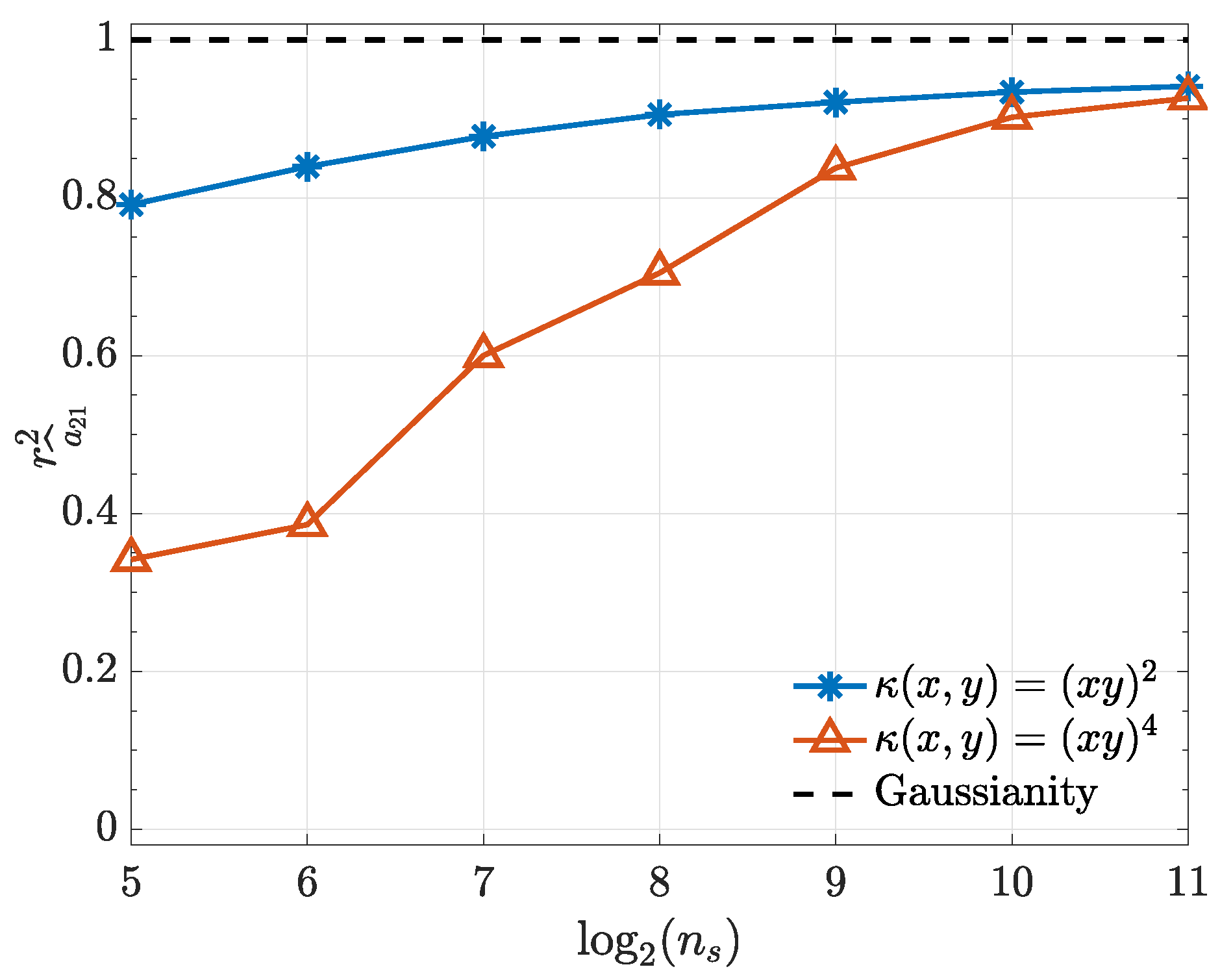
To illustrate and confirm the Gaussian asymptotic behaviour discussed in Section 2.1, normal probability plots for are presented in Figure 3. Further objective quantification of the convergence speed towards normality is provided by the evolution towards 1 of the Filliben squared-correlation coefficient [22,23,24] as a function of (Figure 4).
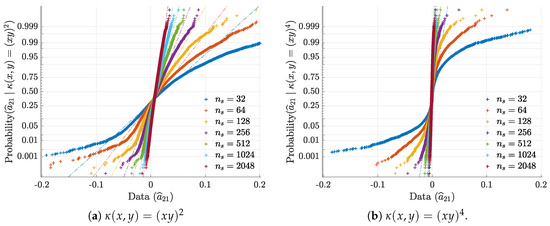
Figure 3.
Ensemble normal probability plots for , respectively for 3a quadratic and 3b quartic kernels, illustrate and confirm asymptotic normality.
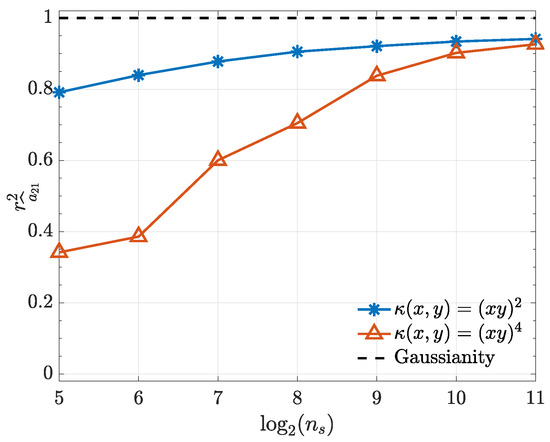
Figure 4.
Filliben squared-correlation coefficient convergence to Gaussianity as a function of for both kernels used in Example 1.
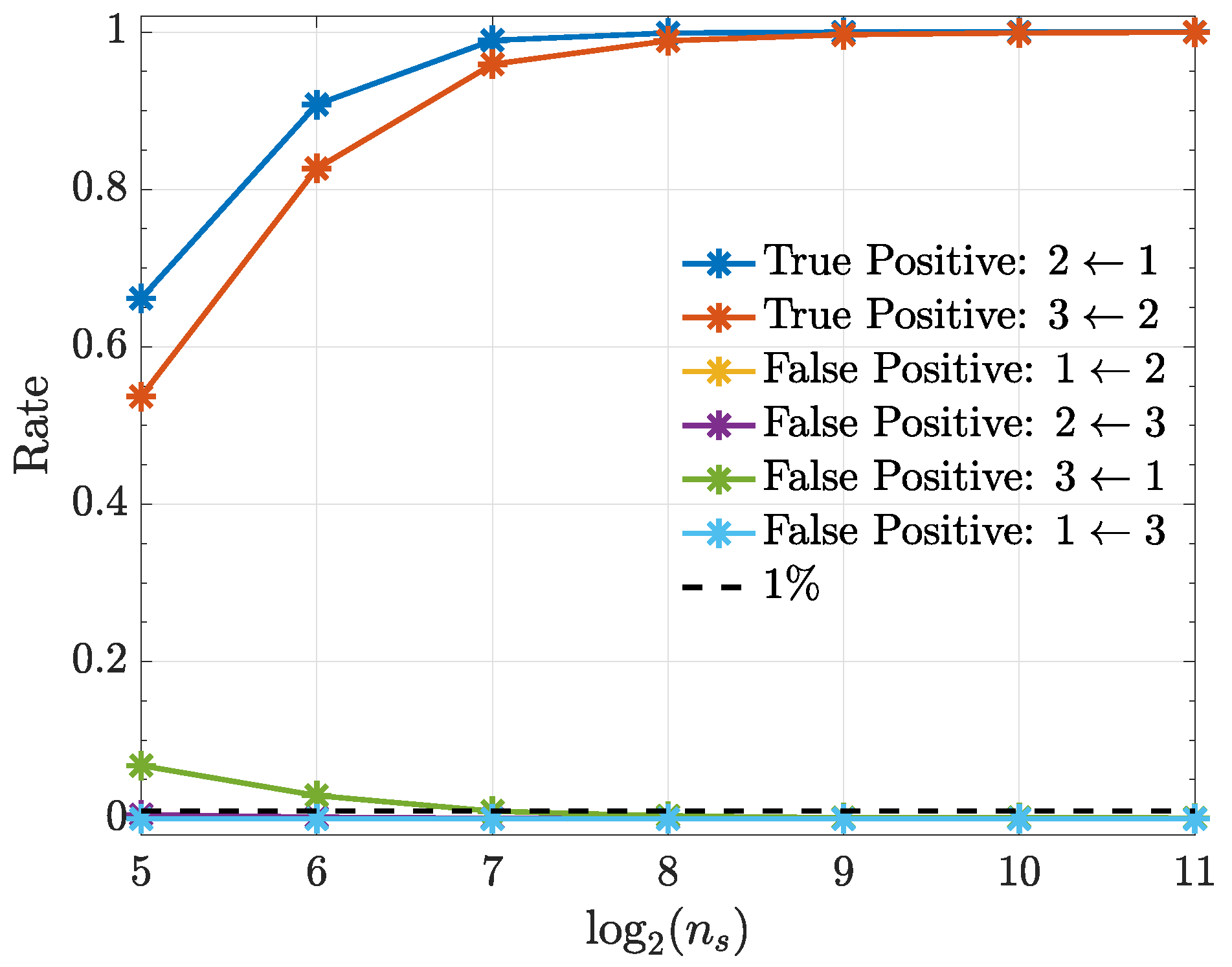
Convergence to normality justifies using (39) to test for null connectivity hypotheses. Test perfomance is depicted in Figure 5.
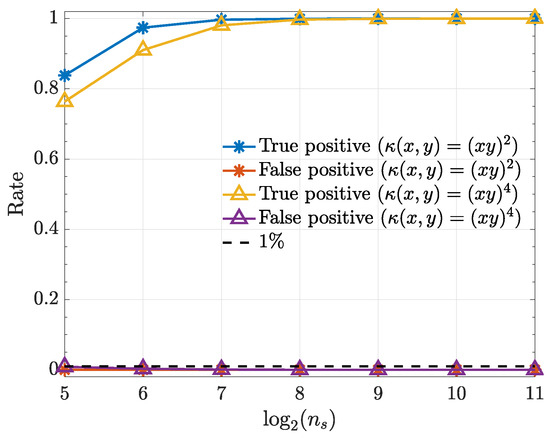
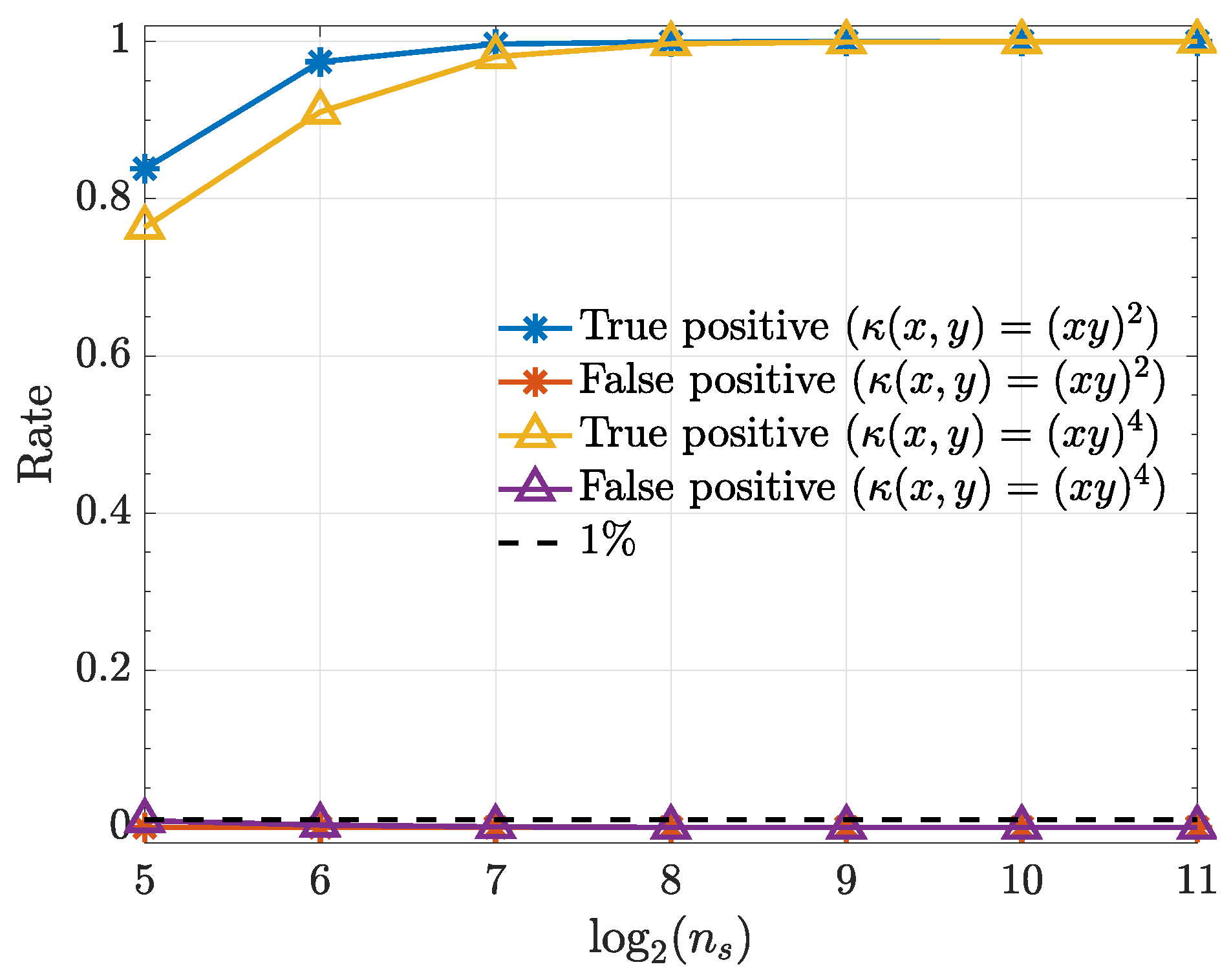
Figure 5.
True positive and false positive rates from the kernelized Granger causality test for various samples sizes () for . Note that the false-positive-rates for both kernels overlap.
3.2. Example 2
Consider , a highly resonant () linear oscillator (at a normalized frequency of ) to be unidirectionally coupled to a low pass system through a delayed squared term
where [17].
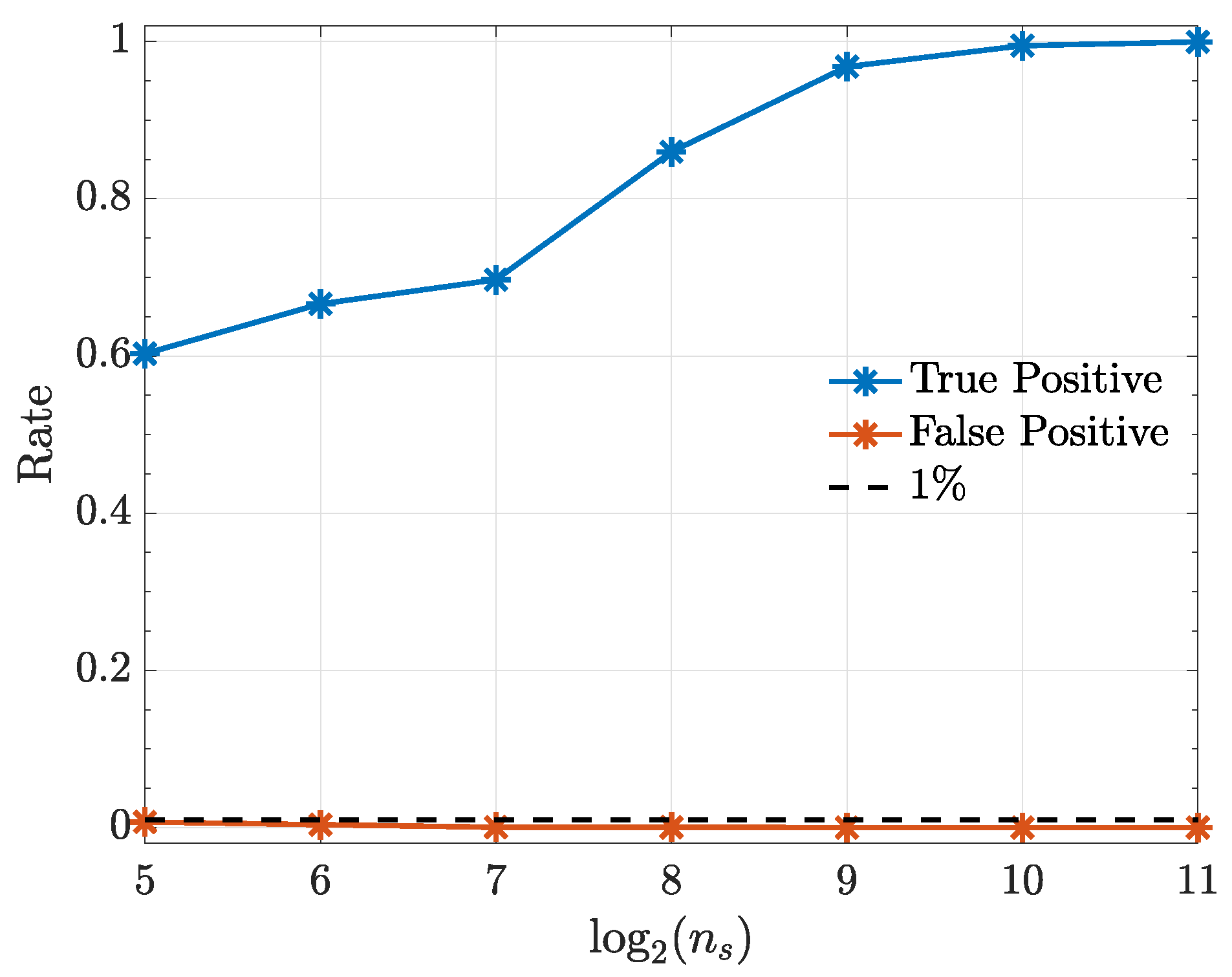
This system was already investigated elsewhere [17,25,26] under a different estimation algorithm and with fewer Monte Carlo replications. The null hypothesis connectivity results are presented in Figure 6 showing adequate asymptotic decision success. A quadratic kernel was used in all cases.
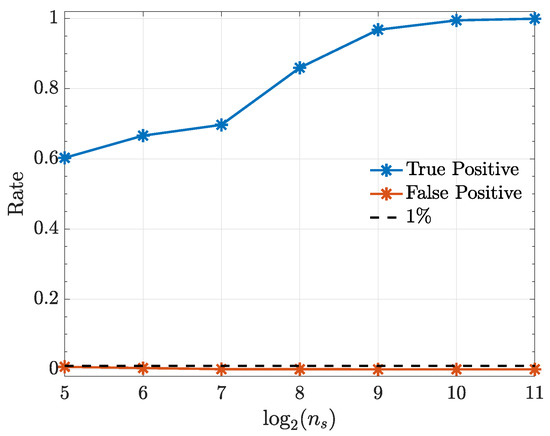
Figure 6.
True positive () and false positive rates () from the kernelized Granger causality test under a quadratic kernel as a function in Example 2.
3.3. Example 3
The present example comes from a model in [27],
This choice was dictated by the nonlinear wideband character of its signals. The values and were adopted.
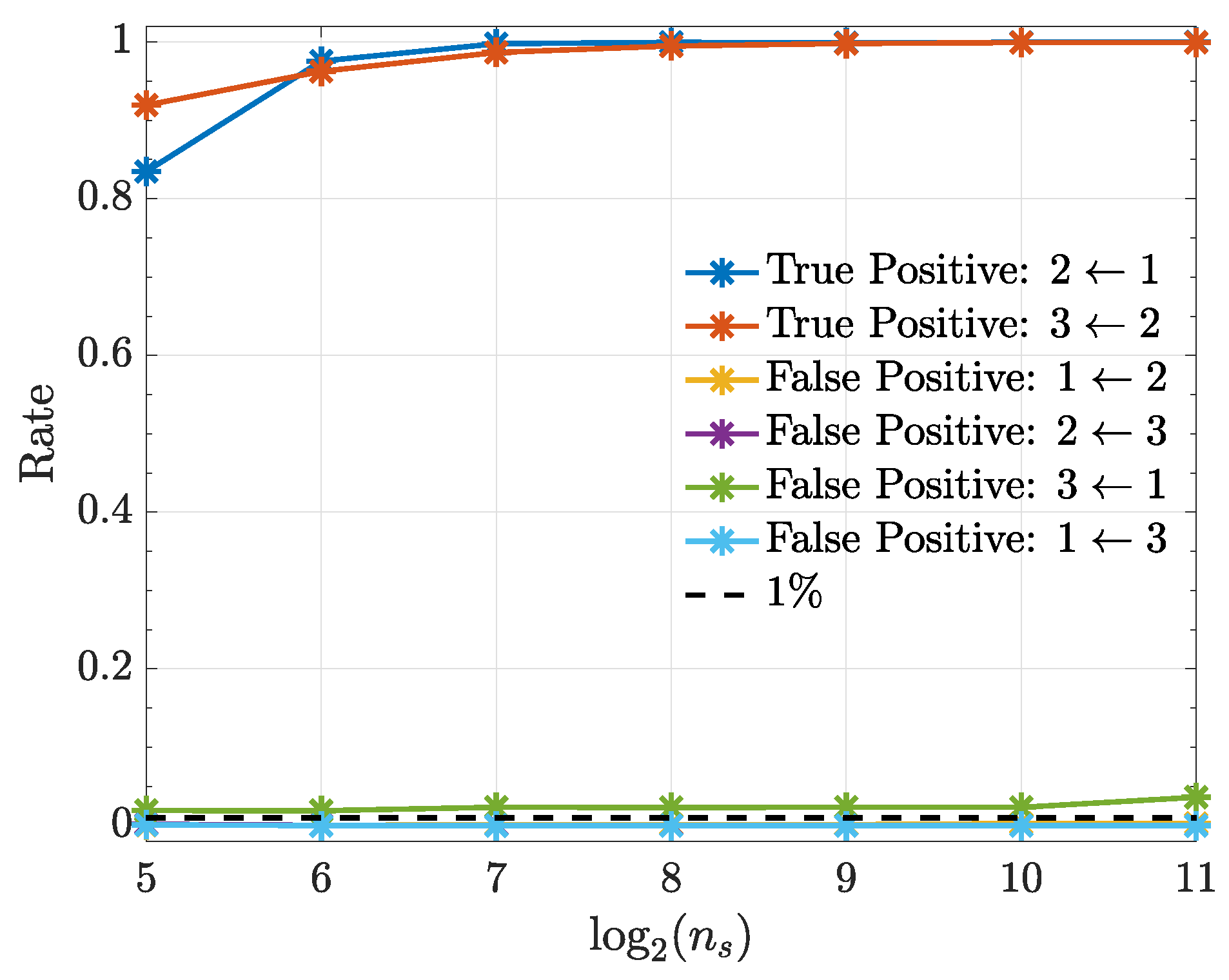
Figure 7 shows that connection detectability improves as signal duration increases except for the nonexisting connection whose performance stays more or less constant with a false positive rate slightly above . All computations used quadratic kernels.
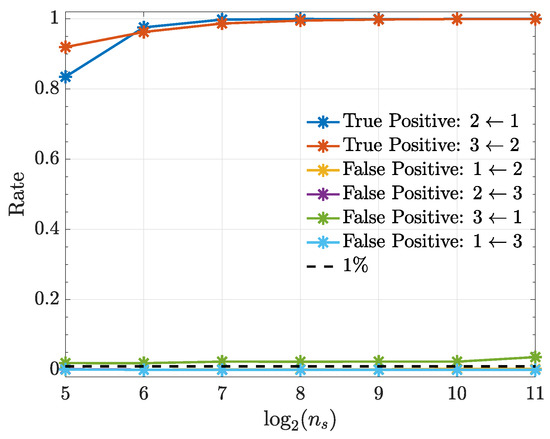
Figure 7.
True positive and false positive rates (Example 3) from the kernelized Granger causality test using a quadratic kernel as a function of . Note that the false-positive-rate for the connections , and overlap over the investigated range.
3.4. Example 4
For this numerical illustration, consider the model presented in [28]
System (48) produces nonlinear wideband signals with a quadratic () coupling factor whose intensity is given by c taken here as .
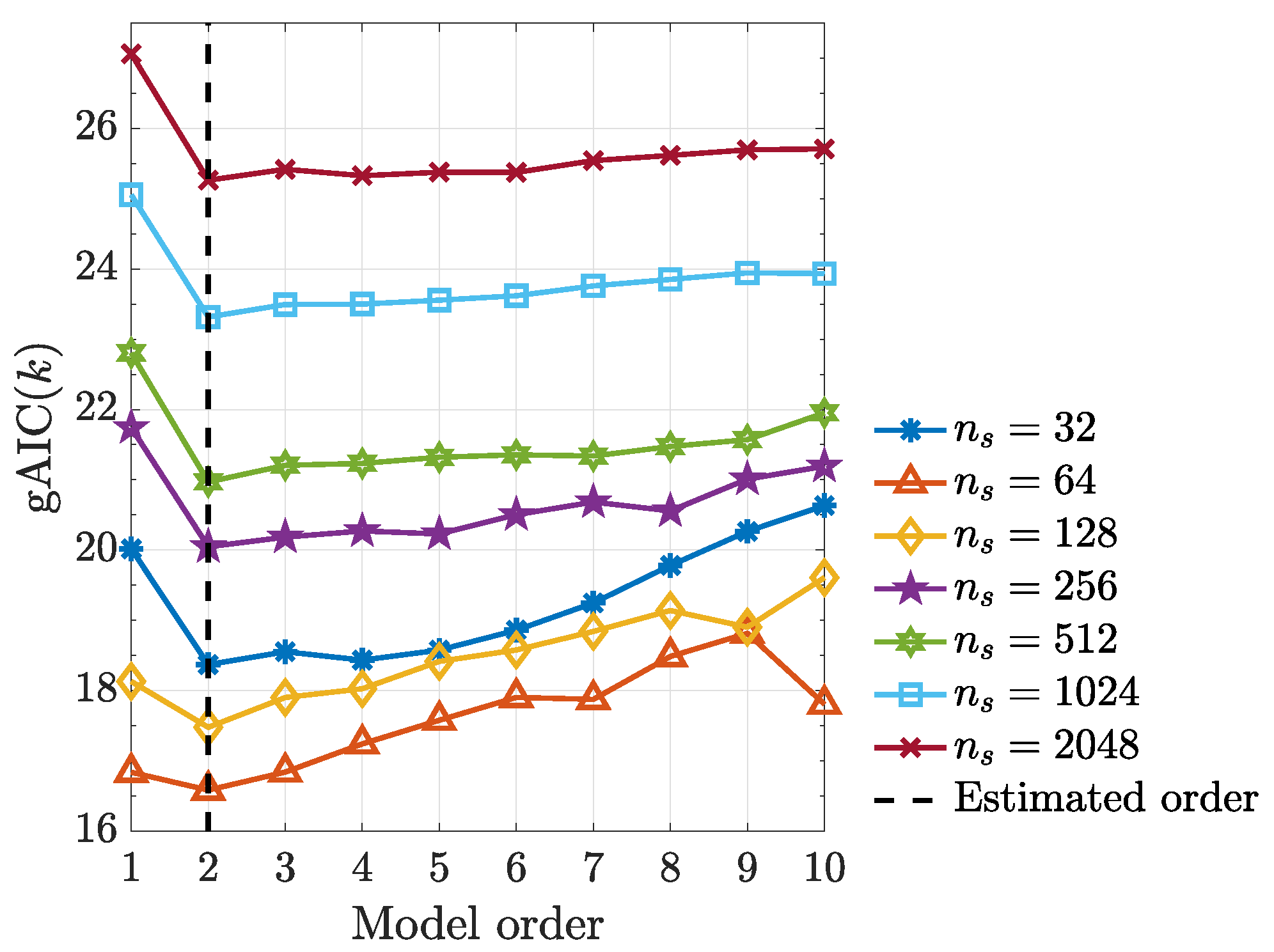
It is worth noting that, kernelized Granger causality true positive rate improves as sample size () increases (Figure 8) and using the generalized Hannan–Quinn criterion, the order of kernelized autoregressive vector models identified for a typical realization was correctly identified and equals 2 as expected (see Figure 9).
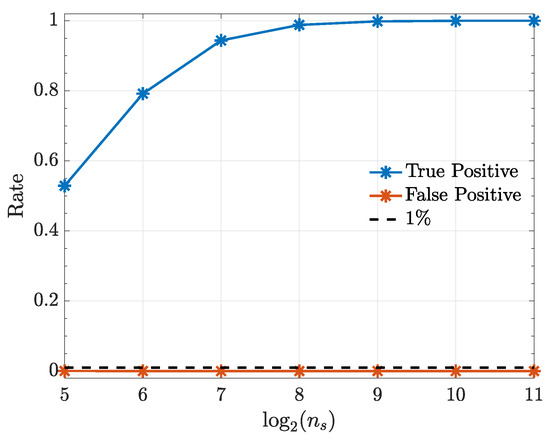
Figure 8.
True positive and false positive rates from the kernelized Granger causality test under a quadratic kernel as function of record length in Example 4.
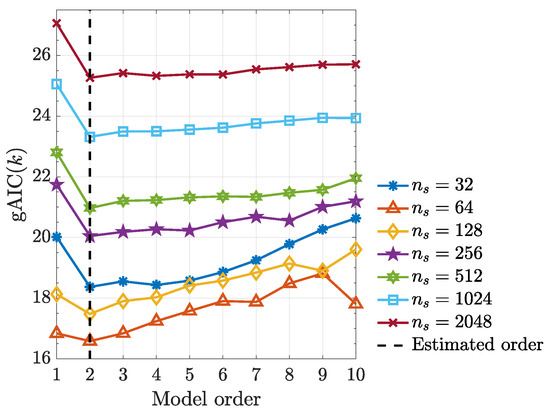
Figure 9.
Generalized Hannan–Quinn criterion () with as a function of model order for various observed record lengths using a typical realization from (48).
3.5. Example 5
As a last numerical illustration, consider data generated by
with and .
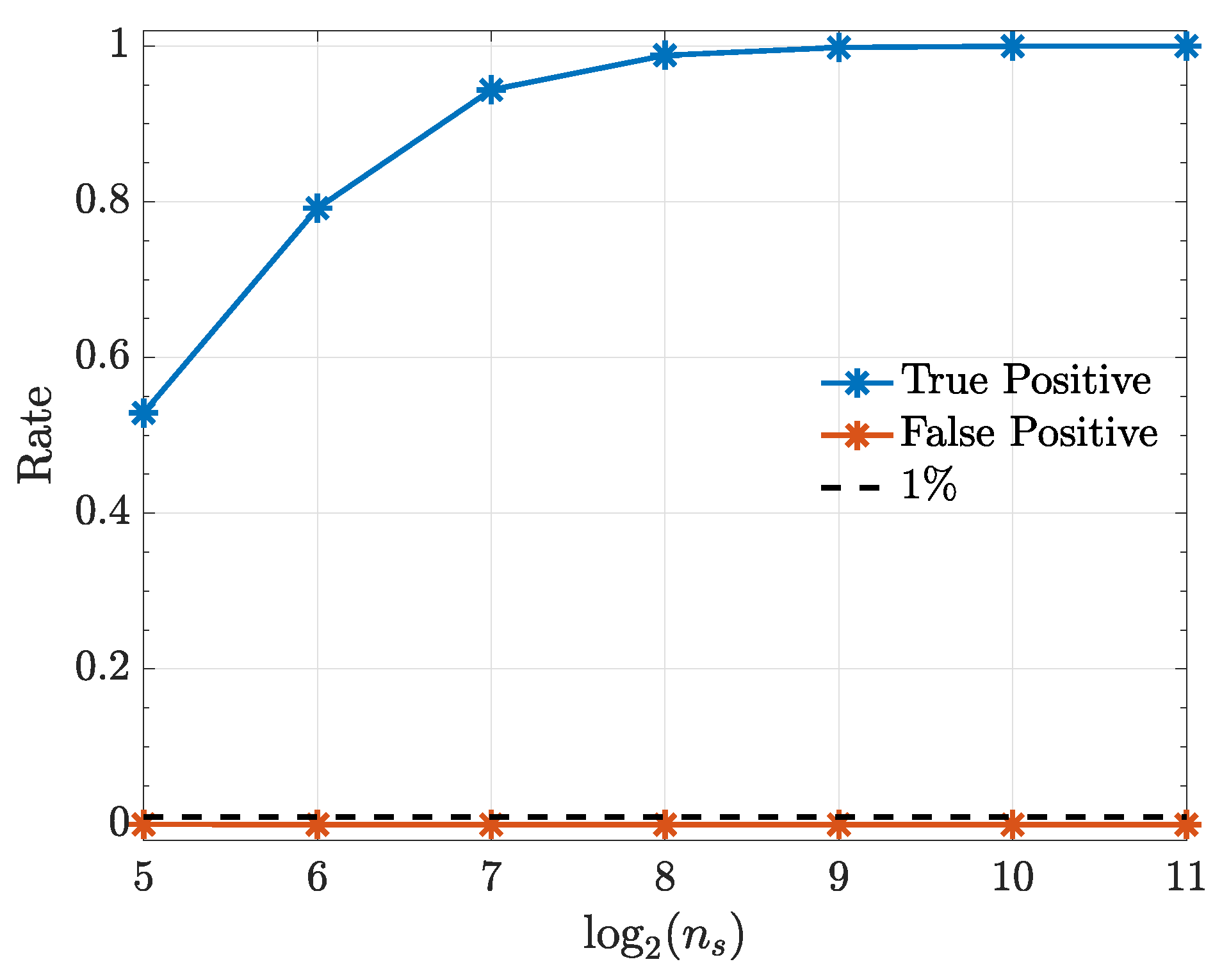
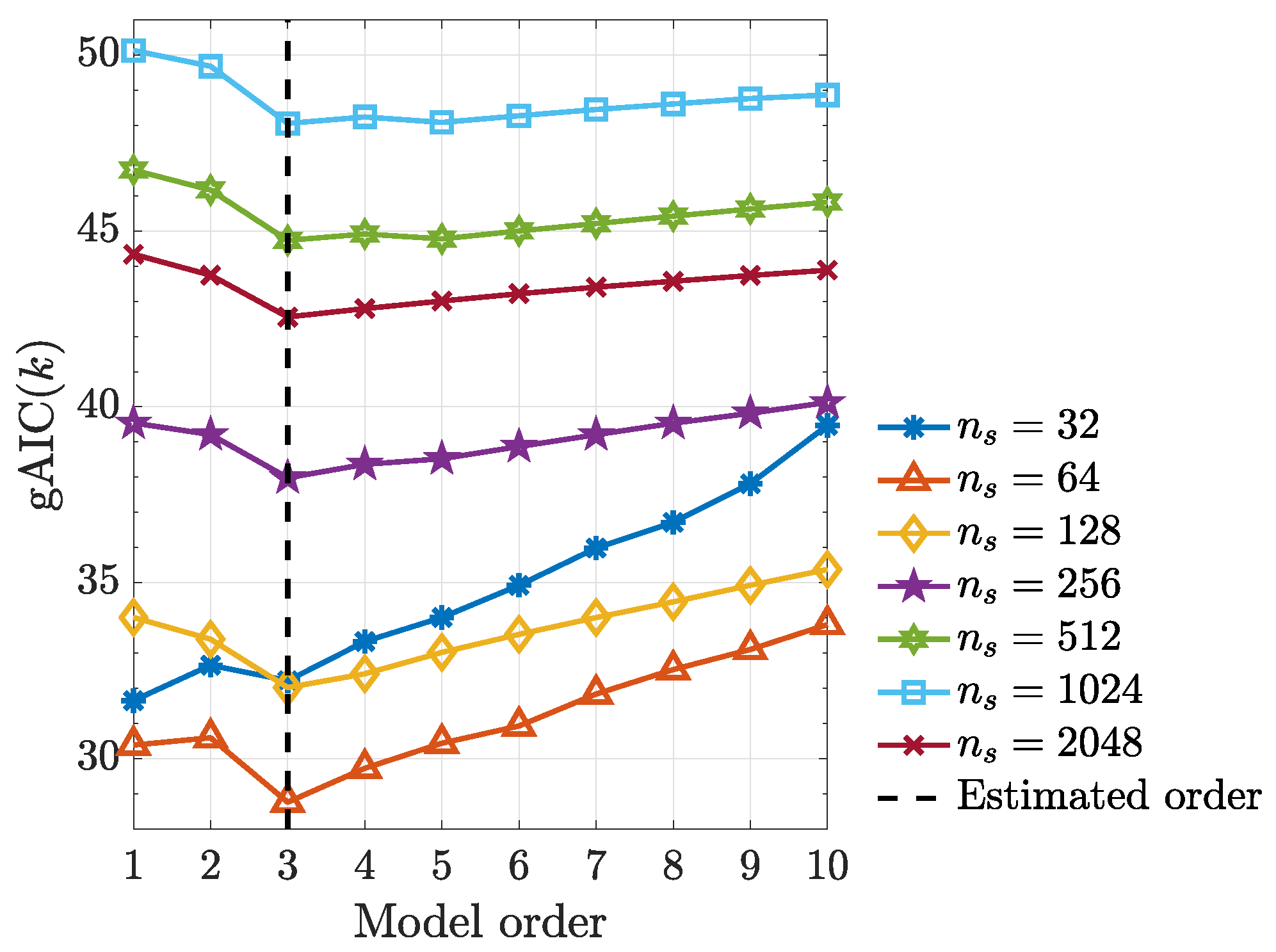
Under the quadratic kernel and employing kernelized Hannan–Quinn information criterion (27) (see Figure 10), one can see that the estimated model order is as expected judging from the term in (49). In addition, kernelized Granger causality detectability improves with record length increase (Figure 11).
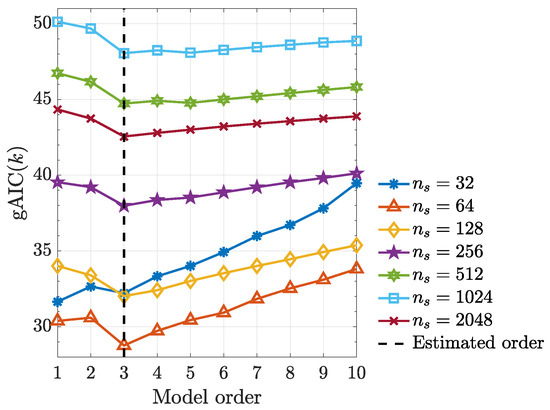
Figure 10.
Generalized Hannan–Quinn criterion () as a function of model order for the various data lengths from a typical realization from (49).
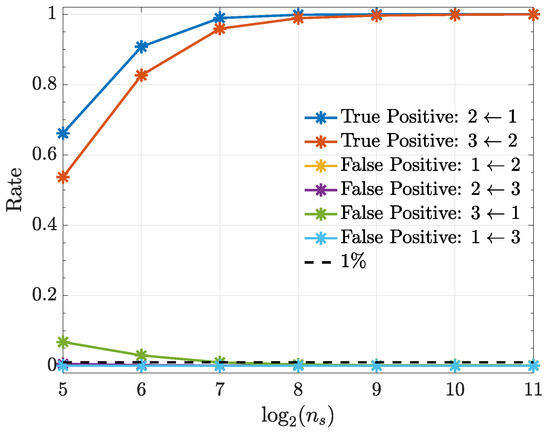
Figure 11.
Observed true positive and false positive rates from the kernelized Granger causality test under a quadratic kernel for various record lengths in Example 5. Note that the false-positive-rate for the connections , and overlap over the range, except for , which, however, attains the same level as the others after .
4. Conclusions and Future Work
After a brief theoretical presentation (Section 2), we have shown that canonical model fitting procedures that involve (a) model specification with order determination and (b) explicit model diagnostic testing can be successfully carried out in the feature space to detect connectivity via reproducing kernels. In dealing with Granger causality detection using kernels as in [29,30], this stands in sharp contrast as the latter depend on solving the reconstruction/pre-image problem to provide prediction error estimates in the original data space . In fact, part of the challenge in pre-image determination lies in its frequently associated numerical ill-condition [31].
The key result behind doing model diagnostics and inference in is (28) by realizing that kernel quantities may be normalized much as correlation coefficients. It should be noted that (28) holds even in the case of (nonkernel) linear modelling by replacing the matrices by auto/crosscorrelation matrices, something that, in practice, is never adopted in classical linear time series modelling because the necessary auto/crosscorrelations are more efficiently computed from model residuals that are easy to obtain as no pre-imaging problem is involved there.
Thus, what importantly sets the present approach apart from previous work is the lack of need for returning to the original input space to gauge model quality as the reconstruction/pre-image problem can be fully circumvented bypassing unnecessary uncertainties.
As such, we showed that, because model adequacy testing can be performed directly in the feature space , directional Granger type connectivity can be detected for a variety of multivariate nonlinear coupling scenarios, thereby totally dispensing with the need for detailed ‘a priori’ model knowledge.
We observed that successful connectivity detection is achievable at the expense of a relatively short time series. A systematic comparison with other approaches [4,5,32,33,34,35] is planned for future work, but, at least for the cases we tested so far, savings of at least one order magnitude in record lengths are feasible.
One of the basic tenants of the present work is that model coefficients in the feature space are asymptotically normal, something whose consistency was successfully illustrated though the need for a more formal proof remains, especially in connection to explicit kernel estimates under the total-least-squares solution to (23). Our choice of TLS was dictated by its apparent superiority when compared to the ‘kernel trick’ [32] whose multivariate version we employed in [26,36,37].
In this context, it is important to note that, contrary to other methods that require time-consuming resampling procedures for adequate inference, the present approach relies on asymptotic statistics and is thus less susceptible to eventual problems derived from data shuffling.
One of the advantages of the present development is that the procedure allows for determining how far in the past to look via the model order criteria we employed (27).
Even though order estimation and model testing were successful upon borrowing from the usual linear modelling practices, further systematic examination is still needed and is under way.
One may rightfully argue that the kernels we chose for illustrating the present work are equivalent to modelling the original time series after the application of a suitable transformation to the data and that they look for the causality evidence present in higher order momenta. This, in fact, explains why quadratic kernels converge much faster than quartic ones in Example 1. The merit of framing the time series transformation discussion for connectivity detection in terms of kernels produces a simple workflow and paves the way to developing future data-driven criteria towards optimum data transformation choice for a given problem. Other kernel choices are being investigated.
The signal model used in the present development does not contemplate additive measurement noise whose impact on connectivity detection we also leave for future examination.
One thing the present type of analysis cannot do is expose details of how the nonlinearity takes place. For example, coupling may be quadratic or involve higher exponential powers or some other function. What the present approach can do, however, is to expose existing connections, so that modelling efforts can be concentrated on them, thereby avoiding modelling parameter waste on non relevant links.
Finally, the present systematic empirical investigation sets the proposal of using feature space-frequency domain descriptions of connectivity like kernel partial directed coherence [26,36], and kernel directed transfer function [37] on sound footing, especially with respect to their asymptotic connectivity behaviour.
Author Contributions
All authors conceptualized, cured the data, did the formal analysis, acquired the funding, did the investigation, obtained the resources, analyzed and interpreted the data, created the software used in the work, did the supervision, validation, visualization, drafted the work, and revised it.
Funding
L.M. was funded by in part by an institutional Ph.D. CAPES Grant at Escola Politécnica, University of São Paulo, São Paulo, Brazil, and by CAPES, grant number (PALEOCEANO Project) and by FAPESP, grant number 2015/50686-1 (PACMEDY Project), both at Instituto de Astronomia, Geofísica e Ciências Atmosféricas, University of São Paulo, São Paulo, Brazil. L.A.B. was funded by CNPq, grant number 308073/2017-7.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Schumacker, R.E.; Lomax, R.G. A Beginner’S Guide to Structural Equation Modeling, 4th ed.; Taylor & Francis: New York, NY, USA, 2016. [Google Scholar]
- Applebaum, D. Probability and Information: An Integrated Approach, 2nd ed.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2008; p. 273. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley Series in Telecommunications; Wiley: New York, NY, USA, 2006; p. 774. [Google Scholar]
- Hlaváčková-Schindler, K.; Paluš, M.; Vejmelka, M.; Bhattacharya, J. Causality detection based on information- theoretic approaches in time series analysis. Phys. Rep. Rev. Sect. Phys. Lett. 2007, 441, 1–46. [Google Scholar] [CrossRef]
- Schreiber, T. Measuring Information transfer. Phys. Rev. Lett. 2000, 85, 461–464. [Google Scholar] [CrossRef] [PubMed]
- Bendat, J.S.; Piersol, A.G. Engineering Applications of Correlation and Spectral Analysis; Wiley: New York, NY, USA; Chichester, UK, 1980. [Google Scholar]
- Baccalá, L.A.; Sameshima, K. Overcoming the limitations of correlation analysis for many simultaneously processed neural structures. Prog. Brain Res. 2001, 130, 33–47. [Google Scholar] [CrossRef] [PubMed]
- Granger, C.W.J. Investigating causal relations by econometric models and cross-spectral methods. Econometrica 1969, 37, 424–438. [Google Scholar] [CrossRef]
- Baccalá, L.A.; Sameshima, K. Multivariate time series brain connectivity: A sum up. Methods in Brain Connectivity Inference Through Multivariate Time Series Analysis; CRC Press: Boca Raton, FL, USA, 2014; pp. 245–251. [Google Scholar]
- Lütkepohl, H. New Introduction to Multiple Time Series Analysis; Springer: Berlin, Germany, 2005. [Google Scholar]
- Baccalá, L.A.; Sameshima, K. Partial directed coherence: A new concept in neural structure determination. Biol. Cybern. 2001, 84, 463–474. [Google Scholar] [CrossRef] [PubMed]
- Vapnik, V.N. Statistical Learning Theory, 1st ed.; John Wiley and Sons: Hoboken, NJ, USA, 1998; p. 736. [Google Scholar]
- Priestley, M.B. Spectral Analysis and Time Series; Probability and Mathematical Statistics; Academic Press London: New York, NY, USA, 1981; p. 890. [Google Scholar]
- Nikias, C.; Petropulu, A.P. Higher Order Spectra Analysis: A Non-linear Signal Processing Framework; Prentice Hall Signal Processing Series; Prentice Hall: Upper Saddle River, NJ, USA, 1993; p. 528. [Google Scholar]
- Subba-Rao, T.; Gabr, M.M. An Introduction to Bispectral Analysis and Bilinear Time Series Models; Lecture Notes in Statistics; Springer: New York, NY, USA, 1984. [Google Scholar]
- Schelter, B.; Winterhalder, M.; Eichler, M.; Peifer, M.; Hellwig, B.; Guschlbauer, B.; Lücking, C.H.; Dahlhaus, R.; Timmer, J. Testing for directed influences among neural signals using partial directed coherence. J. Neurosci. Methods 2006, 152, 210–219. [Google Scholar] [CrossRef] [PubMed]
- Massaroppe, L.; Baccalá, L.A.; Sameshima, K. Semiparametric detection of nonlinear causal coupling using partial directed coherence. In Proceedings of the 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Boston, MA, USA, 30 August–3 September 2011; pp. 5927–5930. [Google Scholar] [CrossRef]
- Schölkopf, B.; Smola, A.J. Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond; MIT Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Mercer, J. Functions of positive and negative type, and their connection with the theory of integral equations. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 1909, A, 415–446. [Google Scholar] [CrossRef]
- Golub, G.H.; van Loan, C.F. Matrix Computations, 4th ed.; Number 3 in Johns Hopkins Studies in the Mathematical Sciences; Johns Hopkins University Press: Baltimore, MD, USA, 2013; p. 784. [Google Scholar]
- Hable, R. Asymptotic normality of support vector machine variants and other regularized kernel methods. J. Multivar. Anal. 2012, 106, 92–117. [Google Scholar] [CrossRef]
- Filliben, J.J. The probability plot correlation coefficient test for normality. Technometrics 1975, 17, 111–117. [Google Scholar] [CrossRef]
- Vogel, R.M. The probability plot correlation coefficient test for the normal, lognormal, and Gumbel distributional hypotheses. Water Resour. Res. 1986, 22, 587–590. [Google Scholar] [CrossRef]
- Vogel, R.M. Correction to “The probability plot correlation coefficient test for the normal, lognormal, and Gumbel distributional hypotheses”. Water Resour. Res. 1987, 23, 2013. [Google Scholar] [CrossRef]
- Massaroppe, L.; Baccalá, L.A. Método semi-paramétrico para inferência de conectividade não-linear entre séries temporais. In Proceedings of the Anais do I Congresso de Matemática e Computacional da Região Sudeste, I CMAC Sudeste, Uberlândia, Brazil, 20–23 September 2011; pp. 293–296. [Google Scholar]
- Massaroppe, L.; Baccalá, L.A. Detecting nonlinear Granger causality via the kernelization of partial directed coherence. In Proceedings of the 60th World Statistics Congress of the International Statistical Institute, ISI2015, Rio de Janeiro, RJ, USA, 26–31 July 2015; pp. 2036–2041. [Google Scholar]
- Gourévitch, B.; Bouquin-Jeannès, R.L.; Faucon, G. Linear and nonlinear causality between signals: Methods, examples and neurophysiological applications. Biol. Cybern. 2006, 95, 349–369. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Rangarajan, G.; Feng, J.; Ding, M. Analyzing multiple nonlinear time series with extended Granger causality. Phys. Lett. A 2004, 324, 26–35. [Google Scholar] [CrossRef]
- Amblard, P.O.; Vincent, R.; Michel, O.J.J.; Richard, C. Kernelizing Geweke’s measures of Granger causality. In Proceedings of the 2012 IEEE International Workshop on Machine Learning for Signal Processing, Santander, Spain, 23–26 September 2012; pp. 1–6. [Google Scholar] [CrossRef]
- Kallas, M.; Honeine, P.; Francis, C.; Amoud, H. Kernel autoregressive models using Yule-Walker equations. Signal Process. 2013, 93, 3053–3061. [Google Scholar] [CrossRef]
- Honeine, P.; Richard, C. Preimage problem in kernel-based machine learning. IEEE Signal Process. Mag. 2011, 28, 77–88. [Google Scholar] [CrossRef]
- Kumar, R.; Jawahar, C.V. Kernel approach to autoregressive modeling. In Proceedings of the Thirteenth National Conference on Communications (NCC 2007), Kanpur, India, 26–28 January 2007; pp. 99–102. [Google Scholar]
- Marinazzo, D.; Pellicoro, M.; Stramaglia, S. Kernel method for nonlinear Granger causality. Phys. Rev. Lett. 2008, 100, 144103. [Google Scholar] [CrossRef] [PubMed]
- Park, I.; Príncipe, J.C. Correntropy based Granger causality. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Las Vegas, NV, USA, 31 March–4 April 2008; pp. 3605–3608. [Google Scholar] [CrossRef]
- Príncipe, J.C. Information Theoretic Learning: Rényi’s Entropy and Kernel Perspectives, 1st ed.; Number XIV in Information Science and Statistics; Springer Publishing Company, Incorporated: New York, NY, USA, 2010; p. 448. [Google Scholar]
- Massaroppe, L.; Baccalá, L.A. Kernel-nonlinear-PDC extends Partial Directed Coherence to detecting nonlinear causal coupling. In Proceedings of the 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milan, Italy, 25–29 August 2015; pp. 2864–2867. [Google Scholar] [CrossRef]
- Massaroppe, L.; Baccalá, L.A. Causal connectivity via kernel methods: Advances and challenges. In Proceedings of the 2016 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 16–20 August 2016. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).