On the Properties of the Reaction Counts Chemical Master Equation
Abstract
1. Introduction
2. Reaction Counts CME
2.1. Formulation
2.2. Analytical Solutions of the Reaction Counts CME
- 1.
- There exists a permutation matrix P such that is lower triangular;
- 2.
- The spectrum of is the set:
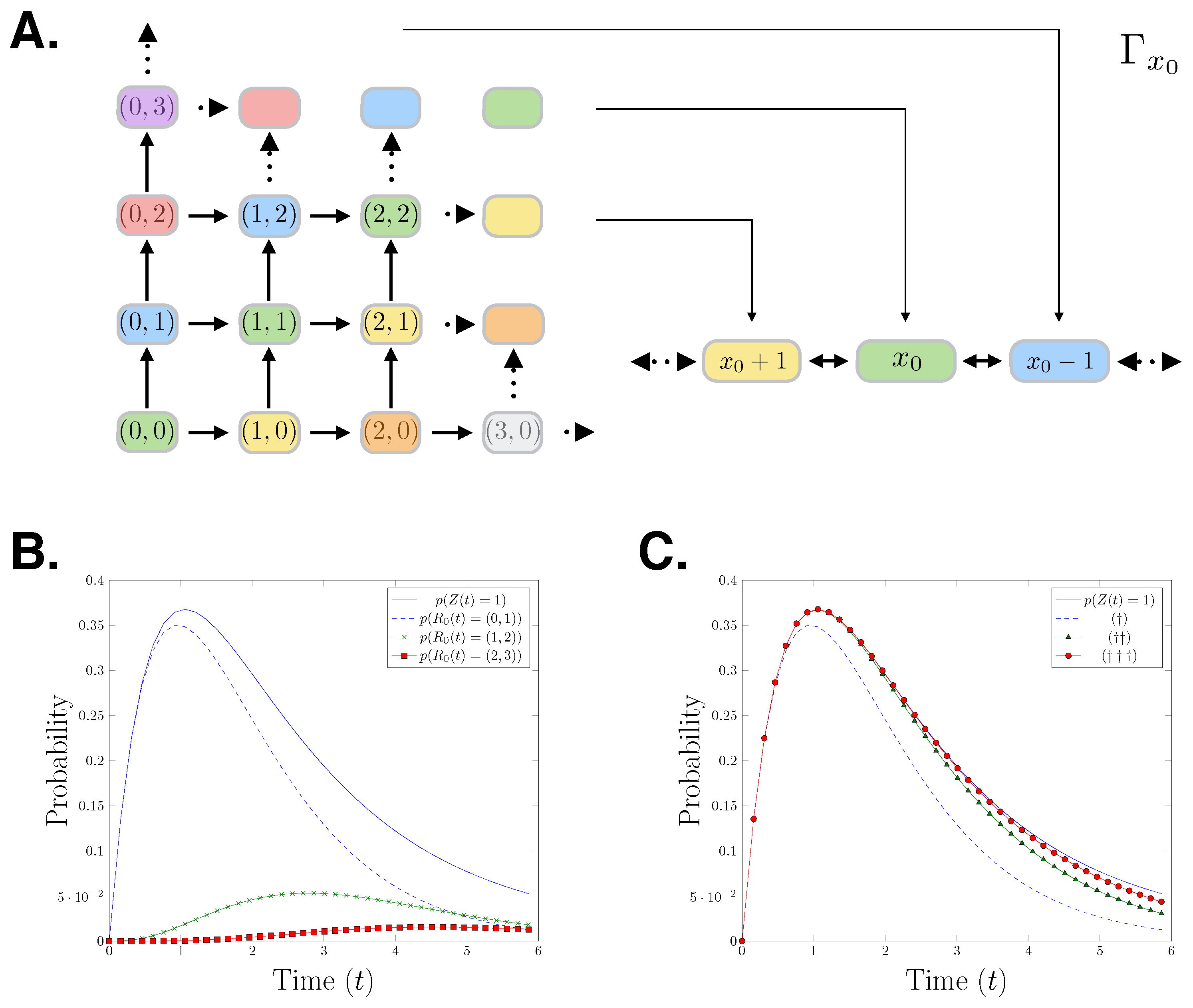
3. Partitioning the State Space
4. Paths
4.1. Path Chains
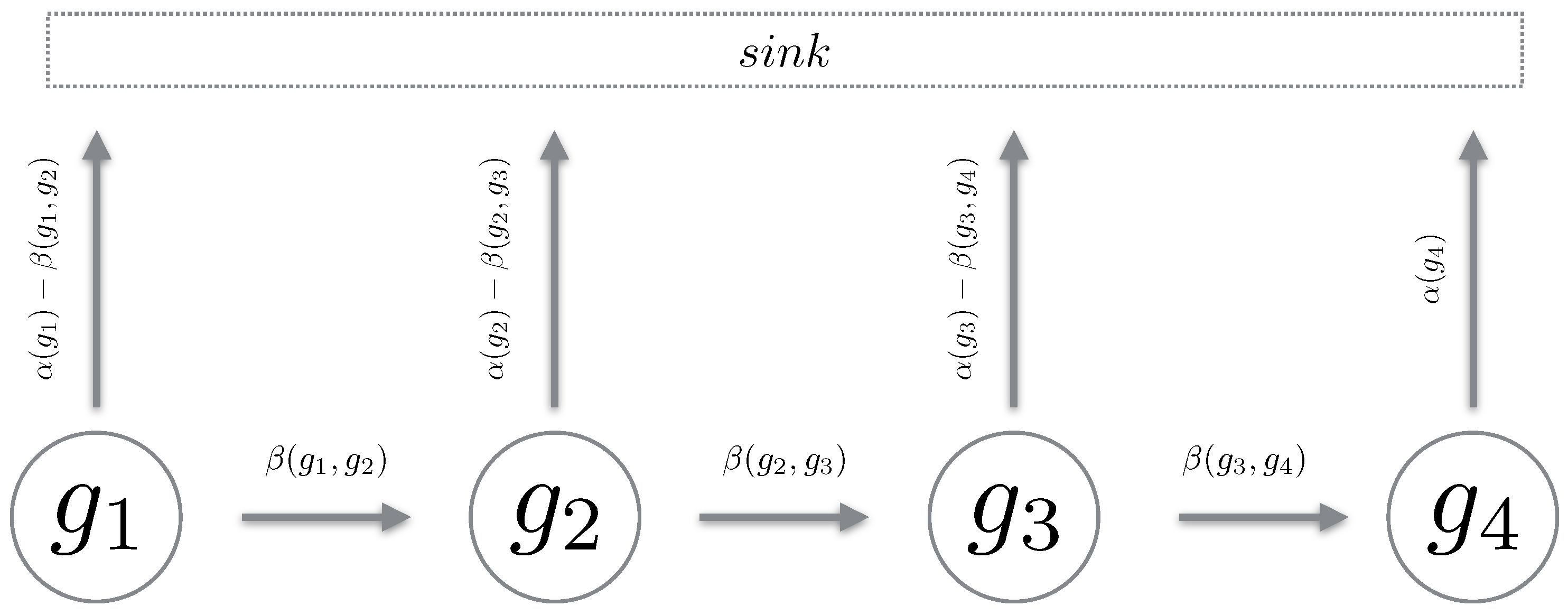
4.2. Gated- and Un-Gated Path Chains
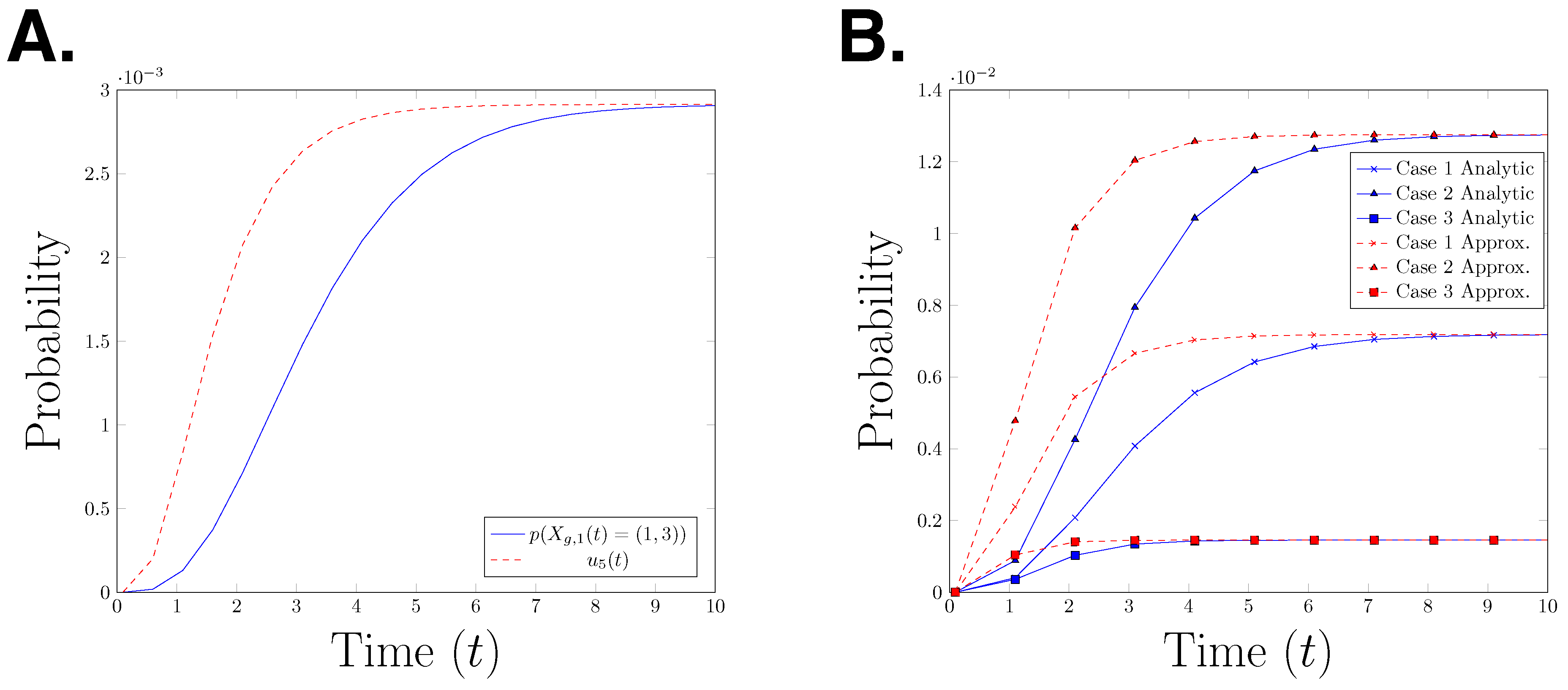
4.3. Cascade of Gating and Un-Gating
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Wilkinson, D.J. Mathematical and Computational Biology Series. In Stochastic Modelling for Systems Biology; Chapman & Hall/CRC: Boca Raton, FL, USA, 2006. [Google Scholar]
- Van Kampen, N.G. Stochastic Processes in Physics and Chemistry, 3rd ed.; North Holland: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Kurtz, T.G. Strong approximation theorems for density dependent Markov chains. Stoch. Process. Their Appl. 1978, 6, 223–240. [Google Scholar] [CrossRef]
- Grima, R.; Thomas, P.; Straube, A.V. How accurate are the nonlinear chemical Fokker-Planck and chemical Langevin equations? J. Chem. Phys. 2011, 135, 084103. [Google Scholar] [CrossRef] [PubMed]
- Higham, D.J. Modeling and Simulating Chemical Reactions. SIAM Rev. 2008, 50, 347–368. [Google Scholar] [CrossRef]
- Hegland, M.; Hellander, A.; Lötstedt, P. Sparse grids and hybrid methods for the chemical master equation. BIT Numer. Math. 2008, 48, 265–283. [Google Scholar] [CrossRef]
- Engblom, S. Spectral approximation of solutions to the chemical master equation. J. Comput. Appl. Math. 2009, 229, 208–221. [Google Scholar] [CrossRef][Green Version]
- Jahnke, T.; Udrescu, T. Solving chemical master equations by adaptive wavelet compression. J. Comput. Phys. 2010, 229, 5724–5741. [Google Scholar] [CrossRef]
- Sunkara, V.; Hegland, M. An Optimal Finite State Projection Method. Procedia Comput. Sci. 2010, 1, 1579–1586. [Google Scholar] [CrossRef]
- Kazeev, V.; Khammash, M.; Nip, M.; Schwab, C. Direct Solution of the chemical master equation Using Quantized Tensor Trains. PLoS Comput. Biol. 2014, 10, e1003359. [Google Scholar] [CrossRef] [PubMed]
- Schnoerr, D.; Sanguinetti, G.; Grima, R. Approximation and inference methods for stochastic biochemical kinetics—A tutorial review. J. Phys. A Math. Theor. 2017, 50, 093001. [Google Scholar] [CrossRef]
- Vlysidis, M.; Kaznessis, Y. Solving Stochastic Reaction Networks with Maximum Entropy Lagrange Multipliers. Entropy 2018, 20, 700. [Google Scholar] [CrossRef]
- Haseltine, E.L.; Rawlings, J.B. Approximate simulation of coupled fast and slow reactions for stochastic chemical kinetics. J. Chem. Phys. 2002, 117, 6959–6969. [Google Scholar] [CrossRef]
- Goutsias, J. Quasiequilibrium approximation of fast reaction kinetics in stochastic biochemical systems. J. Chem. Phys. 2005, 122, 184102. [Google Scholar] [CrossRef] [PubMed]
- Sunkara, V. The chemical master equation with respect to reaction counts. In Proceedings of the 18th World IMACS Congress and (MODSIM09) International Congress on Modelling and Simulation, Cairns, Australia, 13–17 July 2009; Volume 1, pp. 2377–2383. [Google Scholar]
- Menz, S.; Latorre, J.; Schütte, C.; Huisinga, W. Hybrid Stochastic–Deterministic Solution of the Chemical Master Equation. Multiscale Model. Simul. 2012, 10, 1232–1262. [Google Scholar] [CrossRef]
- Black, A.J.; Ross, J.V. Computation of epidemic final size distributions. J. Theor. Biol. 2015, 367, 159–165. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Khammash, M.; Munsky, B. The finite state projection algorithm for the solution of the chemical master equation. J. Chem. Phys. 2006, 124, 1–12. [Google Scholar] [CrossRef]
- Norris, J.R. Markov Chains; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Gillespie, D.T. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 1977, 81, 2340–2361. [Google Scholar] [CrossRef]
- Sunkara, V. Analysis and Numerics of the Chemical Master Equation. Ph.D. Thesis, The Australian National University, Canberra, Australia, 2013. [Google Scholar]

© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sunkara, V. On the Properties of the Reaction Counts Chemical Master Equation. Entropy 2019, 21, 607. https://doi.org/10.3390/e21060607
Sunkara V. On the Properties of the Reaction Counts Chemical Master Equation. Entropy. 2019; 21(6):607. https://doi.org/10.3390/e21060607
Chicago/Turabian StyleSunkara, Vikram. 2019. "On the Properties of the Reaction Counts Chemical Master Equation" Entropy 21, no. 6: 607. https://doi.org/10.3390/e21060607
APA StyleSunkara, V. (2019). On the Properties of the Reaction Counts Chemical Master Equation. Entropy, 21(6), 607. https://doi.org/10.3390/e21060607




