Exergy Analysis of the Heart with a Stenosis in the Arterial Valve
Abstract
1. Introduction
2. Exergy Analysis Methodology Applied to the Human Heart
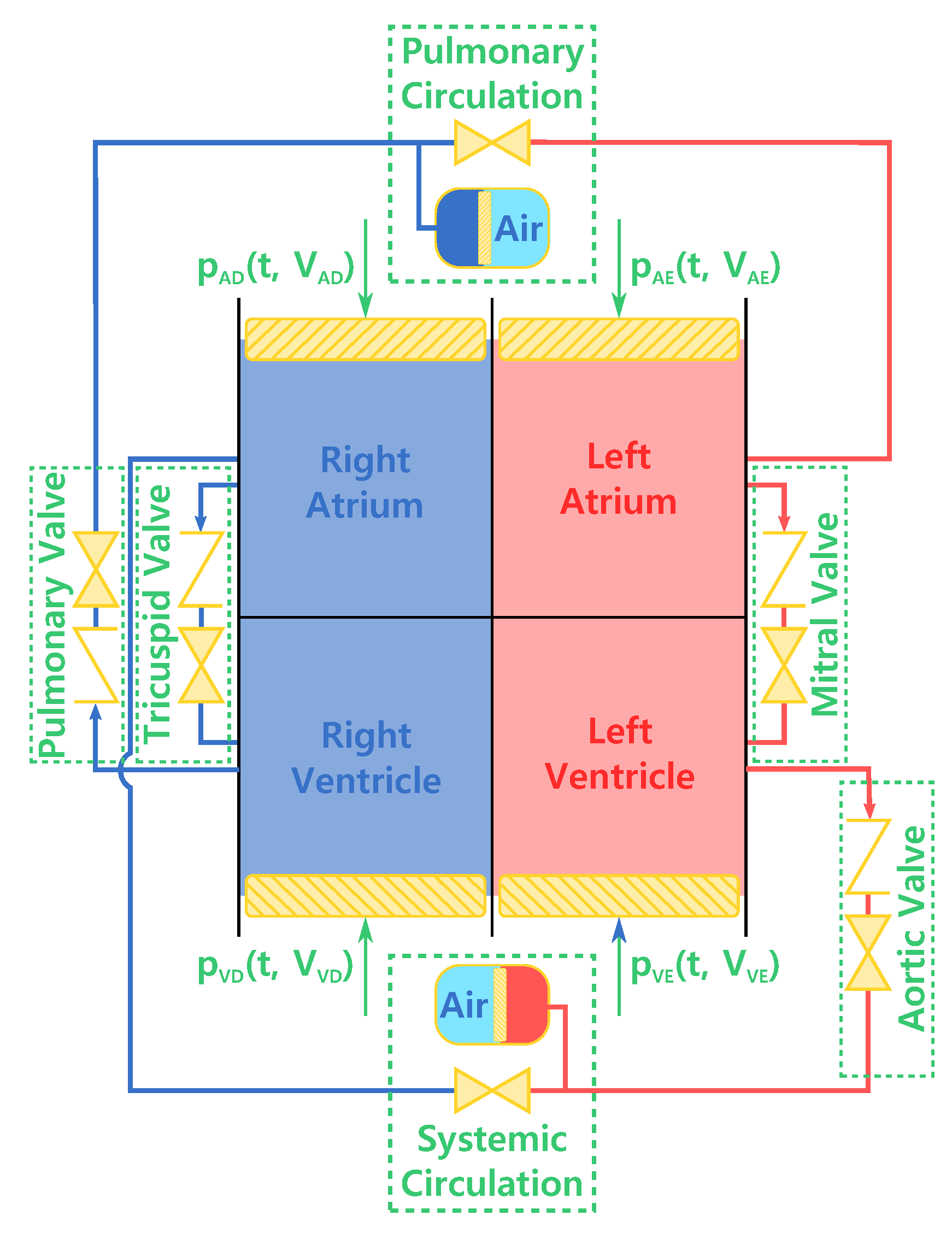
2.1. Phenomenological Model
2.2. Exergy Analysis
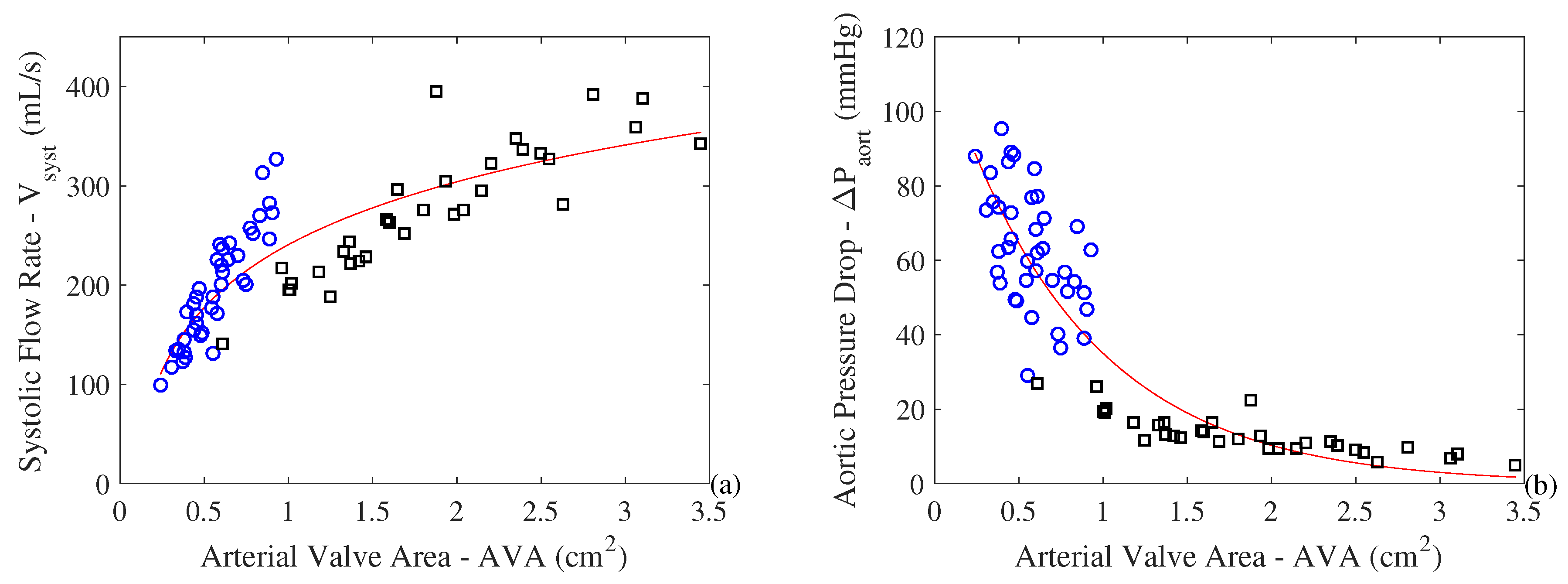
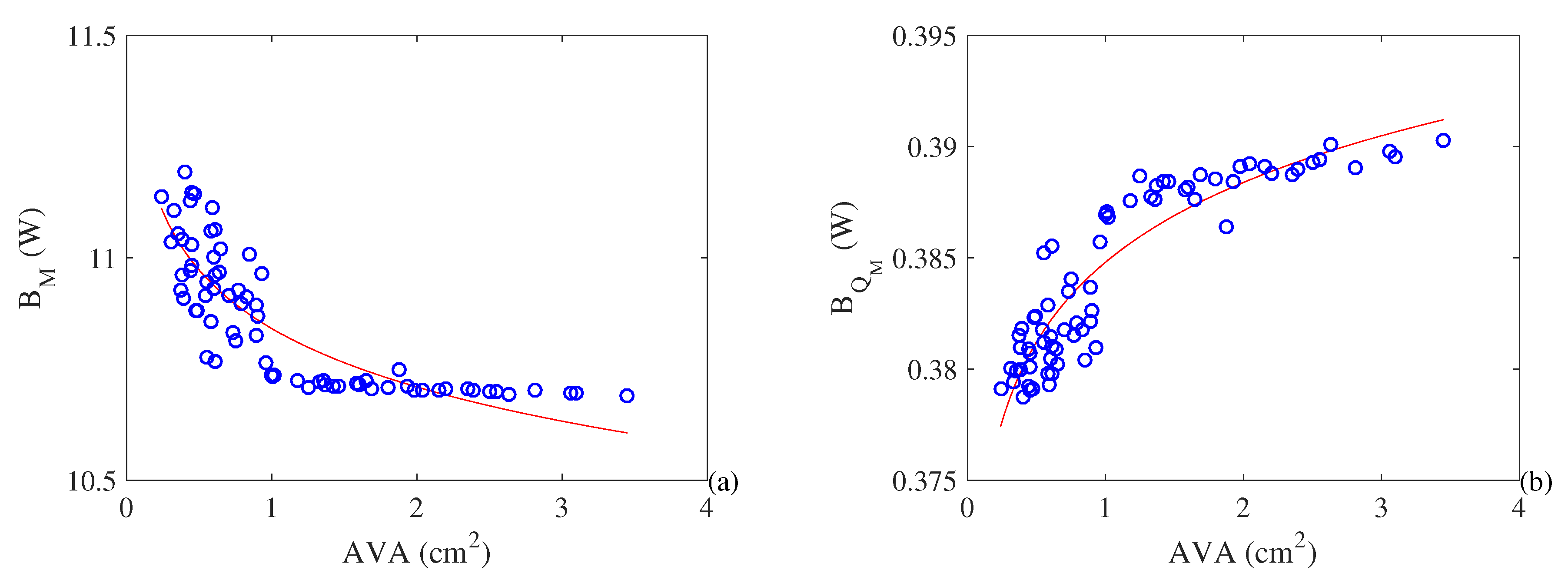
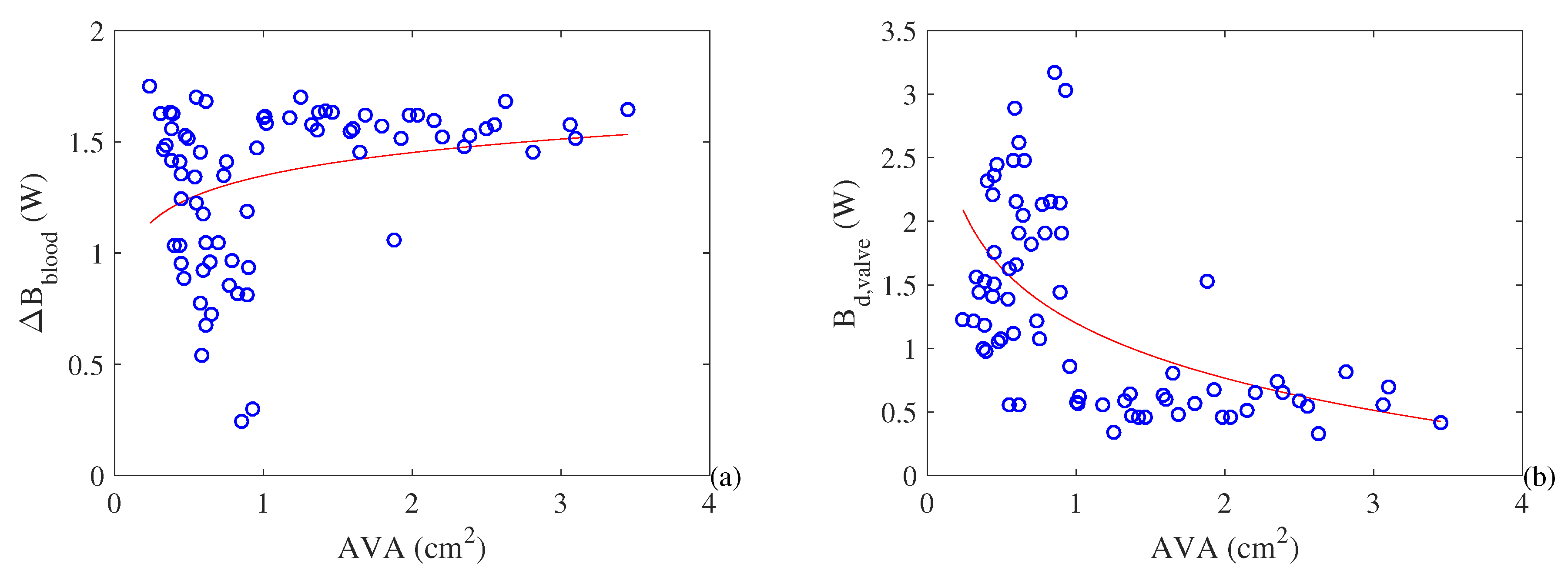
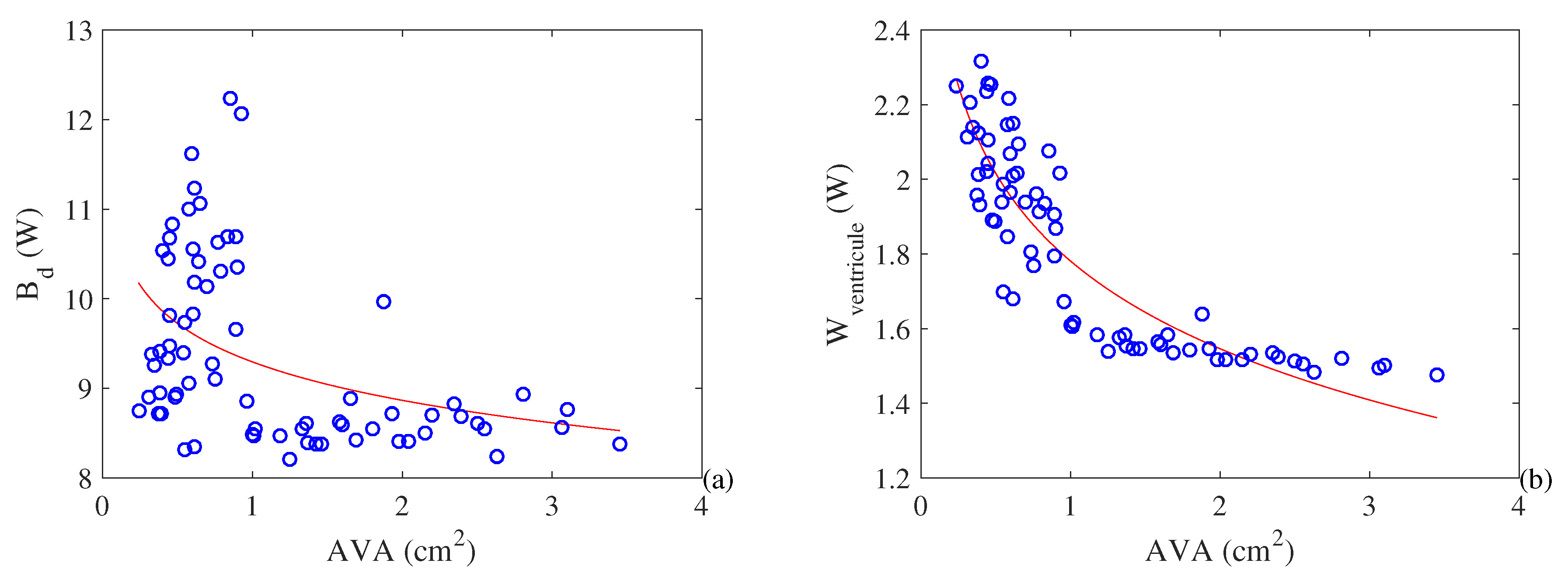
3. Results and Discussions
4. Concluding Remarks
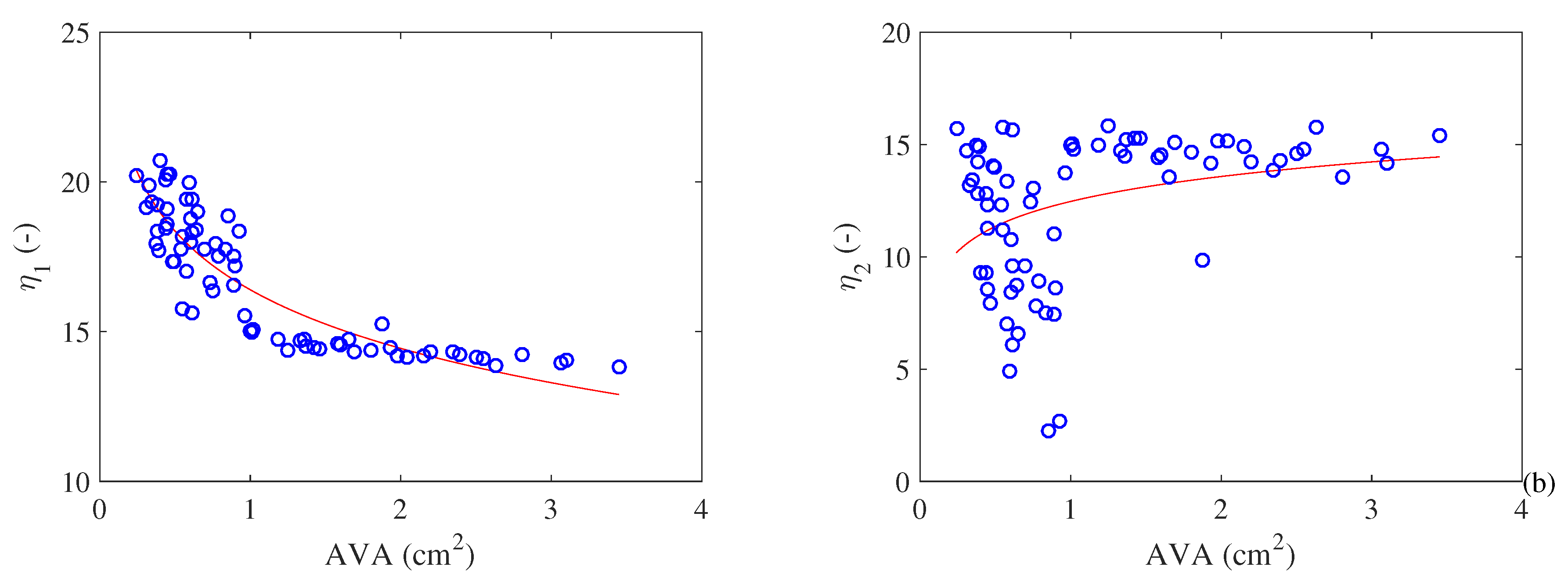
- Both metabolism and cardiac work increase with the increase in the severity of stenosis. T his result explains the hypertrophy that occurs in a pathological heart. Moreover, it is possible to observe an exergy efficiency () increase with the severity of the pathology. In the other hand, the exergy efficiency () based of literature (similar to energy efficiency) increases with the severity of the pathology, which was an unexpected result;
- At the same time, the exergy variation of the blood decreases with the restriction of the AVA (i.e., the quality of the energy variation decreases). Therefore, there is a higher cardiac effort leading to higher losses and higher values of destroyed exergy in the valves. This leads to a decrease in exergy efficiency as the pathology evolves;
- This result may be used to help the medical literature to understand the physiological responses of the heart caused by a pathology—in this case a stenosis in the aortic valve area. The main idea is to use the exergy efficiency as an indicator of the degree of severity of the pathology since its behavior is a consequence of several physiological conditions. Therefore, a modification in the hemodynamics of the blood in the valves causes changes in the Second Law efficiency, which differentiates this physical quantity from the First Law efficiency.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| A | Area (m2) |
| aortic valve area (cm2) | |
| B | Exergy of the control volume (J) |
| Exergy rate (W) | |
| b | Specific exergy (kJ/kg) |
| E | Energy of the control volume (J) |
| Effective orifice area (cm2) | |
| g | Gravitational acceleration (m/s2) |
| Enthalpy rate (W) | |
| h | Specific enthalpy (kJ/kg) |
| Mass flow rate (kg/s) | |
| Energy metabolism (W) | |
| Mitral valve area (cm2) | |
| P | Pressure (Pa, mmHg) |
| Heat transfer rate (W) | |
| Respiratory quotient (-) | |
| Entropy rate (W/K) | |
| s | Specific entropy (kJ/kgK) |
| T | Temperature (°C) |
| t | Time (s) |
| Transvalvular pressure gradient () | |
| Volumetric flow rate (m3/s) | |
| V | Volume (m3) |
| v | Specific volume (m3/s) |
| greek letters: | |
| Efficiency (-) | |
| Specific mass (kg/m3) | |
| subscripts: | |
| 0 | Reference state |
| Blood | |
| Control volume | |
| d | Destroyed |
| e | Exit |
| Associated with the heart | |
| i | Inlet |
| M | Metabolic |
| Associated with the metabolic heat | |
| systolic | |
| Associated with the valve | |
References
- Rant, Z. Energy value and pricing. Strojniski Vestnik 1955, 1, 4–8. [Google Scholar]
- Szargut, J.; Morris, D.; Steward, F. Energy Analysis of Thermal, Chemical, and Metallurgical Processes; Hemisphere Publishing Corporation: New York, NY, USA, 1988. [Google Scholar]
- Oliveira-Junior, S. Exergy: Production, Cost and Renewability; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Luo, L. Entropy production in a cell and reversal of entropy flow as an anticancer therapy. Front. Phys. China 2009, 4, 122–136. [Google Scholar] [CrossRef]
- Lucia, U. Entropy generation approach to cell systems. Phys. A 2014, 406, 1–11. [Google Scholar] [CrossRef]
- Genc, S.; Sorguven, E.; Ozilgen, M.; Aksan Kurnaz, I. Unsteady exergy destruction of the neuron under dynamic stress conditions. Energy 2013, 59, 422–431. [Google Scholar] [CrossRef]
- Spanghero, G.M.; Albuquerque, C.; Lazzaretti Fernandes, T.; Hernandez, A.J.; Keutenedjian Mady, C.E. Exergy Analysis of the Musculoskeletal System Efficiency during Aerobic and Anaerobic Activities. Entropy 2018, 20, 119. [Google Scholar] [CrossRef]
- Cenzi, J.; Albuquerque, C.; Mady, C. The effect of carbon monoxide on the exergy behavior of the lungs. Bioengineering 2018, 5, 108. [Google Scholar] [CrossRef] [PubMed]
- Henriques, I.; Mady, C.; de Oliveira-Junior, S. Exergy model of the human heart. Energy 2016, 117, 612–619. [Google Scholar] [CrossRef]
- Çatak, J.; Özilgen, M.; Olcay, A.B.; Yılmaz, B. Assessment of the work efficiency with exergy method in ageing muscles and healthy and enlarged hearts. Int. J. Exergy 2018, 25, 1–33. [Google Scholar] [CrossRef]
- Prek, M.; Butala, V. Comparison between Fanger’s thermal comfort model and human exergy loss. Energy 2017, 138, 228–237. [Google Scholar] [CrossRef]
- Simone, A.; Kolarik, J.; Iwamatsu, T.; Asada, H.; Dovjak, M.; Schellen, L.; Shukuya, M.; Olesen, B. A relation between calculated human body exergy consumption rate and subjectively assessed thermal sensation. Energy Build. 2011, 43, 1–9. [Google Scholar] [CrossRef]
- Dovjak, M.; Shukuya, M.; Olesen, B.W.; Krainer, A. Analysis on exergy consumption patterns for space heating in Slovenian buildings. Energy Policy 2010, 38, 2998–3007. [Google Scholar] [CrossRef]
- Martinez-Garcia, M.; Une, R.; de Oliveira-Junior, S.; Mady, C. Exergy Analysis and Human Body Thermal Comfort Conditions: Evaluation of Different Body Compositions. Entropy 2018, 20, 265. [Google Scholar] [CrossRef]
- Dovjak, M.; Shukuya, M.; Krainer, A. User-Centred Healing-Oriented Conditions in the Design of Hospital Environments. Int. J. Environ. Res. Public Health 2018, 15, 2140. [Google Scholar] [CrossRef] [PubMed]
- Mosquim, R.; de Oliveira-Junior, S.; Mady, C. Modeling the exergy behavior of São Paulo State in Brazil. J. Clean. Prod. 2018, 197, 643–655. [Google Scholar] [CrossRef]
- Blick, E.; Stein, P. Work of the heart: A general thermodynamics analysis. J. Biomech. 1977, 10, 589–595. [Google Scholar] [CrossRef]
- Henriques, I.; Mady, C.; Marin, J.; Serra, L.; Oliveira-Junior, S. Exergy destroyed in the arteries due to stenosis. In Proceedings of the 29th International Conference on Efficiency, Cost, Optimization, Simulation and Environmental Impact of Energy Systems, Portoroz, Slovenia, 19–23 June 2016. [Google Scholar]
- Roll, J.; Henriques, I.; Mady, C.; Oliveira-Junior, S. Exergy Analysis of the Cardiovascular System. In Proceedings of the 30th International Conference on Efficiency, Cost, Optimization, Simulation and Environmental Impact of Energy Systems, San Diego, CA, USA, 2–6 July 2017. [Google Scholar]
- Klingensmith, M.E. The Washington Manual of Surgery; Lippincott Williams & Wilkins: Philadelphia, PA, USA, 2008. [Google Scholar]
- Borges, M.L.; Abdala, L.; de Oliveira-Junior, S.; Mady, C.E.K. A first approach for an exergy analysis of the human heart with a pathology. In Proceedings of the 17th Brazilian Congress of Thermal Sciences and Engineering, Águas de Lindóia, Brazil, 25–28 November 2018. [Google Scholar]
- Steendijk, P.; Ellen, A. Invasive assessment of cardiac efficiency. Heart Metab. 2008, 39, 33–36. [Google Scholar]
- Hall, J.E. Guyton and Hall Textbook of Medical Physiology E-Book; Elsevier: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Schaldach, M. Electrotherapy Ofthe Heart; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
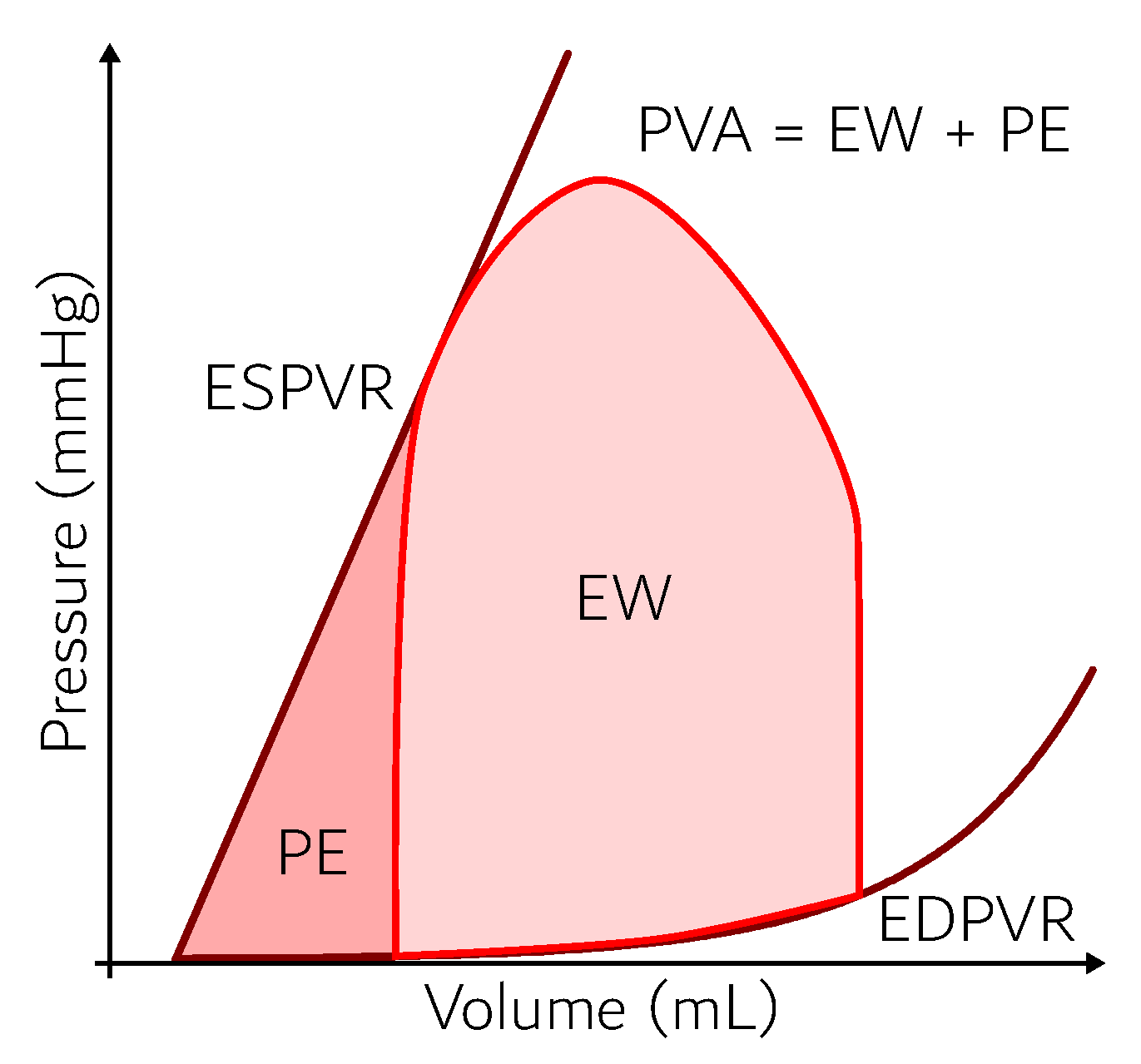
- Suga, H.; Hayashi, T.; Shirahata, M. Ventricular systolic pressure-volume area as predictor of cardiac oxygen consumption. Am. J. Physiol. Heart Circ. Physiol. 1981, 240, H39–H44. [Google Scholar] [CrossRef] [PubMed]
- Izzi, G.; Zile, M.; Gaasch, W. Myocardial oxygen consumption and the left ventricular pressure-volume area in normal and hypertrophic canine hearts. Circulation 1991, 84, 1384–1392. [Google Scholar] [CrossRef]
- Takaoka, H.; Takeuchi, M.; Odake, M.; Yokoyama, M. Assessment of myocardial oxygen consumption (Vo2) and systolic pressure–volume area (PVA) in human hearts. Eur. Heart J. 1992, 13, 85–90. [Google Scholar] [CrossRef]
- Takaoka, H.; Takeuchi, M.; Odake, M.; Hayashi, Y.; Hata, K.; Mori, M.; Yokoyama, M. Comparison of hemodynamic determinants for myocardial oxygen consumption under different contractile states in human ventricle. Circulation 1993, 87, 59–69. [Google Scholar] [CrossRef]
- Mady, C.; Oliveira-Junior, S. Human body exergy metabolism. Int. J. Thermodyn. 2013, 16, 73–80. [Google Scholar] [CrossRef]
- Gorlin, R.; Gorlin, S.G.; Himmelstein, A.; Dresdale, D.; Baldwin, J.; Evans, J.; Ferris, B.; Goodale, W.; Harvey, W.; Eppinger, E.; et al. Hydraulic formula for calculation of the area of the stenotic mitral valve, other cardiac valves, and central circulatory shunts. I. Am. Heart J. 1951, 41, 1–29. [Google Scholar] [CrossRef]
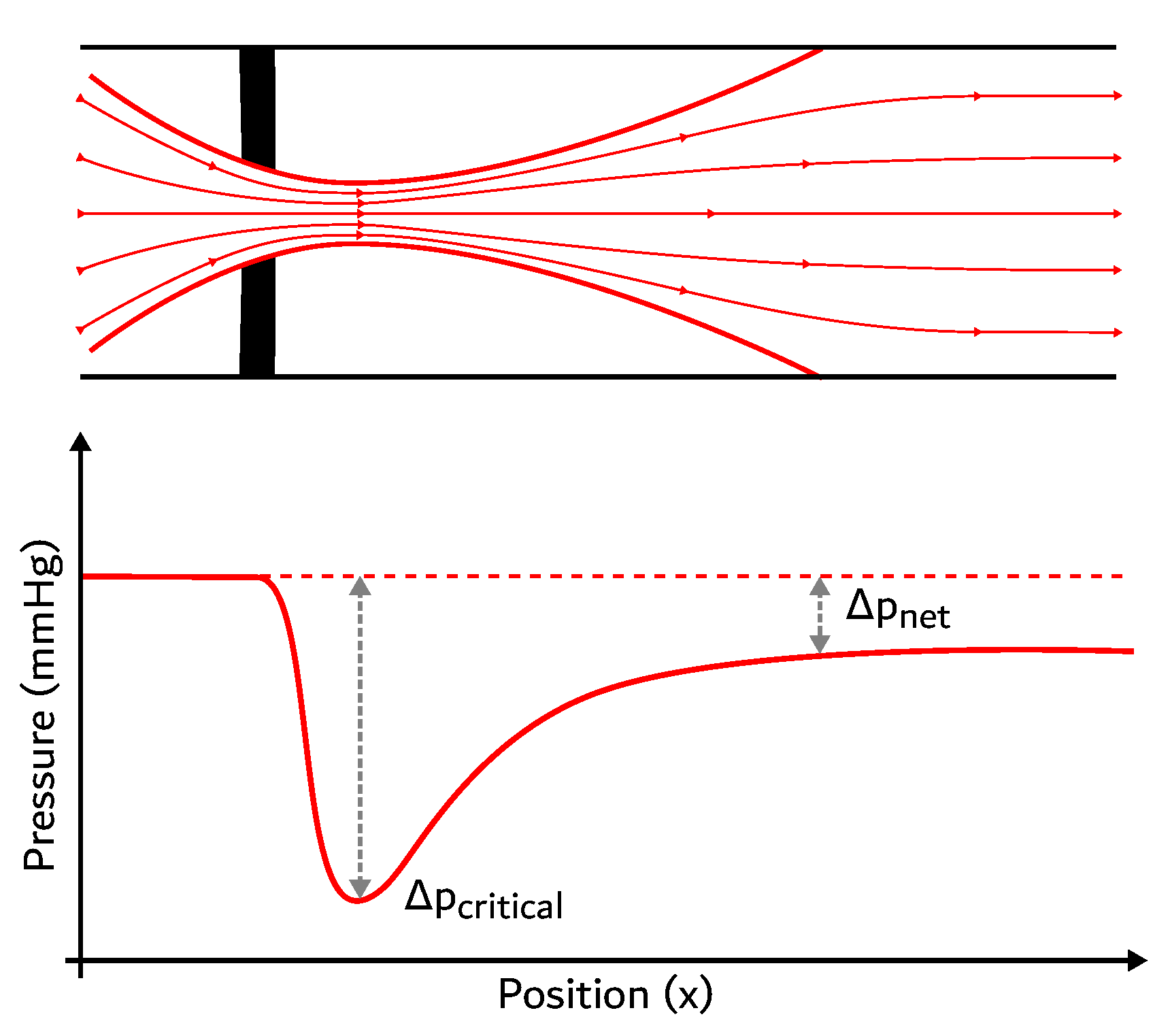
- Garcia, D.; Pibarot, P.; Durand, L.G. Analytical modeling of the instantaneous pressure gradient across the aortic valve. J. Biomech. 2005, 38, 1303–1311. [Google Scholar] [CrossRef] [PubMed]
- Prince, M.R.; Novelline, R.A.; Athanasoulis, C.A.; Simon, M. The diameter of the inferior vena cava and its implications for the use of vena caval filters. Radiology 1983, 149, 687–689. [Google Scholar] [CrossRef] [PubMed]
- Truong, Q.A.; Massaro, J.M.; Rogers, I.S.; Mahabadi, A.A.; Kriegel, M.F.; Fox, C.S.; O’Donnell, C.J.; Hoffmann, U. Reference Values for Normal Pulmonary Artery Dimensions by Noncontrast Cardiac Computed Tomography. Circ. Cardiovasc. Imaging 2012, 5, 147–154. [Google Scholar] [CrossRef] [PubMed]
- Bache, R.J.; Wang, Y.; Greenfield, J.C. Left ventricular ejection time in valvular aortic stenosis. Circulation 1973, 47, 527–533. [Google Scholar] [CrossRef] [PubMed]
- Rosenhek, R.; Binder, T.; Maurer, G.; Baumgartner, H. Normal values for Doppler echocardiographic assessment of heart valve prostheses. J. Am. Soc. Echocardiogr. 2003, 16, 1116–1127. [Google Scholar] [CrossRef]
- Sordelli, C.; Severino, S.; Ascione, L.; Coppolino, P.; Caso, P. Echocardiographic assessment of heart valve prostheses. J. Cardiovasc. Echogr. 2014, 24, 103–113. [Google Scholar] [CrossRef]
- Garcia, D.; Kadem, L. What do you mean by aortic valve area: Geometric orifice area, effective orifice area, or gorlin area? J. Heart Valve Dis. 2006, 15, 601–608. [Google Scholar]
- Zoghbi, W.A.; Chambers, J.B.; Dumesnil, J.G.; Foster, E.; Gottdiener, J.S.; Grayburn, P.A.; Khandheria, B.K.; Levine, R.A.; Marx, G.R.; Miller, F.A.; et al. Recommendations for evaluation of prosthetic valves with echocardiography and Doppler ultrasound: A report from the American Society of Echocardiography’s Guidelines and Standards Committee and the Task Force on Prosthetic Valves, developed in conjunction with the American College of Cardiology Cardiovascular Imaging Committee, Cardiac Imaging Committee of the American Heart Association, the European Association of Echocardiography, a registered branch of the European Society of Cardiology, the Japanese Society of Echocardiography and the Canadian Society of Echocardiography, endorsed by the American College of Cardiology Foundation, American Heart Association, European Association of Echocardiography, a registered branch of the European Society of Cardiology, the Japanese Society of Echocardiography, and Canadian Society of Echocardiography. J. Am. Soc. Echocardiogr. 2009, 22, 975–1014. [Google Scholar]
- Pennes, H. Analysis of tissue and arterial blood temperatures in the resting human forearm. J. Appl. Physiol. 1948, 1, 93–122. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; Holmes, K. Microvascular contributions in tissue heat transfer. Ann. N. Y. Acad. of Sci. 1980, 335, 137–150. [Google Scholar] [CrossRef]
- Mady, C.E.K.; Ferreira, M.S.; Yanagihara, J.I.; Saldiva, P.H.N.; de Oliveira Junior, S. Modeling the exergy behavior of human body. Energy 2012, 45, 546–553. [Google Scholar] [CrossRef]
- Abdala, L. Heart Chamber Modeling Using Navier-Stokes Equations. Master’s Thesis, University of Campinas, Campinas, Brazil, 2018. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brandão Roll, J.; Leone Borges, M.; Keutenedjian Mady, C.E.; de Oliveira Junior, S. Exergy Analysis of the Heart with a Stenosis in the Arterial Valve. Entropy 2019, 21, 563. https://doi.org/10.3390/e21060563
Brandão Roll J, Leone Borges M, Keutenedjian Mady CE, de Oliveira Junior S. Exergy Analysis of the Heart with a Stenosis in the Arterial Valve. Entropy. 2019; 21(6):563. https://doi.org/10.3390/e21060563
Chicago/Turabian StyleBrandão Roll, Julio, Matheus Leone Borges, Carlos Eduardo Keutenedjian Mady, and Silvio de Oliveira Junior. 2019. "Exergy Analysis of the Heart with a Stenosis in the Arterial Valve" Entropy 21, no. 6: 563. https://doi.org/10.3390/e21060563
APA StyleBrandão Roll, J., Leone Borges, M., Keutenedjian Mady, C. E., & de Oliveira Junior, S. (2019). Exergy Analysis of the Heart with a Stenosis in the Arterial Valve. Entropy, 21(6), 563. https://doi.org/10.3390/e21060563