Abstract
The well-known Hölder’s inequality has been recently utilized as an essential tool for solving several optimization problems. However, such an essential role of Hölder’s inequality does not seem to have been reported in the context of generalized entropy, including Rényi–Tsallis entropy. Here, we identify a direct link between Rényi–Tsallis entropy and Hölder’s inequality. Specifically, we demonstrate yet another elegant proof of the Rényi–Tsallis entropy maximization problem. Especially for the Tsallis entropy maximization problem, only with the equality condition of Hölder’s inequality is the q-Gaussian distribution uniquely specified and also proved to be optimal.
1. Introduction
Tsallis entropy [1,2] has been recently utilized as a versatile framework for expanding the realm of Shannon–Boltzmann entropy for nonlinear processes, in particular, those that exhibit power–law behavior. It shares a structure in common with Rényi entropy [3], Daróczy entropy [4], and probability moment presented in Moriguti [5], since the essential part of all these functionals is (or ) for certain constrained probability density functions (or ). This naturally has been of interest for a variety of issues in information theory and related areas. For instance, in his pioneering work, Campbell [6] stated that “Implicit in the use of average code length as a criterion of performance is the assumption that cost varies linearly with code length. This is not always the case.” Then, Campbell [6] introduced a nonlinear average length measure defined as
being an extension of the one by Shannon,
in which D is the size of the alphabet, is the probability for a source to produce symbols , is the length of a codeword mapped from symbol (using D letters of the alphabet) in the context of source coding, and t is an arbitrary parameter (). One of the surprising facts proved in [6] is that the lower bound to the moment-generating function of code lengths, namely, , is given by , namely, Rényi entropy of order of the source . Moreover, Ref. [6] also realizes that, if
which is a mixture of the Shannon code length and Rényi entropy of order , we have the lower bound . So far, Baer [7] has further generalized this result and constructed an algorithm for finding optimal binary codes under quasiarithmetic penalties. In addition, new extensions of [6] were obtained by Bercher [8] and by Bunte and Lapidoth [9].
Such an instance, where “a nonlinear measure” (i.e., generalized entropy) naturally arises, is also known for channel capacities. Daróczy [4] first analyzed a generalized channel capacity, which is a natural consequence of his extension of Shannon entropy (i.e., Daróczy entropy). This result has initiated extensive work in this direction. For instance, Landsberg and Vedral [10] first introduced Rényi entropy and Tsallis entropy for a binary symmetric channel, and they suggested the possibility of “super-Shannon channel capacities.” More recently, Ilić, Djordjević, and Küeppers [11] obtained new expressions for generalized channel capacities by introducing Daróczy–Tsallis entropy even for a weakly symmetric channel, binary erasure channel, and z-channel. Similar extensions have been explored for rate distortion theory. For instance, Venkatesan and Plastino [12] developed nonextensive rate distortion theory by introducing Tsallis entropy and constructed a minimization algorithm for generalized mutual information. More recently, Girardin and Lhote [13] covered the setting in [12] in a general framework of generalized entropy rates, which includes Rènyi–Tsallis entropy.
In the context of generalized entropy just described, the q-Gaussian distribution [1,2] often emerges as a maximizer of Rényi–Tsallis entropy under certain constraints, and, hence, it has been extensively studied. Since the q-Gaussian effectively models power–law behavior with a one-parameter q, its utility is widespread in various areas, including new random number generators proposed by Thistleton, Marsh, Nelson, and Tsallis [14] and by Umeno and Sato [15]. In addition to such an important application in communication systems, queuing theory has recently incorporated the q-Gaussian, reflecting the heavy-tailed traffic characteristics observed in broadband networks [16,17,18,19]. For instance, Karmeshu and Sharma [16] introduced Tsallis entropy maximization, and, there, the q-Gaussian emerges as the queue length distributions, which suggests that Jaynes’ maximum entropy principle [20,21,22] can be generalized to a framework of Tsallis entropy.
Some of the above issues are formulated as nonlinear optimizations with “a nonlinear measure” under certain constraints (which depend on each issue). As mentioned above, Rényi–Tsallis entropy and q-Gaussian is one such instance. In other words, the q-Gaussian maximizes Tsallis entropy under certain constraints. Therefore, it is useful to obtain a deeper understanding of such nonlinear optimization problems. In this study, we find a direct link between Rényi–Tsallis entropy and Hölder’s inequality that leads to yet another elegant proof of Rényi–Tsallis entropy maximization. The idea of the proof is different from those offered in previous studies (for instance, [23,24,25,26,27]) as explained below. Interestingly, the technique developed in this study might possibly be useful for tackling more complicated problems regarding optimization issues in information theory and other research areas, such as the conditional Rényi entropy (as in [28,29,30]), for instance.
Previous studies [23,24,25,26,27] are based on a common standpoint, the generalization of the moment–entropy inequality (cf. [25,26]). Namely, they intend to generalize the situation that a continuous random variable with a given second moment and maximal Shannon entropy is a Gaussian distribution (cf. [3], Theorem 8.6.5). In doing so, a generalized relative entropy is devised, which takes a different form (and has a different name) depending on the problem. First of all, Tsukada and Suyari’s beautiful work [23] has given proofs for Rényi entropy maximization, which is also known as a bound of Moriguti’s probability moment [5] (as posed in R1 in Section 2). Namely, they prove that the q-Gaussian distribution [1,2] is a unique optimal solution by utilizing the fact that all feasible solutions constitute a convex set. Although [23] does not explicitly construct a generalized relative entropy, the essential structure of the proofs inherits the one in the proof of the moment-entropy inequality ([3], Theorem 8.6.5)).
Moreover, they have identified an explicit one-to-one correspondence between feasible solutions to the problems of Rényi entropy maximization and Tsallis entropy maximization, which is also shown in ([31], p. 754). This implies that an ‘indirect’ proof to Tsallis entropy maximization (as posed in T1 in Section 2) has been first obtained in [23]. In contrast to this proof, the first ‘direct’ proof to Tsallis entropy maximization is obtained in Furuichi’s elegant work [24]. The proof in [24] utilizes nonnegativity of the Tsallis relative entropy defined between the q-Gaussian distribution (i.e., a possible maximizer) and any other feasible solution. On the other hand, the remarkable work of Lutwak, Yang, and Zhang first clarified that generalized Gaussians maximize -Rényi entropy power under a constraint on the p-th moment of the distribution, for univariate distributions [25] and for the associated n-dimensional extensions [26].The essential point in the proofs in [25,26] is construction of relative -Rényi entropy power, which is nonnegative and takes a quite different form compared to the Tsallis relative entropy in [24]. (More precisely, in [25], they prove nonnegativity of the relative -Rényi entropy ([25], Lemma 1). Starting from this nonnegativity:, they construct a series of inequalities that saturate at the generalized Gaussian ([25], Lemma 2). Note, however, that, as observed in this , they start by giving a candidate of the maximizer ab initio, which is the generalized Gaussian .) Furthermore, Vignat, Hero, and Costa [32] obtained a general, sharp result using the Bregman information divergence for an n-dimensional extension of Tsallis entropy. In addition to [25,26,32], Eguchi, Komori, and Kato’s interesting results [27] include the same n-dimensional extension to Tsallis entropy. (Ref. [32] has also identified an elegant structure regarding the projective divergence and the -loss functions in maximum likelihood estimation.)Similar to [24,25,26,32], the key component of the proof in [27] is the projective power divergence, which again takes a quite different form compared to the ones in [24,25,26,32]. To prove nonnegativity of the generalized relative entropy, Refs. [25,26,27] utilize Hölder’s inequality, but Refs. [23,24,32] do not. Namely, Hölder’s inequality has been an auxiliary useful tool, and it has never played an essential role in these previous studies. In addition to the construction of generalized relative entropies, the optimal q-Gaussian distribution needs to be ‘given ab initio’ [23,24,25,26,27,32], inheriting the framework showing that the Gaussian distribution maximizes Shannon entropy ([3], Theorem 8.6.5).
Now natural questions arise: is it possible to systematically solve the problems of Rényi–Tsallis entropy maximization in a different (and hopefully simpler) way than the previous study? In addition, is it possible to ‘construct’ the q-Gaussian distribution? These questions are positively answered from a new viewpoint as follows. First, only by the equality (i.e., saturation) condition of Hölder’s inequality, the q-Gaussian distribution is specified, and, at the same time, its optimality is proved by Hölder’s inequality for a Tsallis entropy maximization of (Theorem 1) and of (Theorems 2 and 3). This clarifies how and why the q-Gaussian distribution emerges as the maximizer in an explicit way for the first time in the literature. (To the authors’ knowledge, such a characterization of the q-Gaussian distribution has never been reported.) However, for a Rényi entropy maximization of (Theorem 4) and of (Theorem 5), the q-Gaussian distribution is specified with the aid of the equality condition of Hölder’s inequality. In addition, the proof of its optimality requires a simple inequality inspired from Moriguti [5]. Note that we do not intend to provide an explicit characterization of the q-Gaussian distribution in terms of the parameter q, since numerous previous studies (including [23,24,25,26,27]) have already clarified this. Nevertheless, regarding Tsallis entropy maximization when , which has previously been studied in [2], a rigorous result (as in Theorem 3) is now obtained for the first time thanks to Hölder’s inequality. (For instance, in the framework of [24], the case for cannot be incorporated because the Tsallis relative entropy is not defined adequately.)
We note that Hölder’s inequality has been recently utilized as an essential tool for optimization in Campbell [6], Bercher [8], and Bunte and Lapidoth [9]; on source coding, in Bercher [33,34]; on generalized Cramér–Rao inequalities; and in Tanaka [35,36] on a physical limit of injection locking. However, such an essential role of Hölder’s inequality does not seem to be reported in the context of generalized entropy, including Rényi entropy (cf. [37]), except for the use as a means for proving nonnegativity of a generalized relative entropy, as mentioned above.
In what follows, Section 2 introduces basic definitions required for the analysis. Section 3 includes the main results regarding Rényi–Tsallis entropy maximization problems, and it also contains an explanation on the link to Moriguti’s argument in [5]. Section 4 lists the proofs to the results presented in Section 3. Finally, one Appendix at the end provides further supplementary information.
2. Basic Definitions and Problem Formulation
In this section, we first define Tsallis entropy [1,24] and Rényi entropy ([3], pp. 676–679). Next, we reformulate Rényi–Tsallis entropy maximization problems in a unified way. Finally, we introduce Hölder’s inequality in relation to the problems in this study.
2.1. Tsallis Entropy and Rényi Entropy
Tsallis entropy is beautifully presented in the context of q-analysis (cf. [1], p. 41) as follows. First, the q-exponential function , whose domain and range satisfies
is defined by
While, the inverse of the q-exponential function, namely q-logarithmic function, is defined by
Note that, as , we have and . We also note that the above definition of and has been recently revised by Oikonomou and Bagci [38]. (In [38], they have further developed ‘complete’ q-exponentials and q-logarithms.) Then, the Tsallis entropy is defined by
for univariate probability density functions (PDFs) p on , which is a natural generalization of Boltzmann–Gibbs entropy and Shannon entropy. Hereafter, in (1) is used for notational simplicity. The reason why is used, instead of , is due to the fact that is generally used for the expectation value. On the other hand, Rényi entropy is well-known and can be found in textbooks of information theory (cf. [3], pp. 676–679), which is defined simply by
Finally, we note that only differential entropies (i.e., continuous probability distributions) are considered in this study, although our technique with Hölder’s inequality can be applied to discrete probability distributions.
2.2. Problem Formulation
Let be the set of all PDFs on . We then define the set, as introduced in [24],
Following the problem formulation in [1,2,23,24,31], we first introduce the Tsallis entropy maximization problem for univariate PDFs p on :
in which q and have fixed values, and . Note that and are assumed in T1. is often called the escort probability [27,31]. This somewhat unusual form of expectation is called the q-normalized expectation [31], which has been usually assumed in Tsallis statistics. In contrast to the q-normalized expectation, as [31] pointed out, the usual expectation is also valid in Tsallis statistics. We note the Tsallis entropy maximization problem under the constraint of this usual expectation is considered later in problem R2.
For problem T1, using Tsallis relative entropy, Furuichi [24] first proved that for the q-Gaussian distribution maximizes the Tsallis entropy among any univariate PDFs in , where and are constants determined by q and .
Here, we formulate a slightly generalized optimization problem T2, as follows. First, replace (2c) with
Note that now, as opposed to T1, it is not necessarily required that both and are finite, and hence, is not required, and it is replaced with . Next, notice that Tsallis entropy is maximal at , such that is minimal (or correspondingly, maximal at , such that is maximal) for (correspondingly, for ). Then, by introducing an additional arbitrary parameter , T1 is reformulated as
where the constant is multiplied with in the first term of (3a) simply due to notational convenience for later analysis in Section 4.
As opposed to the Tsallis entropy maximization problem T1, the Rényi entropy maximization problem is usually considered under the constraint of the usual expectation , in other words,
which is equivalent to:
We note this very problem for was first posed and solved by Moriguti in 1952 [5]. (Later in [39], cases and are both analyzed in an n-dimensional spherical symmetric extension of [5] with the same approach as [5].)Similar to T1, by introducing an additional parameter and the constraint
which is obtained from (5b) and (5c), R1 is now reformulated as
2.3. Hölder’s Inequality for Later Analysis
Here, we provide minimum information about Hölder’s inequality for later analysis in Section 3 and Section 4. The standard Hölder’s inequality is given by
with , and (cf. [40] for the one-demensional case and [41] for general measurable functions). In general, f and g are measurable functions defined on a subset and , and we employ a compact notation as
Although and are no longer norms for , now in the context of this study, we set and . Then, Hölder’s inequality (8) is given in the following form:
For the case , the equality in (9) holds if and only if there exists constants A and B, not both 0 (cf. [40], p. 140), (More specifically, if f is null (i.e., ), then . In addition, if g is null, .) such that
In addition, for the exceptional case (as well as ), we can argue a condition for the equality in (9) separately, as shown in Section 4.3, although the expression of (10) is no more valid for this case.
In contrast to (9), reverse Hölder’s inequality is given by
which is directly obtained from Hölder’s inequality [40]. We note that f can be 0 over any subset . As for g, on the other hand, we assume for almost everywhere (a.e.) , taking care that in (11) (cf. [40], p. 140). Then, for the case , the equality in (11) holds if and only if there exists , such that
3. Main Results
In this study, we focus on the univariate PDFs on , and we consider and defined on as a special case of general and in Section 2.3. Hereafter, we refer to (10) and (12), as the equality condition of Hölder’s inequality and reverse Hölder’s inequality, respectively. Thanks to these equality conditions, we obtained our results systematically.
Let be a univariate PDF defined on . Assume that is a measurable function which is integrable with respect to x. In addition, let denote the Beta function (cf. [42], p. 253). Then, we can form the following statements.
Theorem 1.
(Tsallis entropy maximization for ): Suppose . , defined by
is the unique maximizer of the Tsallis entropy in (2a) under the constraints of (3b) and of (3c) inT2.
Corollary 1.
For , Tsallis entropy is bounded, but has no maximizer. Namely, there exist PDFs , such that , in other words, . (The idea for constructing such PDFs is from Tsukada and Suyari [23], where they proved thatR1for becomes unbounded, i.e., .)
The proof of this theorem (and corollary) is given in Section 4.1. As mentioned in Section 1, the above statement itself has already appeared in [24]. However, our proof is quite different to the one in [24], in the sense that it does not require generalized relative entropy, and the maximizer is explicitly ‘specified’ (not ‘given ab initio’). Namely, reverse Hölder’s inequality aids in finding the optimal solution.
The outline of the proof is as follows. First, for , the maximization of the Tsallis entropy , in other words, the minimization of in (3a), is related to reverse Hölder’s inequality in (11). Second, we observe that has the lower bound through reverse Hölder’s inequality. Third, the minimizer achieving this bound is explicitly and uniquely constructed from the equality condition (12):
where and .
Remark 1.
Even if we assume the additional constraint: inT2, the proof of this theorem (as well as of Theorems 2 and 3) remains the same, since we do not require the finiteness of and (i.e., ) in the proof.
Remark 2.
Theorem 2.
(Tsallis entropy maximization for ): Suppose . , as defined by
is the unique maximizer of the Tsallis entropy in (2a) under the constraints of (3b) and of (3c) inT2.
The proof of this theorem is given in Section 4.2. In the case for , the maximization of is recast as Hölder’s inequality in (9), where, similar to the argument in the proof of Theorem 1, construction of and and verification of its optimality are carried out simultaneously. The maximizer for is uniquely determined from the equality condition (10):
where and are uniquely determined, and the associated is uniquely determined as .
Remark 3.
Another simple proof for optimality of is given by following Moriguti’s argument ([5], p. 288). Similar to the case for in Remark 2, (14) holds for . As for , from (17). We then have
where is used for notational simplicity. Integrating (18) over , for any p satisfying the constraints (3b) and (3c), we find
since the first term on the right-hand side as , the second term from the definition of and the fact that , and the third term because of the definition of . Since the equality in (19) holds only if , this implies that in (17) is a unique optimal solution toT2.
Theorem 3.
(Tsallis entropy maximization for ): Suppose . , defined by
is the unique representation of the maximizer of the Tsallis entropy in (2a) under the constraints of (3b) and of (3c) inT2.
The proof of this theorem is given in Section 4.3, where the associated Hölder’s inequality is given as , and we follow the arguments in the proof of Theorem 2 for . (This exceptional case () is also considered in T1, where the same result is obtained through a more direct graphical argument, after proving that any candidate for the maximizer is defined only on a simply connected interval that is symmetric about the origin . The proof is straightforward but lengthy, so we omit it here.) However, as opposed to the case for , the equality condition is not available in the form of (10) for , and we directly verify that
is the unique solution satisfying the equality in (9), as shown in Lemma 1. Namely, for any feasible solutions satisfying the constraints (3b) and (3c), we find that is associated with the unique maximizer of from (52), and hence, for is obtained as in (20).
Remark 4.
Theorem 4.
(Rényi entropy maximization for ): Suppose . , as defined by
is the unique maximizer of Rényi entropy in (4a) under the constraints of (5b) (or (7b)) and of (5c) (or (7c)).
The proof of this theorem is given in Section 4.4. The minimization of in (7b) for is related to reverse Hölder’s inequality in (11). In contrast to those of Theorems 1–3, the proof of Theorem 4, which can be found in Section 4.4, follows from two steps. In the first step, we construct a candidate for the minimizer (i.e., , see (61) below), whose support becomes , and we determine the associated and through the equality condition of reverse Hölder’s inequality. In doing so, as shown in Figure 1, we introduce a subset of feasible solutions , in other words, , which satisfies the constraints (5b) and (5c), and an additional constraint: . In the second step, after obtaining a candidate , we verify that this is indeed the unique minimizer of by directly comparing and for any feasible solutions satisfying the constraints (5b) and (5c).
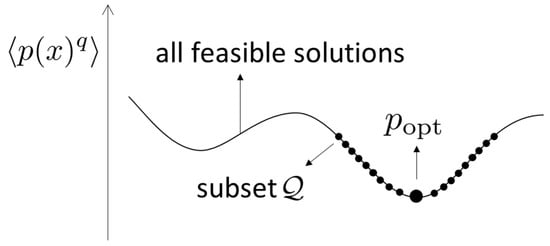
Figure 1.
This figure illustrates how our approach for Theorem 4 works in a possible structure of our optimization problem. The whole curve represents all feasible solutions, and the dotted points represent the subset in all feasible solutions.
Remark 5.
We note that the first proof for this optimality of has been given in Moriguti [5], in which the essential idea is the Taylor expansion shown in the argument below (18).
Theorem 5.
(Rényi entropy maximization for ): Suppose . , defined by
is the unique maximizer of Rényi entropy (4a) under the constraints (5b) and (5c) (or (7b) and (7c)).
The proof of this theorem is given in Section 4.5. Maximization of is related to Hölder’s inequality in (9) and the proof follows two steps, similar to the proof for Theorem 4. In the first step, we construct a candidate for the maximizer (i.e., , given below by (72)) and determine through the equality condition of Hölder’s inequality. In the second step, after obtaining a candidate , we verify that this is indeed the unique maximizer of by directly comparing and for any feasible solutions satisfying the constraints (5b) and (5c). This verification is done as in the proofs for Theorem 4. Although omitted here, using essentially the same argument as in Remark 1, another simple proof based on Moriguti [5] is possible.
Remark 6.
Tsukada and Suyari [23] have proved thatR1for becomes unbounded. As for the exceptional case of , the upper and lower bounds of are argued as follows. First, if we consider the Gaussian distribution that satisfies (5b) and (5c), this gives us , and it implies there is no maximizer. Next, consider a particular distribution given by
with . This satisfies in (5b), and it also satisfies in (5c) when δ is arbitrary small, in other words,
and, this particular distribution gives , which implies there is no minimizer. Therefore, problemR1(andR2) has no maximizer nor minimizer for .
4. Proof of Main Results
Following the outlines leading to Theorems 1–5 in Section 3, here we give their proofs.
4.1. Proof of Theorem 1
Proof.
Let p be arbitrary feasible solutions to T2 for , and let be its optimal solution, which is eventually constructed in (25). Let be a particular value of the additional parameter in T2, which is associated with and is eventually constructed in (29). Then, for any p and a particular ( in (29)), we define f and g as
First, we show is minimized in the following way:
The first “=” in (24a) follows from the fact that in (3a) is independent from the value of , since any feasible solution p satisfies in (3c), and the second “=” in (24a) is immediate from (23). The “=” in (24b) follows from and in (23b), since in (29) , and it satisfies . The “≥” in (24b) follows from reverse Hölder’s inequality (11). The “=” in (24c) follows from . (24c) implies that has the lower bound (i.e., the Tsallis entropy in (1) has the upper bound).
Next, we construct a maximizer achieving this bound and show its uniqueness, which is done by checking the conditions where the “≥” in (24) become “=”; the only “≥” in (24b) becomes “=” if and only if the equality condition (12) is satisfied. Now, we rewrite the equality condition (12) (after assuming in (12)) by using (23), which constructs (a candidate of) :
where A and are uniquely determined, and hence, and are also uniquely determined, as shown in the following calculations. We note the formula ([42], p. 253):
is repeatedly used for the integrations below. (More precisely, for (26), we set , , , and is satisfied. For (27b), we set , , , , and is satisfied.)First, by substituting in (25) into the constraint (3b), and for (finiteness of the left-hand side of (3b) requires the condition ), we have
On the other hand, substituting (25) into and in the constraint (3c), we have
and substitution of (27a) and (27b) into (3c) yields
Then, using the formula ([42], p. 254) in (28), is uniquely determined as
and from (26) and (29) A is uniquely determined as
In (25), equating the second term to the third term, is uniquely determined as
and from (29) and (30), is uniquely determined as
This proves that in (25) is a unique minimizer to T2 for .
Finally, we prove the Corollary to Theorem 1 in Section 3. For , let be the distribution satisfying (3b) and (3c), defined as
where a normalization factor and . What we are going to prove is , which is done as follows. First, straightforward integrations yield:
where . Second, from the constraint in (3c), is obtained, and this shows that becomes finite and is determined by , q, and . Finally, substituting (31a) into (31b), we obtain
and hence , since for in (32) and in (32). □
4.2. Proof of Theorem 2
Proof.
Let p be arbitrary feasible solutions to T2 for , and let be its optimal solution, which is eventually constructed in (38). Let be a particular value of the additional parameter in T2, which is associated with and is eventually constructed in (42). Then, for any p and a particular ( in (42)), we define f and g as
and we define an interval
First, we show that is maximized in the following way:
where , , and . The first “=” in (34a) follows from the fact that in (3a) is independent from the value of , since any feasible solution p satisfies in (3c), and the second “=” in (34a) is immediate from (33). The “≤” in (34b) is obtained from the following observation. By plotting the graph of for (any negative) , we observe that is the set of x on which becomes positive. For any f and g in (34a), we also observe from this graph that for any set but , since
On the other hand, the “=” in (34b) is immediate from . The first “=” in (34c) follows from the definition of , and the inequality in (34c) follows from Hölder’s inequality (9). In view of (33a), the final “≤” in (34d) follows from
and the resulting implies the upper bound of if exists for a given q and .
Next, we construct a maximizer achieving this bound and show its uniqueness, which is done by checking the conditions where all three “≤” in (34) become “=”. As for the “≤” in (34b), it becomes “=” if and only if becomes positive only in . Namely,
In other words, the “≤” in (34b) becomes “<” if the above condition (36) is violated, which is easily verified from the graph of and the above argument for the “≤” in (34b). On the other hand, in (34c), the “≤” becomes “=” if and only if the equality condition (10) is satisfied for , in other words,
If p satisfies (36), it is immediate that and in (37), since , and A and B are not both 0 (cf. [40], p. 140). The conclusion is that, if these two conditions (36) and (37) are satisfied, a maximizer achieving the upper bound of is uniquely determined:
in which , , , , and are uniquely determined, as shown in the following calculations. We note the formula ([42], p. 253):
is repeatedly used for the integrations below. (More precisely, for (39), we set , , and . For (40b), we set , , , and .)By substituting in (38) into the constraint (3b), we have
On the other hand, by substituting (38) into and in the constraint (3c), we have
and substitution of (40a) and (40b) into (3c) yields
Then, using the formula ([42], p. 254) in (41), is uniquely determined as
and from (39) and (42) is uniquely determined as
In (38), equating the second term to the third term, is uniquely determined as
and from (29) and (30), is uniquely determined as
To see that makes all “≤” in (34) “=”, finally, we check the last “≤” in (34d) becomes “=”, which is immediate since in (34c) . Therefore, it is concluded that is uniquely maximized by in (38) for . □
4.3. Proof of Lemma 1 and Theorem 3
Let p be arbitrary feasible solutions to T2 for , and let be its optimal solution, which is eventually constructed in (53). Let be a particular value of the additional parameter in T2, which is associated with and is eventually constructed in (54). Then, for any p and a particular ( in (54)), we define f and g as
and we define an interval
We note this particular is proved to be the unique maximizer of in the following Lemma 1 (as a minor modification of Lemma 4 in [35]).
Lemma 1.
(cf. Lemma 4 in [35]). Let S be an arbitrary subset in , with . For and , assume . Then, is the unique maximizer of the functional in (9).
Proof of Lemma 1.
First, thanks to Hölder’s inequality, see (9), is maximized by , since
Second, the unique representation of this maximizer is shown by proof by contradiction, as follows. Suppose another maximizer exists and it maximizes , in other words, . Then, for any given , the following is satisfied:
Now, using the identities and , we obtain and , respectively, resulting in the equality
Now, keeping and the assumption that in mind, (50) implies
where takes either or 1. However, among such functions having either or 1 values, it is clear that is the only one that makes maximal. Thus, no can exist except for , and the uniqueness of the maximizer is verified. □
Proof of Theorem 3.
First, we show that is maximized in the following way:
where , , and , and is the infinity norm of , in other words, the essential supremum of . The first “=” in (51a) follows from the fact that in (3a) is independent from the value of , since any feasible solution satisfies in (3c), and the second “=” in (51a) is immediate from (45). The “≤” in (51b) is obtained from the same argument of the inequality (34b) and (35) in the proof of Theorem 2. On the other hand, the equality in (51b) is immediate from . The first “=” in (51c) follows from the definition of , and the “≤” in (51c) follows from the Hölder’s inequality (9). The final “≤” in (51d) follows from the definition of in (45a), in other words, , and the resulting implies the upper bound of if exists for given q and .
Next, we construct a maximizer achieving this bound and show its uniqueness, which is done by checking the conditions where all three “≤” in (51) become “=”. As for the first “≤” in (51b), it becomes “=” if and only if becomes positive only in . Namely,
in other words, the “≤” in (51b) becomes “<” if the above condition (52) is violated, which is easily verified from the graph of and the above argument for the “≤” in (51b). On the other hand, in (51c), the second “≤” becomes “=” if and only if due to Lemma 1 (simply by replacing S with , in Lemma 1). The final “≤” in (51d) becomes “=” if and only if in (51c). From these three conditions, f is uniquely determined as in (47), and from (45a) the associated maximizer for is obtained as
where should satisfy . Finally, substituting (53) into the constraint (3c), we have , and from (46) and are uniquely obtained as
respectively. This shows the uniqueness of the representation of in (53). (This exceptional case is also argued in T1, where the same result is obtained through a more direct graphical argument, after proving that any candidate for the maximizer is defined only on a simply connected interval that is symmetric about the origin . The proof is straightforward but lengthy, and we omit it here.) □
4.4. Proof of Theorem 4
Proof.
Let p be arbitrary feasible solutions to R2 for , and let be its optimal solution, which is eventually constructed in (61). Let be a particular value of the additional parameter in R2, which is associated with and is eventually constructed in (65). First, for any p and a particular , in (65), we define f and g as
and we define a set in :
Next, we introduce a subset of the feasible solutions p,
which is proved to be non-empty in Appendix A.1.
First, we show that the following holds: if ,
where , , and . The first “=” in (58a) follows from the fact that in (7c) is independent from the value of , since any feasible solution satisfies in (6), and the second “=” in (58a) is immediate from the definitions (56) and (57). The first “=” in (58b) is also immediate from (56). The “≥” in (58c) follows from reverse Hölder’s inequality (11).
If achieves the lower bound, and in (58c) saturates at this bound for and , then, from (58), the following has to be satisfied:
Therefore, to construct a candidate achieving this bound, we consider the condition where the “≥” in (58c) becomes “=”. Namely, we rewrite the equality condition (12) by using (55):
where . From (59b), it is immediate that
and, hence,
since because and ) in (60). On the other hand, for , it is also immediate that from (56) and (57). Thereby, a candidate of the minimizer (in ) is constructed as:
where . (The distribution in (61) is called the -Gaussian [31].) In (61), is now specified and , , and are uniquely determined as , , and , respectively, as shown in the following calculations. We note the formula ([42], p. 253):
is repeatedly used for the integrations below. (More precisely, for (62) we set , , and .) For (63), we set , , and . Substituting (61) into the constraint (5b), we have
where r is defined by Note that as shown in (65). On the other hand, substituting (61) into the constraint (5c), we have
Substitution of (62) and (63) (multiplied with to its both sides) into (7a) yields
in which ([42], p. 254) is used. Thus, is obtained as
Since
While, from (62), or (63), and (64) that determines r with q and , is uniquely obtained for any given and , and hence, C is also uniquely determined from (65):
Therefore, from (61), (62), and (65), is uniquely determined as in (61). Note that , since
is immediate from (61).
Next, to prove that the candidate in (61) is the unique minimizer, we directly compare and in the following way:
Note that (66a) follows from in (5b) and in (5c), (66b) follows from (61), in other words, , and (66c) follows from (66a) by using , which is immediate from (61). Finally, substituting in (65) into (66b), we obtain
in which the equality holds if and only if , since
and hence,
On the other hand, the term (66c) can be expressed as
4.5. Proof of Theorem 5
Proof.
Let p be arbitrary feasible solutions to R2 for , and let be its optimal solution, which is eventually constructed in (72). Let be a particular value of the additional parameter in R2, which is associated with and is eventually constructed in (76). Then, for any p and a particular , in (76), we define f and g as
First, we show the following holds for any feasible solution p,
The first “=” in (69a) follows from the fact that in (7c) is independent from the value of , since any feasible solution satisfies in (6), and the second “=” in (69a) is immediate from (68). The first “≤” in (69b) follows from , since is always nonnegative but in (68b) can be negative on some intervals in by choosing certain . The second “≤” in (69b) follows from Hölder’s inequality (9). The final “=” in (69c) follows from in (69b).
Next, if achieves the upper bound, and in (69c) saturates at this bound for and , then from (69) the following has to be satisfied:
Therefore, to construct a candidate achieving this bound, we consider the condition where the two “≤” in (69) become “=”. As for the first “≤” in (69b), it becomes “=” if , in other words,
which is eventually verified in (78). On the other hand, the second “≤” in (69b) becomes “=” if and only if the equality condition (10) is satisfied, , in other words,
where . Note that 0 and because of (70). From (70) and (71), a candidate of the maximizer is uniquely constructed:
in which C =, , , and are uniquely determined, and is verified, as shown in the following calculations. We note the formula ([42], p. 253):
is repeatedly used for the integrations below. (More precisely, for (73) we set , , , and is satisfied.) For (74), we set , , , and is satisfied. Substituting (72) into the constraint (5b), we have
where r is defined by Note that as shown in (76). On the other hand, substituting (72) into the constraint (5c), we have
Substitution of (73) and (74) after multiplying to both sides into (7a) yields
in which ([42], p. 254) is used. Thus, we first obtain as
since
Meanwhile, from (73), or (74), and (75) that determines r with q and , () is uniquely determined for any q () and , and hence, C () is also uniquely determined from (76):
Now, we verify (70) is satisfied by . Note that if , using (76) we have
and hence (70) is satisfied by :
which is immediate from (71), (72), and (77). Thus, is uniquely determined as in (72).
Finally, to prove that this candidate (72) is the unique maximizer, we directly compare and as follows. Similar to (66), the following holds here:
Note that (79a) follows from in (5b) and in (5c), and (79b) follows from (79a) by using , which is immediate from (72). Because for , for any and because only when , (79b) is not positive, and it becomes 0 if and only if , in other words, (). This proves that in (72) is the unique maximizer to R2 for . □
5. Conclusions and Discussion
We obtained a new insight about a direct link between generalized entropy and Hölder’s inequality, and yet another proof for Rényi–Tsallis entropy maximization; the q-Gaussian distribution is directly obtained from the equality condition of Hölder’s inequality, and its optimality is proved by Hölder’s inequality through Moriguti’s argument. The simplicity in the proofs of Tsallis entropy maximization (Theorem 1, 2, and 3) is worth noting; essentially, several lines of inequalities (including Hölder’s inequality) are sufficient for the proof.
As an analogy, what we have described in this study can be explained as mountain climbing; as for Tsallis entropy maximization, the top of the mountain, in other words, the upper/lower bound is clearly seen from the starting point. Namely, the bounds in (24c), (34d), and (51d) are explicitly given by q and . Therefore, all we need to do is to keep climbing to the top, in other words, to construct a series of inequalities (24), (34), and (51) that saturate at the bound. On the other hand, for Rényi entropy maximization, the top of the mountain is not clearly seen from the starting point. Namely, the upper/lower bound is not given only by q and but contains , as in (58c) or (69c). Even in such a case, Hölder’s inequality is still useful for finding a peak of the mountain, in other words, it leads to a candidate of the global optimal, and then we verify this candidate is really the top by using a GPS (global positioning system). In addition, this GPS is obtained as in (66) or (79), thanks to Moriguti [5].
Our technique with Hölder’s inequality plus the additional parameter can be useful for other inequalities (e.g., Young’s inequality), and it seems an interesting open problem to clarify what sort of optimization problems can be solved from such a technique.
Author Contributions
Conceptualization, H.-A.T.; methodology, H.-A.T.; writing–original draft preparation, H.-A.T.; writing–review and editing, H.-A.T. and M.N.; supervision, Y.O.; funding acquisition, H.-A.T.
Funding
This work has been supported by the Japan Ministry of Education, Culture, Sports, Science and Technology (MEXT) (Grant No. 26286086) and by the Support Center for Advanced Telecommunications Technology Research (SCAT).
Acknowledgments
The authors would like to express their gratitude to the referees for their careful reading of an earlier draft of this paper and valuable suggestions for improving the paper. The authors are indebted to Hiroki Suyari, Makoto Tsukada, Hideki Takayasu, Hayato Waki, Hayato Chiba, Yutaka Jitsumatsu, Fumito Mori, Yasuhiro Tsubo, Takashi Shimada, Akitoshi Takayasu, Masahide Kashiwagi, and Shinichi Oishi for their enlightening suggestions. One of the authors (H. T.) appreciates Norikazu Takahashi for his critical reading of the manuscript and valuable suggestions which improved the manuscript. H. T. appreciates Jürgen Kurths and Istvan Z. Kiss for their inspiring suggestion that motivated this work, and H. T. also appreciates Constantino Tsallis for his critical comments at Social Modeling and Simulations + Econophysics Colloquium (SMSEC2014). One of the authors (H. T.) would like to dedicate this work to the memory of Sigeiti Moriguti.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Appendix A.1. Example of Non-Empty set Q
Here, we illustrate an example of introduced in Section 4.4. Having obtained and in Section 4.4, an element , which satisfies (5b), (5c), and
is constructed from in (61) as follows. Figure A1 shows how we are going to construct p from ; the basic idea is that such p is obtained only by slightly modifying at its edge while keeping the constraint (A1). First, we choose small adjacent intervals and inside the interval . This choice is consistent to the fact that the constraint (A1) is equivalent to
and hence can be 0 in (as observed in the inset of Figure A1). Second, we shift , , and the associated value of originally defined on and , altogether, while keeping the original value of at 0. As shown in the inset of Figure A1, an option for this shift is: to the right and to the left. Such an option for small shifts always exists because of the continuity of integration with respect to and . Note that the resulting p shown in the inset of Figure A1 satisfies (5b), (5c), and (A1). The above constructed p constitutes a non-empty set and it is straightforwardly verified to be convex.
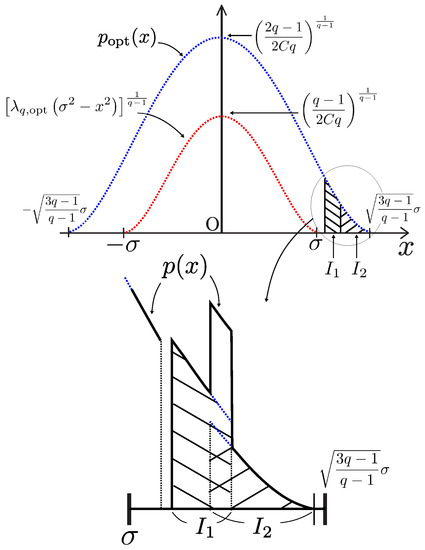
Figure A1.
Construction of from .
References
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics; Springer: New York, NY, USA, 2009; ISBN 978-0-387-85358-1. [Google Scholar]
- Prato, D.; Tsallis, C. Nonextensive foundation of Lévy distributions. Phys. Rev. E 1999, 60, 2398–2401. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006; ISBN 978-0-471-24195-9. [Google Scholar]
- Daróczy, Z. Generalized information functions. Inf. Control 1970, 16, 36–51. [Google Scholar] [CrossRef] [Green Version]
- Moriguti, S. A lower bound for a probability moment of any absolutely continuous distribution with finite variance. Ann. Math. Stat. 1952, 23, 286–289. [Google Scholar] [CrossRef]
- Campbell, L.L. A coding theorem and Rényi’s entropy. Inf. Control 1965, 8, 423–429. [Google Scholar] [CrossRef]
- Baer, M.B. Source coding for quasiarithmetic penalties. IEEE Trans. Inf. Theory 2006, 52, 4380–4393. [Google Scholar] [CrossRef]
- Bercher, J.-F. Source coding with scaled distributions and Rényi entropy bounds. Phys. Lett. A 2009, 373, 3235–3238. [Google Scholar] [CrossRef]
- Bunte, C.; Lapidoth, A. Encoding tasks and Rényi entropy. IEEE Trans. Inf. Theory 2014, 60, 5065–5076. [Google Scholar] [CrossRef]
- Landsberg, P.T.; Vedral, V. Distributions and channel capacities in generalized statistical mechanics. Phys. Lett. A 1998, 247, 211–217. [Google Scholar] [CrossRef]
- Ilić, V.M.; Djordjević, I.B.; Küeppers, F. On the Daróczy–Tsallis capacities of discrete channels. In Sciforum Electronic Conference Series, Proceedings of the 2nd International Electronic Conference on Entropy and Its Applications, 15–30 November 2015; MDPI: Basel, Switzerland, 2015; B004; pp. 1–11. [Google Scholar]
- Venkatesan, R.C.; Plastino, A. Generalized statistics framework for rate distortion theory. Phys. A 2009, 388, 2337–2353. [Google Scholar] [CrossRef] [Green Version]
- Girardin, V.; Lhote, L. Rescaling entropy and divergence rates. IEEE Trans. Inf. Theory 2015, 61, 5868–5882. [Google Scholar] [CrossRef]
- Thistleton, W.J.; Marsh, J.A.; Nelson, K.; Tsallis, C. Generalized Box-Müller method for generating q-Gaussian random deviates. IEEE Trans. Inf. Theory 2007, 53, 4805–4810. [Google Scholar] [CrossRef]
- Umeno, K.; Sato, A. Chaotic method for generating q-Gaussian random variables. IEEE Trans. Inf. Theory 2013, 59, 3199–3209. [Google Scholar] [CrossRef]
- Karmeshu; Sharma, S. Queue length distribution of network packet traffic: Tsallis entropy maximization with fractional moments. IEEE Commun. Lett. 2006, 10, 34–36. [Google Scholar] [CrossRef]
- Sharma, S.; Karmeshu. Power law characteristic and loss probability: finite buffer queueing systems. IEEE Commun. Lett. 2009, 13, 971–973. [Google Scholar] [CrossRef]
- Singh, A.K.; Karmeshu. Power law behavior of queue size: Maximum entropy principle with shifted geometric mean constraint. IEEE Commun. Lett. 2014, 18, 1335–1338. [Google Scholar] [CrossRef]
- Singh, A.K.; Singh, H.P.; Karmeshu. Analysis of finite buffer queue: Maximum entropy probability distribution with shifted fractional geometric and arithmetic means. IEEE Commun. Lett. 2015, 19, 163–166. [Google Scholar] [CrossRef]
- Jaynes, E.T. On the rationale of maximum-entropy methods. Proc. IEEE 1982, 70, 939–952. [Google Scholar] [CrossRef]
- Shore, J.E.; Johnson, R.W. Axiomatic derivation of the principle of maximum entropy and the principle of minimum cross-entropy. IEEE Trans. Inf. Theory 1980, 26, 26–37. [Google Scholar] [CrossRef] [Green Version]
- Shore, J.E.; Johnson, R.W. Properties of cross-entropy minimization. IEEE Trans. Inf. Theory 1981, 27, 427–482. [Google Scholar] [CrossRef]
- Tsukada, M.; Suyari, H.; Kato, M. On the probability distribution max imizing generalized entropies. In Proceedings of 2005 Symposium on Applied Functional Analysis: Information Sciences and Related Fields; Murohashi, T., Takahashi, W., Tsukada, M., Eds.; Yokohama Publisher: Yokohama, Japan, 2007; pp. 99–111. [Google Scholar]
- Furuichi, S. On the maximum entropy principle and the minimization of the Fisher information in Tsallis statistics. J. Math. Phys. 2009, 50, 013303:1–013303:13. [Google Scholar] [CrossRef]
- Lutwak, E.; Yang, D.; Zhang, G. Cramér-Rao and moment-entropy inequalities for Renyi entropy and generalized Fisher information. IEEE Trans. Inf. Theory 2005, 51, 473–478. [Google Scholar] [CrossRef]
- Lutwak, E.; Yang, D.; Zhang, G. Moment-entropy inequalities for a random vector. IEEE Trans. Inf. Theory 2007, 53, 1603–1607. [Google Scholar] [CrossRef]
- Eguchi, S.; Komori, O.; Kato, S. Projective power entropy and maximum Tsallis entropy distributions. Entropy 2011, 13, 1746–1764. [Google Scholar] [CrossRef]
- Watanabe, S.; Oohama, Y. Secret key agreement from vector Gaussian sources by rate limited public communication. IEEE Trans. Inf. Forensic Secur. 2011, 6, 541–550. [Google Scholar] [CrossRef]
- Fehr, S.; Berens, S. On the conditional Rényi entropy. IEEE Trans. Inf. Theory 2014, 60, 6801–6810. [Google Scholar] [CrossRef]
- Sakai, Y.; Iwata, K. Sharp bounds on Arimoto’s conditional Rényi entropies between two distinct orders. In Proceedings of the 2017 IEEE International Symposium on Information Theory (ISIT), Aachen, Germany, 25–30 June 2017; pp. 2985–2989. [Google Scholar] [CrossRef]
- Suyari, H.; Tsukada, M. Law of error in Tsallis statistics. IEEE Trans. Inf. Theory 2005, 51, 753–757. [Google Scholar] [CrossRef]
- Vignat, C.; Hero, A.O., III; Costa, J.A. About closedness by convolution of the Tsallis maximizers. Phys. A 2004, 340, 147–152. [Google Scholar] [CrossRef]
- Bercher, J.-F. On generalized Cramér-Rao inequalities, generalized Fisher information and characterizations of generalized q-Gaussian distributions. J. Phys. A Math. Gen. 2012, 45, 255303:1–255303:15. [Google Scholar] [CrossRef]
- Bercher, J.-F. On multidimensional generalized Cramér-Rao inequalities, uncertainty relations and characterizations of generalized q-Gaussian distributions. J. Phys. A Math. Theor. 2013, 46, 095303:1–095303:18. [Google Scholar] [CrossRef]
- Tanaka, H.-A. Optimal entrainment with smooth, pulse, and square signals in weakly forced nonlinear oscillators. Phys. D 2014, 288, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Tanaka, H.-A. Synchronization limit of weakly forced nonlinear oscillators. J. Phys. A Math. Theor. 2014, 47, 402002:1–402002:10. [Google Scholar] [CrossRef]
- Dembo, A.; Cover, T.M.; Thomas, J.A. Information theoretic inequalities. IEEE Trans. Inf. Theory 1991, 37, 1501–1518. [Google Scholar] [CrossRef]
- Oikonomou, T.; Bagci, G.B. A note on the definition of deformed exponential and logarithm functions. J. Math. Phys. 2009, 50, 103301:1–103301:9. [Google Scholar] [CrossRef]
- Dehesa, J.S.; Galvez, F.J.; Porras, I. Bounds to density-dependent quantities of D-dimensional many-particle systems in position and momentum spaces: Applications to atomic systems. Phys. Rev. A 1989, 40, 35–40. [Google Scholar] [CrossRef]
- Hardy, G.; Littlewood, J.E.; Pólya, G. Inequalities, 2nd ed.; Cambridge University Press: Cambridge, UK, 1988; ISBN 978-0-521-35880-4. [Google Scholar]
- Rudin, W. Real and Complex Analysis, 3rd ed.; McGraw-Hill: New York, NY, USA, 1987; pp. 63–65. ISBN1 0070542341. ISBN2 9780070542341. [Google Scholar]
- Whittaker, E.T.; Watson, G.N. A Course of Modern Analysis, 4th ed.; Cambridge University Press: Cambridge, UK, 1927. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).