Stationary Wavelet-Fourier Entropy and Kernel Extreme Learning for Bearing Multi-Fault Diagnosis
Abstract
1. Introduction
2. Shannon Entropy Measures
2.1. Stationary Wavelet Packet Fourier Entropy
2.2. Stationary Wavelet Packet Permutation Entropy
- Step 1:
- Create a set of m-dimensional vectors as follows:where m is the embedding dimension of the vector .
- Step 2:
- Each vector is sorted in ascending order with permutation pattern as follows:where each vector in m-dimensional space can be mapped to one of the ordinal patterns .
- Step 3:
- Calculate the probability of occurrence for each permutation pattern as follows:where denotes the total amount of embedding vectors.
- Step 4:
- Calculate the normalized SWPPE of the wavelet sub-band signal using Equation (6):
2.3. Stationary Wavelet Packet Dispersion Entropy
- Step 1:
- The wavelet sub-band signal is normalized between zero and one using the normal cumulative distribution function as follows:where and are the mean and standard deviation of the raw vibration signal of N data points.
- Step 2:
- The normalized signal is mapped into c classes with integer indices from 1–c using the equation as follows:where denotes the rounding operation.
- Step 3:
- Create multiple m-dimensional vectors as follows:
- Step 4:
- Each embedding vector is mapped into a dispersion pattern , where . Thus, the number of possible dispersion patterns is equal to .
- Step 5:
- Calculate the probability of occurrence for each permutation pattern as follows:where denotes the total of embedding vectors.
- Step 6:
- Calculate the normalized SWPDE of the wavelet sub-band signal using Equation (11):
2.4. Stationary Wavelet Packet Transform
3. Bearing Fault Diagnosis Algorithm
3.1. Proposed Diagnosis Algorithm
- Step 1:
- Divide the discrete time raw vibration signal into multiple non-overlapped signals of N data points.
- Step 2:
- Step 3:
- Create a D-dimensional features vector based on multi-scale wavelet Shannon entropy as follows:where represents one of the SWPFE/SWPPE/SWPDE values of the ith wavelet sub-band signal and k corresponds to the kth raw non-overlapping vibration signal.
- Step 4:
- Normalize the features matrix Z as follows:where corresponds to the ith column of the features matrix Z and and denote the minimum value and maximum value of the vector, respectively.
- Step 5:
- Create the KELM classifier based on both the features matrix Z and the k-fold cross-validation method.
3.2. Kernel-ELM Classifier
3.3. Experimental Setup
4. Experiments and Results
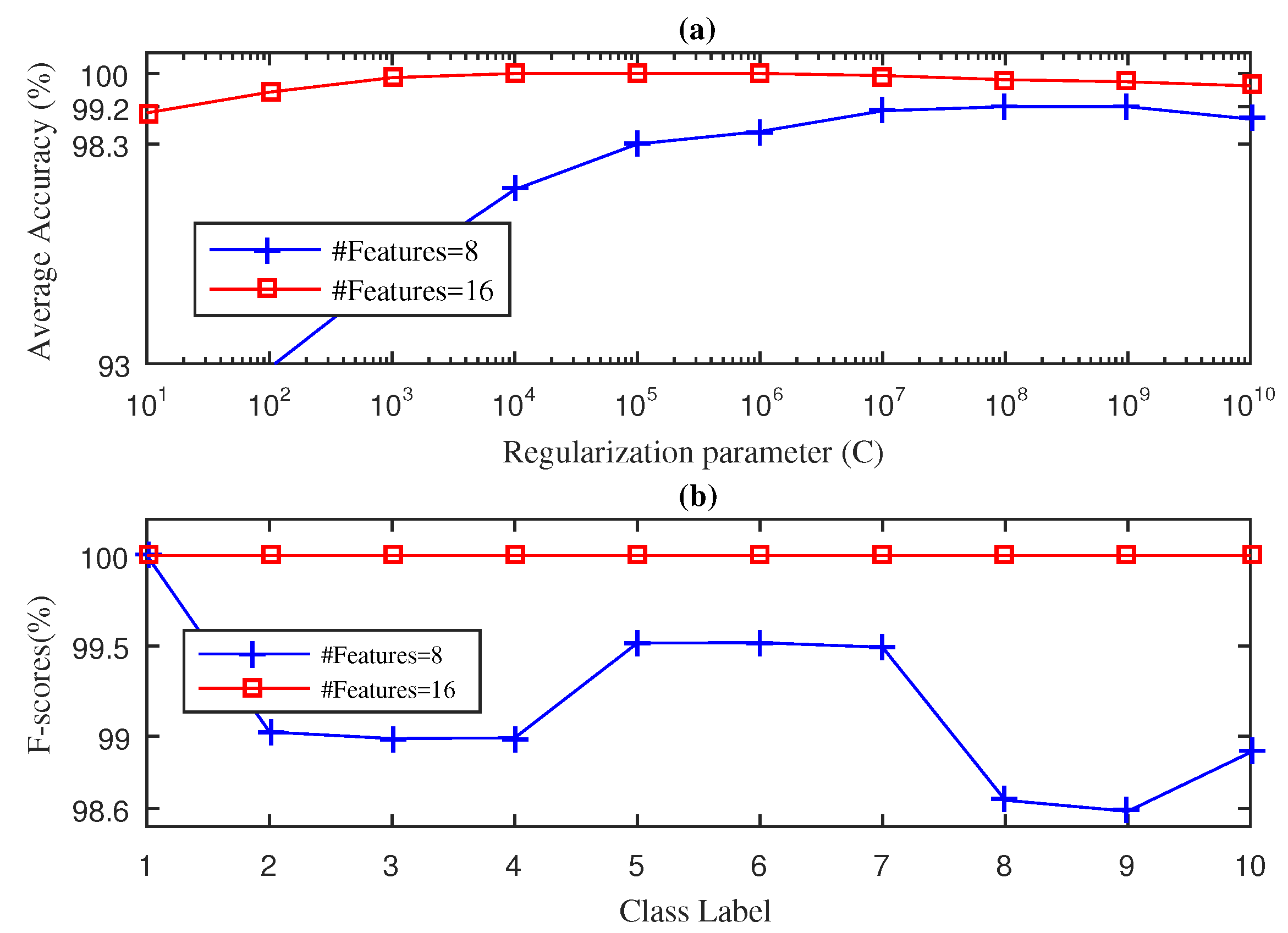
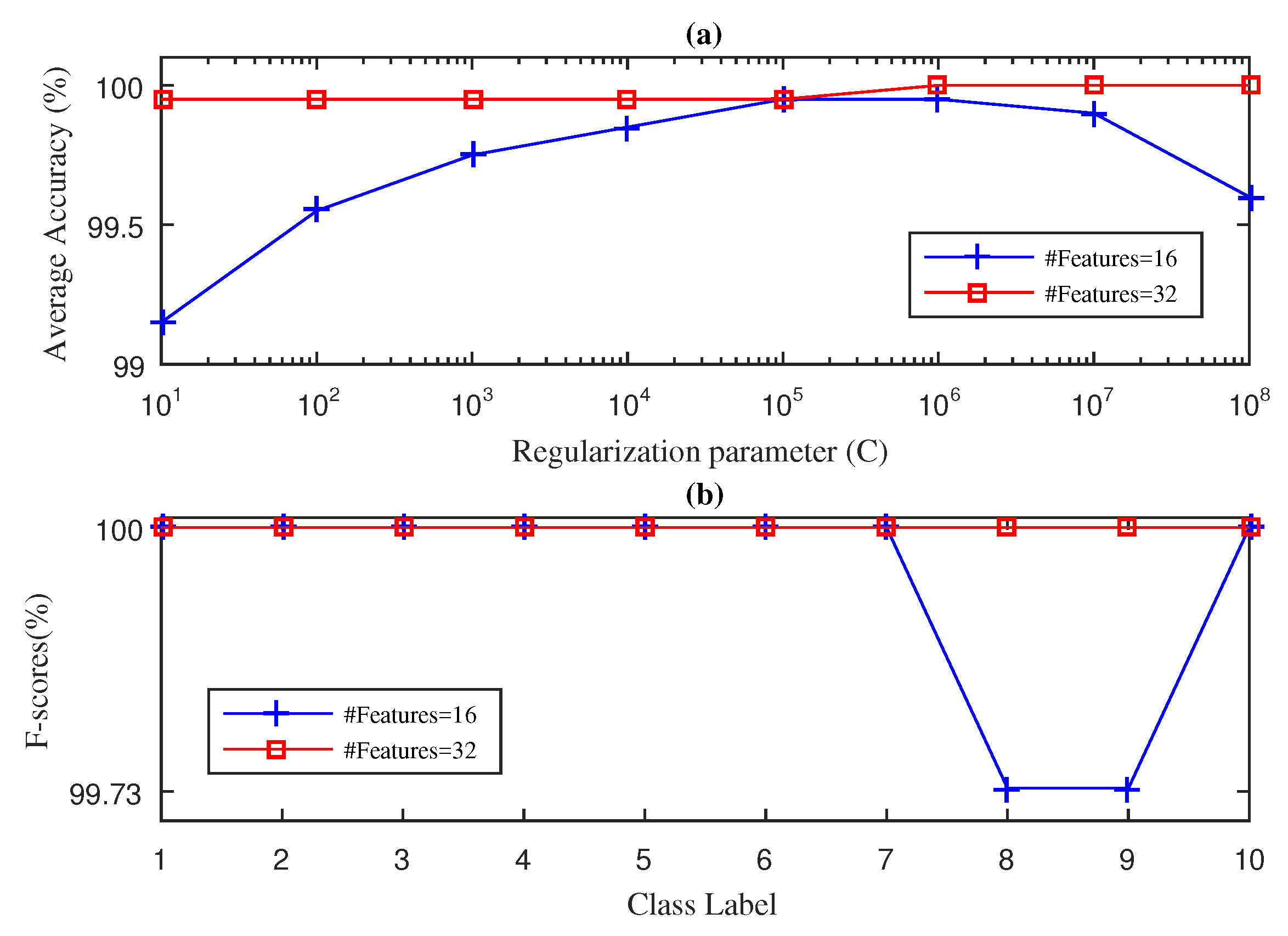
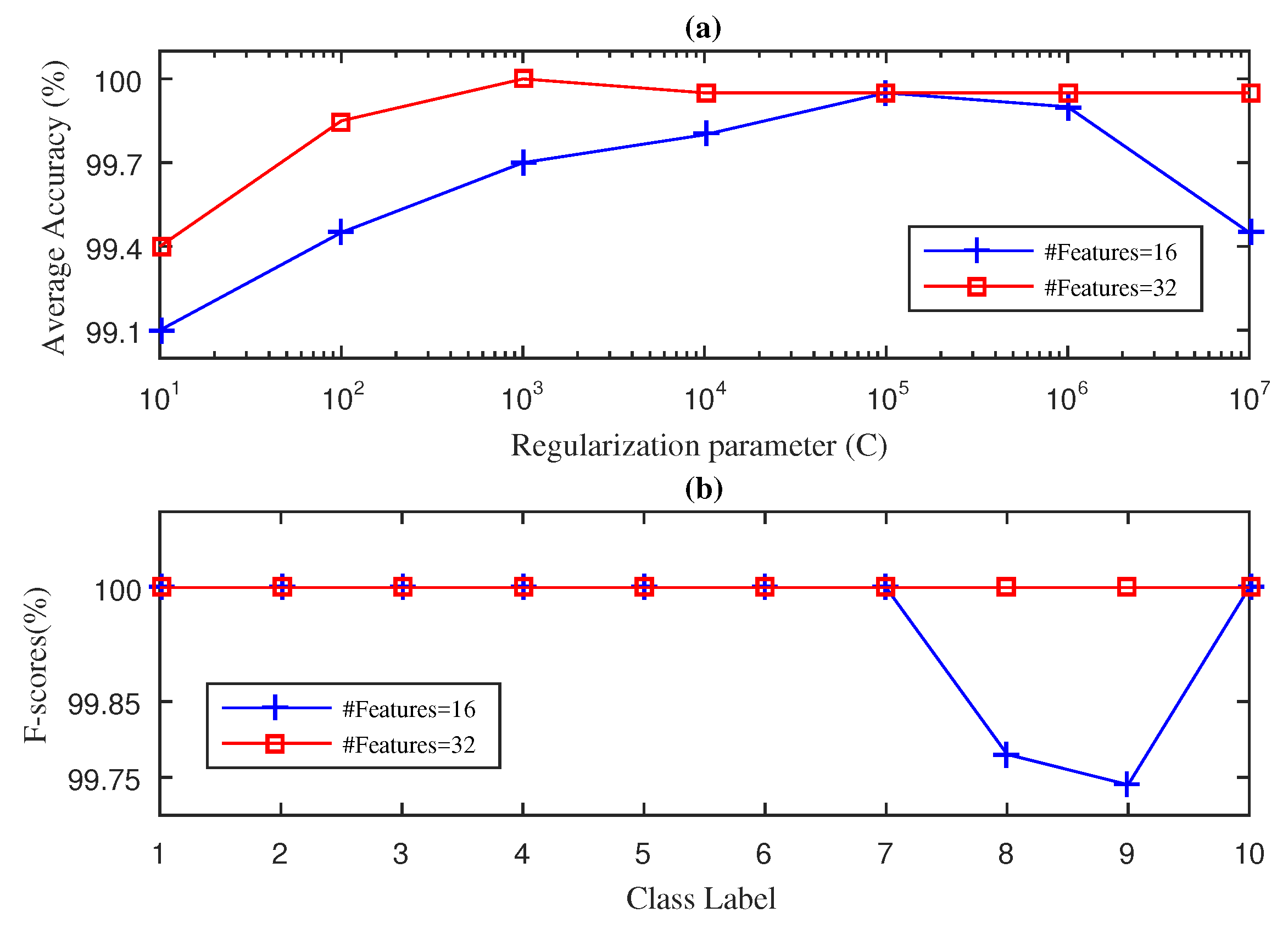
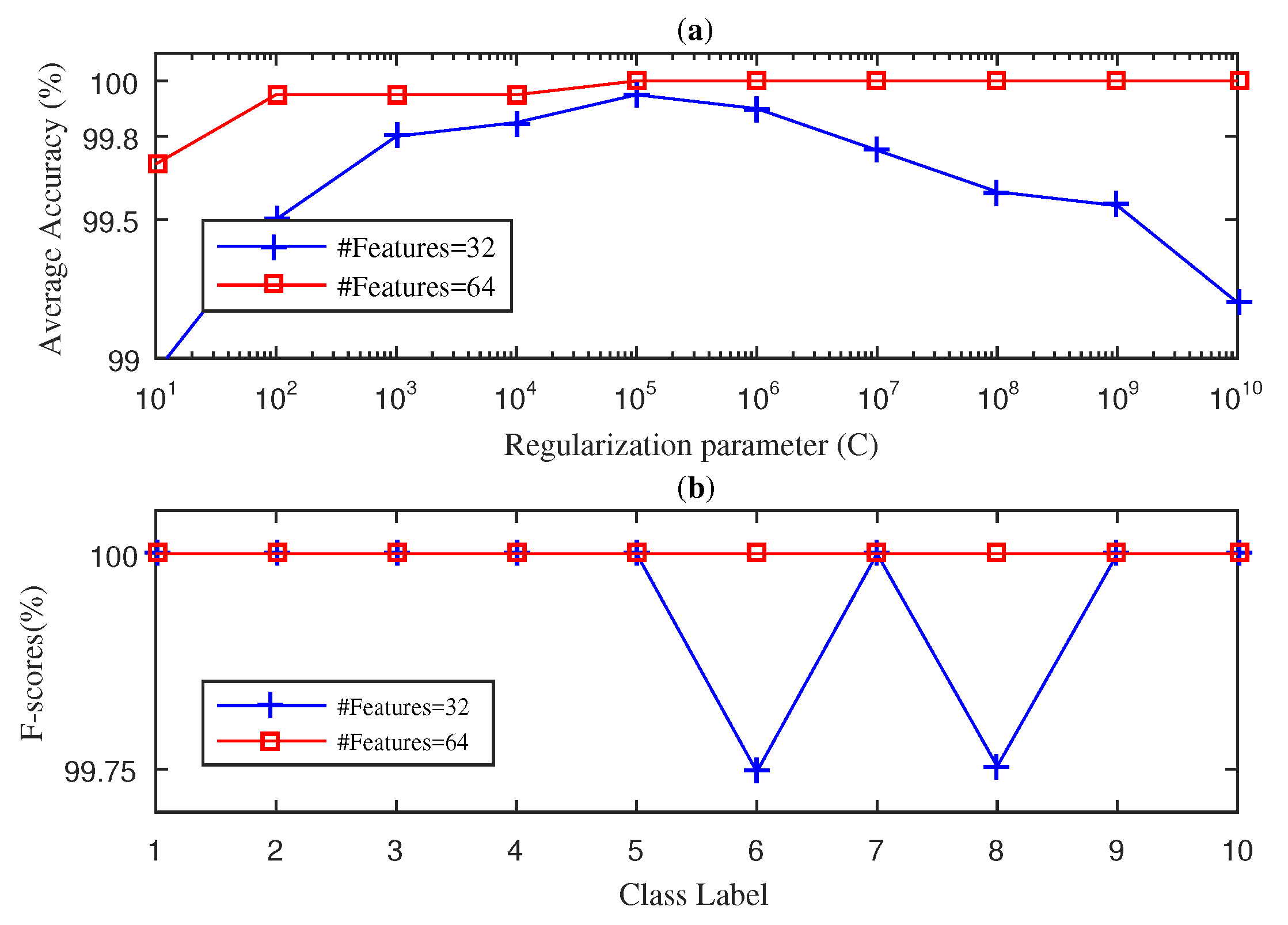
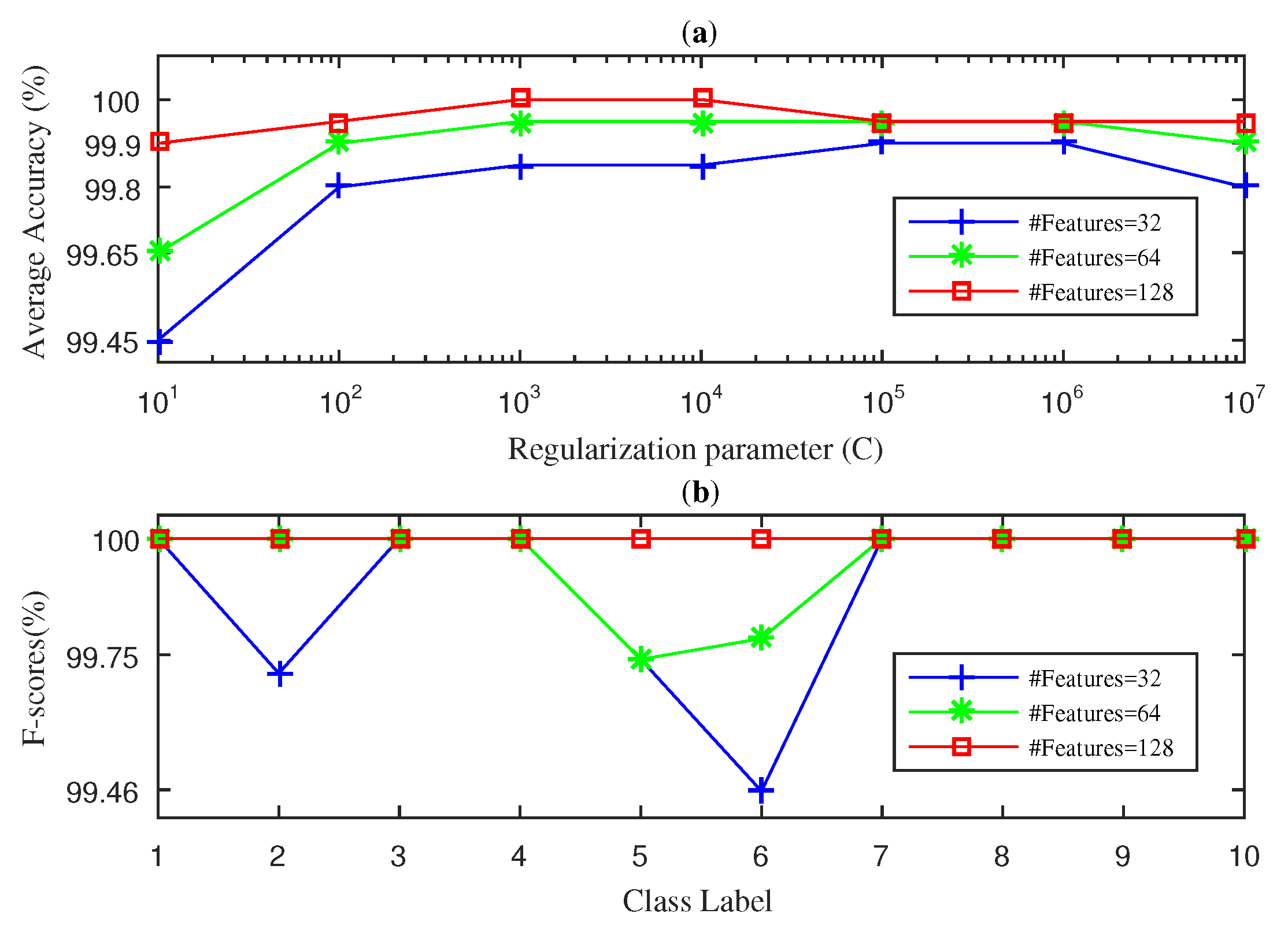
4.1. Case 1: Fan-End Bearing
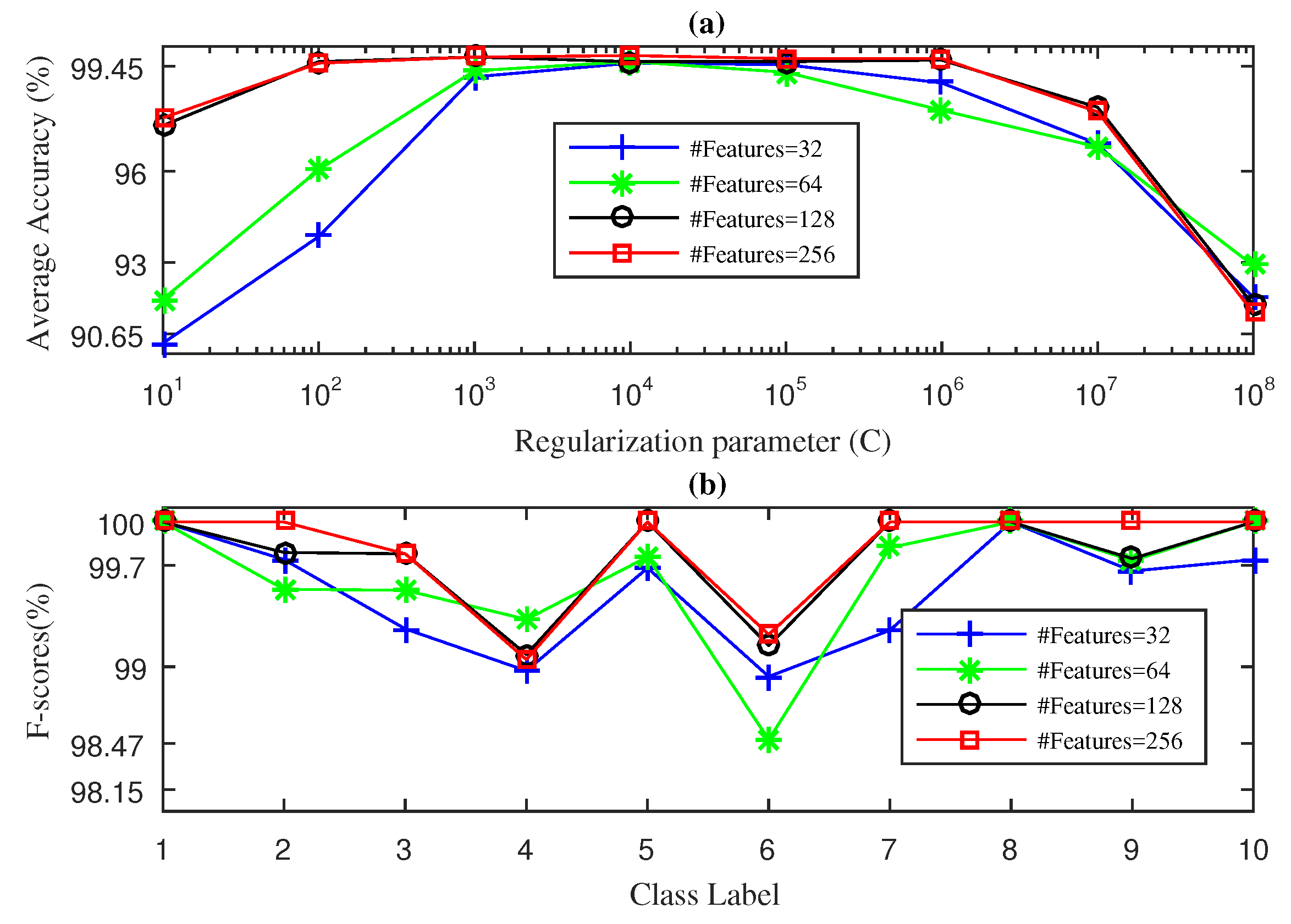
4.2. Case 2: Drive-End Bearing
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bozchalooi, I.S.; Liang, M. A smoothness index-guided approach to wavelet parameter selection in signal de-noising and fault detection. J. Sound Vib. 2007, 308, 246–267. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, L.; Xiang, J.; Yang, J.; He, S. A hybrid approach to fault diagnosis of roller bearings under variable speed conditions. Meas. Sci. Technol. 2017, 28, 125104. [Google Scholar] [CrossRef]
- Miao, Y.; Zhao, M.; Lin, J. Improvement of kurtosis-guided-grams via Gini index for bearing fault feature identification. Meas. Sci. Technol. 2017, 28, 125001. [Google Scholar] [CrossRef]
- Wang, D. Spectral L2/L1 norm: A new perspective for spectral kurtosis for characterizing non-stationary signals. Mech. Syst. Signal Proc. 2018, 104, 290–293. [Google Scholar] [CrossRef]
- Wang, D. Some further thoughts about spectral kurtosis, spectral L2/L1 norm, spectral smoothness index and spectral Gini index for characterizing repetitive transients. Mech. Syst. Signal Proc. 2018, 108, 360–368. [Google Scholar] [CrossRef]
- Immovilli, F.; Bellini, A.; Rubini, R.; Tassoni, C. Diagnosis of Bearing Faults in Induction Machines by Vibration or Current Signals: A Critical Comparison. IEEE Trans. Ind. Appl. 2010, 46, 1350–1359. [Google Scholar] [CrossRef]
- Henao, H.; Capolino, G.; Fernandez-Cabanas, M.; Filippetti, F.; Bruzzese, C.; Strangas, E.; Pusca, R.; Estima, J.; Riera-Guasp, M.; Hedayati-Kia, S. Trends in Fault Diagnosis for Electrical Machines: A Review of Diagnostic Techniques. IEEE Ind. Electron. Mag. 2014, 8, 31–42. [Google Scholar] [CrossRef]
- Tang, J.; Qiao, J.; Wu, Z.; Chai, T.; Zhang, J.; Yu, W. Vibration and acoustic frequency spectra for industrial process modeling using selective fusion multi-condition samples and multi-source features. Mech. Syst. Signal Proc. 2018, 99, 142–168. [Google Scholar] [CrossRef]
- Frosini, L.; Harlişca, C.; Szabo, L. Induction Machine Bearing Fault Detection by Means of Statistical Processing of the Stray Flux Measurement. IEEE Trans. Ind. Electron. 2015, 62, 1846–1854. [Google Scholar] [CrossRef]
- Antoni, J. The spectral kurtosis: a useful tool for characterising non-stationary signals. Mech. Syst. Signal Proc. 2006, 20, 282–307. [Google Scholar] [CrossRef]
- Antoni, J.; Randall, R. The spectral kurtosis: application to the vibratory surveillance and diagnostics of rotating machines. Mech. Syst. Signal Proc. 2006, 20, 308–331. [Google Scholar] [CrossRef]
- Antoni, J. Fast computation of the kurtogram for the detection of transient faults. Mech. Syst. Signal Proc. 2007, 21, 108–124. [Google Scholar] [CrossRef]
- Sawalhi, N.; Randall, R.; Endo, H. The enhancement of fault detection and diagnosis in rolling element bearings using minimum entropy deconvolution combined with spectral kurtosis. Mech. Syst. Signal Proc. 2007, 21, 2616–2633. [Google Scholar] [CrossRef]
- Lei, Y.; Lin, J.; He, Z.; Zi, Y. Application of an improved kurtogram method for fault diagnosis of rolling element bearings. Mech. Syst. Signal Proc. 2011, 25, 1738–1749. [Google Scholar] [CrossRef]
- Wang, D.; Tse, P.W.; Tsui, K.L. An enhanced Kurtogram method for fault diagnosis of rolling element bearings. Mech. Syst. Signal Proc. 2013, 35, 176–199. [Google Scholar] [CrossRef]
- Antoni, J. The infogram: Entropic evidence of the signature of repetitive transients. Mech. Syst. Signal Proc. 2016, 74, 73–94. [Google Scholar] [CrossRef]
- Moshrefzadeh, A.; Fasana, A. The Autogram: An effective approach for selecting the optimal demodulation band in rolling element bearings diagnosis. Mech. Syst. Signal Proc. 2018, 105, 294–318. [Google Scholar] [CrossRef]
- Li, H.; Liu, T.; Wu, X.; Chen, Q. Application of EEMD and improved frequency band entropy in bearing fault feature extraction. ISA Trans. 2019, 88, 170–185. [Google Scholar] [CrossRef]
- Han, M.; Pan, J. A fault diagnosis method combined with LMD, sample entropy and energy ratio for roller bearings. Measurement 2015, 76, 7–19. [Google Scholar] [CrossRef]
- Gong, T.; Yuan, X.; Yuan, Y.; Lei, X.; Wang, X. Application of tentative variational mode decomposition in fault feature detection of rolling element bearing. Measurement 2019, 135, 481–492. [Google Scholar] [CrossRef]
- Rodriguez, N.; Alvarez, P.; Barba, L.; Cabrera-Guerrero, G. Combining Multi-Scale Wavelet Entropy and Kernelized Classification for Bearing Multi-Fault Diagnosis. Entropy 2019, 21, 152. [Google Scholar] [CrossRef]
- Rodriguez, N.; Cabrera, G.; Lagos, C.; Cabrera, E. Stationary Wavelet Singular Entropy and Kernel Extreme Learning for Bearing Multi-Fault Diagnosis. Entropy 2017, 19, 541. [Google Scholar] [CrossRef]
- Brkovic, A.; Gajic, D.; Gligorijevic, J.; Savic-Gajic, I.; Georgieva, O.; Gennaro, S.D. Early fault detection and diagnosis in bearings for more efficient operation of rotating machinery. Energy 2017, 136, 63–71. [Google Scholar] [CrossRef]
- Luo, M.; Li, C.; Zhang, X.; Li, R.; An, X. Compound feature selection and parameter optimization of ELM for fault diagnosis of rolling element bearings. ISA Trans. 2016, 65, 556–566. [Google Scholar] [CrossRef]
- Zheng, J.; Pan, H.; Yang, S.; Cheng, J. Generalized composite multiscale permutation entropy and Laplacian score based rolling bearing fault diagnosis. Mech. Syst. Signal Proc. 2018, 99, 229–243. [Google Scholar] [CrossRef]
- Mao, W.; Feng, W.; Liang, X. A novel deep output kernel learning method for bearing fault structural diagnosis. Mech. Syst. Signal Proc. 2019, 117, 293–318. [Google Scholar] [CrossRef]
- Hoang, D.T.; Kang, H.J. Rolling element bearing fault diagnosis using convolutional neural network and vibration image. Cogn. Syst. Res. 2019, 53, 42–50. [Google Scholar] [CrossRef]
- Yang, Y.; Zheng, H.; Li, Y.; Xu, M.; Chen, Y. A fault diagnosis scheme for rotating machinery using hierarchical symbolic analysis and convolutional neural network. ISA Trans. 2019. [Google Scholar] [CrossRef]
- Zhu, Z.; Peng, G.; Chen, Y.; Gao, H. A convolutional neural network based on a capsule network with strong generalization for bearing fault diagnosis. Neurocomputing 2019, 323, 62–75. [Google Scholar] [CrossRef]
- Huang, G.B. Universal Approximation Using Incremental Constructive Feedforward Networks with Random Hidden Nodes. IEEE Trans. Neur. Netw. 2006, 17, 879–892. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhou, H.; Ding, X.; Zhang, R. Extreme Learning Machine for Regression and Multiclass Classification. IEEE Trans. Syst. Man Cybern. Part B 2012, 42, 513–529. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Lan, Y.; Huang, G.; Xu, Z. Universal approximation of extreme learning machine with adaptive growth of hidden nodes. IEEE Trans. Neur. Netw. Learn. Syst. 2012, 23, 365–371. [Google Scholar] [CrossRef] [PubMed]
- Bearing Data Center. Technical Report, Case Western Reserve University. Available online: https://csegroups.case.edu/bearingdatacenter/home (accessed on 27 May 2019).
- Lou, X.; Loparo, K.A. Bearing fault diagnosis based on wavelet transform and fuzzy inference. Mech. Syst. Signal Proc. 2004, 18, 1077–1095. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation Entropy: A Natural Complexity Measure for Time Series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
- Rostaghi, M.; Azami, H. Dispersion Entropy: A Measure for Time-Series Analysis. IEEE Signal Proc. Lett. 2016, 23, 610–614. [Google Scholar] [CrossRef]
- Rostaghi, M.; Ashory, M.R.; Azami, H. Application of dispersion entropy to status characterization of rotary machines. J. Sound Vib. 2019, 438, 291–308. [Google Scholar] [CrossRef]
- Azami, H.; Rostaghi, M.; Abásolo, D.; Escudero, J. Refined Composite Multiscale Dispersion Entropy and its Application to Biomedical Signals. IEEE Trans. Biomed. Eng. 2017, 64, 2872–2879. [Google Scholar]
- Yan, X.; Jia, M. Intelligent fault diagnosis of rotating machinery using improved multiscale dispersion entropy and mRMR feature selection. Knowl. Syst. 2019, 163, 450–471. [Google Scholar] [CrossRef]
- Coifman, R.; Donoho, D. Translation-invariant de-noising. Wavelets Stat. Lect. Notes Stat. 1995, 102, 125–150. [Google Scholar]
- Nason, G.; Silverman, B. The stationary wavelet transform and some statistical applications. Wavelets Stat. Lect. Notes Stat. 1995, 103, 281–300. [Google Scholar]
- Pesquet, J.C.; Krim, H.; Carfantan, H. Time-invariant orthonormal wavelet representations. IEEE Trans. Signal Proc. 1996, 44, 1964–1970. [Google Scholar] [CrossRef]
- Daubechies, I. Ten Lectures on Wavelet; Society for Industrial and Applied Mathematics Philadelphia: Philadelphia, PA, USA, 1992. [Google Scholar]
- Mallat, S. A Wavelet Tour of Signal Processing; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Rodriguez, N.; Lagos, C.; Cabrera, E.; Canete, L. Extreme learning machine based on stationary wavelet singular values for bearing failure diagnosis. Stud. Inf. Control 2017, 26, 287–294. [Google Scholar] [CrossRef]
- Huang, G.; Chen, L. Convex incremental extreme learning machine. Neurocomputing 2007, 70, 3056–3062. [Google Scholar] [CrossRef]
- Serre, D. Matrices: Theory and Applications; Springer: New York, NY, USA, 2002. [Google Scholar]
- Stone, M. Cross-Validatory Choice and Assessment of Statistical Predictions. J. R. Stat. Soc. Ser. B 1974, 36, 111–142. [Google Scholar] [CrossRef]
- Geisser, S. The predictive sample reuse method with applications. J. Am. Stat. Assoc. 1975, 70, 320–328. [Google Scholar] [CrossRef]
- Ferri, C.; Hernández-Orallo, J.; Modroiu, R. An experimental comparison of performance measures for classification. Pattern Recognit. Lett. 2009, 30, 27–38. [Google Scholar] [CrossRef]
- Sokolova, M.; Lapalme, G. A systematic analysis of performance measures for classification tasks. Inf. Proc. Manag. 2009, 45, 427–437. [Google Scholar] [CrossRef]

| Fault Types | Speed (r/min) | Load (hp) | Fault Diameter (mils) | Samples Numbers | Class Label | Class Label |
|---|---|---|---|---|---|---|
| NB | 1797-1730 | 0-3 | 0 | 200 | 1 | 1 |
| ORF | 1797-1730 | 0-3 | 7 | 200 | 2 | 2 |
| 14 | 200 | 3 | 3 | |||
| 21 | 200 | 4 | 4 | |||
| IRF | 1797-1730 | 0-3 | 7 | 200 | 5 | 5 |
| 14 | 200 | 6 | 6 | |||
| 21 | 200 | 7 | 7 | |||
| BF | 1797-1730 | 0-3 | 7 | 200 | 8 | 8 |
| 14 | 200 | 9 | 9 | |||
| 21 | 200 | 10 | 10 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodriguez, N.; Barba, L.; Alvarez, P.; Cabrera-Guerrero, G. Stationary Wavelet-Fourier Entropy and Kernel Extreme Learning for Bearing Multi-Fault Diagnosis. Entropy 2019, 21, 540. https://doi.org/10.3390/e21060540
Rodriguez N, Barba L, Alvarez P, Cabrera-Guerrero G. Stationary Wavelet-Fourier Entropy and Kernel Extreme Learning for Bearing Multi-Fault Diagnosis. Entropy. 2019; 21(6):540. https://doi.org/10.3390/e21060540
Chicago/Turabian StyleRodriguez, Nibaldo, Lida Barba, Pablo Alvarez, and Guillermo Cabrera-Guerrero. 2019. "Stationary Wavelet-Fourier Entropy and Kernel Extreme Learning for Bearing Multi-Fault Diagnosis" Entropy 21, no. 6: 540. https://doi.org/10.3390/e21060540
APA StyleRodriguez, N., Barba, L., Alvarez, P., & Cabrera-Guerrero, G. (2019). Stationary Wavelet-Fourier Entropy and Kernel Extreme Learning for Bearing Multi-Fault Diagnosis. Entropy, 21(6), 540. https://doi.org/10.3390/e21060540





