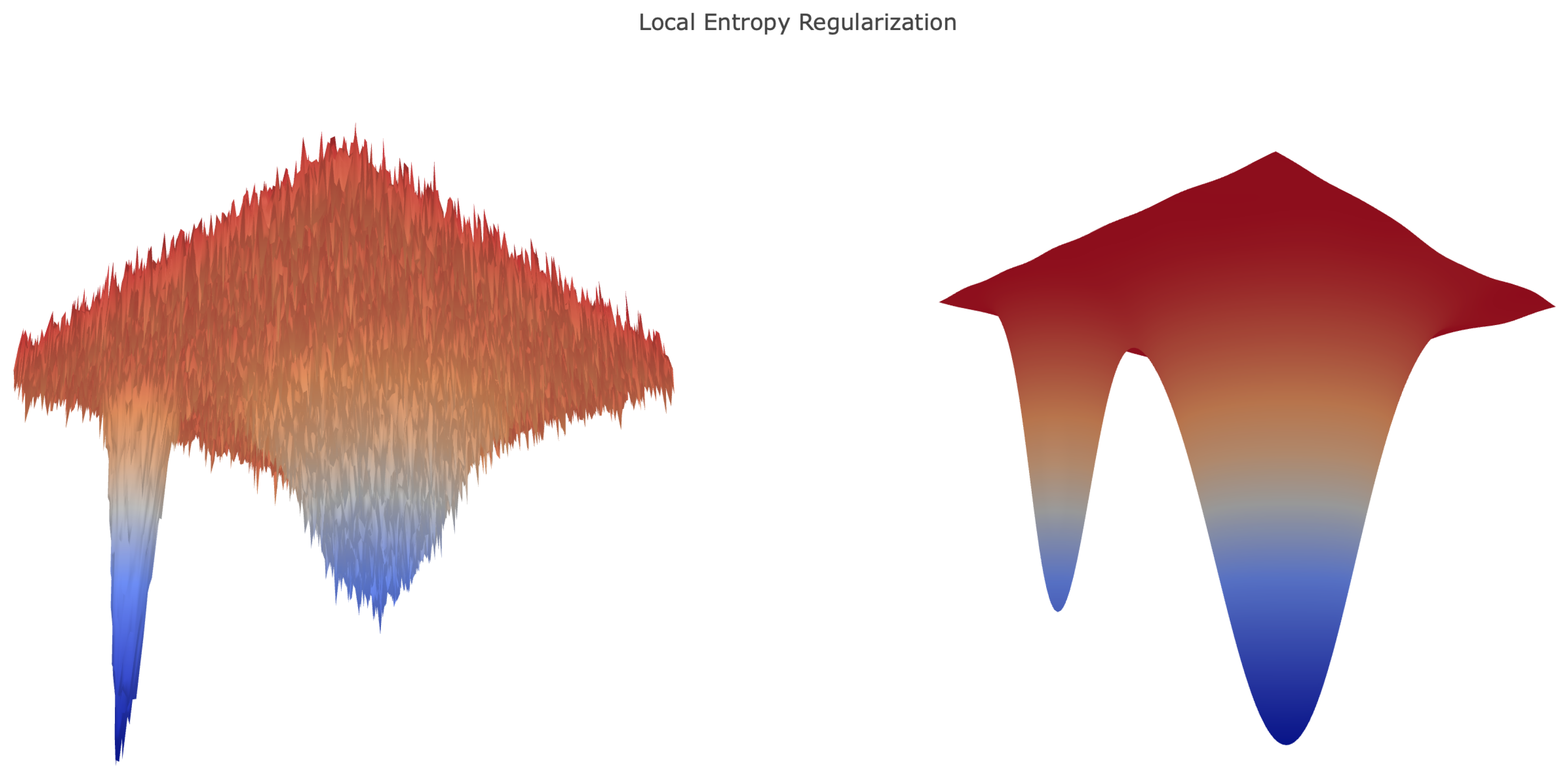
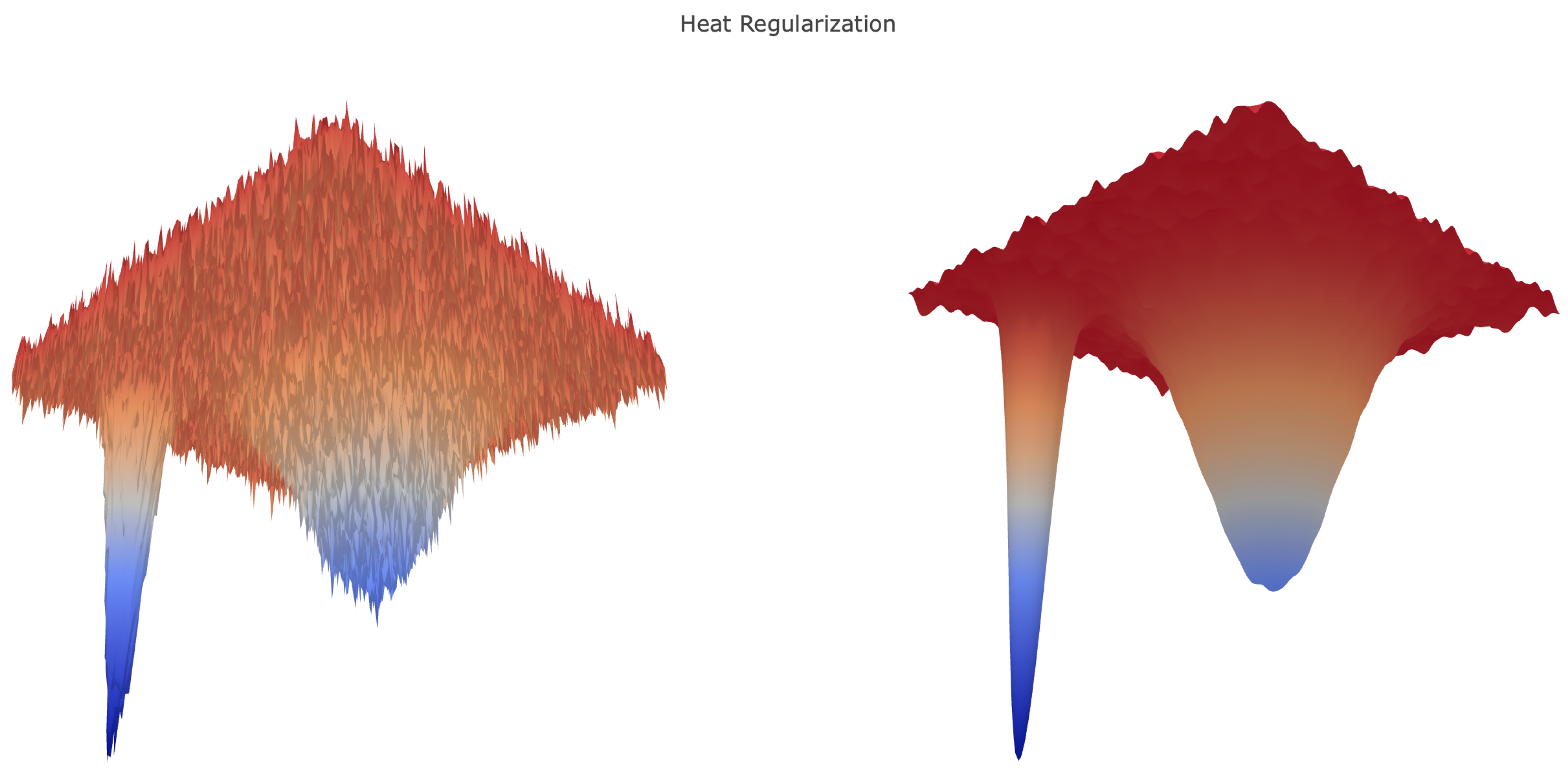
In the following numerical experiments, we investigated the practical use of local entropy and heat regularization in the training of neural networks. We present experiments on dense multilayered networks applied to a basic image classification task, viz. MNIST handwritten digit classification [
21]. Our choice of dataset is standard in machine learning and had been considered in previous work on loss regularizations for deep learning, e.g., [
4,
5]. We implemented Algorithms 3, 4, and 5 in TensorFlow, analyzing the effectiveness of each in comparison to stochastic gradient descent (SGD). We investigated whether the theoretical monotonicity of regularized losses translates into monotonicity of the held-out test data error. Additionally, we explored various choices for the hyperparameter
to illustrate the effects of variable levels of regularization. In accordance with the algorithms specified above, we employed importance sampling (IS) and stochastic gradient Langevin dynamics (SGLD) to approximate the expectation in (
15) and the Robbins–Monro algorithm for heat regularization (HR).
6.2. Training Neural Networks from Random Initialization
Considering the computational burden of computing a Monte Carlo estimate for each weight update, we proposed that Algorithms 3, 4, and 5 are potentially most useful when employed following SGD; although per-update progress is on par or exceeds that of SGD with step size, often called learning rate, equivalent to the value of , the computational load required makes the method unsuited for end-to-end training. Though in this section, we present an analysis of these algorithms used for the entirety of training, this approach is likely too expensive to be practical for contemporary deep networks.
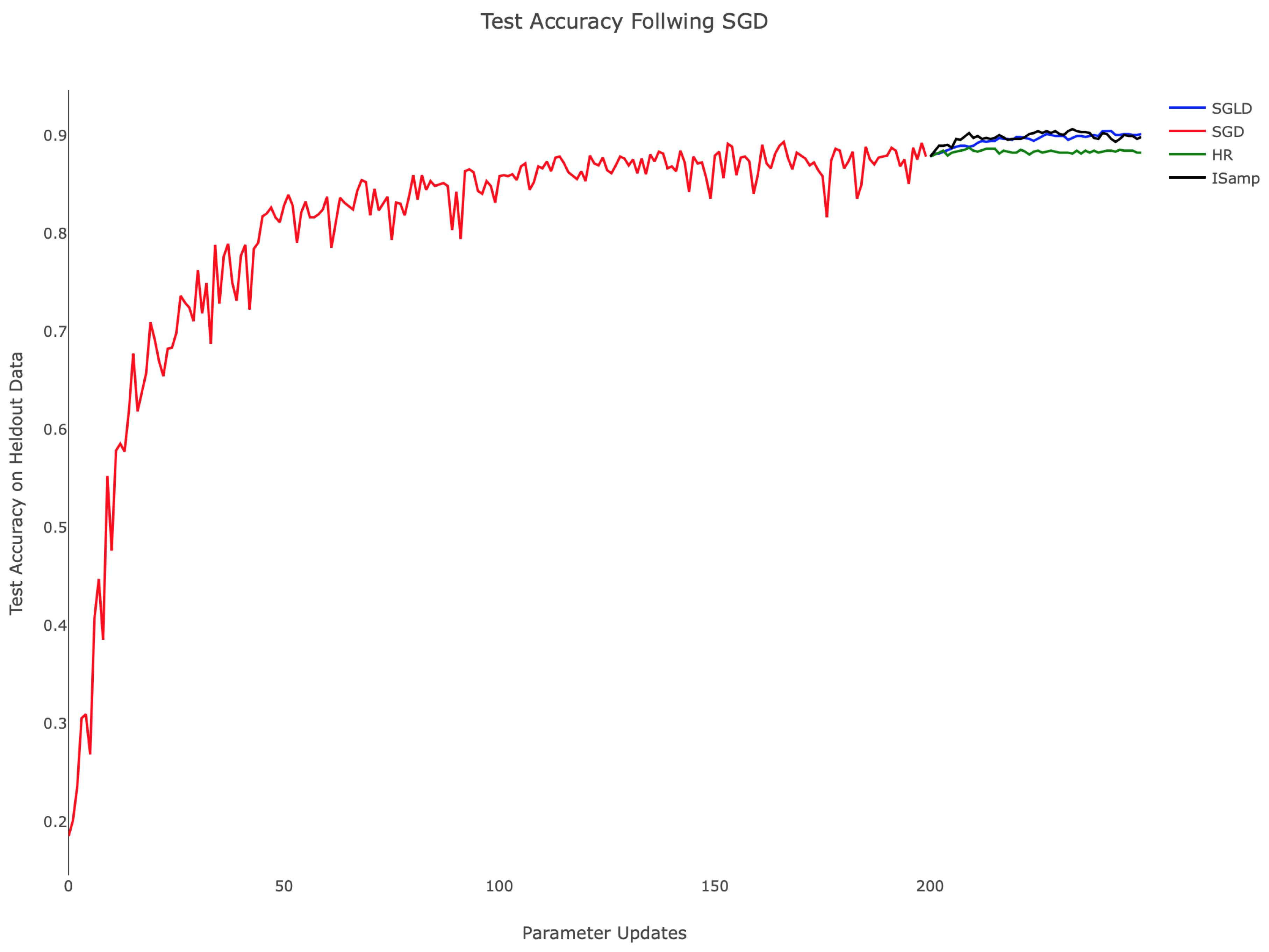
Table 1 and the associated
Figure 4 demonstrate the comparative training behavior for each algorithm, displaying the held-out test accuracy for identical instantiations of the hidden layer network trained with each algorithm for 500 parameter updates. Note that a minibatch size of 20 was used in each case to standardize the amount of training data available to the methods. Additionally, SGLD, IS, and HR each employed
, while SGD utilized an equivalent step size, thus fixing the level of regularization in training. To establish computational equivalence between Algorithms 3, 4, and 5, we computed
with
samples for Algorithms 3 and 4, setting
and performing 30 updates of the chain in Algorithm 5. Testing accuracy was computed by classifying 1000 randomly-selected images from the held-out MNIST test set. In related experiments, we observed consistent training progress across all three algorithms. In contrast, IS and HR trained more slowly, particularly during the parameter updates following initialization. From
Figure 4, we can appreciate that while SGD attempted to minimize training error, it nonetheless behaved in a stable way when plotting held-out accuracy, especially towards the end of training. SGLD on the other hand was observed to be more stable throughout the whole training, with few drops in accuracy along the sequence of optimization iterates.
While SGD, SGLD, and HR utilize gradient information in performing parameter updates, IS does not. This difference in approach contributes to IS’s comparatively poor start; as the other methods advance quickly due to the large gradient of the loss landscape, IS’s progress was isolated, leading to training that depended only on the choice of
. When
was held constant, as shown in
Figure 4, the rate of improvement remained nearly constant throughout. This suggests the need for dynamically updating
, as is commonly performed with annealed learning rates for SGD. Moreover, SGD, SGLD, and HR are all schemes that depend linearly on
f, making minibatching justifiable, something, which is not true for IS.
It is worth noting that the time to train differed drastically between methods.
Table 2 shows the average runtime of each algorithm in seconds. SGD performed roughly
-times faster than the others, an expected result considering the most costly operation in training, filling the network weights, was performed
-times per parameter update. Other factors contributing to the runtime discrepancy are the implementation specifications and the deep learning library; here, we used TensorFlow’s implementation of SGD, a method for which the framework is optimized. More generally, the runtimes in
Table 2 reflected the hyperparameter choices for the number of Monte Carlo samples and will vary according to the number of samples considered.
6.3. Local Entropy Regularization after SGD
Considering the longer runtime of the sampling-based algorithms in comparison to SGD, it is appealing to utilize SGD to train networks initially, then shift to more computationally-intensive methods to identify local minima with favorable generalization properties.
Figure 5 illustrates IS and SGLD performing better than HR when applied after SGD. HR’s smooths the loss landscape, a transformation that is advantageous for generating large steps early in training, but presents challenges as smaller features are lost. In
Figure 5, this effect manifests as constant test accuracy after SGD, and no additional progress is made. The contrast between each method is notable since the algorithms used equivalent step sizes; this suggests that the methods, not the hyperparameter choices, dictate the behavior observed.
Presumably, SGD trains the network into a sharp local minima or saddle point of the non-regularized loss landscape; transitioning to an algorithm that minimizes the local entropy regularized loss, then finds an extremum, which performs better on the test data. However, based on our experiments, in terms of held-out data accuracy, regularization in the later stages does not seem to provide significant improvement over training with SGD on the original loss.
6.4. Algorithm Stability and Monotonicity
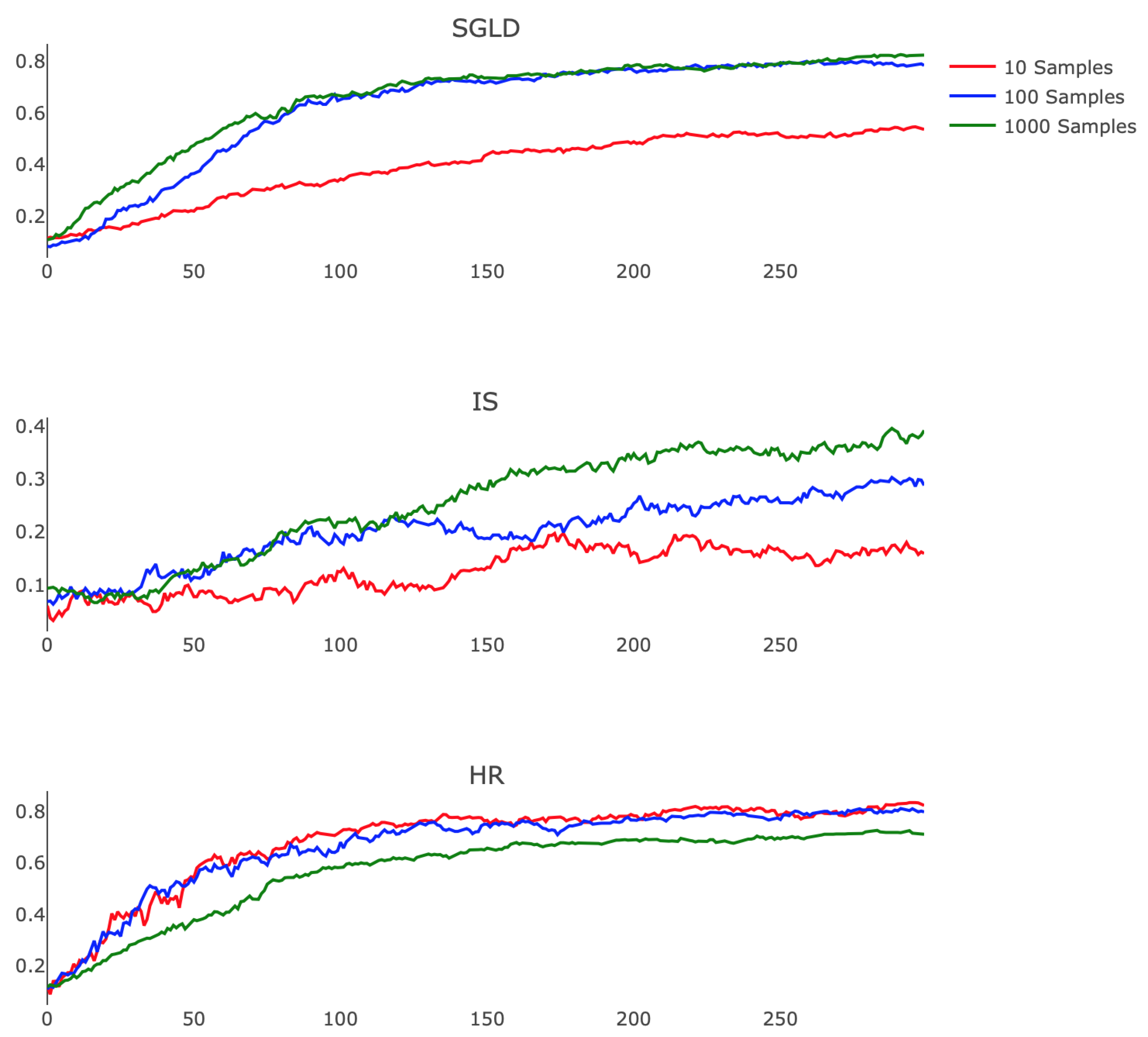
Prompted by the guarantees of Theorems 2 and 4, which prove the effectiveness of these methods when is approximated accurately, we also demonstrated the stability of these algorithms in the case of an inaccurate estimate of the expectation. To do so, we explored the empirical consequences of varying the number of samples used in the Monte Carlo and Robbins–Monro calculations.
Figure 6 shows how each algorithm responds to this change. We observe that IS performed better as we refined our estimate of
, exhibiting less noise and faster training rates. This finding suggests that a highly parallel implementation of IS, which leverages the modern GPU architecture to efficiently compute the relevant expectation, may offer practicality. SGLD also benefits from a more accurate approximation, displaying faster convergence and higher final testing accuracy when comparing 10 and 100 Monte Carlo samples. HR however performs more poorly when we employ longer Robbins–Monro chains, suffering from diminished step size and exchanging quickly realized progress for less oscillatory testing accuracy. Exploration of the choices of
and
for SGLD and HR remains a valuable avenue for future research, specifically in regards to the interplay between these hyperparameters and the variable accuracy of estimating
.
6.5. Choosing
An additional consideration of these schemes is the choice of
, the hyperparameter that dictates the level of regularization in Algorithms 3, 4, and 5. As noted in [
5], large values of
correspond to a nearly uniform local entropy regularized loss, whereas small values of
yield a minimally regularized loss, which is very similar to the original loss function. To explore the effects of small and large values of
, we trained our smaller network with IS and SGLD for many choices of
, observing how regularization alters training rates.
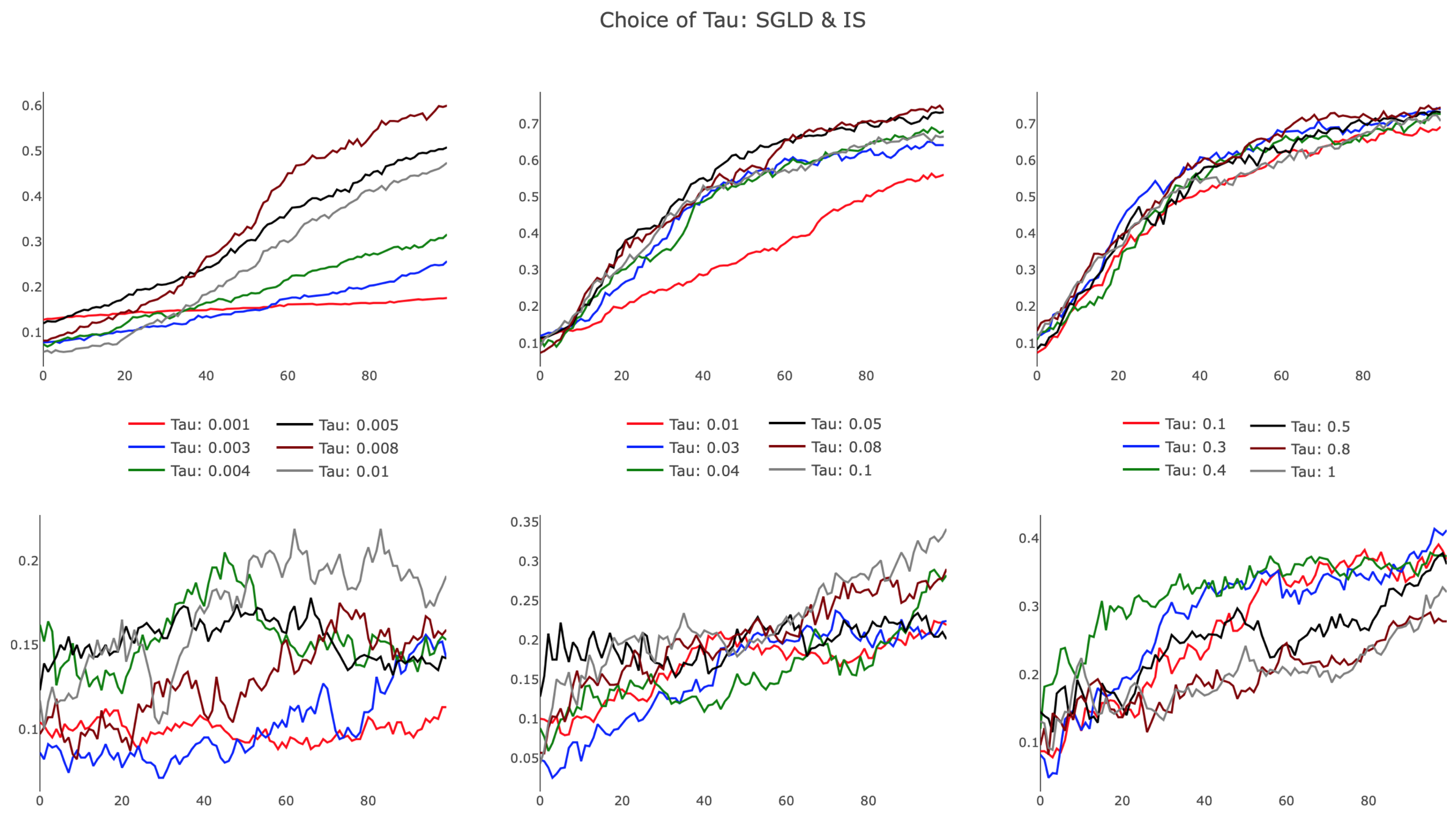
The results, presented in
Figure 7, illustrate differences in SGLD and IS, particularly in the small
regime. As evidenced in the leftmost plots, SGLD trained successfully, albeit slowly, with
. For small values of
, the held-out test accuracy improved almost linearly over parameter updates, appearing characteristically similar to SGD with a small learning rate. IS failed for small
, with highly variant test accuracy improving only slightly during training. Increasing
, we observed SGLD reach a point of saturation, as additional increases in
did not affect the training trajectory. We note that this behavior persisted as
, recognizing that the regularization term in the SGLD algorithm approached a value of zero for growing
. IS demonstrated improved training efficiency in the bottom-center panel, showing that increased
provided favorable algorithmic improvements. This trend dissipated for larger
, with IS performing poorly as
. The observed behavior suggests there exists an optimal
that is architecture and task specific, opening opportunities to further develop a heuristic to tune the hyperparameter.
As suggested in [
5], we investigated annealing the scope of
from large to small values in order to examine the landscape of the loss function at different scales. Early in training, we used comparatively large values to ensure broad exploration, transitioning to smaller values for a comprehensive survey of the landscape surrounding a minima. We used the following schedule for the
kth parameter update:
where
is large and
is set so that the magnitude of the local entropy gradient is roughly equivalent to that of SGD.
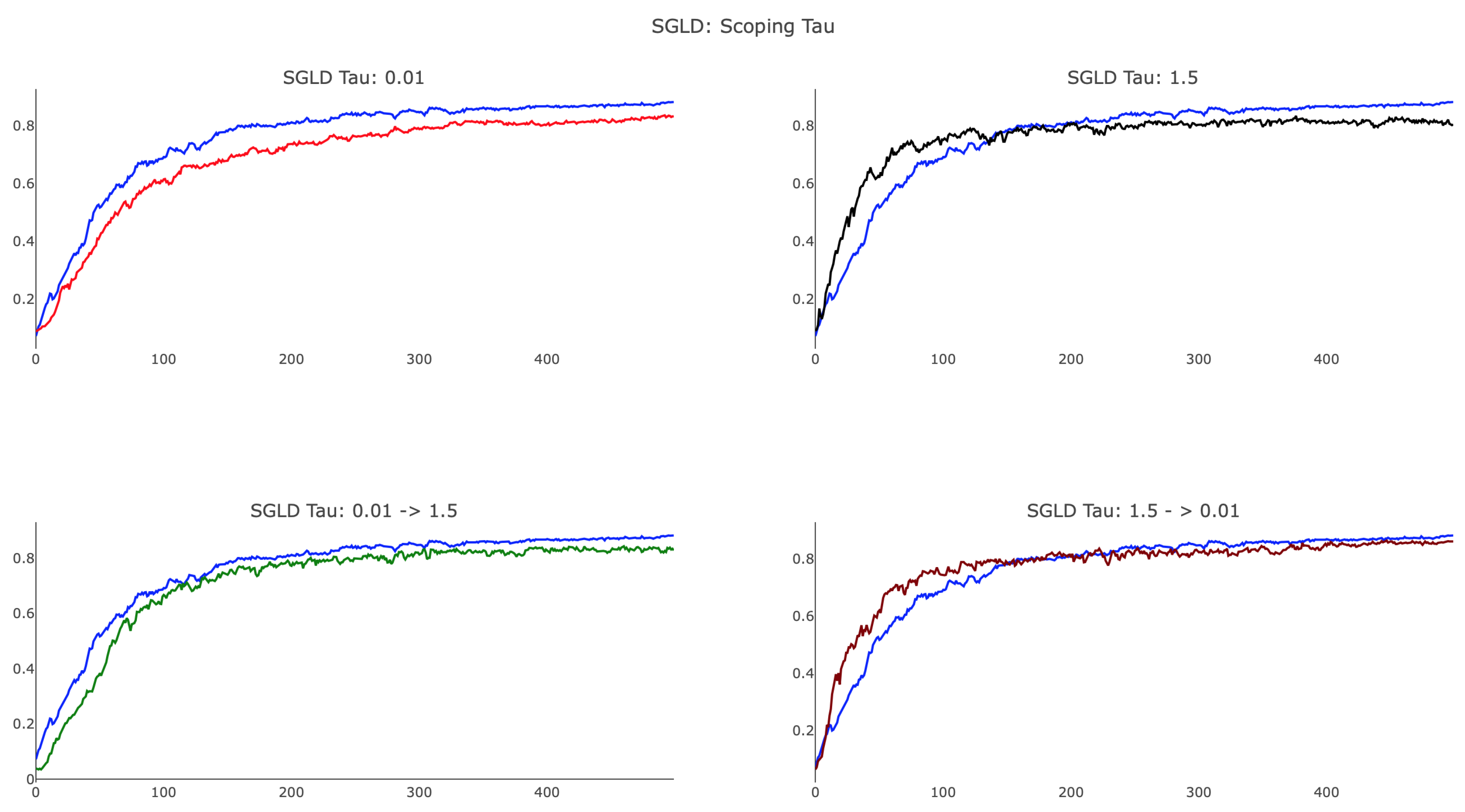
As shown in
Figure 8, annealing
proved to be useful and provided a method by which training can focus on more localized features to improve test accuracy. We observed that SGLD, with a smaller value of
, achieved a final test accuracy close to that of SGD, whereas
was unable to identify the optimal minima. Additionally, the plot shows that large
SGLD trained faster than SGD in the initial 100 parameter updates, whereas small
SGLD lagged behind. When scoping
, we considered both annealing and reverse-annealing, illustrating that increasing
over training produced a network that trained more slowly than SGD and was unable to achieve testing accuracy comparable to that of SGD. Scoping
from
via the schedule (
18) with
and
delivered advantageous results, yielding an algorithm that trains faster than SGD after initialization and achieved analogous testing accuracy. We remark that, while the preceding figures offer some insight into the various behaviors associated with difference choices of
, a considerable amount of detail regarding proper dynamic tuning of the hyperparameter remains unknown, specifying an additional open research question. At the current stage, our recommendation for choosing
would be to use cross-validation over several scoping schedules.