Optimal Microbiome Networks: Macroecology and Criticality
Abstract
1. Introduction
1.1. Microbiome Dynamics and Health
1.2. Microbiome Diversity and Functional Network Organization
1.3. Microbiome Inference, Neutrality and Criticality
2. Material and Methods
2.1. Microbiome Data
2.2. Time Series Reconstruction
2.3. Probabilistic Characterization of the Microbiome
2.4. Network Inference and Dynamical Species Characterization
2.4.1. Information Balance and Exchange
2.4.2. Maximum Entropy Networks
2.4.3. Optimal Information Networks
2.4.4. Assessment of Species Importance and Collectivity
2.5. Macroecological Indicators
2.6. Functional and Structural Network Metrics
3. Results
4. Discussion
5. Conclusions
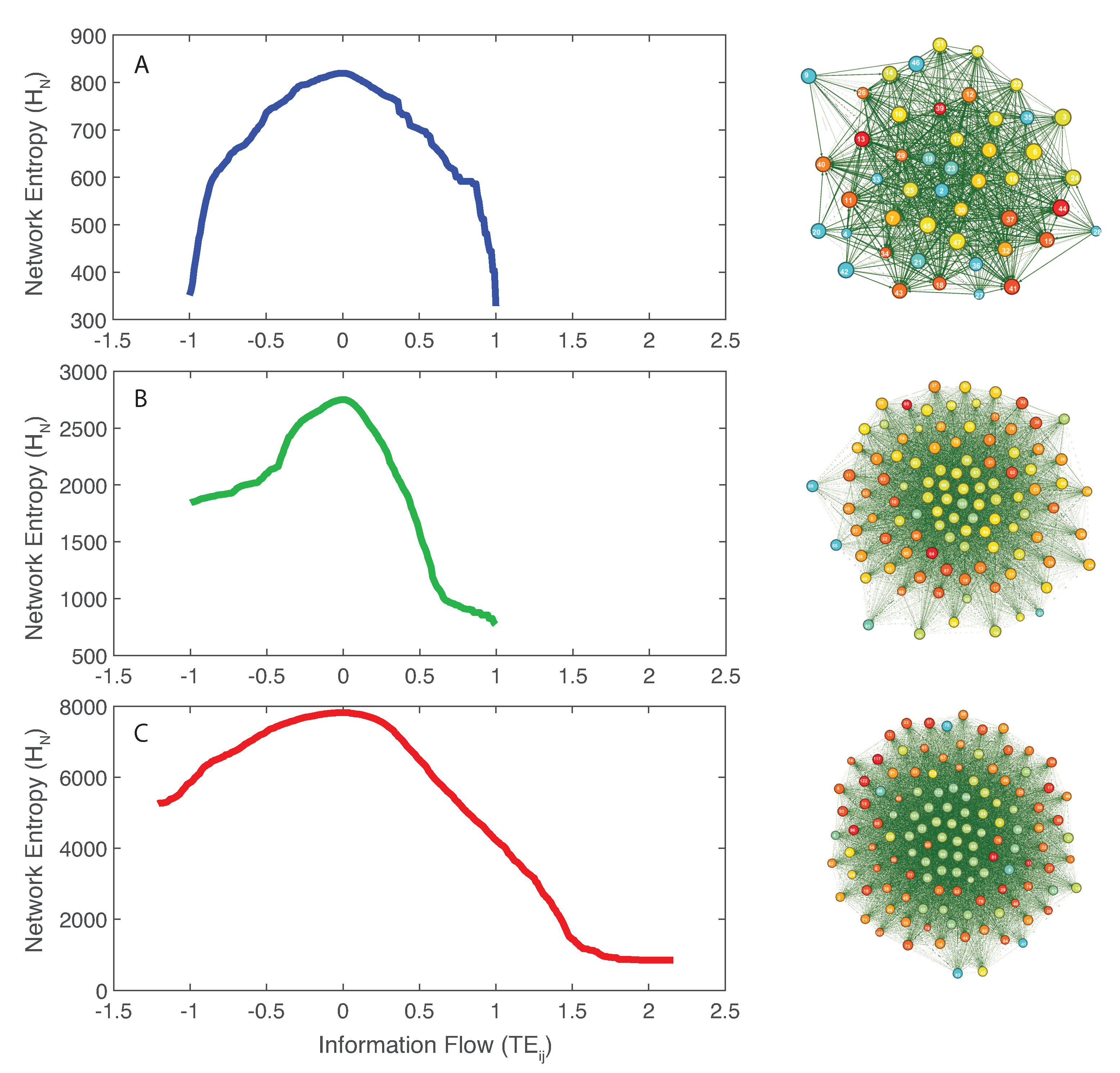
- Directed species interdependencies and phase transitions of the microbiome over time were detected. The healthy microbiome is characterized by balanced positive and negative species interactions vs. the unhealthy microbiome where most species interactions are positive. The balanced interactions were evidenced by the symmetrical pattern of the total network entropy as a function of the pairwise information flow (TE) vs. the positively biased asymmetrical pattern of the dysbiotic microbiome. The healthy symmetrical network entropy pattern underlines the neutral “sum to zero” dynamics of species interactions (based on RSA); the same neutrality was found for biodiversity of large scale ecosystems at stationarity that are driven predominantly by intrinsic ecological stochasticity (ecological drift). On the contrary, unhealthy microbiome entropic patterns are affected by environmental disturbances; the positive bias in information flow (that may relate to infections and antibiotics, as shown in the original data [51]) causes an overgrowth in RSA of many opportunistic species as well as the generation of new detrimental species. The categorization of beneficial and detrimental species was based on published literature; however, we emphasize how important it is to consider collective bacteria topology vs. individual bacteria behavior when defining health and disease;
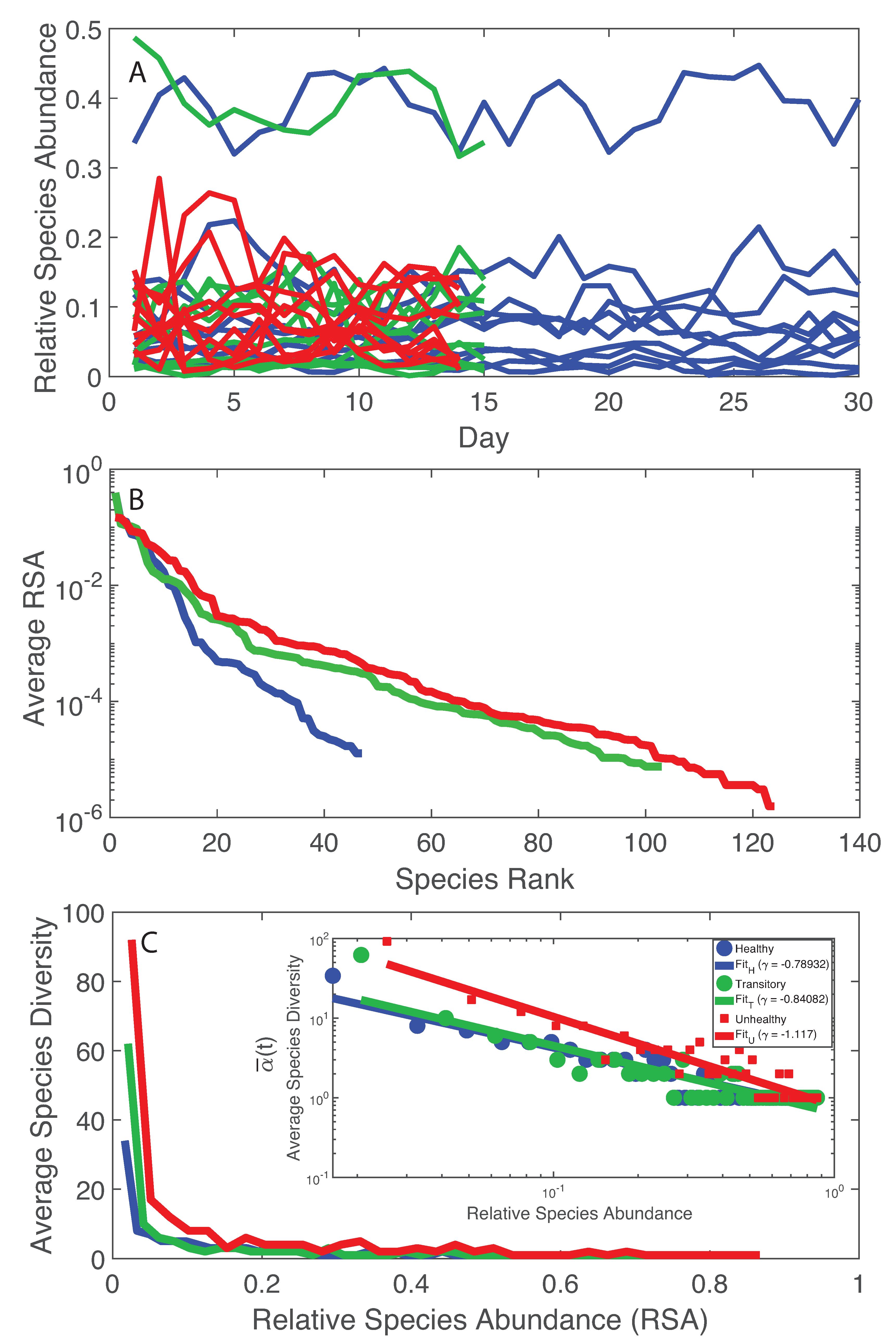
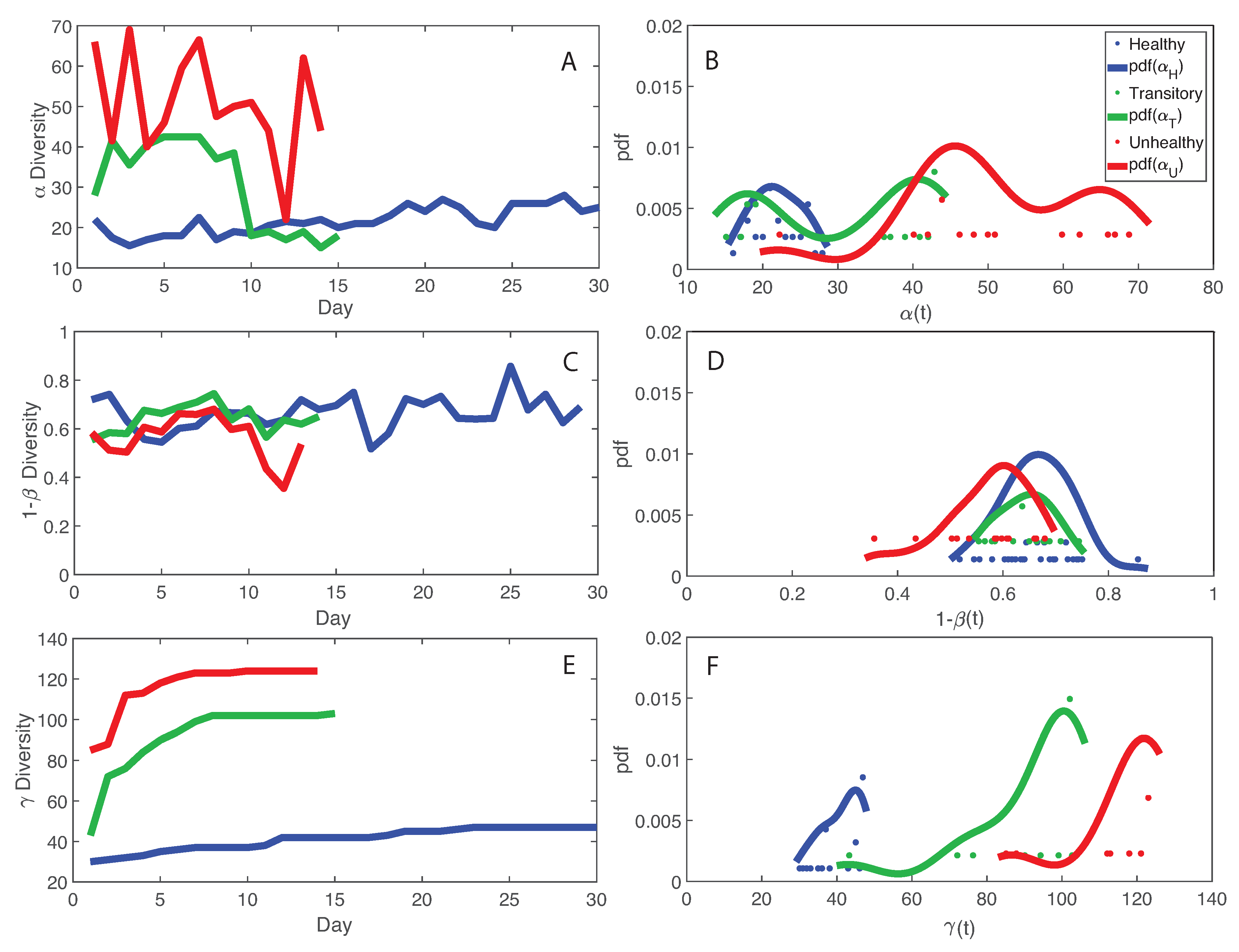
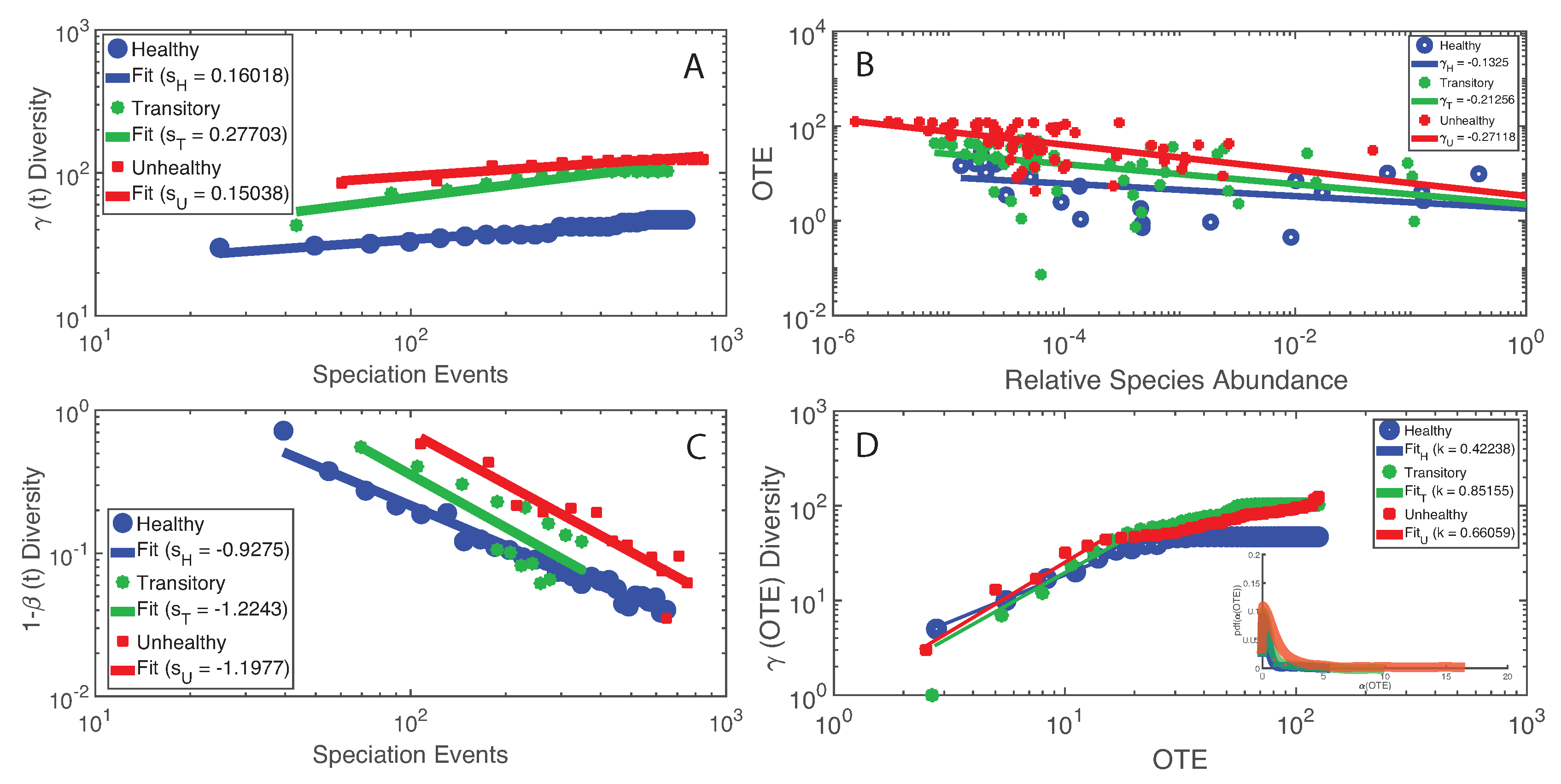
- The healthy state is characterized by the highest total species diversity growth rate (leaving aside the transitory microbiome) and the lowest loss of species similarity over time, i.e., species turnover (). A relationship similar to the species–area relationship for large scale ecosystems [70] was found between -diversity and the number of species generations with an exponent equal to on average. The fact that the healthy microbiome has the lowest average total diversity () is in contrast to what is observed in large-scale ecosystems at stationarity where the highest total diversity correspond to the stable and supposedly healthy state [78]. However, we speculate that an optimal diversity growth is oriented toward maximizing growth rate rather than total diversity (as according to many Pareto portfolio theories). The latter can lead to over-redundancy of microbial interactions and instability as observed for the dysbiotic microbiome; the highest diversity for unhealthy ecosystems is related to non-endemic species. Hence, we tend to challenge the diversity–health–stability hypothesis when for diversity the total systemic diversity is solely considered without the consideration of “invasive” species and ;
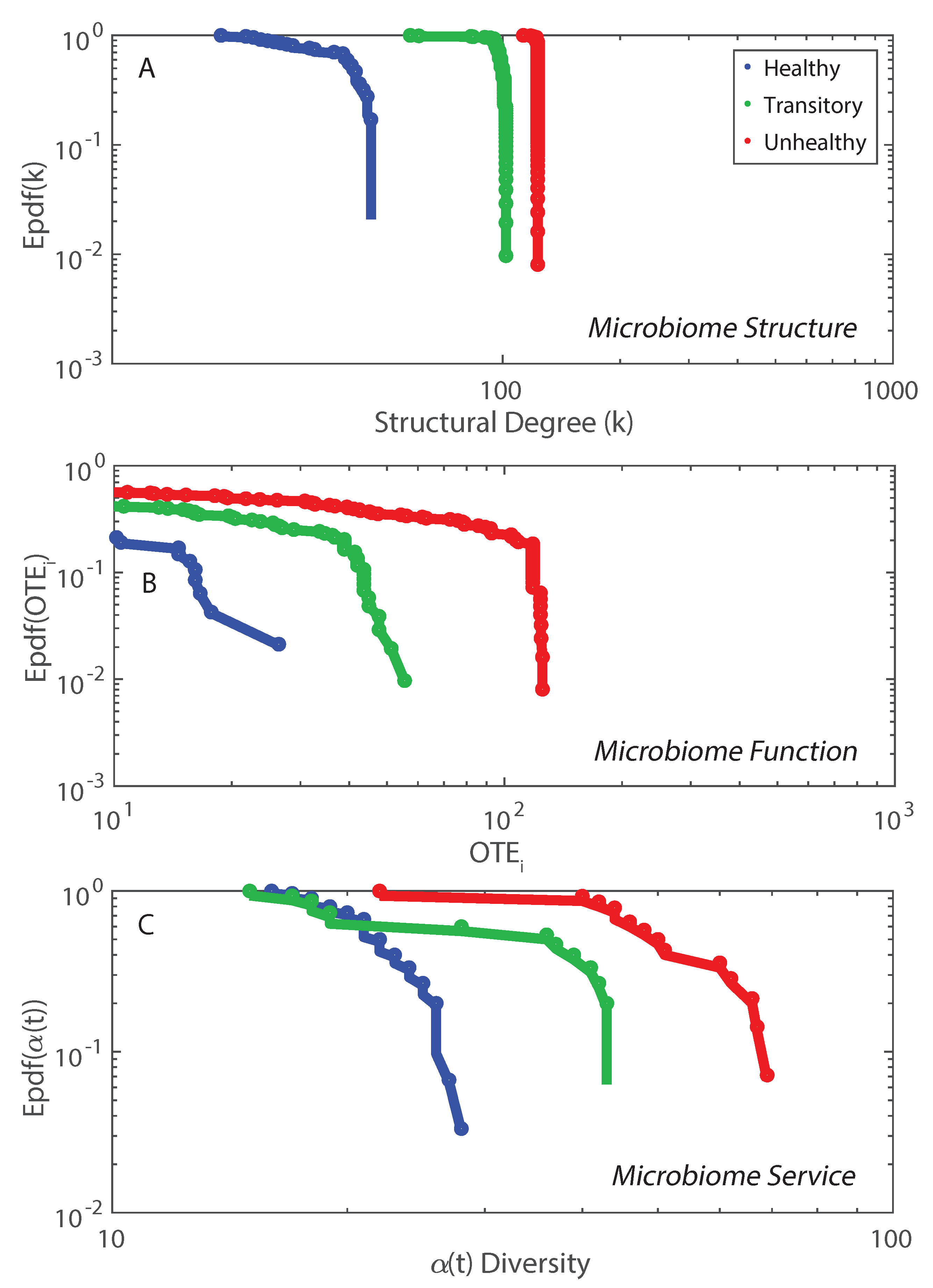
- We observed a phase transition of the second order from the healthy to the unhealthy state and vice versa. The transition from healthy to unhealthy is characterized by typical signs of transitions observed in many complex systems [107], i.e., an increase and a decrease in mean and variance of species diversity while approaching the transition (“critical slowing down”). In the unhealthy state the variance of is higher than in the healthy state and concentrated around two values which underline the likely chaotic-like dynamics of the microbiome. In terms of microbiome functional network topology, a transition between the scale-free to the random network topology is observed. The critical state, defined by a scale-free-like organization of microbial species interactions, coincides with the neutral state (i.e., for the symmetrical network entropy pattern) emphasizing how criticality does not necessarily occur at critical phase transitions, particularly for second-order transitions as in this case. Rather, criticality can coincide with neutrality in open energy dissipative systems, as observed in other complex systems [20]. Criticality at the phase transition can favor gut adaptability but may pose high risks to tip to unhealthy states. Neutrality implies lower topological complexity and higher dynamical stability (corresponding to higher symmetry, higher organized information exchange, lower entropy/total information, higher diversity, and higher predictability (or information content)) considering the scale-free and small-world functional and structural organization of the microbial network. We emphasize how the healthy local stable state is dynamically flexible because of the lower entropy (i.e., higher free energy) and more predictable due to the more organized collective behavior of species; however, due to the gradient in entropy moving from locally stable unhealthy conditions to the globally healthy stable one is hard;
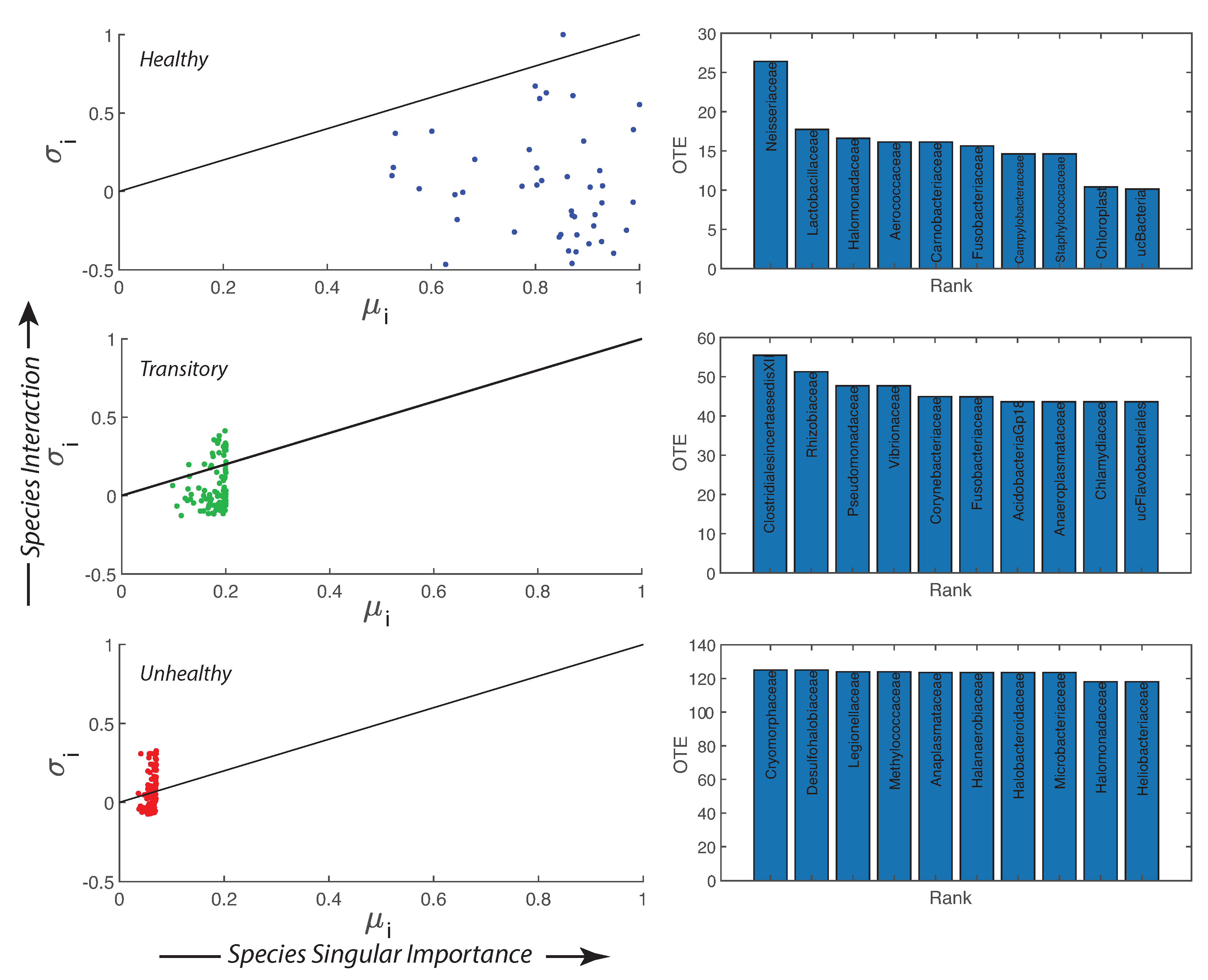
- A probabilistic linkage was found between microbiome function and services, defined by species interaction topology and biodiversity organization, respectively. We did not find any correspondence between microbiome structure and function, which emphasizes the non-linearity between the two and the importance of assessing function rather than structure in biological networks. We propose the total Outgoing Transfer Entropy (OTE) as the measure to identify the most influential nodes (and pairs); these nodes are able to predict the behavior of all other connected nodes, as well as of the whole microbiome. OTE is largely determining the total entropy of the network compared to the sum of nodal entropies whose contribution is negligible. This emphasizes even more the role of collective behavior vs. individual nodes considered in isolation. The highest OTE nodes have the lowest RSA, and these are the most beneficial and the most detrimental bacteria for the dysbiotic and healthy microbiome. A scaling law was found between OTE and RSA with an exponent close to that is similar to the mass-specific Kleiber’s law [81] where the species specific metabolic rate is the OTE and the mass is the RSA. A power-law distribution for the microbiome function (i.e., the sum of nodal OTE) was found for the healthy state (with an exponent ∼2 that implies finite mean but infinite variance suggesting how the healthy condition is prone to perturbations enhancing fluctuations of all sizes) despite no information (or resolution) invariance being detected in the network entropy pattern (see Servadio and Convertino [13]). The lack of scale invariance in the entropy/free-energy phase space may imply the metastability of the microbiome that can indicate its resilience in terms of ability to move quickly from one state to another.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| IBS | Irritable Bowel Syndrome |
| RSA | Relative Species Abundance |
| local time point species diversity | |
| intertemporal species diversity | |
| total species diversity | |
| JSI | Jaccard Similarity Index |
| TE | Transfer Entropy |
| TEI | Transfer Entropy Indices |
| OTE | Outgoing Transfer Entropy |
| ITE | Incoming Transfer Entropy |
| MaxEnt | Maximum Entropy |
| MENets | Maximum Entropy Networks |
| OIN | Optimal Information Network |
References
- Blaser, M.J.; Cardon, Z.G.; Cho, M.K.; Dangl, J.L.; Donohue, T.J.; Green, J.L.; Knight, R.; Maxon, M.E.; Northen, T.R.; Pollard, K.S.; et al. Toward a predictive understanding of Earth’s microbiomes to address 21st century challenges. Am. Soc. Microbiol. 2016. [Google Scholar] [CrossRef] [PubMed]
- Thompson, L.R.; Sanders, J.G.; McDonald, D.; Amir, A.; Ladau, J.; Locey, K.J.; Prill, R.J.; Tripathi, A.; Gibbons, S.M.; Ackermann, G.; et al. A communal catalogue reveals Earth’s multiscale microbial diversity. Nature 2017, 551, 457. [Google Scholar] [CrossRef]
- Coyte, K.Z.; Schluter, J.; Foster, K.R. The ecology of the microbiome: Networks, competition, and stability. Science 2015, 350, 663–666. [Google Scholar] [CrossRef] [PubMed]
- Van de Guchte, M.; Blottière, H.M.; Doré, J. Humans as holobionts: Implications for prevention and therapy. Microbiome 2018, 6, 81. [Google Scholar] [CrossRef] [PubMed]
- Arumugam, M.; Raes, J.; Pelletier, E.; Le Paslier, D.; Yamada, T.; Mende, D.R.; Fernandes, G.R.; Tap, J.; Bruls, T.; Batto, J.M.; et al. Enterotypes of the human gut microbiome. Nature 2011, 473, 174–180. [Google Scholar] [CrossRef] [PubMed]
- Knights, D.; Ward, T.L.; McKinlay, C.E.; Miller, H.; Gonzalez, A.; McDonald, D.; Knight, R. Rethinking “Enterotypes”. Cell Host Microbe 2014, 16, 433–437. [Google Scholar] [CrossRef] [PubMed]
- Caesar, R.; Tremaroli, V.; Kovatcheva-Datchary, P.; Cani, P.D.; Backhed, F. Crosstalk between Gut Microbiota and Dietary Lipids Aggravates WAT Inflammation through TLR Signaling. Cell Metab. 2015, 22, 658–668. [Google Scholar] [CrossRef] [PubMed]
- Martí, J.M.; Martínez-Martínez, D.; Rubio, T.; Gracia, C.; Peña, M.; Latorre, A.; Moya, A.; Garay, C.P. Health and Disease Imprinted in the Time Variability of the Human Microbiome. Am. Soc. Microbiol. 2017, 2. [Google Scholar] [CrossRef]
- Sitkin, S.; Vakhitov, T.; Demyanova, E. Microbiome, gut dysbiosis and inflammatory bowel disease: That moment when the function is more important than taxonomy. Alm. Clin. Med. 2018, 46, 396–425. [Google Scholar] [CrossRef]
- Lezon, T.R.; Banavar, J.R.; Cieplak, M.; Maritan, A.; Fedoroff, N.V. Using the principle of entropy maximization to infer genetic interaction networks from gene expression patterns. Proc. Natl. Acad. Sci. USA 2006, 103, 19033–19038. [Google Scholar] [CrossRef]
- Marsili, M.; Mastromatteo, I.; Roudi, Y. On sampling and modeling complex systems. J. Stat. Mech. Theory Exp. 2013, 2013. [Google Scholar] [CrossRef]
- Gresele, L.; Marsili, M. On Maximum Entropy and Inference. Entropy 2017, 19, 642. [Google Scholar] [CrossRef]
- Servadio, J.L.; Convertino, M. Optimal information networks: Application for data-driven integrated health in populations. Sci. Adv. 2018, 4. [Google Scholar] [CrossRef] [PubMed]
- Layeghifard, M.; Hwang, D.M.; Guttman, D.S. Disentangling Interactions in the Microbiome: A Network Perspective. Trends Microbiol. 2017, 25, 217–228. [Google Scholar] [CrossRef]
- Lizier, J.T.; Prokopenko, M. Differentiating information transfer and causal effect. Eur. Phys. J. B 2010, 73, 605–615. [Google Scholar] [CrossRef]
- Boschetti, F. Models and people: An alternative view of the emergent properties of computational models. Complexity 2015. [Google Scholar] [CrossRef]
- Zillio, T.; Banavar, J.; Green, J.; Harte, J.; Maritan, A. Incipient criticality in ecological communities. Proc. Natl. Acad. Sci. USA 2008, 105, 18714–18717. [Google Scholar] [CrossRef]
- Convertino, M. Neutral metacommunity clustering and SAR: River basin vs. 2-D landscape biodiversity patterns. Ecol. Model. 2011, 222, 1863–1879. [Google Scholar] [CrossRef]
- Azaele, S.; Suweis, S.; Grilli, J.; Volkov, I.; Banavar, J.R.; Maritan, A. Statistical mechanics of ecological systems: Neutral theory and beyond. Rev. Mod. Phys. 2016, 88, 035003. [Google Scholar] [CrossRef]
- Martinello, M.; Hidalgo, J.; Maritan, A.; di Santo, S.; Plenz, D.; Muñoz, M.A. Neutral Theory and Scale-Free Neural Dynamics. Phys. Rev. X 2017, 7, 041071. [Google Scholar] [CrossRef]
- Ofiţeru, I.D.; Lunn, M.; Curtis, T.P.; Wells, G.F.; Criddle, C.S.; Francis, C.A.; Sloan, W.T. Combined niche and neutral effects in a microbial wastewater treatment community. Proc. Natl. Acad. Sci. USA 2010, 107, 15345–15350. [Google Scholar] [CrossRef]
- Jeraldo, P.; Sipos, M.; Chia, N.; Brulc, J.M.; Dhillon, A.S.; Konkel, M.E.; Larson, C.L.; Nelson, K.E.; Qu, A.; Schook, L.B.; et al. Quantification of the relative roles of niche and neutral processes in structuring gastrointestinal microbiomes. Proc. Natl. Acad. Sci. USA 2012, 109, 9692–9698. [Google Scholar] [CrossRef]
- Levy, R.; Borenstein, E. Metabolic modeling of species interaction in the human microbiome elucidates community-level assembly rules. Proc. Natl. Acad. Sci. USA 2013, 110, 12804–12809. [Google Scholar] [CrossRef]
- Shafquat, A.; Joice, R.; Simmons, S.L.; Huttenhower, C. Functional and phylogenetic assembly of microbial communities in the human microbiome. Trends Microbiol. 2014, 22, 261–266. [Google Scholar] [CrossRef]
- Quinn, R.A.; Comstock, W.; Zhang, T.; Morton, J.T.; da Silva, R.; Tran, A.; Aksenov, A.; Nothias, L.F.; Wangpraseurt, D.; Melnik, A.V.; et al. Niche partitioning of a pathogenic microbiome driven by chemical gradients. Sci. Adv. 2018, 4, eaau1908. [Google Scholar] [CrossRef]
- Stein, R.R.; Bucci, V.; Toussaint, N.C.; Buffie, C.G.; Rätsch, G.; Pamer, E.G.; Sander, C.; Xavier, J.B. Ecological modeling from time-series inference: Insight into dynamics and stability of intestinal microbiota. PLoS Comput. Biol. 2013, 9, e1003388. [Google Scholar] [CrossRef]
- Convertino, M.; Bockelie, A.; Kiker, G.A.; Muñoz-Carpena, R.; Linkov, I. Shorebird patches as fingerprints of fractal coastline fluctuations due to climate change. Ecol. Process. 2012, 1. [Google Scholar] [CrossRef]
- Lahti, L.; Salojärvi, J.; Salonen, A.; Scheffer, M.; de Vos, W.M. Tipping elements in the human intestinal ecosystem. Nat. Commun. 2014, 5, 4344. [Google Scholar] [CrossRef]
- Ma, Z.S. Power law analysis of the human microbiome. Mol. Ecol. 2015, 24, 5428–5445. [Google Scholar] [CrossRef]
- Gentile, C.L.; Weir, T.L. The gut microbiota at the intersection of diet and human health. Science 2018, 362, 776–780. [Google Scholar] [CrossRef]
- Gonze, D.; Coyte, K.Z.; Lahti, L.; Faust, K. Microbial communities as dynamical systems. Curr. Opin. Microbiol. 2018, 44, 41–49. [Google Scholar] [CrossRef]
- Bauchinger, F. Self-organized Criticality in the Gut Microbiome. Master’s Thesis, University of Vienna, Wien, Austria, 2015. [Google Scholar]
- Hidalgo, J.; Grilli, J.; Suweis, S.; Muñoz, M.A.; Banavar, J.R.; Maritan, A. Information-based fitness and the emergence of criticality in living systems. Proc. Natl. Acad. Sci. USA 2014, 111, 10095–10100. [Google Scholar] [CrossRef]
- Li, X.; Small, M. Neuronal avalanches of a self-organized neural network with active-neuron-dominant structure. Chaos Interdiscip. J. Nonlinear Sci. 2012, 22, 023104. [Google Scholar] [CrossRef]
- Poil, S.S.; Hardstone, R.; Mansvelder, H.D.; Linkenkaer-Hansen, K. Critical-state dynamics of avalanches and oscillations jointly emerge from balanced excitation/inhibition in neuronal networks. J. Neurosci. 2012, 32, 9817–9823. [Google Scholar] [CrossRef]
- Banavar, J.R.; Colaiori, F.; Flammini, A.; Maritan, A.; Rinaldo, A. Scaling, Optimality, and Landscape Evolution. J. Stat. Phys. 2001, 104, 1–48. [Google Scholar] [CrossRef]
- Convertino, M.; Muneepeerakul, R.; Azaele, S.; Bertuzzo, E.; Rinaldo, A.; Rodriguez-Iturbe, I. On neutral metacommunity patterns of river basins at different scales of aggregation. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Fisher, C.K.; Mehta, P. The transition between the niche and neutral regimes in ecology. Proc. Natl. Acad. Sci. USA 2014, 111, 13111–13116. [Google Scholar] [CrossRef]
- Convertino, M.; Muñoz-Carpena, R.; Kiker, G.; Perz, S. Design of optimal ecosystem monitoring networks: Hotspot detection and biodiversity patterns. Stoch. Environ. Res. Risk Assess. 2015, 29, 1085–1101. [Google Scholar] [CrossRef]
- Convertino, M.; Liu, Y.; Hwang, H. Optimal surveillance network design: A value of information model. Complex Adapt. Syst. Model. 2014, 2, 6. [Google Scholar] [CrossRef]
- Sugihara, G.; May, R.; Ye, H.; Hsieh, C.; Deyle, E.; Fogarty, M.; Munch, S. Detecting Causality in Complex Ecosystems. Science 2012, 338, 496–500. [Google Scholar] [CrossRef]
- Baldassano, S.N.; Bassett, D.S. Topological distortion and reorganized modular structure of gut microbial co-occurrence networks in inflammatory bowel disease. Sci. Rep. 2016, 6, 26087. [Google Scholar] [CrossRef]
- Grimm, V.; Revilla, E.; Berger, U.; Jeltsch, F.; Mooij, W.M.; Railsback, S.F.; Thulke, H.H.; Weiner, J.; Wiegand, T.; DeAngelis, D.L. Pattern-Oriented Modeling of Agent-Based Complex Systems: Lessons from Ecology. Science 2005, 310, 987–991. [Google Scholar] [CrossRef]
- Faust, K.; Bauchinger, F.; Laroche, B.; De Buyl, S.; Lahti, L.; Washburne, A.D.; Gonze, D.; Widder, S. Signatures of ecological processes in microbial community time series. Microbiome 2018, 6, 120. [Google Scholar] [CrossRef]
- Hastings, A.; Abbott, K.C.; Cuddington, K.; Francis, T.; Gellner, G.; Lai, Y.C.; Morozov, A.; Petrovskii, S.; Scranton, K.; Zeeman, M.L. Transient phenomena in ecology. Science 2018, 361. [Google Scholar] [CrossRef]
- Mastromatteo, I.; Marsili, M. On the criticality of inferred models. J. Stat. Mech. Theory Exp. 2011, 2011, P10012. [Google Scholar] [CrossRef]
- Chisholm, R.A.; Pacala, S.W. Niche and neutral models predict asymptotically equivalent species abundance distributions in high-diversity ecological communities. Proc. Natl. Acad. Sci. USA 2010, 107, 15821–15825. [Google Scholar] [CrossRef] [PubMed]
- Latombe, G.; Hui, C.; McGeoch, M.A. Beyond the continuum: A multi-dimensional phase space for neutral–niche community assembly. Proc. R. Soc. B Biol. Sci. 2015, 282, 20152417. [Google Scholar] [CrossRef]
- Li, L.; Ma, Z.S. Testing the neutral theory of biodiversity with human microbiome datasets. Sci. Rep. 2016, 6, 31448. [Google Scholar] [CrossRef]
- Leibold, M.A.; Urban, M.C.; De Meester, L.; Klausmeier, C.A.; Vanoverbeke, J. Regional neutrality evolves through local adaptive niche evolution. Proc. Natl. Acad. Sci. USA 2019, 116, 2612–2617. [Google Scholar] [CrossRef]
- Durbán, A.; Abellán, J.J.; Jiménez-Hernández, N.; Artacho, A.; Garrigues, V.; Ortiz, V.; Ponce, J.; Latorre, A.; Moya, A. Instability of the faecal microbiota in diarrhoea-predominant irritable bowel syndrome. FEMS Microbiol. Ecol. 2013, 86, 581–589. [Google Scholar] [CrossRef]
- Crandall, R.; Pomerance, C.B. Prime Numbers: A Computational Perspective; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006; Volume 182. [Google Scholar]
- Villaverde, A.F.; Ross, J.; Morán, F.; Banga, J.R. MIDER: Network Inference with Mutual Information Distance and Entropy Reduction. PLoS ONE 2014, 9, 1–15. [Google Scholar] [CrossRef]
- Convertino, M.; Simini, F.; Catani, F.; Linkov, I.; Kiker, G.A. Power-law of aggregate-size spectra in natural systems. ICST Trans. Complex Syst. 2013. [Google Scholar] [CrossRef]
- James, C.; Azaele, S.; Maritan, A.; Simini, F. Zipf’s and Taylor’s laws. Phys. Rev. E 2018, 98, 032408. [Google Scholar] [CrossRef]
- Lizier, J.T. JIDT: An Information-Theoretic Toolkit for Studying the Dynamics of Complex Systems. Front. Robot. AI 2014, 1, 11. [Google Scholar] [CrossRef]
- Tsilimigras, M.C.; Fodor, A.A. Compositional data analysis of the microbiome: Fundamentals, tools, and challenges. Ann. Epidemiol. 2016, 26, 330–335. [Google Scholar] [CrossRef]
- Razak, F.A.; Jeldtoft Jensen, H. Quantifying “causality” in complex systems: Understanding Transfer Entropy. PLoS ONE 2014. [Google Scholar] [CrossRef]
- Wollstadt, P.; Meyer, U.; Wibral, M. A graph algorithmic approach to separate direct from indirect neural interactions. PLoS ONE 2015, 10, e0140530. [Google Scholar] [CrossRef] [PubMed]
- Bossomaier, T.; Barnett, L.; Harré, M.; Lizier, J.T. An Introduction to Transfer Entropy; Springer International Publishing: Cham, Germany, 2016. [Google Scholar]
- Hanel, R.; Thurner, S. A comprehensive classification of complex statistical systems and an axiomatic derivation of their entropy and distribution functions. EPL (Europhys. Lett.) 2011, 93, 20006. [Google Scholar] [CrossRef]
- James, R.G.; Barnett, N.; Crutchfield, J.P. Information flows? A critique of transfer entropies. Phys. Rev. Lett. 2016, 116, 238701. [Google Scholar] [CrossRef] [PubMed]
- Borile, C.; Muñoz, M.A.; Azaele, S.; Banavar, J.R.; Maritan, A. Spontaneously Broken Neutral Symmetry in an Ecological System. Phys. Rev. Lett. 2012, 109, 038102. [Google Scholar] [CrossRef] [PubMed]
- Hanel, R.; Thurner, S.; Gell-Mann, M. How multiplicity determines entropy and the derivation of the maximum entropy principle for complex systems. Proc. Natl. Acad. Sci. USA 2014, 111, 6905–6910. [Google Scholar] [CrossRef]
- Ma, L.; Cordero, O. Solving the structure-function puzzle. Nat. Microbiol. 2018, 3, 750–751. [Google Scholar] [CrossRef] [PubMed]
- Rivett, D.W.; Bell, T. Abundance determines the functional role of bacterial phylotypes in complex communities. Nat. Microbiol. 2018, 3, 767. [Google Scholar] [CrossRef]
- Banavar, J.R.; Maritan, A.; Rinaldo, A. Size and form in efficient transportation networks. Nature 1999, 399, 130. [Google Scholar] [CrossRef] [PubMed]
- Lüdtke, N.; Panzeri, S.; Brown, M.; Broomhead, D.S.; Knowles, J.; Montemurro, M.A.; Kell, D.B. Information-theoretic sensitivity analysis: A general method for credit assignment in complex networks. J. R. Soc. Interface 2008, 5, 223–235. [Google Scholar] [CrossRef] [PubMed]
- Jost, L. Entropy and diversity. Oikos 2006, 113, 363–375. [Google Scholar] [CrossRef]
- Hubbell, S. The Unified Neutral Theory of Biodiversity and Biogeography; Princeton University Press: Princeton, NJ, USA, 2001. [Google Scholar]
- Seoane, L.F.; Sole, R. Phase transitions in Pareto optimal complex networks. Phys. Rev. E 2015, 92, 032807. [Google Scholar] [CrossRef]
- Vandeputte, D.; Kathagen, G.; D’hoe, K.; Vieira-Silva, S.; Valles-Colomer, M.; Sabino, J.; Wang, J.; Tito, R.Y.; De Commer, L.; Darzi, Y.; et al. Quantitative microbiome profiling links gut community variation to microbial load. Nature 2017, 551, 507. [Google Scholar] [CrossRef] [PubMed]
- Mellin, C.; Bradshaw, C.J.A.; Fordham, D.A.; Caley, M.J. Strong but opposing beta-diversity-stability relationships in coral reef fish communities. Proc. R. Soc. Lond. B Biol. Sci. 2014, 281. [Google Scholar] [CrossRef]
- Zaneveld, J.R.; Burkepile, D.E.; Shantz, A.A.; Pritchard, C.E.; McMinds, R.; Payet, J.P.; Welsh, R.; Correa, A.M.S.; Lemoine, N.P.; Rosales, S.; et al. Overfishing and nutrient pollution interact with temperature to disrupt coral reefs down to microbial scales. Nat. Commun. 2016, 7, 11833. [Google Scholar] [CrossRef]
- Johnson, K.V.A.; Burnet, P.W.J. Microbiome: Should we diversify from diversity? Gut Microbes 2016, 7, 455–458. [Google Scholar] [CrossRef] [PubMed]
- Matthews, T.J.; Whittaker, R.J. On the species abundance distribution in applied ecology and biodiversity management. J. Appl. Ecol. 2015, 52, 443–454. [Google Scholar] [CrossRef]
- Isbell, F.; Calcagno, V.; Hector, A.; Connolly, J.; Harpole, W.S.; Reich, P.B.; Scherer-Lorenzen, M.; Schmid, B.; Tilman, D.; Van Ruijven, J.; et al. High plant diversity is needed to maintain ecosystem services. Nature 2011, 477, 199. [Google Scholar] [CrossRef]
- Wang, S.; Loreau, M. Biodiversity and ecosystem stability across scales in metacommunities. Ecol. Lett. 2016, 19, 510–518. [Google Scholar] [CrossRef] [PubMed]
- Winemiller, K.O. Spatial and temporal variation in tropical fish trophic networks. Ecol. Monogr. 1990, 60, 331–367. [Google Scholar] [CrossRef]
- Csányi, G.; Szendrői, B. Fractal-small-world dichotomy in real-world networks. Phys. Rev. E 2004, 70, 016122. [Google Scholar] [CrossRef]
- DeLong, J.P.; Okie, J.G.; Moses, M.E.; Sibly, R.M.; Brown, J.H. Shifts in metabolic scaling, production, and efficiency across major evolutionary transitions of life. Proc. Natl. Acad. Sci. USA 2010, 107, 12941–12945. [Google Scholar] [CrossRef]
- Bashan, A.; Gibson, T.E.; Friedman, J.; Carey, V.J.; Weiss, S.T.; Hohmann, E.L.; Liu, Y.Y. Universality of human microbial dynamics. Nature 2016, 534, 259. [Google Scholar] [CrossRef]
- Zaneveld, J.R.; McMinds, R.; Thurber, R.V. Stress and stability: Applying the Anna Karenina principle to animal microbiomes. Nat. Microbiol. 2017, 2, 17121. [Google Scholar] [CrossRef]
- Chao, A.; Chazdon, R.L.; Colwell, R.K.; Shen, T.J. A new statistical approach for assessing similarity of species composition with incidence and abundance data. Ecol. Lett. 2005, 8, 148–159. [Google Scholar] [CrossRef]
- Weiss, S.; Van Treuren, W.; Lozupone, C.; Faust, K.; Friedman, J.; Deng, Y.; Xia, L.C.; Xu, Z.Z.; Ursell, L.; Alm, E.J.; et al. Correlation detection strategies in microbial data sets vary widely in sensitivity and precision. ISME J. 2016, 10, 1669. [Google Scholar] [CrossRef]
- Foster, K.R.; Schluter, J.; Coyte, K.Z.; Rakoff-Nahoum, S. The evolution of the host microbiome as an ecosystem on a leash. Nature 2017, 548, 43–51. [Google Scholar] [CrossRef]
- Pareto, V. Manual of Political Economy; Augustus M. Kelley: New York, NY, USA, 1971. [Google Scholar]
- Albert, R.; Jeong, H.; Barabási, A.L. Error and attack tolerance of complex networks. Nature 2000, 406, 378. [Google Scholar] [CrossRef]
- Mori, A.S.; Isbell, F.; Seidl, R. β-diversity, community assembly, and ecosystem functioning. Trends Ecol. Evol. 2018, 33, 549–564. [Google Scholar] [CrossRef]
- Tria, F.; Loreto, V.; Servedio, V. Zipf’s, Heaps’ and Taylor’s Laws are Determined by the Expansion into the Adjacent Possible. Entropy 2018, 20, 752. [Google Scholar] [CrossRef]
- Whittaker, R.J.; Fernández-Palacios, J.M.; Matthews, T.J.; Borregaard, M.K.; Triantis, K.A. Island biogeography: Taking the long view of nature’s laboratories. Science 2017, 357. [Google Scholar] [CrossRef]
- Kauffman, S.A. The Origins of Order: Self-Organization and Selection in Evolution; Oxford University Press: New York, NY, USA, 1993. [Google Scholar]
- West, G.B.; Brown, J.H.; Enquist, B.J. A general model for the origin of allometric scaling laws in biology. Science 1997, 276, 122–126. [Google Scholar] [CrossRef]
- Seoane, L.F.; Solé, R. Systems poised to criticality through Pareto selective forces. arXiv 2015, arXiv:1510.08697. [Google Scholar]
- Tendler, A.; Mayo, A.; Alon, U. Evolutionary tradeoffs, Pareto optimality and the morphology of ammonite shells. BMC Syst. Biol. 2015, 9, 12. [Google Scholar] [CrossRef]
- Koçillari, L.; Fariselli, P.; Trovato, A.; Seno, F.; Maritan, A. Signature of Pareto optimization in the Escherichia coli proteome. Sci. Rep. 2018, 8, 9141. [Google Scholar] [CrossRef]
- Suweis, S.; Grilli, J.; Banavar, J.R.; Allesina, S.; Maritan, A. Effect of localization on the stability of mutualistic ecological networks. Nat. Commun. 2015, 6, 10179. [Google Scholar] [CrossRef]
- Tu, C.; Suweis, S.; Grillib, J.; Formentin, M.; Maritan, A. Reconciling cooperation, biodiversity and stability in complex ecological communities. arXiv 2018, arXiv:1805.03527. [Google Scholar] [CrossRef]
- Kilpatrick, A.M.; Ives, A.R. Species interactions can explain Taylor’s power law for ecological time series. Nature 2003, 422, 65–68. [Google Scholar] [CrossRef] [PubMed]
- Grilli, J.; Barabás, G.; Michalska-Smith, M.J.; Allesina, S. Higher-order interactions stabilize dynamics in competitive network models. Nature 2017, 548, 210–213. [Google Scholar] [CrossRef]
- Levine, J.; Bascompte, J.; Adler, P.; Allesina, S. Beyond pairwise mechanisms of species coexistence in complex communities. Nature 2017, 546, 56–64. [Google Scholar] [CrossRef] [PubMed]
- Quax, R.; Apolloni, A.; Sloot, P.M. The diminishing role of hubs in dynamical processes on complex networks. J. R. Soc. Interface 2013, 10, 20130568. [Google Scholar] [CrossRef] [PubMed]
- Granovetter, M. The strength of weak ties: A network theory revisited. Sociol. Theory 1983, 1, 201–233. [Google Scholar] [CrossRef]
- García-Jiménez, B.; de la Rosa, T.; Wilkinson, M.D. MDPbiome: Microbiome engineering through prescriptive perturbations. Bioinformatics 2018, 34, i838–i847. [Google Scholar] [CrossRef]
- Toju, H.; Peay, K.G.; Yamamichi, M.; Narisawa, K.; Hiruma, K.; Naito, K.; Fukuda, S.; Ushio, M.; Nakaoka, S.; Onoda, Y.; et al. Core microbiomes for sustainable agroecosystems. Nat. Plants 2018, 4, 247–257. [Google Scholar] [CrossRef] [PubMed]
- Allen, A.P.; Dinan, T.G.; Clarke, G.; Cryan, J.F. A psychology of the human brain–gut–microbiome axis. Soc. Personal. Psychol. Compass 2017, 11, e12309. [Google Scholar] [CrossRef] [PubMed]
- Scheffer, M.; Carpenter, S.R.; Lenton, T.M.; Bascompte, J.; Brock, W.; Dakos, V.; Van de Koppel, J.; Van de Leemput, I.A.; Levin, S.A.; Van Nes, E.H.; et al. Anticipating critical transitions. Science 2012, 338, 344–348. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Convertino, M. Optimal Microbiome Networks: Macroecology and Criticality. Entropy 2019, 21, 506. https://doi.org/10.3390/e21050506
Li J, Convertino M. Optimal Microbiome Networks: Macroecology and Criticality. Entropy. 2019; 21(5):506. https://doi.org/10.3390/e21050506
Chicago/Turabian StyleLi, Jie, and Matteo Convertino. 2019. "Optimal Microbiome Networks: Macroecology and Criticality" Entropy 21, no. 5: 506. https://doi.org/10.3390/e21050506
APA StyleLi, J., & Convertino, M. (2019). Optimal Microbiome Networks: Macroecology and Criticality. Entropy, 21(5), 506. https://doi.org/10.3390/e21050506