State and Parameter Estimation from Observed Signal Increments
Abstract
1. Introduction
2. Mathematical Problem Formulation
3. Parameter Estimation from Noiseless Data
3.1. Feedback Particle Filter
3.2. Ensemble Kalman–Bucy Filter
4. State Estimation for Noisy Data
4.1. Generalised Feedback Particle Filter Formulation
4.2. Generalised Kalman–Bucy Filter
4.3. Ensemble Kalman–Bucy Filter
5. Combined State and Parameter Estimation
5.1. Feedback Particle Filter Formulation
5.2. Ensemble Kalman–Bucy Filter
6. Numerical Results
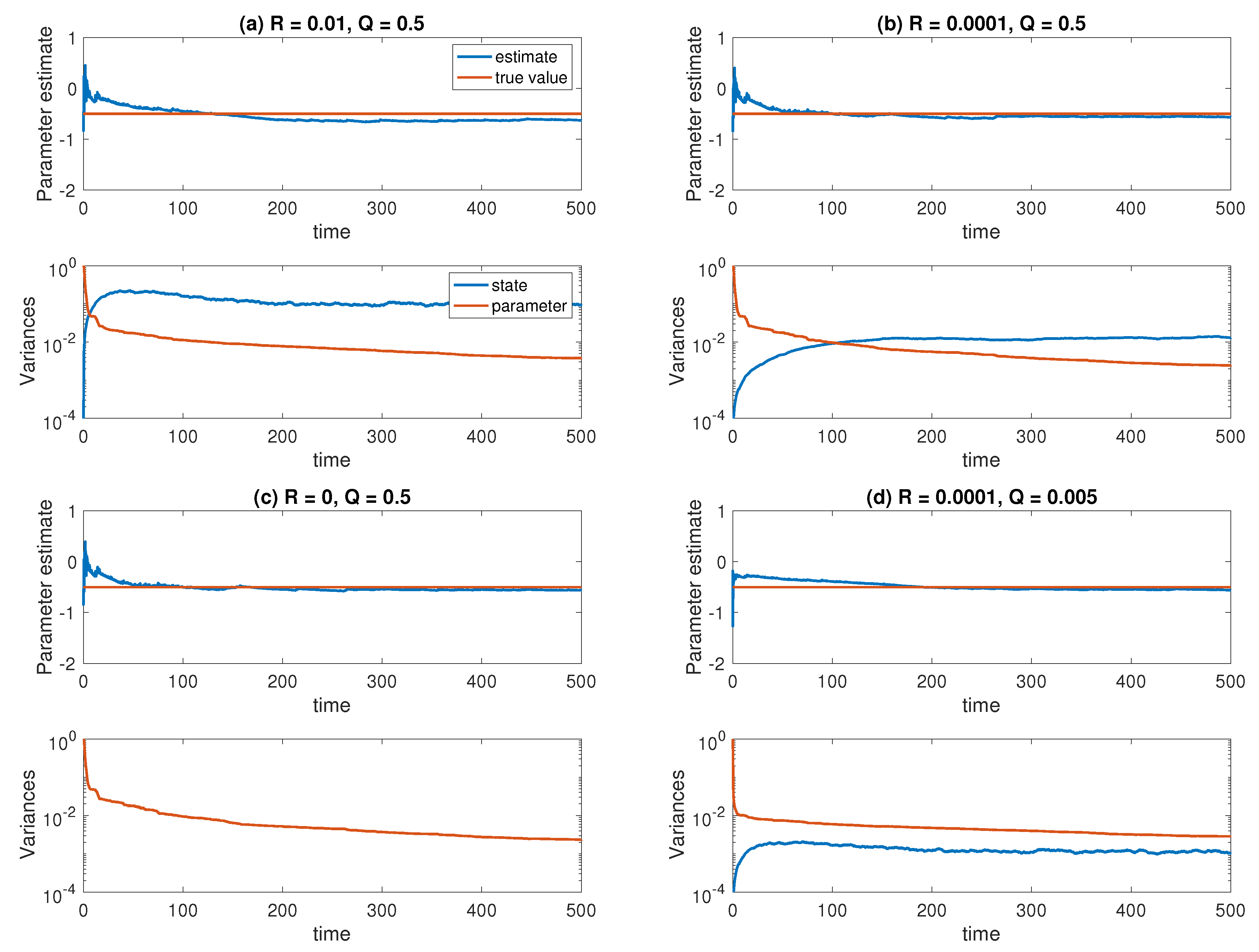
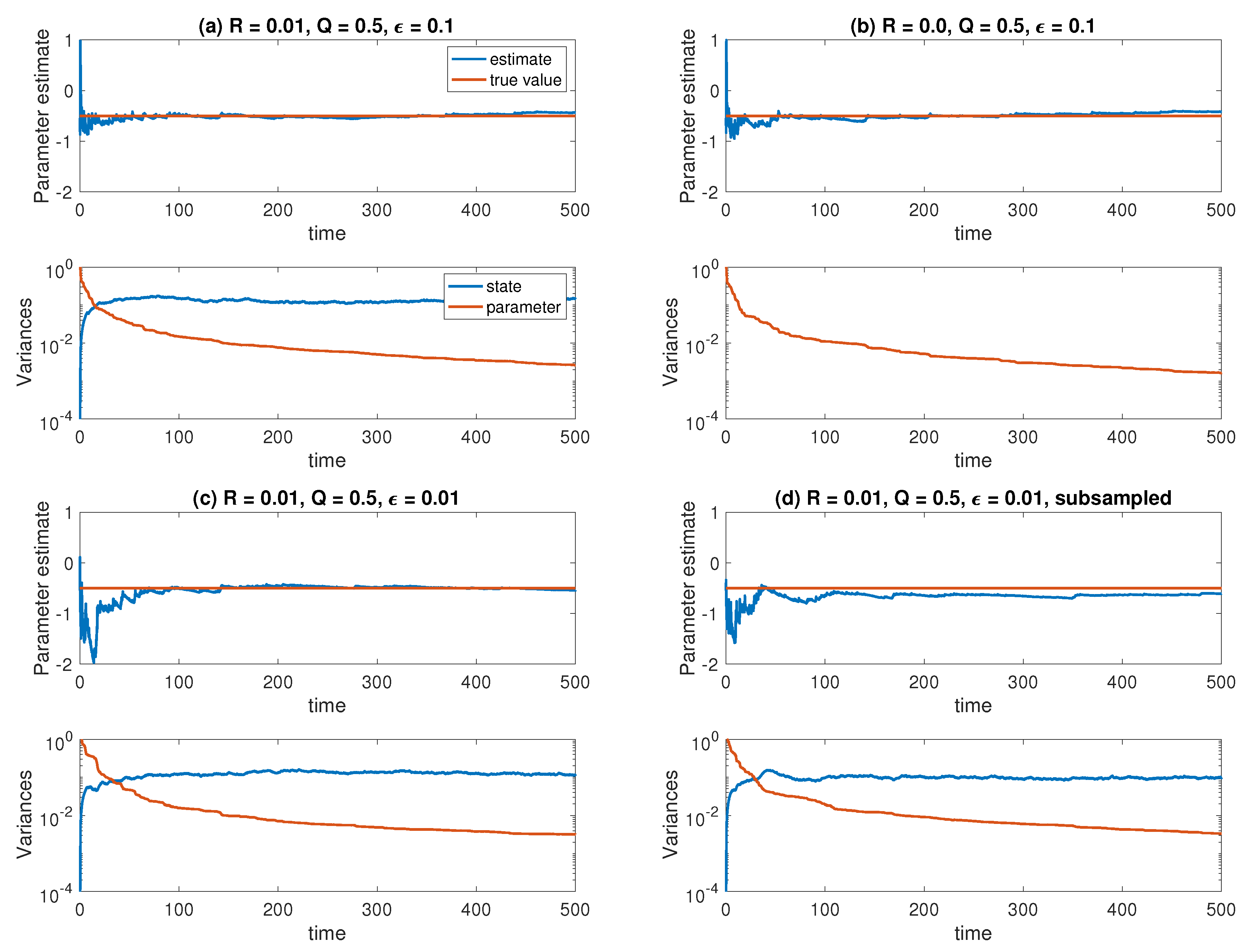
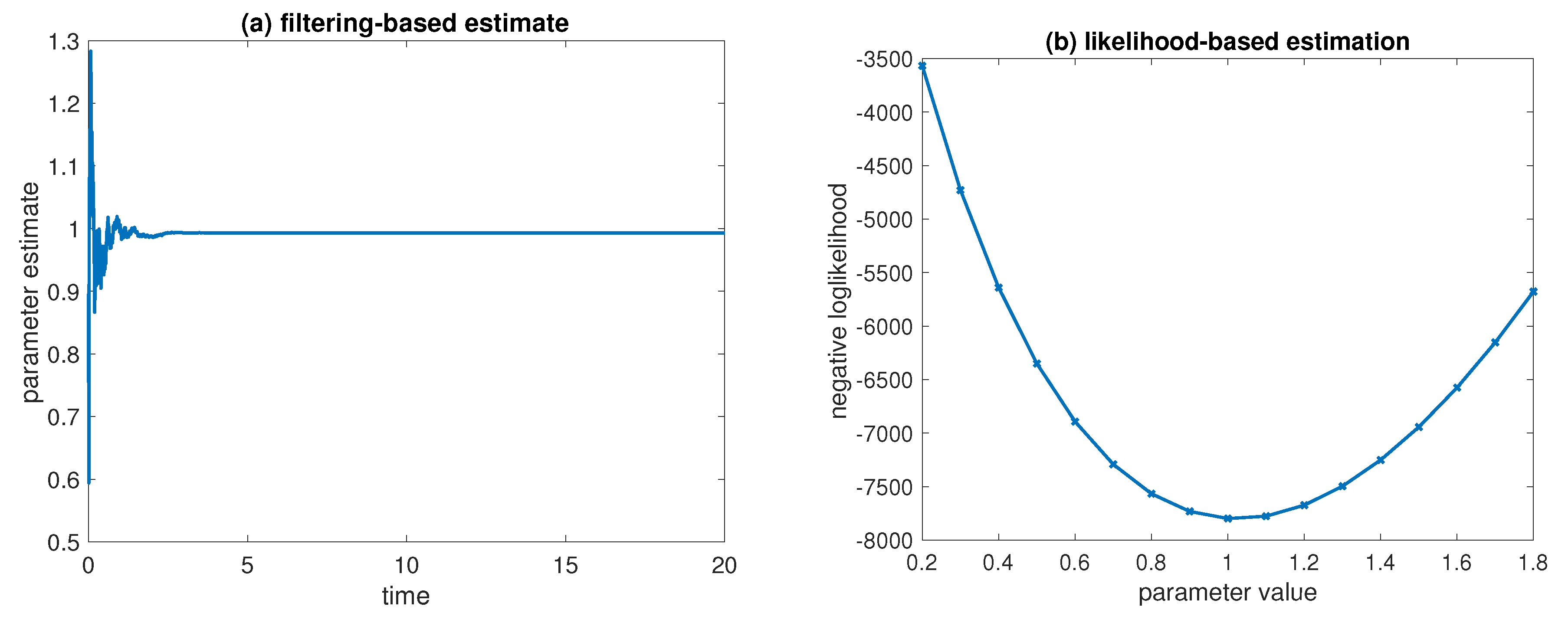
6.1. Parameter Estimation for the Ornstein–Uhlenbeck Process
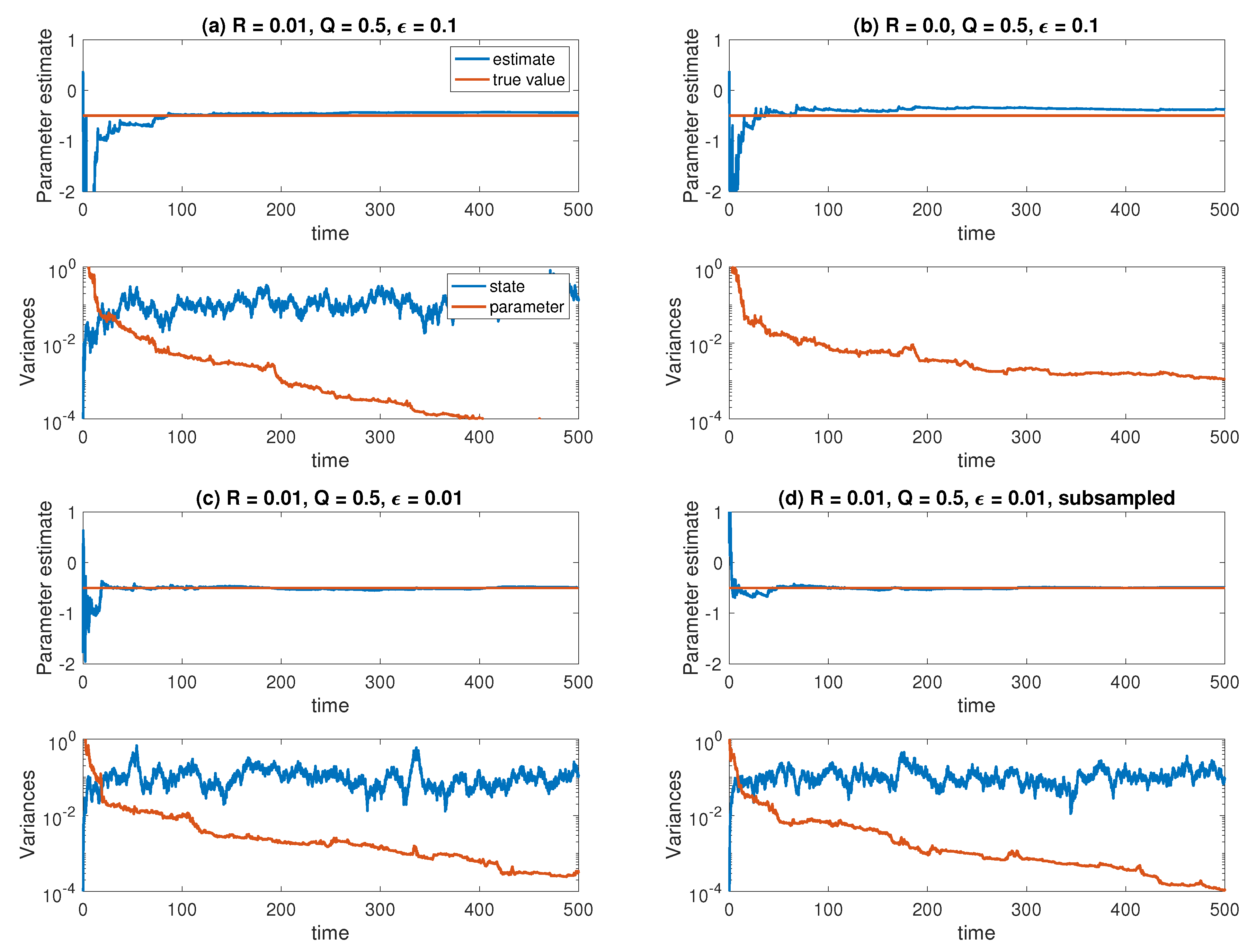
6.2. Averaging
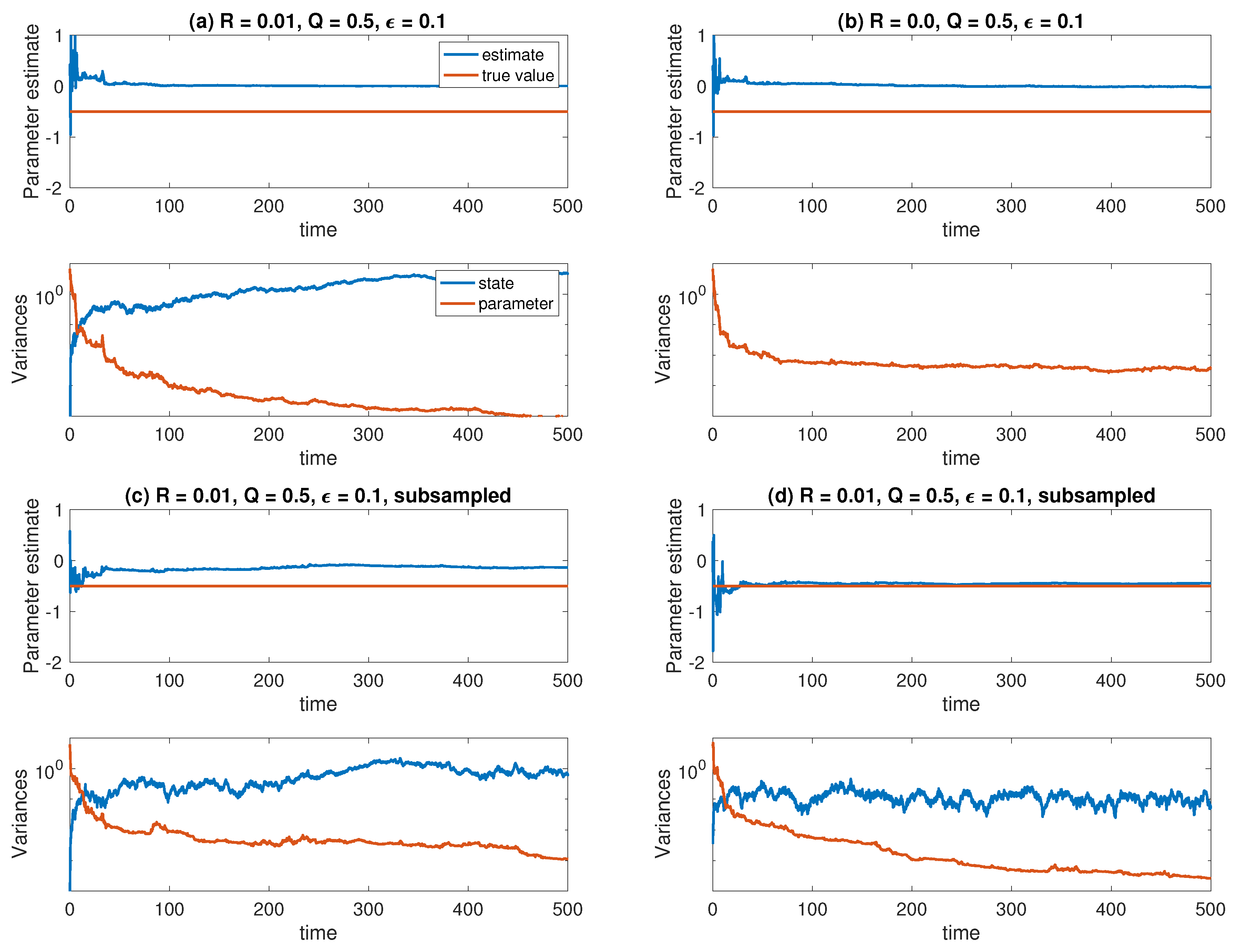
6.3. Homogenisation
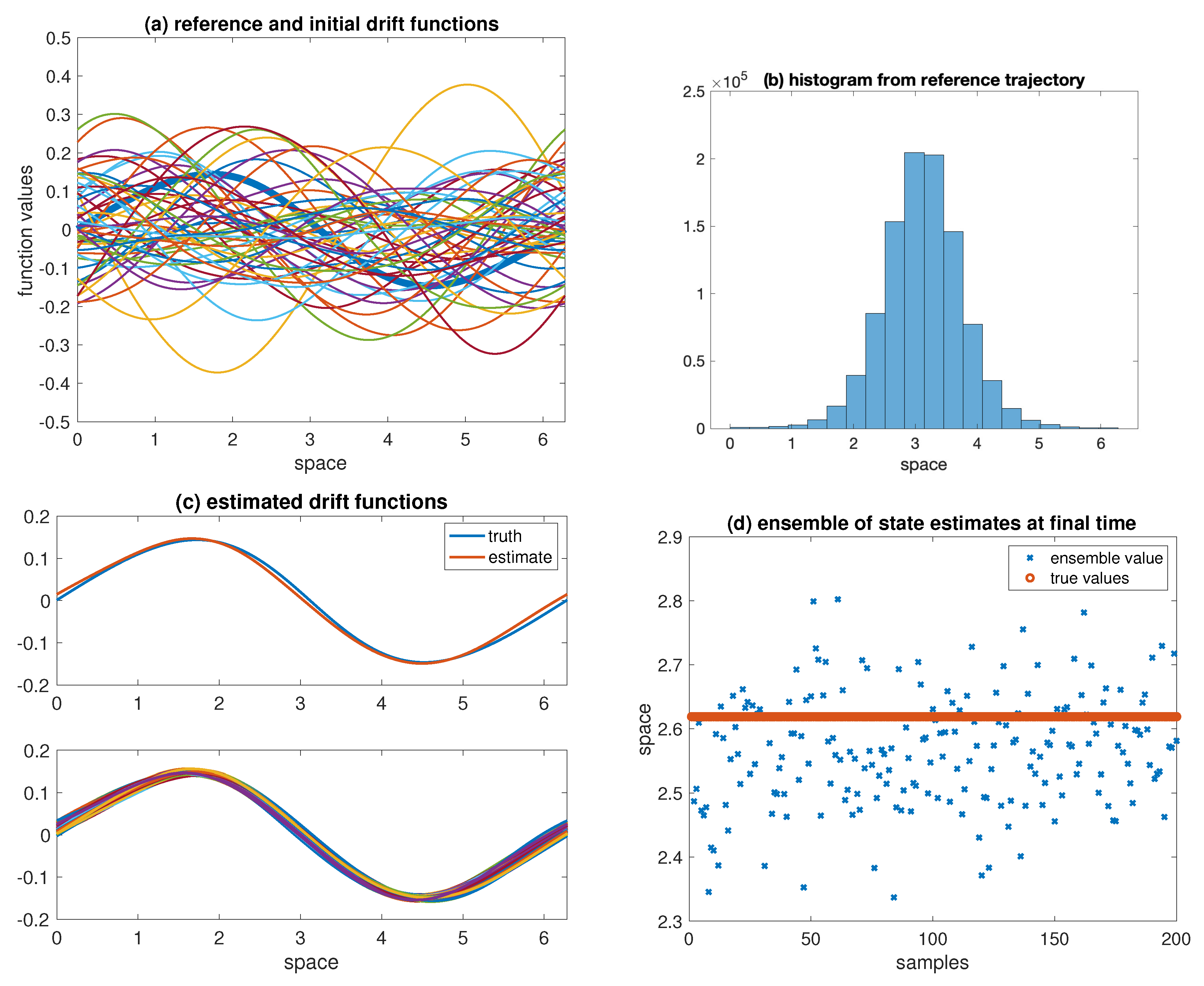
6.4. Nonparametric Drift and State Estimation
6.5. Spde Parameter Estimation
6.6. Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. The Filtering Equations for Correlated Noise
References
- Kutoyants, Y. Statistical Inference for Ergodic Diffusion Processes; Springer: New York, NY, USA, 2004. [Google Scholar]
- Pavliotis, G. Stochastic Processes and Applications; Springer: New York, NY, USA, 2014. [Google Scholar]
- Apte, A.; Hairer, M.; Stuart, A.; Voss, J. Sampling the posterior: An approach to non-Gaussian data assimilation. Phys. D Nonlinear Phenom. 2007, 230, 50–64. [Google Scholar] [CrossRef]
- Salman, H.; Kuznetsov, L.; Jones, C.; Ide, K. A method for assimilating Lagrangian data into a shallow-water-equation ocean model. Mon. Weather Rev. 2006, 134, 1081–1101. [Google Scholar] [CrossRef]
- Apte, A.; Jones, C.; Stuart, A. A Bayesian approach to Lagrangian data assimilation. Tellus A 2008, 60, 336–347. [Google Scholar] [CrossRef]
- Simon, D. Optimal State Estimation; Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]
- Bain, A.; Crisan, D. Fundamentals of Stochastic Filtering; Springer: New York, NY, USA, 2009. [Google Scholar]
- Liu, J. Monte Carlo Strategies in Scientific Computing; Springer: New York, NY, USA, 2001. [Google Scholar]
- Crisan, D.; Xiong, J. Approximate McKean-Vlasov representation for a class of SPDEs. Stochastics 2010, 82, 53–68. [Google Scholar] [CrossRef]
- McKean, H. A class of Markov processes associated with nonlinear parabolic equations. Proc. Natl. Acad. Sci. USA 1966, 56, 1907–1911. [Google Scholar] [CrossRef] [PubMed]
- Yang, T.; Mehta, P.; Meyn, S. Feedback particle filter. IEEE Trans. Autom. Control 2013, 58, 2465–2480. [Google Scholar] [CrossRef]
- Reich, S. Data assimilation: The Schrödinger perspective. Acta Numer. 2019, 28, 635–710. [Google Scholar]
- Majda, A.; Harlim, J. Filtering Complex Turbulent Systems; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Bergemann, K.; Reich, S. An ensemble Kalman–Bucy filter for continuous data assimilation. Meteorol. Z. 2012, 21, 213–219. [Google Scholar] [CrossRef]
- Taghvaei, A.; de Wiljes, J.; Mehta, P.; Reich, S. Kalman filter and its modern extensions for the continuous-time nonlinear filtering problem. ASME. J. Dyn. Syst. Meas. Control 2017, 140. [Google Scholar] [CrossRef]
- Law, K.; Stuart, A.; Zygalakis, K. Data Assimilation: A Mathematical Introduction; Springer: New York, NY, USA, 2015. [Google Scholar]
- Reich, S.; Cotter, C. Probabilistic Forecasting and Bayesian Data Assimilation; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Moral, P.D. Mean Field Simulation for Monte Carlo Integration; Chapman and Hall/CRC: London, UK, 2013. [Google Scholar]
- Pavliotis, G.; Stuart, A. Multiscale Methods; Springer: New York, NY, USA, 2008. [Google Scholar]
- Altmeyer, R.; Reiß, M. Nonparametric Estimation for Linear SPDEs from Local Measurements; Technical Report; Humboldt University Berlin: Berlin, Germany, 2019. [Google Scholar]
- Saha, S.; Gustafsson, F. Particle filtering with dependent noise processes. IEEE Trans. Signal Process. 2012, 60, 4497–4508. [Google Scholar] [CrossRef]
- Berry, T.; Sauer, T. Correlations between systems and observation errors in data assimilation. Mon. Weather Rev. 2018, 146, 2913–2931. [Google Scholar] [CrossRef]
- Mitchell, H.L.; Daley, R. Discretization error and signal/error correlation in atmospheric data assimilation: (I). All scales resolved. Tellus A 1997, 49, 32–53. [Google Scholar] [CrossRef]
- Papaspiliopoulos, O.; Pokern, Y.; Roberts, G.; Stuart, A. Nonparametric estimation of diffusion: A differential equation approach. Biometrika 2012, 99, 511–531. [Google Scholar] [CrossRef]
- Särkkä, S. Bayesian Filtering and Smoothing; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Laugesen, R.S.; Mehta, P.G.; Meyn, S.P.; Raginsky, M. Poisson’s equation in nonlinear filtering. SIAM J. Control Optim. 2015, 53, 501–525. [Google Scholar] [CrossRef]
- Taghvaei, A.; Mehta, P.; Meyn, S. Gain Function Approximation in the Feedback Particle Filter; Technical Report; University of Illinois at Urbana-Champaign: Champaign, IL, USA, 2019. [Google Scholar]
- Amezcua, J.; Kalnay, E.; Ide, K.; Reich, S. Ensemble transform Kalman-Bucy filters. Q. J. R. Meteorol. Soc. 2014, 140, 995–1004. [Google Scholar] [CrossRef]
- De Wiljes, J.; Reich, S.; Stannat, W. Long-time stability and accuracy of the ensemble Kalman–Bucy filter for fully observed processes and small measurement noise. SIAM J. Appl. Dyn. Syst. 2018, 17, 1152–1181. [Google Scholar] [CrossRef]
- Blömker, D.; Schillings, C.; Wacker, P. A strongly convergent numerical scheme for ensemble Kalman inversion. SIAM J. Numer. Anal. 2018, 56, 2537–2562. [Google Scholar] [CrossRef]
- Harlim, J. Model error in data assimilation. In Nonlinear and Stochastic Climate Dynamics; Franzke, C., Kane, T.O., Eds.; Cambridge University Press: Cambridge, UK, 2017; pp. 276–317. [Google Scholar]
- Krumscheid, S.; Pavliotis, G.; Kalliadasis, S. Semi-parametric drift and diffusion estimation for multiscale diffusions. SIAM J. Multiscale Model. Simul. 2011, 11, 442–473. [Google Scholar] [CrossRef]
- Van Waaij, J.; van Zanten, H. Gaussian process methods for one-dimensional diffusion: Optimal rates and adaptation. Electron. J. Stat. 2016, 10, 628–645. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nüsken, N.; Reich, S.; Rozdeba, P.J. State and Parameter Estimation from Observed Signal Increments. Entropy 2019, 21, 505. https://doi.org/10.3390/e21050505
Nüsken N, Reich S, Rozdeba PJ. State and Parameter Estimation from Observed Signal Increments. Entropy. 2019; 21(5):505. https://doi.org/10.3390/e21050505
Chicago/Turabian StyleNüsken, Nikolas, Sebastian Reich, and Paul J. Rozdeba. 2019. "State and Parameter Estimation from Observed Signal Increments" Entropy 21, no. 5: 505. https://doi.org/10.3390/e21050505
APA StyleNüsken, N., Reich, S., & Rozdeba, P. J. (2019). State and Parameter Estimation from Observed Signal Increments. Entropy, 21(5), 505. https://doi.org/10.3390/e21050505




