An Analysis of China’s Onshore and Offshore Exchange Rates—Adjusted Thermal Optimal Path Approach Based on Pruning and Path Segmentation
Abstract
1. Introduction
2. Methodology
2.1. Thermal Optimal Path Method
2.2. Improvement of TOP Method
| Algorithm 1. Adjusted TOP method based on pruning and path segmentation algorithm |
| Pruning and Path Segmentation algorithm |
|
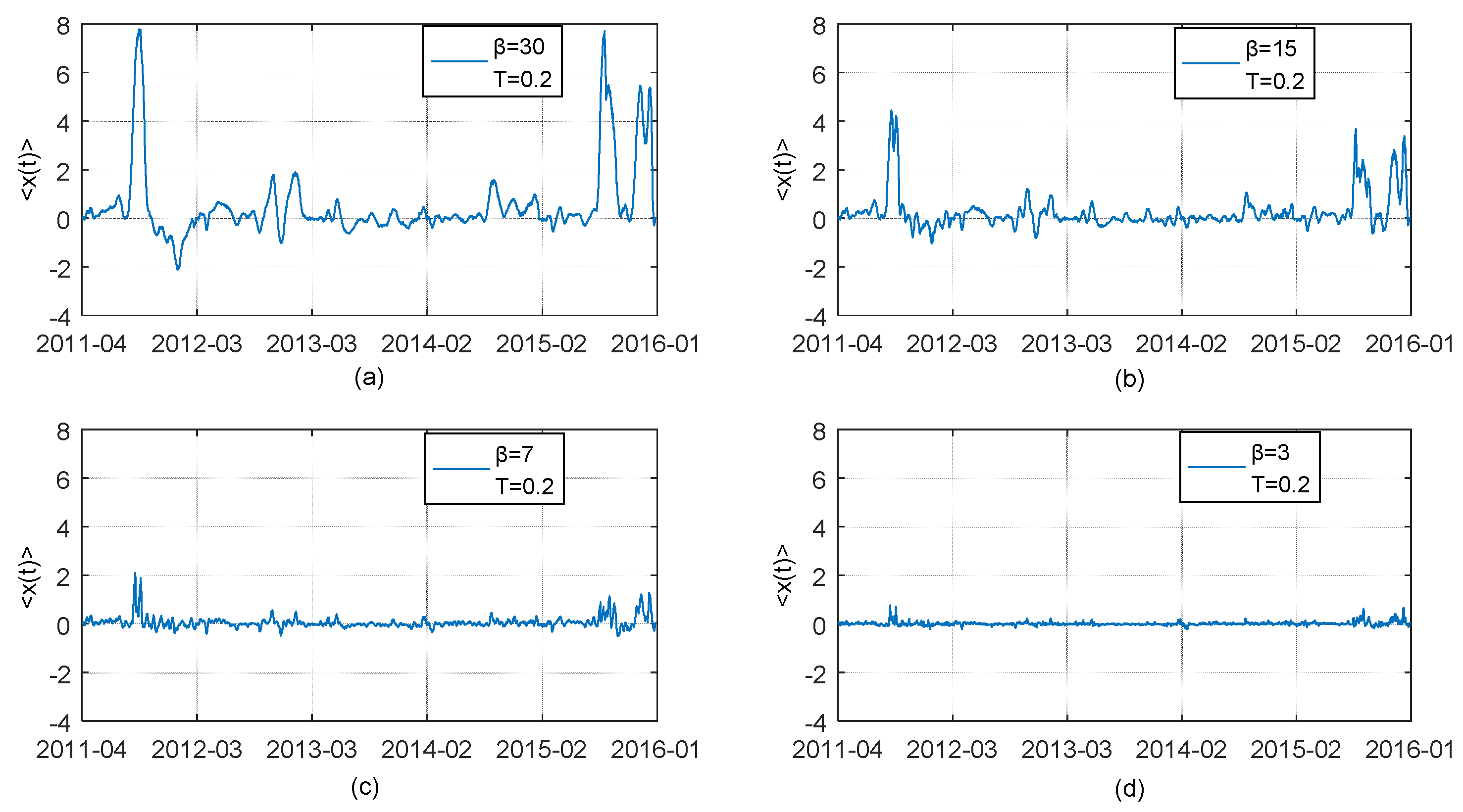
| Note: the concrete definition and description of n*, n1 in Algorithm 1 can be funded in Appendix. In the following empirical study, n = 1249 (time-series data size) and we set n1 = 420 (a partition coefficient), n* = 510 (a threshold), and β = 30 (the possible maximum lag). Furthermore, the adjusted TOP method and existing TOP are the same for the case of small data (small time-series data size). |
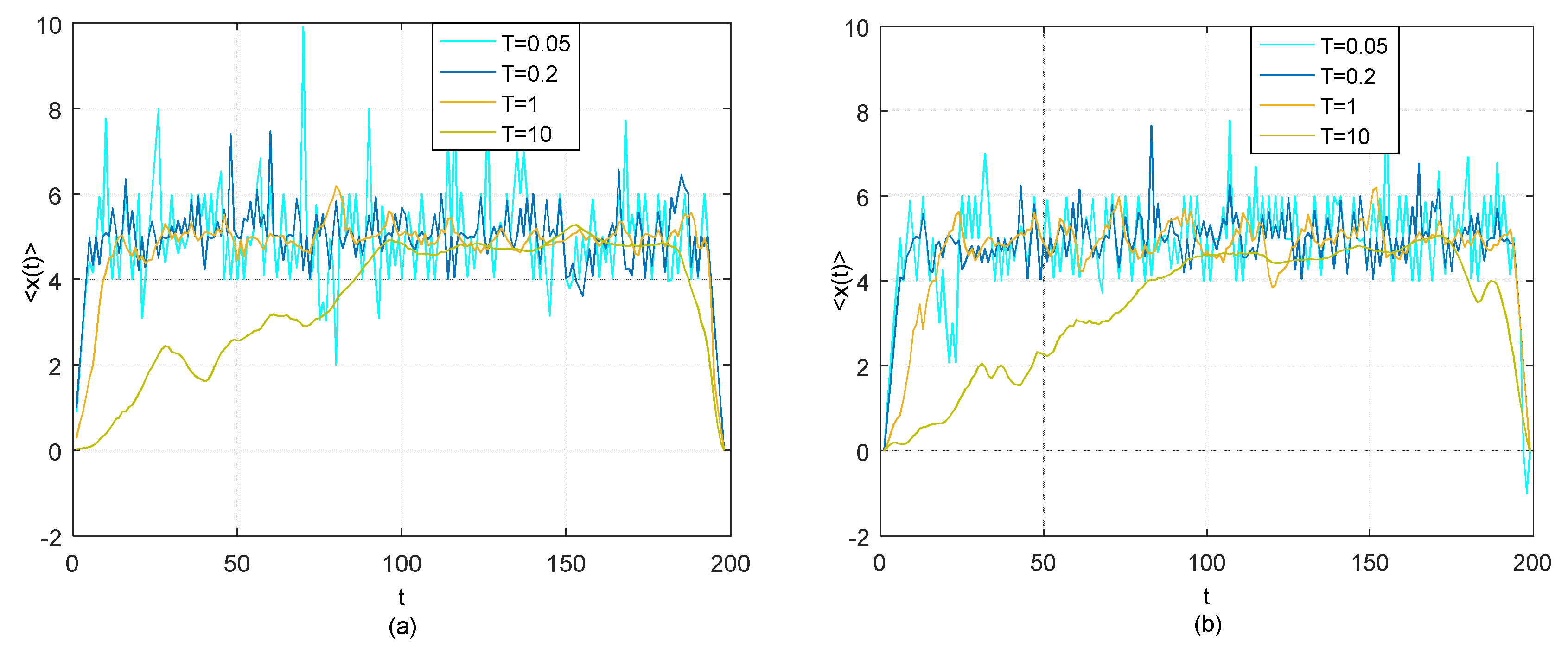
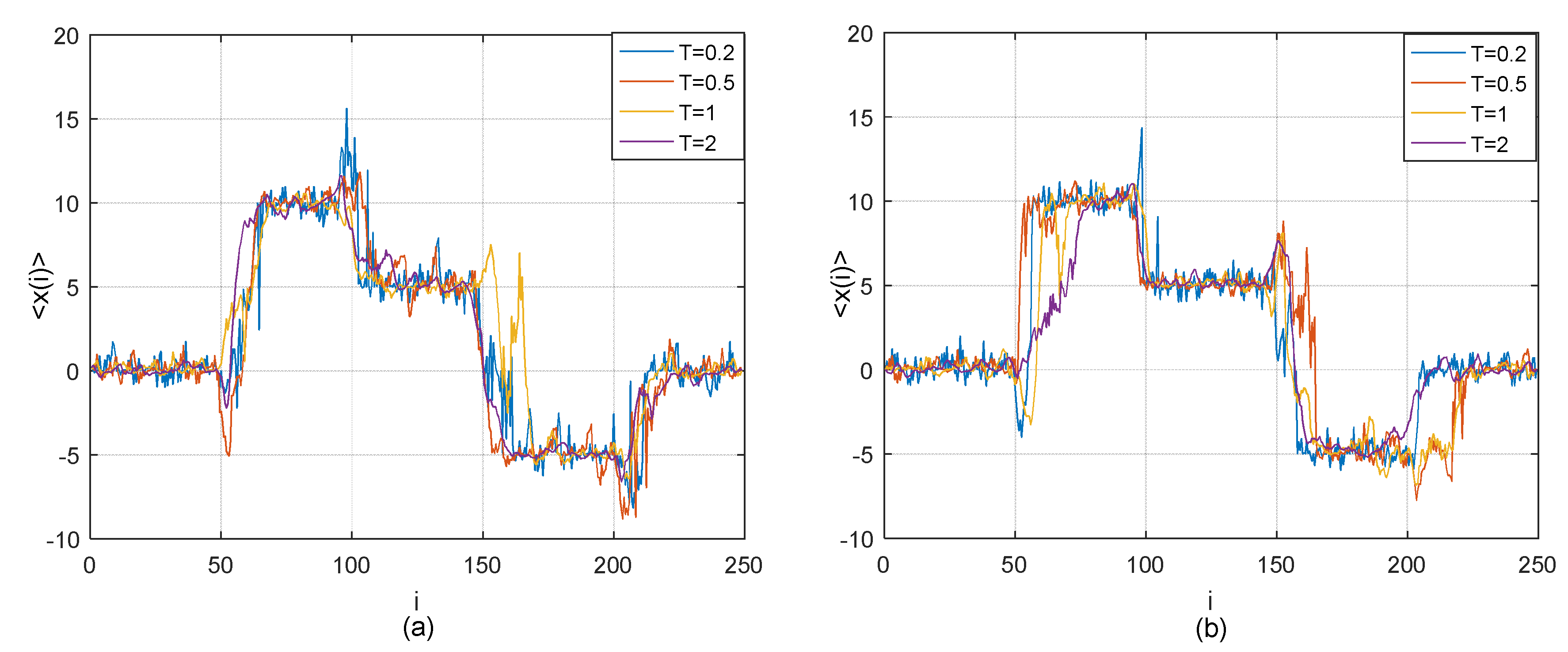
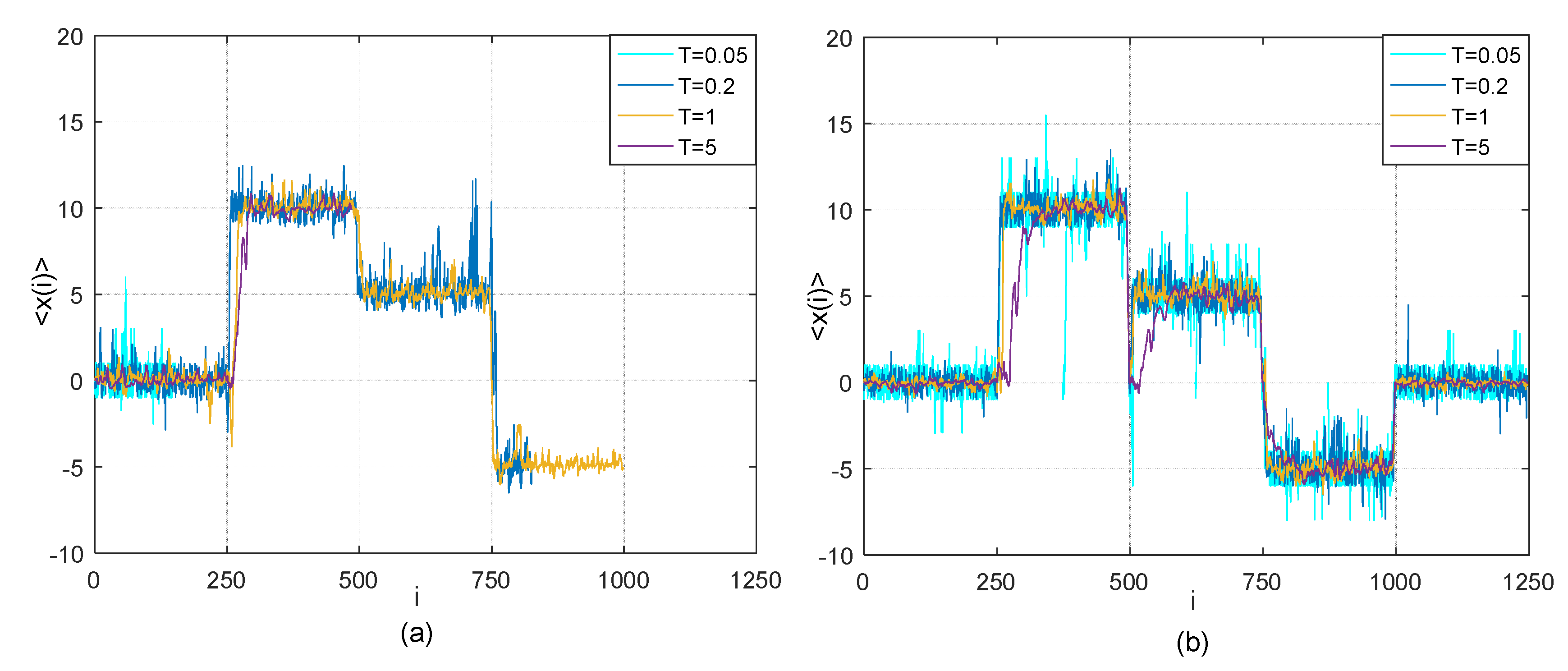
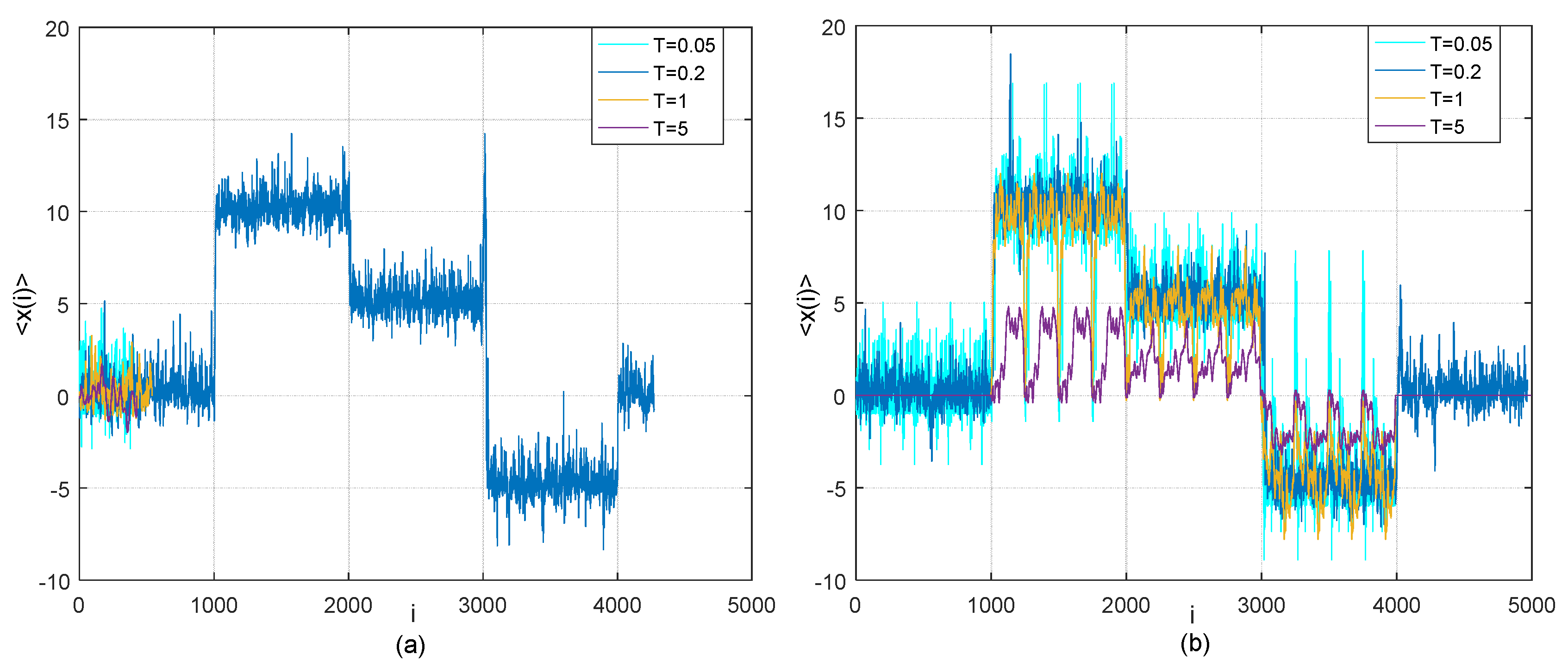
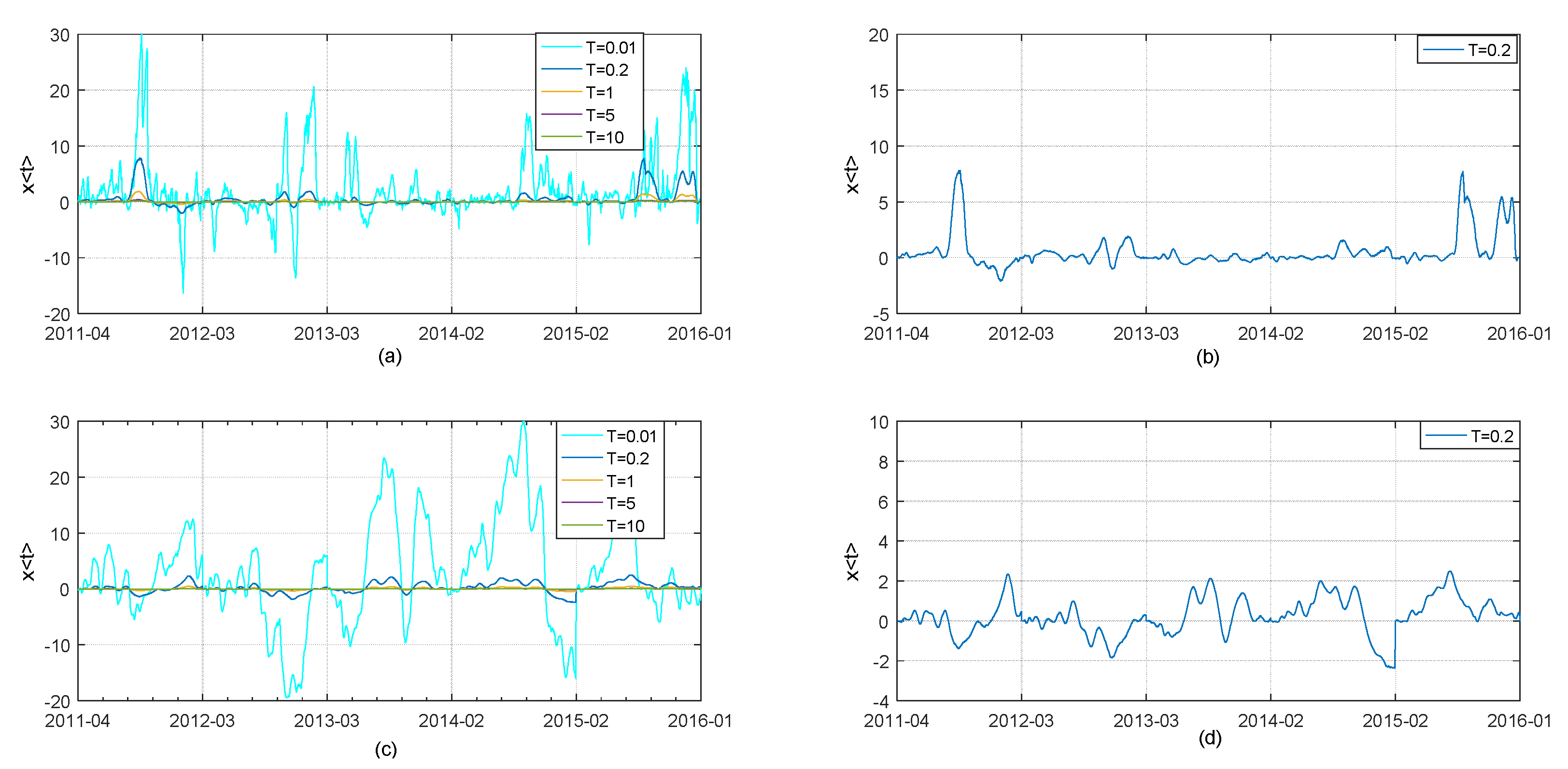
2.3. Numerical Tests on Simple Examples
2.3.1. Comparison on Single-Change-of-Regime in Time Lag
2.3.2. Comparison on Multiple-Change-of-Regime in Time Lag
2.3.3. Comparison on Multiple-Change-of-Regime in Time Lag with Big Data
3. Empirical Results
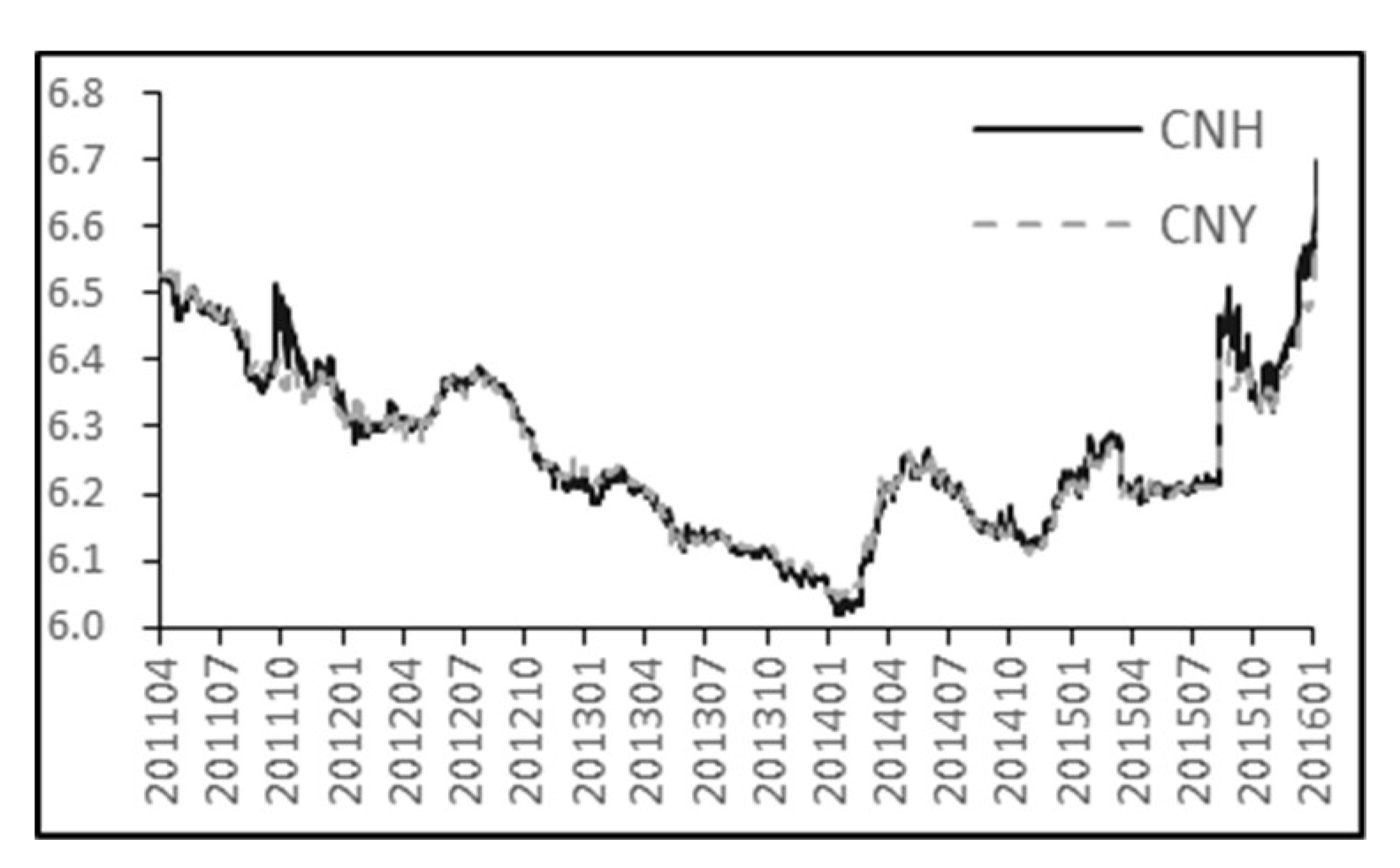
3.1. Data Source and Description
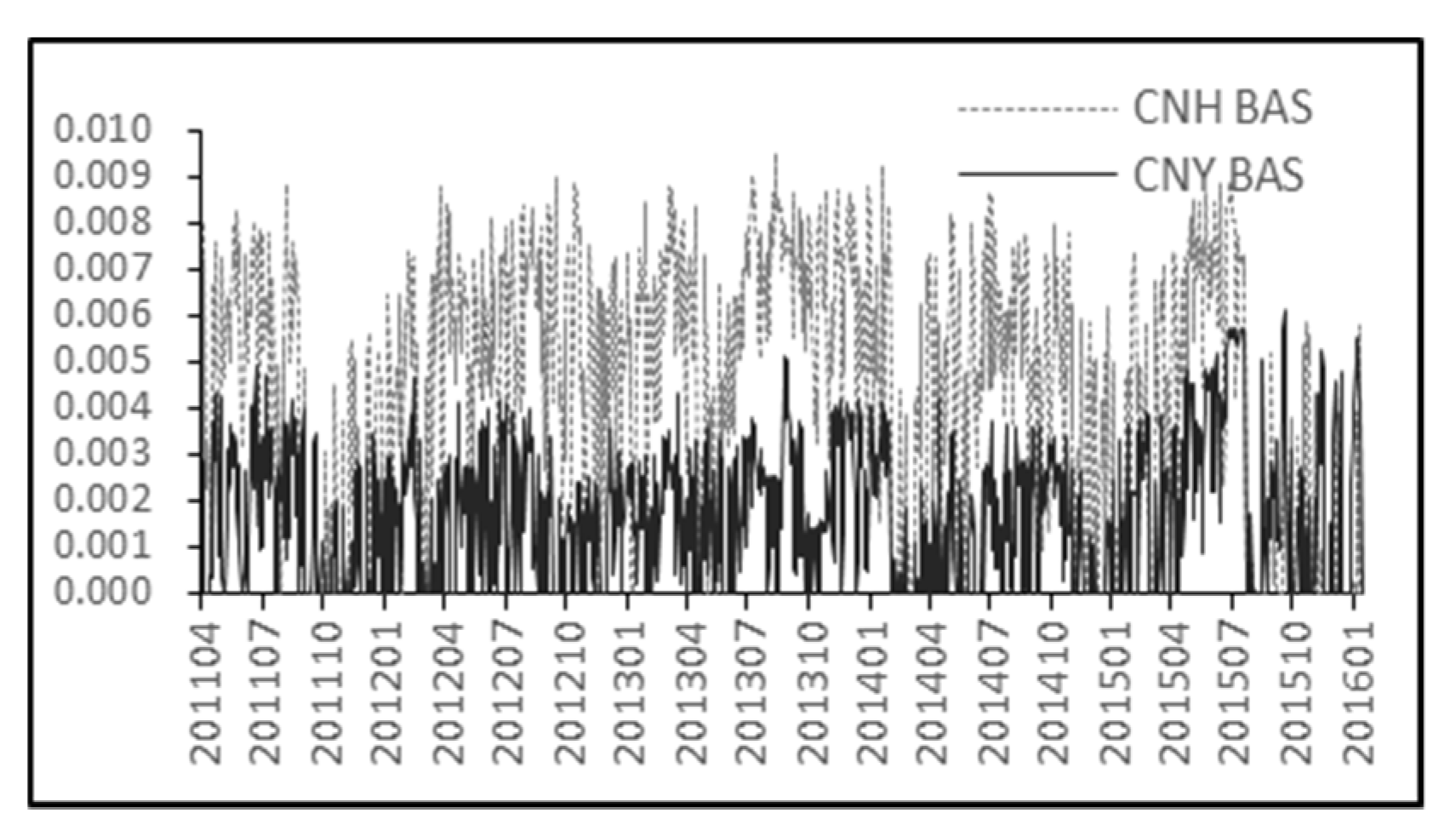
3.2. Liquidity Measure
3.3. Preliminary Analysis by Vector Auto-Regression Model
3.4. Analysis on Results of Thermal Optimal Causality Paths
3.4.1. The Results from Adjusted TOP Method
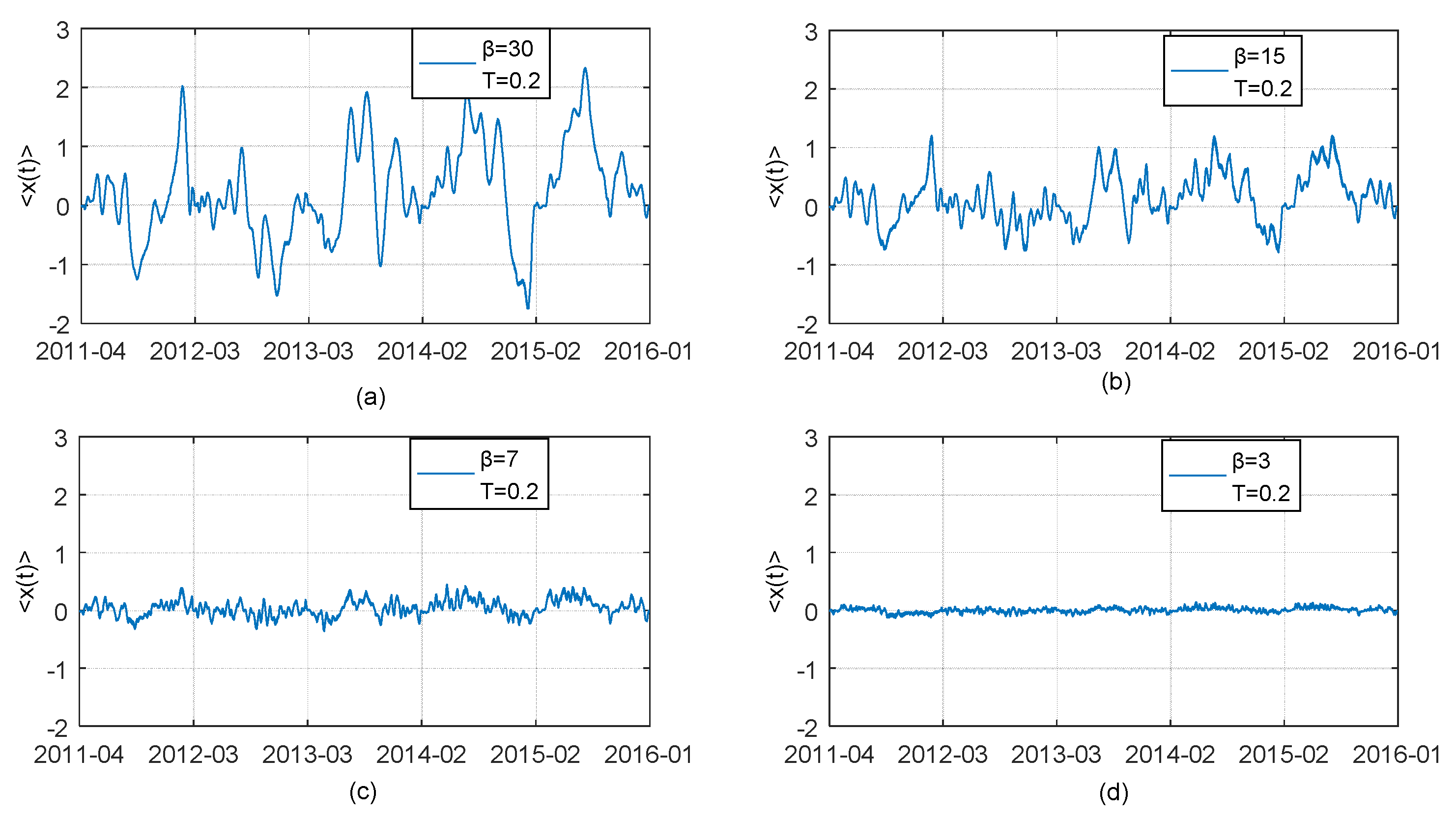
3.4.2. Analysis on Influence of Maximum Lag Results on Thermal Optimal Path
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Ding, D.K.; Tse, Y.; Williams, M. The price discovery puzzle in offshore yuan trading: different contributions for different contracts. J. Futures Mark. 2014, 34, 103–123. [Google Scholar] [CrossRef]
- Cheung, Y.; Rime, D. The offshore renminbi exchange rate: Microstructure and links to the onshore market. J. Int. Money Finance 2014, 49, 170–189. [Google Scholar] [CrossRef]
- Wu, G.; Pei, C. A quantitative research on the relationship among onshore spot exchange rate, offshore spot exchange rate and offshore NDF rate. J. Financ. Res. 2012, 9, 62–73. [Google Scholar]
- Leung, D.; Fu, J. Interactions between CNY and CNH Money and Forward Exchange Markets; Research Working Papers No. 13; Hong Kong Institute for Monetary: Hong Kong, China, 2014. [Google Scholar]
- Du, J.; Lai, K.K. Copula-based risk management models for multivariable RMB exchange rate in the process of RMB internationalization. J. Syst. Sci. Complex. 2017, 30, 660–679. [Google Scholar] [CrossRef]
- Shi, L. Research of coupling effects between the offshore RMB exchange rate and onshore exchange rate. Asian J. Empir. Res. 2016, 6, 201–209. [Google Scholar]
- Sornette, D.; Zhou, W. Non-parametric determination of real-time lag structure between two time series: The ’optimal thermal causal path’ method. Quant. Finance 2005, 5, 577–591. [Google Scholar] [CrossRef]
- Zhou, W.; Sornette, D. Non-parametric determination of real-time lag structure between two time series: The “optimal thermal causal path” method with applications to economic data. J. Macroecon. 2006, 28, 195–224. [Google Scholar] [CrossRef]
- Zhou, W.; Sornette, D. Lead-lag cross-sectional structure and detection of correlated–anticorrelated regime shifts: application to the volatilities of inflation and economic growth rates. Phys. A Stat. Mech. Its Appl. 2007, 380, 287–296. [Google Scholar] [CrossRef][Green Version]
- Stoop, M. Credit Creation and Its Contribution to Financial Crises. Master’s Thesis, Swiss Federal institute of Technology Zurich, Zurich, Switzerland, 2010. [Google Scholar]
- Guo, C.; Zhou, W.X.; Cheng, S.W. Economy barometer analysis of China stock market—A dynamic analysis based on the thermal optimal path method. J. Manag. Sci. China 2012, 15, 1–10. [Google Scholar]
- Guo, K.; Sun, Y.; Qian, X. Can investor sentiment be used to predict the stock price? Dynamic analysis based on China stock market. Phys. A Stat. Mech. Its Appl. 2017, 469, 390–396. [Google Scholar] [CrossRef]
- Gong, C.; Ji, S.; Su, L.; Li, S.; Ren, F. The lead–lag relationship between stock index and stock index futures: A thermal optimal path method. Phys. A Stat. Mech. Its Appl. 2016, 444, 63–72. [Google Scholar] [CrossRef]
- Meng, H.; Zhou, W.; Sornette, D. Symmetric thermal optimal path and time-dependent lead-lag relationship: novel statistical tests and application to UK and US real-estate and monetary policies. Quant. Finance 2017, 17, 959–977. [Google Scholar] [CrossRef]
- Wang, D.; Tu, J.; Chang, X.; Li, S. The lead-lag relationship between the spot and futures markets in China. Quant. Finance 2017, 17, 1447–1456. [Google Scholar] [CrossRef]
- Jia, R.; Wang, D.; Tu, J.; Li, S. Correlation between agricultural markets in dynamic perspective—Evidence from China and the US futures markets. Phys. A Stat. Mech. Its Appl. 2016, 464, 83–92. [Google Scholar] [CrossRef]
- Wang, X.; Guo, K.; Lu, X. The long-run dynamic relationship between exchange rate and its attention index: Based on DCCA and TOP method. Phys. A Stat. Mech. Its Appl. 2016, 453, 108–115. [Google Scholar] [CrossRef]
- Xu, H.; Zhou, W.; Sornette, D. Time-dependent lead-lag relationship between the onshore and offshore Renminbi exchange rates. J. Int. Financ. Mark. Inst. Money 2017, 49, 173–183. [Google Scholar] [CrossRef]
- Galati, G. Trading Volumes, Volatility and Spreads in Foreign Exchange Markets: Evidence from Emerging Market Countries; Working Paper, No. 93; Bank for International Settlements: Basel, Switzerland, 2000. [Google Scholar]
- Eraslan, S. Asymmetric arbitrage trading on offshore and onshore renminbi markets. Empir. Econ. 2018, 1–23. [Google Scholar] [CrossRef]
- Cushnie, L. Opinion: Regulators need to do more to improve CNH liquidity. Asia Money 2012, 23, 38. [Google Scholar]
- Craig, R.; Hua, C.; Ng, P.; Yuen, R. Chinese Capital Account Liberalization and the Internationalization of the Renminbi; IMF Working Paper WP/13/268; IMF: Washington, DC, USA, 2013. [Google Scholar]
- Funke, M.; Shu, C.; Cheng, X.; Eraslan, S. Assessing the CNH-CNY pricing differential: Role of fundamentals, contagion and policy. J. Int. Money Finance 2015, 59, 245–262. [Google Scholar] [CrossRef]
- Danese, P. HKMA boosts CNH liquidity in time of need. Global Capital. 2016, 11, 212. [Google Scholar]
- Hui, R. HKEX highlights need for better CNH liquidity. Global Capital. 2017, 1, 1. [Google Scholar]
- Corwin, S.A.; Schultz, P.H. A simple way to estimate bid-ask spreads from daily high and low prices. J. Finance 2012, 67, 719–760. [Google Scholar] [CrossRef]
- Ma, Y.; Kanas, A. Testing for a nonlinear relationship among fundamentals and exchange rates in the ERM. J. Int. Money Finance 2000, 19, 135–152. [Google Scholar] [CrossRef]
- Bekiros, S.D.; Diks, C.G.H. The nonlinear dynamic relationship of exchange rates: Parametric and nonparametric causality testing. J. Macroecon. 2008, 30, 1641–1650. [Google Scholar] [CrossRef]
| Notation | Explanation |
|---|---|
| USD / CNY closing price on day t, t = 0,1,2,…,n | |
| USD / CNH closing price on day t, t = 0,1,2,…,n | |
| the highest USD / CNY spot rate over the two days t and t + 1, t = 0,1,2,…,n − 1 | |
| the lowest USD / CNH spot rate over the two days t and t + 1, t = 0,1,2,…,n − 1 | |
| the spread between bid and ask price of CNY spot on day t, t = 0,1,2,…,n − 1 | |
| the spread between bid and ask price of CNH spot on day t, t = 0,1,2,…,n − 1 |
| Variable | Mean | Stand Deviation | Maximum | Minimum |
|---|---|---|---|---|
| 0.0017 | 0.0015 | 0.0061 | 0 | |
| 0.0044 | 0.0028 | 0.0095 | 0 |
| H0: Time Series Has a Unit Root; H1: Time Series Is Stationary | ||
|---|---|---|
| Time Series | ADF Statistic | p-Value |
| 0.17939 | 0.99 | |
| −0.30993 | 0.99 | |
| −9.7336 | 0.01 *** | |
| −10.797 | 0.01 *** | |
| −6.8676 | 0.01 *** | |
| −4.5958 | 0.01 *** | |
| Null Hypothesis H0 | Does Not Cause | Does Not Cause | CNY BAS Does Not Cause CNHBAS | CNH BAS Does Not Cause CNYBAS |
|---|---|---|---|---|
| F-Statistic | 2.13577 | 8.48935 | 1.93456 | 3.20295 |
| p-Value | 0.0589 | 7E−08 | 0.0859 | 0.0070 |
| Test result | Reject H0 | Reject H0 | Reject H0 | Reject H0 |
| Parameter | ||||||||
|---|---|---|---|---|---|---|---|---|
| Estimation p-Value | Estimation p-Value | Estimation p-Value | Estimation p-Value | |||||
| α0 | 3.3E−05 | 0.4408 | 0.0001 | 0.3814 | 0.0003 | 3.4E−06 | 0.0007 | 3.48E−11 |
| α1 | −0.1522 | 0.0792 * | −0.0505 | 0.0875 | 0.5133 | 6E−58 *** | 0.7191 | 6.67E−102 |
| α2 | −0.1319 | 0.0002 *** | −0.0177 | 0.0203 | 0.0430 | 0.1356 | −0.0845 | 0.0114 |
| α3 | 0.0128 | 0.3660 | −0.1474 | 4.83E−5 *** | 0.0034 | 0.4602 | 0.1158 | 0.0009 *** |
| α4 | −0.0281 | 0.2227 | −0.0984 | 0.0047 | 0.0734 | 0.0158 | 0.0123 | 0.3697 |
| α5 | 0.0217 | 0.2738 | 0.0009 | 0.4903 | 0.0948 | 0.0010 | 0.0782 | 0.0053 |
| β1 | 0.1380 | 1.5E−8 *** | 0.1522 | 0.0032 *** | 0.0732 | 9E−05 *** | 0.0404 | 0.1986 |
| β2 | 0.1014 | 3.1E−5 *** | 0.0690 | 0.2468 | −0.0349 | 0.0698 | −0.0557 | 0.0060 *** |
| β3 | 0.0047 | 0.4253 | 0.0385 | 0.0517 | 0.0048 | 0.4197 | −0.1001 | 0.0309 |
| β4 | 0.0260 | 0.1506 | 0.0905 | 0.0517 | −0.0183 | 0.2190 | 0.1346 | 0.1488 |
| β5 | 0.0475 | 0.0283 | 0.0134 | 0.4026 | 0.0073 | 0.3534 | −0.0427 | 0.1871 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, D.; Lai, K.K. An Analysis of China’s Onshore and Offshore Exchange Rates—Adjusted Thermal Optimal Path Approach Based on Pruning and Path Segmentation. Entropy 2019, 21, 499. https://doi.org/10.3390/e21050499
Yan D, Lai KK. An Analysis of China’s Onshore and Offshore Exchange Rates—Adjusted Thermal Optimal Path Approach Based on Pruning and Path Segmentation. Entropy. 2019; 21(5):499. https://doi.org/10.3390/e21050499
Chicago/Turabian StyleYan, Dawen, and Kin Keung Lai. 2019. "An Analysis of China’s Onshore and Offshore Exchange Rates—Adjusted Thermal Optimal Path Approach Based on Pruning and Path Segmentation" Entropy 21, no. 5: 499. https://doi.org/10.3390/e21050499
APA StyleYan, D., & Lai, K. K. (2019). An Analysis of China’s Onshore and Offshore Exchange Rates—Adjusted Thermal Optimal Path Approach Based on Pruning and Path Segmentation. Entropy, 21(5), 499. https://doi.org/10.3390/e21050499




