A Novel Uncertainty Management Approach for Air Combat Situation Assessment Based on Improved Belief Entropy
Abstract
1. Introduction
2. Preliminaries
2.1. Dempster–Shafer Evidence Theory
2.2. Improved Belief Entropy
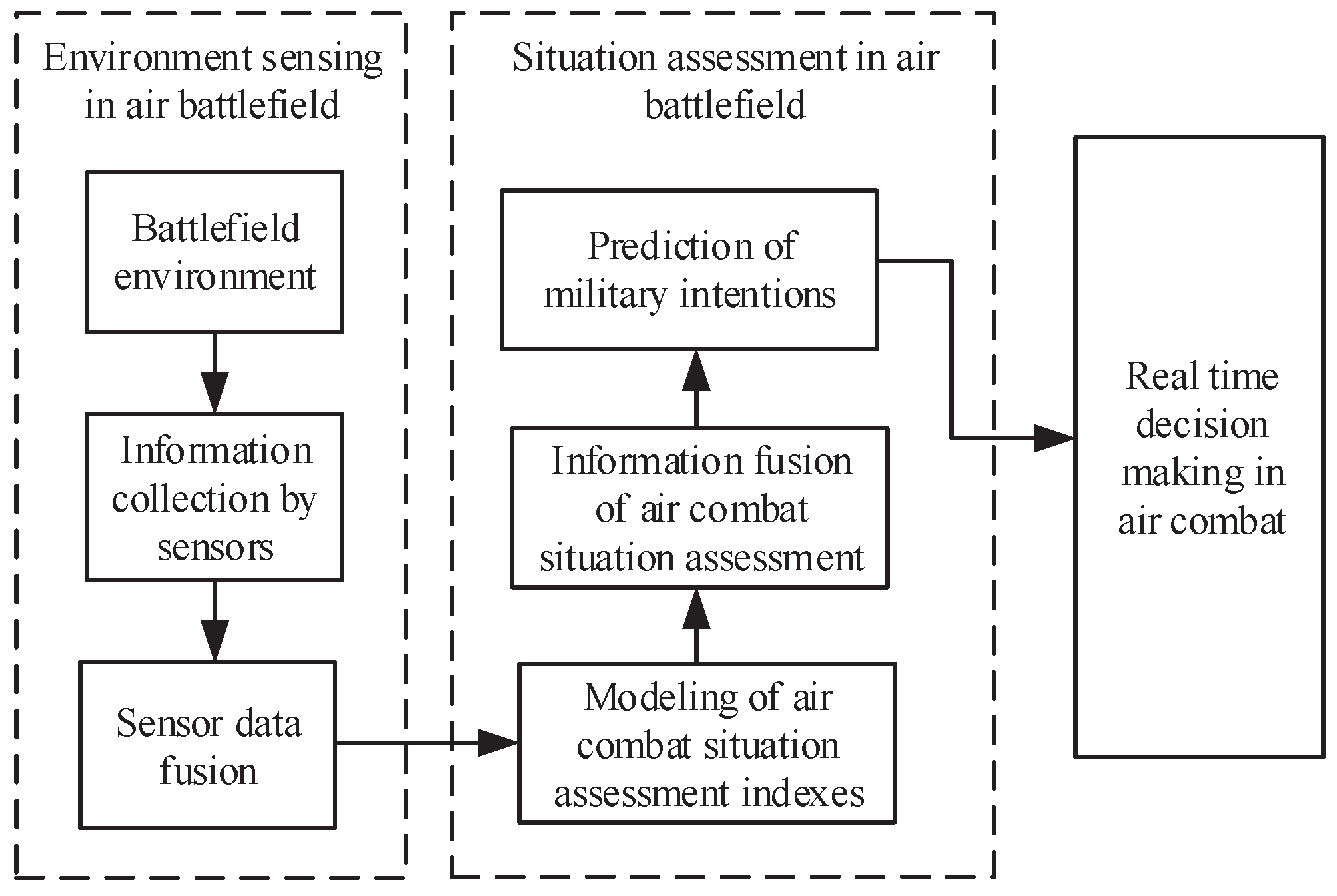
3. Improved Belief Entropy-Based Situation Assessment Method for Air Combat
- Step 1: battlefield environment information modelingAll the information about the two sides in the battlefield, the weather, the terrain, the international political situation, and the military expert assessment information should be included in the model of the battlefield environment.
- Step 2: sensor information acquisitionBattlefield information acquisition will be based on many kinds of sensors, including satellites, air reconnaissance aircraft, ground-based radar, airborne radars, and intelligence agent.
- Step 3: sensor data fusionThe heterogeneous sensor information acquired from the previous step will be fused for air combat situation assessment. The sensor data fusion method needs to be chosen cautiously, which is another important issue.
- Step 4: air combat situation understanding and evidence modelingSensor data fusion results shall be modeled in the DST framework based on air combat situation understanding. The knowledge in the military domain includes clustering analysis of multi-enemy targets, behavior analysis of the enemy, etc.
- Step 5: IBE-based uncertainty measure and preprocessing of the evidence for situation assessmentBefore applying evidence fusion of the situation assessment information, the uncertainty of each evidence is measured and applied for evidence modification. If evidence has a high degree of uncertainty, which is represented by a high value of IBE, then the reliability of the evidence is low, which means the evidence makes a small contribution to the final decision. Based on this cautious rule, the preprocessing of the evidence based on the uncertainty measure results will be based on the following function:where means the modified evidence after preprocessing, () is the ith piece of evidence coming from air combat situation understanding and evidence modeling, and is the IBE defined in Equation (4).
- Step 6: information fusion of air combat situation assessment and the prediction of military intentionIn this paper, Dempster’s rule of combination is chosen for information fusion after evidence modification. The prediction of military intention will be based on the fused situation assessment information. If the evidence modification is based on () pieces of evidence, the time of information fusion for the modified evidence is n.where ⊕ refers to the information fusion of the modified evidence , which is based on Dempster’s rule of combination in Equation (3).
- Step 7: real-time decision-making of air combatReal-time decision-making in air combat situation assessment aided by the aforementioned intelligent information fusion method will be used to support the pilots and commanders.
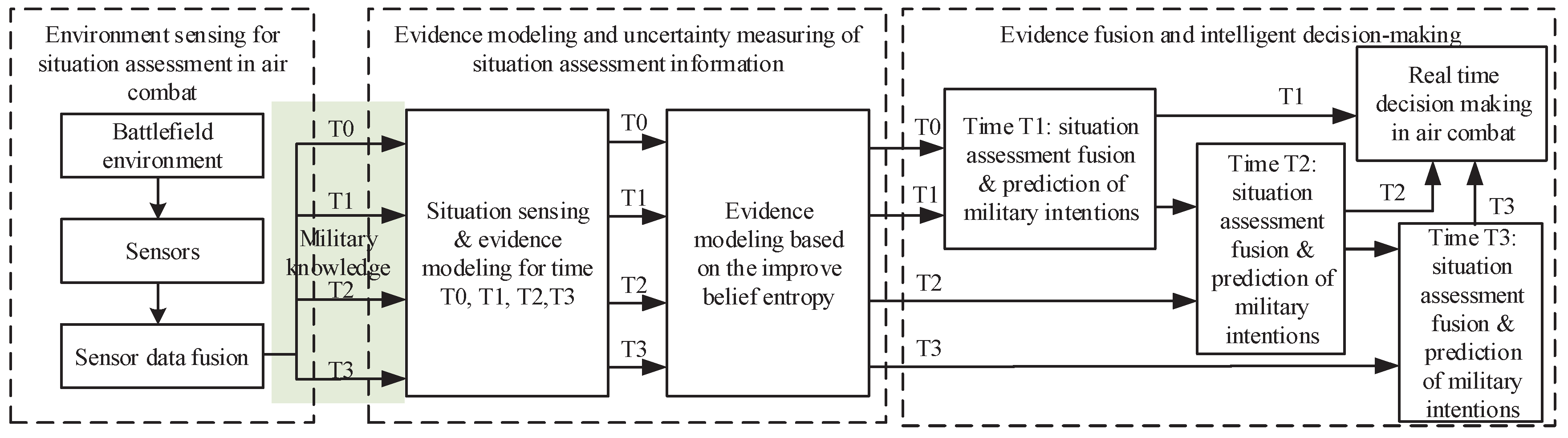
4. Example
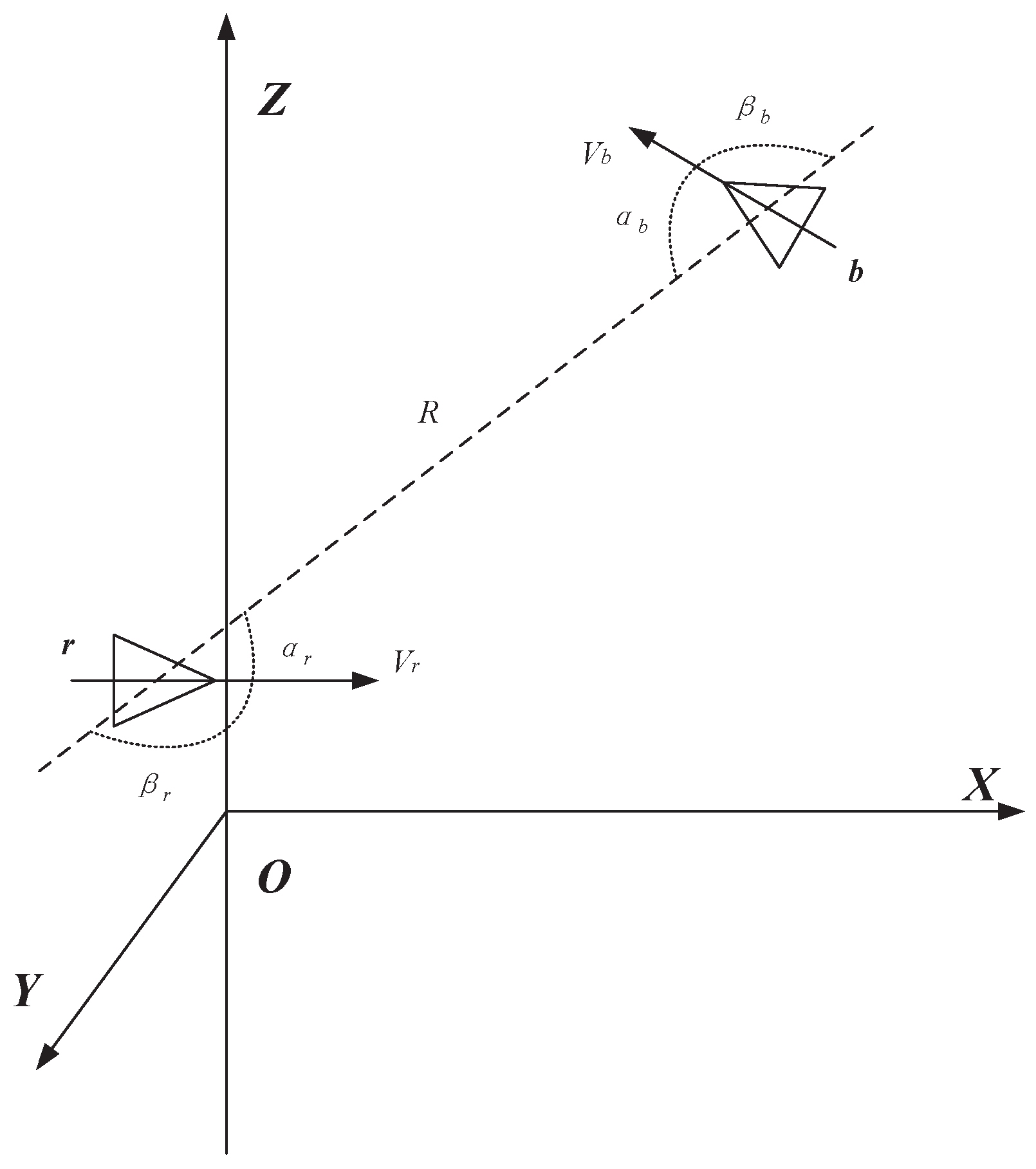
4.1. Problem Description
4.2. Implementation Steps
- At time T0, the sensor reports event , and a fighter plane appears. The distance is 100 km, the speed is Mach 1.2, and the military intentions are not clear. The evidence modeling based on the military knowledge is .
- At time T1, the sensor reports event , and the fighter plane is approaching at Mach 1.8. The evidence modeling based on military knowledge is .
- At time T2, the sensor reports event , and the fighter plane is approaching at Mach 2.2. The evidence modeling based on the military knowledge is .
- At time T3, the sensor reports event , and the fighter plane is still approaching at a high speed. In addition, its fire control radar is turned on, the attack situation becomes obvious, and the evidence modeling based on the military knowledge is .
5. Discussion and Open Issues
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ernest, N.; Carroll, D.; Schumacher, C.; Clark, M.; Cohen, K.; Lee, G. Genetic fuzzy based artificial intelligence for unmanned combat aerial vehicle control in simulated air combat missions. J. Def. Manag. 2016, 6, 2167-0374. [Google Scholar] [CrossRef]
- Lei, X.; Huang, A.; Zhao, T.; Su, Y.; Ren, C. A New Machine Learning Framework for Air Combat Intelligent Virtual Opponent. J. Phys. Conf. Ser. 2018, 1069, 012031. [Google Scholar] [CrossRef]
- Jin, X. Simulation Game System: A Possible Way to Realize Intelligent Command and Control. In Advances in Computer Science and Ubiquitous Computing; Springer: Berlin, Germany, 2017; pp. 560–565. [Google Scholar]
- Duan, H.; Shao, S.; Su, B.; Zhang, L. New development thoughts on the bio-inspired intelligence based control for unmanned combat aerial vehicle. Sci. China Technol. Sci. 2010, 53, 2025–2031. [Google Scholar] [CrossRef]
- Shetty, V.K.; Sudit, M.; Nagi, R. Priority-based assignment and routing of a fleet of unmanned combat aerial vehicles. Comput. Oper. Res. 2008, 35, 1813–1828. [Google Scholar] [CrossRef]
- Xu, X.; Yang, R.; Fu, Y. Situation assessment for air combat based on novel semi-supervised naive Bayes. J. Syst. Eng. Electron. 2018, 29, 768–779. [Google Scholar]
- Das, S.; Grey, R.; Gonsalves, P. Situation assessment via Bayesian belief networks. In Proceedings of the Fifth International Conference on Information Fusion, FUSION 2002, Annapolis, MD, USA, 8–11 July 2002; Volume 1, pp. 664–671. [Google Scholar]
- Wang, L.; Wang, M. Modeling of combined Bayesian networks and cognitive framework for decision-making in C2. J. Syst. Eng. Electron. 2010, 21, 812–820. [Google Scholar] [CrossRef]
- Prabhu, A.; Manivannan, H.; Sridhar, K.; Ahmed, S.; Shrinivasan, L. Decision fusion using type-1 fuzzy logic for situation assessment in aviation scenarios. In Proceedings of the 2014 International Conference on Advances in Electronics Computers and Communications, Bangalore, India, 10–11 October 2014; pp. 1–6. [Google Scholar]
- McAnally, K.; Davey, C.; White, D.; Stimson, M.; Mascaro, S.; Korb, K. Inference in the Wild: A Framework for Human Situation Assessment and a Case Study of Air Combat. Cogn. Sci. 2018, 42, 2181–2204. [Google Scholar] [CrossRef]
- Chen, G.; Shen, D.; Kwan, C.; Cruz, J.B.; Kruger, M. Game Theoretic Approach to Threat Prediction and Situation Awareness. In Proceedings of the 2006 9th International Conference on Information Fusion, Florence, Italy, 10–13 July 2006; pp. 1–8. [Google Scholar]
- Dempster, A.P. Upper and Lower Probabilities Induced by a Multi-valued Mapping. Ann. Math. Stat. 1967, 38, 325–339. [Google Scholar] [CrossRef]
- Shafer, G. A Mathematical Theory of Evidence; Princeton University Press: Princeton, NJ, USA, 1976. [Google Scholar]
- Zhou, K.; Martin, A.; Pan, Q.; Liu, Z. SELP: Semi–supervised evidential label propagation algorithm for graph data clustering. Int. J. Approx. Reason. 2017, 92, 139–154. [Google Scholar] [CrossRef]
- Liu, Z.G.; Pan, Q.; Dezert, J.; Martin, A. Adaptive imputation of missing values for incomplete pattern classification. Pattern Recognit. 2016, 52, 85–95. [Google Scholar] [CrossRef]
- Xiao, F. Multi-sensor data fusion based on the belief divergence measure of evidences and the belief entropy. Inf. Fusion 2019, 46, 23–32. [Google Scholar] [CrossRef]
- Liu, Z.G.; Pan, Q.; Dezert, J.; Martin, A. Combination of Classifiers with Optimal Weight Based on Evidential Reasoning. IEEE Trans. Fuzzy Syst. 2018, 26, 1217–1230. [Google Scholar] [CrossRef]
- Su, X.; Mahadevan, S.; Xu, P.; Deng, Y. Dependence Assessment in Human Reliability Analysis Using Evidence Theory and AHP. Risk Anal. 2015, 35, 1296–1316. [Google Scholar] [CrossRef]
- Zhou, D.; Tang, Y.; Jiang, W. An Improved Belief Entropy and Its Application in Decision-Making. Complexity 2017, 4359195. [Google Scholar] [CrossRef]
- Wang, X.; Song, Y. Uncertainty measure in evidence theory with its applications. Appl. Intell. 2017, 48, 1672–1688. [Google Scholar] [CrossRef]
- Cui, H.; Liu, Q.; Zhang, J.; Kang, B. An improved Deng entropy and its application in pattern recognition. IEEE Access 2019. [Google Scholar] [CrossRef]
- Ozkan, K. Comparing Shannon entropy with Deng entropy and improved Deng entropy for measuring biodiversity when a priori data is not clear. J. Fac. For.-Istanb. Univ. 2018, 68, 136–140. [Google Scholar]
- Song, Y.; Wang, X.; Lei, L.; Yue, S. Uncertainty measure for interval-valued belief structures. Measurement 2015, 80, 241–250. [Google Scholar] [CrossRef]
- Pan, L.; Deng, Y. A New Belief Entropy to Measure Uncertainty of Basic Probability Assignments Based on Belief Function and Plausibility Function. Entropy 2018, 20, 842. [Google Scholar] [CrossRef]
- Tang, Y.; Zhou, D.; Chan, F.T. Extending Deng Entropy to the Open World in the Evidence Theory. In Proceedings of the 2018 21st International Conference on Information Fusion (FUSION), Cambridge, UK, 10–13 July 2018; pp. 629–634. [Google Scholar]
- Tang, Y.; Zhou, D.; Chan, F. An extension to Deng’s entropy in the open world assumption with an application in sensor data fusion. Sensors 2018, 18, 1902. [Google Scholar] [CrossRef]
- Jiroušek, R.; Shenoy, P.P. A new definition of entropy of belief functions in the Dempster–Shafer theory. Int. J. Approx. Reason. 2018, 92, 49–65. [Google Scholar] [CrossRef]
- Deng, Y. Deng entropy. Chaos Solitons Fractals 2016, 91, 549–553. [Google Scholar] [CrossRef]
- Tang, Y.; Zhou, D.; Xu, S.; He, Z. A Weighted Belief Entropy-Based Uncertainty Measure for Multi-Sensor Data Fusion. Sensors 2017, 17, 928. [Google Scholar] [CrossRef]
- Nguyen, X.T. Threat assessment in tactical airborne environments. In Proceedings of the Fifth International Conference on Information Fusion, FUSION 2002, (IEEE Cat. No. 02EX5997), Annapolis, MD, USA, 8–11 July 2002; Volume 2, pp. 1300–1307. [Google Scholar]
- Mulgund, S.; Rinkus, G.; Illgen, C.; Friskie, J. Olipsa: On-line intelligent processor for situation assessment. In Proceedings of the Second Annual Symposium and Exhibition on Situational Awareness in the Tactical Air Environment, Patuxent River, MD, USA, 3–4 June 1997. [Google Scholar]
- Hix, D.; Swan, J.E.; Gabbard, J.L.; McGee, M.; Durbin, J.; King, T. User-centered design and evaluation of a real-time battlefield visualization virtual environment. In Proceedings of the IEEE Virtual Reality (Cat. No. 99CB36316), Houston, TX, USA, 13–17 March 1999; pp. 96–103. [Google Scholar]
- Jameson, S.M. Architectures for distributed information fusion to support situation awareness on the digital battlefield. In Proceedings of the 4th International Conference on Data Fusion, New York, NY, USA, 2–6 April 2001; pp. 7–10. [Google Scholar]
- Zhou, W.; Xiao-yuan, P.; Ning, L. Key Technologies in Construction of Network-Centric Warfare Concept Based Virtual Battlefield. J. Syst. Simul. 2005, 17, 1294–1298. [Google Scholar]
- Deng, X.; Liu, Q.; Deng, Y.; Mahadevan, S. An improved method to construct basic probability assignment based on the confusion matrix for classification problem. Inf. Sci. 2016, 340, 250–261. [Google Scholar] [CrossRef]
- Tang, Y.; Zhou, D.; Jiang, W. A New Fuzzy-Evidential Controller for Stabilization of the Planar Inverted Pendulum System. PLoS ONE 2016, 11, e0160416. [Google Scholar] [CrossRef]
- Kurniawati, H.; Yadav, V. An online POMDP solver for uncertainty planning in dynamic environment. In Robotics Research; Springer: Berlin, Germany, 2016; pp. 611–629. [Google Scholar]
- Marco, E.; Meuleman, W.; Huang, J.; Glass, K.; Pinello, L.; Wang, J.; Kellis, M.; Yuan, G.C. Multi-scale chromatin state annotation using a hierarchical hidden Markov model. Nat. Commun. 2017, 8, 15011. [Google Scholar] [CrossRef]
- Ramasso, E. Contribution of belief functions to hidden Markov models with an application to fault diagnosis. In Proceedings of the 2009 IEEE International Workshop on Machine Learning for Signal Processing, Grenoble, France, 1–4 September 2009; pp. 1–6. [Google Scholar]
| Evaluation Code | ||||
|---|---|---|---|---|
| Situation Type | Attack | Defense | Escape | Feint |
| Time T0, | 0.25 | 0.25 | 0.25 | 0.25 |
| Time T1, | 0.3 | 0.2 | 0.2 | 0.3 |
| Time T2, | 0.4 | 0.1 | 0.2 | 0.3 |
| Time T3, | 0.7 | 0.1 | 0.1 | 0.1 |
| Evidence Modification | |||
|---|---|---|---|
| m(SA1) | 0.2754 | 0.3208 | 0.4623 |
| m(SA2) | 0.2246 | 0.1792 | 0.1496 |
| m(SA3) | 0.2246 | 0.2156 | 0.1725 |
| m(SA4) | 0.2754 | 0.2844 | 0.2156 |
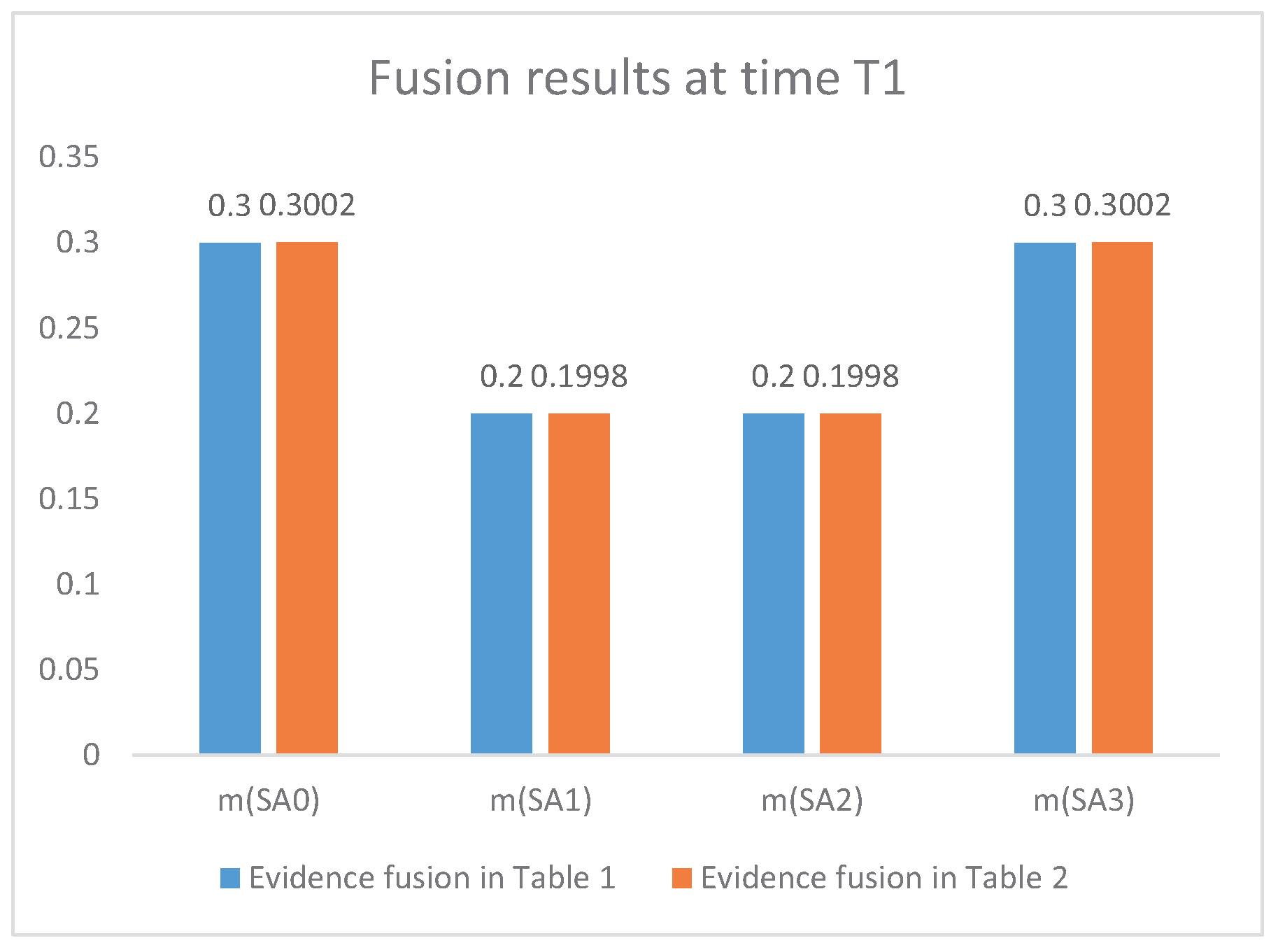
| Evidence Fusion | ||||
|---|---|---|---|---|
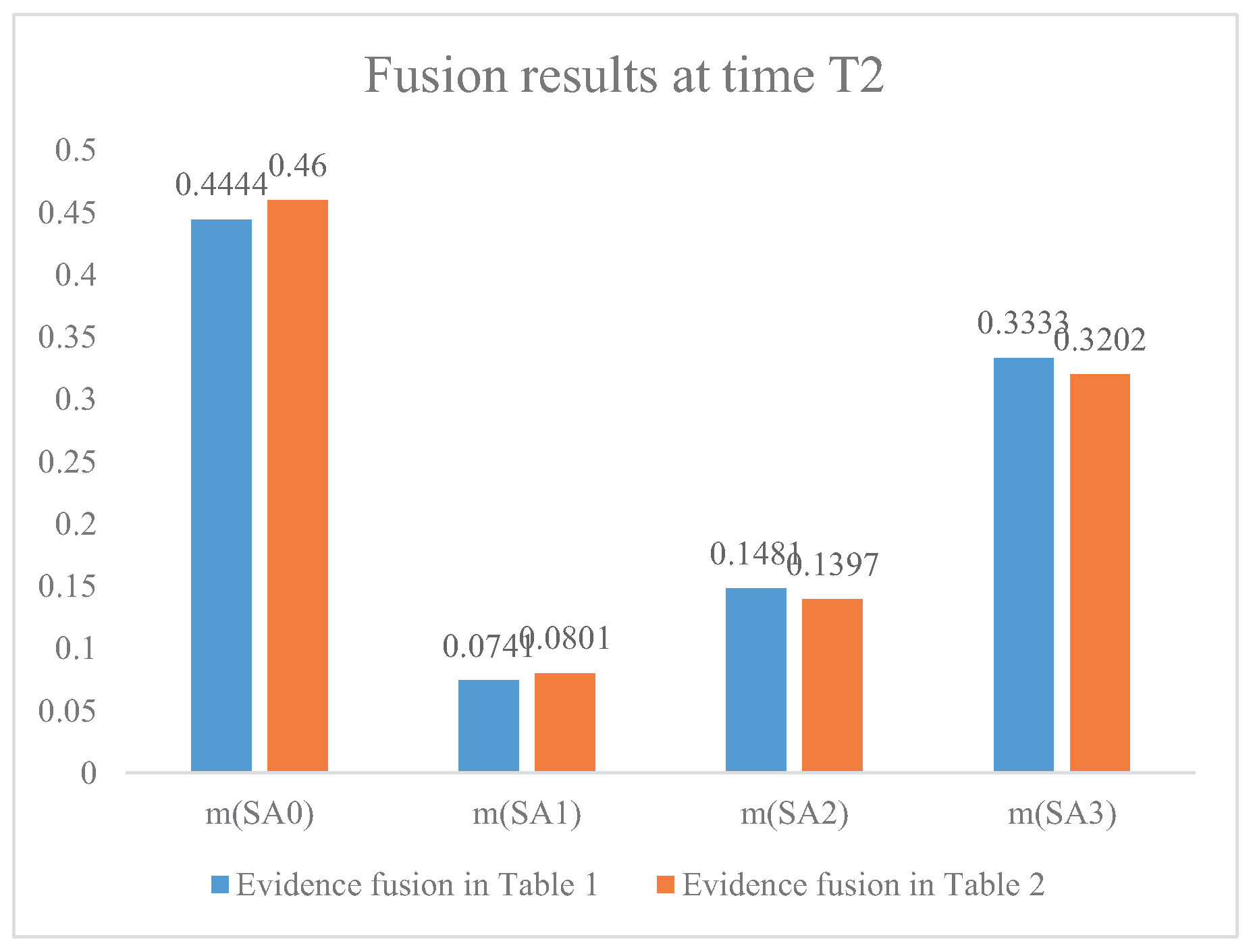
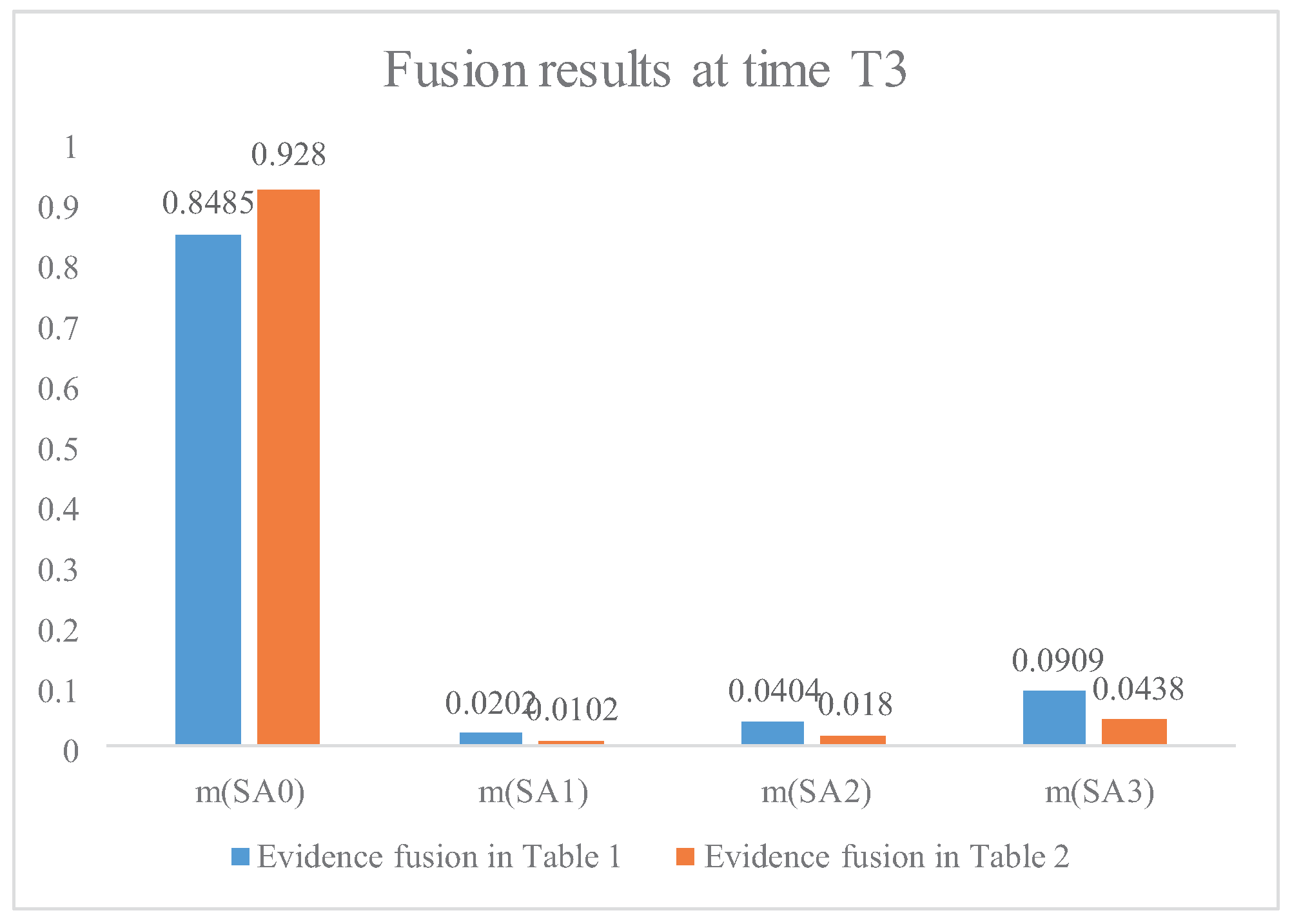
| Fusion of Table 1 | m(SA1) | 0.3000 | 0.4444 | 0.8485 |
| m(SA2) | 0.2000 | 0.0741 | 0.0202 | |
| m(SA3) | 0.2000 | 0.1481 | 0.0404 | |
| m(SA4) | 0.3000 | 0.3333 | 0.0909 | |
| Fusion of Table 2 | m(SA1) | 0.3002 | 0.4600 | 0.9280 |
| m(SA2) | 0.1998 | 0.0801 | 0.0102 | |
| m(SA3) | 0.1998 | 0.1397 | 0.0180 | |
| m(SA4) | 0.3002 | 0.3202 | 0.0438 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Tang, Y.; Zhao, X. A Novel Uncertainty Management Approach for Air Combat Situation Assessment Based on Improved Belief Entropy. Entropy 2019, 21, 495. https://doi.org/10.3390/e21050495
Zhou Y, Tang Y, Zhao X. A Novel Uncertainty Management Approach for Air Combat Situation Assessment Based on Improved Belief Entropy. Entropy. 2019; 21(5):495. https://doi.org/10.3390/e21050495
Chicago/Turabian StyleZhou, Ying, Yongchuan Tang, and Xiaozhe Zhao. 2019. "A Novel Uncertainty Management Approach for Air Combat Situation Assessment Based on Improved Belief Entropy" Entropy 21, no. 5: 495. https://doi.org/10.3390/e21050495
APA StyleZhou, Y., Tang, Y., & Zhao, X. (2019). A Novel Uncertainty Management Approach for Air Combat Situation Assessment Based on Improved Belief Entropy. Entropy, 21(5), 495. https://doi.org/10.3390/e21050495





