Numerical Simulation of Entropy Generation for Power-Law Liquid Flow over a Permeable Exponential Stretched Surface with Variable Heat Source and Heat Flux
Abstract
1. Introduction
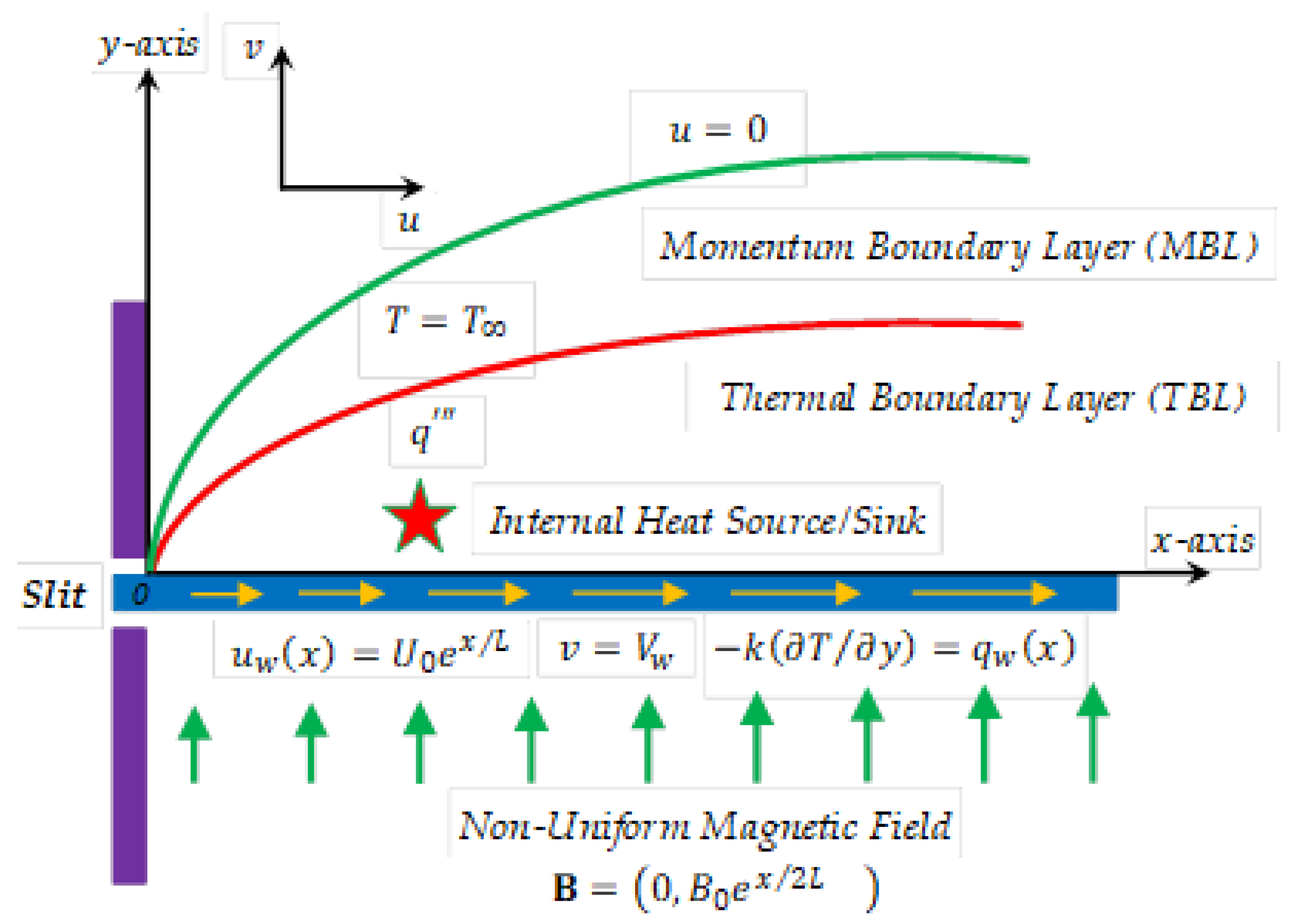
2. Definition of the Problem
3. Relevant Physical Measures
4. Entropy Generation and Bejan Number
5. Solution Methodology and Validation of Results
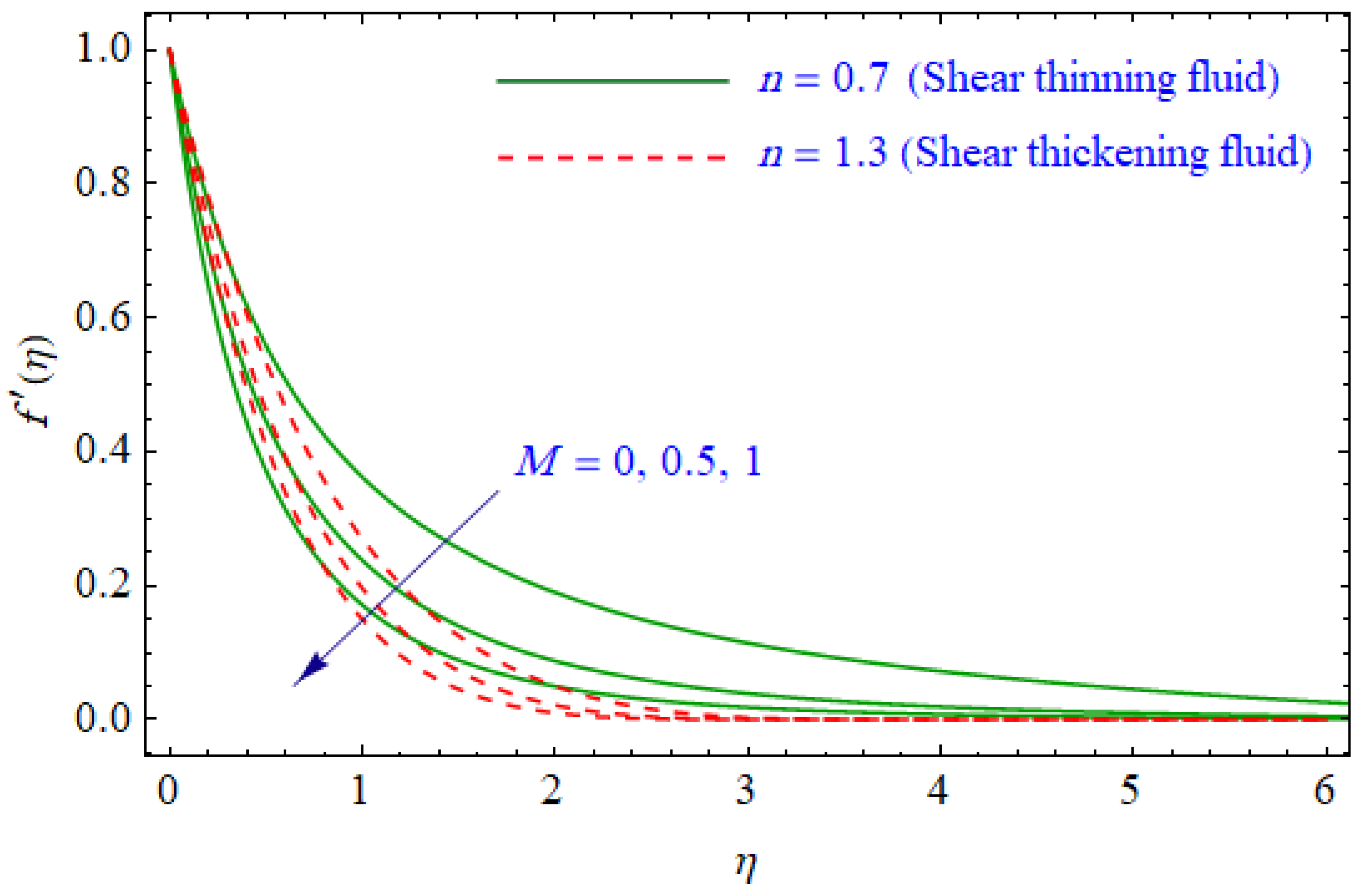
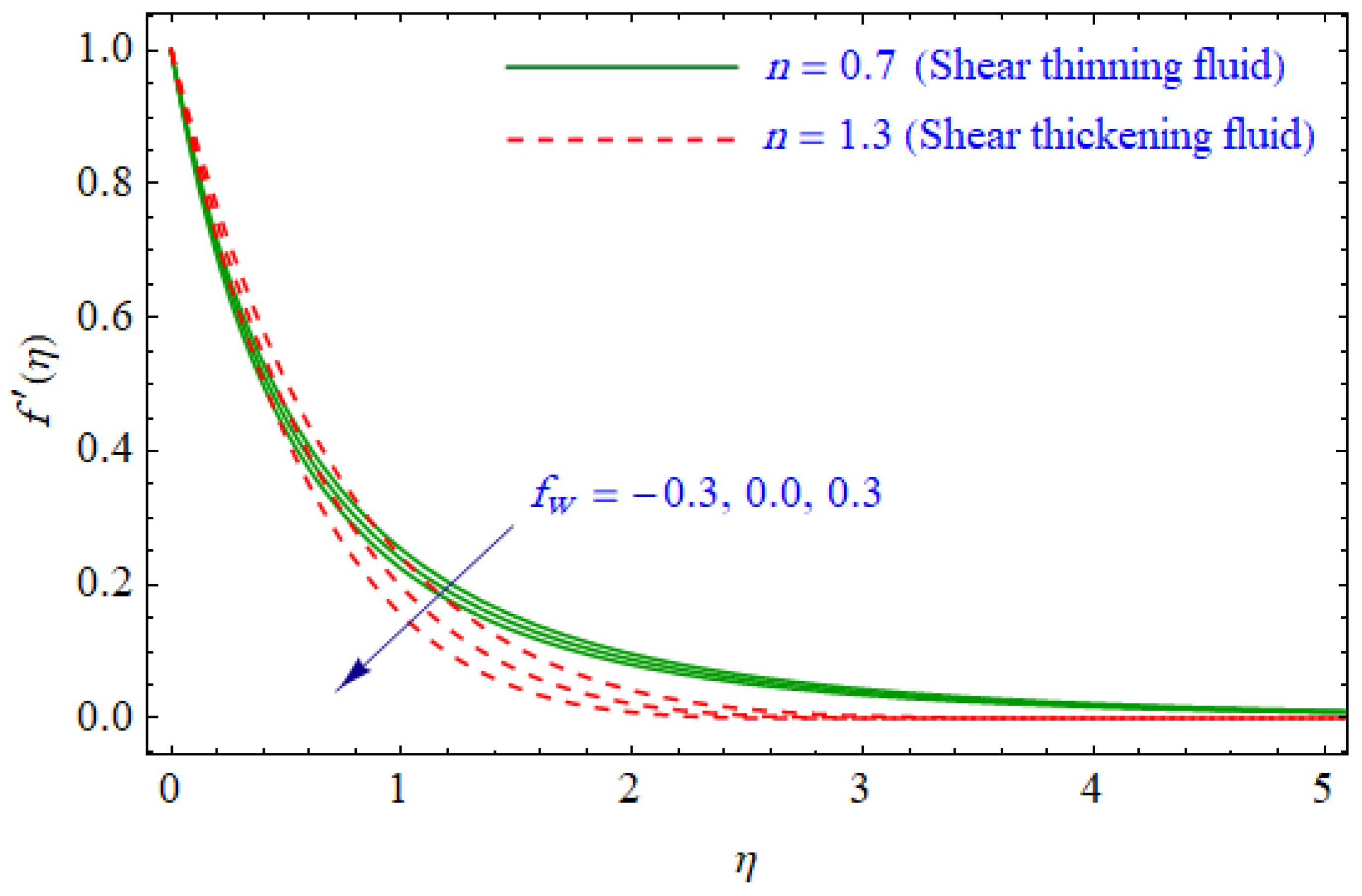
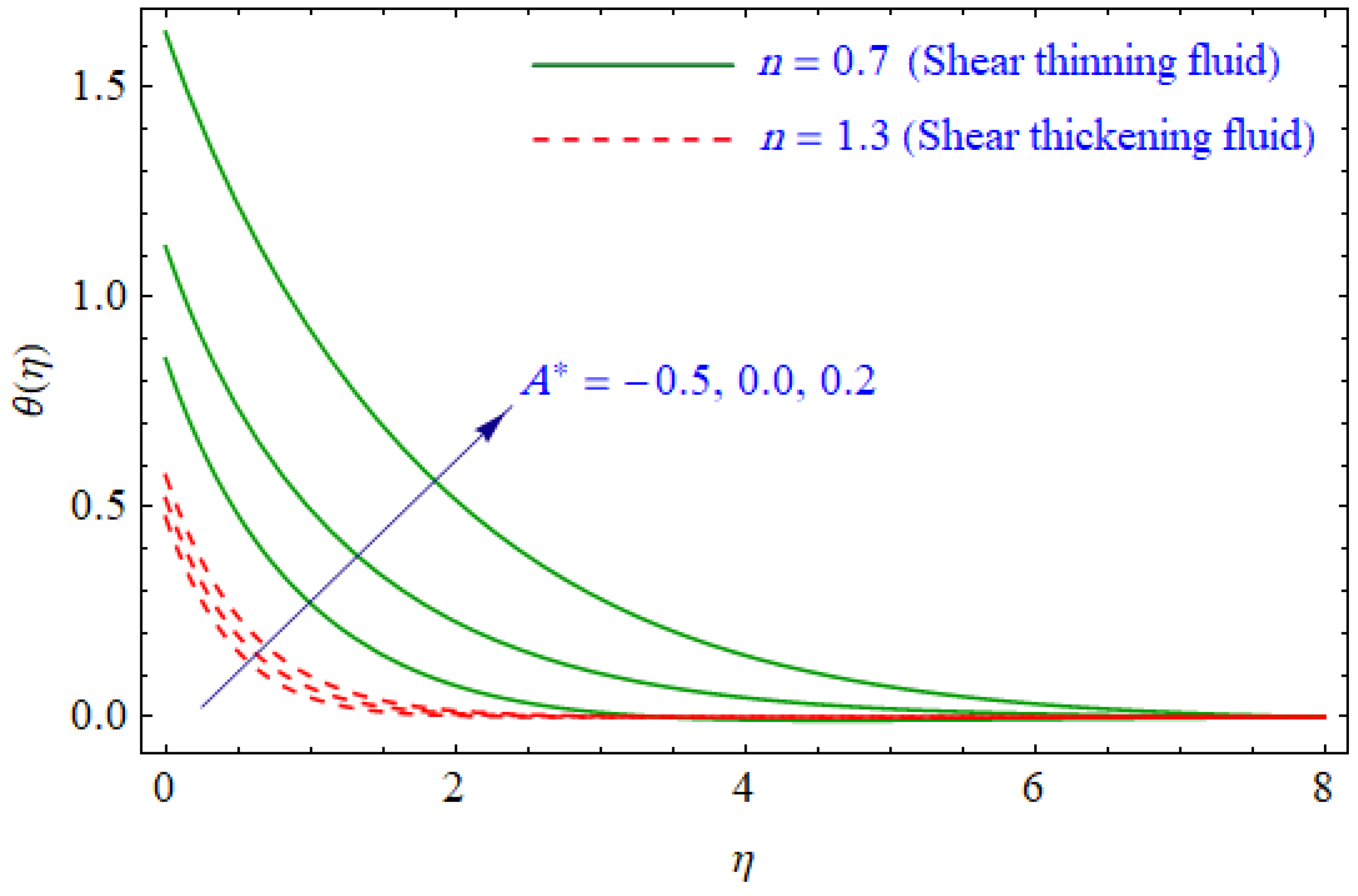
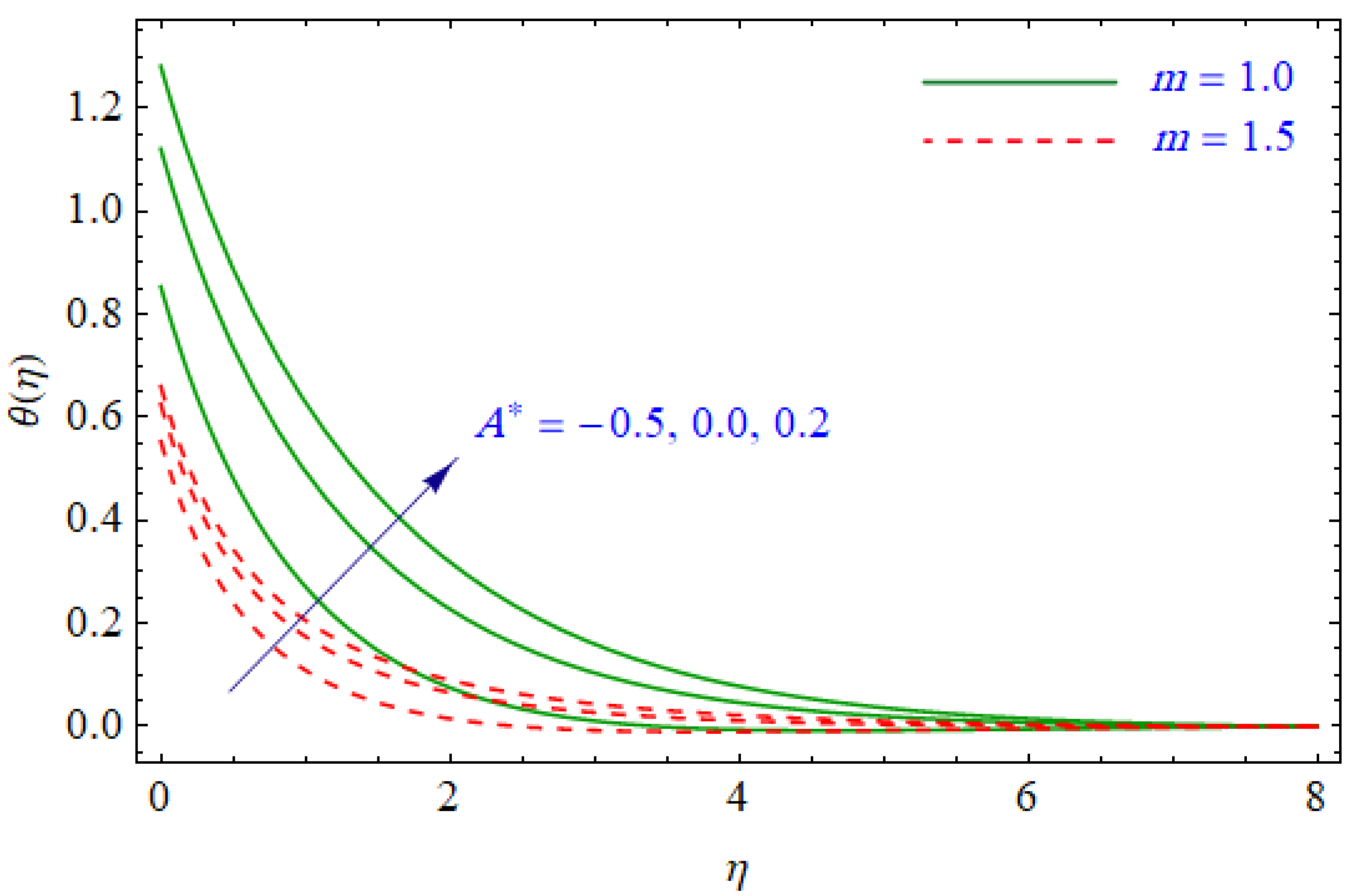
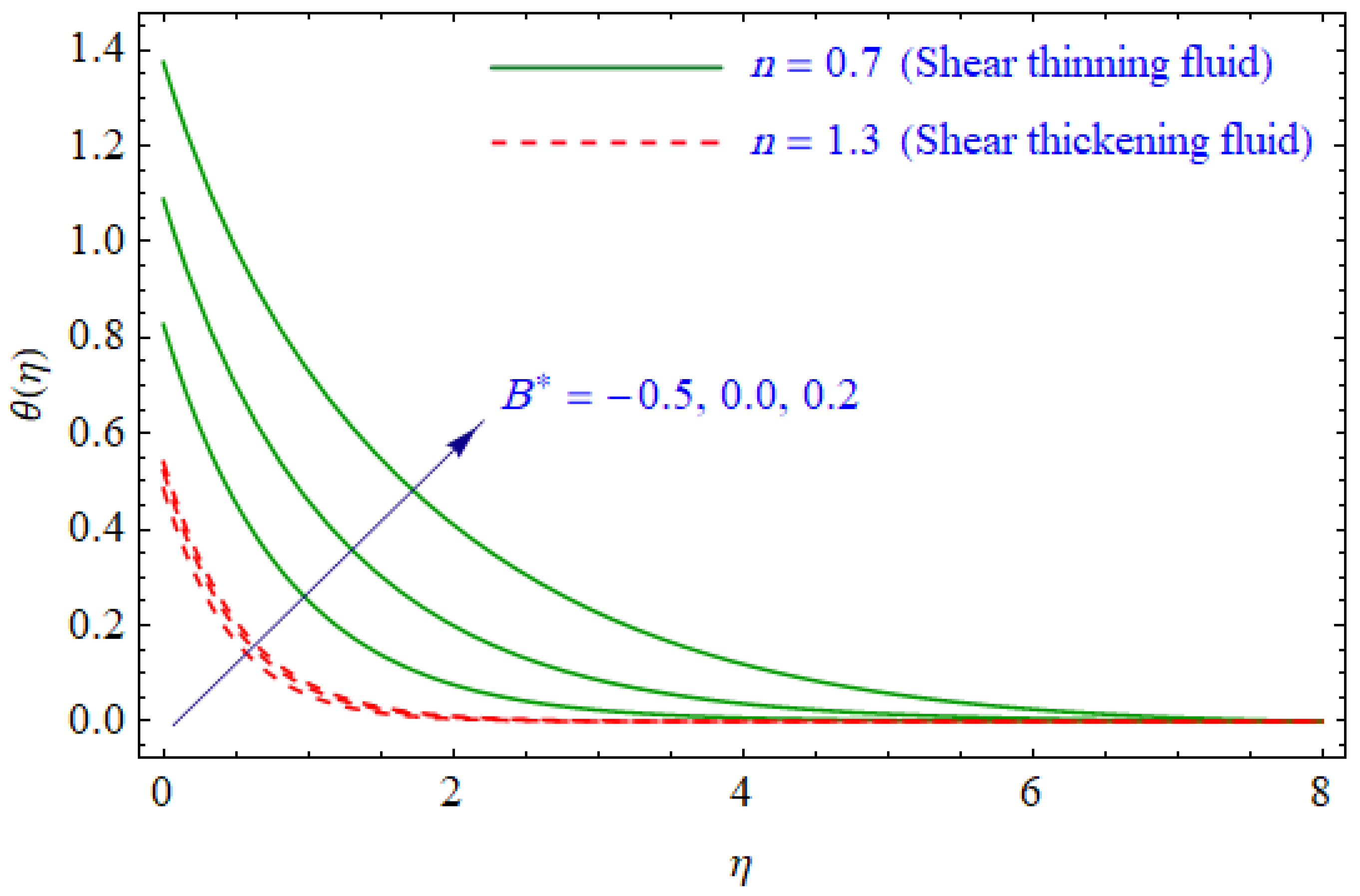
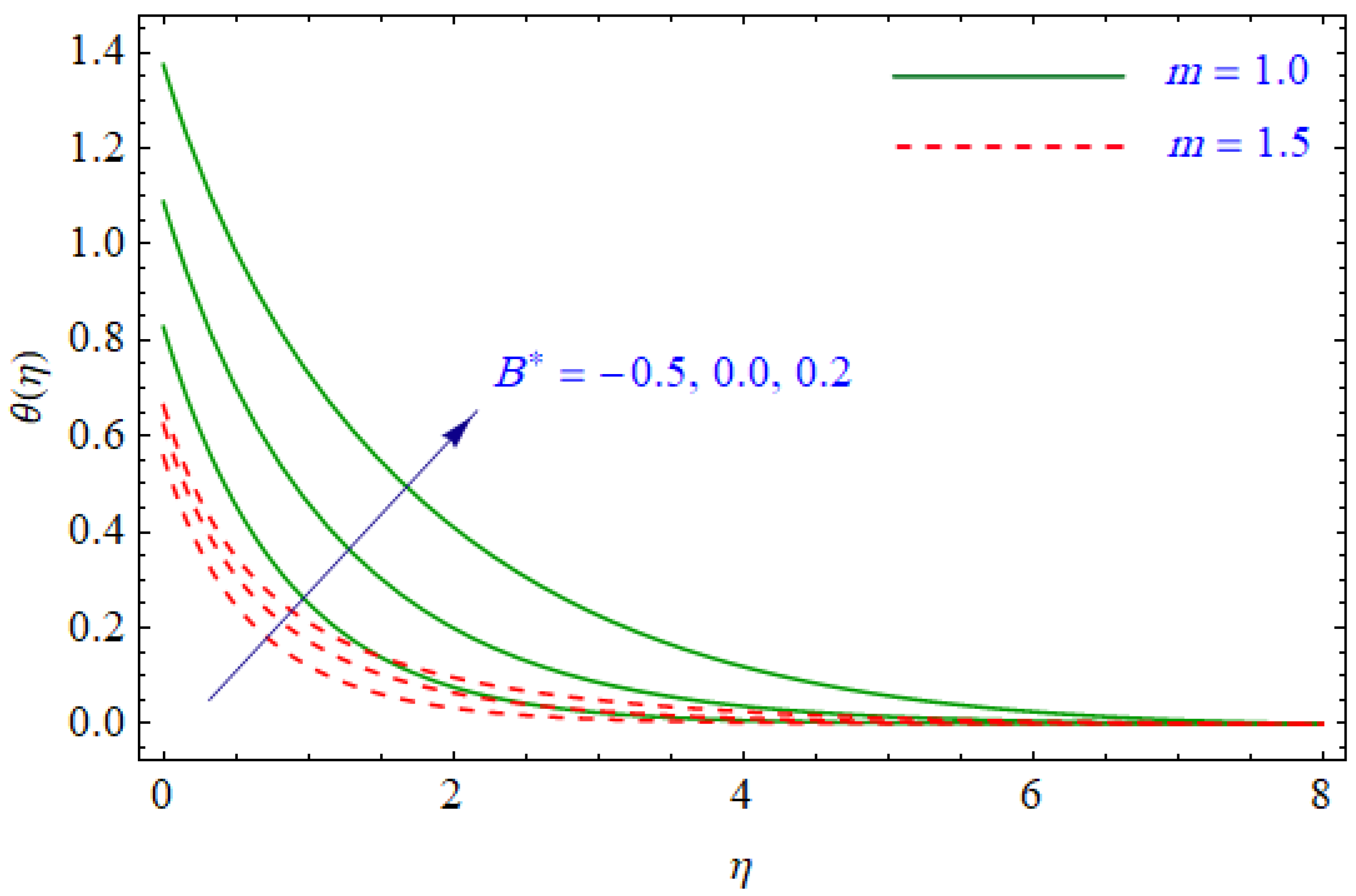
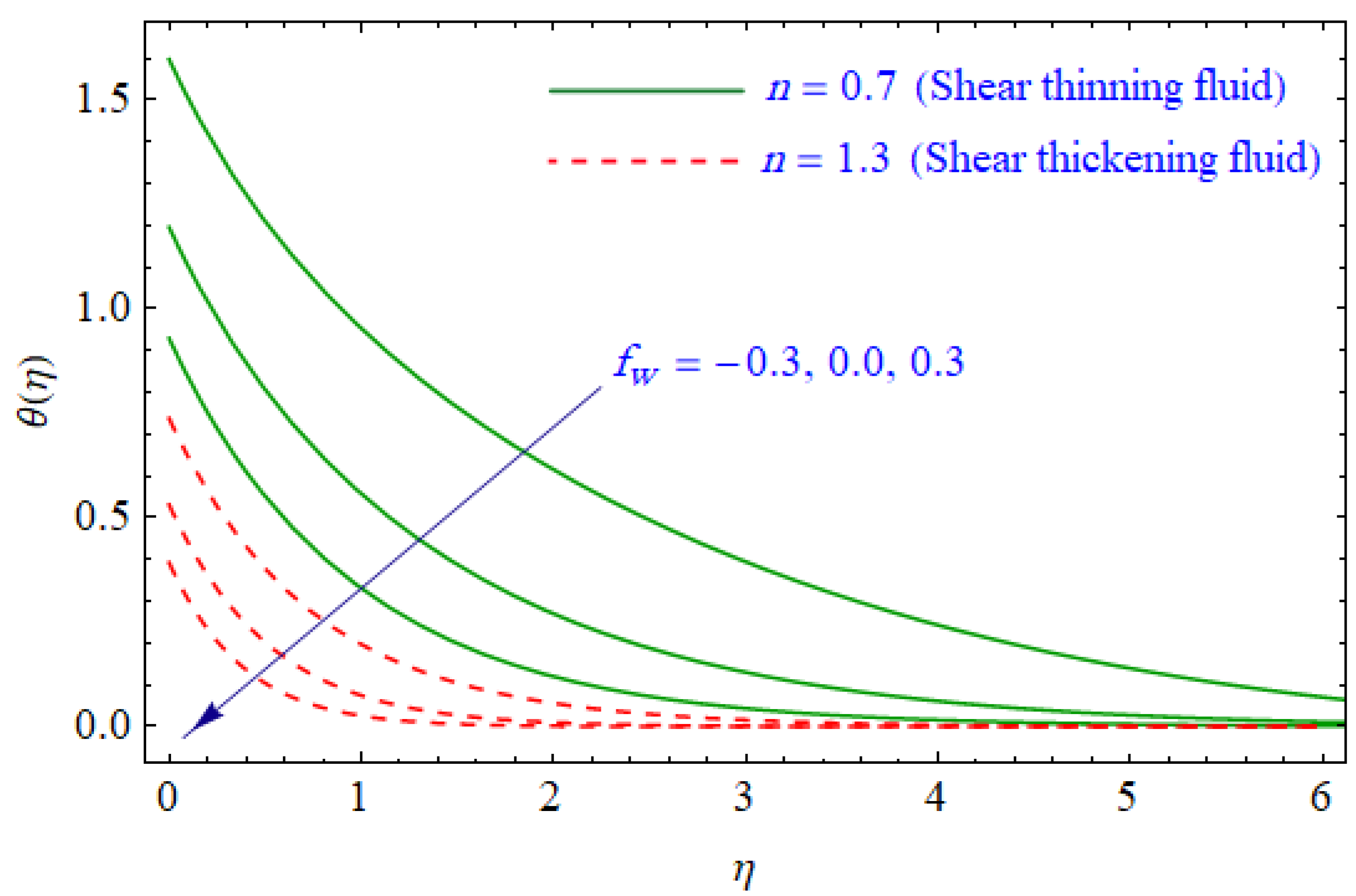
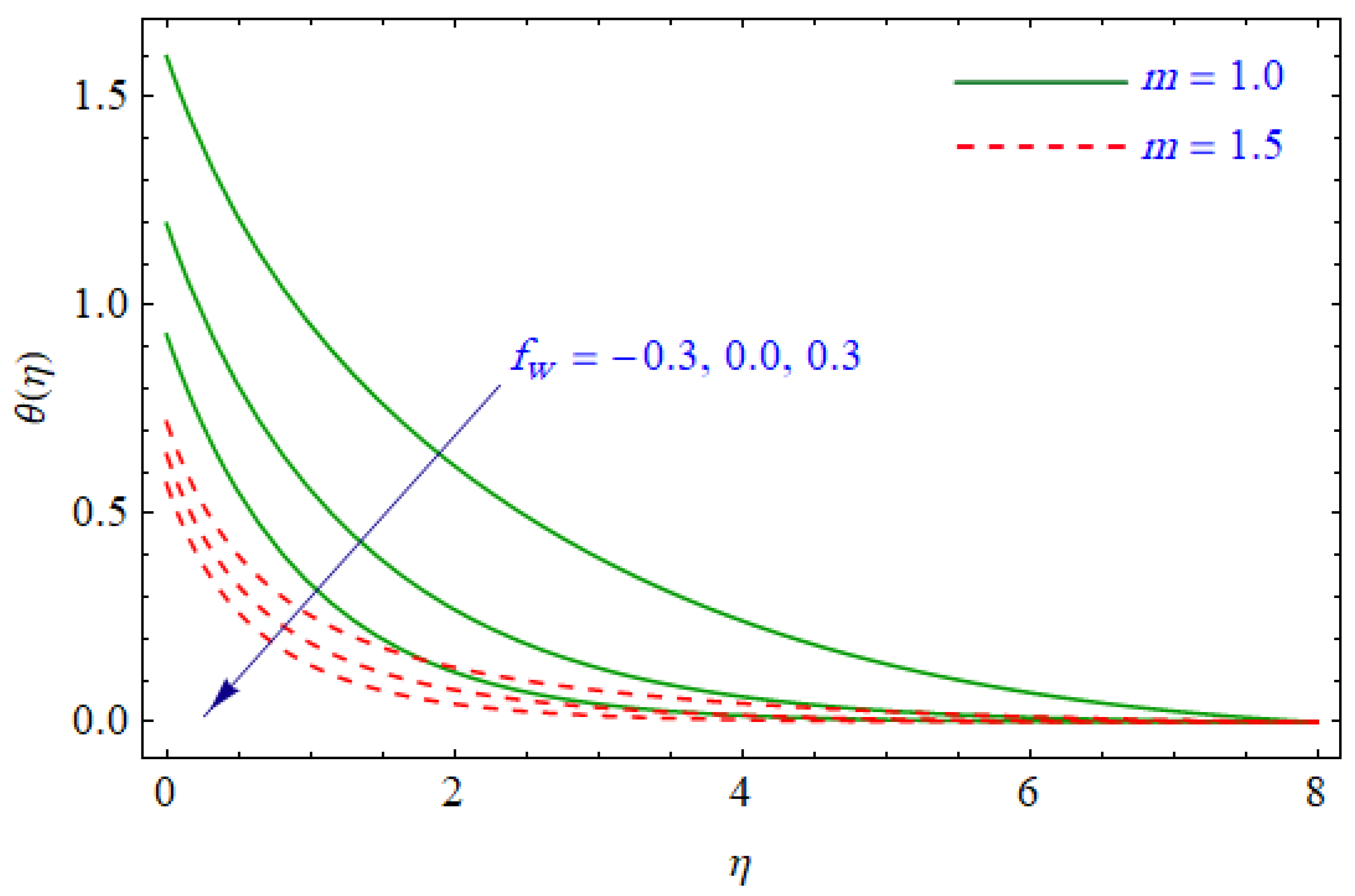
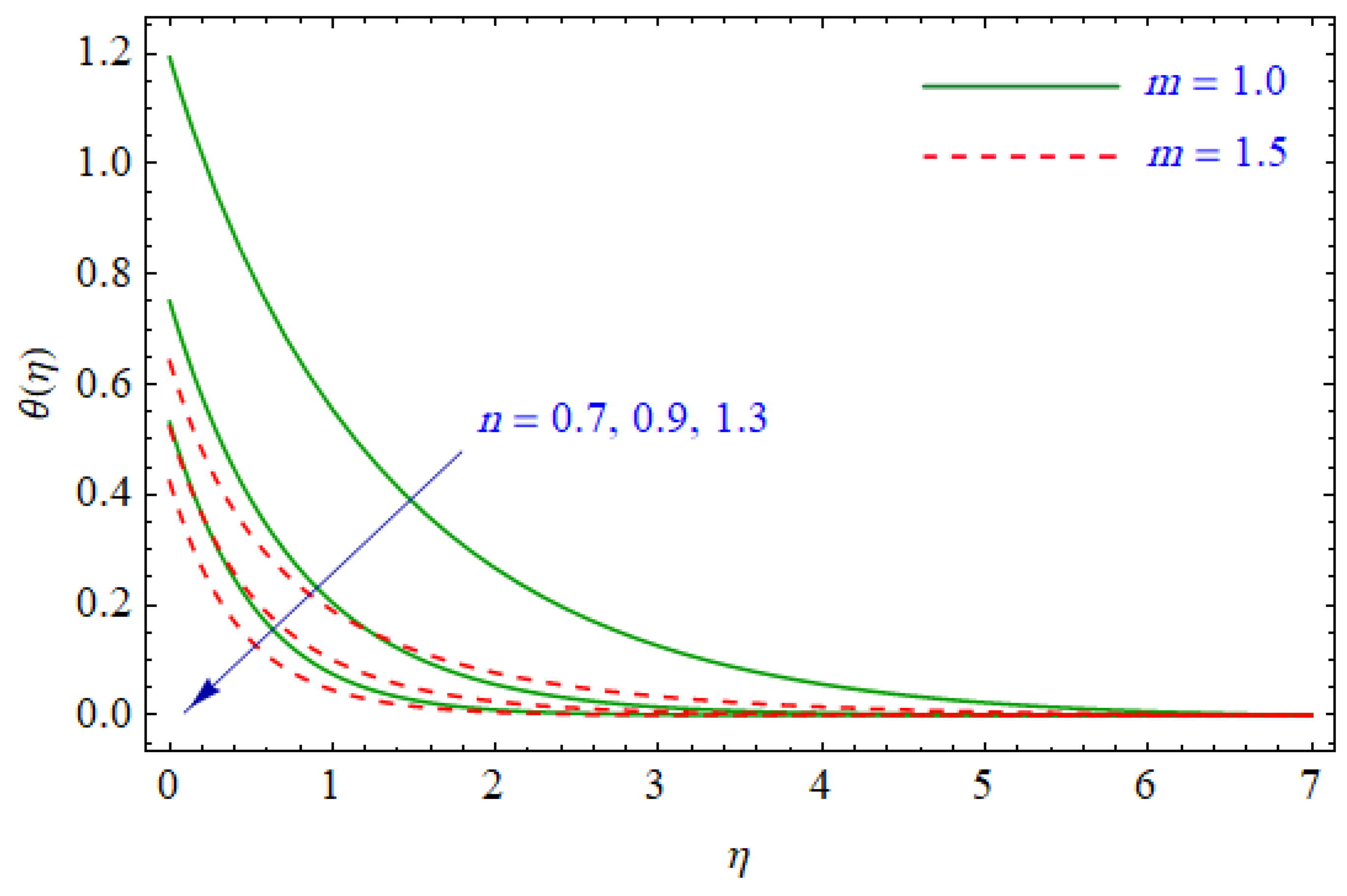
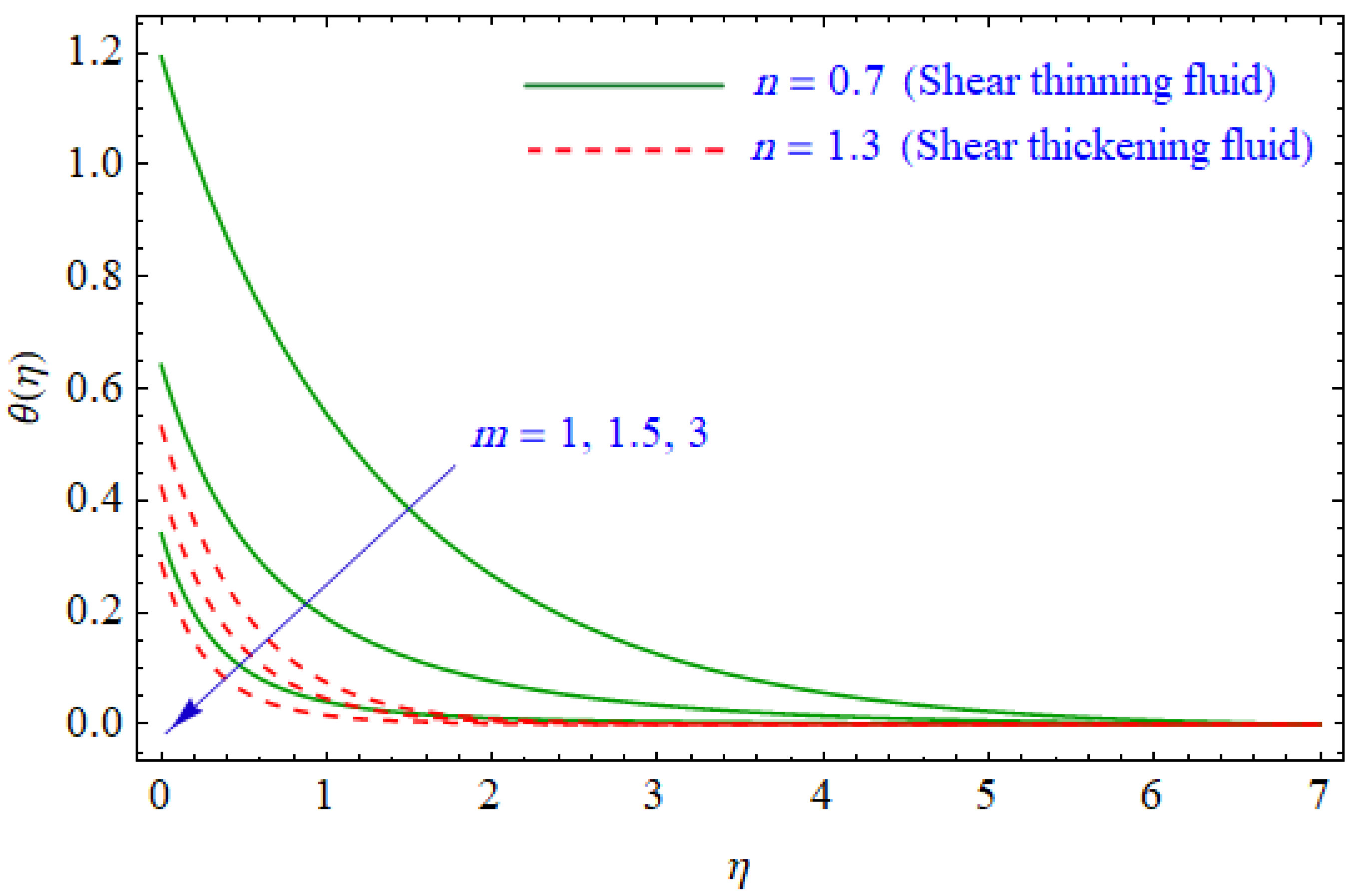
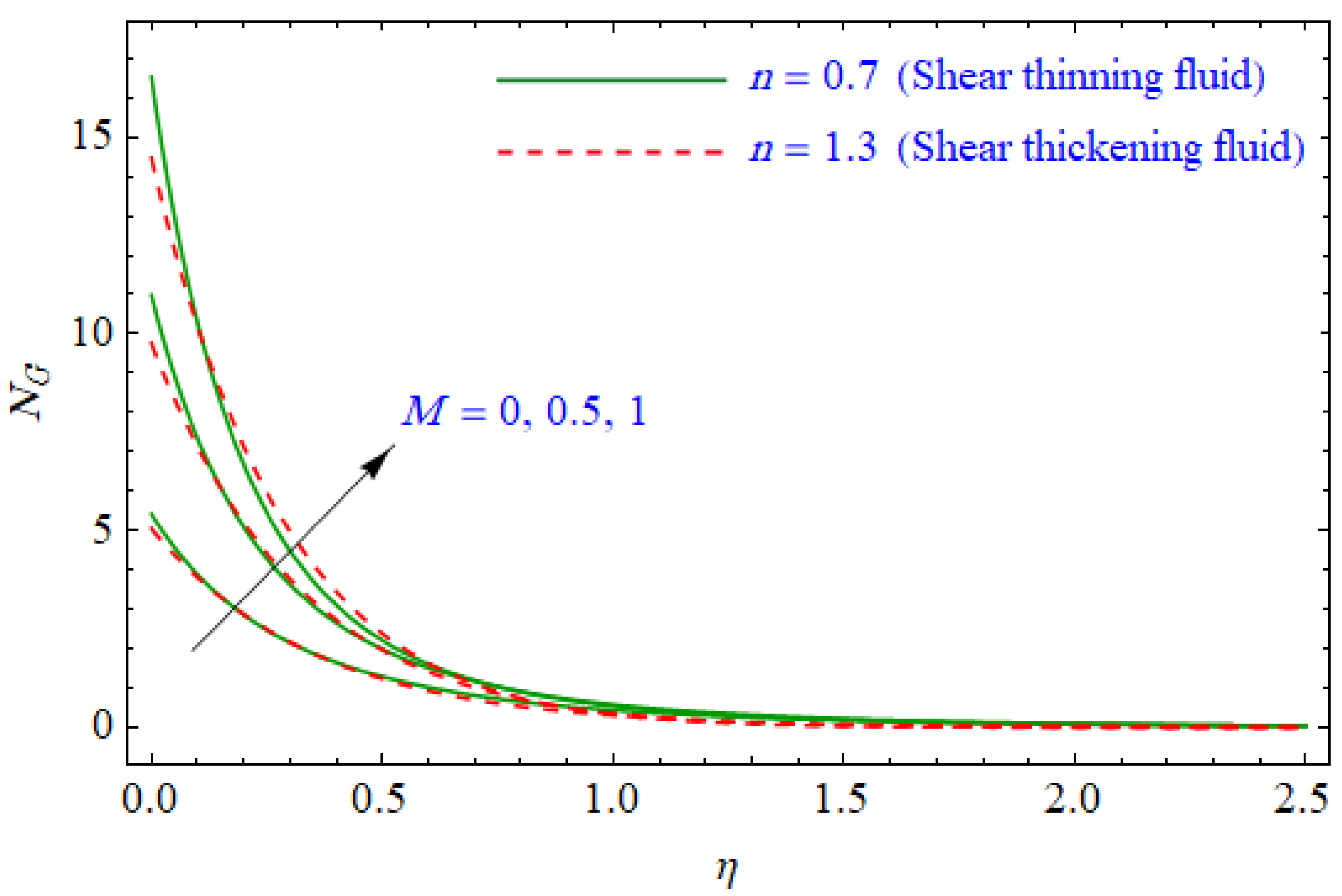
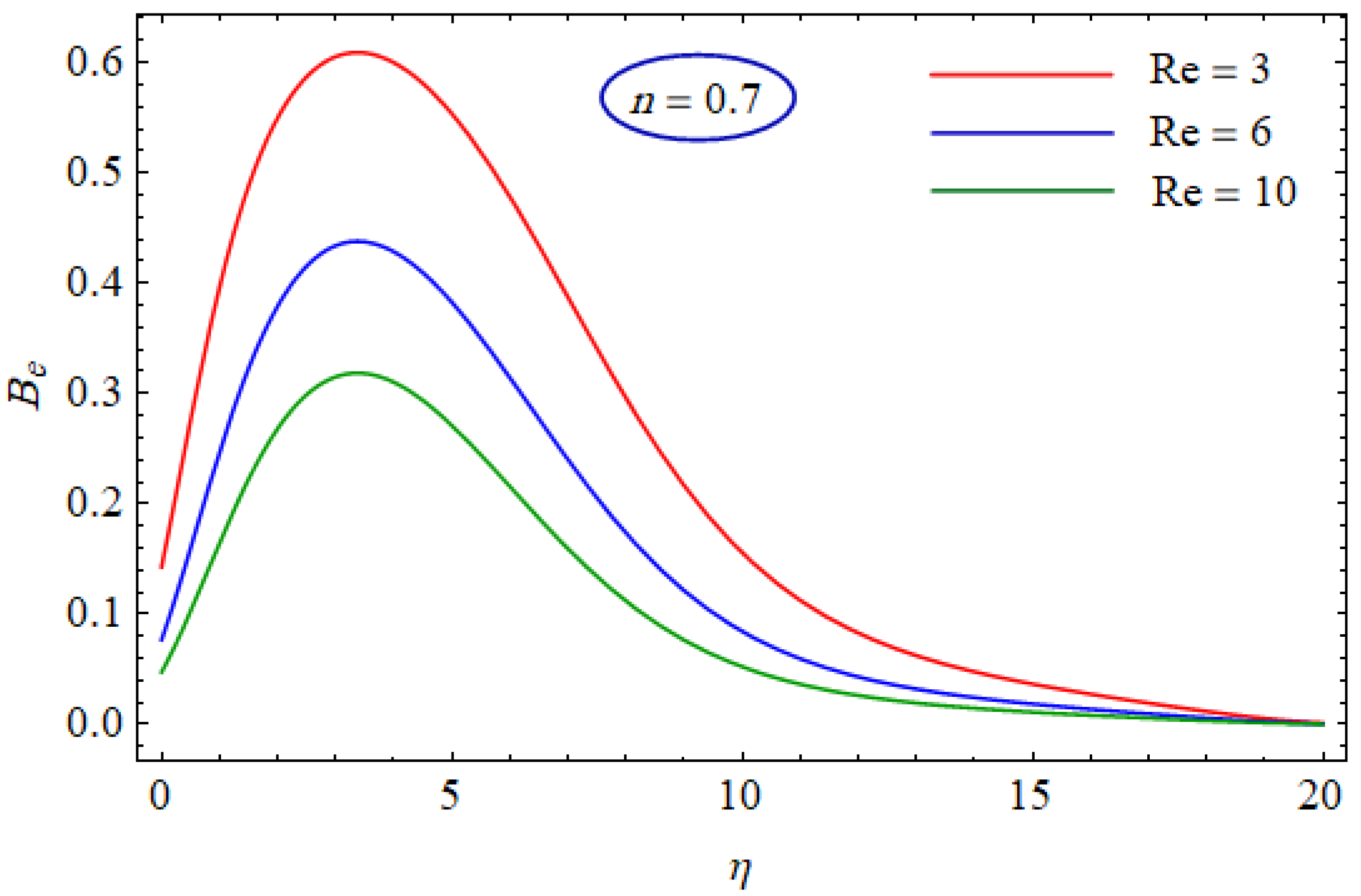
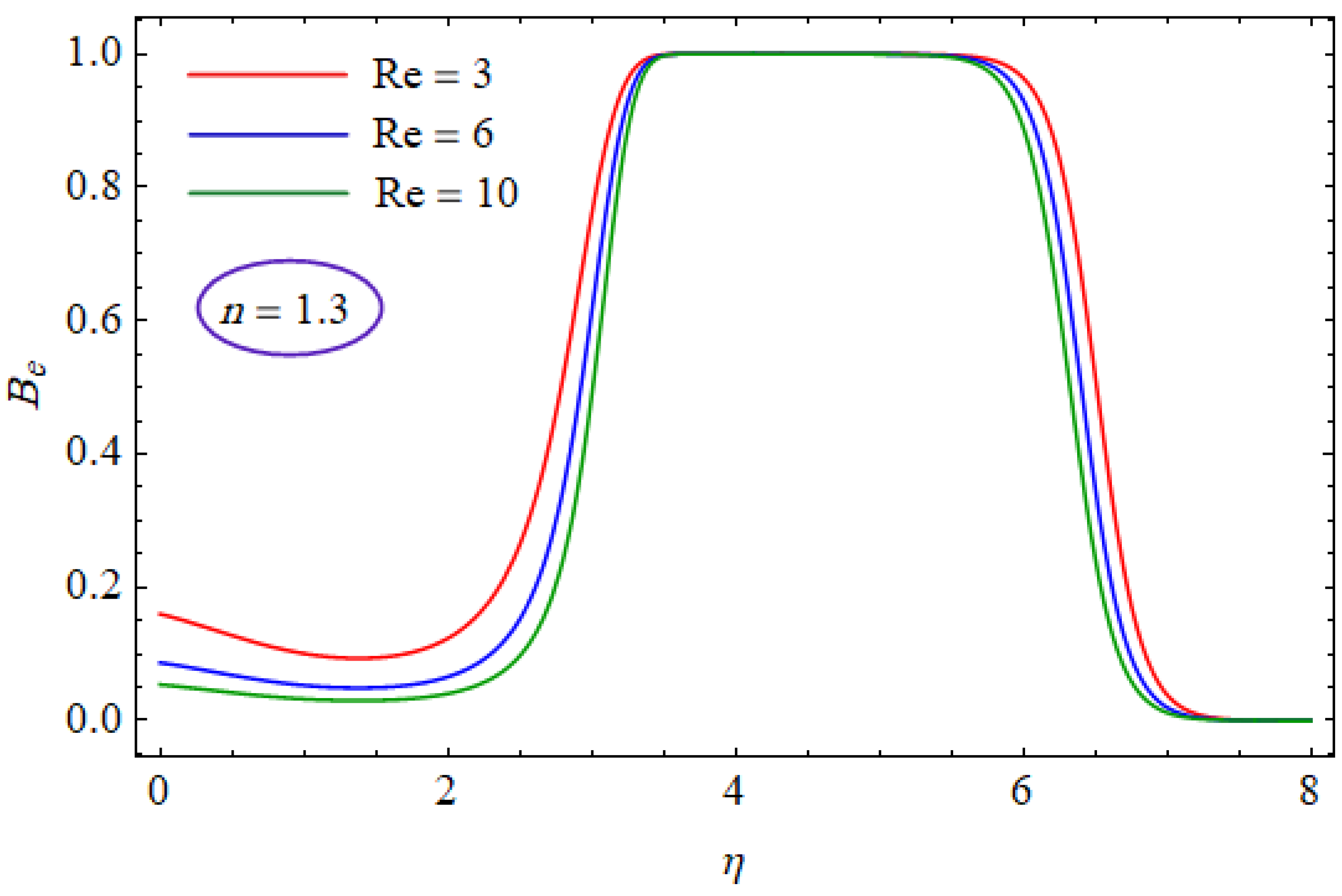
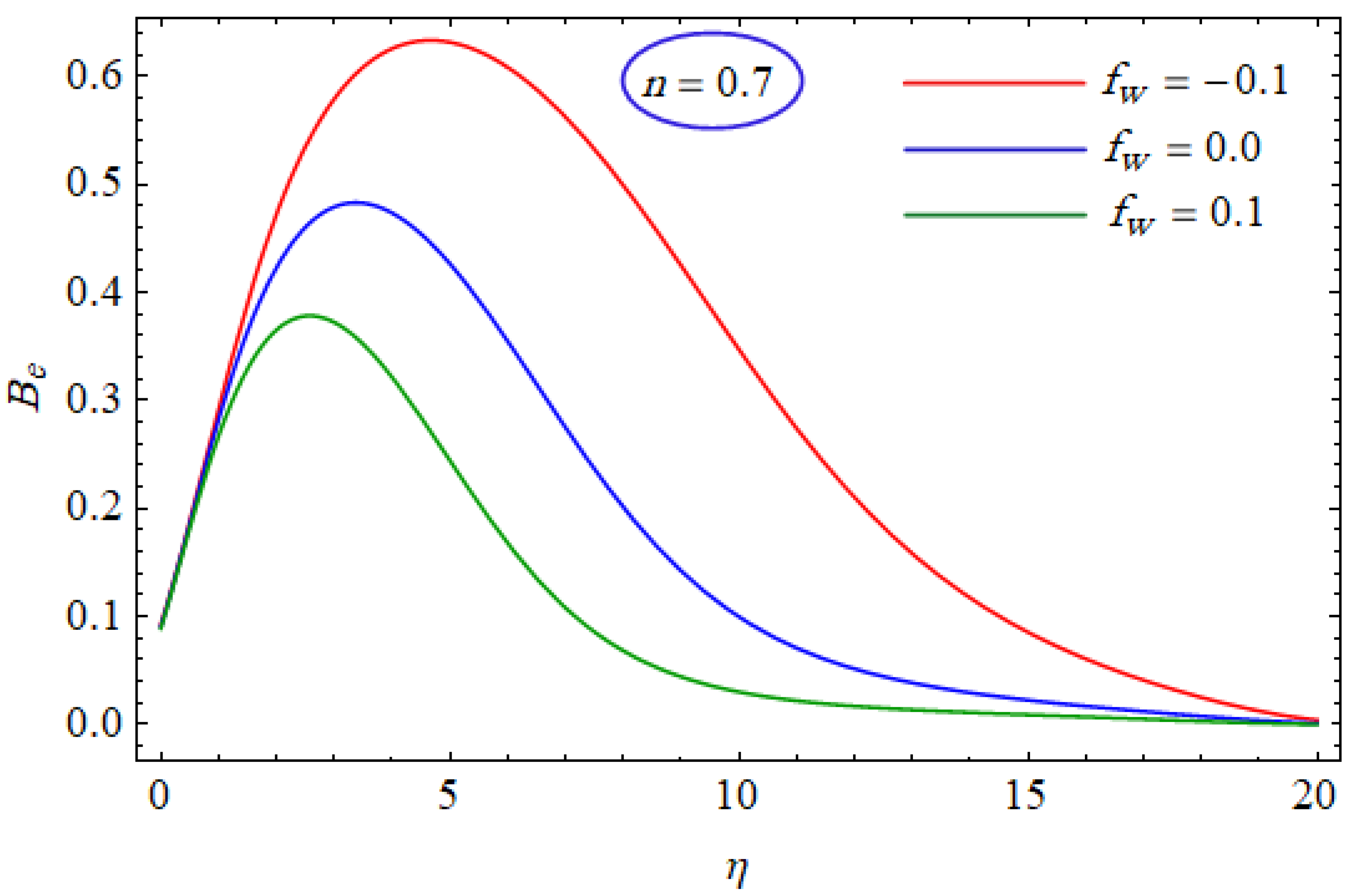
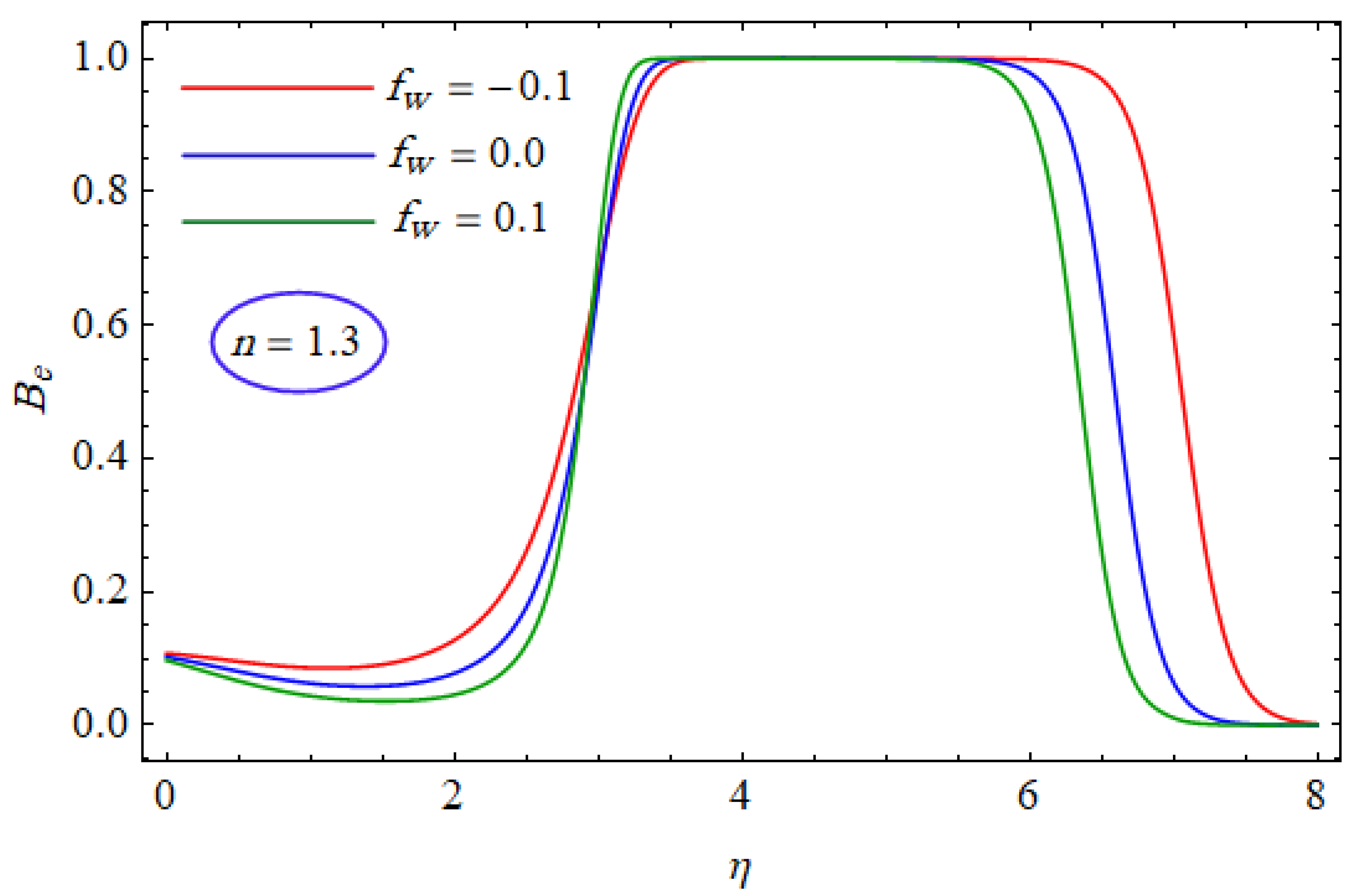
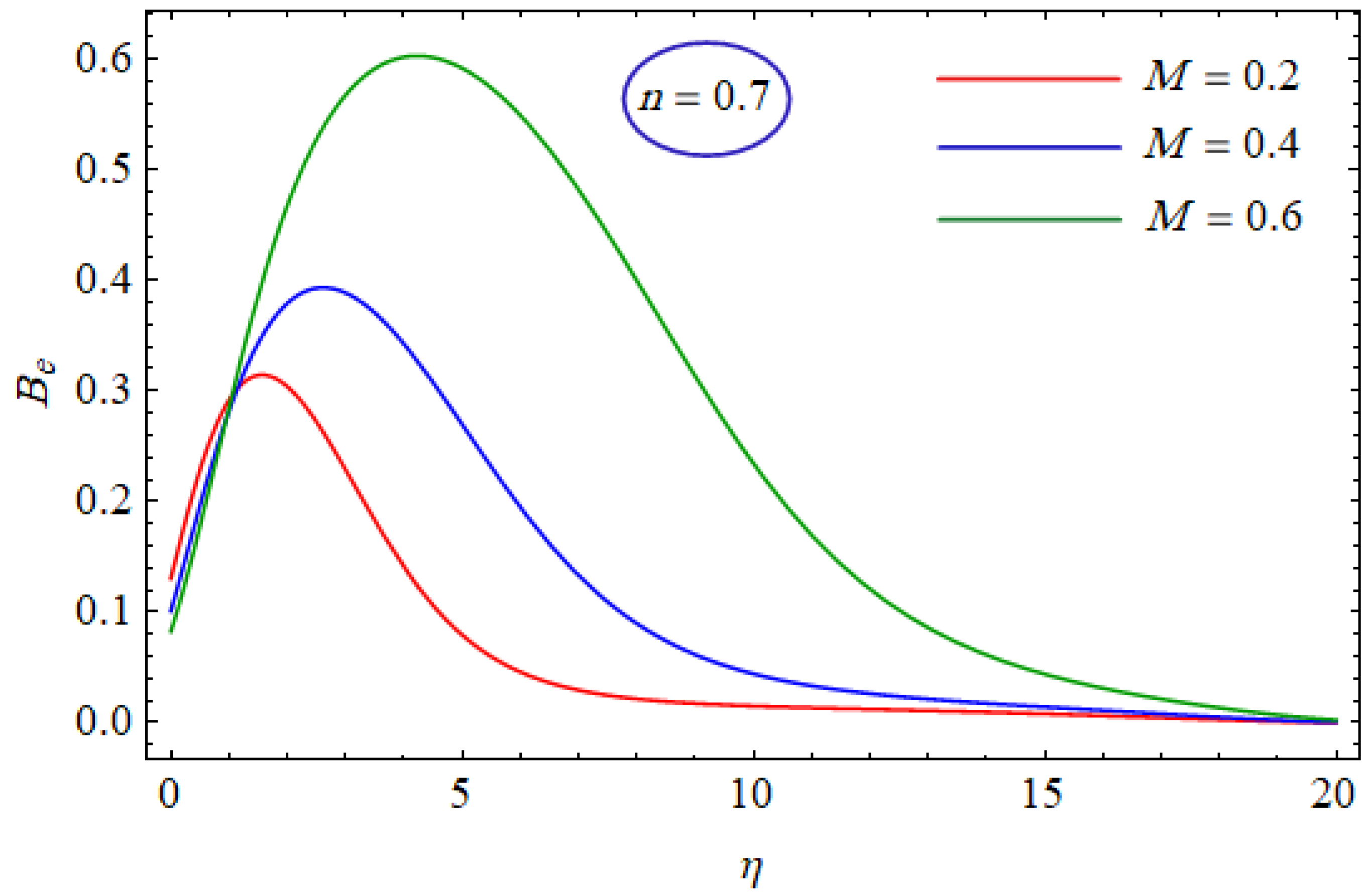
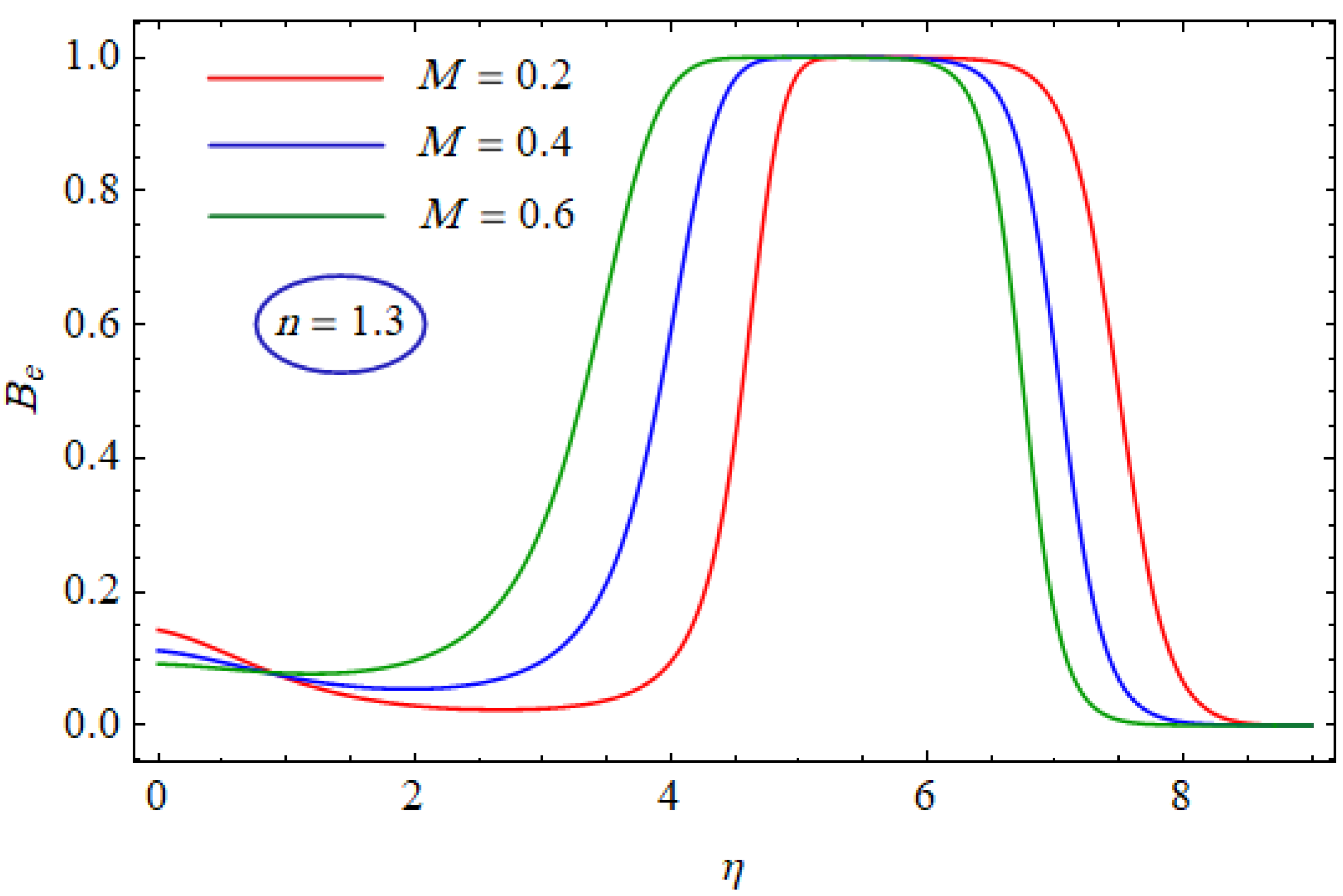
6. Results and Discussion
7. Conclusions
- The Bejan number expressively decreased and the total entropy generation was augmented with the growing Reynolds number.
- The quality of energy reduces, i.e., entropy generation is enhanced, with large magnetic and group parameters.
- The velocity of the power-law fluid varies indirectly with the suction/injection parameter.
- The heat transfer rate decay under the presence of an internal heat source and magnetic field was established.
- Thermal boundary layer decreases with an increasing heat flux index during the phenomenon.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bejan, A. Entropy Generation through Heat and Fluid Flow; Willey: New York, NY, USA, 1982. [Google Scholar]
- Kaushik, P.; Mondal, K.P.; Pati, S.; Chakraborty, S. Heat transfer and entropy generation characteristics of a non-Newtonian fluid squeezed and extruded between two parallel plates. J. Heat Transf. 2017, 139, 022004. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Darzi, M.; Li, Z. Experimental investigation for entropy generation and exergy loss of nano-refrigerant condensation process. Int. J. Heat Mass Transf. 2018, 125, 1087–1095. [Google Scholar] [CrossRef]
- Afridi, M.I.; Wakif, A.; Qasim, M.; Hussanan, A. Second law analysis of dissipative nanofluid flow over a curved surface in the presence of Lorentz force: Utilization of the Chebyshev-Gauss-Lobatto spectral method. Nanomaterials 2019, 9, 195. [Google Scholar] [CrossRef] [PubMed]
- Nouri, D.; Pasandideh-Fard, M.; Oboodi, M.J.; Mahian, O.; Sahin, A.Z. Entropy generation analysis of nanofluid flow over a spherical heat source inside a channel with sudden expansion and contraction. Int. J. Heat Mass Transf. 2018, 116, 1036–1043. [Google Scholar] [CrossRef]
- Dormohammadi, R.; Farzaneh-Gord, M.; Ebrahimi-Moghadam, A.; Ahmadi, M.H. Heat transfer and entropy generation of the nanofluid flow inside sinusoidal wavy channels. J. Mol. Liq. 2018, 269, 229–240. [Google Scholar] [CrossRef]
- Sheremet, M.A.; Oztop, H.F.; Pop, I.; Abu-Hamdeh, N. Analysis of entropy generation in natural convection of nanofluid inside a square cavity having hot solid block: Tiwari and Das’ Model. Entropy 2016, 18, 9. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Ali, M.; Freidoonimehr, N.; Nazari, F. Parametric analysis and optimization of entropy generation in unsteady MHD flow over a stretching rotating disk using artificial neural network and particle swarm optimization algorithm. Energy 2013, 55, 497–510. [Google Scholar] [CrossRef]
- Liu, Y.; Jian, Y.; Tan, W. Entropy generation of electromagnetohydrodynamic (EMHD) flow in a curved rectangular microchannel. Int. J. Heat Mass Transf. 2018, 127, 901–913. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Kavyani, N.; Abelman, S. Investigation of entropy generation in MHD and slip flow over a rotating porous disk with variable properties. Int. J. Heat. Mass Transf. 2014, 70, 892–917. [Google Scholar] [CrossRef]
- Rehman, A.U.; Mehmood, R.; Nadeem, S. Entropy analysis of radioactive rotating nanofluid with thermal slip. Appl. Therm. Eng. 2017, 112, 832–840. [Google Scholar] [CrossRef]
- Akbarzadeh, M.; Rashidi, S.; Karimi, N.; Ellahi, R. Convection of heat and thermodynamic irreversibilities in two-phase, turbulent nanofluid flows in solar heaters by corrugated absorber plates. Adv. Powder Technol. 2018, 29, 2243–2254. [Google Scholar] [CrossRef]
- Qasim, M.; Afridi, M.I.; Wakif, A.; Thoi, T.N.; Hussanan, A. Second Law Analysis of Unsteady MHD Viscous Flow over a Horizontal Stretching Sheet Heated Non-Uniformly in the Presence of Ohmic Heating: Utilization of Gear-Generalized Differential Quadrature Method. Entropy 2019, 21, 240. [Google Scholar] [CrossRef]
- Afridi, M.I.; Qasim, M.; Saleem, S. Second law analysis of three dimension dissipative flow of Hybrid nanofluid. J. Nanofluids 2018, 7, 1272–1280. [Google Scholar] [CrossRef]
- Abbas, M.A.; Bai, Y.; Rashidi, M.M.; Bhatti, M.M. Analysis of entropy generation in the flow of peristaltic nanofluids in channels with compliant walls. Entropy 2016, 18, 90. [Google Scholar] [CrossRef]
- Oztop, H.F.; Al-Salem, K. A review on entropy generation in natural and mixed convection heat transfer for energy systems. Renew. Sustain. Energy Rev. 2012, 16, 911–920. [Google Scholar] [CrossRef]
- Makinde, O.D.; Osalusi, E. ESecond law analysis of laminar flow in a channel filled with saturated porous media. Entropy 2005, 7, 148–160. [Google Scholar] [CrossRef]
- Qasim, M.; Khan, Z.H.; Khan, I.; Al-Mdallal, Q.M. Analysis of entropy generation in flow of methanol-based nanofluid in a sinusoidal wavy channel. Entropy 2017, 19, 490. [Google Scholar] [CrossRef]
- Ellahi, R.; Hassan, M.; Zeeshan, A. Shape effects of nanosize particles in Cu-H2O nanofluid on entropy generation. Int. J. Heat Mass Transf. 2015, 81, 449–456. [Google Scholar] [CrossRef]
- Scott, S.H.; Abt, S.R. Hydraulic transport of fine and coarse sediment mixtures in pipelines. J. Transp. Eng. 2002, 128, 1–8. [Google Scholar] [CrossRef]
- Sadiq, M.A.; Khan, A.U.; Saleem, S.; Nadeem, S. Numerical simulation of oscillatory oblique stagnation point flow of a magneto micropolar nanofluid. RSC Adv. 2019, 9, 4751–4764. [Google Scholar] [CrossRef]
- Saleem, S.; Firdous, H.; Nadeem, S.; Khan, A.U. Convective heat and mass transfer in magneto Walter’s B nanofluid flow induced by a rotating cone. Arab. J. Sci. Eng. 2019, 44, 1515–1523. [Google Scholar] [CrossRef]
- Malik, M.Y.; Salahuddin, T.; Hussain, A.; Bilal, S. MHD flow of tangent hyperbolic fluid over a stretching cylinder: Using Keller box method. J. Magn. Magn. Mater. 2015, 395, 271–276. [Google Scholar] [CrossRef]
- Sadaf, H.; Akbar, M.U.; Nadeem, S. Induced magnetic field analysis for the peristaltic transport of non-Newtonian nanofluid in an annulus. Math. Comput. Simul. 2018, 148, 16–36. [Google Scholar] [CrossRef]
- Raju, C.S.K.; Saleem, S.; Al-Qarni, M.M.; Mamatha Upadhya, S. Unsteady nonlinear convection on Eyring-Powell radiated flow with suspended graphene and dust particles. Microsyst. Technol. 2018. [Google Scholar] [CrossRef]
- Haque, A.; Nayak, A.K.; Soni, B.; Majhi, M. Thermosolutal hydromagnetic convection of power-law fluids in an enclosure with periodic active zones. Int. J. Heat Mass Transf. 2018, 127C, 622–642. [Google Scholar] [CrossRef]
- El-Aziz, M.A.; Afify, A.A. Lie group analysis of hydromagnetic flow and heat transfer of a power-law fluid over stretching surface with temperature-dependent viscosity and thermal conductivity. Int. J. Mod. Phys. C 2016, 27, 1650150. [Google Scholar] [CrossRef]
- Sasmal, C.; Gupta, A.K.; Chhabra, R.P. Natural convection heat transfer in a power-law fluid from a heated rotating cylinder in a square duct. Int. J. Heat Mass Transf. 2019, 129, 975–996. [Google Scholar] [CrossRef]
- Salem, A.M.; El-Aziz, M.A.; Abo-Eldahab, E.M.; Abd-Elfatah, I. Effect of variable density on hydromagnetic mixed convection flow of a non-Newtonian fluid past a moving vertical plate. Commun. Nonlinear Sci. Numer. Simul. 2009, 15, 1485–1493. [Google Scholar] [CrossRef]
- Mohebbi, R.; Nazari, M.; Kayhani, M. Comparative study of forced convection of a power-law fluid in a channel with a built-in square cylinder. J. Appl. Mech. Technol. Phys. 2016, 57, 55–68. [Google Scholar] [CrossRef]
- El-Aziz, M.A.; Yahya, A.S. Heat and Mass Transfer of Unsteady Hydromagnetic Free Convection Flow Through Porous Medium Past a Vertical Plate with Uniform Surface Heat Flux. J. Theor. Appl. Mech. 2017, 47, 25–58. [Google Scholar] [CrossRef][Green Version]
- Metri, P.G.; Metri, P.G.; Abel, S.; Silvestrov, S. Heat transfer in MHD mixed convection viscoelastic fluid flow over a stretching sheet embedded in a porous medium with viscous dissipation and non-uniform heat source/sink. Procedia Eng. 2016, 157, 309–316. [Google Scholar] [CrossRef]
- Shehzad, N.; Zeeshan, A.; Ellahi, R.; Rashidi, S. Modelling Study on Internal Energy Loss Due to Entropy Generation for Non-Darcy Poiseuille Flow of Silver-Water Nanofluid: An Application of Purification. Entropy 2018, 20, 851. [Google Scholar] [CrossRef]
- Hayat, T.; Nadeem, S. Flow of 3D Eyring-Powell fluid by utilizing Cattaneo-Christov heat flux model and chemical processes over an exponentially stretching surface. Results Phys. 2018, 8, 397–403. [Google Scholar] [CrossRef]
- Patil, P.M.; Latha, D.N.; Roy, S. Ebrahim Momoniat, Double diffusive mixed convection flow from a vertical exponentially stretching surface in presence of the viscous dissipation. Int. J. Heat Mass Transf. 2017, 112, 758–766. [Google Scholar] [CrossRef]
- Hayat, T.; Ijaz Khan, M.; Farooq, M.; Alsaedi, A.; Waqas, M. Tabassam Yasmeen, Impact of Cattaneo–Christov heat flux model in flow of variable thermal conductivity fluid over a variable thicked surface. Int. J. Heat Mass Transf. 2016, 99, 702–710. [Google Scholar] [CrossRef]
- Nadeem, S.; Lee, C. Boundary layer flow of nanofluid over an exponentially stretching surface. Nanoscale Res. Lett. 2012, 7, 94. [Google Scholar] [CrossRef]
- Irfan, M.; Khan, M.; Khan, W.A. Impact of non-uniform heat sink/source and convective condition in radiative heat transfer to Oldroyd-B nanofluid: A revised proposed relation. Phys. Lett. A 2019, 383, 376–382. [Google Scholar] [CrossRef]
- Animasaun, I.L.; Mahanthesh, B.; Jagun, A.O.; Bankole, T.D.; Sivaraj, R.; Shah, N.A.; Saleem, S. Significance of Lorentz Force and Thermoelectric on the Flow of 29 nm CuO–Water Nanofluid on an Upper Horizontal Surface of a Paraboloid of Revolution. J. Heat Transf. 2019, 141, 022402. [Google Scholar] [CrossRef]
- Saleem, S.; AlQarni, M.M.; Nadeem, S.; Sandeep, N. Convective heat and mass transfer in magneto Jeffrey fluid flow on a rotating cone with heat source and chemical reaction. Commun. Theor. Phys. 2018, 70, 534–540. [Google Scholar] [CrossRef]
- Hayat, T.; Ijaz Khan, M.; Farooq, M.; Yasmeen, T.; Alsaedi, A. Stagnation point flow with Cattaneo-Christov heat flux and homogeneous-heterogeneous reactions. J. Mol. Liq. 2016, 220, 49–55. [Google Scholar] [CrossRef]
- Afridi, M.I.; Wakif, A.; Qasim, M.; Hussanan, A. Irreversibility Analysis of Dissipative Fluid Flow Over A Curved Surface Stimulated by Variable Thermal Conductivity and Uniform Magnetic Field: Utilization of Generalized Differential Quadrature Method. Entropy 2018, 20, 943. [Google Scholar] [CrossRef]
- Wakif, A.; Boulahia, Z.; Ali, F.; Eid, M.R.; Sehaqui, R. Numerical Analysis of the Unsteady Natural Convection MHD Couette Nanofluid Flow in the Presence of Thermal Radiation Using Single and Two-Phase Nanofluid Models for Cu–Water Nanofluids. Int. J. Appl. Comput. Math. 2018, 4, 1–27. [Google Scholar] [CrossRef]
- Zeeshan, A.; Shehzad, N.; Abbas, T.; Ellahi, R. Effects of Radiative Electro-Magnetohydrodynamics Diminishing Internal Energy of Pressure-Driven Flow of Titanium Dioxide-Water Nanofluid due to Entropy Generation. Entropy 2019, 21, 236. [Google Scholar] [CrossRef]
- Amanulla, C.H.; Saleem, S.; Wakif, A.; AlQarni, M.M. MHD Prandtl fluid flow past an isothermal permeable sphere with slip effects. Case Stud. Therm. Eng. 2019, 14, 100447. [Google Scholar] [CrossRef]
- Makinde, O.D.; Omojola, M.T.; Mahanthesh, B.; Alao, F.I.; Adegbie, K.S.; Animasaun, I.L.; Wakif, A.; Sivaraj, R.; Tshehla, M.S. Significance of Buoyancy, Velocity Index and Thickness of an Upper Horizontal Surface of a Paraboloid of Revolution: The Case of Non-Newtonian Carreau Fluid. Defect. Diffus. Forum 2018, 387, 550–561. [Google Scholar] [CrossRef]
- Qasim, M.; Afridi, M.I.; Wakif, A.; Saleem, S. Influence of Variable Transport Properties on Nonlinear Radioactive Jeffrey Fluid Flow Over a Disk: Utilization of Generalized Differential Quadrature Method. Arab. J. Sci. Eng. 2019, 1–10. [Google Scholar] [CrossRef]
- Wakif, A.; Boulahia, Z.; Mishra, S.R.; Mehdi Rashidi, M.; Sehaqui, R. Influence of a uniform transverse magnetic field on the thermo-hydrodynamic stability in water-based nanofluids with metallic nanoparticles using the generalized Buongiorno’s mathematical model. Eur. Phys. J. Plus. 2018, 133, 181. [Google Scholar] [CrossRef]
- Wakif, A.; Boulahia, Z.; Sehaqui, R. A Semi-Analytical Analysis of Electro-Thermo-Hydrodynamic Stability in Dielectric Nanofluids Using Buongiorno’s Mathematical Model Together with More Realistic Boundary Conditions. Results Phys. 2018, 9, 1438–1454. [Google Scholar] [CrossRef]
- Saleem, S.; Nadeem, S.; Rashidi, M.M.; Raju, C.S.K. An optimal analysis of radiated nanomaterial flow with viscous dissipation and heat source. Microsyst. Technol. 2019, 25, 683–689. [Google Scholar] [CrossRef]
- Saleem, S.; El-Aziz, M.A. Entropy generation and convective heat transfer of radiated non-Newtonian power-law fluid past an exponentially moving surface under slip effects. Eur. Phys. J. Plus. 2019, 134, 184. [Google Scholar] [CrossRef]
- Amanulla, C.H.; Wakif, A.; Boulahia, Z.; Fazuruddin, S.; Mohammed, S.N. A Study on Non-Newtonian Transport Phenomena in MHD Fluid Flow from a Vertical Cone with Navier Slip and Convective Heating. Nonlinear Eng. 2019, 8, 534–545. [Google Scholar] [CrossRef]
- Wakif, A.; Boulahia, Z.; Amine, A.; Animasaun, I.L.; Afridi, M.I.; Qasim, M.; Sehaqui, R. Magneto-Convection of Alumina—Water Nanofluid Within Thin Horizontal Layers Using the Revised Generalized Buongiorno’s Model. Front. Heat Mass Transf. 2019, 12, 1–15. [Google Scholar] [CrossRef]
- Amanulla, C.H.; Wakif, A.; Boulahia, Z.; Suryanarayana Reddy, M.; Nagendra, N. Numerical investigations on magnetic field modeling for Carreau non-Newtonian fluid flow past an isothermal sphere. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 462. [Google Scholar] [CrossRef]
- Cimpean, D.; Lungu, N.; Pop, I. A problem of entropy generation in a channel filled with a porous medium. Creative Math. Inform. 2008, 17, 357–362. [Google Scholar]
- Magyari, E.; Keller, B. Heat and mass transfer in the boundary layers on an exponentially stretching continuous surface. J. Phys. D Appl. Phys. 1999, 32, 577–585. [Google Scholar] [CrossRef]
- Elbashbeshy, E.M.A. Heat transfer over an exponentially stretching continuous surface with suction. Arc. Mech. 2001, 53, 643–651. [Google Scholar]
- Sahoo, B.; Poncet, S. Flow and heat transfer of a third grade fluid past an exponentially stretching sheet with partial slip boundary condition. Int. J. Heat Mass Transf. 2011, 54, 5010–5019. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.; Moindal, I.C.; Hayat, T. MHD boundary layer flow of Casson fluid passing through an exponentially stretching permeable surface with thermal radiation. Chin. Phys. B 2014, 23, 104701. [Google Scholar] [CrossRef]
- Sajid, M.; Hayat, T. Influence of thermal radiation on the boundary layer flow due to an exponentially stretching sheet. Int. Commun. Heat Mass Transf. 2008, 35, 347–356. [Google Scholar] [CrossRef]
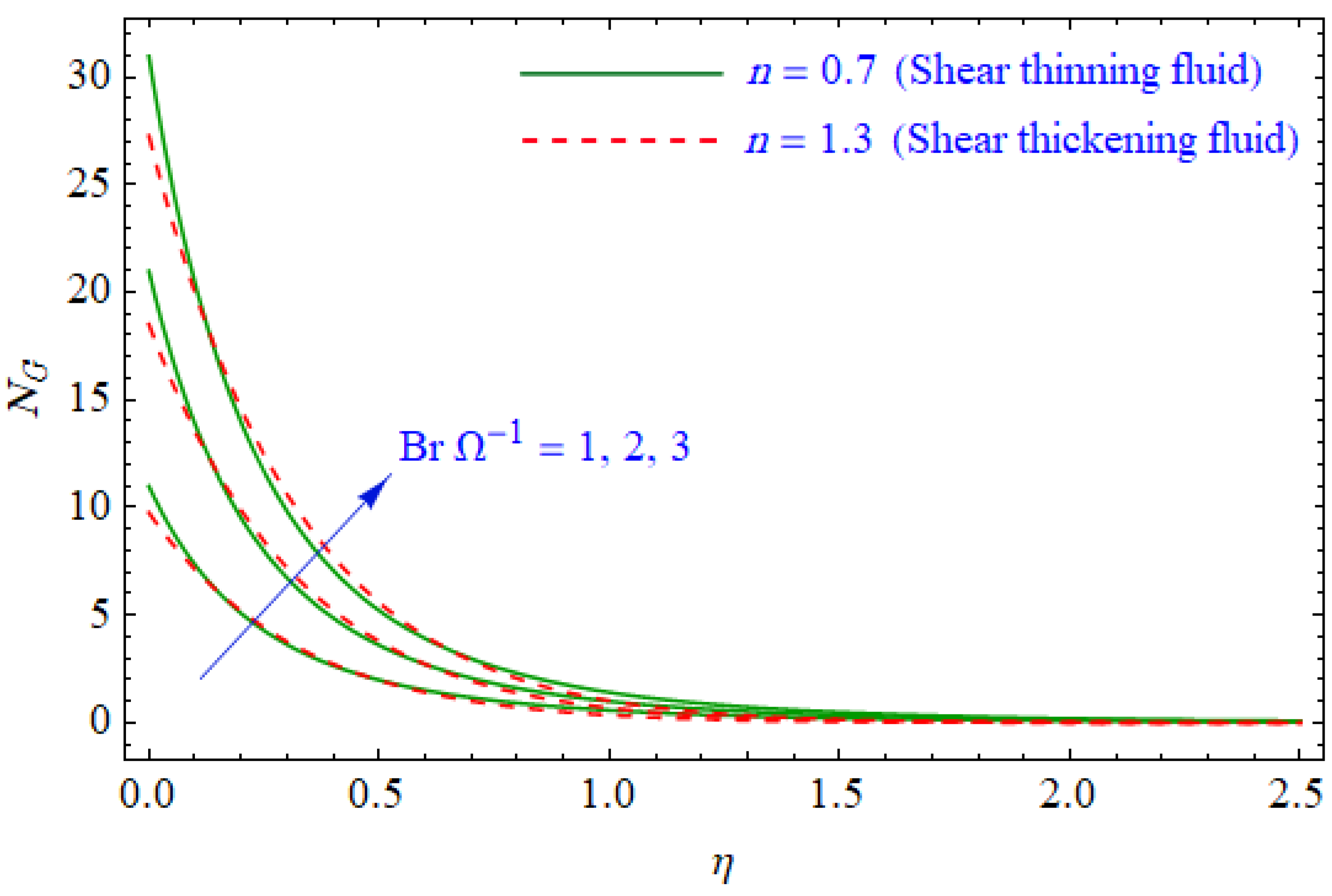
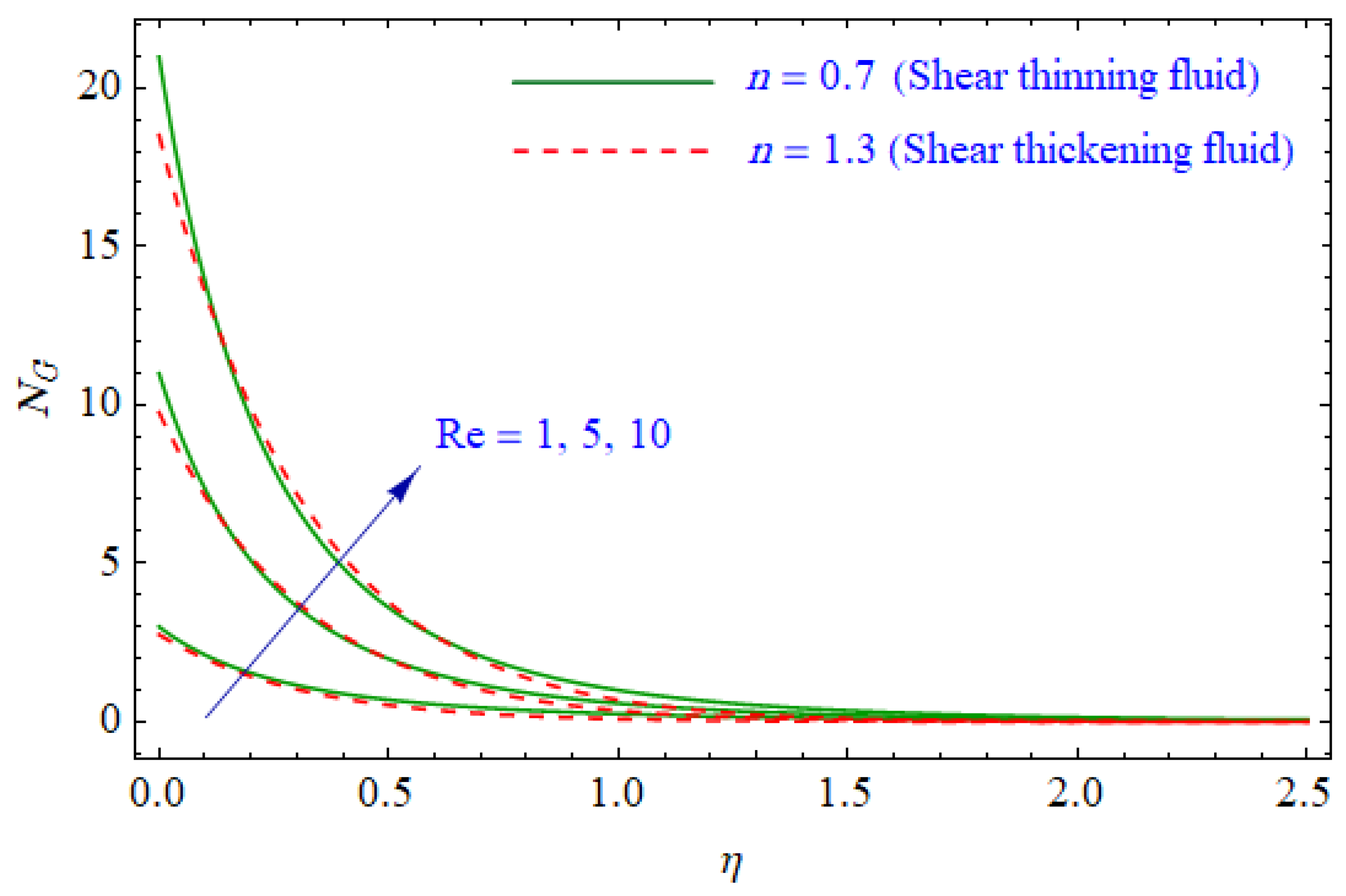
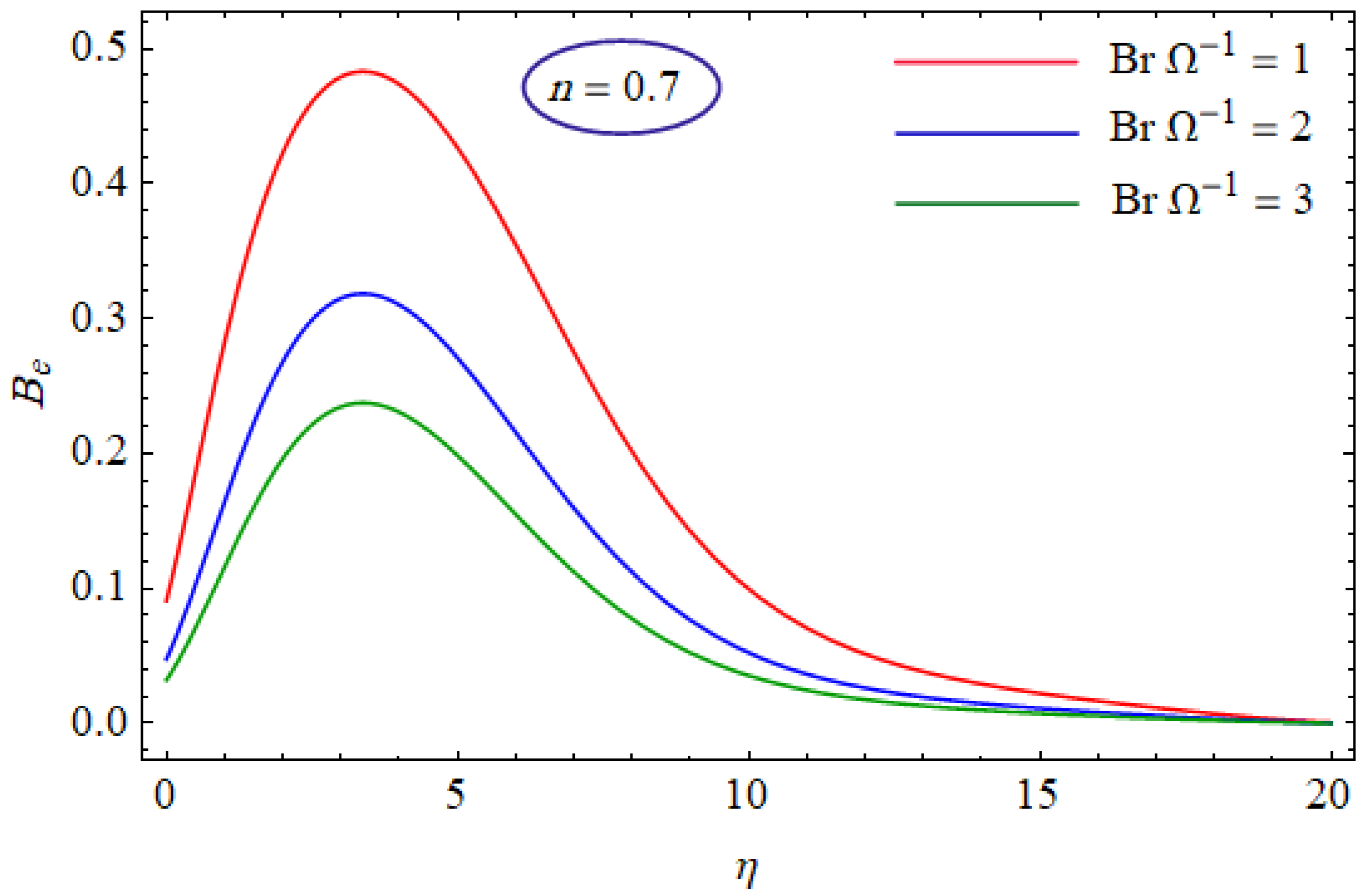
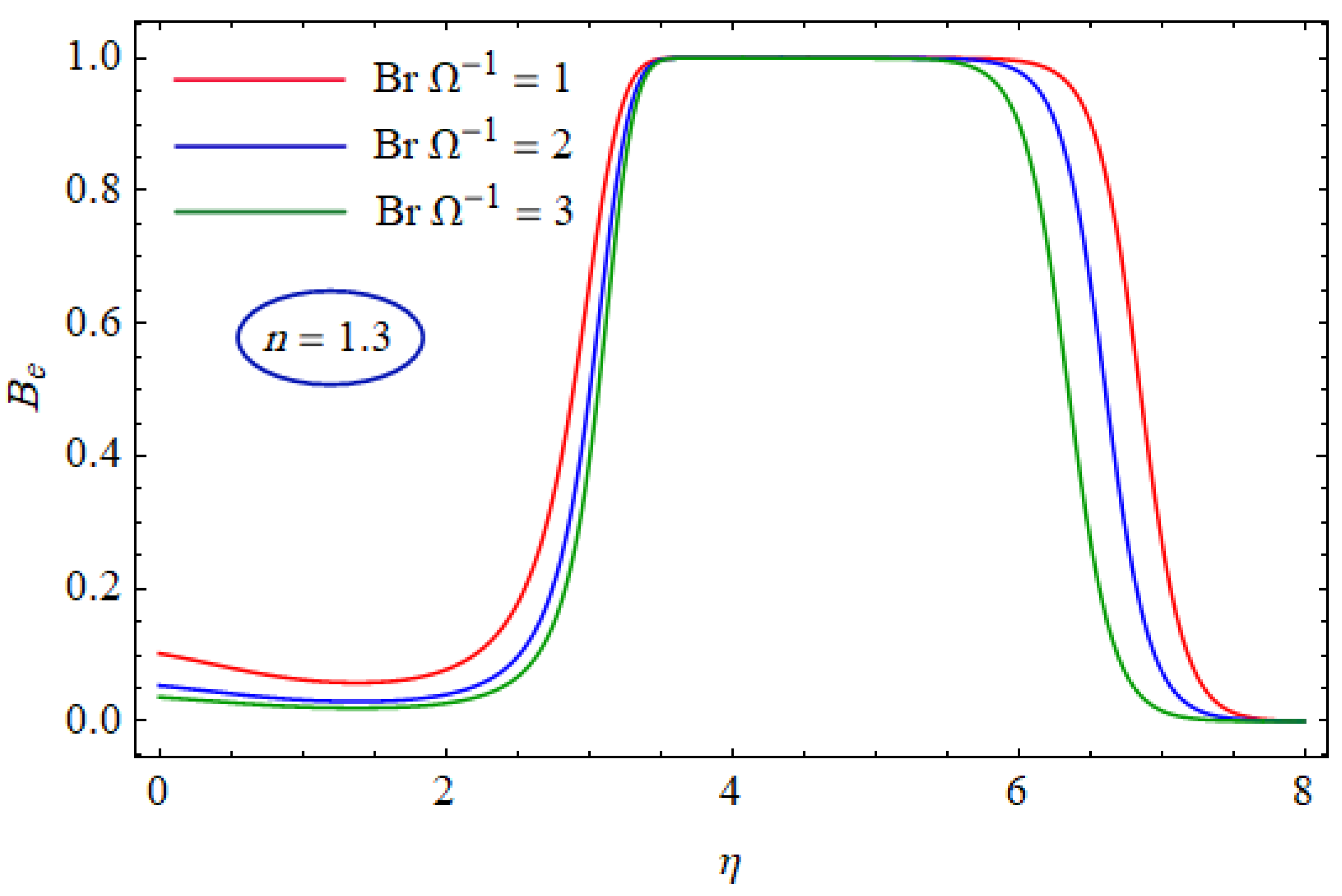
| Existing Results for | Present Result for | ||||
|---|---|---|---|---|---|
| [56] | [57] | [58] | [59] | [60] | SRKFM |
| −1.28180 | −1.28181 | −1.281811 | −1.281812 | −1.28181 | −1.2818098 |
| M | ||||||
|---|---|---|---|---|---|---|
| 0.0 | −1.264728 | 0.957247 | ||||
| 0.5 | 0.0 | 1.0 | 0.1 | 0.1 | −1.570997 | 0.836066 |
| 1.0 | −1.808090 | 0.731285 | ||||
| −0.3 | −1.513345 | 0.625733 | ||||
| 0.5 | 0.1 | 1.0 | 0.1 | 0.1 | −1.590886 | 0.913095 |
| 0.3 | −1.631743 | 1.075468 | ||||
| 0.8 | −1.570988 | 0.441335 | ||||
| 0.5 | 0.0 | 1.5 | 0.1 | 0.1 | −1.571019 | 1.556417 |
| 3.0 | −1.571019 | 2.930572 | ||||
| −0.5 | −1.570997 | 1.171080 | ||||
| 0.5 | 0.0 | 0.1 | 0.0 | 0.1 | −1.570997 | 0.891902 |
| 0.5 | −1.570997 | 0.441335 | ||||
| −0.5 | −1.570997 | 1.208040 | ||||
| 0.5 | 0.0 | 0.1 | 0.1 | 0.0 | −1.570997 | 0.918485 |
| 0.2 | −1.570997 | 0.727479 |
| M | ||||||
|---|---|---|---|---|---|---|
| 0.0 | −1.313498 | 1.956119 | ||||
| 0.5 | 0.0 | 1.0 | 0.1 | 0.1 | −1.679224 | 1.883365 |
| 1.0 | −1.992612 | 1.822293 | ||||
| −0.3 | −1.470333 | 1.354459 | ||||
| 0.5 | 0.1 | 1.0 | 0.1 | 0.1 | −1.754932 | 2.089481 |
| 0.3 | −1.915439 | 2.546558 | ||||
| 0.8 | −1.679185 | 1.668265 | ||||
| 0.5 | 0.0 | 1.5 | 0.1 | 0.1 | −1.679185 | 2.355932 |
| 3.0 | −1.679185 | 3.474166 | ||||
| −0.5 | −1.679185 | 2.099785 | ||||
| 0.5 | 0.0 | 0.1 | 0.0 | 0.1 | −1.679185 | 1.917798 |
| 0.5 | −1.679185 | 1.735811 | ||||
| −0.5 | −1.679185 | 2.060122 | ||||
| 0.5 | 0.0 | 0.1 | 0.1 | 0.0 | −1.679185 | 1.913069 |
| 0.2 | −1.679185 | 1.848783 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abd El-Aziz, M.; Saleem, S. Numerical Simulation of Entropy Generation for Power-Law Liquid Flow over a Permeable Exponential Stretched Surface with Variable Heat Source and Heat Flux. Entropy 2019, 21, 484. https://doi.org/10.3390/e21050484
Abd El-Aziz M, Saleem S. Numerical Simulation of Entropy Generation for Power-Law Liquid Flow over a Permeable Exponential Stretched Surface with Variable Heat Source and Heat Flux. Entropy. 2019; 21(5):484. https://doi.org/10.3390/e21050484
Chicago/Turabian StyleAbd El-Aziz, Mohamed, and Salman Saleem. 2019. "Numerical Simulation of Entropy Generation for Power-Law Liquid Flow over a Permeable Exponential Stretched Surface with Variable Heat Source and Heat Flux" Entropy 21, no. 5: 484. https://doi.org/10.3390/e21050484
APA StyleAbd El-Aziz, M., & Saleem, S. (2019). Numerical Simulation of Entropy Generation for Power-Law Liquid Flow over a Permeable Exponential Stretched Surface with Variable Heat Source and Heat Flux. Entropy, 21(5), 484. https://doi.org/10.3390/e21050484





