On Properties of Distance-Based Entropies on Fullerene Graphs
Abstract
:1. Introduction
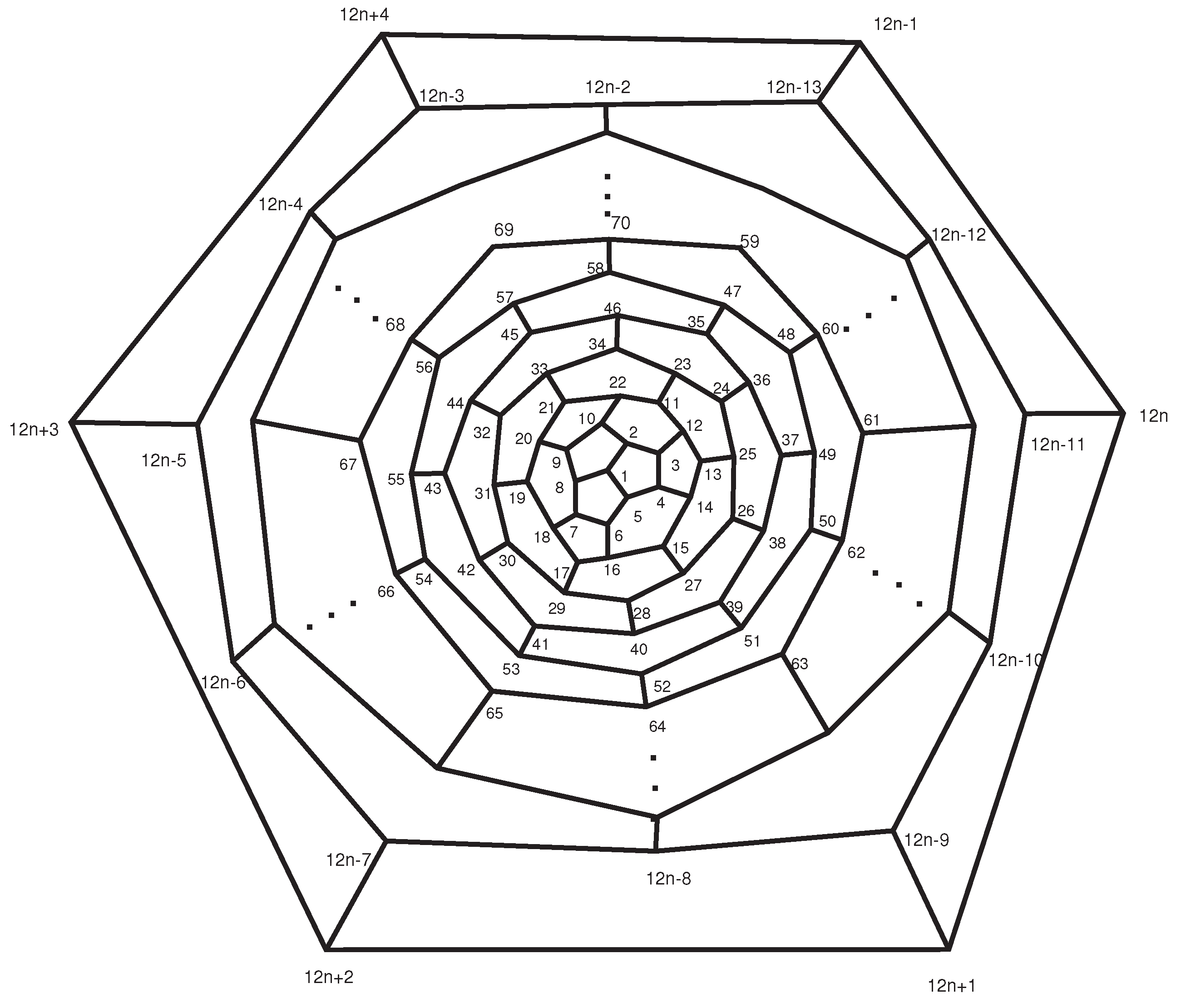
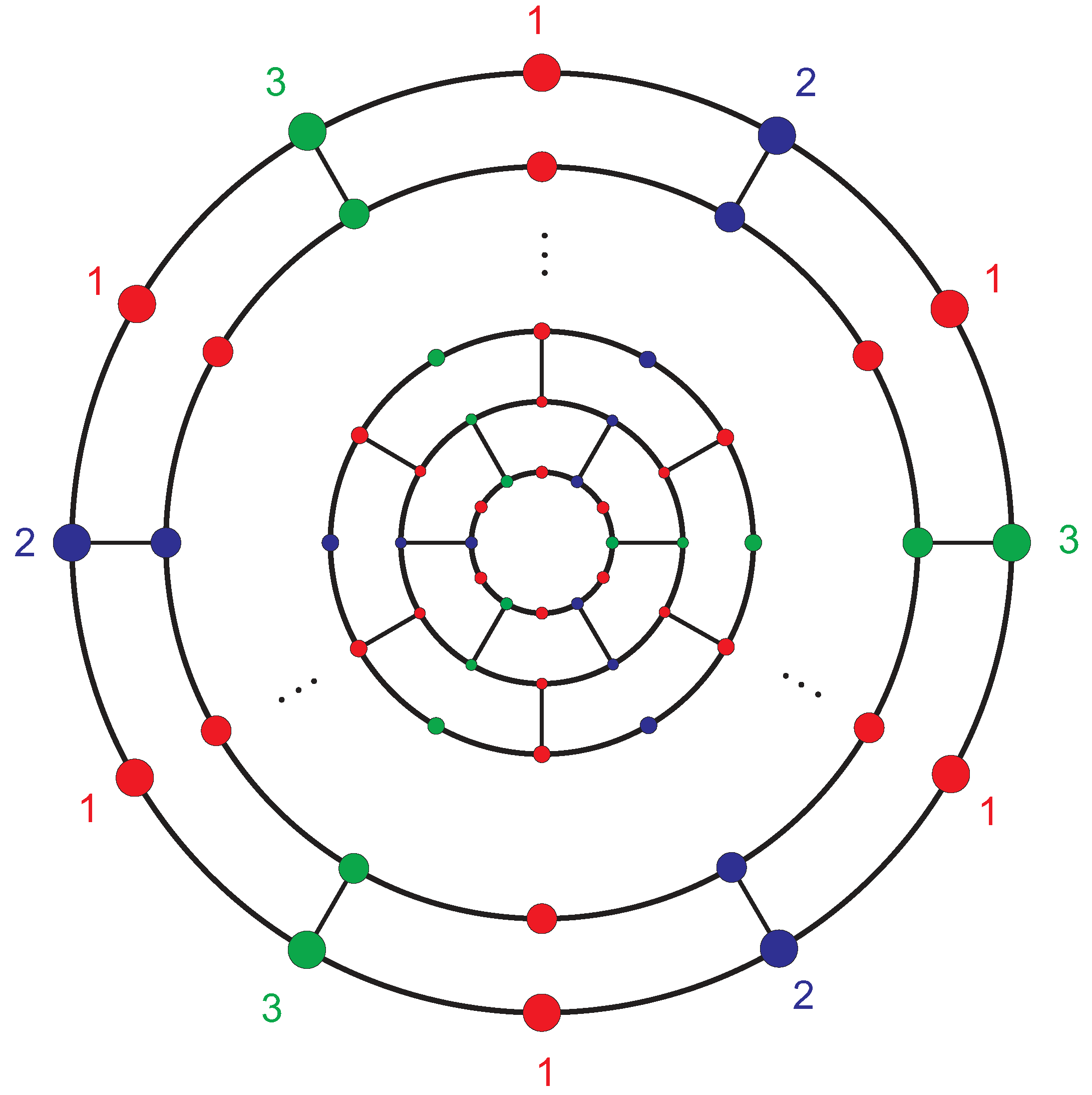
2. Concepts and Terminology
3. Entropy of Graphs
4. Main Results
Correlation Analysis
5. Summary and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dehmer, M.; Mowshowitz, A. A history of graph entropy measures. Inf. Sci. Int. J. 2011, 181, 57–78. [Google Scholar] [CrossRef]
- Dehmer, M.; Mowshowitz, A.; Emmert-Streib, F. Connections between classical and parametric network entropies. PLoS ONE 2011, 6, e15733. [Google Scholar] [CrossRef]
- Mowshowitz, A. Entropy and the complexity of the graphs I: An index of the relative complexity of a graph. Bull. Math. Biophys. 1968, 30, 175–204. [Google Scholar] [CrossRef]
- Rashevsky, N. Life, Information Theory, and Topology. Bull. Math. Biophys. 1955, 17, 229–235. [Google Scholar] [CrossRef]
- Mowshowitz, A. Entropy and the complexity of graphs II: The information content of digraphs and infinite graphs. Bull. Math. Biophys. 1968, 30, 225–240. [Google Scholar] [CrossRef] [PubMed]
- Mowshowitz, A. Entropy and the complexity of graphs III: Graphs with prescribed information content. Bull. Math. Biophys. 1968, 30, 387–414. [Google Scholar] [CrossRef]
- Mowshowitz, A. Entropy and the complexity of graphs IV: Entropy measures and graphical structure. Bull. Math. Biophys. 1968, 30, 533–546. [Google Scholar] [CrossRef]
- Mowshowitz, A.; Dehmer, M. The Hosoya entropy of a graph. Entropy 2015, 17, 1054–1062. [Google Scholar] [CrossRef]
- Dehmer, M. Strukturelle Analyse web-basierter Dokumente. In Multimedia und Telekooperation; Deutscher Universitats Verlag: Wiesbaden, Germany, 2006. [Google Scholar]
- Dehmer, M.; Emmert-Streib, F.; Shi, Y. Interrelations of graph distance measures based on topological indices. PLoS ONE 2014, 9, e94985. [Google Scholar] [CrossRef] [PubMed]
- Dehmer, M.; Emmert-Streib, F.; Shi, Y. Graph distance measures based on topological indices revisited. Appl. Math. Comput. 2015, 266, 623–633. [Google Scholar] [CrossRef]
- Dehmer, M.; Mehler, A. A new method of measuring similarity for a special class of directed graphs. Tatra Mt. Math. Publ. 2007, 36, 39–59. [Google Scholar]
- Dehmer, M.; Mowshowitz, A. Generalized graph entropies. Complexity 2011, 17, 45–50. [Google Scholar] [CrossRef]
- Dehmer, M.; Sivakumar, L.; Varmuza, K. Uniquely discriminating molecular structures using novel eigenvalue-based descriptors. MATCH Commun. Math. Comput. Chem. 2012, 67, 147–172. [Google Scholar]
- Dehmer, M.; Shi, Y.; Emmert-Streib, F. Structural differentiation of graphs using Hosoya-based indices. PLoS ONE 2014, 9, e102459. [Google Scholar] [CrossRef] [PubMed]
- Dehmer, M.; Varmuza, K.; Borgert, S.; Emmert-Streib, F. On entropy-based molecular descriptors: Statistical analysis of real and synthetic chemical structures. J. Chem. Inf. Model. 2009, 49, 1655–1663. [Google Scholar] [CrossRef] [PubMed]
- Kroto, H.W.; Heath, J.R.; O’Brien, S.C.; Curl, R.F.; Smalley, R.E. C60: buckminsterfullerene. Nature 1985, 318, 162–163. [Google Scholar] [CrossRef]
- Fowler, P.W.; Manolopoulos, D.E. An Atlas of Fullerenes; Clarendon Press: Oxford, UK, 1995. [Google Scholar]
- Ori, O.; Cataldo, F.; Graovac, A. Topological ranking of C28 fullerenes reactivity. Fullerene Nanotube Carbon Nanostruct. 2009, 17, 308–323. [Google Scholar] [CrossRef]
- Ori, O.; D’Mello, M. A topological study of the structure of the C76 fullerene. Chem. Phys. Lett. 1992, 197, 49–54. [Google Scholar] [CrossRef]
- Sabirov, D.S.; Ori, O.; Laszlo, I.; Graovac, A. Isomers of the C84 fullerene: A theoretical consideration within energetic, structural, and topological approaches. Fuller. Nanotub. Carbon Nanostruct. 2018, 26, 100–110. [Google Scholar] [CrossRef]
- Ghorbani, M. Connective eccentric index of fullerenes. J. Math. Nanosci. 2011, 1, 43–50. [Google Scholar]
- Aleskovskii, V.B. Information as a factor of self-organization and organization of matter. Russ. J. Gen. Chem. 2002, 72, 569–574. [Google Scholar] [CrossRef]
- Talanov, V.M.; Ivanov, V.V. Structure as the source of information on the chemical organization of substance. Russ. J. Gen. Chem. 2013, 83, 2225–2336. [Google Scholar] [CrossRef]
- Sabirov, D.S.; Osawa, E. Information entropy of fullerenes. J. Chem. Inf. Model. 2015, 55, 1576–1584. [Google Scholar] [CrossRef]
- Sabirov, D.S.; Terentyev, A.O.; Sokolov, V.I. Activation energies and information entropies of helium penetration through fullerene walls. Insights into the formation of endofullerenes nX@C60/70 (n = 1 and 2) from the information entropy approach. RSC Adv. 2016, 6, 72230–72237. [Google Scholar] [CrossRef]
- Shannon, C.E.; Weaver, W. The Mathematical Theory of Communication; University of Illinois Press: Urbana, IL, USA, 1949. [Google Scholar]
- Ghorbani, M.; Dehmer, M.; Zangi, S. On certain aspects of graph entropies of fullerenes. MATCH Commun. Math. Comput. Chem. 2019, 81, 163–174. [Google Scholar]
- Ghorbani, M.; Dehmer, M.; Rajabi-Parsa, M.; Mowshowitz, A.; Emmert-Streib, F. Hosoya entropy of fullerene graph. Appl. Math. Comput. 2019, 352, 88–98. [Google Scholar] [CrossRef]
- Das, K.C.; Shi, Y. Some properties on entropies of graphs, MATCH Commun. Math. Comput. Chem. 2017, 78, 259–272. [Google Scholar]
- Eliasi, M. On extremal properties of general graph entropies. MATCH Commun. Math. Comput. Chem. 2018, 79, 645–657. [Google Scholar]
- Gutman, I.; Furtula, B.; Katanić, V. Randić index and information. AKCE Int. J. Graphs Comb. 2018, 18. [Google Scholar] [CrossRef]
- Kazemi, R. Entropy of weighted graphs with the degree-based topological indices as weights. MATCH Commun. Math. Comput. Chem. 2016, 76, 69–80. [Google Scholar]
- Li, X.; Qin, Z.; Wei, M.; Gutman, I. Novel inequalities for generalized graph entropies-graph energies and topological indices. Appl. Math. Comput. 2015, 259, 470–479. [Google Scholar] [CrossRef]
- Bonchev, D. Information Theoretic Indices for Characterization of Chemical Structures; Research Studies Press: Chichester, UK, 1983. [Google Scholar]
- Todeschini, R.; Consonni, V. Handbook of Molecular Descriptors; WILEY-VCH: Hoboken, NJ, USA, 2000. [Google Scholar]
- Ashrafi, A.R.; Ghorbani, M. Eccentric Connectivity Index of Fullerenes. In Novel Molecular Structure Descriptors-Theory and Applications II; Gutman, I., Furtula, B., Eds.; Kragujevac University, Faculty of Science: Kragujevac, Serbia, 2008; pp. 183–192. [Google Scholar]
- Ghorbani, M.; Dehmer, M.; Zangi, S. Graph operations based on using distance-based graph entropies. Appl. Math. Comput. 2018, 333, 547–555. [Google Scholar] [CrossRef]
- Gutman, I. The energy of a graph Berichte der Mathematisch-Statistischen. Sektionim Forschungszentrum Graz 1978, 103, 1–22. [Google Scholar]
- Gutman, I. The energy of a graph: Old and new results. In Algebraic Combinatorics and Applications; Betten, A., Kohner, A., Laue, R., Wassermann, A., Eds.; Springer: Berlin, Germany, 2001; pp. 196–211. [Google Scholar]
- Doslić, T. The Smallest Eigenvalue of Fullerene Graphs Closing the Gap. MATCH Commun. Math. Comput. Chem. 2013, 70, 73–78. [Google Scholar]
- Fath-Tabar, G.H.; Ashrafi, A.R.; Stevanovic, D. Spectral properties of fullerenes. J. Comput. Theor. Nanosci. 2012, 9, 327–329. [Google Scholar] [CrossRef]
- Ghorbani, M. Remarks on markaracter table of fullerene graphs. J. Comput. Theor. Nanosci. 2014, 11, 363–379. [Google Scholar] [CrossRef]
- Ghorbani, M.; Bani-Asadi, E. Remarks on characteristic coefficients of fullerene graphs. Appl. Math. Comput. 2014, 230, 428–435. [Google Scholar] [CrossRef]
- Harary, F. Graph Theory; Addison-Wesley: Reading, MA, USA, 1969. [Google Scholar]
- Jalali-Rad, M. Which fullerenes are stable? J. Math. Nanosci. 2015, 5, 23–29. [Google Scholar]
- Manolopoulos, D.E.; Woodall, D.R.; Fowler, P.W. Electronic stability of fullerenes: Eigenvalues theorems for leapfrog carbon clusters. J. Chem. Soc. Faraday Trans. 1992, 88, 2427–2435. [Google Scholar] [CrossRef]
- Shiu, W.C. On the spectra of the fullerenes that contain a nontrivial cyclic-5-cutset. Aust. J. Comb. 2010, 47, 41–51. [Google Scholar]
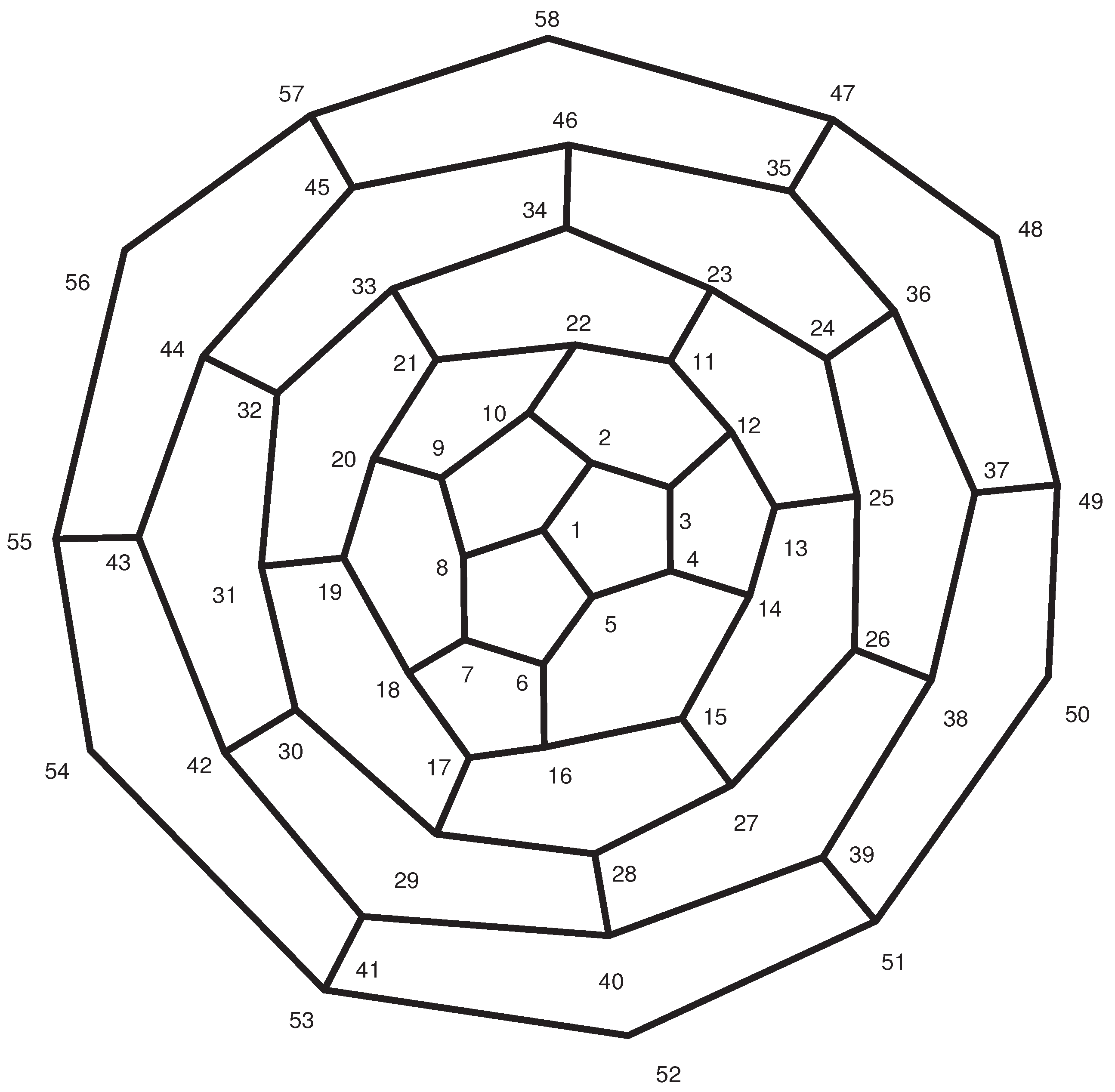
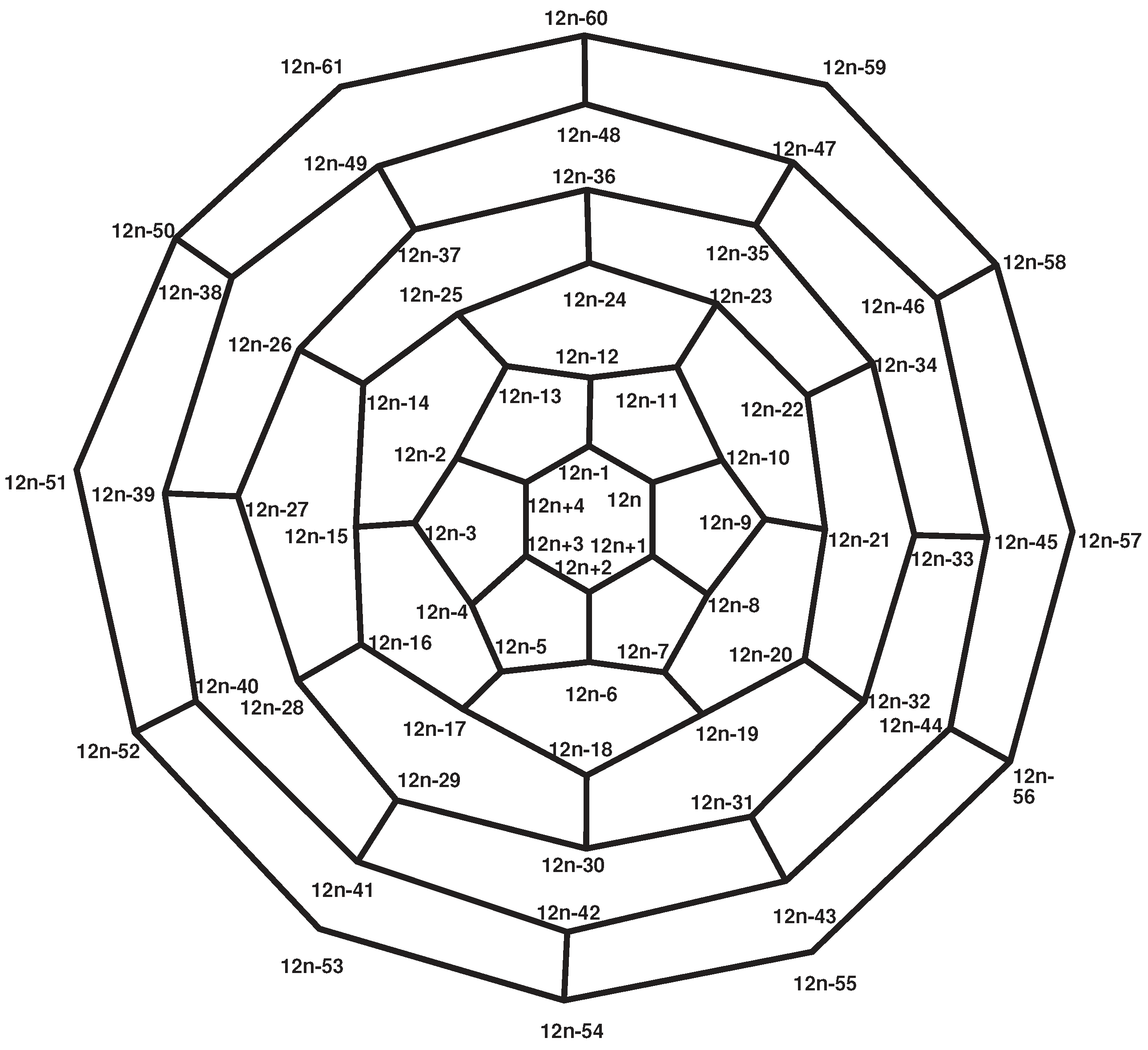

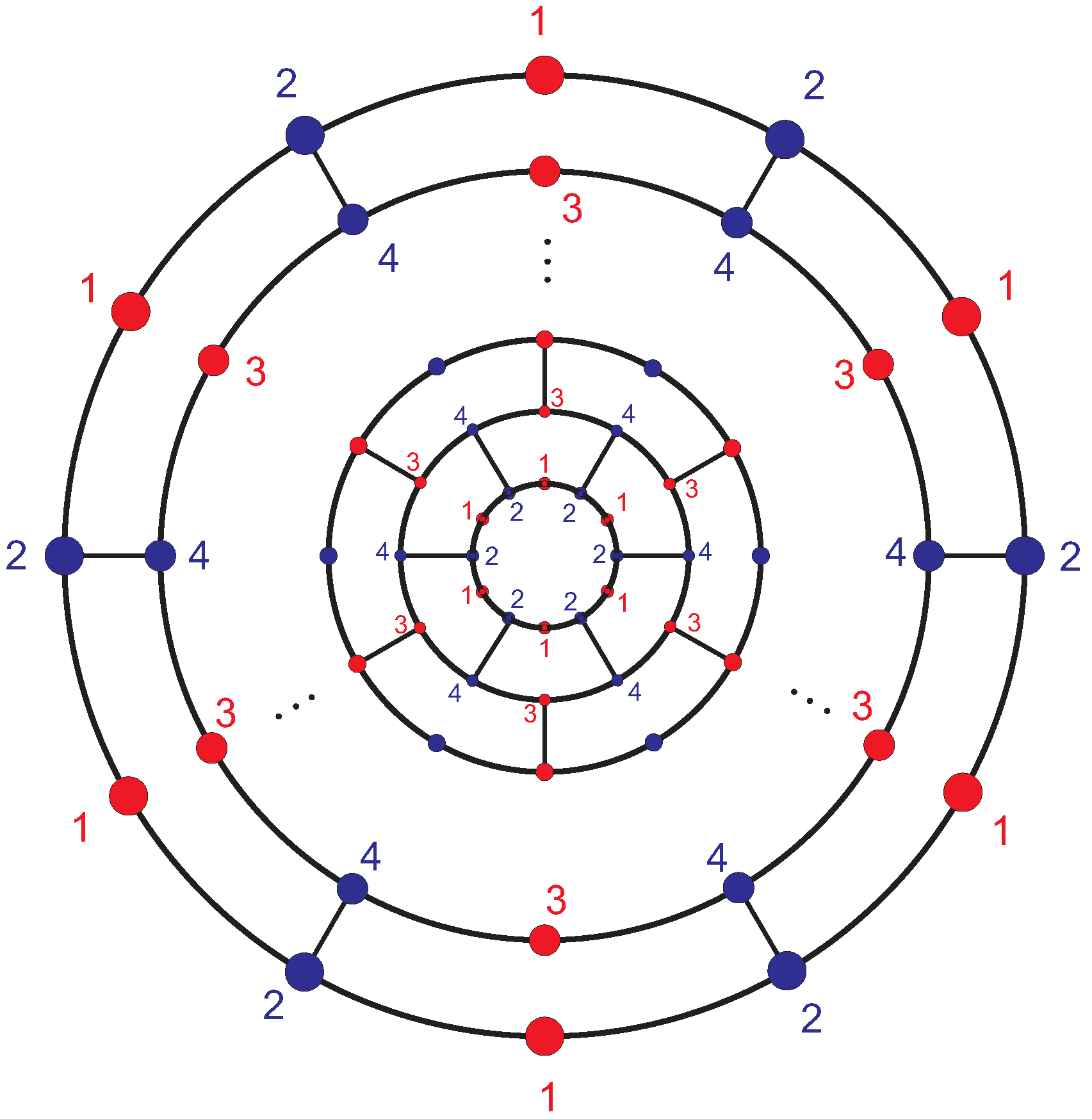
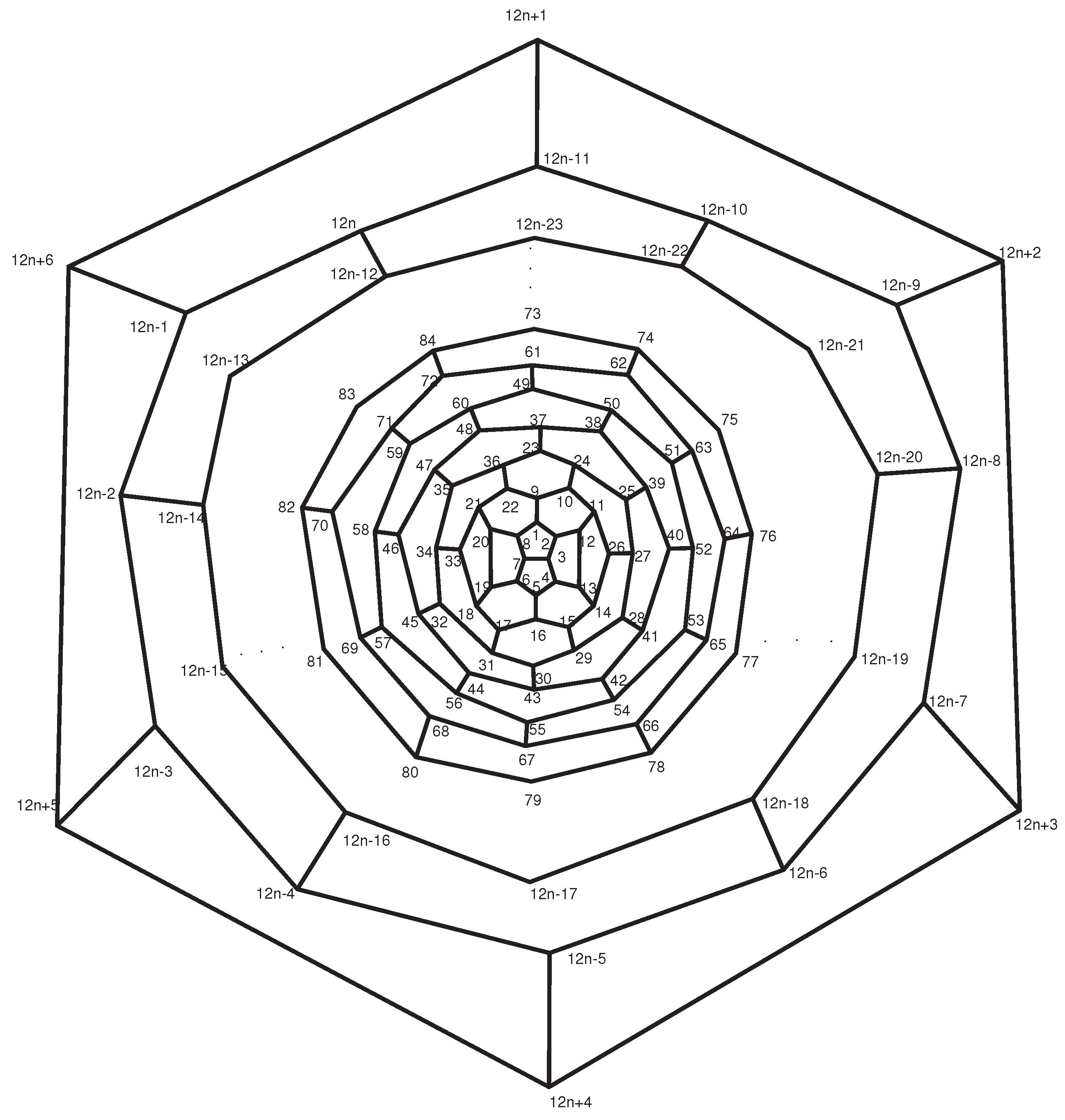
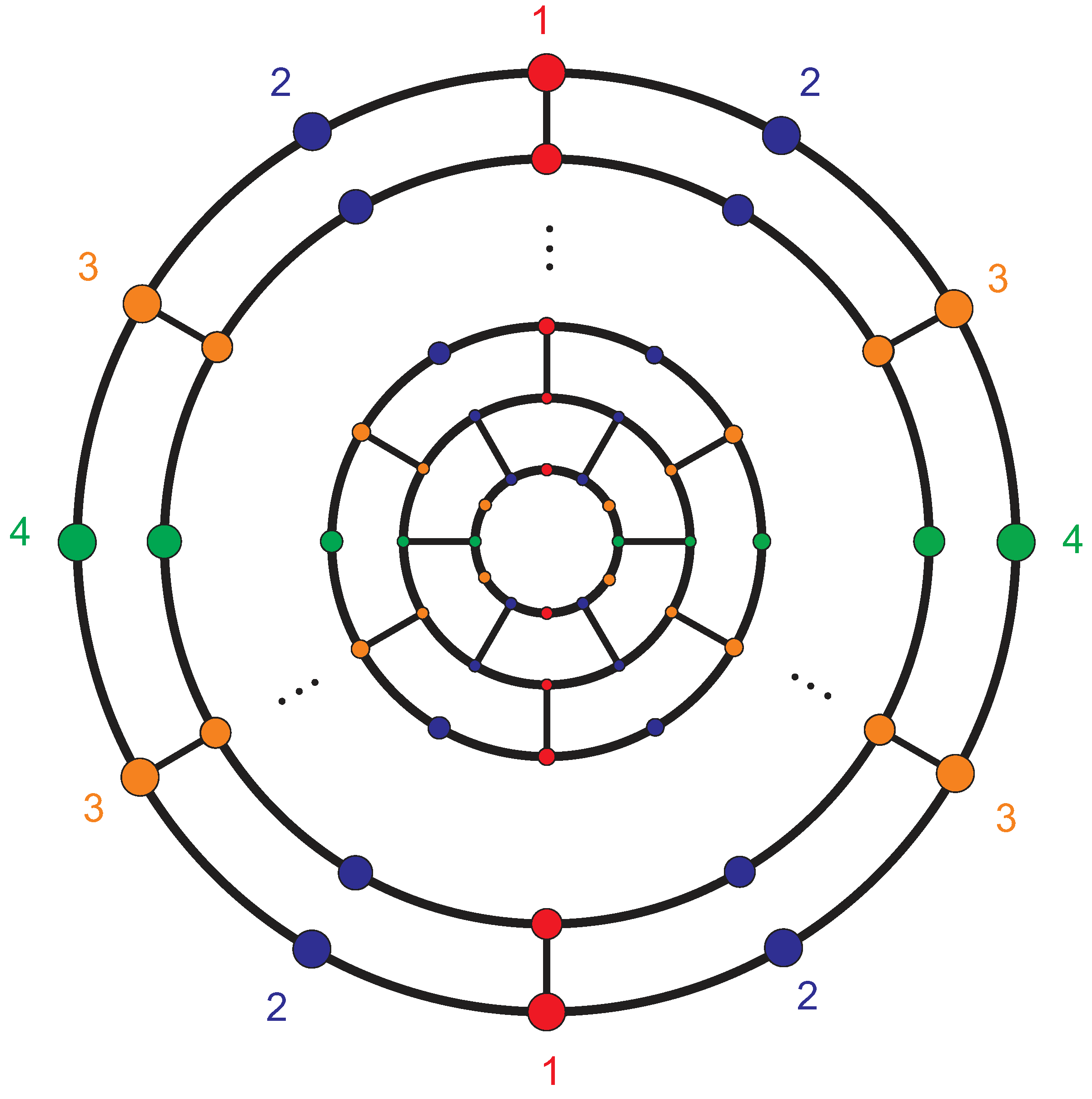

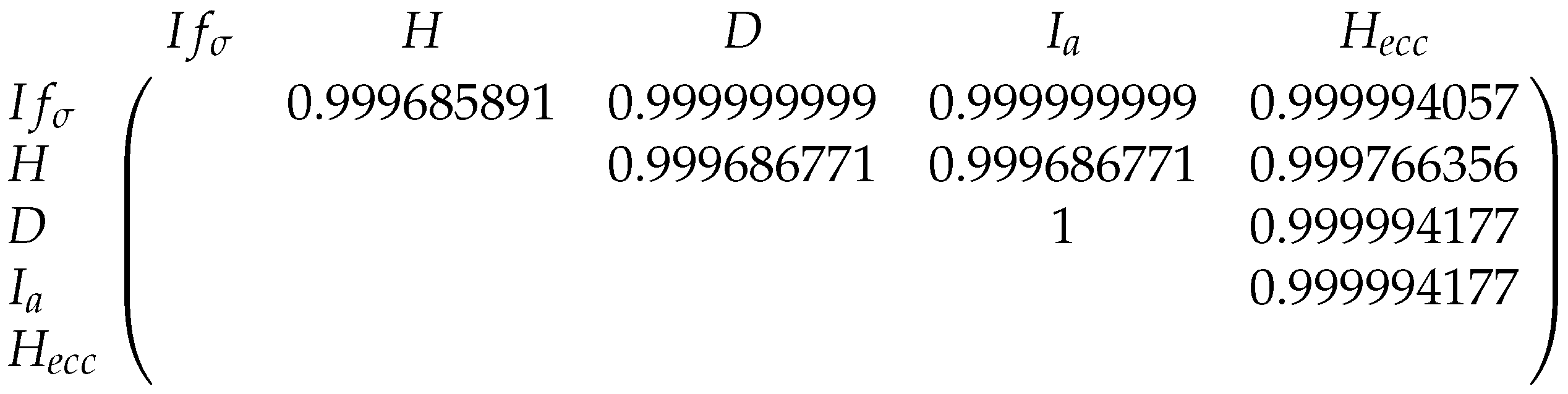
| Partitions | Elements | ecc |
|---|---|---|
| 1 | ||
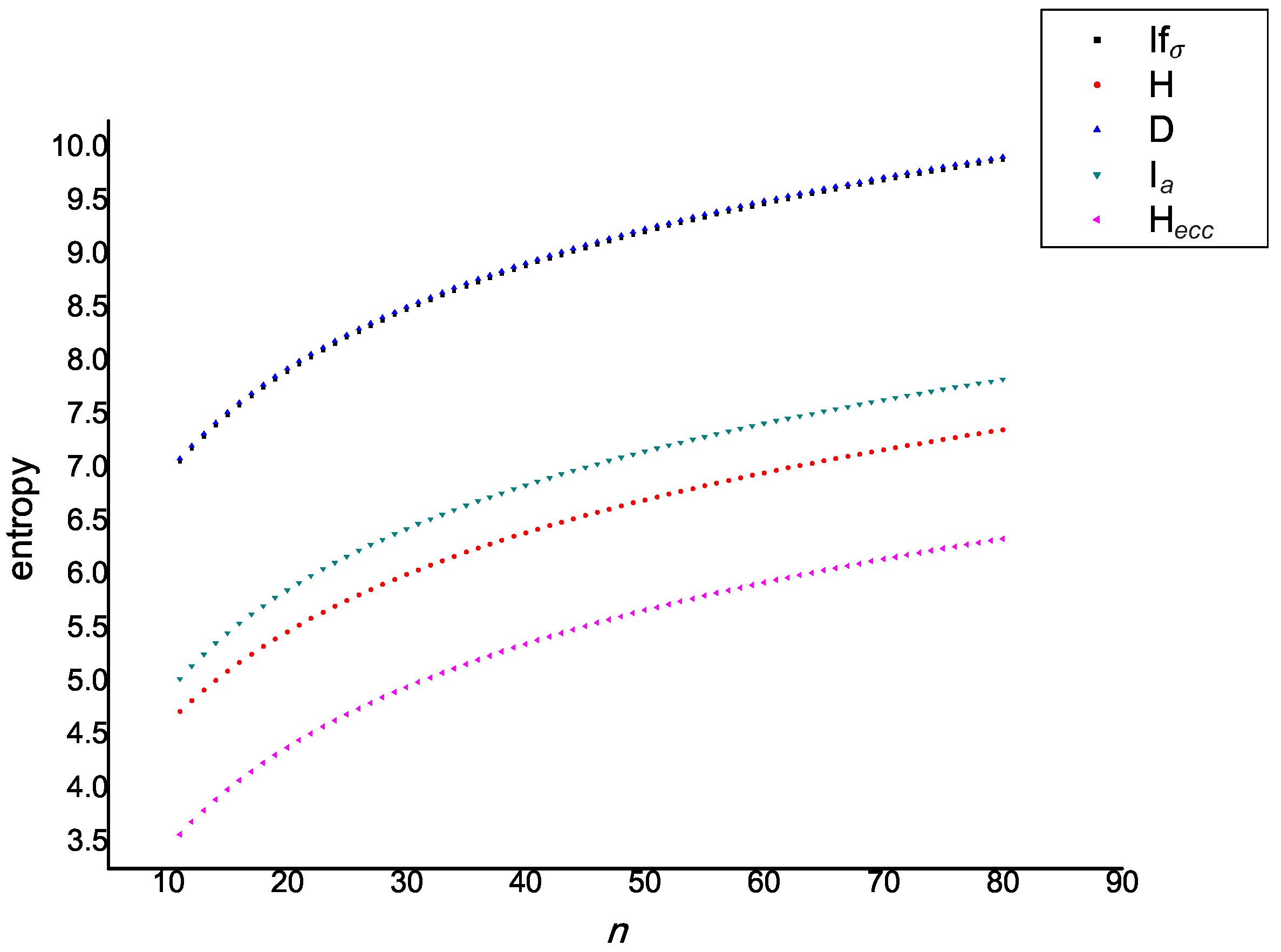
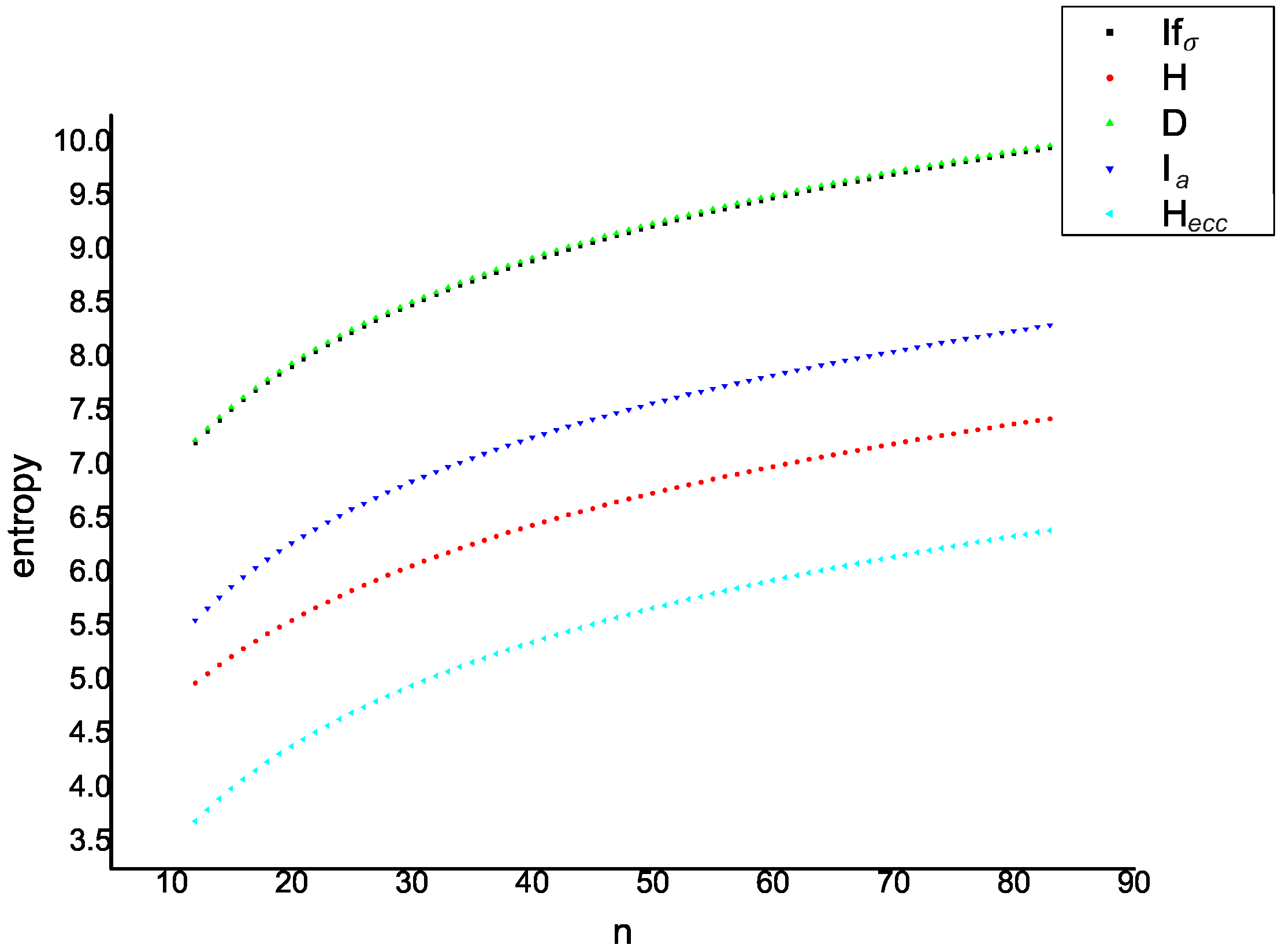
| n | E | D | H | |||
|---|---|---|---|---|---|---|
| 11 | 212.87 | 7.08 | 7.06 | 5.02 | 4.72 | 3.57 |
| 12 | 231.73 | 7.2 | 7.18 | 5.14 | 4.82 | 3.68 |
| 13 | 250.59 | 7.32 | 7.29 | 5.25 | 4.92 | 3.79 |
| 14 | 269.46 | 7.42 | 7.39 | 5.36 | 5.01 | 3.89 |
| 15 | 288.32 | 7.52 | 7.49 | 5.45 | 5.09 | 3.98 |
| 16 | 307.19 | 7.61 | 7.58 | 5.54 | 5.18 | 4.07 |
| 17 | 326.05 | 7.7 | 7.67 | 5.63 | 5.25 | 4.15 |
| 18 | 344.91 | 7.78 | 7.75 | 5.71 | 5.33 | 4.23 |
| 19 | 363.78 | 7.85 | 7.83 | 5.78 | 5.4 | 4.31 |
| 20 | 382.64 | 7.93 | 7.9 | 5.86 | 5.46 | 4.38 |
| Cor | 0.9964006 | 0.9972326 | 0.99673 | 0.9975728 | 0.9974525 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghorbani, M.; Dehmer, M.; Rajabi-Parsa, M.; Mowshowitz, A.; Emmert-Streib, F. On Properties of Distance-Based Entropies on Fullerene Graphs. Entropy 2019, 21, 482. https://doi.org/10.3390/e21050482
Ghorbani M, Dehmer M, Rajabi-Parsa M, Mowshowitz A, Emmert-Streib F. On Properties of Distance-Based Entropies on Fullerene Graphs. Entropy. 2019; 21(5):482. https://doi.org/10.3390/e21050482
Chicago/Turabian StyleGhorbani, Modjtaba, Matthias Dehmer, Mina Rajabi-Parsa, Abbe Mowshowitz, and Frank Emmert-Streib. 2019. "On Properties of Distance-Based Entropies on Fullerene Graphs" Entropy 21, no. 5: 482. https://doi.org/10.3390/e21050482
APA StyleGhorbani, M., Dehmer, M., Rajabi-Parsa, M., Mowshowitz, A., & Emmert-Streib, F. (2019). On Properties of Distance-Based Entropies on Fullerene Graphs. Entropy, 21(5), 482. https://doi.org/10.3390/e21050482






