Synchronization of Fractional-Order Complex Chaotic Systems Based on Observers
Abstract
1. Introduction
2. Problem Statement
3. Problem Description and Synchronization Scheme
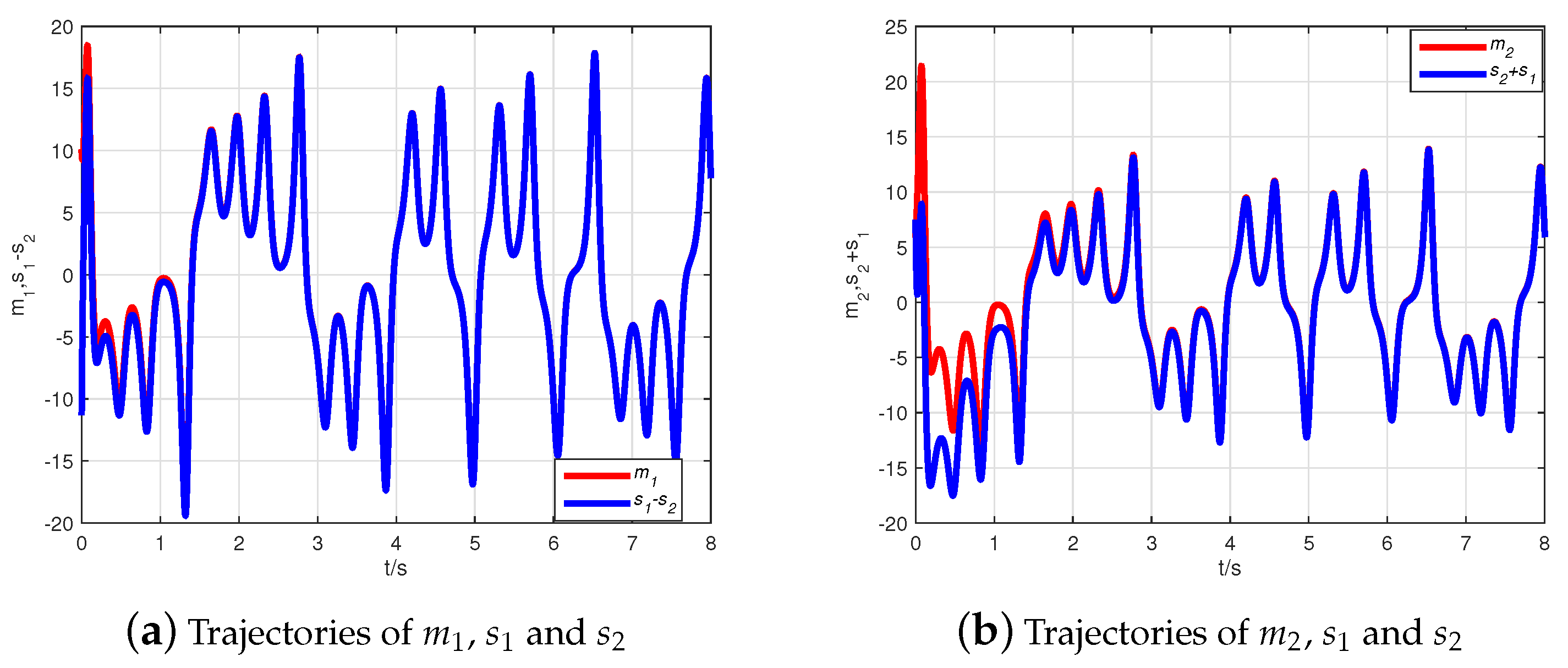
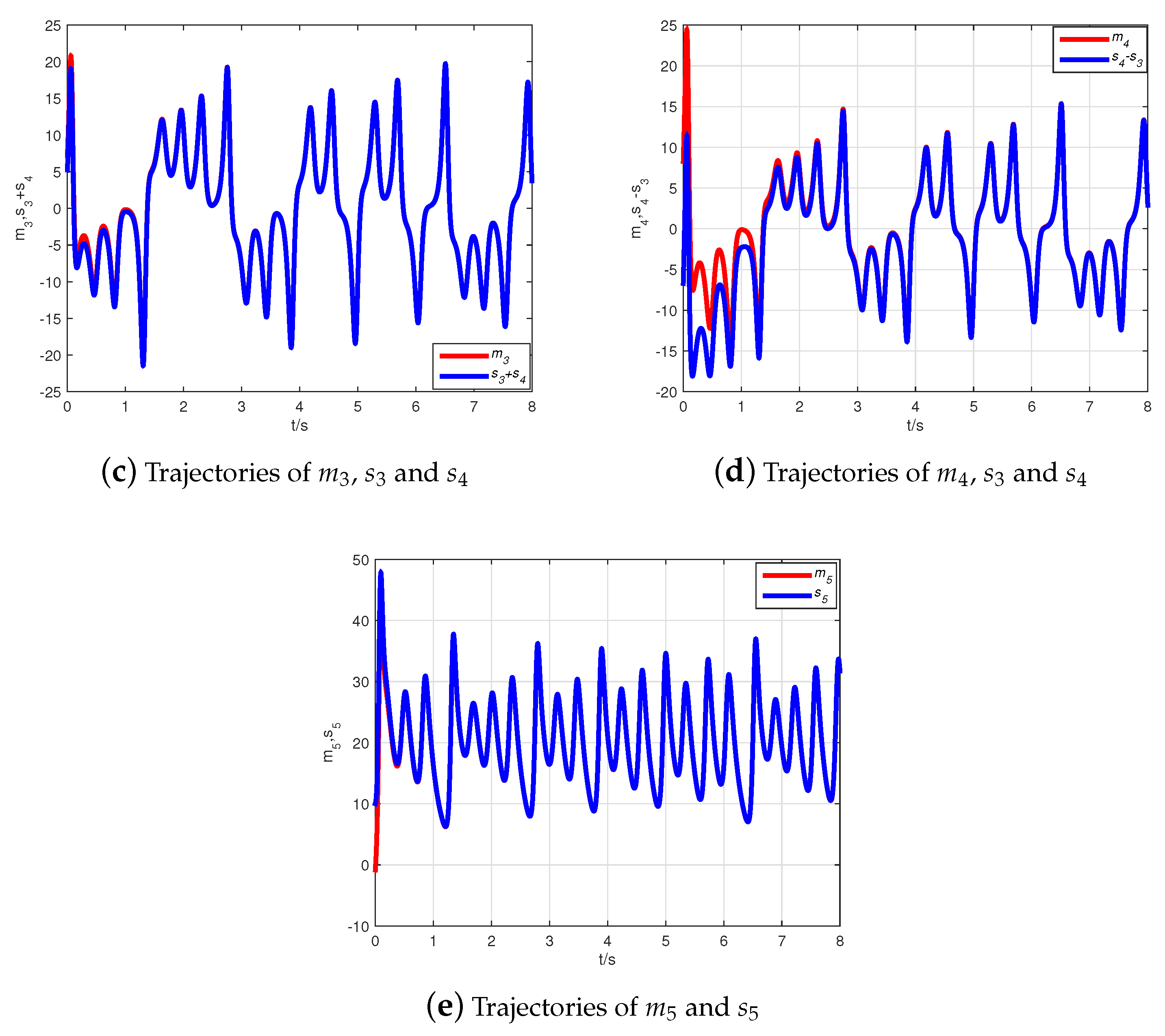
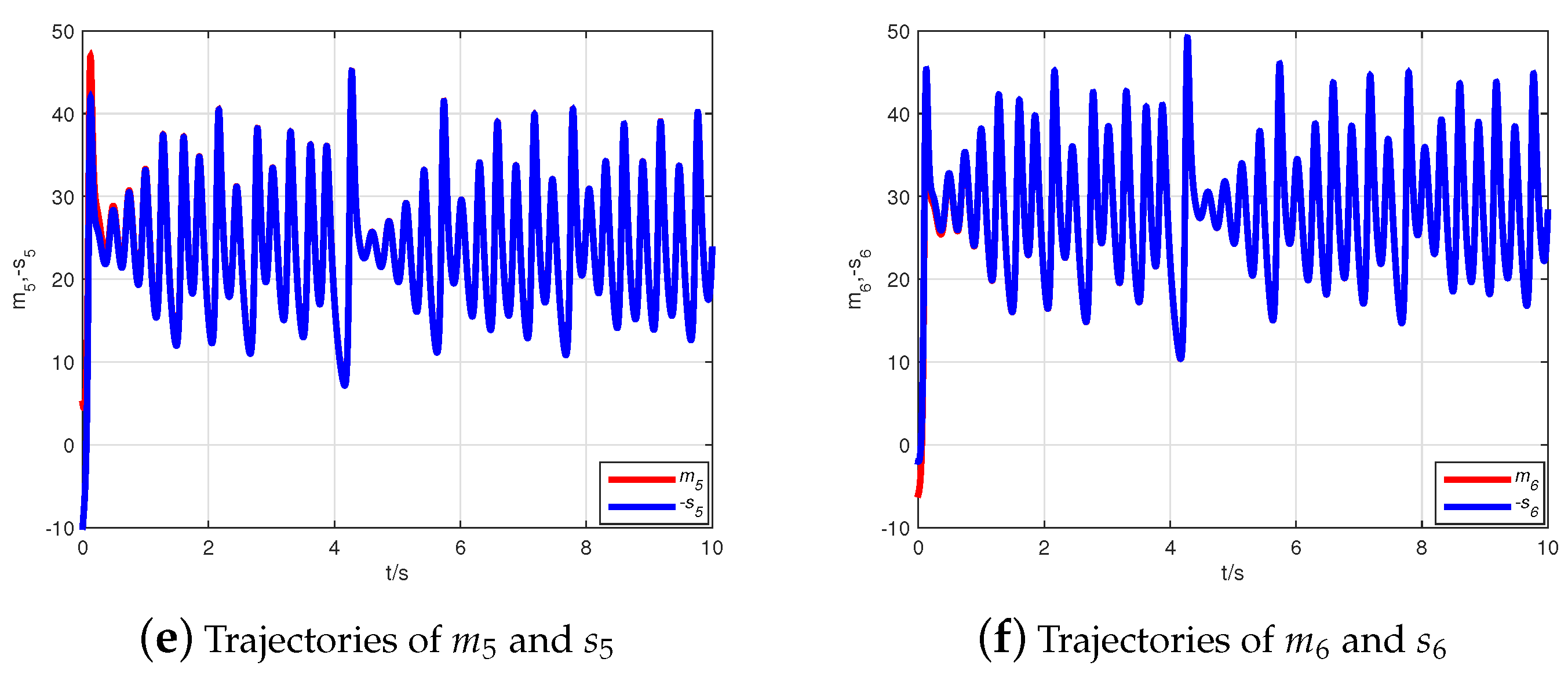
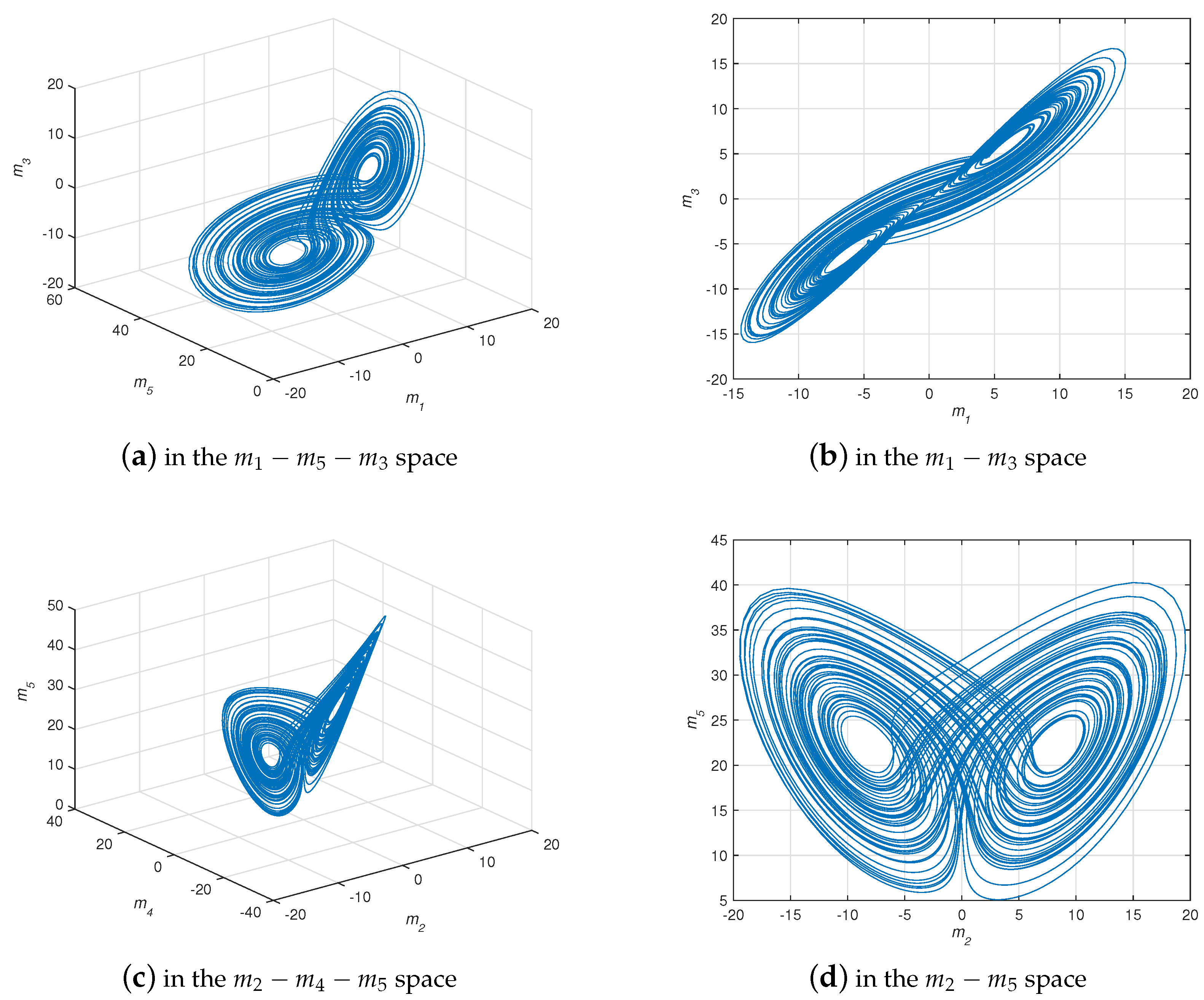
4. Numerical Simulations
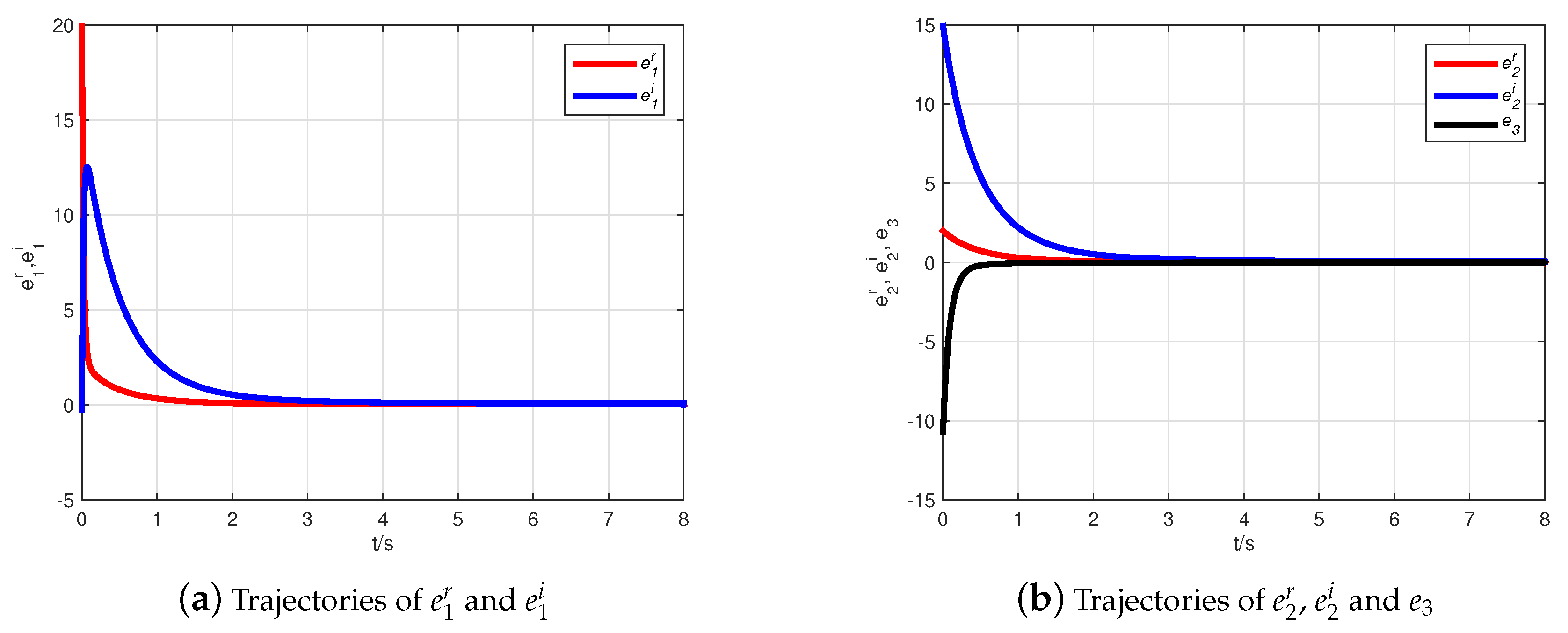
4.1. CMPS of the Fractional-Order Complex Lü Systems
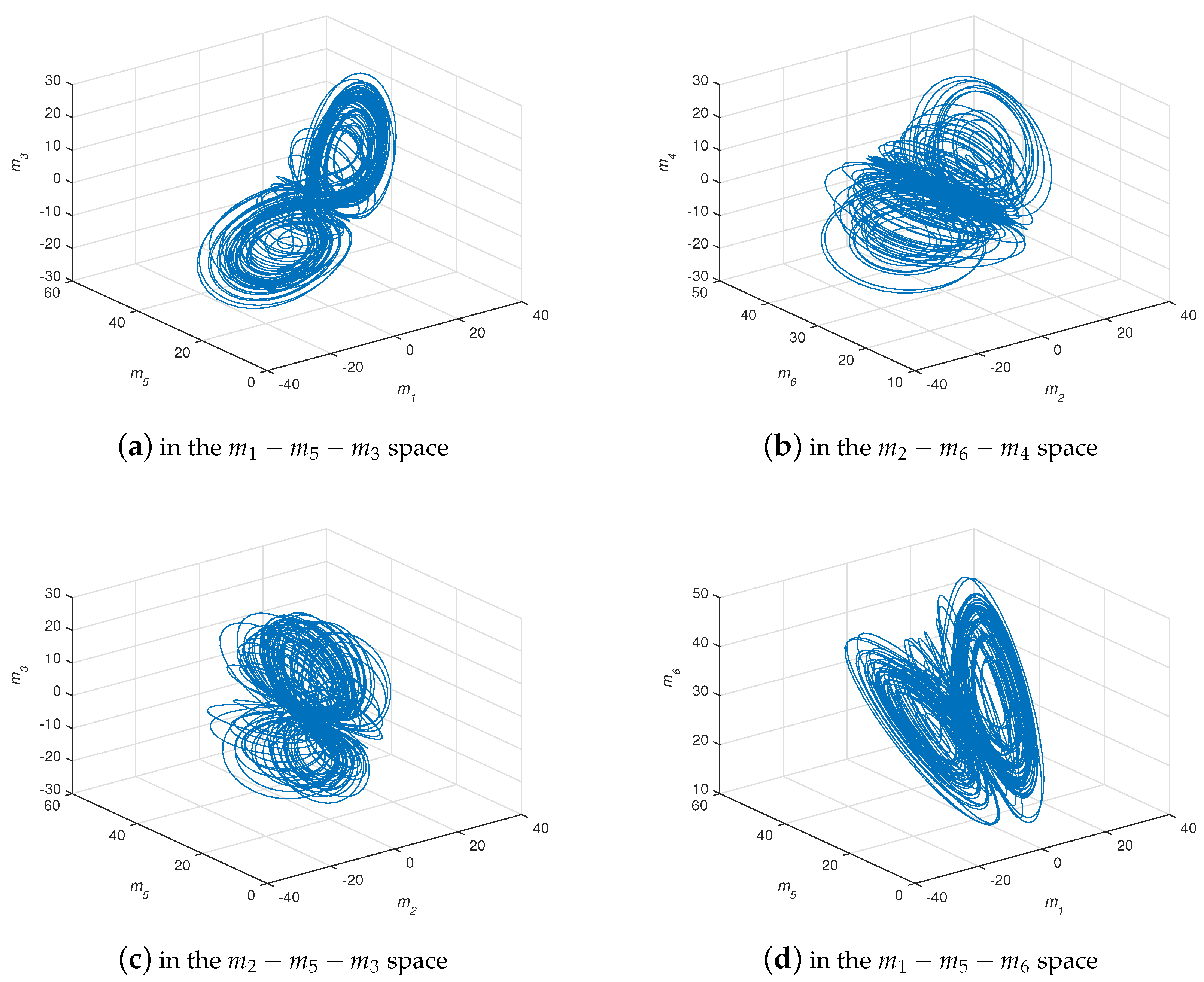
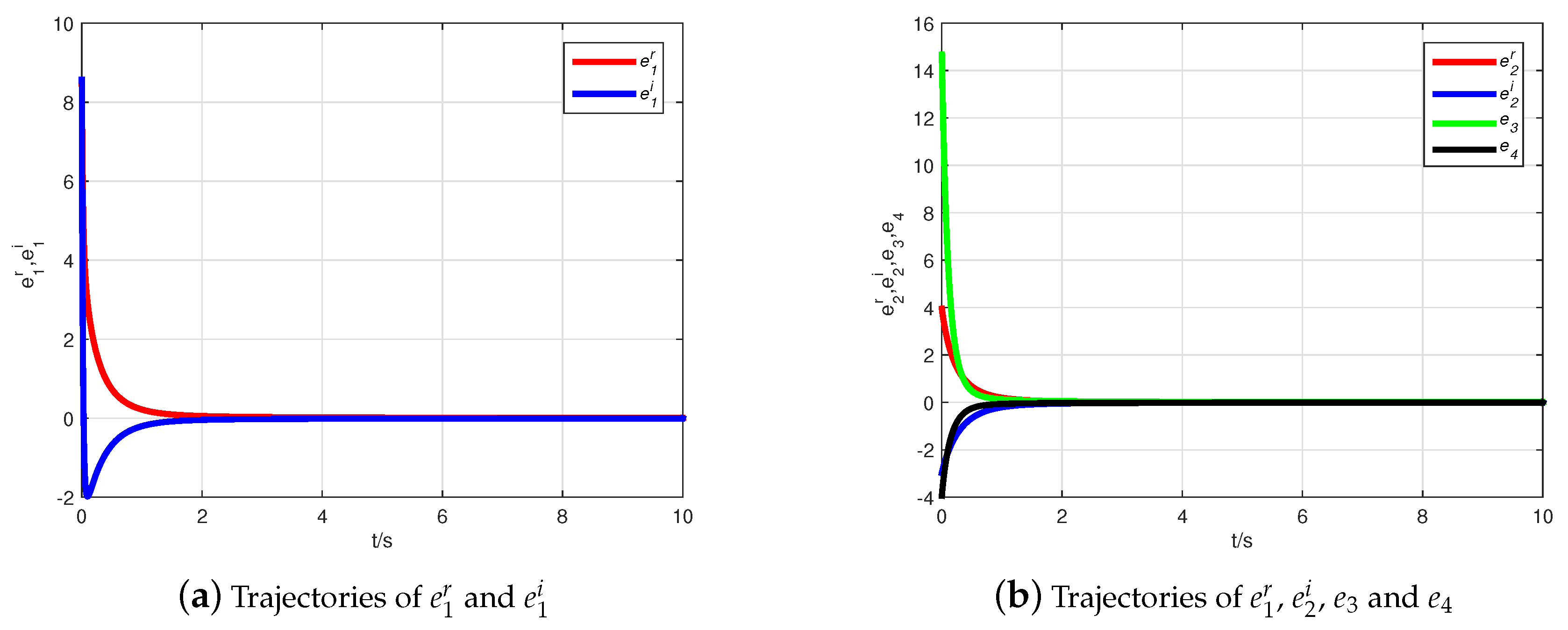
4.2. CMPS of the Fractional-Order Hyper-Chaotic Complex Lü System
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gao, X.; Yu, J.B. Chaos in the fractional order periodically forced complex Duffing’s oscillators. Chaos Solitons Fractals 2005, 24, 1097–1104. [Google Scholar] [CrossRef]
- El-Sayed, A.M.A.; Ahmed, E.; El-Saka, H.A.A. Dynamic properties of the fractional-order Logistic equation of complex variables. Abstr. Appl. Anal. 2012, 2012, 1–12. [Google Scholar] [CrossRef]
- Luo, C.; Wang, X.Y. Chaos in the fractional-order complex Lorenz system and its synchronization. Nonlinear Dyn. 2013, 71, 241–257. [Google Scholar] [CrossRef]
- Luo, C.; Wang, X.Y. Chaos generated from the fractional-order complex Chen system and its application to digital secure communication. Int. J. Mod. Phys. C 2013, 24, 1350025. [Google Scholar] [CrossRef]
- Liu, X.J.; Hong, L.; Yang, L.X. Fractional-order complex T system: Bifurcations, chaos control, and synchronization. Nonlinear Dyn. 2014, 75, 589–602. [Google Scholar] [CrossRef]
- Jiang, C.M.; Liu, S.T.; Luo, C. A new fractional-order chaotic complex system and its antisynchronization. Abstr. Appl. Anal. 2014, 2014, 326354. [Google Scholar] [CrossRef]
- Yang, L.X.; Jiang, J. Complex dynamical behavior and modified projective synchronization in fractional-order hyper-chaotic complex Lü system. Chaos Solitons Fractals 2015, 78, 267–276. [Google Scholar] [CrossRef]
- Singh, A.K.; Yadav, V.K.; Das, S. Synchronization between fractional order complex chaotic systems. Int. J. Dyn. Control 2017, 5, 756–770. [Google Scholar] [CrossRef]
- Zhang, R.X.; Liu, Y.L.; Yang, S.P. Adaptive synchronization of fractional-order complex chaotic systems with unknown complex parameters. Entropy 2019, 21, 207. [Google Scholar] [CrossRef]
- Jiang, C.M.; Zhang, F.F.; Li, T.X. Synchronization and antisynchronization of N-coupled fractional-order complex chaotic systems with ring connection. Math. Meth. Appl. Sci. 2018, 41, 2625–2638. [Google Scholar] [CrossRef]
- Velmurugan, G.; Rakkiyappan, R. Hybrid projective synchronization of fractional-order chaotic complex nonlinear systems with time delays. ASME J. Comput. Nonlinear Dyn. 2016, 11, 031016. [Google Scholar] [CrossRef]
- Delavari, H.; Mohadeszadeh, M. Adaptive modified hybrid robust projective synchronization between identical and nonidentical fractional-order complex chaotic systems with fully unknown parameters. ASME J. Comput. Nonlinear Dyn. 2016, 11, 041023. [Google Scholar] [CrossRef]
- Sun, J.W.; Deng, W.; Cui, G.Z.; Wang, Y.F. Real combination synchronization of three fractional-order complex-variable chaotic systems. Optik 2016, 127, 11460–11468. [Google Scholar] [CrossRef]
- Jiang, C.M.; Liu, S.T.; Wang, D. Generalized combination complex synchronization for fractional-order chaotic complex systems. Entropy 2015, 17, 5199–5217. [Google Scholar] [CrossRef]
- Mahmoud, G.M.; Ahmed, M.E.; Abed-Elhameed, T.M. Generalization of combination-combination synchronization of chaotic n-dimensional fractional-order dynamical systems. Nonlinear Dyn. 2016, 83, 1885–1893. [Google Scholar] [CrossRef]
- Jiang, C.M.; Liu, S.T.; Zhang, F.F. Complex modified projective synchronization for fractional-order chaotic complex systems. Int. J. Autom. Comput. 2018, 15, 599–611. [Google Scholar] [CrossRef]
- Liu, J. Complex modified hybrid projective synchronization of different dimensional fractional-order complex chaos and real hyper-chaos. Entropy 2014, 16, 6195–6211. [Google Scholar] [CrossRef]
- Tian, X.M.; Zhong, Y. Adaptive complex modified projective synchronization of two fractional-order complex-variable chaotic systems with unknown parameters. Eng. Lett. 2017, 25, 4. [Google Scholar]
- Mahmoud, G.M.; Ahmed, M.E.; Abed-Elhameed, T.M. On fractional-order hyperchaotic complex systems and their generalized function projective combination synchronization. Optik 2017, 130, 398–406. [Google Scholar] [CrossRef]
- Peng, D.X.; Li, X.D.; Aouiti, C.; Miaadi, F. Finite-time synchronization for Cohen-Grossberg neural networks with mixed time-delays. Neurocomputing 2018, 294, 39–47. [Google Scholar] [CrossRef]
- Wang, P.G.; Li, C.R.; Zhang, J.; Li, T.X. Quasilinearization method for first-order impulsive integro-differential equations. Electron. J. Differ. Eq. 2019, 46, 1–14. [Google Scholar]
- Yang, D.; Li, X.D.; Qiu, J.L. Output tracking control of delayed switched systems via state-dependent switching and dynamic output feedback. Nonlinear Anal. Hybrid Syst. 2019, 32, 294–305. [Google Scholar] [CrossRef]
- Li, X.D.; Ho, D.W.C.; Cao, J.D. Finite-time stability and settling-time estimation of nonlinear impulsive systems. Automatica 2019, 99, 361–368. [Google Scholar] [CrossRef]
- Singh, A.K.; Yadav, V.K.; Das, S. Dual combination synchronization of the fractional order complex chaotic systems. ASME J. Comput. Nonlinear Dyn. 2017, 12, 011017. [Google Scholar] [CrossRef]
- Yadav, V.K.; Srikanth, N.; Das, S. Dual function projective synchronization of fractional order complex chaotic systems. Optik 2016, 127, 10527–10538. [Google Scholar] [CrossRef]
- Mahmoud, G.M.; Mahmoud, E.E. Complex modified projective synchronization of two chaotic complex nonlinear systems. Nonlinear Dyn. 2013, 73, 2231–2240. [Google Scholar] [CrossRef]
- Zhang, F.F.; Liu, S.T.; Yu, W.Y. Modified projective synchronization with complex scaling factors of uncertain real chaos and complex chaos. Chin. Phys. B 2013, 22, 120505. [Google Scholar] [CrossRef]
- Wu, Z.Y.; Duan, J.Q.; Fu, X.C. Complex projective synchronization in coupled chaotic complex dynamical systems. Nonlinear Dyn. 2012, 69, 771–779. [Google Scholar] [CrossRef]
- Mahmoud, E.E. Complex complete synchronization of two nonidentical hyperchaotic complex nonlinear systems. Math. Methods Appl. Sci. 2014, 37, 321–328. [Google Scholar] [CrossRef]
- Mahmoud, E.E.; Abo-Dahab, S.M. Dynamical properties and complex anti synchronization with applications to secure communications for a novel chaotic complex nonlinear model. Chaos Solitons Fractals 2018, 106, 273–284. [Google Scholar] [CrossRef]
- Wang, S.B.; Wang, X.Y.; Zhou, Y.F. A memristor-based complex Lorenz system and its modified projective synchronization. Entropy 2015, 17, 7628–7644. [Google Scholar] [CrossRef]
- Mahmoud, G.M.; Mahmoud, E.; Arafa, A.A. Projective synchronization for coupled partially linear complex-variable systems with known parameters. Math. Methods Appl. Sci. 2017, 40, 1214–1222. [Google Scholar] [CrossRef]
- Liu, J.; Liu, S.T.; Yuan, C.H. Adaptive complex modified projective synchronization of complex chaotic (hyperchaotic) systems with uncertain complex parameters. Nonlinear Dyn. 2015, 79, 1035–1047. [Google Scholar] [CrossRef]
- Hebertt, S.; Cruz-Hernández, C. Synchronization of chaotic systems: A generalized Hamiltonian systems approach. Int. J. Bifurc. Chaos 2001, 11, 1381–1395. [Google Scholar]
- Liao, T.L.; Huang, N.S. An observer-based approach for chaotic synchronization with application to secure communications. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1999, 46, 1144–1150. [Google Scholar] [CrossRef]
- Nijmeijer, H.; Mareels, I.M.Y. An observer looks at synchronization. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1997, 44, 882–890. [Google Scholar] [CrossRef]
- Ushio, T. Synthesis of synchronized chaotic systems based on observers. Int. J. Bifurc. Chaos 1999, 9, 541–546. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Matignon, D. Stability results for fractional differential equations with applications to control processing. In Proceedings of the IMACS IEEE-SMC Proceedings, Lille, France, 9–12 July 1996. [Google Scholar]
- Pano-Azucena, A.D.; Ovilla-Martinez, B.; Tlelo-Cuautle, E.; Mu noz-Pacheco, J.M.; de la Fraga, L.G. FPGA-based implementation of different families of fractional-order chaotic oscillators applying Grünwald-Letnikov method. Commun. Nonlinear Sci. Numer. Simulat. 2019, 72, 516–527. [Google Scholar] [CrossRef]
- Tolba, M.F.; Said, L.A.; Madian, A.H.; Radwan, A.G. FPGA implementation of the fractional order integrator/differentiator: Two approaches and applications. IEEE Trans. Circuits Syst. I Regul. Pap. 2019, 66, 1484–1495. [Google Scholar] [CrossRef]
- Tolba, M.F.; AboAlNaga, B.M.; Said, L.A.; Madian, A.H.; Radwan, A.G. Fractional order integrator/differentiator: FPGA implementation and FOPID controller application. AEU-Int. J. Electron. Commun. 2019, 98, 220–229. [Google Scholar] [CrossRef]
- He, S.B.; Sun, K.H.; Wang, H.H. Generalized synchronization of fractional-order hyperchaotic systems and its DSP implementation. Nonlinear Dyn. 2018, 92, 85–96. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J.; Freed, A.D. A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn. 2002, 29, 3–22. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Xia, T.; Jiang, C. Synchronization of Fractional-Order Complex Chaotic Systems Based on Observers. Entropy 2019, 21, 481. https://doi.org/10.3390/e21050481
Li Z, Xia T, Jiang C. Synchronization of Fractional-Order Complex Chaotic Systems Based on Observers. Entropy. 2019; 21(5):481. https://doi.org/10.3390/e21050481
Chicago/Turabian StyleLi, Zhonghui, Tongshui Xia, and Cuimei Jiang. 2019. "Synchronization of Fractional-Order Complex Chaotic Systems Based on Observers" Entropy 21, no. 5: 481. https://doi.org/10.3390/e21050481
APA StyleLi, Z., Xia, T., & Jiang, C. (2019). Synchronization of Fractional-Order Complex Chaotic Systems Based on Observers. Entropy, 21(5), 481. https://doi.org/10.3390/e21050481