Abstract
We revisit the distributed hypothesis testing (or hypothesis testing with communication constraints) problem from the viewpoint of privacy. Instead of observing the raw data directly, the transmitter observes a sanitized or randomized version of it. We impose an upper bound on the mutual information between the raw and randomized data. Under this scenario, the receiver, which is also provided with side information, is required to make a decision on whether the null or alternative hypothesis is in effect. We first provide a general lower bound on the type-II exponent for an arbitrary pair of hypotheses. Next, we show that if the distribution under the alternative hypothesis is the product of the marginals of the distribution under the null (i.e., testing against independence), then the exponent is known exactly. Moreover, we show that the strong converse property holds. Using ideas from Euclidean information theory, we also provide an approximate expression for the exponent when the communication rate is low and the privacy level is high. Finally, we illustrate our results with a binary and a Gaussian example.
1. Introduction
In the distributed hypothesis testing (or hypothesis testing with communication constraints) problem, some observations from the environment are collected by the sensors in a network. They describe these observations over the network which are finally received by the decision center. The goal is to guess the joint distribution governing the observations at terminals. In particular, there are two possible hypotheses or , where the joint distribution of the observations is specified under each of them. The performance of this system is characterized by two criteria: the type-I and the type-II error probabilities. The probability of deciding on (respectively ) when the original hypothesis is (respectively ) is referred to as the type-I error (type-II error) probability. There are several approaches for defining the performance of a hypothesis test. First, we can maximize the exponent (exponential rate of decay) of the Bayesian error probability. Second, we can impose that the type-II error probability decays exponentially fast and we can then maximize the exponent of the type-I error probability; this is known as the Hoeffding regime. The approach in this work is the Chernoff-Stein regime in which we upper bound the type-II error probability by a non-vanishing constant and we maximize the exponent of the type-II error probability.
A special case of interest is testing against independence where the joint distribution under is the product of the marginals under . The optimal exponent of type-II error probability for testing against independence is determined by Ahlswede and Csiszár in [1]. Several extensions of this basic problem are studied for a multi-observer setup [2,3,4,5,6], a multi-decision center setup [7,8] and a setup with security constraints [9]. The main idea of the achievable scheme in these works is typicality testing [10,11]. The sensor finds a jointly typical codeword with its observation and sends the corresponding bin index to the decision center. The final decision is declared based on typicality check of the received codeword with the observation at the center. We note that the coding scheme employed here is reminiscent of those used for source coding with side information [12] and for different variants of the information bottleneck problem [13,14,15,16].
1.1. Injecting Privacy Considerations into Our System
We revisit the distributed hypothesis testing problem from a privacy perspective. In many applications such as healthcare systems, there is a need to randomize the data before publishing it. For example, hospitals often have large amounts of medical records of their patients. These records are useful for performing various statistical inference tasks, such as learning about causes of a certain ailment. However, due to privacy considerations of the patients, the data cannot be published as is. The data needs to be sanitized, quantized, perturbed and then be fed to a management center before statistical inference, such as hypothesis testing, is being done.
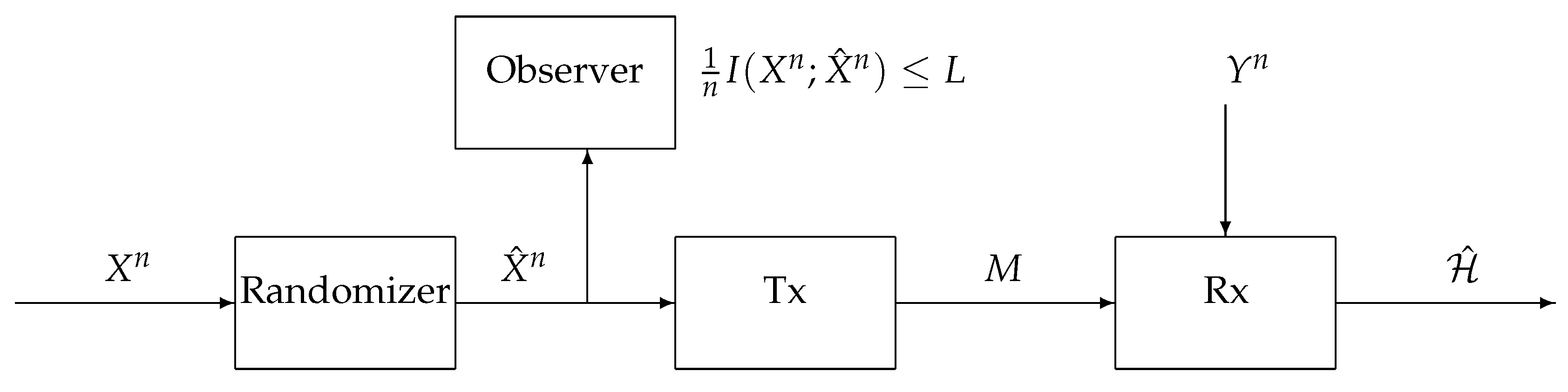
In the proposed setup, we use a privacy mechanism to sanitize the observation at the terminal before it is compressed; see Figure 1. The compression is performed at a separate terminal called transmitter, which communicates the randomized data over a noiseless link of rate R to a receiver. The hypothesis testing is performed using the received data (the compression index and additional side information) to determine the correct hypothesis governing the original observations. The privacy criterion is defined by the mutual information [17,18,19,20] of the published and original data.
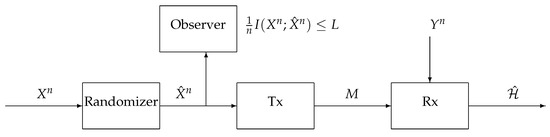
Figure 1.
Hypothesis testing with communication and privacy constraints.
There is a long history of research to provide appropriate metrics to measure privacy. To quantify the information leakage an observation can induce on a latent variable X, Shannon’s mutual information is considered in [17,18,19,20]. Smith [18] proposed to use Arimoto’s mutual information of order ∞, . Barthe and Köpf [21,22,23] proposed the maximal information leakage . We refer the reader to [24] for a survey on the existing information leakage measures. A different line of works, in statistics, computer science, and other related fields, concerns differential privacy, initially proposed in [25]. Furthermore, a generalized notion—-differential privacy [26]—provides a unified mathematical framework for data privacy. The reader is referred to the survey by Dwork [27] and the statistical framework studied by Wasserman and Zhou [28] and the references therein.
The privacy mechanism can be either memoryless or non-memoryless. In the former, the distribution of the randomized data at each time instant depends on the original sequence at the same time and not on the previous history of the data.
1.2. Description of Our System Model
We propose a coding scheme for the proposed setup. The idea is that the sensor, upon observing the source sequence, performs a typicality test and obtains its belief of the hypothesis. If the belief is , it publishes the randomized data based on a specific memoryless mechanism. However, if its belief is , it sends an all-zero sequence to let the transmitter know about its decision. The transmitter communicates the received data, which is a sanitized version of the original data or an all-zero sequence, over the noiseless link to the receiver. In this scheme, the whole privacy mechanism is non-memoryless since the typicality check of the source sequence which uses the history of the observation, determines the published data. It is shown that the achievable error exponent recovers previous results on hypothesis testing with zero and positive communication rates in [10]. Our work is related to a recent work [29] where a general hypothesis testing setup is considered from a privacy perspective. However, in [29], the problem at hand is different from ours. The authors consider equivocation and average distortion as possible measures of privacy whereas we constrain the mutual information between the original and released (published) data.
A difference of the proposed scheme with some previous works is highlighted as follows. The privacy mechanism even if it is memoryless, cannot be viewed as a noiseless link of a rate equivalent to the privacy criterion. Particularly, the proposed model is different from cascade hypothesis testing problem of [8] or similar works [3,4] which consider consecutive noiseless links for data compression and distributed hypothesis testing. The difference comes from the fact that in these works, a codeword is chosen jointly typical with the observed sequence at the terminal and its corresponding index is sent over the noiseless link. However, in our model, the randomized sequence is not necessarily jointly typical with the original sequence. Thus, there is a need for an achievable scheme which lets the transmitter know whether the original data is typical or not.
The problem of hypothesis testing against independence with a memoryless privacy mechanism is also considered. A coding scheme is proposed where the sensor outputs the randomized data based on the memoryless privacy mechanism. The optimality of the achievable type-II error exponent is shown by providing a strong converse. Specializing the optimal error exponent to a binary example shows that an increase in the privacy criterion (a less stringent privacy mechanism) results in a larger type-II error exponent. Thus, there exists a trade-off between privacy and hypothesis testing criteria. The optimal type-II error exponent is further studied for the case of restricted privacy mechanism and zero-rate communication. The Euclidean approach of [30,31,32,33] is used to approximate the error exponent for this regime. The result confirms the trade-off between the privacy criterion and type-II error exponent. Finally, a Gaussian setup is proposed and its optimal error exponent is established.
1.3. Main Contributions
The contributions of the paper are listed in the following:
- An achievable type-II error exponent is proposed using a non-memoryless privacy mechanism (Theorem 1 in Section 3);
- The optimal error exponent of testing against independence with a memoryless privacy mechanism is determined. In addition, a strong converse is also proved (Theorem 2 in Section 4.1);
- A binary example is proposed to show the trade-off between the privacy and error exponent (Section 4.3);
- An Euclidean approximation [30] of the error exponent is provided (Section 4.4);
- A Gaussian setup is proposed and its optimal error exponent is derived (Proposition 2 in Section 4.5).
1.4. Notation
The notation mostly follows [34]. Random variables are denoted by capital letters, e.g., X, Y, and their realizations by lower case letters, e.g., x, y. The alphabet of the random variable X is denoted as . Sequences of random variables and their realizations are denoted by and and are abbreviated as and . We use the alternative notation when . Vectors and matrices are denoted by boldface letters, e.g., , . The -norm of is denoted as . The notation denotes the transpose of .
The probability mass function (pmf) of a discrete random variable X is denoted as , the conditional pmf of X given Y is denoted as . The notation denotes the Kullback-Leibler (KL) divergence between two pmfs and . The total variation distance between two pmfs and is denoted by . We use to denote the joint type of .
For a given and a positive number , we denote by , the set of jointly -typical sequences [34], i.e., the set of all whose joint type is within of (in the sense of total-variation distance). The notation denotes for the type class of the type .
The notation denotes the binary entropy function, its inverse over , and for . The differential entropy of a continuous random variable X is . All logarithms are taken with respect to base 2.
1.5. Organization
The remainder of the paper is organized as follows. Section 2 describes a mathematical setup for our proposed problem. Section 3 discusses hypothesis testing with general distributions. The results for hypothesis testing against independence with a memoryless privacy mechanism are provided in Section 4. The paper is concluded in Section 5.
2. System Model
Let , , and be arbitrary finite alphabets and let n be a positive integer. Consider the hypothesis testing problem with communication and privacy constraints depicted in Figure 1. The first terminal in the system, the Randomizer, receives the sequence and outputs the sequence , which is a noisy version of under a privacy mechanism determined by the conditional probability distribution ; the second terminal, the Transmitter, receives the sequence ; the third terminal, the Receiver, observes the side-information sequence . Under the null hypothesis
whereas under the alternative hypothesis
for two given pmfs and .
The privacy mechanism is described by the conditional pmf which maps each sequence to a sequence . For any , the joint distributions considering the privacy mechanism are given by
A memoryless/local privacy mechanism is defined by a conditional pmf which stochastically and independently maps each entry of to a released to construct . Consequently, for the memoryless privacy mechanism, the conditional pmf factorizes as follows:
There is a noise-free bit pipe of rate R from the transmitter to the receiver. Upon observing , the transmitter computes the message using a possibly stochastic encoding function and sends it over the bit pipe to the receiver.
The goal of the receiver is to produce a guess of using a decoding function based on the observation and the received message M. Thus the estimate of the hypothesis is .
This induces a partition of the sample space into an acceptance region defined as follows:
and a rejection region denoted by .
Definition 1.
For any and for a given rate-privacy pair , we say that a type-II exponent is -achievable if there exists a sequence of functions and conditional pmfs , such that the corresponding sequences of type-I and type-II error probabilities at the receiver are defined as
respectively, and they satisfy
Furthermore, the privacy measure
satisfies
The optimal exponent is the supremum of all -achievable .
3. General Hypothesis Testing
3.1. Achievable Error Exponent
The following presents an achievable error exponent for the proposed setup.
Theorem 1.
For a given and a rate-privacy pair , the optimal type-II error exponent for the multiterminal hypothesis testing setup under the privacy constraint L and the rate constraint R satisfies
where the set is defined as
Given and , the mutual informations in (11) are calculated according to the following joint distribution:
Proof.
The coding scheme is given in the following section. For the analysis, see Appendix A. □
3.2. Coding Scheme
In this section, we propose a coding scheme for Theorem 1, under fixed rate and privacy constraints . Fix the joint distribution as in (13). Let be the marginal distribution of defined as
Fix positive and , an arbitrary blocklength n and two conditional pmfs and over finite auxiliary alphabets and . Fix also the rate and privacy leakage level as
Codebook Generation: Randomly and independently generate a codebook
by drawing in an i.i.d. manner according to . The codebook is revealed to all terminals.
Randomizer: Upon observing , it checks whether If successful, it outputs the sequence where its i-th component is generated based on , according to . If the typicality check is not successful, the randomizer then outputs which is an all-zero sequence of length n, where .
Transmitter: Upon observing , if , the transmitter finds an index m such that If successful, it sends the index m over the noiseless link to the receiver. Otherwise, if the typicality check is not successful or , it sends .
Receiver: Upon observing and receiving the index m, if , the receiver declares . If , it checks whether If the test is successful, the receiver declares ; otherwise, it sets .
Remark 1.
In the above scheme, the sequence is chosen to be an n-length zero-sequence when the randomizer finds that is not typical according to . Thus, the privacy mechanism is not memoryless and the sequence is not identically and independently distributed (i.i.d.). A detailed analysis in Appendix A shows that the privacy criterion is not larger than L as the blocklength .
3.3. Discussion
In the following, we discuss some special cases. First, suppose that . The following corollary shows that Theorem 1 recovers Han’s result [1] for distributed hypothesis testing with zero-rate communication.
Corollary 1
(Theorem 5 in [10]). Suppose that . For all , the optimal error exponent of the zero-rate communication for any privacy mechanism (including non-memoryless mechanisms) is given by the following:
Proof.
The proof of achievability follows by Theorem 1, in which is arbitrary and the auxiliary due to the zero-rate constraint. The proof of the strong converse follows along the same lines as [35]. □
Remark 2.
Consider the case of and where is independent of X. Using Theorem 1, the optimal error exponent is lower bounded as follows:
However, there is no known converse result in this case where the communication rate is positive. Comparing this special case with the one in Corollary 1 shows that the proposed model does not, in general, admit symmetry between the rate and privacy constraints. However, we will see from some specific examples in the following that the roles of R and L are symmetric.
Now, suppose that L is so large such that . The following corollary shows that Theorem 1 recovers Han’s result in [10] for distributed hypothesis testing over a rate-R communication link.
Corollary 2
(Theorem 2 in [10]). Assuming , the optimal error exponent is lower bounded as the following:
Proof.
The proof follows from Theorem 1 by specializing to . □
The above two special cases reveal a trade-off between the privacy criterion and the achievable error exponent when the communication rate is positive, i.e., . An increase in L results in a larger achievable error exponent. This observation is further illustrated by an example in Section 4.3 to follow.
4. Hypothesis Testing against Independence with a Memoryless Privacy Mechanism
In this section, we consider testing against independence where the joint pmf under factorizes as follows:
The privacy mechanism is assumed to be memoryless here.
4.1. Optimal Error Exponent
The following theorem, which includes a strong converse, states the optimal error exponent for this special case.
Theorem 2.
For any , define
Then, for any and any , the optimal error exponent for testing against independence when using a memoryless privacy mechanism is given by (21), where it suffices to choose and according to Caratheodory’s theorem [36] (Theorem 15.3.5).
Proof.
The coding scheme is given in the following section. For the rest of proof, see Appendix B. □
4.2. Coding Scheme
In this section, we propose a coding scheme for Theorem 2. Fix the joint distribution as in (13), and the rate and privacy constraints as in (15). Generate the codebook as in (16).
Randomizer: Upon observing , it outputs the sequence in which the i-th component is generated based on , according to .
Transmitter: It finds an index m such that If successful, it sends the index m over the noiseless link to the receiver. Otherwise, it sends .
Receiver: Upon observing and receiving the index m, if , the receiver declares . If , it checks whether If the test is successful, the receiver declares ; otherwise, it sets .
Remark 3.
In the above scheme, the sequence is i.i.d. since it is generated based on the memoryless mechanism .
When the communication rate is positive, there exists a trade-off between the optimal error exponent and the privacy criterion. The following example elucidates this trade-off.
4.3. Binary Example
In this section, we study hypothesis testing against independence for a binary example. Suppose that under both hypotheses, we have . Under the null hypothesis,
for some , where N is independent of X. Under the alternative hypothesis
where Y is independent of X. The cardinality constraint shows that it suffices to choose . Among all possible privacy mechanisms, the choice of and minimizes the mutual information . Thus, we restrict to this choice which also results in .
The cardinality bound on the auxiliary random variable U is . The following proposition states that it is also optimal to choose to be a BSC.
Proposition 1.
The optimal error exponent of the proposed binary setup is given by the following:
Proof.
For the proof of achievability, choose the following auxiliary random variables:
for some where and Z are independent of X and , respectively. The optimal error exponent of Theorem 2 reduces to the following:
which can be simplified to (24). For the proof of the converse, see Appendix C. □
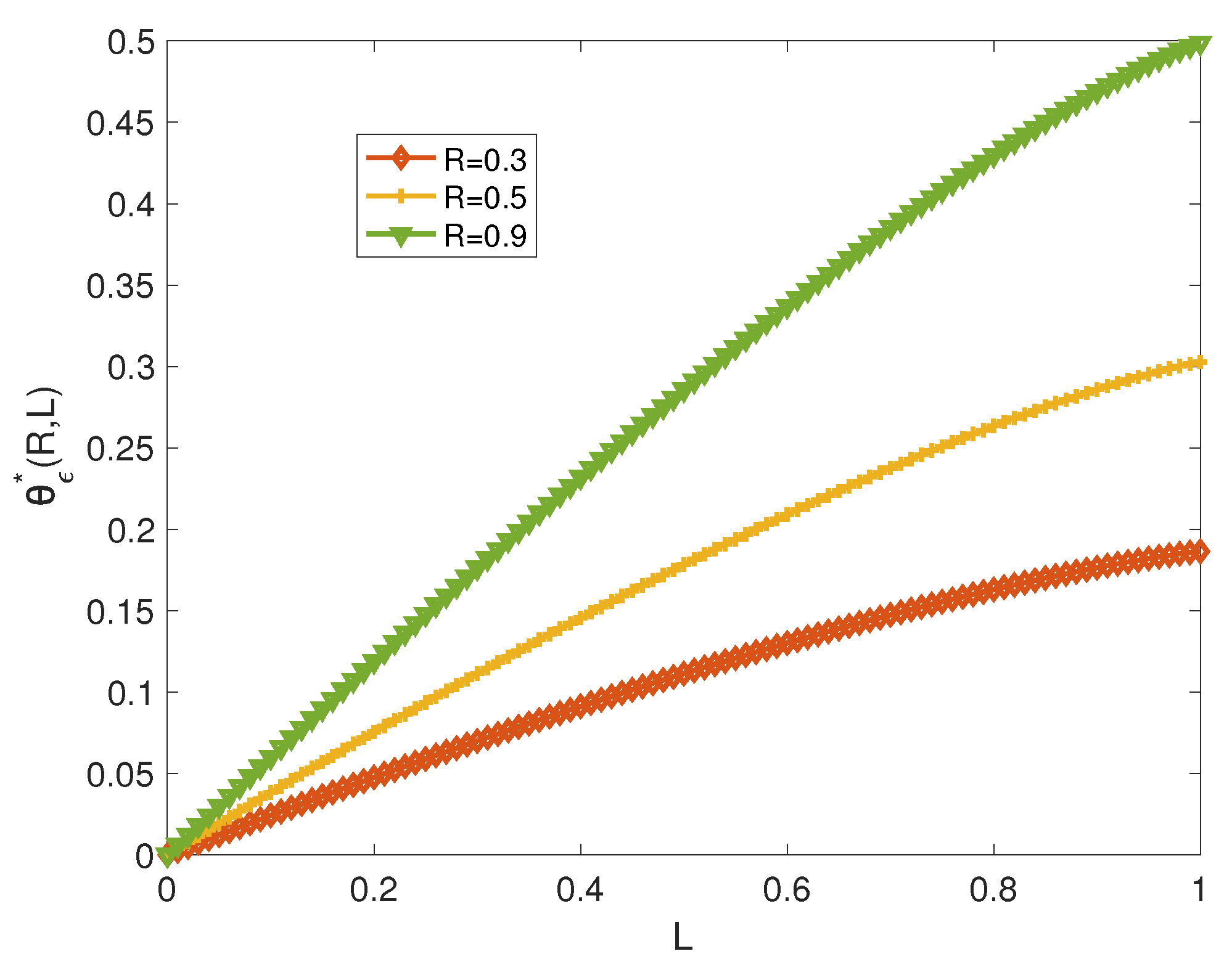
Figure 2 illustrates the error exponent versus the privacy parameter L for a fixed rate R. There is clearly a trade-off between and L. For a less stringent privacy requirement (large L), the error exponent increases.
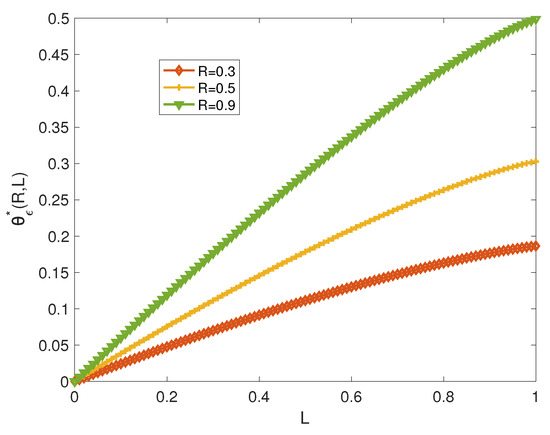
Figure 2.
versus L for and various values of R.
4.4. Euclidean Approximation
In this section, we propose Euclidean approximations [30,31] for the optimal error exponent of testing against independence scenario (Theorem 2) when and . Consider the optimal error exponent as follows:
Let of dimension , denote the transition matrix , which is itself induced by and the joint distribution . Now, consider the rate constraint as follows:
Assuming , we let be a local perturbation from , where we have
for a perturbation satisfying
in order to preserve the row stochasticity of . Using a -approximation [30], we can write:
where denotes the length- column vector of weighted perturbations whose -th component is defined as:
Using the above definition, the rate constraint in (29) can be written as:
Similarly, consider the privacy constraint as the following:
Assuming , we let be a local perturbation from where
for a perturbation that satifies:
Again, using a -approximation, we obtain the following:
where is a length- column vector and its x-th component is defined as follows:
Thus, the privacy constraint in (35) can be written as:
For any and , we define the following:
and the corresponding length- column vector defined as follows:
where denotes a diagonal -matrix, so that its -th element () is , and is defined similarly. Moreover, refers to the -matrix defined as follows:
Let be the inverse of diagonal -matrix . As shown in Appendix D, the optimization problem in (28) can be written as follows:
The following example specializes the above approximation to the binary case.
Example 1.
Consider the binary setup of Example 4.3 and the choice of auxiliary random variables in (26). Since the privacy mechanism is assumed to be a BSC, we have
Now, we consider the vectors and defined as
for some positive . This yields the following:
We also choose the vectors and as follows:
which results in
Notice that the matrix is given by
Solving the above optimization yields
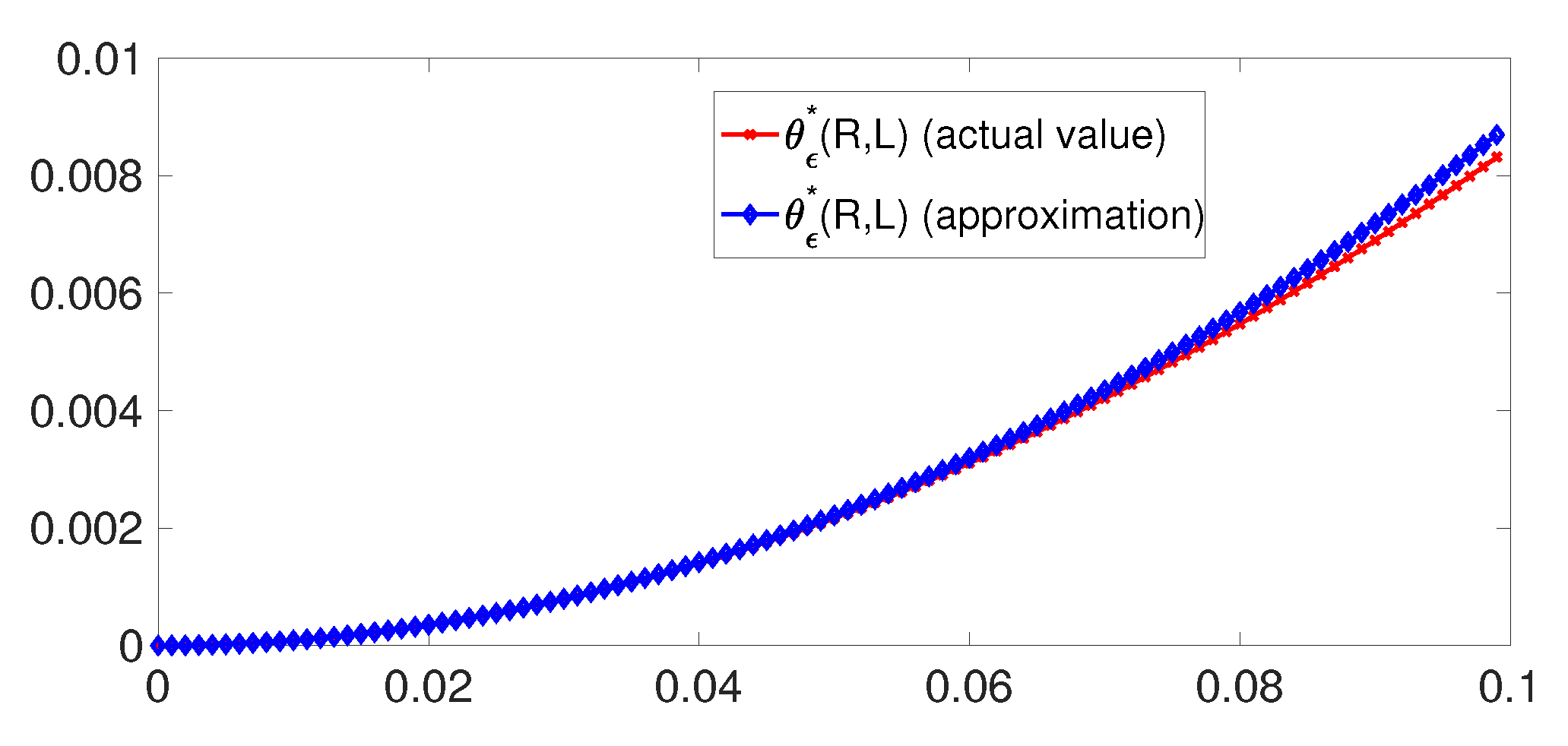
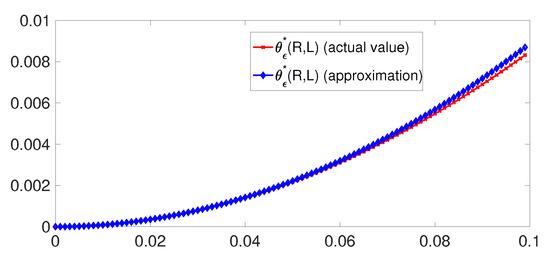
For some values of parameters, the approximation in (60) is compared to the error exponent of (24) in Figure 3. We observe that when , the approximation turns out to be excellent.

Figure 3.
versus L for and .
Remark 4.
The trade-off between the optimal error exponent and the privacy can again be verified from (60) in the case of and . As L becomes larger (which corresponds to a less stringent privacy requirement), the error exponent also increases. For a fixed error exponent, a trade-off between R and L exists. An increase in R results in a decrease of L.
4.5. Gaussian Setup
In this section, we consider hypothesis testing against independence over a Gaussian example. Suppose that and under the null hypothesis , the sources X and Y are jointly Gaussian random variables distributed as , where is defined as the following:
for some .
Under the alternative hypothesis , we assume that X and Y are independent Gaussian random variables, each distributed as . Consider the privacy constraint as follows:
For a Gaussian source X, the conditional entropy is maximized for a jointly Gaussian . This choice minimizes the RHS of (62). Thus, without loss of optimality, we choose
where Z is independent of . The following proposition states that it is optimal to choose U jointly Gaussian with .
Proposition 2.
The optimal error exponent of the proposed Gaussian setup is given by
Proof.
For the proof of achievability, we choose as in (63). Also, let
for some , where is independent of U. It can be shown that Theorem 2 remains valid when it is extended to the continuous alphabet [5]. For the details of the simplification and also the proof of converse, see Appendix E. □
Remark 5.
If , the above proposition recovers the optimal error exponent of Rahman and Wagner [5] (Corollary 7) for testing against independence of Gaussian sources over a noiseless link of rate R.
5. Summary and Discussion
In this paper, distributed hypothesis testing with privacy constraints is considered. A coding scheme is proposed where the sensor decides on one of hypotheses and generates the randomized data based on its decision. The transmitter describes the randomized data over a noiseless link to the receiver. The privacy mechanism in this scheme is non-memoryless. The special case of testing against independence with a memoryless privacy mechanism is studied in detail. The optimal type-II error exponent of this case is established, together with a strong converse. A binary example is proposed where the trade-off between the privacy criterion and the error exponent is reported. Euclidean approximations are provided for the case in which the privacy level is high and and the communication rate is vanishingly small. The optimal type-II error exponent of a Gaussian setup is also established.
A future line of research is to study the second-order asymptotics of our model. The second-order analysis of distributed hypothesis testing without privacy constraints and with zero-rate communication was studied in [37]. In our proposed model, the trade-off between the privacy and type-II error exponent is observed, i.e., a less stringent privacy requirement yields a larger error exponent. The next step is to see whether the trade-off between privacy and error exponent affects the second-order term.
Another potential line for future research is to consider other metrics of privacy instead of the mutual information. A possible candidate is to use the maximal leakage [21,22,23] and to analyze the performance in tandem with distributed hypothesis testing problem.
Author Contributions
Investigation, A.G.; Supervision, S.S. and V.Y.F.T.; Writing—original draft, S.B.A.
Funding
This research was partially funded by grants R-263-000-C83-112 and R-263-000-C54-114.
Acknowledgments
The authors would like to thank Lin Zhou (National University of Singapore) and Daming Cao (Southeast University) for helpful discussions during the preparation of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Proof of Theorem 1
The analysis is based on the scheme described in Section 3.2.
Error Probability Analysis: We analyze the type-I and type-II error probabilities averaged over all random codebooks. By standard arguments [36] (p. 204), it can be shown that there exists at least one codebook that satisfies constraints on the error probabilities.
For the considered and the considered blocklength n, let be the set of all joint types over which satisfy the following constraints:
First, we analyze the type-I error probability. For the case of , we define the following event:
Thus, type-I error probability can be upper bounded as follows:
where (A7) follows from AEP [36] (Theorem 3.1.1); (A8) follows from the covering lemma [34] (Lemma 3.3) and the rate constraint (15), (A10) follows from Markov lemma [34] (Lemma 12.1). In all justifications, n is taken to be sufficiently large.
Next, we analyze the type-II error probability. The acceptance region at the receiver is
The set is contained within the following acceptance region :
Let . Therefore, the average of type-II error probability over all codebooks is upper bounded as follows:
where
and (A16) follows from the upper bound of Sanov’s theorem [36] (Theorem 11.4.1). Hence,
where as . Equality (A20) follows from the rate constraint in (15) and (A21) holds because .
Privacy Analysis: We first analyze the privacy under . Notice that is not necessarily i.i.d. because according to the scheme in Section 3.2, is forced to be an all-zero sequence if the Randomizer decides that is not typical. However, conditioned on the event that , the sequence is i.i.d. according to the conditional pmf . The privacy measure satisfies
We now provide a lower bound on as follows
For any and for , it holds that
where (A26) is true because for any , it holds that , and (A27) follows because the conditional typicality lemma [34] (Chapter 2) implies that for n sufficiently large.
Combining (A23) and (A27), we obtain
where (A29) follows because the AEP [36] (Theorem 3.1.1) implies that for n sufficiently large.
Hence, we have
where , and .
Next, consider the privacy analysis under . Please note that when , the analysis is similar to that of . Thus, we assume that in the following. From (A22), the privacy measure satisfies:
To upper bound , we calculate the probability for as follows:
where exponentially fast as . Here, (A38) follows because if , then , (A39) follows because when , then and (A41) follows from Sanov’s theorem and the continuity of the relative entropy in its first argument [38] (Lemma 1.2.7).
Write as and let be the distribution on that places all its probability mass on . Since , by the uniform continuity of entropy [38] (Lemma 1.2.7),
Since exponentially fast, the same holds true for and so by (A42), . Therefore, under , we have as .
Letting and then letting , we obtain and , with given by the RHS of (11). This establishes the proof of Theorem 1.
Appendix B. Proof of Theorem 2
Achievability: The analysis is based on the scheme of Section 4.2. It follows similar steps as in [1]. Recall the definition of the event in (A4). Consider the type-I error probability as follows:
where (A46) follows from covering lemma [34] (Lemma 3.3) and the rate constraint in (15), and also the Markov lemma [34] (Lemma 12.1). Now, consider the type-II error probability as follows:
where the last equality follows from the symmetry of the code construction. Now, the average of type-II error probability over all codebooks satisfies:
where is a function that tends to zero as . The privacy analysis is straightforward since the privacy mechanism is memoryless whence we have
where the last equality follows from the privacy constraint in (15). This concludes the proof of achievability.
Converse: Now, we prove the strong converse. It involves an extension of the -image characterization technique [4,38]. The proof steps are given as follows. First, we find a truncated distribution which is arbitrarily close to in terms of entropy. Then, we analyze the type-II error probability under a constrained type-I error probability. Finally, a single-letter characterization of the rate and privacy constraints is given.
- (1)
- Construction of a Truncated Distribution:
Since the privacy machanism is memoryless, we conclude that is i.i.d. according to . For a given , define for all and . A set is an -image of the set over the channel if
The privacy mechanism is the same under both hypotheses, thus, we can define the acceptance region based on as follows:
For any encoding function and an acceptance region , let denote the cardinality of codebook and define the following sets:
The acceptance region can be written as follows:
where for all . Define the set as follows:
Fix and notice that the type-I error probability is upper-bounded as
which we can write equivalently as
where the first term is because ; and the second term is because for any , we have .
In what follows, let . Inequality (A62) implies
Let . For the typical set , we have
Hence,
For any and for sufficiently large n,
We can also write as
Combining the above equations, we get
Let denote the type which maximizes the -probability of the type class among all such types. As there exist at most possible types, it holds that
Define the set . We can write the probability in (A70) as
where as due to the fact that and so the entropies are also arbitrarily close. It then follows from (A70) and (A73) that
where as .
The encoding function partitions the set into non-intersecting subsets such that for any . Define the following distribution:
Please note that this distribution, henceforth denoted as , corresponds to a uniform distribution over because all sequences in have the same type , and the probability is uniform on a type class under any i.i.d. measure.
Finally, define the following truncated joint distribution:
- (2)
- Analysis of Type-II Error Exponent:
The proof of the upper bound on the error exponent relies on the following Lemma A1. For a set , let denote the collection of all -images of A, define and
This quantity is a generalization of the minimum cardinality of the -images in [38] and is closely related to the minimum type-II error probability associated with the set A.
For the testing against independence setup, , and thus
and is simply written as and is given by
Lemma A1
(Lemma 3 in [4]). For any set , consider a distribution over A and let be its corresponding output distribution induced by the channel , i.e.,
Then, for every , , we have
for sufficiently large n.
Let be the distribution of the random variable given . The type-II error probability can be lower-bounded as:
where (A84) follows from the definition of , (A86) follows because Lemma A1 implies that for any distribution over the set it holds that , (A87) follows because of the convexity of the function , and (A88) follows by (A70) and the fact that . Hence,
where .
- (3)
- Single-letterization Steps and Analyses of Rate and Privacy Constraints:
In the following, we proceed to provide a single-letter characterization of the upper bound in (A89). Considering the fact that , the right-hand-side of (A89) can be upper-bounded as follows:
Here, (A96)–(A99) are justified in the following:
- (A96) follows by the chain rule;
- (A97) follows from the Markov chain ;
- (A98) follows from the definition
- (A99) follows by defining a time-sharing random variable T over and the following
This leads to the following upper-bound on the type-II error exponent:
Next, the rate constraint satisfies the following:
where (A106) follows because the distribution is uniform over the set ; (A107) follows from (A74); (A109) follows from the definition in (A100); (A110) follows by defining .
Finally, the privacy measure satisfies the following:
where (A112) follows because are functions of and from data processing inequality, (A114) follows because is uniform over the set (see definition in (A75)), (A115) follows from (A74), and (A118) follows by defining , and choosing T uniformly over .
Since , for any ,
Recall that with . Hence, from (A121), it holds that . By the definitions of , and , we have and . The random variable U is chosen over the same alphabet as and such that .
Since for all , letting and and the uniform continuity of the involved information-theoretic quantities yields the following upper bound on the optimal error exponent:
subject to the rate constraint:
and the privacy constraint:
This concludes the proof of converse.
Appendix C. Proof of Converse of Proposition 1
We simplify Theorem 2 for the proposed binary setup. As discussed in Section 4.3, from the fact that and the symmetry of the source X on its alphabet, without loss of optimality, we can choose to be a BSC. First, consider the rate constraint:
which can be equivalently written as the following:
Also, the privacy criterion can be simplified as follows:
which can be equivalently written as
Appendix D. Euclidean Approximation of Testing agianst Independence
We analyze the Euclidean approximation with the parameters, , , and defined in Section 4.4. Notice that since forms a Markov chain, it holds that, for any ,
Now, consider the following chain of equalities for any :
where (A143)—(A146) are justified in the following:
- (A143) follows from the Markov chain where given , U and X are independent;
With the definition of in (42), we can write
Thus, we get
Applying the -approximation and using (A150), we can rewrite as follows:
Appendix E. Proof of Proposition 2
Achievability: We specialize the achievable scheme of Theorem 2 to the proposed Gaussian setup. We choose the auxiliary random variables as in (63) and (65). Notice that from the Markov chain and also the Gaussian choice of in (63) which was discussed in Section 4.5, we can write where is independent of . These choices of auxiliary random variables lead to the following rate constraint:
which can be equivalently written as:
The optimal error exponent is also lower bounded as follows
Converse: Consider the following upper bound on the optimal error exponent in Theorem 2:
where (A159) follows from the entropy power inequality (EPI) [34] (Chapter 2). Now, consider the rate constraint as follows:
which is equivalent to
Considering (A160) with (A164) yields the following upper bound on the error exponent:
This concludes the proof of the proposition.
References
- Ahlswede, R.; Csiszàr, I. Hypothesis testing with communication constraints. IEEE Trans. Inf. Theory 1986, 32, 533–542. [Google Scholar] [CrossRef]
- Zhao, W.; Lai, L. Distributed testing against independence with multiple terminals. In Proceedings of the 2014 52nd Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 30 September–3 October 2014; pp. 1246–1251. [Google Scholar]
- Xiang, Y.; Kim, Y.H. Interactive hypothesis testing against independence. In Proceedings of the 2013 IEEE International Symposium on Information Theory, Istanbul, Turkey, 7–12 July 2013; pp. 2840–2844. [Google Scholar]
- Tian, C.; Chen, J. Successive refinement for hypothesis testing and lossless one-helper problem. IEEE Trans. Inf. Theory 2008, 54, 4666–4681. [Google Scholar] [CrossRef]
- Rahman, M.S.; Wagner, A.B. On the optimality of binning for distributed hypothesis testing. IEEE Trans. Inf. Theory 2012, 58, 6282–6303. [Google Scholar] [CrossRef]
- Sreekuma, S.; Gündüz, D. Distributed Hypothesis Testing Over Noisy Channels. In Proceedings of the 2017 IEEE International Symposium on Information Theory (ISIT), Aachen, Germany, 25–30 June 2017. [Google Scholar]
- Salehkalaibar, S.; Wigger, M.; Timo, R. On hypothesis testing against independence with multiple decision centers. arXiv 2017, arXiv:1708.03941. [Google Scholar] [CrossRef]
- Salehkalaibar, S.; Wigger, M.; Wang, L. Hypothesis Testing In Multi-Hop Networks. arXiv 2017, arXiv:1708.05198. [Google Scholar]
- Mhanna, M.; Piantanida, P. On secure distributed hypothesis testing. In Proceedings of the 2015 IEEE International Symposium on Information Theory (ISIT), Hong Kong, China, 14–19 June 2015; pp. 1605–1609. [Google Scholar]
- Han, T.S. Hypothesis testing with multiterminal data compression. IEEE Trans. Inf. Theory 1987, 33, 759–772. [Google Scholar] [CrossRef]
- Shimokawa, H.; Han, T.; Amari, S.I. Error bound for hypothesis testing with data compression. IEEE Trans. Inf. Theory 1994, 32, 533–542. [Google Scholar]
- Ugur, Y.; Aguerri, I.E.; Zaidi, A. Vector Gaussian CEO Problem Under Logarithmic Loss and Applications. arXiv 2018, arXiv:1811.03933. [Google Scholar]
- Zaidi, A.; Aguerri, I.E.; Caire, G.; Shamai, S. Uplink oblivious cloud radio access networks: An information theoretic overview. In Proceedings of the 2018 Information Theory and Applications Workshop (ITA), San Diego, CA, USA, 11–16 February 2018. [Google Scholar]
- Aguerri, I.E.; Zaidi, A.; Caire, G.; Shamai, S. On the capacity of cloud radio access networks with oblivious relaying. In Proceedings of the 2017 IEEE International Symposium on Information Theory (ISIT), Aachen, Germany, 25–30 June 2017. [Google Scholar]
- Aguerri, I.E.; Zaidi, A. Distributed information bottleneck method for discrete and Gaussian sources. In Proceedings of the 2018 International Zurich Seminar on Information and Communication (IZS), Zurich, Switzerland, 21–23 February 2018. [Google Scholar]
- Aguerri, I.E.; Zaidi, A. Distributed variational representation learning. arXiv 2018, arXiv:1807.04193. [Google Scholar]
- Evfimievski, A.V.; Gehrke, J.; Srikant, R. Limiting privacy breaches in privacy preserving data mining. In Proceedings of the Twenty-Second Symposium on Principles of Database Systems, San Diego, CA, USA, 9–11 June 2003; pp. 211–222. [Google Scholar]
- Smith, G. On the Foundations of Quantitative Information Flow. In Proceedings of the 12th International Conference on Foundations of Software Science and Computational Structures: Held as Part of the Joint European Conferences on Theory and Practice of Software, ETAPS 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 288–302. [Google Scholar]
- Sankar, L.; Rajagopalan, S.R.; Poor, H.V. Utility-Privacy Tradeoffs in Databases: An Information-Theoretic Approach. IEEE Trans. Inf. Forensics Secur. 2013, 8, 838–852. [Google Scholar] [CrossRef]
- Liao, J.; Sankar, L.; Tan, V.Y.F.; Calmon, F. Hypothesis Testing Under Mutual Information Privacy Constraints in the High Privacy Regime. IEEE Trans. Inf. Forensics Secur. 2018, 13, 1058–1071. [Google Scholar] [CrossRef]
- Barthe, G.; Köpf, B. Information-theoretic bounds for differentially private mechanisms. In Proceedings of the 2011 IEEE 24th Computer Security Foundations Symposium, Cernay-la-Ville, France, 27–29 June 2011; pp. 191–204. [Google Scholar]
- Issa, I.; Wagner, A.B. Operational definitions for some common information leakage metrics. In Proceedings of the 2017 IEEE International Symposium on Information Theory (ISIT), Aachen, Germany, 25–30 June 2017; pp. 769–773. [Google Scholar]
- Liao, J.; Sankar, L.; Calmon, F.; Tan, V.Y.F. Hypothesis testing under maximal leakage privacy constraints. In Proceedings of the 2017 IEEE International Symposium on Information Theory (ISIT), Aachen, Germany, 25–30 June 2017; pp. 779–783. [Google Scholar]
- Wagner, I.; Eckhoff, D. Technical Privacy Metrics: A Systematic Survey. ACM Comput. Surv. (CSUR) 2018, 51. to appear. [Google Scholar] [CrossRef]
- Dwork, C. Differential Privacy. In Proceedings of the 33rd International Colloquium on Automata, Languages and Programming, Part II (ICALP 2006); Springer: Venice, Italy, 2006; Volume 4052, pp. 1–12. [Google Scholar]
- Dwork, C.; Kenthapadi, K.; McSherry, F.; Mironov, I.; Naor, M. Our Data, Ourselves: Privacy Via Distributed Noise Generation. In Advances in Cryptology (EUROCRYPT 2006); Springer: Saint Petersburg, Russia, 2006; Volume 4004, pp. 486–503. [Google Scholar]
- Dwork, C. Differential Privacy: A Survey of Results; Chapter Theory and Applications of Models of Computation; TAMC 2008; Lecture Notes in Computer Science; Springer: Heidelberg, Germany, 2008; Volume 4978. [Google Scholar]
- Wasserman, L.; Zhou, S. A statistical framework for differential privacy. J. Am. Stat. Assoc. 2010, 105, 375–389. [Google Scholar] [CrossRef]
- Sreekumar, A.C.; Gunduz, D. Distributed hypothesis testing with a privacy constraint. arXiv 2018, arXiv:1806.02015. [Google Scholar]
- Borade, S.; Zheng, L. Euclidean Information Theory. In Proceedings of the 2008 IEEE International Zurich Seminar on Communications, Zurich, Switzerland, 12–14 March 2008; pp. 14–17. [Google Scholar]
- Huang, S.; Suh, C.; Zheng, L. Euclidean information theory of networks. IEEE Trans. Inf. Theory 2015, 61, 6795–6814. [Google Scholar] [CrossRef]
- Viterbi, A.J.; Omura, J.K. Principles of Digital Communication and Coding; McGraw-Hill: New York, NY, USA, 1979. [Google Scholar]
- Weinberger, N.; Merhav, N. Optimum tradeoffs between the error exponent and the excess-rate exponent of variable rate Slepian-Wolf coding. IEEE Trans. Inf. Theory 2015, 61, 2165–2190. [Google Scholar] [CrossRef]
- El Gamal, A.; Kim, Y.H. Network Information Theory; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Shalaby, H.M.H.; Papamarcou, A. Multiterminal detection with zero-rate data compression. IEEE Trans. Inf. Theory 1992, 38, 254–267. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]
- Watanabe, S. Neyman-Pearson Test for Zero-Rate Multiterminal Hypothesis Testing. IEEE Trans. Inf. Theory 2018, 64, 4923–4939. [Google Scholar] [CrossRef]
- Csiszàr, I.; Körner, J. Information theory: Coding Theorems for Discrete Memoryless Systems; Academic Press: New York, NY, USA, 1982. [Google Scholar]
- Wyner, A.D.; Ziv, J. A theorem on the entropy of certain binary sequences and applications (Part I). IEEE Trans. Inf. Theory 1973, 19, 769–772. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).