Controlling and Optimizing Entropy Production in Transient Heat Transfer in Graded Materials
Abstract
1. Introduction
“Evaluations of most appropriate temperature distribution, for the development of analytical models have to be studied precisely for accurate evaluation of plate deformations.”
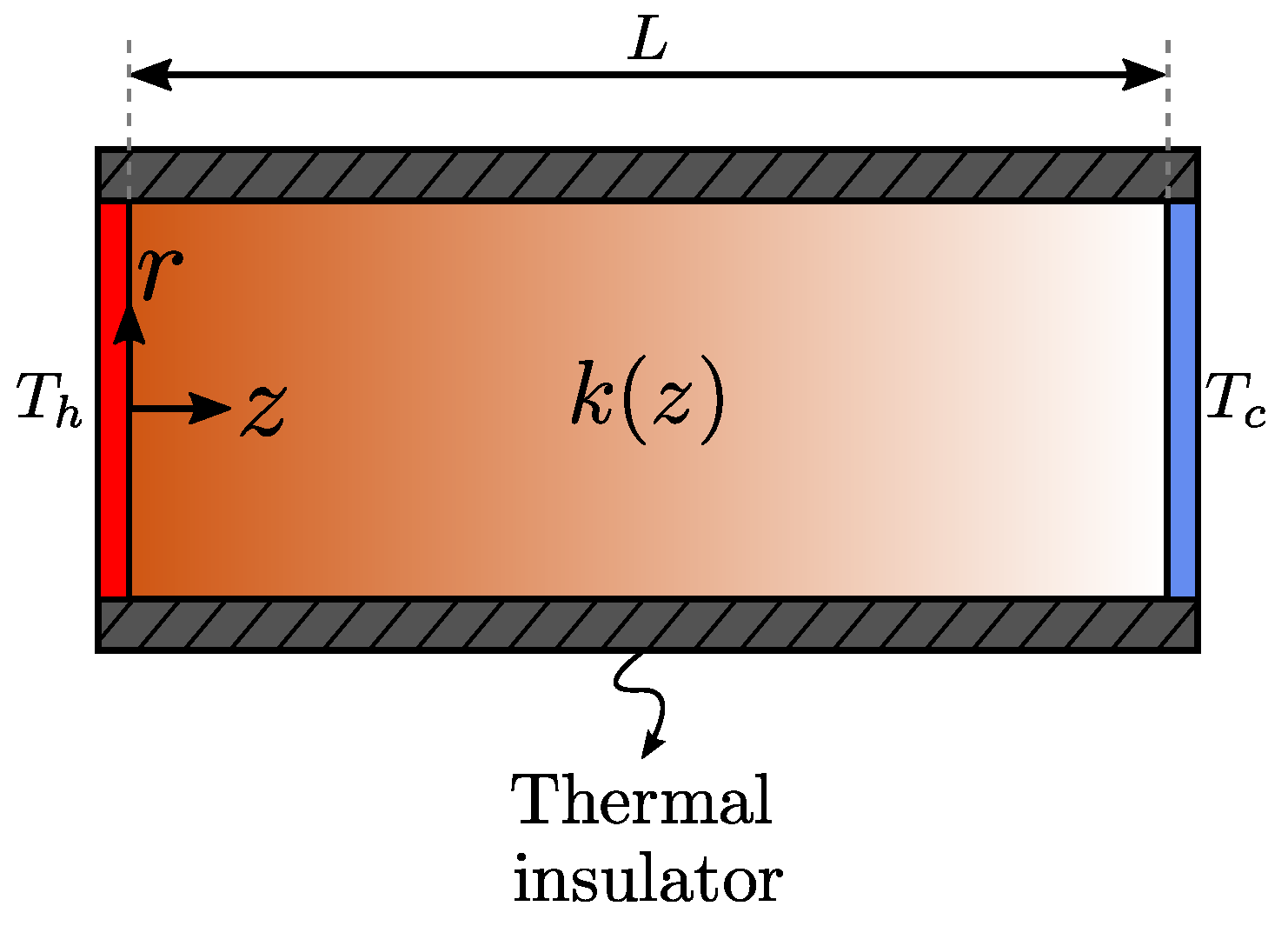
2. Mathematical Modeling
2.1. Initial and Boundary Conditions
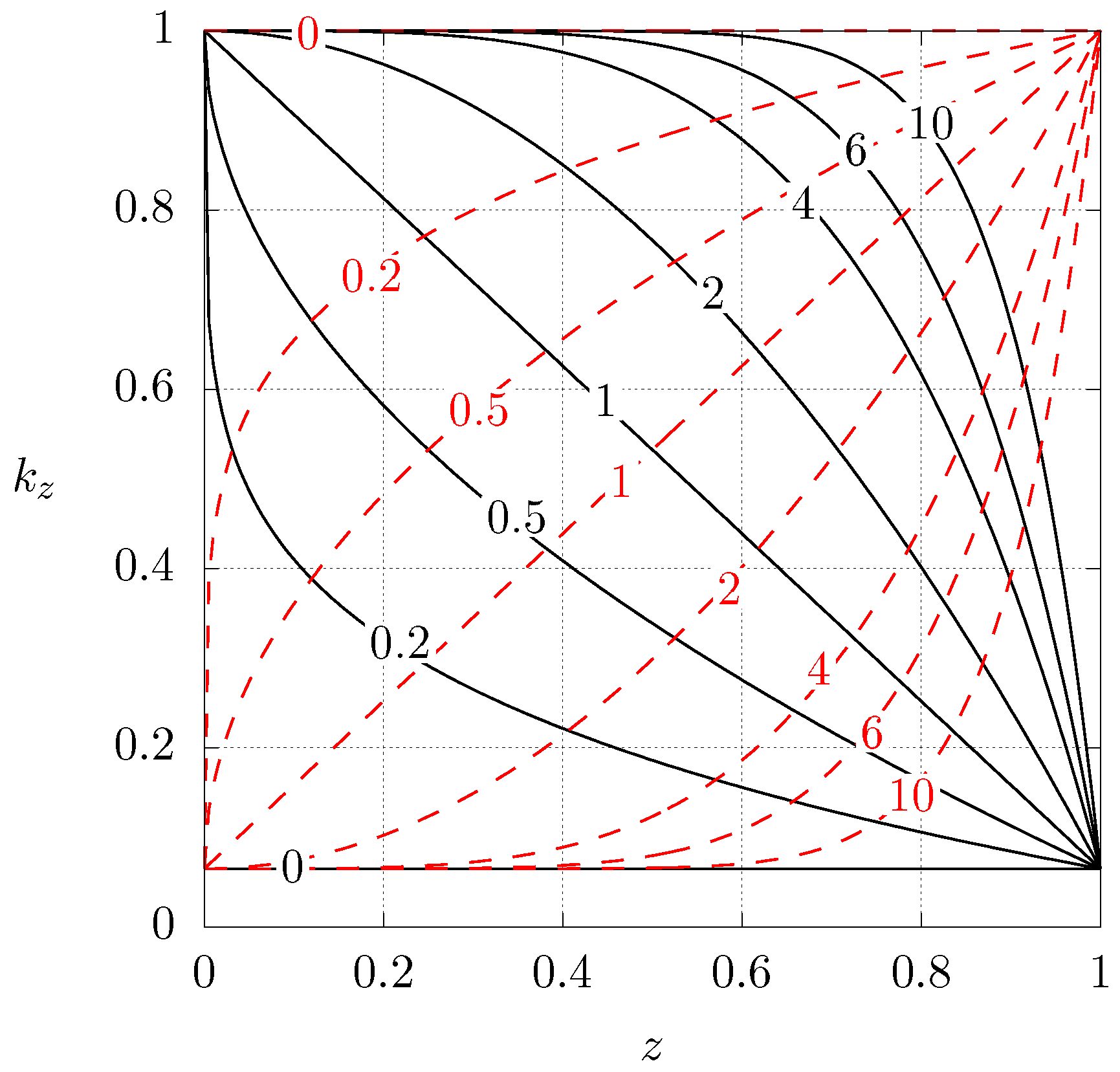
2.2. Grading of the Material
- Using a low thermal conductivity () matrix to be graded with a high thermal conductivity () material
- Using a high thermal conductivity matrix to be graded with a low thermal conductivity material
2.3. Entropy Calculation
2.4. Numerical Methodology
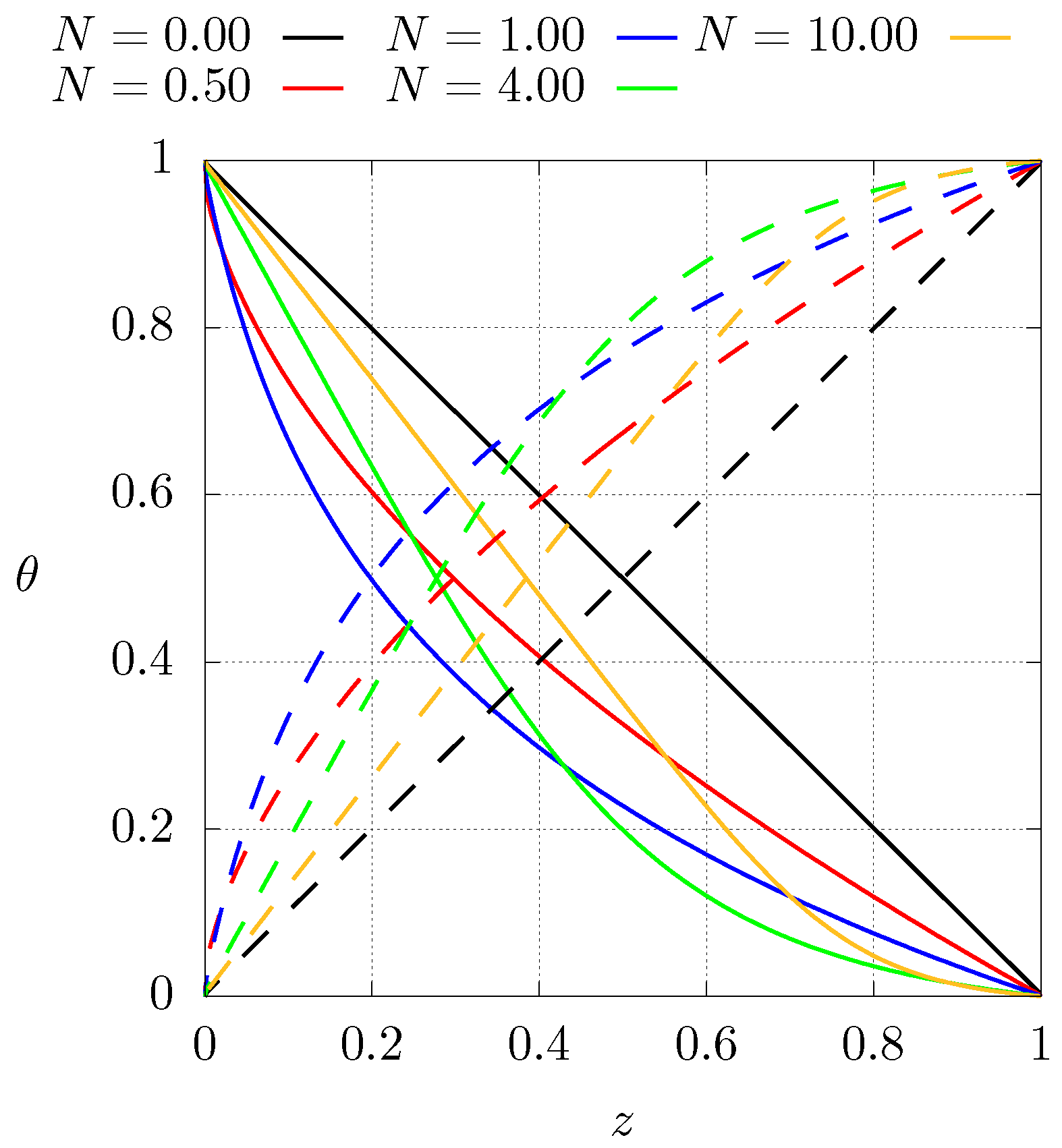
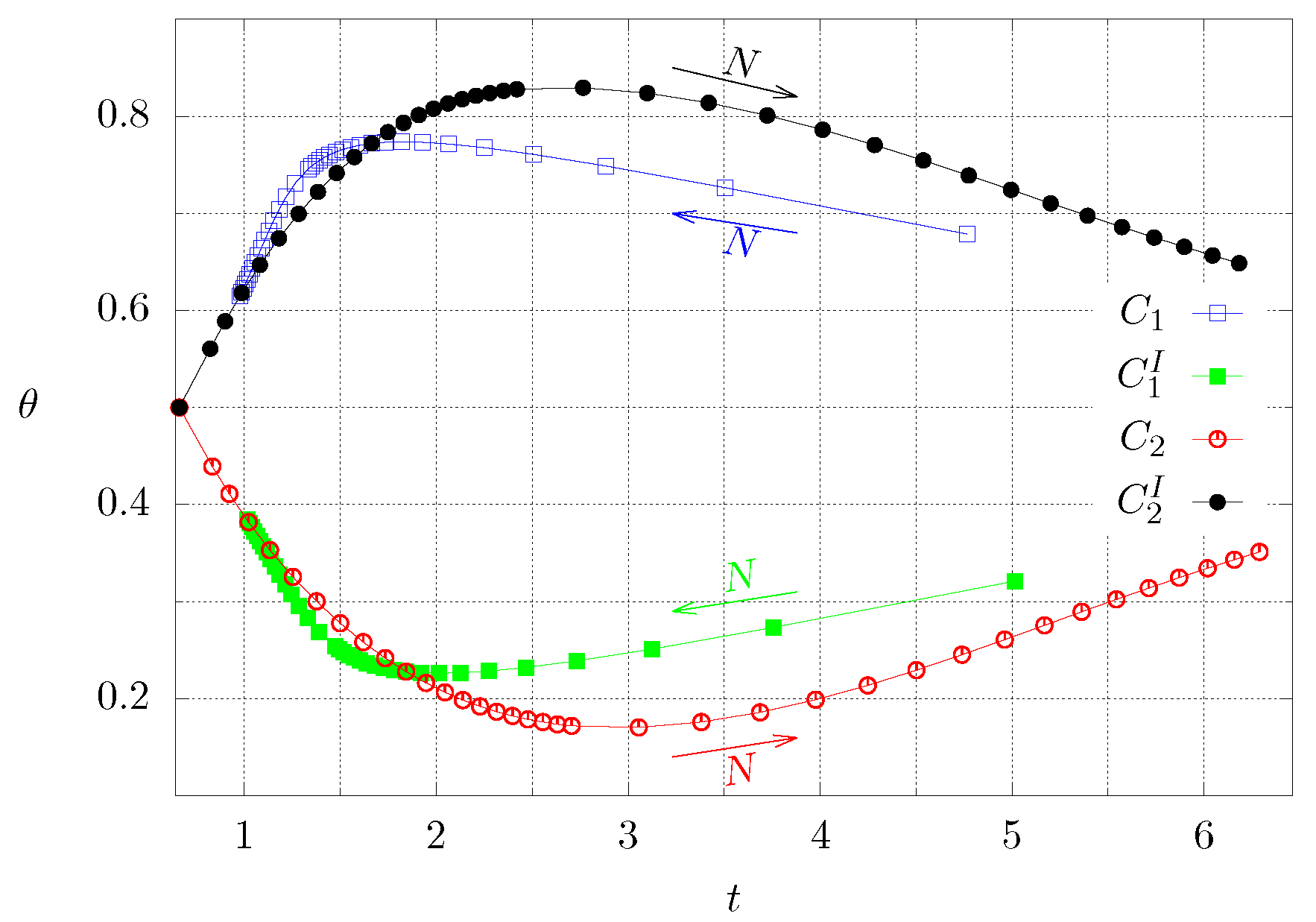
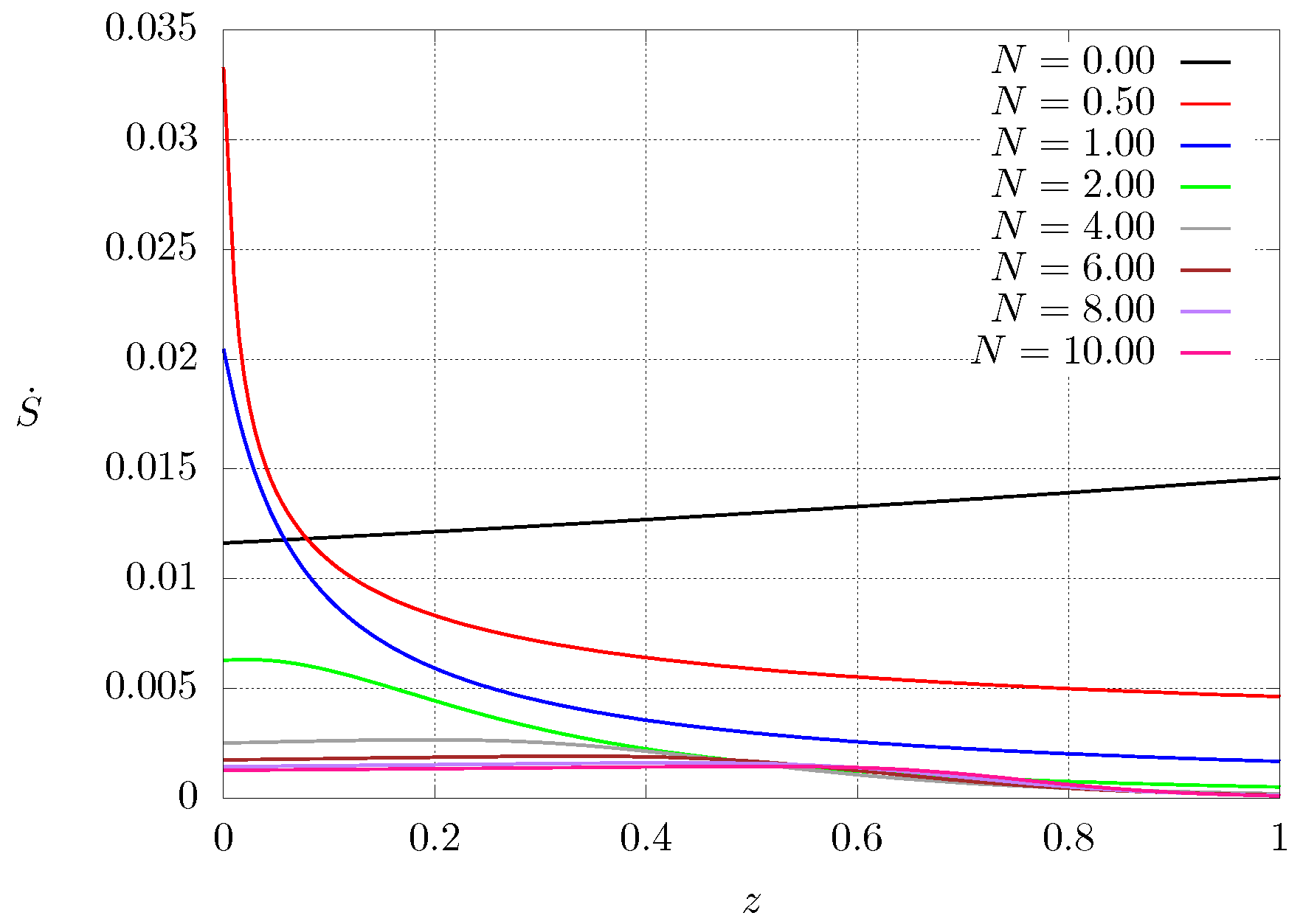
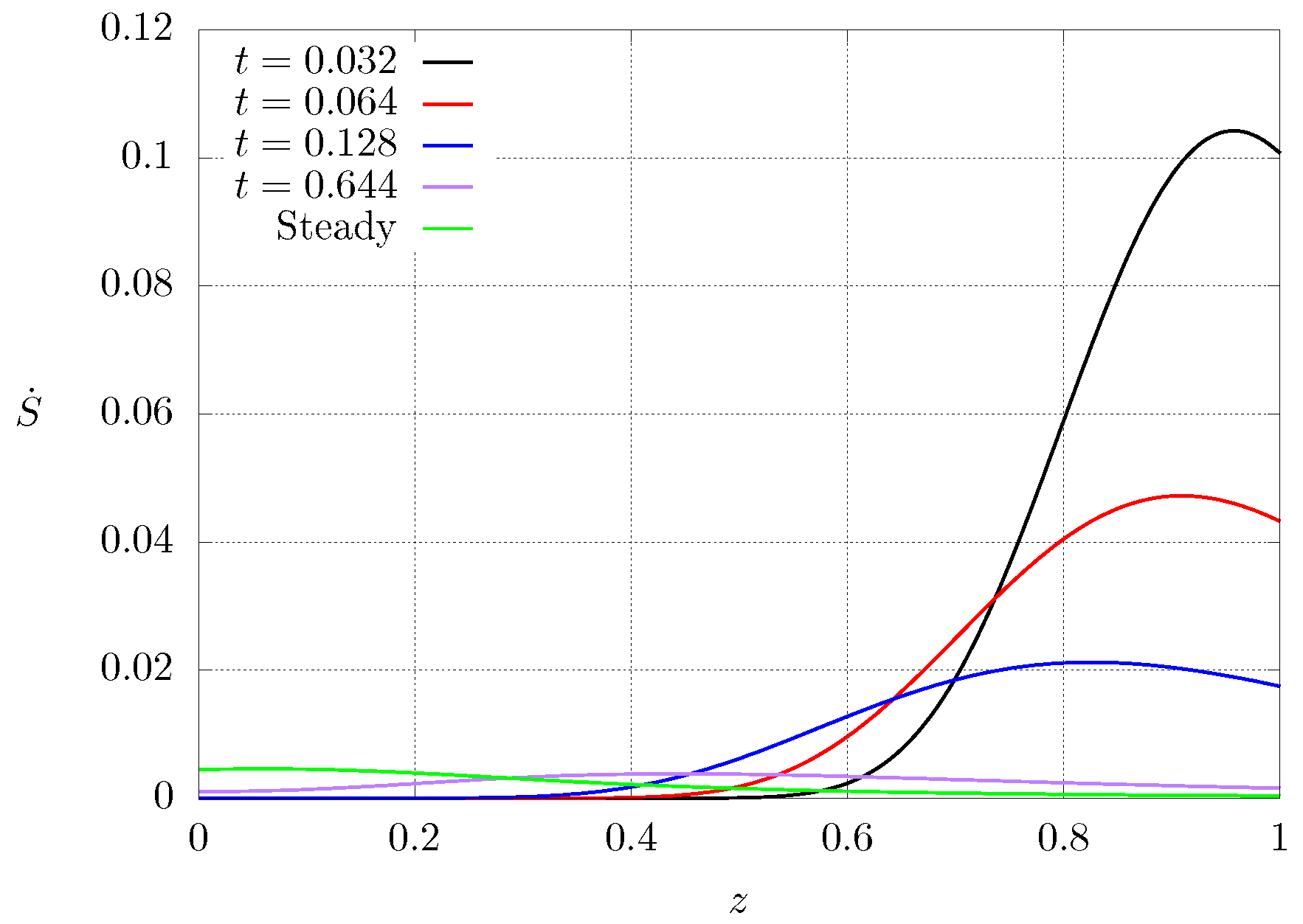
3. Numerical Results
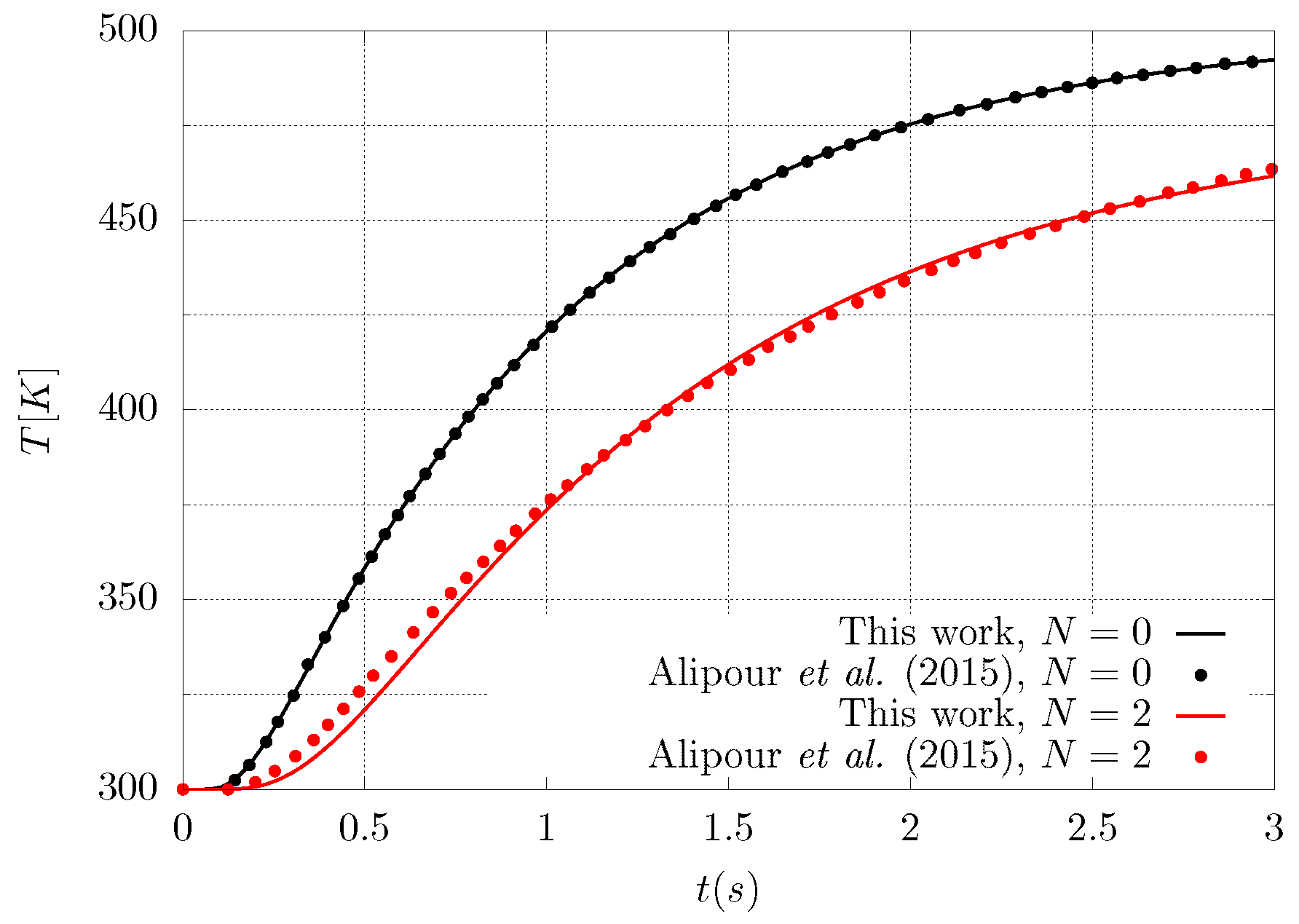
3.1. Validation of the Numerical Code
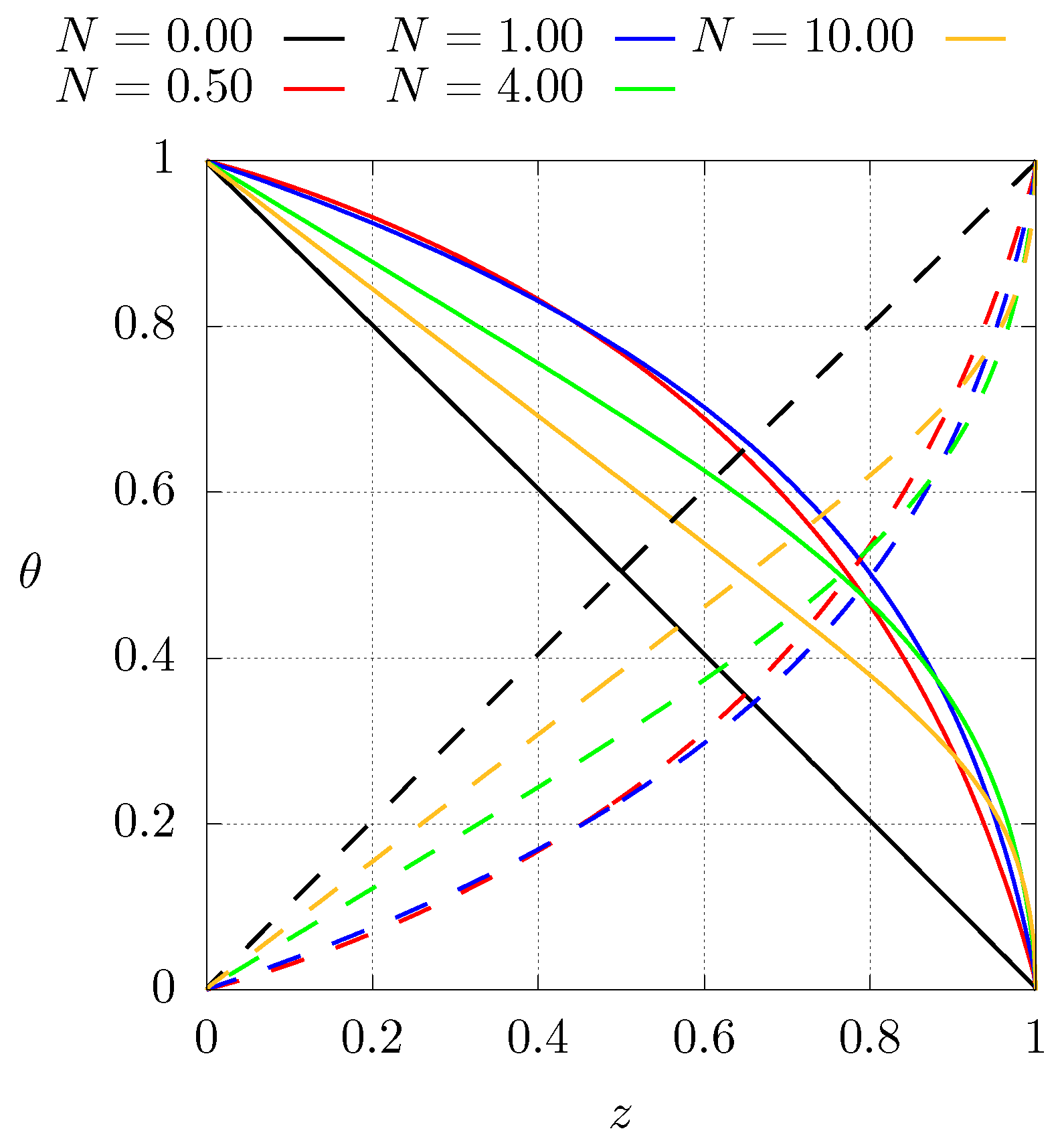
3.2. Numerical Results for the Present Case
4. Discussion
5. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Thai, H.T.; Kim, S.E. A review of theories for the modeling and analysis of functionally graded plates and shells. Compos. Struct. 2015, 128, 70–86. [Google Scholar] [CrossRef]
- D’Ans, P.; Degrez, M. How to minimise thermal fatigue in surface multi-treatments and coatings? Comput. Mater. Sci. 2012, 62, 276–281. [Google Scholar] [CrossRef]
- Birman, V.; Byrd, L.W. Modeling and Analysis of Functionally Graded Materials and Structures. Appl. Mech. Rev. 2007, 60, 195–216. [Google Scholar] [CrossRef]
- Hamza-Cherif, S.M.; Houmat, A.; Hadjoui, A. Transient heat conduction in functionally graded materials. Int. J. Comput. Methods 2007, 4, 603–619. [Google Scholar] [CrossRef]
- Sakurai, H. Transient and steady-state heat conduction analysis of two-dimensional functionally graded materials using particle method. WIT Trans. Eng. Sci. 2009, 64, 45–54. [Google Scholar] [CrossRef]
- Ma, C.C.; Chen, Y.T. Theoretical analysis of heat conduction problems of nonhomogeneous functionally graded materials for a layer sandwiched between two half-planes. Acta Mech. 2011, 221, 223–237. [Google Scholar] [CrossRef]
- Zhao, N.; Cao, L.; Guo, H. Transient heat conduction in functionally graded materials by LT-MFS. Adv. Mater. Res. 2011, 189, 1664–1669. [Google Scholar] [CrossRef]
- Rahideh, H.; Malekzadeh, P.; Haghighi, M.G. Heat conduction analysis of multi-layered FGMs considering the finite heat wave speed. Energy Convers. Manag. 2012, 55, 14–19. [Google Scholar] [CrossRef]
- Khan, W.A.; Aziz, A. Transient heat transfer in a functionally graded convecting longitudinal fin. Heat Mass Transf. 2012, 48, 1745–1753. [Google Scholar] [CrossRef]
- Zajas, J.; Heiselberg, P. Determination of the local thermal conductivity of functionally graded materials by a laser flash method. Int. J. Heat Mass Transf. 2013, 60, 542–548. [Google Scholar] [CrossRef]
- Akbarzadeh, A.H.; Chen, Z.T. Dual phase lag heat conduction in functionally graded hollow spheres. Int. J. Appl. Mech. 2014, 6, 1450002. [Google Scholar] [CrossRef]
- Li, M.; Wen, P.H. Finite block method for transient heat conduction analysis in functionally graded media. Int. J. Numer. Methods Eng. 2014, 99, 372–390. [Google Scholar] [CrossRef]
- Li, G.; Guo, S.; Zhang, J.; Li, Y.; Han, L. Transient heat conduction analysis of functionally graded materials by a multiple reciprocity boundary face method. Eng. Anal. Bound. Elem. 2015, 60, 81–88. [Google Scholar] [CrossRef]
- Yang, Y.C.; Wang, S.; Lin, S.C. Dual-phase-lag heat conduction in a furnace wall made of functionally graded materials. Int. Commun. Heat Mass Transf. 2016, 74, 76–81. [Google Scholar] [CrossRef]
- Cimmelli, V.A.; Jou, D.; Sellito, A. Heat transport equations with phonons and electrons. Acta Appl. Math. 2012, 122, 117–126. [Google Scholar] [CrossRef]
- Jou, D.; Carlomagno, I.; Cimmelli, V.A. A thermodynamic model for heat transport and thermal wave propagation in graded systems. Phys. E Low-Dimens. Syst. Nanostruct. 2015, 73, 242–249. [Google Scholar] [CrossRef]
- Jou, D.; CarIomagno, I.; Cimmelli, V.A. Rectification of low-frequency thermal wave in graded SicGe1−c. Phys. Lett. A 2016, 380, 1824–1829. [Google Scholar] [CrossRef]
- Swaminathan, K.; Sangeetha, D. Thermal analysis of FGM plates—A critical review of various modelling techniques and solution methods. Compos. Struct. 2017, 160, 43–60. [Google Scholar] [CrossRef]
- Hahn, D.W.; Özisik, M.N. Heat Conduction; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012. [Google Scholar]
- Dettori, R.; Melis, C.; Cartoixà, X.; Rurali, R.; Colombo, L. Thermal boundary resistance in semiconductors by non-equilibrium thermodynamics. Adv. Phys. X 2016, 1, 246–261. [Google Scholar] [CrossRef]
- Machrafi, H.; Lebon, G.; Jou, D. Thermal rectifier efficiency of various bulk-nanoporous silicon devices. Int. J. Heat Mass Transf. 2016, 97, 603–610. [Google Scholar] [CrossRef]
- Tamura, S.; Ogawa, K. Thermal rectificatioin in nonmetalic solid junctions: Effect of Kapitza resistance. Solid State Commun. 2012, 152, 1906–1911. [Google Scholar] [CrossRef]
- Saha, B.; Koh, Y.K.; Feser, J.P.; Sadasivam, S.; Fisher, T.S.; Shakouri, A.; Sands, T.D. Phonon wave effects in the thermal transport of epitaxial TiN/(Al,Sc)N metal/semiconductor superlattices. J. Appl. Phys. 2017, 121, 015109. [Google Scholar] [CrossRef]
- Ezzahri, Y.; Dilhaire, S.; Grauby, S.; Rampnoux, J.M.; Claeys, W. Study of thermomechanical properties of Si/SiGe superlattices using femtosecond transient thermoreflectance technique. Appl. Phys. Lett. 2005, 87, 103506. [Google Scholar] [CrossRef]
- Vo, T.Q.; Barisik, M.; Kim, B.H. Atomic density effects on temperature characteristics and thermal transport at grain boundaries through a proper bin size selection. J. Chem. Phys. 2016, 144, 194707. [Google Scholar] [CrossRef]
- Gonzalez-Valle, C.U.; Ramos-Alvarado, B. Spectral mapping of thermal transport across SiC-water interfaces. Int. J. Heat Mass Transf. 2018, 131, 645–653. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, L. Optimization of ceramic strength using elastic gradients. Acta Mater. 2009, 57, 2721–2729. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Sun, M.J.; Zhang, D. Designing functionally graded materials with superior load-bearing properties. Acta Biomater. 2012, 8, 1101–1108. [Google Scholar] [CrossRef]
- Shen, H.S. Functionally Graded Materials Nonlinear Analysis of Plates and Shells; Taylor & Francis: Abingdon, UK, 2009. [Google Scholar]
- Carrera, E.; Fazzolari, F.A.; Cinefra, M. Thermal Stress Analysis of Composite Beams, Plates and Shells: Computational Modelling and Applications; Academic Press, Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Kreuzer, H.J. Nonequilibrium Thermodynamics and Its Statistical Foundations; Clarendon Press: Oxford, UK, 1981. [Google Scholar]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method; Longman Scientific & Technical: Harlow, UK, 1995. [Google Scholar]
- Núñez, J.; Ramos, E.; Lopez, J.M. A mixed Fourier–Galerkin–finite-volume method to solve the fluid dynamics equations in cylindrical geometries. Fluid Dyn. Res. 2012, 44, 031414. [Google Scholar] [CrossRef]
- Alipour, S.M.; Kiani, Y.; Eslami, M.R. Rapid heating of FGM rectangular plates. Acta Mech. 2015, 227, 421–436. [Google Scholar] [CrossRef]
- Hassanzadeh, R.; Bilgili, M. Improvement of thermal efficiency in computer heat sink using functionally graded materials. Commun. Adv. Comput. Sci. Appl. 2014, 2014, cacsa-00018. [Google Scholar] [CrossRef][Green Version]

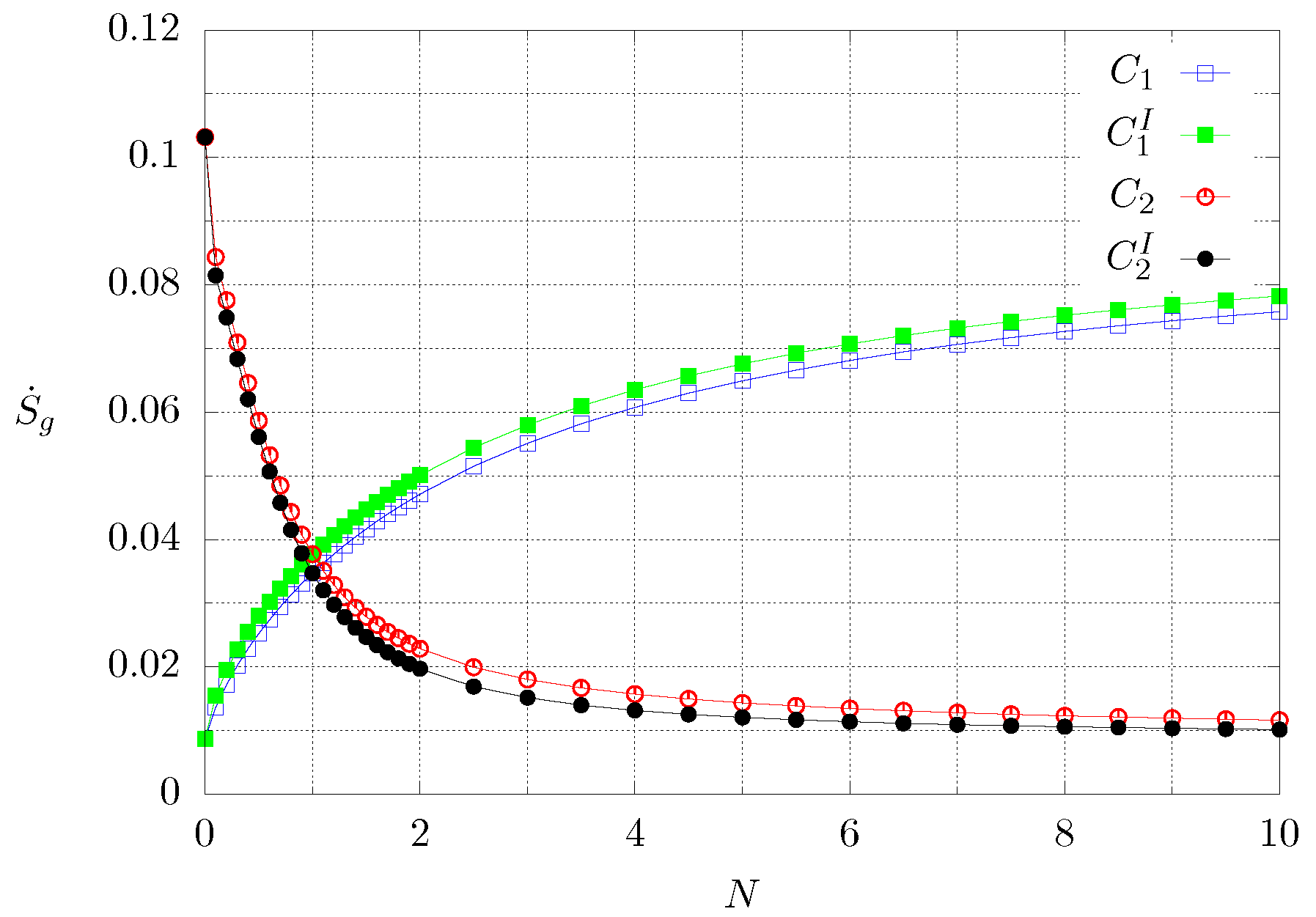
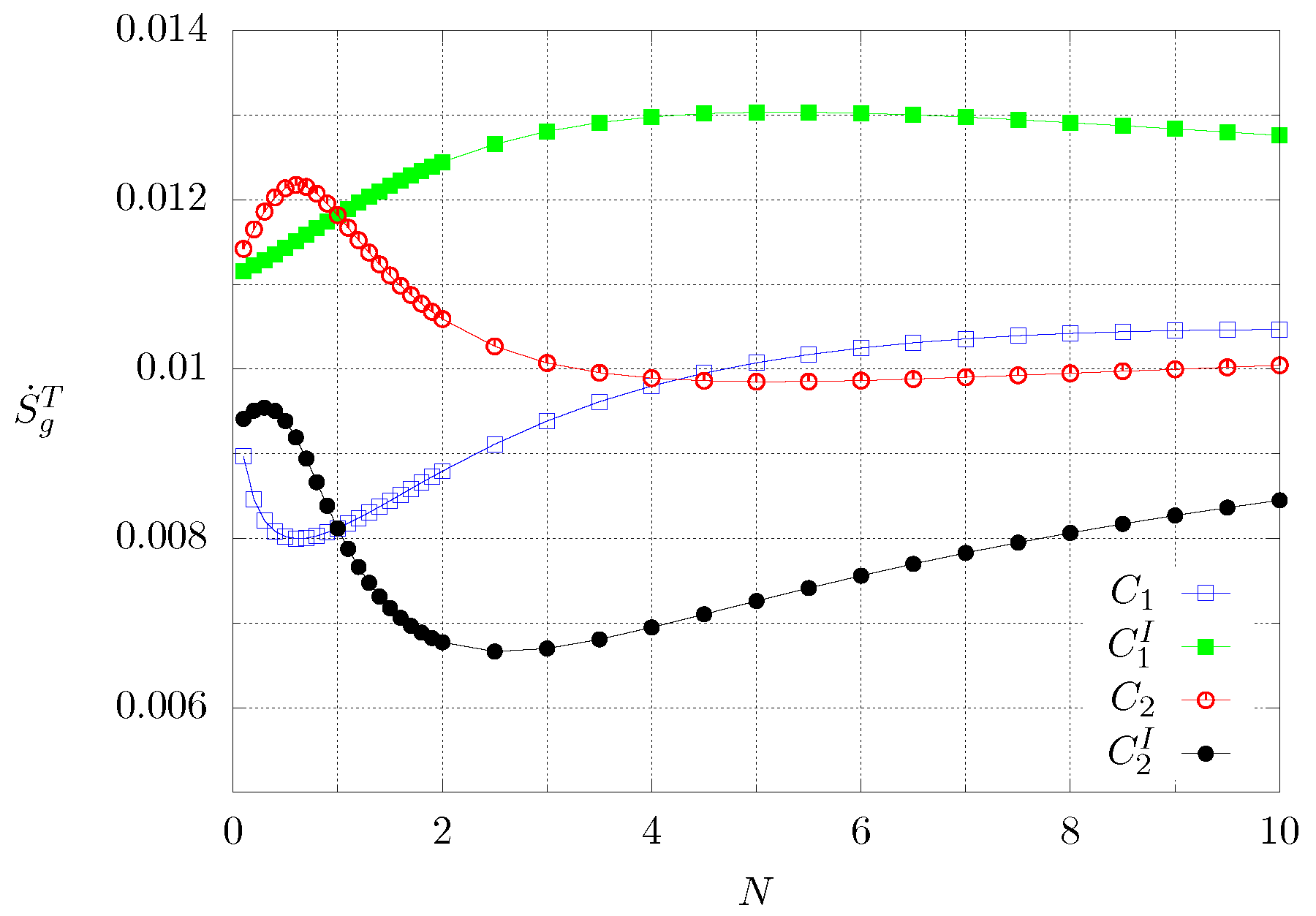
| Material | Min/Max | N | |||
|---|---|---|---|---|---|
| Min | 0.6 | 0.008 | 0.025 | 0.32 | |
| Max | 5.5 | 0.013 | 0.069 | 0.19 | |
| Max | 0.6 | 0.0122 | 0.053 | 0.23 | |
| Min | 5 | 0.0098 | 0.014 | 0.7 | |
| Max | 0.3 | 0.0095 | 0.062 | 0.15 | |
| Min | 2.5 | 0.0067 | 0.017 | 0.39 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pérez-Barrera, J.; Figueroa, A.; Vázquez, F. Controlling and Optimizing Entropy Production in Transient Heat Transfer in Graded Materials. Entropy 2019, 21, 463. https://doi.org/10.3390/e21050463
Pérez-Barrera J, Figueroa A, Vázquez F. Controlling and Optimizing Entropy Production in Transient Heat Transfer in Graded Materials. Entropy. 2019; 21(5):463. https://doi.org/10.3390/e21050463
Chicago/Turabian StylePérez-Barrera, James, Aldo Figueroa, and Federico Vázquez. 2019. "Controlling and Optimizing Entropy Production in Transient Heat Transfer in Graded Materials" Entropy 21, no. 5: 463. https://doi.org/10.3390/e21050463
APA StylePérez-Barrera, J., Figueroa, A., & Vázquez, F. (2019). Controlling and Optimizing Entropy Production in Transient Heat Transfer in Graded Materials. Entropy, 21(5), 463. https://doi.org/10.3390/e21050463






