Second Law Analysis of Spectral Radiative Transfer and Calculation in One-Dimensional Furnace Cases
Abstract
1. Introduction
1.1. Radiative Thermodynamics
1.2. Second Law in Radiation Transfer Calculations
1.3. Summary
2. Spectral Radiative Exergy Theories Review and Comments
2.1. Equivalent Temperature
2.2. Previous Research Review
2.3. Comments
3. Thermodynamic Analysis of Spectral Radiation Transfer
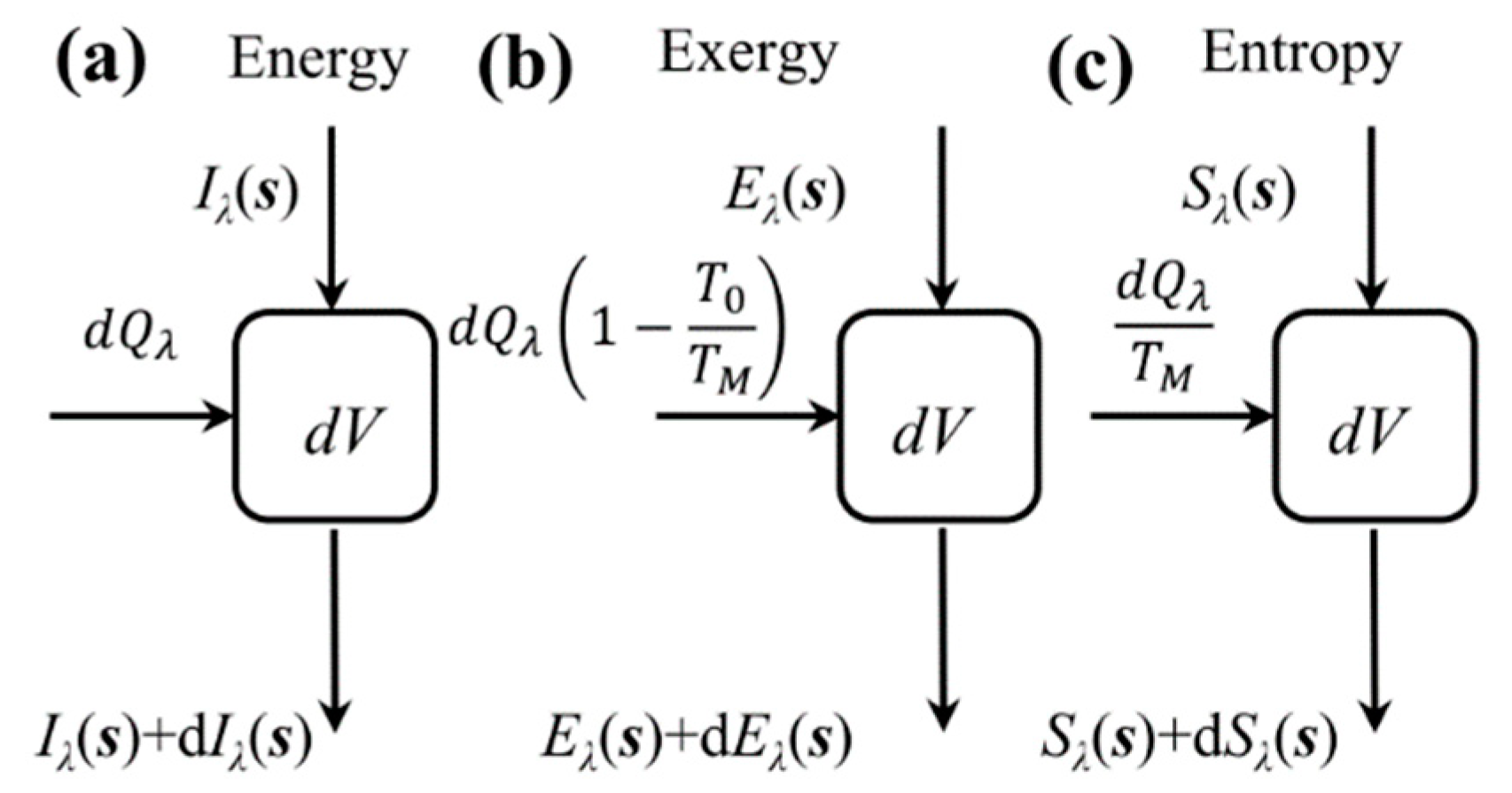
3.1. Spectral Radiative Exergy Transfer
3.2. Spectral Radiative Entropy Transfer
3.3. Verification
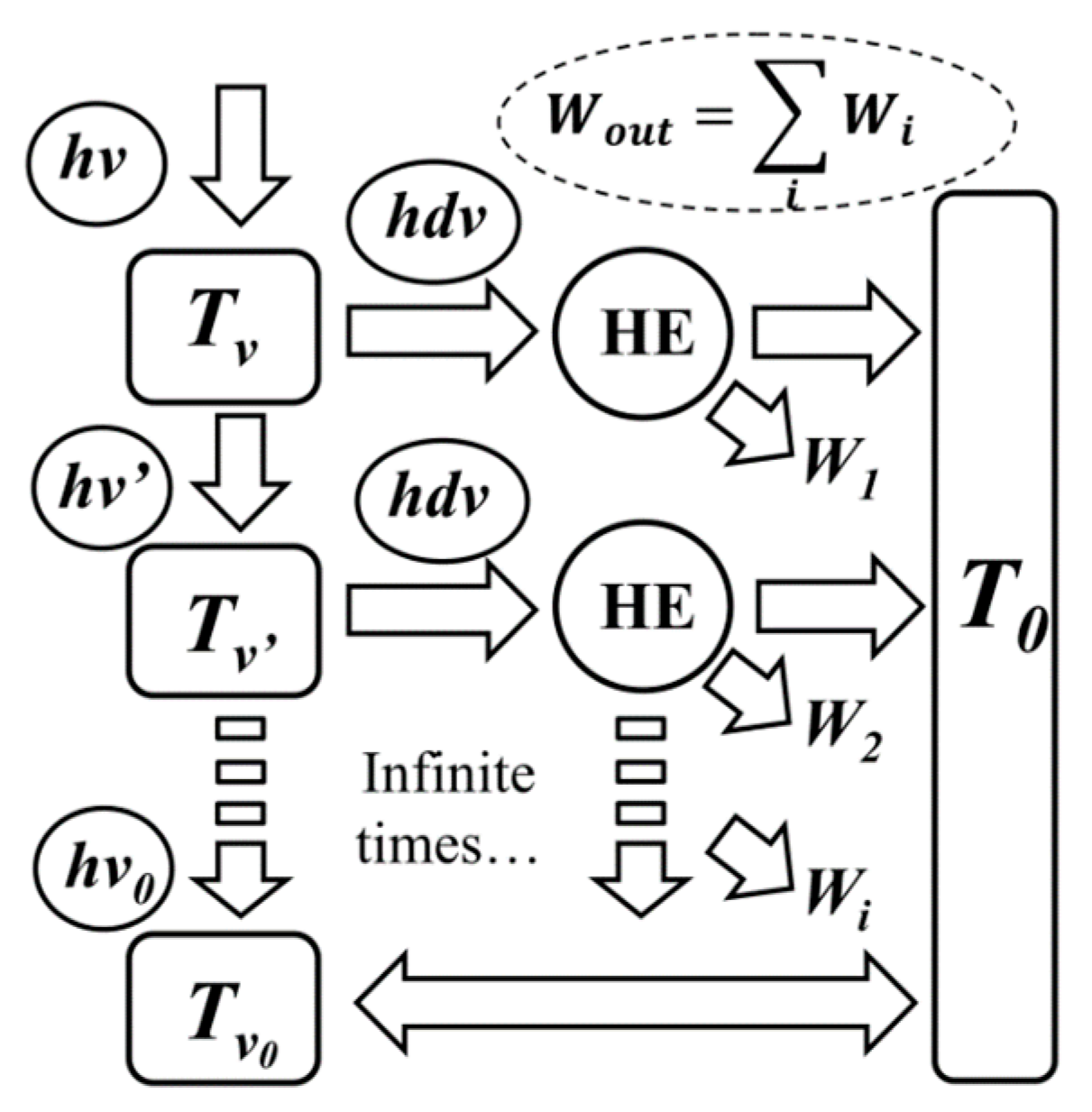
3.3.1. Thermodynamic Relationship Verification
3.3.2. Numerical Verification
4. One-Dimensional Cases Studies
4.1. Cases and Calculation Method
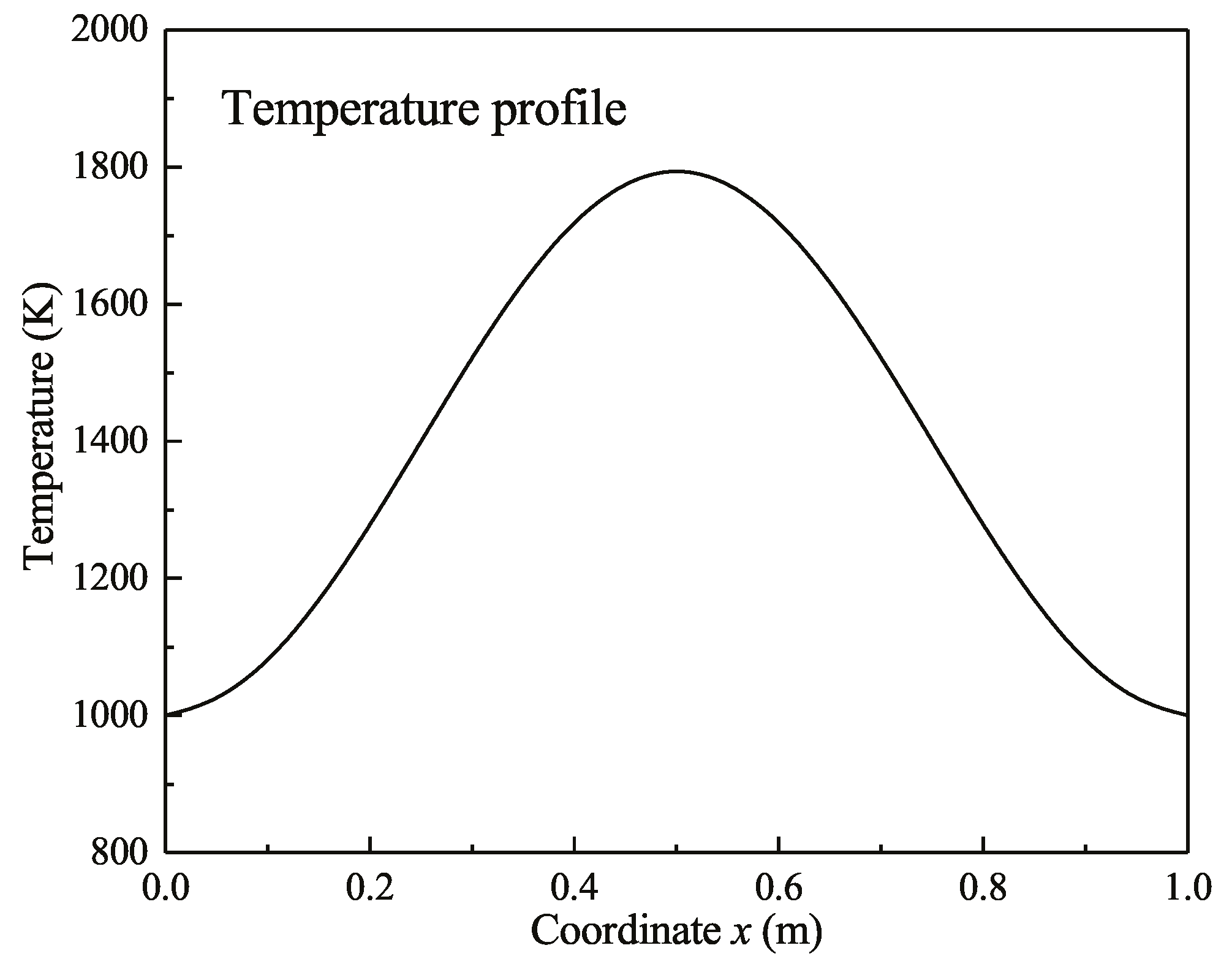
4.1.1. One-Dimensional Cases
4.1.2. Calculation Method
4.2. Calculation Results
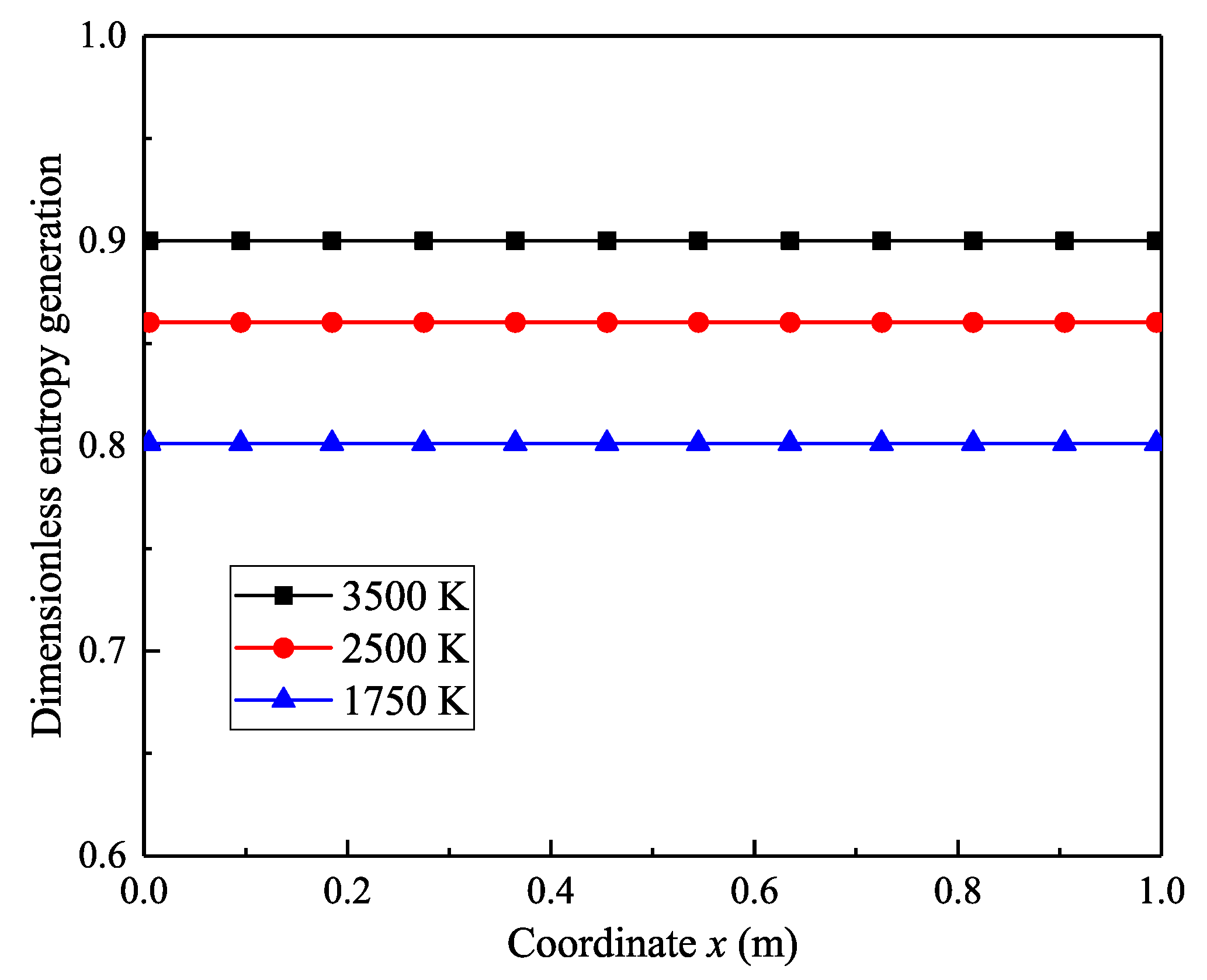
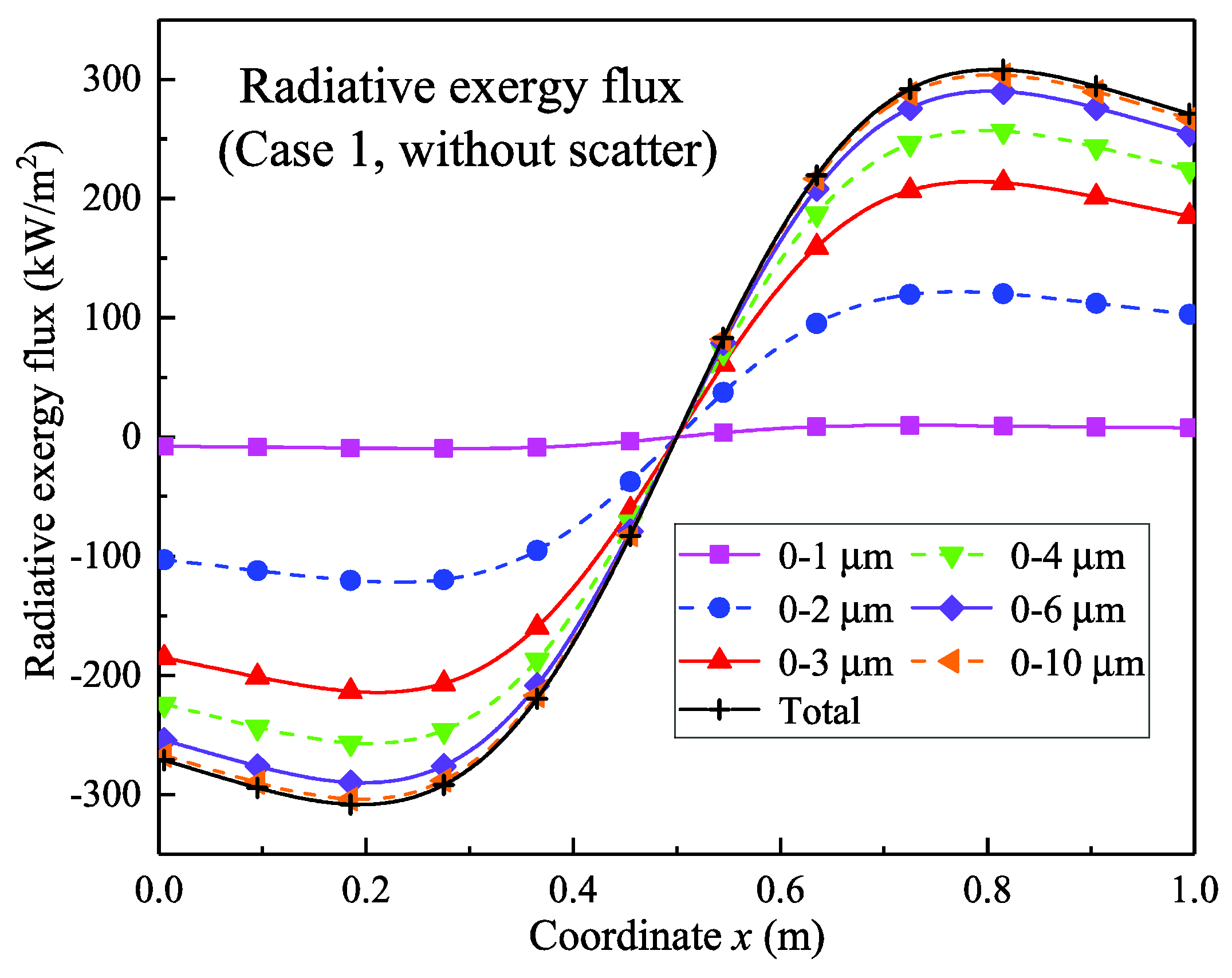
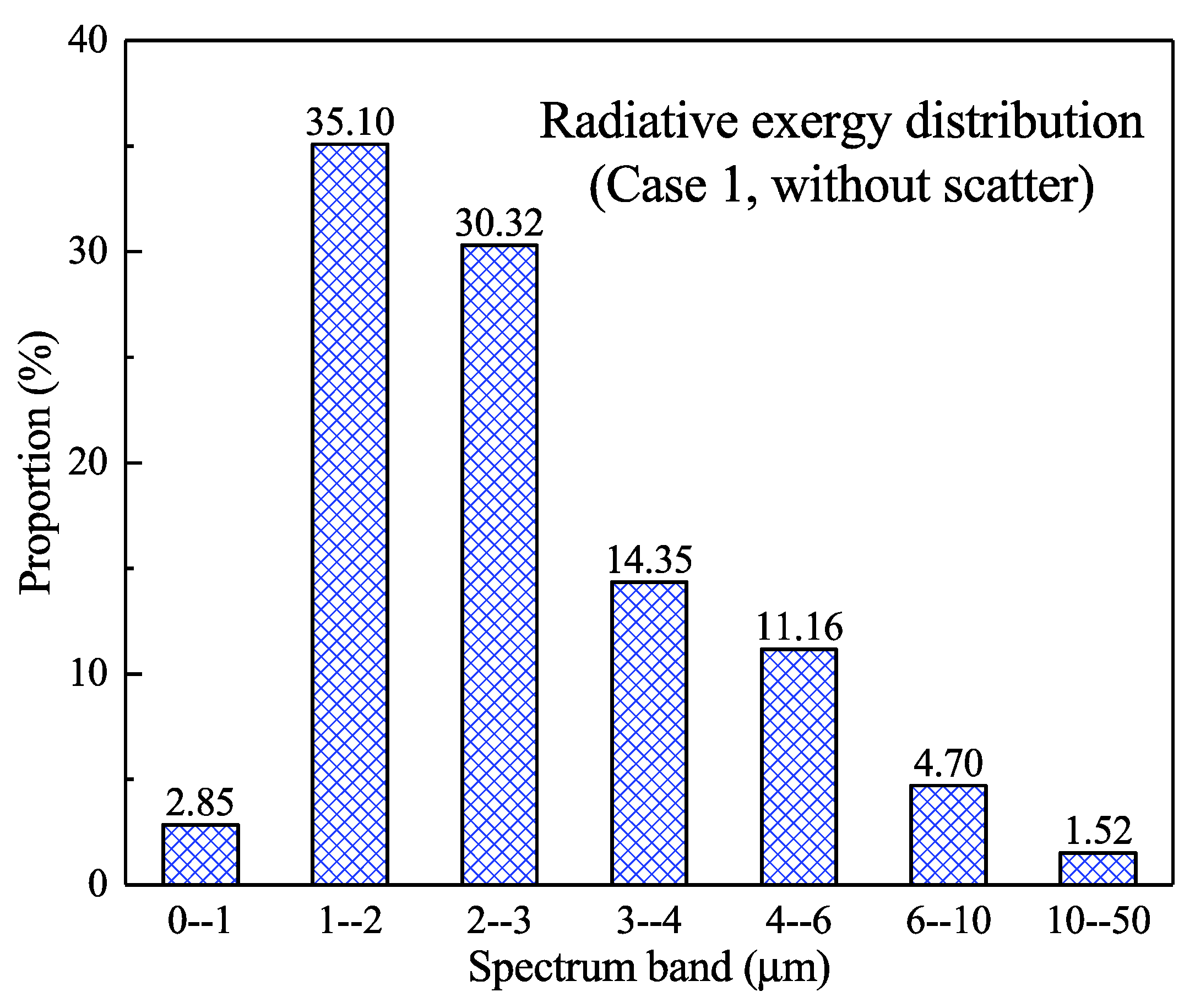
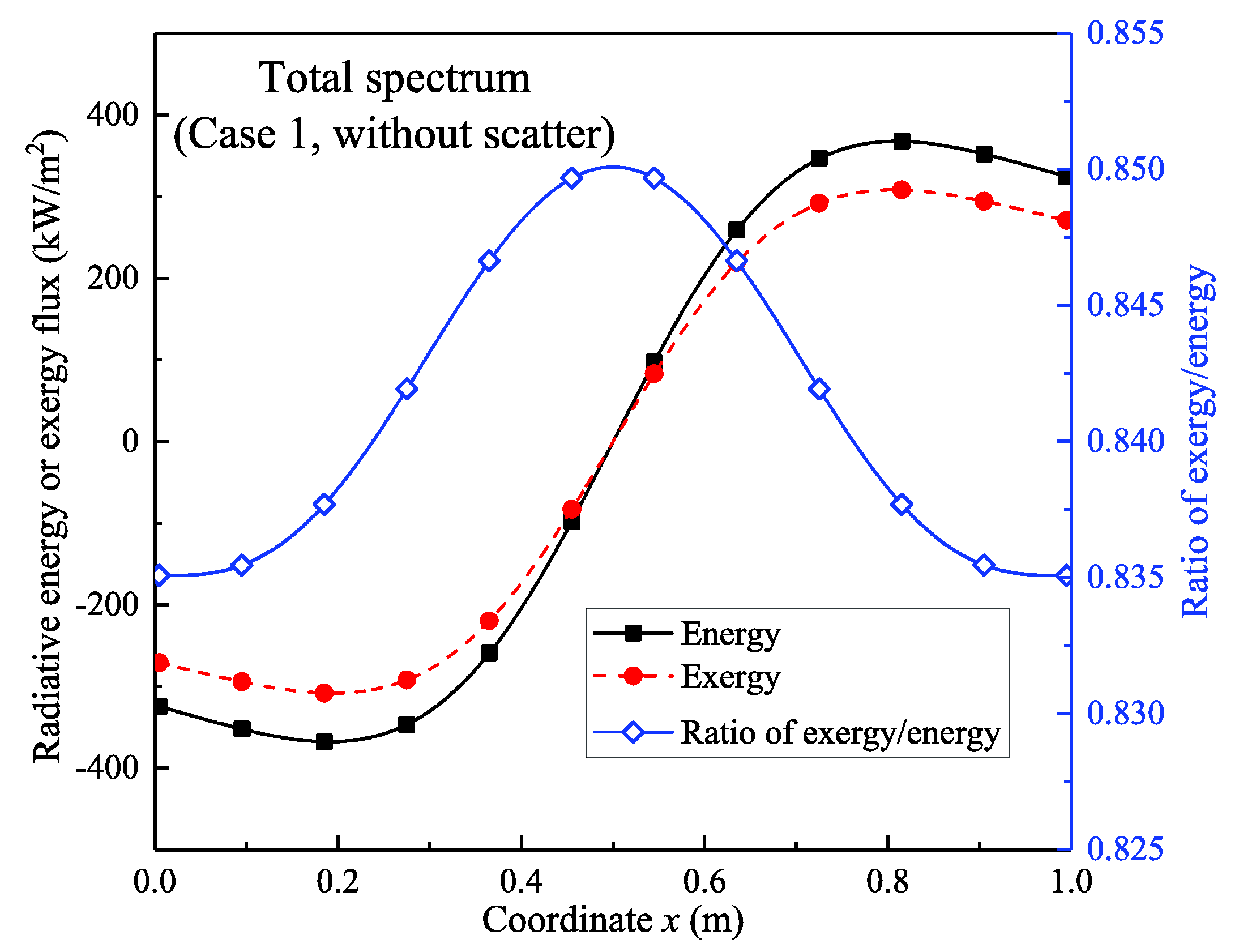
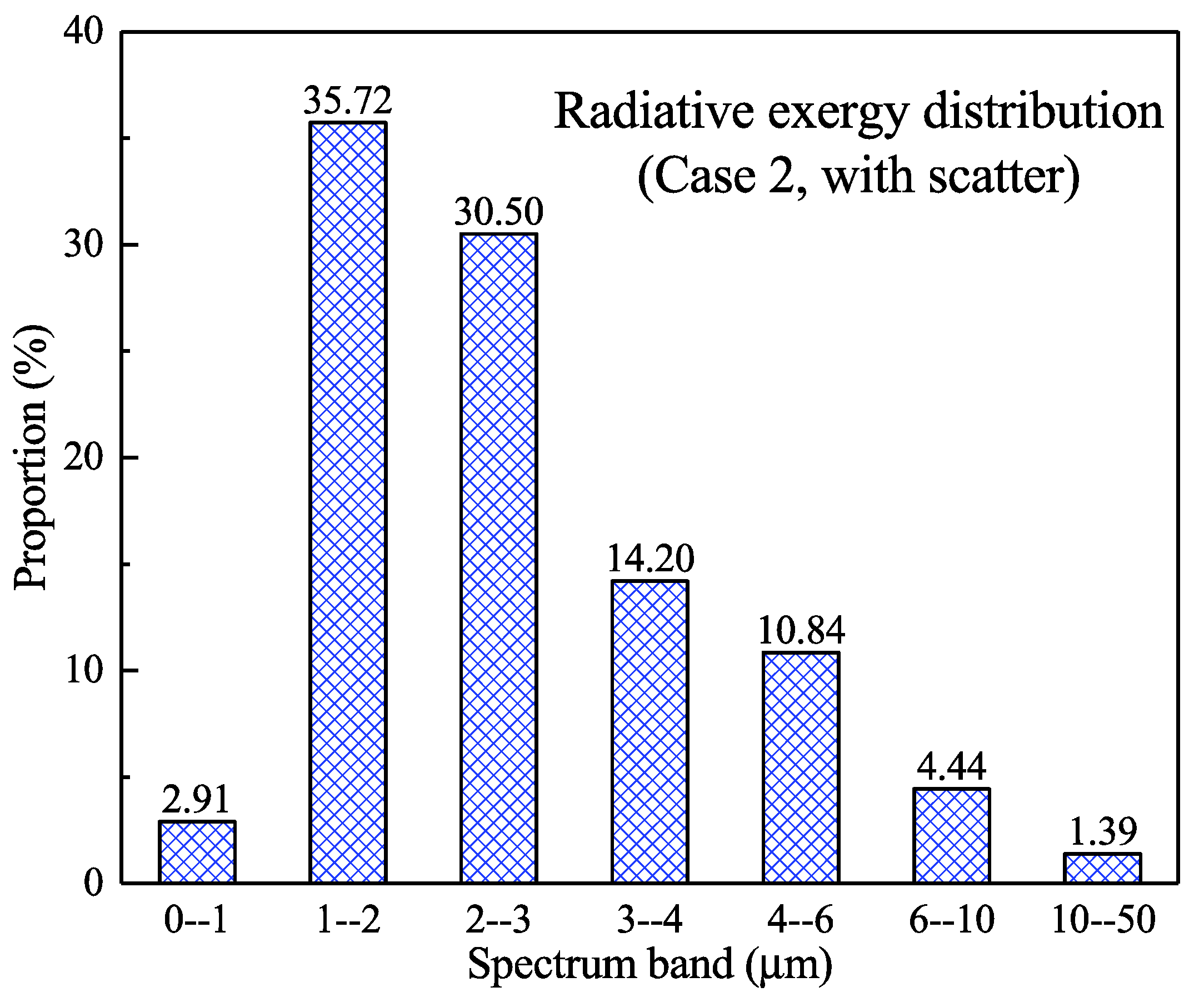
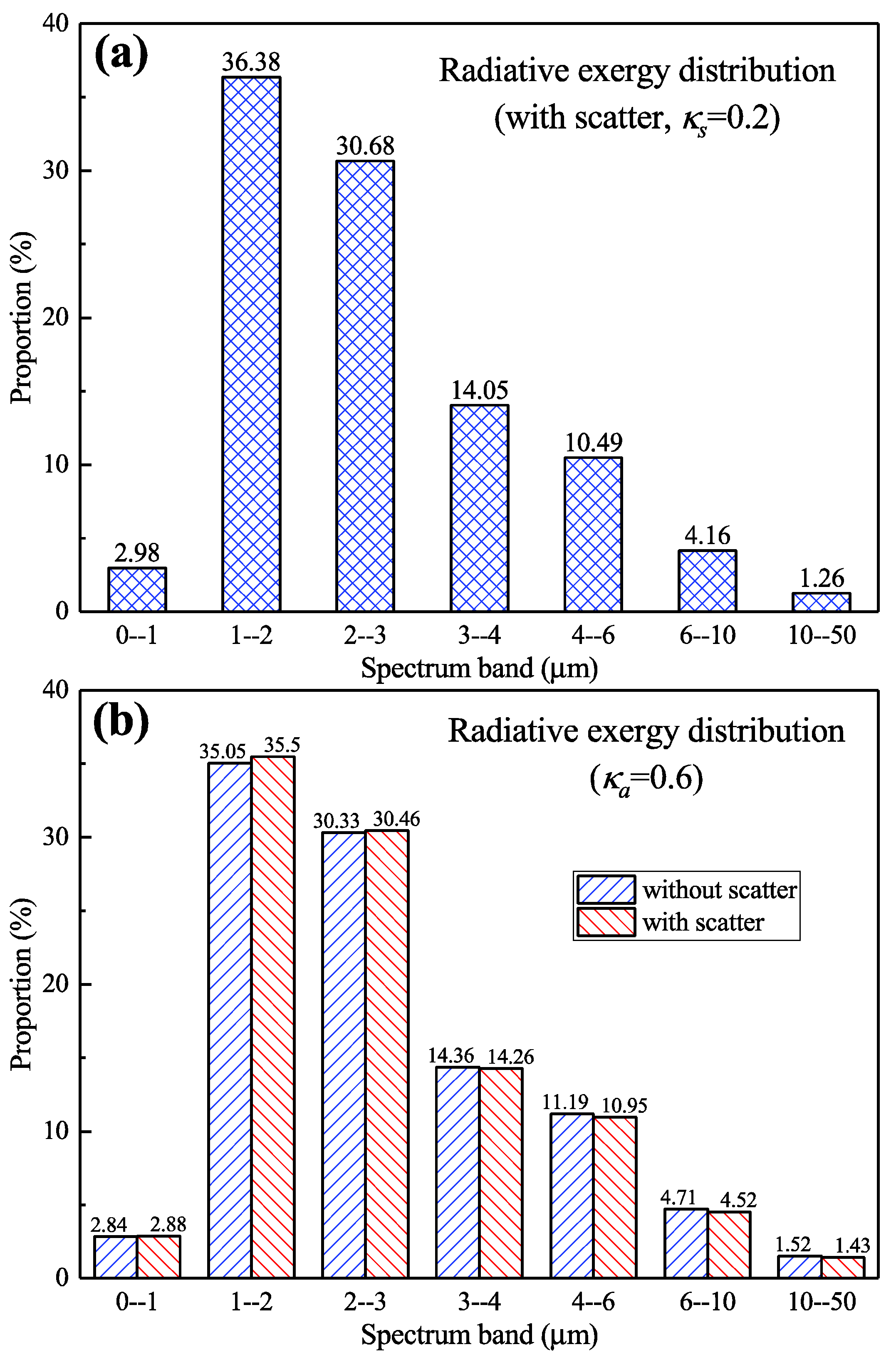
4.2.1. Results of the Temperature Field without Scattering
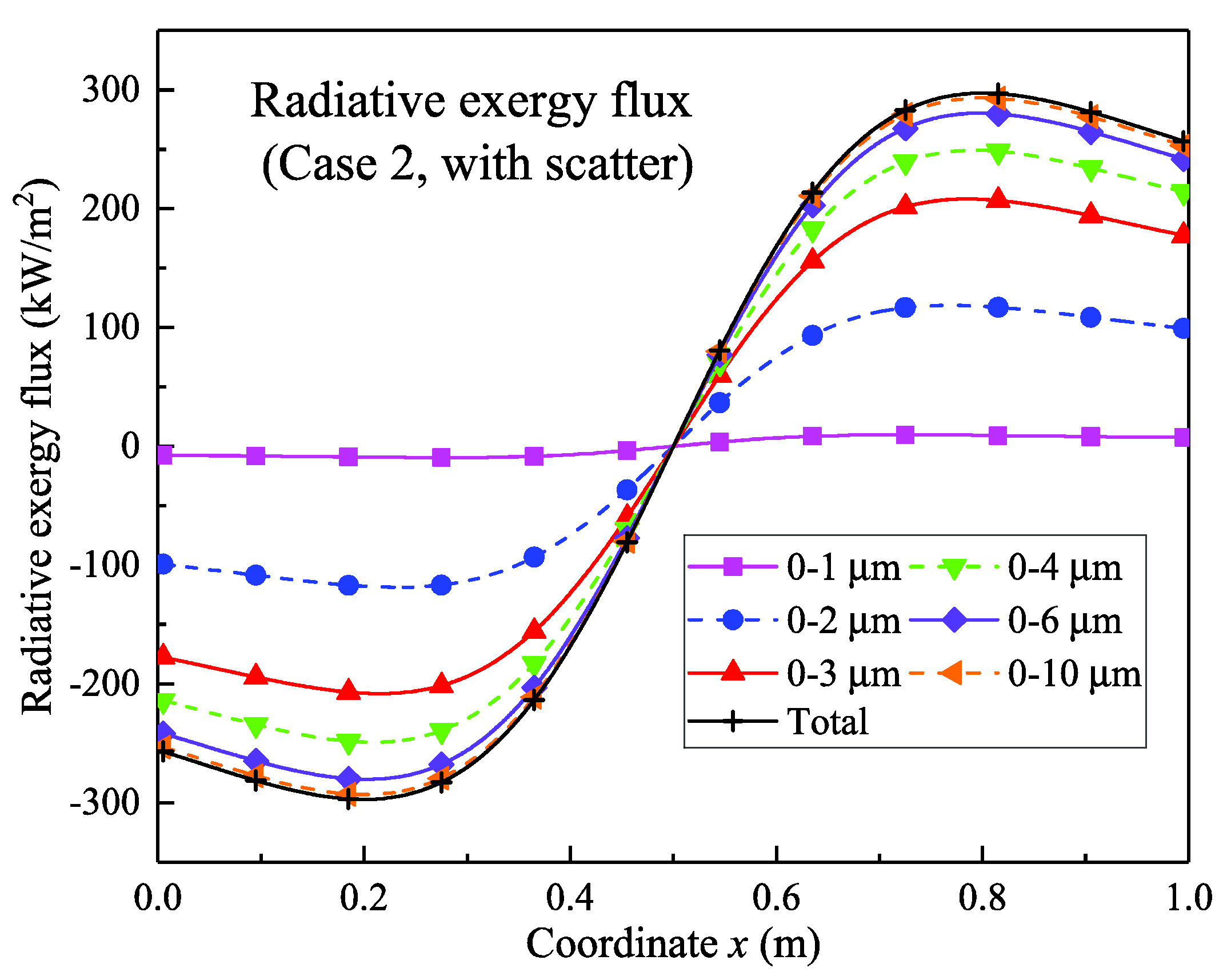
4.2.2. Results of the Temperature Field with Scattering
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| e | radiative exergy flux |
| E | radiative exergy intensity |
| Ev | exergy of monochromatic photon |
| f | coefficient of equivalent temperature |
| h | Planck constant |
| H | enthalpy |
| I | radiative intensity |
| L | distance between one dimensional parallel infinite plates |
| Q | thermal energy |
| s | direction of radiation transfer |
| s′ | direction of incident scattering radiation |
| S | radiative entropy intensity |
| Sv | entropy of monochromatic photon |
| T | temperature |
| T0 | ambient temperature |
| V | volume |
| x | length coordinate |
| Geek symbols | |
| ΓG | radiative entropy generation in one-dimensional space |
| η | exergy-to-energy coefficient |
| θ | zenith angle |
| κ | absorption coefficient |
| λ | Wavelength |
| ν | Frequency |
| ξ | entropy-to-energy coefficient |
| ΠG | dimensionless radiative entropy generation in one-dimensional space |
| Φ | scattering phase function |
| Ω | solid angle |
| Ω′ | solid angle of incident scattering |
| Subscripts | |
| a | absorption |
| b | blackbody |
| H | high |
| L | low |
| M | media |
| R | radiation field |
| s | scattering |
| 0 | reference state |
References
- Modest, M.F. Radiative Heat Transfer, 3rd ed.; Academic press: Amsterdam, The Netherland, 2013. [Google Scholar]
- Gungor, A. Second law analysis of heat transfer surfaces in circulating fluidized beds. Appl. Energy 2009, 86, 1344–1353. [Google Scholar] [CrossRef]
- Jarray, K.; Mazgar, A.; Nejma, F.B. Numerical analysis of entropy generation through non-grey gas radiation in a cylindrical annulus. Int. J. Hydrog. Energy 2017, 42, 8795–8803. [Google Scholar] [CrossRef]
- Hossain, M.I.; Bousselham, A.; Alharbi, F.H. Optical concentration effects on conversion efficiency of a split-spectrum solar cell system. J. Phys. D Appl. Phys. 2014, 47, 075101. [Google Scholar] [CrossRef]
- Shan, S.; Zhou, Z.; Cen, K. An innovative integrated system concept between oxy-fuel thermo-photovoltaic device and a Brayton-Rankine combined cycle and its preliminary thermodynamic analysis. Energy Convers Manag. 2019, 180, 1139–1152. [Google Scholar] [CrossRef]
- Yin, E.; Li, Q.; Xuan, Y. A novel optimal design method for concentration spectrum splitting photovoltaic–thermoelectric hybrid system. Energy 2018, 163, 519–532. [Google Scholar] [CrossRef]
- Yang, Z.; Li, W.; Chen, X.; Su, S.; Lin, G.; Chen, J. Maximum efficiency and parametric optimum selection of a concentrated solar spectrum splitting photovoltaic cell-thermoelectric generator system. Energy Convers Manag. 2018, 174, 65–71. [Google Scholar] [CrossRef]
- Wright, S. Comparative analysis of the entropy of radiative heat transfer and heat conduction. Int. J. Thermody. 2007, 10, 27–35. [Google Scholar]
- Liu, L.H.; Chu, S.X. On the entropy generation formula of radiation heat transfer processes. J. Heat Transf. Trans. ASME 2006, 128, 504–506. [Google Scholar] [CrossRef]
- Petela, R. Exergy of heat radiation. J. Heat. Transf. Trans. ASME 1964, 86, 187–192. [Google Scholar] [CrossRef]
- Jeter, S.M. Maximum conversion efficiency for the utilization of direct solar radiation. Sol. Energy 1981, 26, 231–236. [Google Scholar] [CrossRef]
- Spanner, D.C. Introduction to Thermodynamics; Academic Press: London, UK, 1964. [Google Scholar]
- Bejan, A. Unification of three different theories concerning the ideal conversion of enclosed radiation. J. Sol. Energy Eng. 1987, 109, 46–51. [Google Scholar] [CrossRef]
- Landsberg, P.T.; Baruch, P. The thermodynamics of the conversion of radiation energy for photovoltaics. J. Phys. A Math. Gen. 1989, 22, 1911–1926. [Google Scholar] [CrossRef]
- Badescu, V. On the thermodynamics of the conversion of diluted radiation. J. Phys. D Appl. Phys. 1990, 23, 289–292. [Google Scholar] [CrossRef]
- Sieniutycz, S.; Kuran, P. Modeling thermal behavior and work flux in finite-rate systems with radiation. Int. J. Heat Mass Transf. 2006, 49, 3264–3283. [Google Scholar] [CrossRef]
- Laptev, V.I. Conversion of solar heat into work: A supplement to the actual thermodynamic description. J. Appl. Phys. 2005, 98, 124905. [Google Scholar] [CrossRef]
- Wright, S.E.; Rosen, M.A. Exergetic efficiencies and the exergy content of terrestrial solar radiation. J. Sol. Energy Eng. 2004, 126, 673–676. [Google Scholar] [CrossRef]
- Saidur, R.; BoroumandJazi, G.; Mekhlif, S.; Jameel, M. Exergy analysis of solar energy applications. Renew. Sust. Energ Rev. 2012, 16, 350–356. [Google Scholar] [CrossRef]
- Peng, S.; Hong, H. Exergy analysis of solar gas turbine system coupled with Kalina cycle. Int. J. Exergy 2015, 18, 192–213. [Google Scholar] [CrossRef]
- Saxena, G.; Gaur, M.K. Exergy analysis of evacuated tube solar collectors: A review. Int. J. Exergy 2018, 25, 54–74. [Google Scholar] [CrossRef]
- Zhou, Z.; Shan, S.; Chen, L.; Zhang, Y. Exergy of Blackbody Radiation and Monochromatic Photon. Int. J. Thermophys. 2017, 38, 57. [Google Scholar] [CrossRef]
- Candau, Y. On the exergy of radiation. Sol. Energy 2003, 75, 241–247. [Google Scholar] [CrossRef]
- Chen, Z.; Mo, S. Effective temperature and exergy of monochromic blackbody radiation. Prog. Nat. Sci. 2007, 17, 1250–1254. [Google Scholar] [CrossRef]
- Chen, Z.; Mo, S.; Hu, P. Recent progress in thermodynamics of radiation—exergy of radiation, effective temperature of photon and entropy constant of photon. Sci. Chin. Ser. E 2008, 51, 1096. [Google Scholar] [CrossRef]
- Lior, N.; Sarmiento-Darkin, W.; Al-Sharqawi, H.S. The exergy fields in transport processes: Their calculation and use. Energy 2006, 31, 553–578. [Google Scholar] [CrossRef]
- Caldas, M.; Semiao, V. Entropy generation through radiative transfer in participating media: Analysis and numerical computation. J. Quant. Spectrosc. Radiat. Transf. 2005, 96, 423–437. [Google Scholar] [CrossRef]
- Caldas, M.; Semiao, V. The effect of turbulence–radiation interaction on radiative entropy generation and heat transfer. J. Quant. Spectrosc. Radiat. Transf. 2007, 104, 12–23. [Google Scholar] [CrossRef]
- Liu, L.H.; Chu, S.X. Verification of numerical simulation method for entropy generation of radiation heat transfer in semitransparent medium. J. Quant. Spectrosc. Radiat. Transf. 2007, 103, 43–56. [Google Scholar] [CrossRef]
- Liu, L.H.; Chu, S.X. Radiative exergy transfer equation. J. Thermophys. Heat Transf. 2007, 21, 819–822. [Google Scholar] [CrossRef]
- Chu, S.X.; Liu, L.H. Entropy generation analysis of two-dimensional high-temperature confined jet. Int. J. Therm. Sci. 2009, 48, 998–1006. [Google Scholar] [CrossRef]
- Makhanlall, D.; Liu, L.H.; Zhang, H.C. Determination of loss coefficients for high-temperature flow devices: An entropy-based approach. Int. J. Therm. Sci. 2010, 49, 1848–1855. [Google Scholar] [CrossRef]
- Makhanlall, D.; Liu, L.H. Second law analysis of coupled conduction–radiation heat transfer with phase change. Int. J. Therm. Sci. 2010, 49, 1829–1836. [Google Scholar] [CrossRef]
- Bejan, A. Advanced Engineering Thermodynamics; Wiley: New York, NY, USA, 1988. [Google Scholar]
- Juretić, D.; Županović, P. Photosynthetic models with maximum entropy production in irreversible charge transfer steps. Comput. Biol. Chem. 2003, 27, 541–553. [Google Scholar] [CrossRef] [PubMed]
- Lems, S.; Van Der Kooi, H.J.; De Swaan Arons, J. Exergy analyses of the biochemical processes of photosynthesis. Int. J. Exergy 2010, 7, 333–351. [Google Scholar] [CrossRef]
- Meszéna, G.; Westerhoff, H.V.; Somsen, O. Reply to Comment on ‘Non-equilibrium thermodynamics of light absorption’. J. Phys. A Math. Gen. 2000, 33, 1301. [Google Scholar] [CrossRef]
- Shan, S.; Qian, B.; Zhou, Z.; Wang, Z.; Cen, K. New pressurized WSGG model and the effect of pressure on the radiation heat transfer of H2O/CO2 gas mixtures. Int. J. Heat Mass Transf. 2018, 121, 999–1010. [Google Scholar] [CrossRef]
- Shan, S.; Zhou, Z.; Chen, L.; Wang, Z.; Cen, K. New weighted-sum-of-gray-gases model for typical pressurized oxy-fuel conditions. Int. J. Energy Res. 2017, 41, 2576–2595. [Google Scholar] [CrossRef]
- Becher, V.; Goanta, A.; Spliethoff, H. Validation of spectral gas radiation models under oxy-fuel conditions–Part C: Validation of simplified models. Int. J. Greenh. Gas Control. 2012, 11, 34–51. [Google Scholar] [CrossRef]
- Kirdyashkin, A.I.; Orlovskii, V.M.; Sosnin, E.A.; Tarasenko, V.F.; Gushchin, A.N.; Panarin, V.A. Energy and spectral characteristics of radiation during filtration combustion of natural gas. Combust. Explos. 2010, 46, 523–527. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shan, S.; Zhou, Z. Second Law Analysis of Spectral Radiative Transfer and Calculation in One-Dimensional Furnace Cases. Entropy 2019, 21, 461. https://doi.org/10.3390/e21050461
Shan S, Zhou Z. Second Law Analysis of Spectral Radiative Transfer and Calculation in One-Dimensional Furnace Cases. Entropy. 2019; 21(5):461. https://doi.org/10.3390/e21050461
Chicago/Turabian StyleShan, Shiquan, and Zhijun Zhou. 2019. "Second Law Analysis of Spectral Radiative Transfer and Calculation in One-Dimensional Furnace Cases" Entropy 21, no. 5: 461. https://doi.org/10.3390/e21050461
APA StyleShan, S., & Zhou, Z. (2019). Second Law Analysis of Spectral Radiative Transfer and Calculation in One-Dimensional Furnace Cases. Entropy, 21(5), 461. https://doi.org/10.3390/e21050461




