Gaze Information Channel in Cognitive Comprehension of Poster Reading
Abstract
1. Introduction
2. Background
3. Information Measures and Information Channel
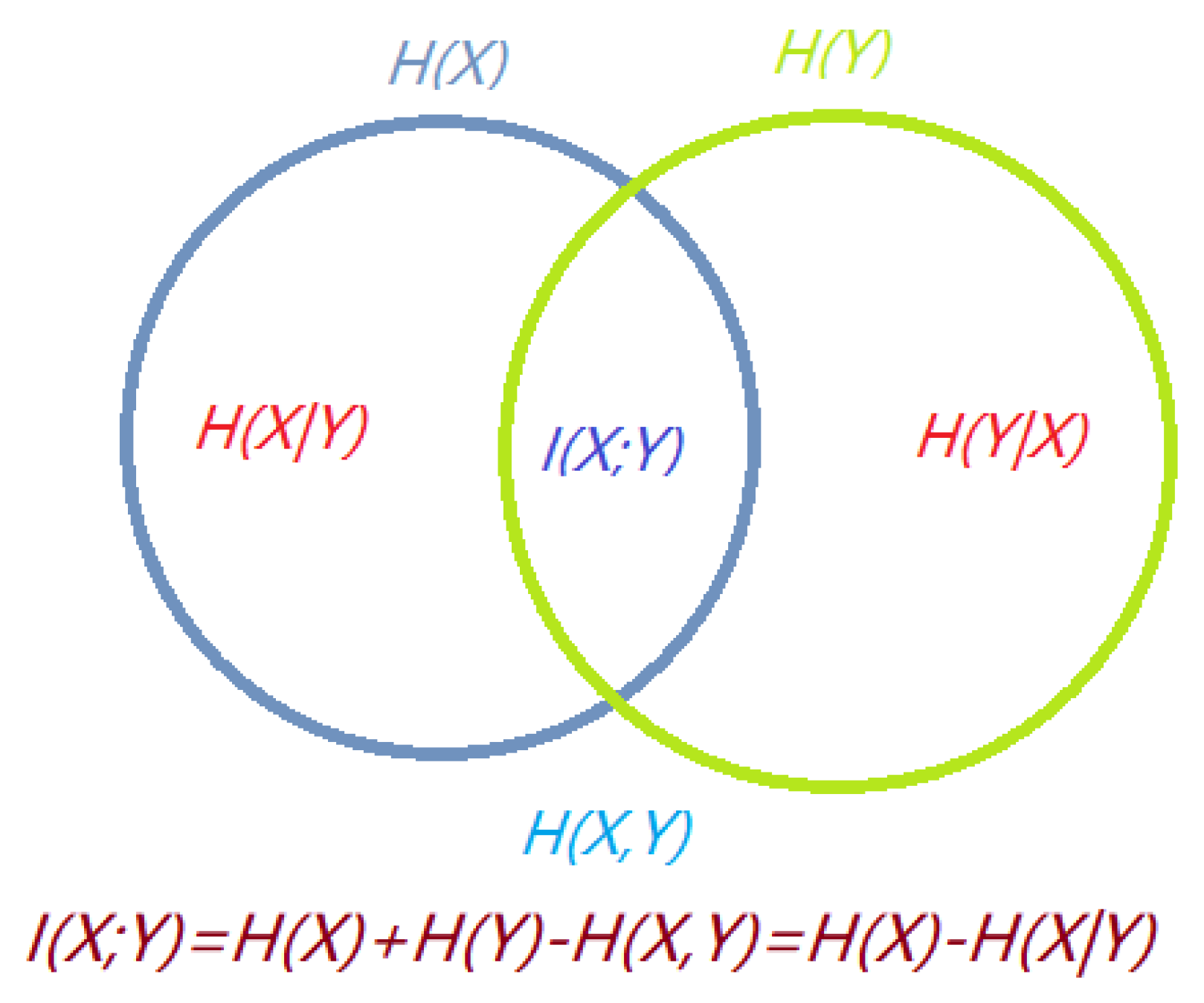
3.1. Basic Information-Theoretic Measures
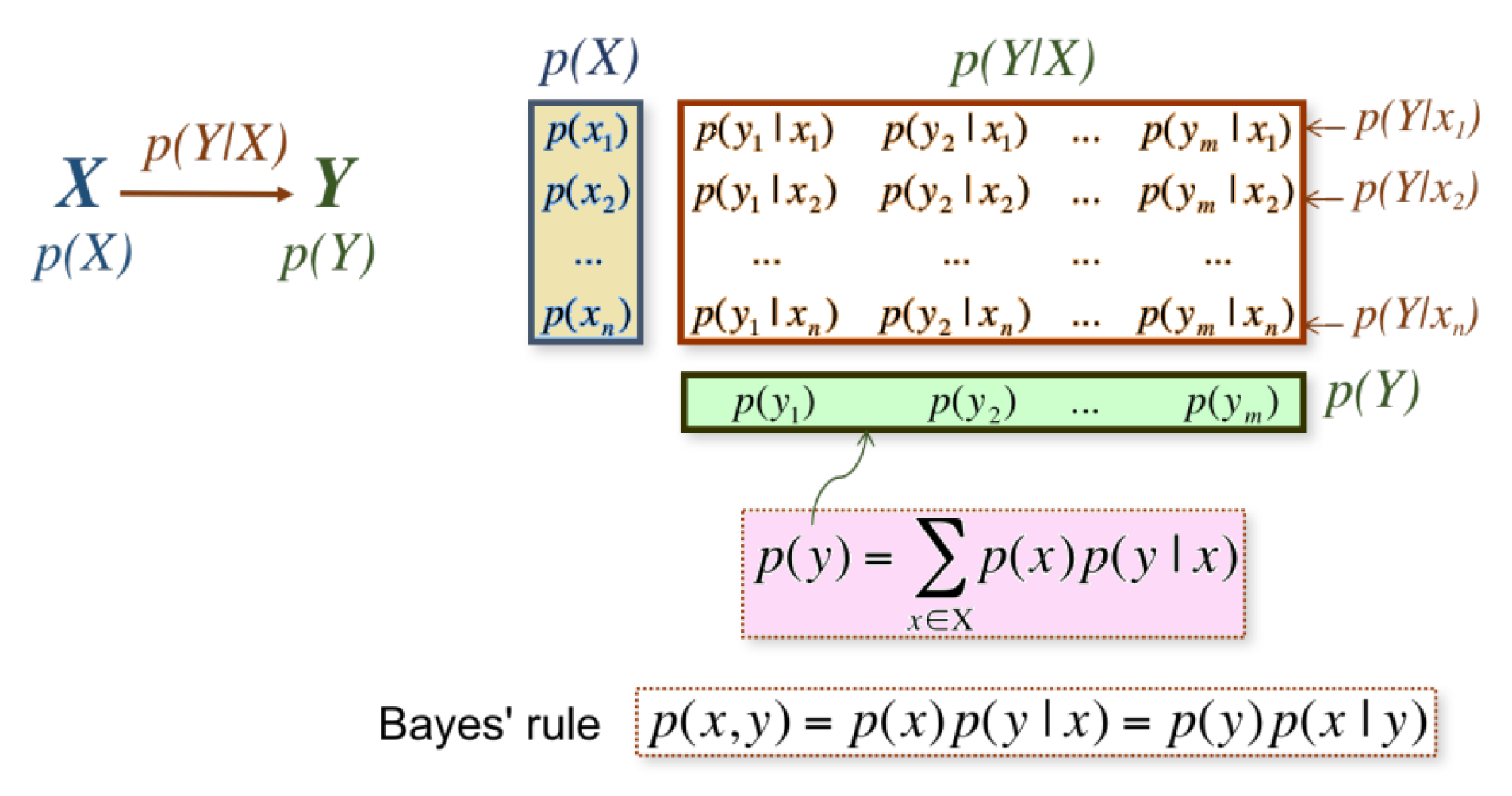
3.2. Information Channel
- and represent the probability distributions of input and output variables X and Y, respectively.
- Probability transition matrix composed of conditional probabilities , which gives the output distribution given the input distribution . Each row of can be seen as a probability distribution, denoted by .
4. Method
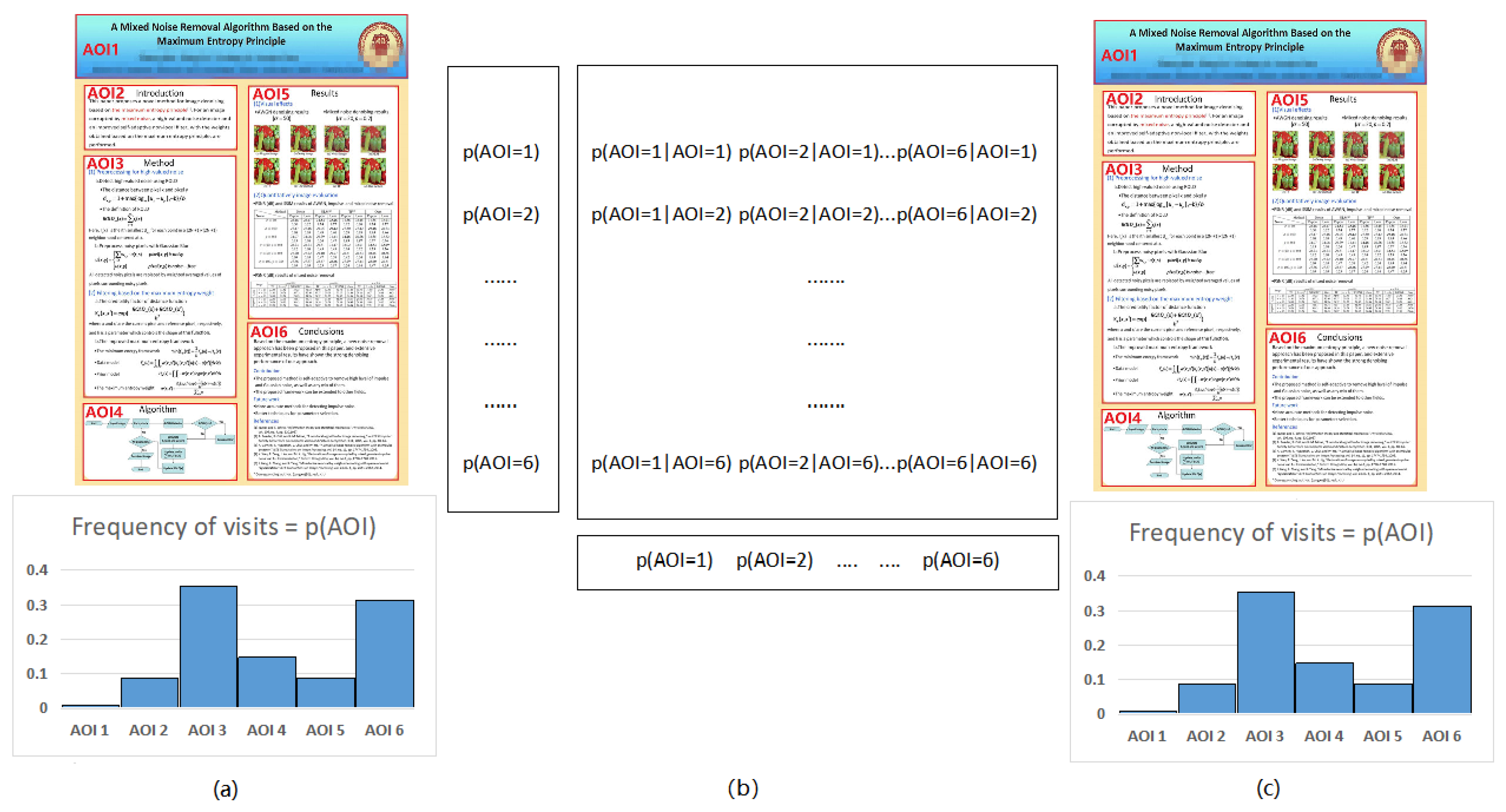
4.1. Gaze Information Channel
- The conditional probability is given by , which represents the estimated probability of transitioning from AOI to any AOI given AOI as the starting point. Matrix elements are set to the number of transitions from source AOI to destination AOI for each participant and then the matrix is normalized relative to each source AOI (i.e., per row), . Conditional probabilities fulfill ,, that is, .
- The marginal probabilities of input X and output Y, ) and , are both given by the stationary probability , , giving the frequency of visits of each AOI.
4.2. Entropy and Mutual Information in Gaze Information Channel
5. Experiment and Data Collection
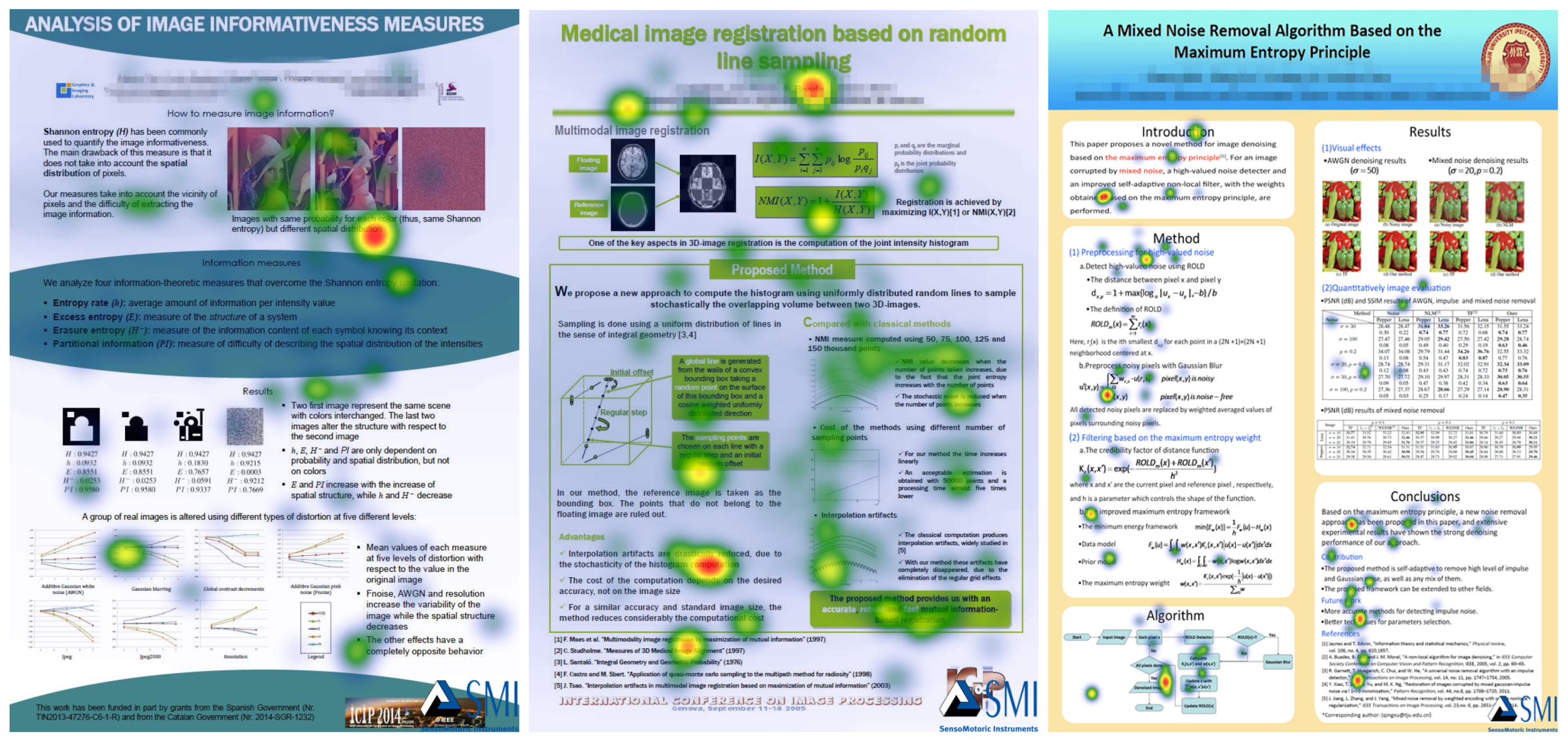
5.1. Materials
5.2. Participants
5.3. Procedure
5.4. Apparatus and Site Setting
5.5. Data Collection
6. Results Analysis
6.1. Traditional Metrics
6.2. Entropy and Mutual Information in Gaze Information Channel
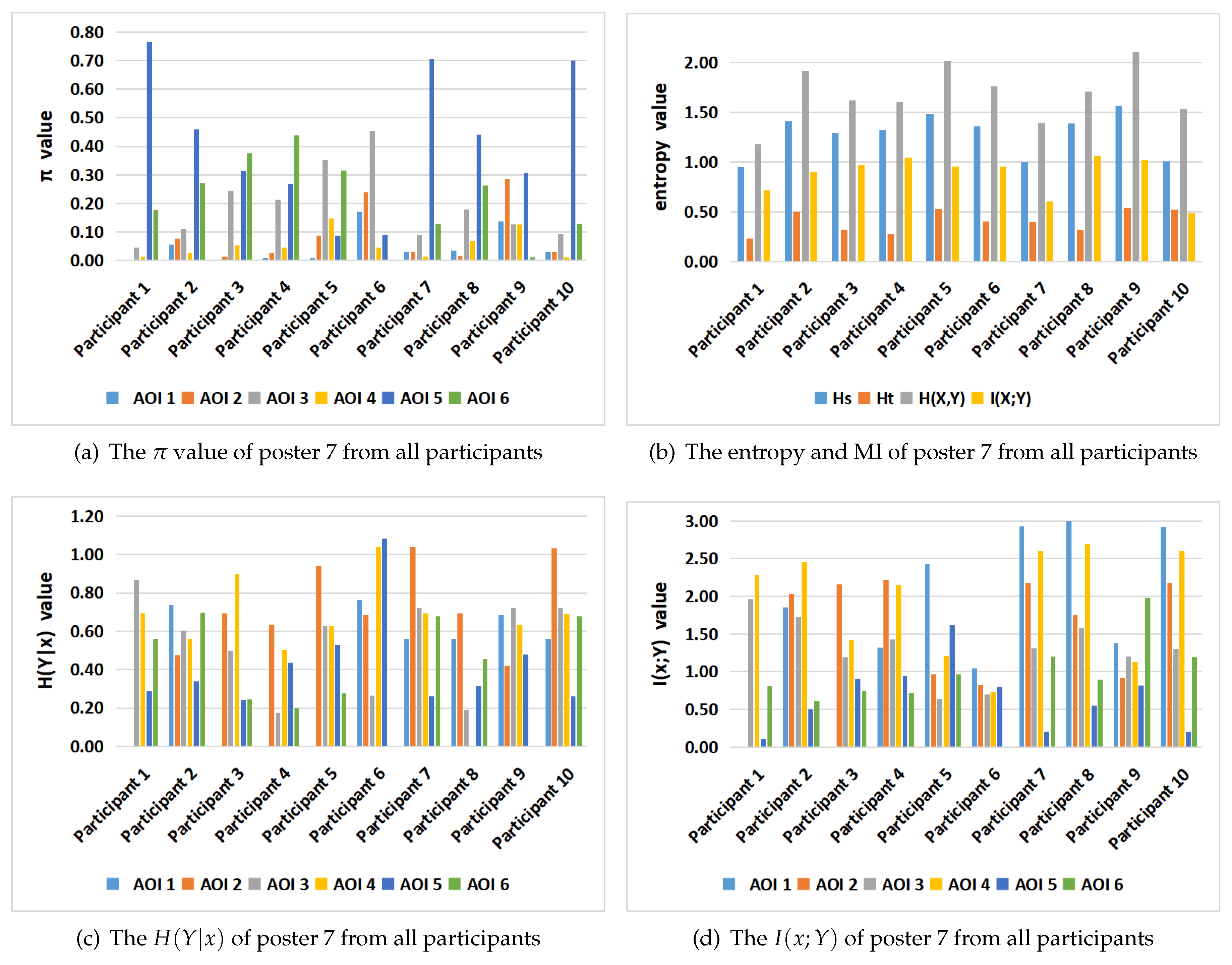
6.2.1. Transition Matrices
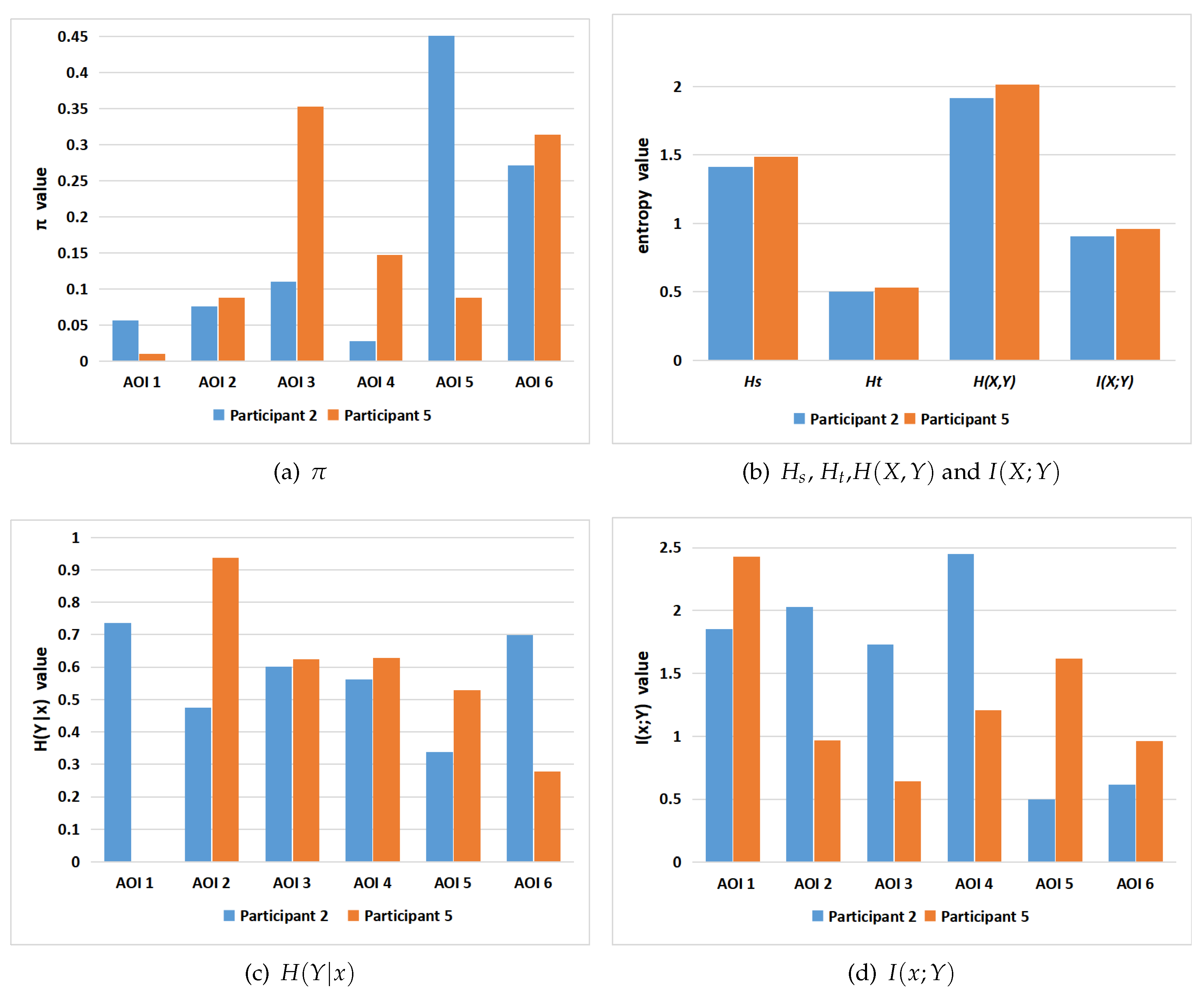
6.2.2. Comparison between Two Participants for Poster 7
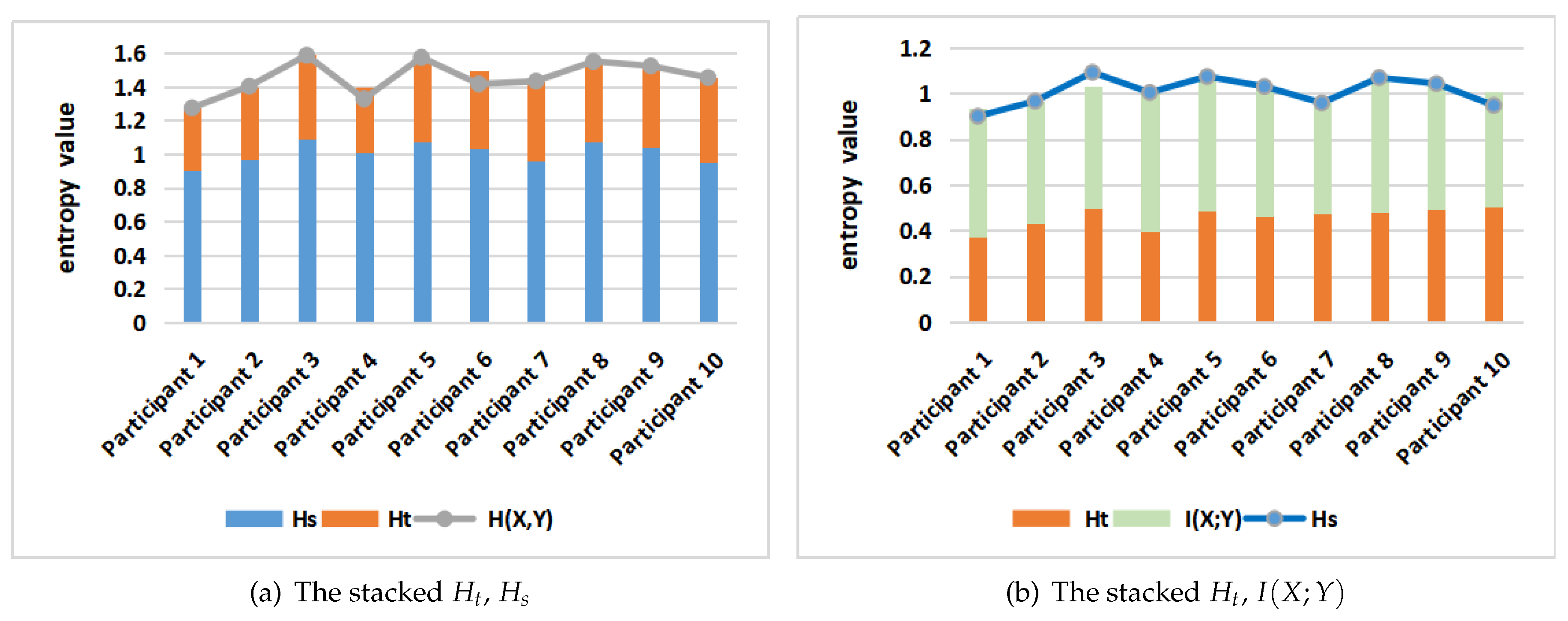
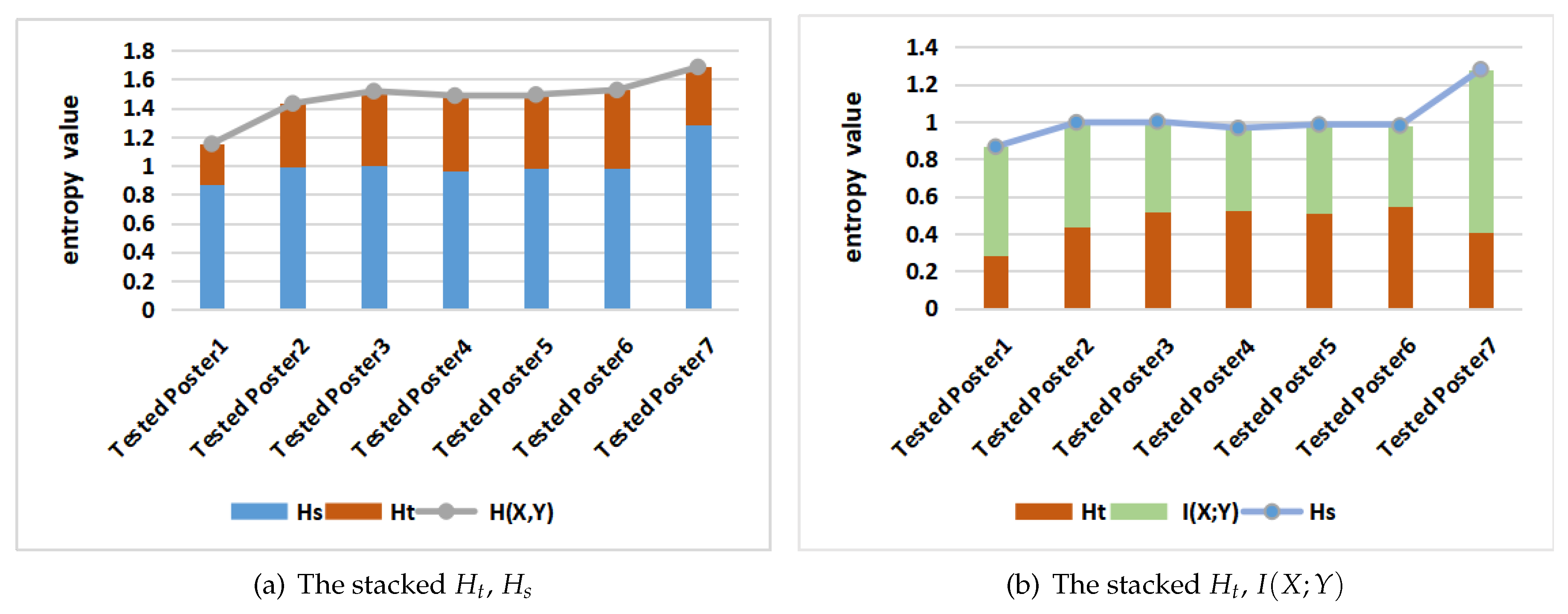
6.2.3. Averaging Results for All Posters and Participants
7. Discussion
8. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| MI | Tested Poster1 | Tested Poster2 | Tested Poster3 | Tested Poster4 | Tested Poster5 | Tested Poster6 | Tested Poster7 | Average Value | Standard Deviation |
|---|---|---|---|---|---|---|---|---|---|
| Participant 1 | 0.422 | 0.489 | 0.584 | 0.474 | 0.548 | 0.474 | 0.716 | 0.530 | 0.091 |
| Participant 2 | 0.469 | 0.608 | 0.377 | 0.545 | 0.411 | 0.398 | 0.908 | 0.531 | 0.172 |
| Participant 3 | 0.782 | 0.557 | 0.533 | 0.394 | 0.512 | 0.428 | 0.969 | 0.596 | 0.191 |
| Participant 4 | 0.664 | 0.641 | 0.582 | 0.411 | 0.351 | 0.587 | 1.043 | 0.611 | 0.207 |
| Participant 5 | 0.655 | 0.542 | 0.422 | 0.415 | 0.671 | 0.449 | 0.958 | 0.587 | 0.180 |
| Participant 6 | 0.497 | 0.786 | 0.301 | 0.429 | 0.544 | 0.481 | 0.956 | 0.571 | 0.208 |
| Participant 7 | 0.575 | 0.508 | 0.512 | 0.439 | 0.464 | 0.294 | 0.609 | 0.486 | 0.095 |
| Participant 8 | 0.638 | 0.544 | 0.611 | 0.412 | 0.452 | 0.406 | 1.062 | 0.589 | 0.211 |
| Participant 9 | 0.512 | 0.498 | 0.470 | 0.427 | 0.497 | 0.397 | 1.023 | 0.546 | 0.198 |
| Participant 10 | 0.581 | 0.415 | 0.437 | 0.514 | 0.288 | 0.370 | 0.484 | 0.441 | 0.089 |
| Average Value | 0.580 | 0.559 | 0.483 | 0.446 | 0.474 | 0.428 | 0.873 | – | – |
| Standard Deviation | 0.103 | 0.097 | 0.095 | 0.047 | 0.103 | 0.074 | 0.189 | – | – |
| Tested Poster1 | Tested Poster2 | Tested Poster3 | Tested Poster4 | Tested Poster5 | Tested Poster6 | Tested Poster7 | Average Value | Standard Deviation | |
|---|---|---|---|---|---|---|---|---|---|
| Participant 1 | 0.711 | 0.833 | 0.939 | 0.930 | 1.021 | 0.924 | 0.948 | 0.901 | 0.093 |
| Participant 2 | 0.889 | 0.942 | 0.744 | 1.15 | 0.755 | 0.88 | 1.412 | 0.967 | 0.221 |
| Participant 3 | 1.008 | 1.051 | 1.077 | 1.087 | 1.022 | 1.115 | 1.293 | 1.093 | 0.088 |
| Participant 4 | 0.904 | 0.936 | 1.061 | 0.903 | 0.930 | 0.980 | 1.323 | 1.005 | 0.139 |
| Participant 5 | 0.851 | 1.025 | 1.050 | 0.970 | 1.229 | 0.915 | 1.487 | 1.075 | 0.201 |
| Participant 6 | 0.919 | 0.918 | 0.941 | 0.930 | 1.023 | 1.128 | 1.360 | 1.031 | 0.152 |
| Participant 7 | 0.836 | 0.998 | 1.030 | 0.918 | 0.929 | 0.999 | 1.004 | 0.959 | 0.063 |
| Participant 8 | 0.914 | 1.066 | 1.011 | 0.808 | 1.184 | 1.120 | 1.386 | 1.070 | 0.174 |
| Participant 9 | 0.798 | 1.092 | 1.055 | 0.996 | 1.015 | 0.780 | 1.569 | 1.044 | 0.242 |
| Participant 10 | 0.822 | 1.093 | 1.094 | 0.959 | 0.727 | 0.934 | 1.009 | 0.948 | 0.126 |
| Average Value | 0.865 | 0.995 | 1.000 | 0.965 | 0.984 | 0.978 | 1.279 | – | – |
| Standard Deviation | 0.077 | 0.082 | 0.099 | 0.091 | 0.152 | 0.109 | 0.206 | – | – |
| Tested Poster1 | Tested Poster2 | Tested Poster3 | Tested Poster4 | Tested Poster5 | Tested Poster6 | Tested Poster7 | Average Value | Standard Deviation | |
|---|---|---|---|---|---|---|---|---|---|
| Participant 1 | 0.289 | 0.344 | 0.355 | 0.456 | 0.473 | 0.467 | 0.232 | 0.374 | 0.088 |
| Participant 2 | 0.420 | 0.333 | 0.367 | 0.616 | 0.344 | 0.466 | 0.504 | 0.436 | 0.094 |
| Participant 3 | 0.226 | 0.494 | 0.543 | 0.693 | 0.509 | 0.687 | 0.324 | 0.497 | 0.160 |
| Participant 4 | 0.240 | 0.295 | 0.478 | 0.492 | 0.580 | 0.393 | 0.280 | 0.394 | 0.118 |
| Participant 5 | 0.196 | 0.483 | 0.627 | 0.555 | 0.558 | 0.453 | 0.529 | 0.486 | 0.129 |
| Participant 6 | 0.422 | 0.132 | 0.639 | 0.505 | 0.479 | 0.647 | 0.404 | 0.461 | 0.161 |
| Participant 7 | 0.261 | 0.491 | 0.518 | 0.480 | 0.465 | 0.704 | 0.396 | 0.474 | 0.123 |
| Participant 8 | 0.276 | 0.523 | 0.398 | 0.396 | 0.732 | 0.714 | 0.324 | 0.480 | 0.169 |
| Participant 9 | 0.286 | 0.592 | 0.582 | 0.569 | 0.518 | 0.383 | 0.537 | 0.495 | 0.108 |
| Participant 10 | 0.238 | 0.678 | 0.658 | 0.445 | 0.439 | 0.557 | 0.525 | 0.506 | 0.139 |
| Average Value | 0.285 | 0.437 | 0.517 | 0.521 | 0.510 | 0.547 | 0.406 | – | – |
| Standard Deviation | 0.073 | 0.152 | 0.108 | 0.084 | 0.097 | 0.124 | 0.108 | – | – |
| H(X,Y) | Tested Poster1 | Tested Poster2 | Tested Poster3 | Tested Poster4 | Tested Poster5 | Tested Poster6 | Tested Poster7 | Average Value | Standard Deviation |
|---|---|---|---|---|---|---|---|---|---|
| Participant 1 | 1.000 | 1.176 | 1.293 | 1.385 | 1.494 | 1.391 | 1.180 | 1.274 | 0.155 |
| Participant 2 | 1.310 | 1.275 | 1.111 | 1.765 | 1.099 | 1.346 | 1.916 | 1.403 | 0.293 |
| Participant 3 | 1.234 | 1.544 | 1.620 | 1.781 | 1.532 | 1.802 | 1.617 | 1.590 | 0.175 |
| Participant 4 | 1.144 | 1.231 | 1.539 | 1.395 | 1.510 | 1.373 | 1.603 | 1.399 | 0.155 |
| Participant 5 | 1.047 | 1.508 | 1.678 | 1.526 | 1.787 | 1.367 | 2.016 | 1.561 | 0.287 |
| Participant 6 | 1.341 | 1.050 | 1.580 | 1.435 | 1.502 | 1.775 | 1.764 | 1.492 | 0.234 |
| Participant 7 | 1.097 | 1.489 | 1.548 | 1.398 | 1.393 | 1.703 | 1.400 | 1.433 | 0.172 |
| Participant 8 | 1.190 | 1.589 | 1.409 | 1.204 | 1.915 | 1.835 | 1.710 | 1.550 | 0.270 |
| Participant 9 | 1.083 | 1.683 | 1.637 | 1.566 | 1.532 | 1.164 | 2.015 | 1.539 | 0.316 |
| Participant 10 | 1.060 | 1.771 | 1.752 | 1.404 | 1.166 | 1.492 | 1.534 | 1.454 | 0.250 |
| Average Value | 1.151 | 1.432 | 1.517 | 1.486 | 1.493 | 1.525 | 1.685 | – | – |
| Standard Deviation | 0.109 | 0.224 | 0.184 | 0.170 | 0.232 | 0.223 | 0.268 | – | – |
| Normalized MI | Tested Poster1 | Tested Poster2 | Tested Poster3 | Tested Poster4 | Tested Poster5 | Tested Poster6 | Tested Poster7 | Average Value | Standard Deviation |
|---|---|---|---|---|---|---|---|---|---|
| Participant 1 | 0.594 | 0.587 | 0.622 | 0.510 | 0.537 | 0.513 | 0.755 | 0.588 | 0.079 |
| Participant 2 | 0.528 | 0.645 | 0.507 | 0.474 | 0.544 | 0.452 | 0.643 | 0.542 | 0.071 |
| Participant 3 | 0.776 | 0.530 | 0.495 | 0.362 | 0.501 | 0.384 | 0.749 | 0.542 | 0.151 |
| Participant 4 | 0.735 | 0.685 | 0.549 | 0.455 | 0.377 | 0.599 | 0.788 | 0.598 | 0.138 |
| Participant 5 | 0.770 | 0.529 | 0.402 | 0.428 | 0.546 | 0.491 | 0.644 | 0.544 | 0.118 |
| Participant 6 | 0.541 | 0.856 | 0.320 | 0.461 | 0.532 | 0.426 | 0.703 | 0.548 | 0.166 |
| Participant 7 | 0.688 | 0.509 | 0.497 | 0.478 | 0.499 | 0.294 | 0.607 | 0.510 | 0.113 |
| Participant 8 | 0.698 | 0.510 | 0.604 | 0.510 | 0.382 | 0.363 | 0.766 | 0.548 | 0.141 |
| Participant 9 | 0.642 | 0.456 | 0.445 | 0.429 | 0.490 | 0.509 | 0.652 | 0.517 | 0.086 |
| Participant 10 | 0.707 | 0.380 | 0.399 | 0.536 | 0.396 | 0.396 | 0.480 | 0.471 | 0.110 |
| Average Value | 0.668 | 0.569 | 0.484 | 0.464 | 0.480 | 0.443 | 0.679 | – | – |
| Standard Deviation | 0.084 | 0.127 | 0.090 | 0.048 | 0.065 | 0.084 | 0.089 | – | – |
| Normalized MI | Tested Poster1 | Tested Poster2 | Tested Poster3 | Tested Poster4 | Tested Poster5 | Tested Poster6 | Tested Poster7 | Average Value | Standard Deviation |
|---|---|---|---|---|---|---|---|---|---|
| Participant 1 | 0.422 | 0.416 | 0.452 | 0.342 | 0.367 | 0.341 | 0.607 | 0.421 | 0.092 |
| Participant 2 | 0.358 | 0.477 | 0.339 | 0.309 | 0.374 | 0.296 | 0.474 | 0.375 | 0.073 |
| Participant 3 | 0.634 | 0.361 | 0.329 | 0.221 | 0.334 | 0.238 | 0.599 | 0.388 | 0.165 |
| Participant 4 | 0.580 | 0.521 | 0.378 | 0.295 | 0.232 | 0.428 | 0.651 | 0.441 | 0.152 |
| Participant 5 | 0.626 | 0.359 | 0.251 | 0.272 | 0.375 | 0.328 | 0.475 | 0.384 | 0.130 |
| Participant 6 | 0.371 | 0.749 | 0.191 | 0.299 | 0.362 | 0.271 | 0.542 | 0.398 | 0.189 |
| Participant 7 | 0.524 | 0.341 | 0.331 | 0.314 | 0.333 | 0.173 | 0.435 | 0.350 | 0.109 |
| Participant 8 | 0.536 | 0.342 | 0.434 | 0.342 | 0.236 | 0.221 | 0.621 | 0.390 | 0.149 |
| Participant 9 | 0.473 | 0.296 | 0.287 | 0.273 | 0.324 | 0.341 | 0.508 | 0.357 | 0.094 |
| Participant 10 | 0.548 | 0.234 | 0.249 | 0.366 | 0.247 | 0.248 | 0.316 | 0.315 | 0.113 |
| Average Value | 0.507 | 0.410 | 0.324 | 0.303 | 0.318 | 0.289 | 0.523 | – | – |
| Standard Deviation | 0.099 | 0.145 | 0.083 | 0.042 | 0.058 | 0.074 | 0.103 | – | – |
References
- Was, C.; Sansosti, F.; Morris, B. Eye-Tracking Technology Applications in Educational Research; IGI Global: Hershey, PA, USA, 2016. [Google Scholar]
- Prieto, L.P.; Sharma, K.; Wen, Y.; Dillenbourg, P. The Burden of Facilitating Collaboration: Towards Estimation of Teacher Orchestration Load Using Eye-tracking Measures; International Society of the Learning Sciences, Inc. [ISLS]: Albuquerque, NM, USA, 2015. [Google Scholar]
- Ellis, E.M.; Borovsky, A.; Elman, J.L.; Evans, J.L. Novel Word Learning: An Eye-tracking Study. Are 18-month-old Late Talkers Really Different From Their Typical Peers? J. Commun. Disord. 2015, 58, 143–157. [Google Scholar] [CrossRef]
- Fox, S.E.; Faulkner-Jones, B.E. Eye-Tracking in the Study of Visual Expertise: Methodology and Approaches in Medicine. Frontline Learn. Res. 2017, 5, 29–40. [Google Scholar] [CrossRef]
- Jarodzka, H.; Boshuizen, H.P. Unboxing the Black Box of Visual Expertise in Medicine. Frontline Learn. Res. 2017, 5, 167–183. [Google Scholar] [CrossRef][Green Version]
- Fong, A.; Hoffman, D.J.; Zachary Hettinger, A.; Fairbanks, R.J.; Bisantz, A.M. Identifying Visual Search Patterns in Eye Gaze Data; Gaining Insights into Physician Visual Workflow. J. Am. Med. Inform. Assoc. 2016, 23, 1180–1184. [Google Scholar] [CrossRef]
- McLaughlin, L.; Bond, R.; Hughes, C.; McConnell, J.; McFadden, S. Computing Eye Gaze Metrics for the Automatic Assessment of Radiographer Performance During X-ray Image Interpretation. Int. J. Med. Inform. 2017, 105, 11–21. [Google Scholar] [CrossRef]
- Holzman, P.S.; Proctor, L.R.; Hughes, D.W. Eye-tracking Patterns in Schizophrenia. Science 1973, 181, 179–181. [Google Scholar] [CrossRef]
- Pavlidis, G.T. Eye Movements in Dyslexia: Their Diagnostic Significance. J. Learn. Disabil. 1985, 18, 42–50. [Google Scholar] [CrossRef]
- Zhang, L.; Wade, J.; Bian, D.; Fan, J.; Swanson, A.; Weitlauf, A.; Warren, A.; Sarkar, N. Cognitive Load Measurement in A Virtual Reality-based Driving System for Autism Intervention. IEEE Trans. Affect. Comput. 2017, 8, 176–189. [Google Scholar] [CrossRef] [PubMed]
- Vidal, M.; Bulling, A.; Gellersen, H. Pursuits: Spontaneous Eye-based Interaction for Dynamic Interfaces. GetMobile Mob. Comput. Commun. 2015, 18, 8–10. [Google Scholar] [CrossRef]
- Strandvall, T. Eye Tracking in Human-computer Interaction and Usability Research. In IFIP Conference on Human-Computer Interaction; Springer: Berlin/Heidelberg, Germany, 2010; pp. 936–937. [Google Scholar]
- Wang, Q.; Yang, S.; Liu, M.; Cao, Z.; Ma, Q. An Eye-tracking Study of Website Complexity from Cognitive Load Perspective. Decis. Support Syst. 2014, 62, 1–10. [Google Scholar] [CrossRef]
- Schiessl, M.; Duda, S.; Tholke, A.; Fischer, R. Eye tracking and Its Application in Usability and Media Research. MMI-interaktiv J. 2003, 6, 41–50. [Google Scholar]
- Steiner, G.A. The People Look at Commercials: A Study of Audience Behavior. J. Bus. 1966, 39, 272–304. [Google Scholar] [CrossRef]
- Lunn, D.; Harper, S. Providing Assistance to Older Users of Dynamic Web Content. Comput. Hum. Behav. 2011, 27, 2098–2107. [Google Scholar] [CrossRef]
- Van Gog, T.; Scheiter, K. Eye Tracking as A Tool to Study and Enhance Multimedia Learning; Elsevier: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Navarro, O.; Molina, A.I.; Lacruz, M.; Ortega, M. Evaluation of Multimedia Educational Materials Using Eye Tracking. Procedia-Soc. Behav. Sci. 2015, 197, 2236–2243. [Google Scholar] [CrossRef]
- Van Wermeskerken, M.; van Gog, T. Seeing the Instructor’s Face and Gaze in Demonstration Video Examples Affects Attention Allocation but not Learning. Comput. Educ. 2017, 113, 98–107. [Google Scholar] [CrossRef]
- Stuijfzand, B.G.; van der Schaaf, M.F.; Kirschner, F.C.; Ravesloot, C.J.; van der Gijp, A.; Vincken, K.L. Medical Students’ Cognitive Load in Volumetric Image Interpretation: Insights from Human-computer Interaction and Eye Movements. Comput. Hum. Behav. 2016, 62, 394–403. [Google Scholar] [CrossRef]
- Ju, U.; Kang, J.; Wallraven, C. Personality Differences Predict Decision-making in An Accident Situation in Virtual Driving. In Proceedings of the 2016 IEEE Virtual Reality, Greenville, SC, USA, 19–23 March 2016; pp. 77–82. [Google Scholar]
- Chen, X.; Starke, S.D.; Baber, C.; Howes, A. A Cognitive Model of How People Make Decisions through Interaction with Visual Displays. In Proceedings of the 2017 CHI Conference on Human Factors in Computing Systems, Denver, CO, USA, 6–11 May 2017; pp. 1205–1216. [Google Scholar]
- Duchowski, A.T.; Driver, J.; Jolaoso, S.; Tan, W.; Ramey, B.N.; Robbins, A. Scanpath Comparison Revisited. In Proceedings of the 2010 Symposium on Eye-Tracking Research & Applications, Austin, TX, USA, 22–24 March 2010; pp. 219–226. [Google Scholar]
- De Bruin, J.A.; Malan, K.M.; Eloff, J.H.P. Saccade Deviation Indicators for Automated Eye Tracking Analysis. In Proceedings of the 2013 Conference on Eye Tracking South Africa, Cape Town, South Africa, 29–31 August 2013; pp. 47–54. [Google Scholar]
- Peysakhovich, V.; Hurter, C. Scanpath visualization and comparison using visual aggregation techniques. J. Eye Mov. Res. 2018, 10, 1–14. [Google Scholar]
- Mishra, A.; Kanojia, D.; Nagar, S.; Dey, K.; Bhattacharyya, P. Scanpath Complexity: Modeling Reading Effort Using Gaze Information. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017. [Google Scholar]
- Li, A.; Zhang, Y.; Chen, Z. Scanpath Mining of Eye Movement Trajectories for Visual Attention Analysis. In Proceedings of the 2017 IEEE International Conference on Multimedia and Expo (ICME), Hong Kong, China, 10–14 July 2017; pp. 535–540. [Google Scholar]
- Grindinger, T.; Duchowski, A.T.; Sawyer, M. Group-wise Similarity and Classification of Aggregate Scanpaths. In Proceedings of the 2010 Symposium on Eye-Tracking Research & Applications, Austin, TX, USA, 22–24 March 2010; pp. 101–104. [Google Scholar]
- Isokoski, P.; Kangas, J.; Majaranta, P. Useful Approaches to Exploratory Analysis of Gaze Data: Enhanced Heatmaps, cluster Maps, and Transition Maps. In Proceedings of the 2018 ACM Symposium on Eye Tracking Research & Applications, Warsaw, Poland, 14–17 June 2018; p. 68. [Google Scholar]
- Gu, Z.; Jin, C.; Dong, Z.; Chang, D. Predicting Webpage Aesthetics with Heatmap Entropy. arXiv 2018, arXiv:1803.01537. [Google Scholar]
- Shiferaw, B.; Downey, L.; Crewther, D. A review of gaze entropy as a measure of visual scanning efficiency. Neurosci. Biobehav. Rev. 2019, 96, 353–366. [Google Scholar] [CrossRef]
- Ma, L.J.; Sbert, M.; Xu, Q.; Feixas, M. Gaze Information Channel. In Pacific Rim Conference on Multimedia; Springer: Cham, Switzerland, September 2018; pp. 575–585. [Google Scholar]
- Qiang, Y.; Fu, Y.; Guo, Y.; Zhou, Z.H.; Sigal, L. Learning to Generate Posters of Scientific Papers. In Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016. [Google Scholar]
- Bavdekar, S.B.; Vyas, S.; Anand, V. Creating Posters for Effective Scientific Communication. J. Assoc. Phys. India 2017, 65, 82–88. [Google Scholar]
- Berg, J.; Hicks, R. Successful Design and Delivery of A Professional Poster. J. Am. Assoc. Nurse Pract. 2017, 29, 461–469. [Google Scholar] [CrossRef] [PubMed]
- Rezaeian, M.; Rezaeian, M.; Rezaeian, M. How to Prepare A Poster for A Scientific Presentation. Middle East J. Fam. Med. 2017, 7, 133. [Google Scholar] [CrossRef]
- Ponsoda, V.; Scott, D.; Findlay, J.M. A Probability Vector and Transition Matrix Analysis of Eye Movements During Visual Search. Acta Psychol. 1995, 88, 167–185. [Google Scholar] [CrossRef]
- Ellis, S.R.; Stark, L. Statistical Dependency in Visual Scanning. Hum. Factors 1986, 28, 421–438. [Google Scholar] [CrossRef]
- Liechty, J.; Pieters, R.; Wedel, M. Global and Local Covert Visual Attention: Evidence from A Bayesian Hidden Markov Model. Psychometrika 2003, 68, 519–541. [Google Scholar] [CrossRef]
- Helmert, J.R.; Joos, M.; Pannasch, S.; Velichkovsky, B.M. Two Visual Systems and Their Eye Movements: Evidence from Static and Dynamic Scene Perception. In Proceedings of the 2005 Annual Meeting of the Cognitive Science Society, Stresa, Italy, 21–23 July 2005; p. 27. [Google Scholar]
- Hwang, A.D.; Wang, H.C.; Pomplun, M. Semantic Guidance of Eye Movements in Real-world Scenes. Vision Res. 2011, 51, 1192–1205. [Google Scholar] [CrossRef] [PubMed]
- Bonev, B.; Chuang, L.L.; Escolano, F. How do Image Complexity, Task Demands and Looking Biases Influence Human Gaze Behavior? Pattern Recognit. Lett. 2013, 34, 723–730. [Google Scholar] [CrossRef]
- Besag, J.; Mondal, D. Exact Goodness-of-Fit Tests for Markov Chains. Biometrics 2013, 69, 488–496. [Google Scholar] [CrossRef] [PubMed]
- Krejtz, K.; Duchowski, A.; Szmidt, T.; Krejtz, I.; González Perilli, F.; Pires, A.; Vilaro, A.; Villalobos, N. Gaze Transition Entropy. ACM Trans. Appl. Percept. 2015, 13, 4. [Google Scholar] [CrossRef]
- Krejtz, K.; Szmidt, T.; Duchowski, A.; Krejtz, I.; Perilli, F.G.; Pires, A.; Vilaro, A.; Villalobos, N. Entropy-based Statistical Analysis of Eye Movement Transitions. In Proceedings of the 2014 Symposium on Eye Tracking Research and Applications, Safety Harbor, FL, USA, 26–28 March 2014; pp. 159–166. [Google Scholar]
- Raptis, G.E.; Fidas, C.A.; Avouris, N.M. On Implicit Elicitation of Cognitive Strategies using Gaze Transition Entropies in Pattern Recognition Tasks. In Proceedings of the 2017 CHI Conference Extended Abstracts on Human Factors in Computing Systems, Denver, CO, USA, 6–11 May 2017; pp. 1993–2000. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley and Sons: Hoboken, NJ, USA, 1991; pp. 33–36. [Google Scholar]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Chen, M.; Feixas, M.; Viola, I.; Bardera, A.; Shen, H.W.; Sbert, M. Information Theory Tools for Visualization; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Ruiz, F.E.; Perez, P.S.; Bonev, B.I. Information Theory in Computer Vision and Pattern Recognition; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Yeung, R.W. Information Theory and Network Coding; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Gagniuc, P.A. Markov Chains: From Theory to Implementation and Experimentation; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Feixas, M.; del Acebo, E.; Bekaert, P.; Sbert, M. An Information Theory Framework for the Analysis of Scene Complexity. Comput. Gr. Forum 1999, 18, 95–106. [Google Scholar] [CrossRef]
- Hu, B.-G. Information Theoretic Learning in Pattern Classification. In Proceedings of the ICONIP Tutorial, Guangzhou, China, 14–18 November 2017. [Google Scholar]
- Tishby, N.; Pereira, F.C.; Bialek, W. The Information Bottleneck Method. In Proceedings of the 37th Annual Allerton Conference on Communication, Control and Computing, Monticello, IL, USA, 22–24 September 1999; pp. 368–377. [Google Scholar]



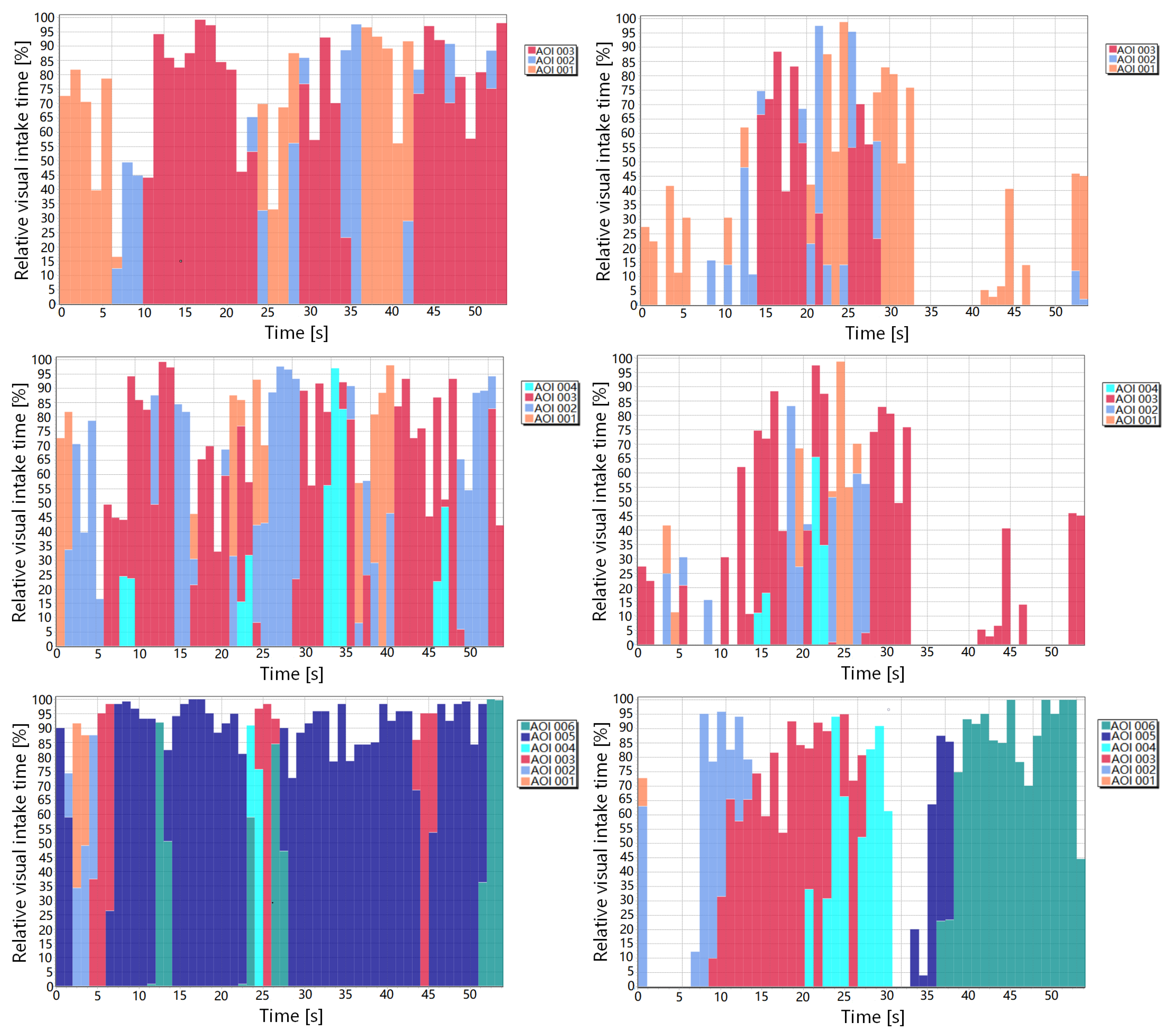
| Tested Posters | Tested Poster 1 | Tested Poster 2 | Tested Poster 3 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AOI1 | AOI2 | AOI3 | AOI1 | AOI2 | AOI3 | AOI1 | AOI2 | AOI3 | ||||
| AOI1 | 419 | 25 | 0 | AOI1 | 337 | 42 | 4 | AOI1 | 241 | 54 | 1 | |
| Transition matrix | AOI2 | 24 | 518 | 19 | AOI2 | 41 | 138 | 42 | AOI2 | 45 | 537 | 50 |
| AOI3 | 2 | 19 | 64 | AOI3 | 6 | 41 | 506 | AOI3 | 10 | 45 | 269 | |
| Tested Posters | Tested Poster 4 | Tested Poster 5 | Tested Poster 6 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AOI1 | AOI2 | AOI3 | AOI4 | AOI1 | AOI2 | AOI3 | AOI4 | AOI1 | AOI2 | AOI3 | AOI4 | ||||
| AOI1 | 50 | 32 | 2 | 1 | AOI1 | 71 | 23 | 1 | 0 | AOI1 | 56 | 32 | 1 | 0 | |
| AOI2 | 31 | 253 | 52 | 0 | AOI2 | 19 | 149 | 45 | 0 | AOI2 | 25 | 159 | 49 | 0 | |
| AOI3 | 4 | 50 | 636 | 21 | AOI3 | 5 | 43 | 690 | 29 | AOI3 | 8 | 38 | 700 | 38 | |
| AOI4 | 0 | 1 | 21 | 38 | AOI4 | 1 | 0 | 31 | 63 | AOI4 | 1 | 4 | 36 | 52 | |
| Observers | Participant 2 | Participant 5 | ||
|---|---|---|---|---|
| AOI1 AOI2 AOI3 AOI4 AOI5 AOI6 | AOI1 AOI2 AOI3 AOI4 AOI5 AOI6 | |||
| AOI1 | 0.750 0.125 0.000 0.000 0.125 0.000 | AOI1 | 0.000 1.000 0.000 0.000 0.000 0.000 | |
| AOI2 | 0.000 0.818 0.182 0.000 0.000 0.000 | AOI2 | 0.111 0.333 0.556 0.000 0.000 0.000 | |
| AOI3 | 0.000 0.125 0.813 0.063 0.000 0.000 | AOI3 | 0.000 0.111 0.806 0.083 0.000 0.000 | |
| AOI4 | 0.000 0.000 0.000 0.750 0.000 0.250 | AOI4 | 0.000 0.000 0.133 0.800 0.067 0.000 | |
| AOI5 | 0.000 0.000 0.000 0.000 0.894 0.106 | AOI5 | 0.000 0.000 0.000 0.000 0.778 0.222 | |
| AOI6 | 0.026 0.000 0.000 0.026 0.180 0.769 | AOI6 | 0.000 0.031 0.000 0.000 0.031 0.934 | |
| Observers | Participant 2 | Participant 5 |
|---|---|---|
| (0.056, 0.076, 0.11, 0.028, 0.458, 0.271) | (0.010, 0.088, 0.353, 0.147, 0.088, 0.314) | |
| 1.412 | 1.487 | |
| 0.504 | 0.529 | |
| (0.736, 0.474, 0.602, 0.562, 0.338, 0.698) | (0.000, 0.937, 0.625, 0.628, 0.529, 0.277) | |
| 1.916 | 2.016 | |
| 0.908 | 0.958 | |
| (1.851, 2.030, 1.729, 2.452, 0.498, 0.613) | (2.428, 0.965, 0.643, 1.207, 1.616, 0.961) |
| Tested Poster | Tested Poster 1 | Tested Poster 2 | Tested Poster 3 | Tested Poster 4 | Tested Poster 5 | Tested Poster 6 | Tested Poster7 |
|---|---|---|---|---|---|---|---|
| Basic Group | 4 | 7 | 6 | 6 | 4 | 4 | 5 |
| Keywords Group | 6 | 3 | 4 | 4 | 6 | 6 | 5 |
| MI | 0.580 | 0.559 | 0.483 | 0.446 | 0.474 | 0.428 | 0.873 |
| MI normalized by | 0.668 | 0.569 | 0.484 | 0.464 | 0.480 | 0.443 | 0.679 |
| MI normalized by | 0.507 | 0.410 | 0.324 | 0.303 | 0.318 | 0.289 | 0.523 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, Q.; Sbert, M.; Ma, L. Gaze Information Channel in Cognitive Comprehension of Poster Reading. Entropy 2019, 21, 444. https://doi.org/10.3390/e21050444
Hao Q, Sbert M, Ma L. Gaze Information Channel in Cognitive Comprehension of Poster Reading. Entropy. 2019; 21(5):444. https://doi.org/10.3390/e21050444
Chicago/Turabian StyleHao, Qiaohong, Mateu Sbert, and Lijing Ma. 2019. "Gaze Information Channel in Cognitive Comprehension of Poster Reading" Entropy 21, no. 5: 444. https://doi.org/10.3390/e21050444
APA StyleHao, Q., Sbert, M., & Ma, L. (2019). Gaze Information Channel in Cognitive Comprehension of Poster Reading. Entropy, 21(5), 444. https://doi.org/10.3390/e21050444





