Unstable Limit Cycles and Singular Attractors in a Two-Dimensional Memristor-Based Dynamic System
Abstract
:1. Introduction
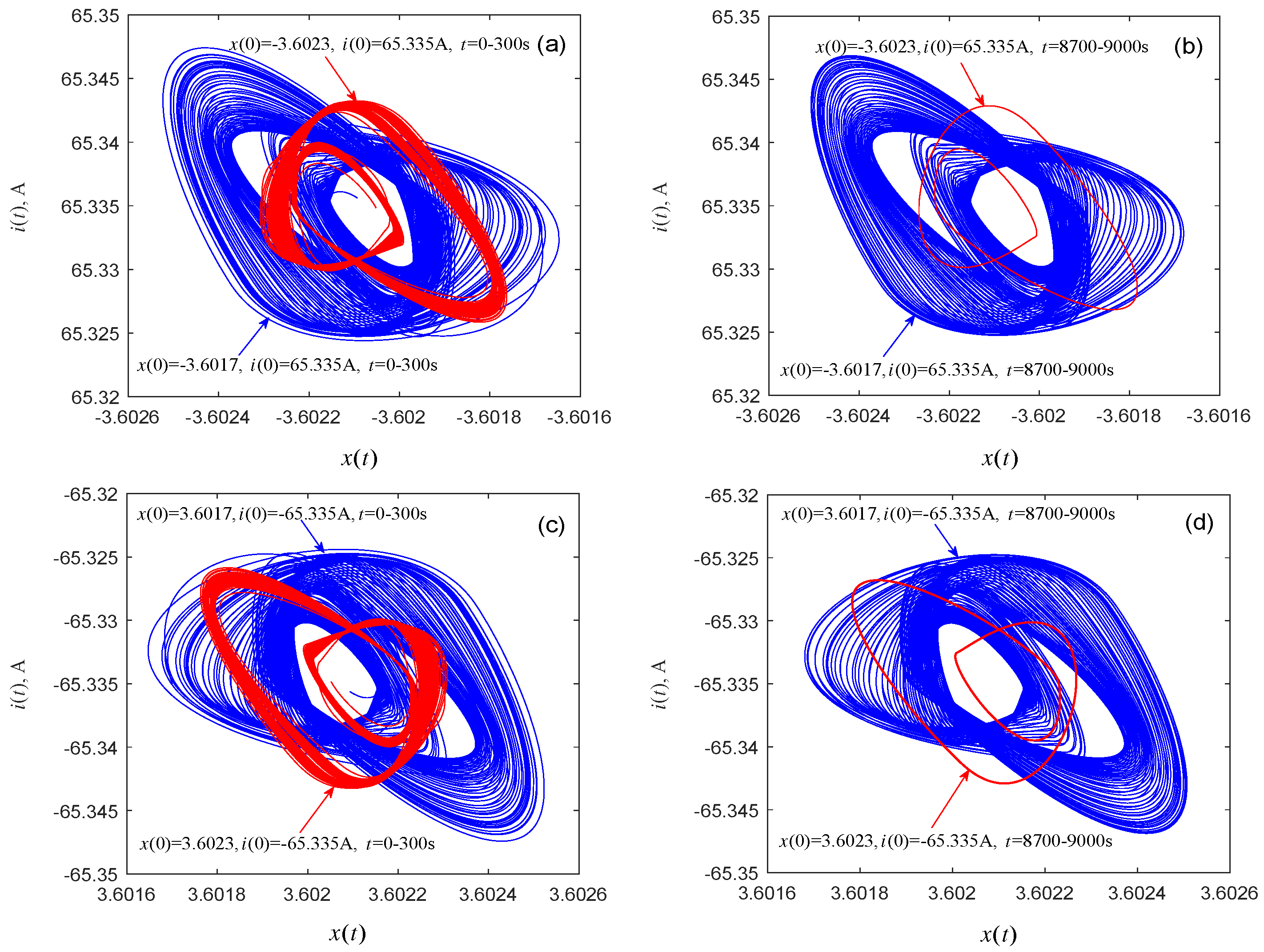
2. Unstable Limit Cycles of the Memristor-Based Dynamic System
| Algorithm 1: An algorithm for finding unstable limit cycles. |
|
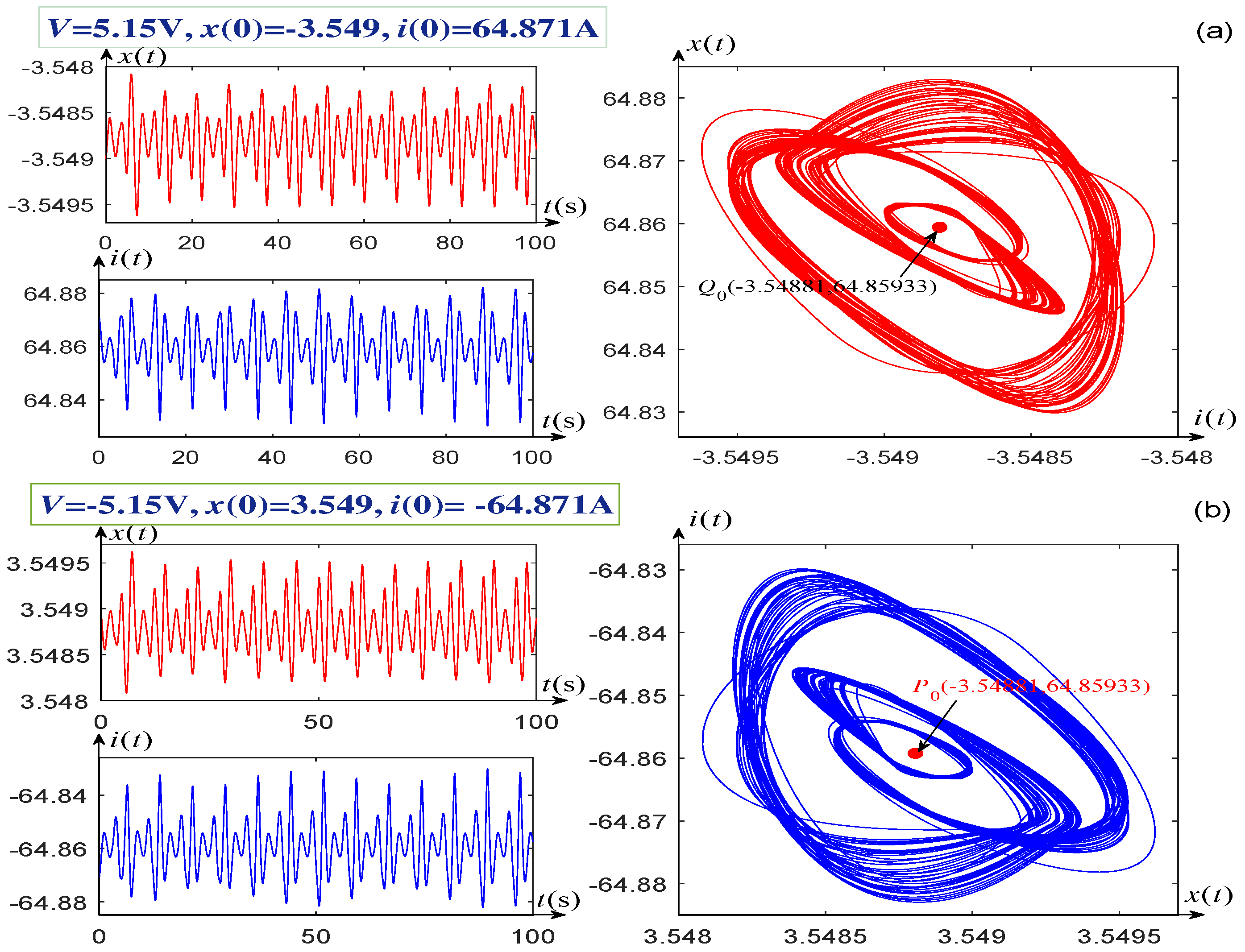
3. Coexisting SingularAttractors of the Memristor-Based Dynamic System
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chua, L.O. Memristors-the missing circuit element. IEEE Trans. Circuit Theory 1971, 18, 507–519. [Google Scholar] [CrossRef]
- Chua, L.O. Everything you wish to know about memristors but are afraid to ask. Radioengineering 2015, 24, 319–368. [Google Scholar] [CrossRef]
- Chua, L.O. If it’s pinched it’s a memristor. Semicond. Sci. Technol. 2014, 29, 104001. [Google Scholar] [CrossRef]
- Strukov, D.B.; Snider, G.S.; Stewart, G.R.; Williams, R.S. The missing memristor found. Nature 2008, 453, 80–83. [Google Scholar] [CrossRef] [PubMed]
- Wen, S.; Zeng, Z.; Huang, T.; Chen, Y. Passivity analysis of memristor-based recurrent neural networks with time-varying delays. J. Frankl. Inst. 2013, 350, 2354–2370. [Google Scholar] [CrossRef]
- Huang, X.; Fan, Y.; Jia, J.; Wang, Z.; Li, Y. Quasi-synchronization of fractional-order memristor-based neural networks with parameter mismatches. IET Control Thory Appl. 2017, 11, 2317–2327. [Google Scholar] [CrossRef]
- Li, L.; Wang, Z.; Lu, J.; Li, Y. Adaptive synchronization of fractional-order complex-valued neural networks with discrete and distributed delays. Entropy 2018, 20, 124. [Google Scholar] [CrossRef]
- Azghadi, M.R.; Linares-Barranco, B.; Abbott, D.; Leong, P.H. A hybrid CMOS-memristor neuromorphic synapse. IEEE Trans. Biomed. Circuits Syst. 2016, 11, 434–445. [Google Scholar] [CrossRef]
- Li, Y.; Huang, X.; Song, Y.; Lin, J. A new fourth-order memristive chaotic system and its generation. Int. J. Bifurc. Chaos 2015, 25, 1550151. [Google Scholar] [CrossRef]
- Xi, H.; Li, Y.; Huang, X. Generation and nonlinear dynamical analyses of fractional-order memristor-based Lorenz systems. Entropy 2014, 16, 6240–6253. [Google Scholar] [CrossRef]
- Huang, X.; Jia, J.; Li, Y.; Wang, Z. Complex nonlinear dynamics in fractional and integer order memristor-based systems. Neurocomputing 2016, 218, 296–306. [Google Scholar] [CrossRef]
- Guo, M.; Xue, Y.; Gao, Z.; Zhang, Y.; Dou, G.; Li, Y. Dynamic analysis of a physical SBT memristor-Based chaotic circuit. Int. J. Bifurc. Chaos 2017, 27, 1730047. [Google Scholar] [CrossRef]
- Li, C.; Thio, W.J.-C.; Iu, H.H.C.; Lu, T. A memristive chaotic oscillator with increasing amplitude and frequency. IEEE Access 2017, 6, 12945–12950. [Google Scholar] [CrossRef]
- Lin, Z.; Wang, H. Efficient Image Encryption Using a Chaos-based PWL Memristor. IETE Tech. Rev. 2010, 27, 318–325. [Google Scholar] [CrossRef]
- Liu, P.; Xi, R.; Ren, P.; Hou, J.; Li, X. Analysis and Implementation of a New Switching Memristor Scroll Hyperchaotic System and Application in Secure Communication. Complexity 2018, 2018, 1–15. [Google Scholar] [CrossRef]
- Chai, X.; Gan, Z.; Yang, K.; Chen, Y.; Liu, X. An image encryption algorithm based on the memristive hyperchaotic system, cellular automata and DNA sequence operations. Signal Process. 2017, 52, 6–19. [Google Scholar] [CrossRef]
- Hamdioui, S.; Taouil, M.; Haron, N. Testing open defects in memristor-based memories. IEEE Trans. Comput. 2014, 64, 247–259. [Google Scholar] [CrossRef]
- Chua, L.O.; Sbitnev, V.; Kim, H. Hodgkin-Huxley axon is made of memristor. Int. J. Bifurc. Chaos 2012, 22, 1230011. [Google Scholar] [CrossRef]
- Chua, L.O.; Sbitnev, V.; Kim, H. Neurons are poised near the edge of chaos. Int. J. Bifurc. Chaos 2012, 22, 1250098. [Google Scholar] [CrossRef]
- Sah, M.P.; Eroglu, A.; Chua, L.O. Memristive model of the barnacle giant muscle fibers. Int. J. Bifurc. Chaos 2016, 26, 1630001. [Google Scholar] [CrossRef]
- Rajamani, V.; Sah, M.P.; Mannan, Z.; Kim, H.; Chua, L. Third-order memristor Morris-Lecar model of barnacle muscle fiber. Int. J. Bifurc. Chaos 2017, 27, 1730015. [Google Scholar] [CrossRef]
- Mannan, Z.I.; Choi, H.; Kim, H. Chua corsage memristor oscillator via Hopf bifurcation. Int. J. Bifurc. Chaos 2016, 25, 1530010. [Google Scholar] [CrossRef]
- Mannan, Z.I.; Choi, H.; Kim, H.; Chua, L.O. Chua Corsage Memristor: Phase portraits, basin of attraction, and coexisting pinched hysteresis loops. Int. J. Bifurc. Chaos 2017, 27, 1730011. [Google Scholar] [CrossRef]
- Mainzer, K.; Chua, L.O. Local Activity Principle: The Cause of Complexity and Symmetry Breaking; World Scientific, Imperial College Press: Singapore, 2013; pp. 9–33. [Google Scholar]
- Chang, H.; Wang, Z.; Li, Y.; Chen, G. Dynamic analysis of a bistable bi-local active memristor and its associated oscillator system. Int. J. Bifurc. Chaos 2018, 28, 1850105. [Google Scholar] [CrossRef]
- Cang, S.; Qi, G.; Chen, Z. A four-wing hyper-chaotic attractor and transient chaos generated from a new 4-D quadratic autonomous system. Nonlinear Dyn. 2010, 59, 515–527. [Google Scholar] [CrossRef]
- Yuan, F.; Li, Y.; Wang, G.; Chen, G. Complex dynamics in a memcapacitor-based circuit. Entropy 2019, 21, 188. [Google Scholar] [CrossRef]
- Yuan, F.; Deng, Y.; Li, Y.; Wang, G. The amplitude, frequency and parameter space boosting in a memristor-meminductor-based circuit. Nonlinear Dyn. 2019. [Google Scholar] [CrossRef]
- Li, C.; Chen, G. Coexisting chaotic attractors in a single neuron model with adapting feedback synapse. Chaos Soliton Fract. 2005, 23, 1599–1604. [Google Scholar] [CrossRef]
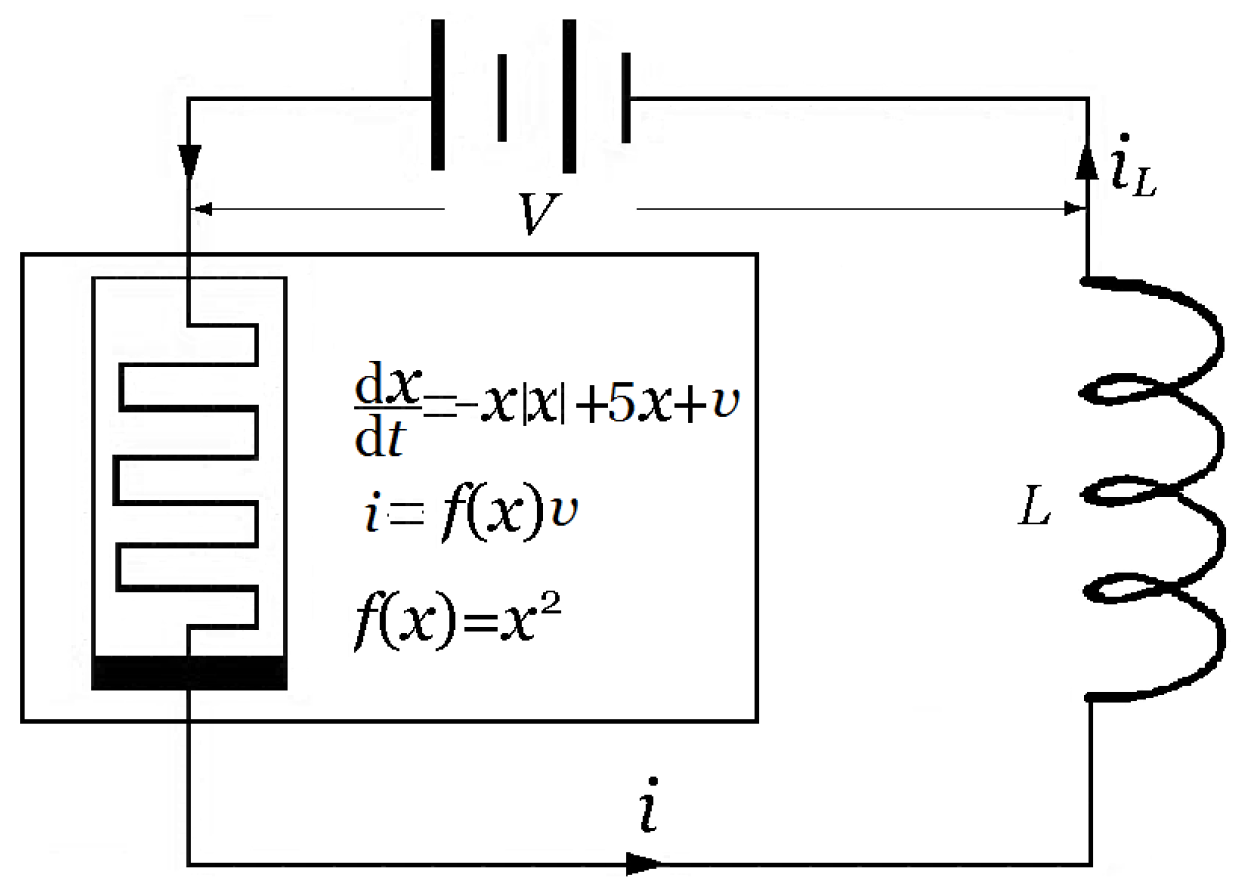
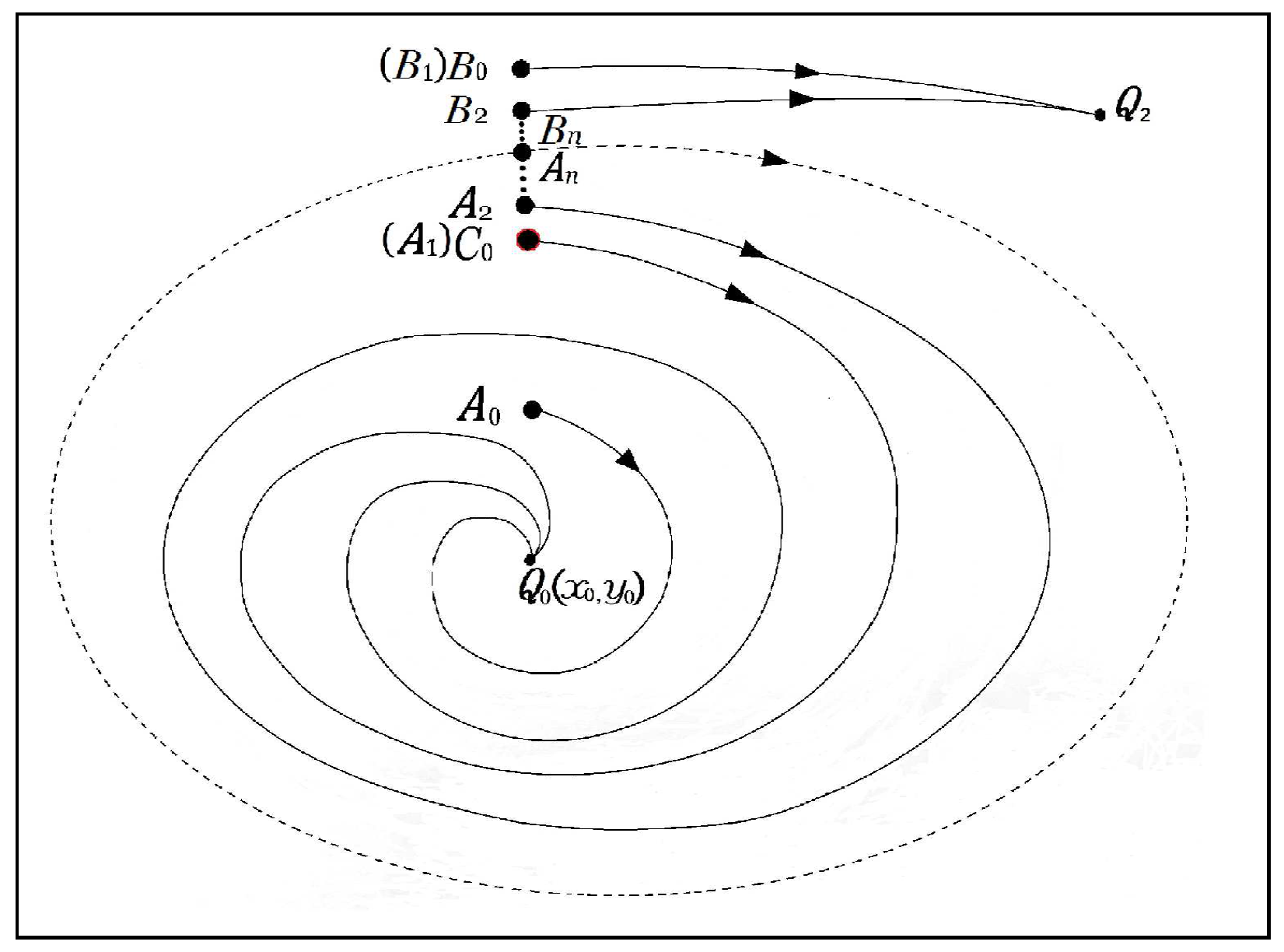
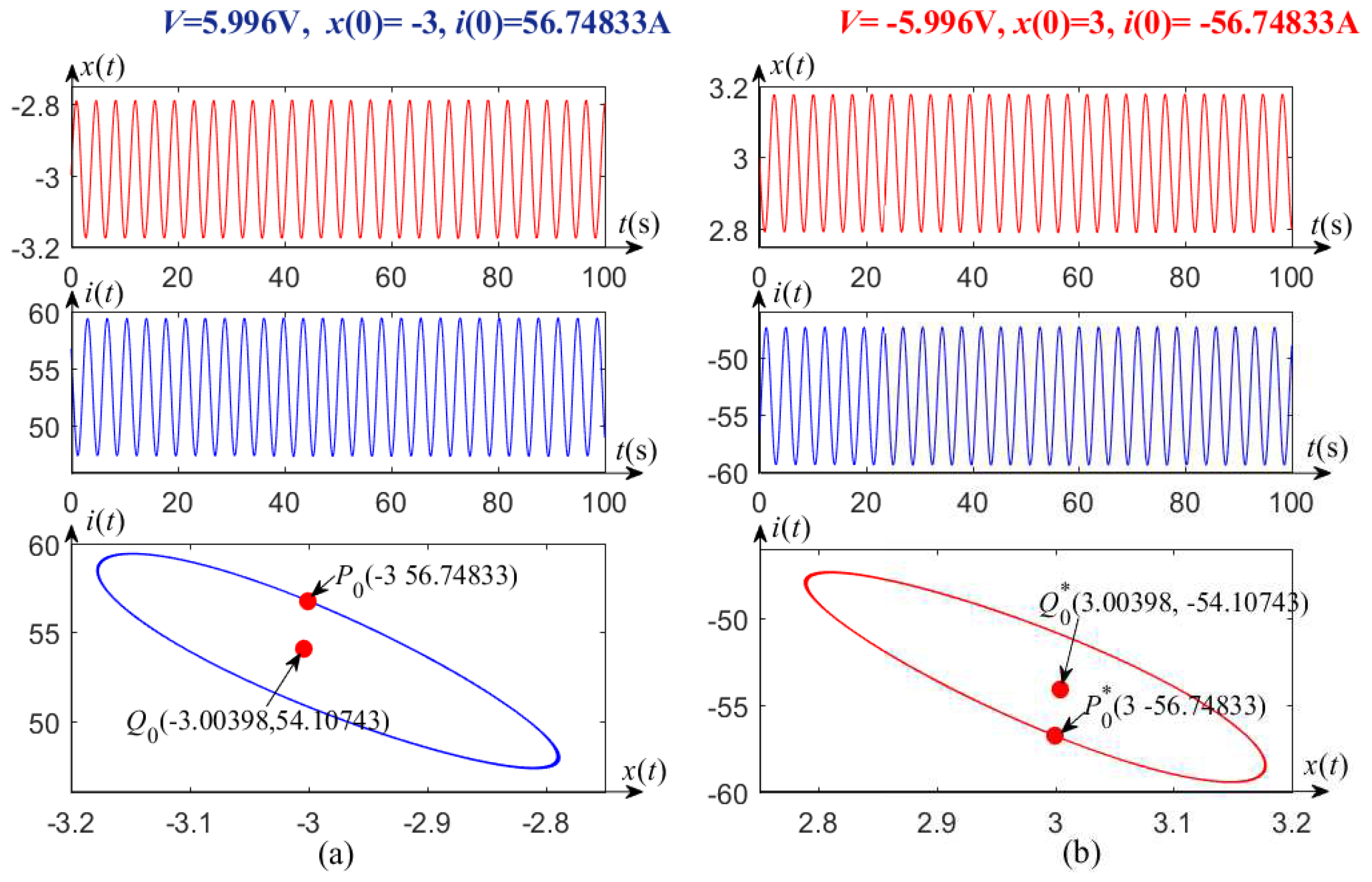


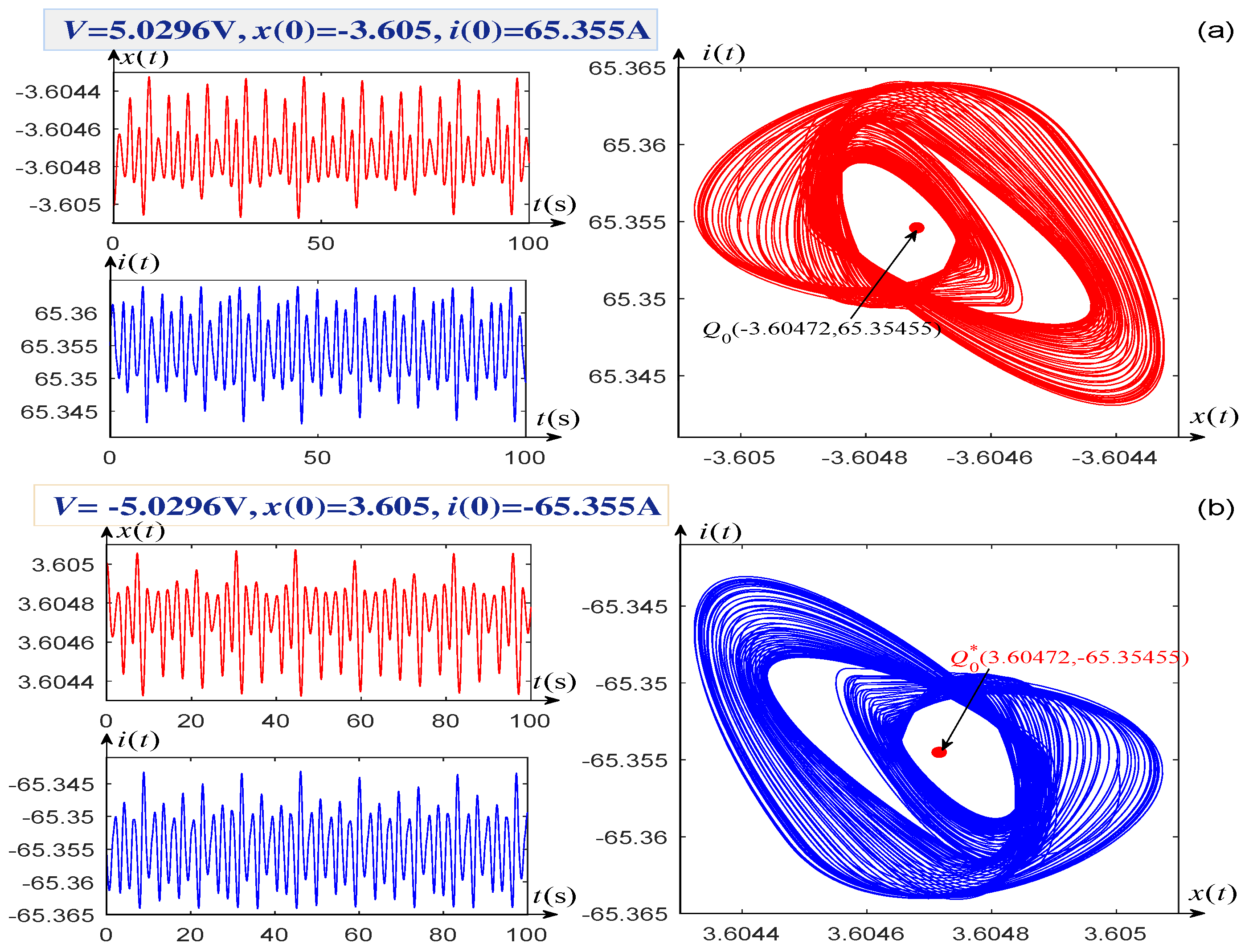

| Local activity domain 1: | V V, A A |
| Local activity domain 2: | V V, A A |
| Hopf bifurcation region 1: | V V, A A |
| Hopf bifurcation region 2: | V V, 54 A A |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, H.; Song, Q.; Li, Y.; Wang, Z.; Chen, G. Unstable Limit Cycles and Singular Attractors in a Two-Dimensional Memristor-Based Dynamic System. Entropy 2019, 21, 415. https://doi.org/10.3390/e21040415
Chang H, Song Q, Li Y, Wang Z, Chen G. Unstable Limit Cycles and Singular Attractors in a Two-Dimensional Memristor-Based Dynamic System. Entropy. 2019; 21(4):415. https://doi.org/10.3390/e21040415
Chicago/Turabian StyleChang, Hui, Qinghai Song, Yuxia Li, Zhen Wang, and Guanrong Chen. 2019. "Unstable Limit Cycles and Singular Attractors in a Two-Dimensional Memristor-Based Dynamic System" Entropy 21, no. 4: 415. https://doi.org/10.3390/e21040415
APA StyleChang, H., Song, Q., Li, Y., Wang, Z., & Chen, G. (2019). Unstable Limit Cycles and Singular Attractors in a Two-Dimensional Memristor-Based Dynamic System. Entropy, 21(4), 415. https://doi.org/10.3390/e21040415






