Model Development and Exergy Analysis of a Microreactor for the Steam Methane Reforming Process in a CFD Environment
Abstract
1. Introduction
2. Process and Exergy
2.1. Process Description
2.2. Exergy Concept
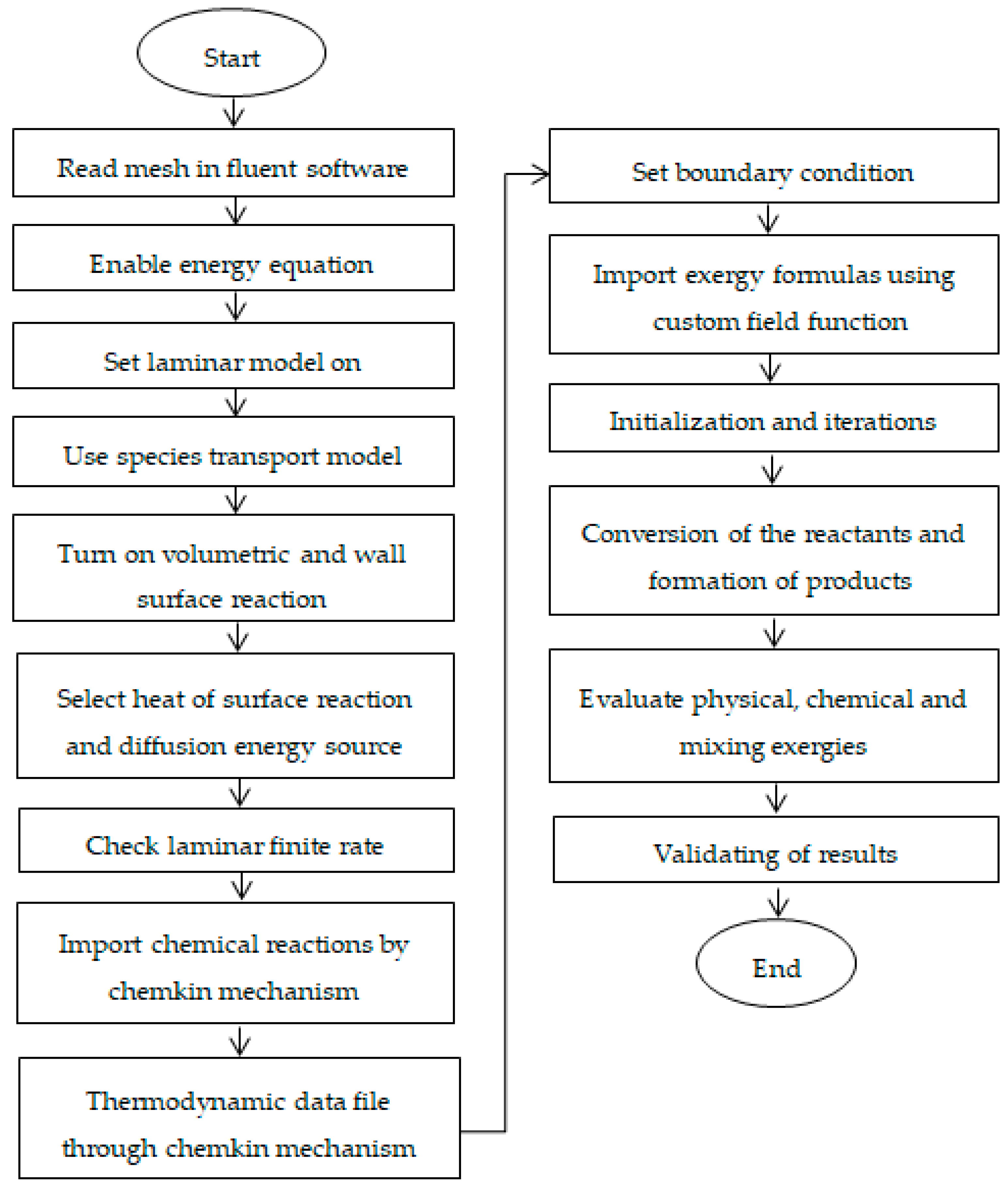
3. Model Development
- The equilibrium state is reached and the maximum yield is achieved.
- There is negligible heat loss from the reactor wall to the surroundings.
- The catalytic wall is isothermal in condition.
- The flow regime is laminar in the reaction channel, and steady-state operation is reached.
- The gas mixture is treated as an incompressible ideal gas. The density of the mixture is constant as calculated from ideal gas law.
- The gas-phase non-catalytic reaction can be neglected so that only the surface reactions are modeled.
3.1. Geometry and Meshing
3.2. Boundary and Cell Zone Conditions
3.3. CFD Model Describing the Flow Field
3.4. Kinetic Models Describing the Surface Catalytic Reactions
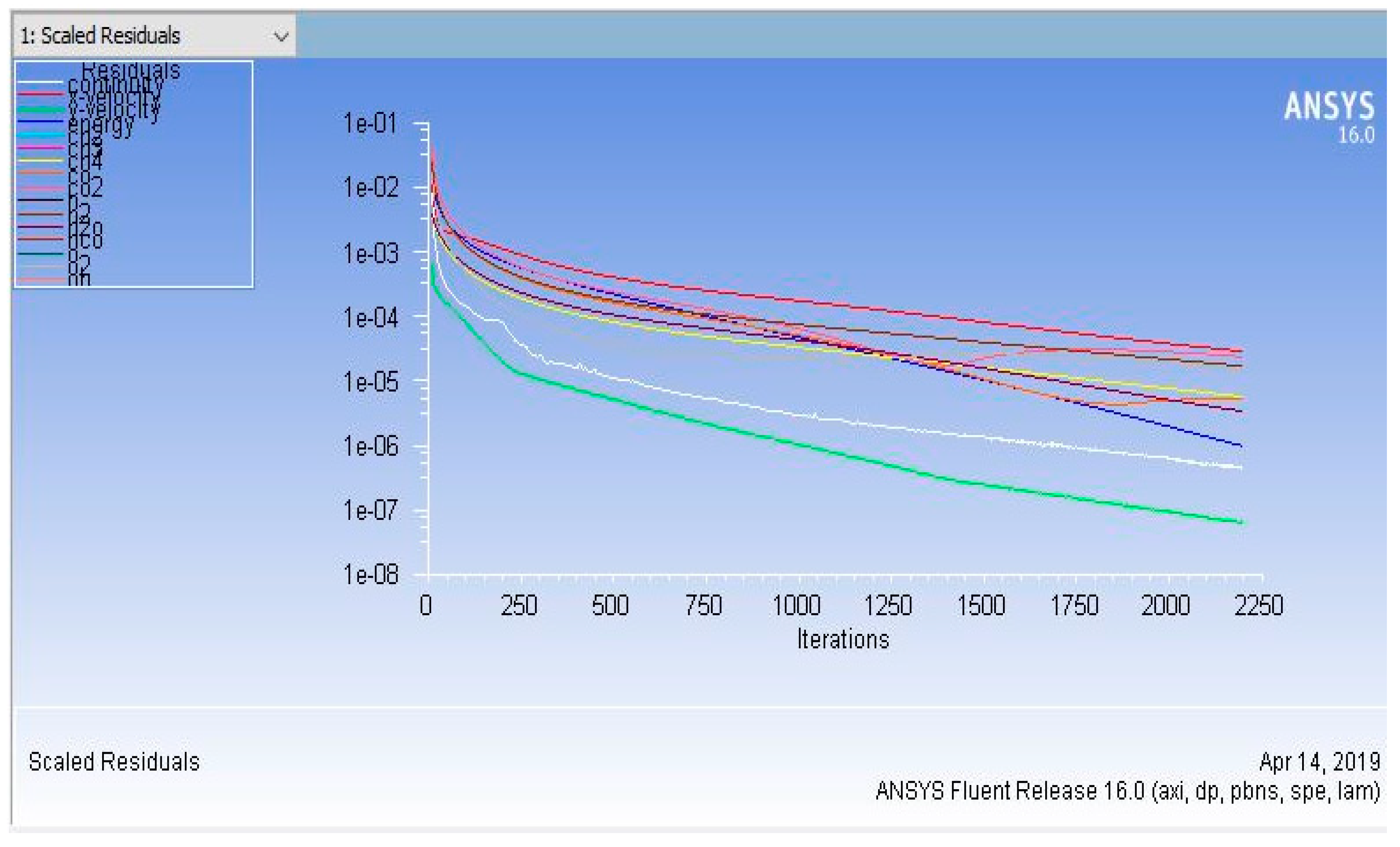
3.5. Computational Schemes
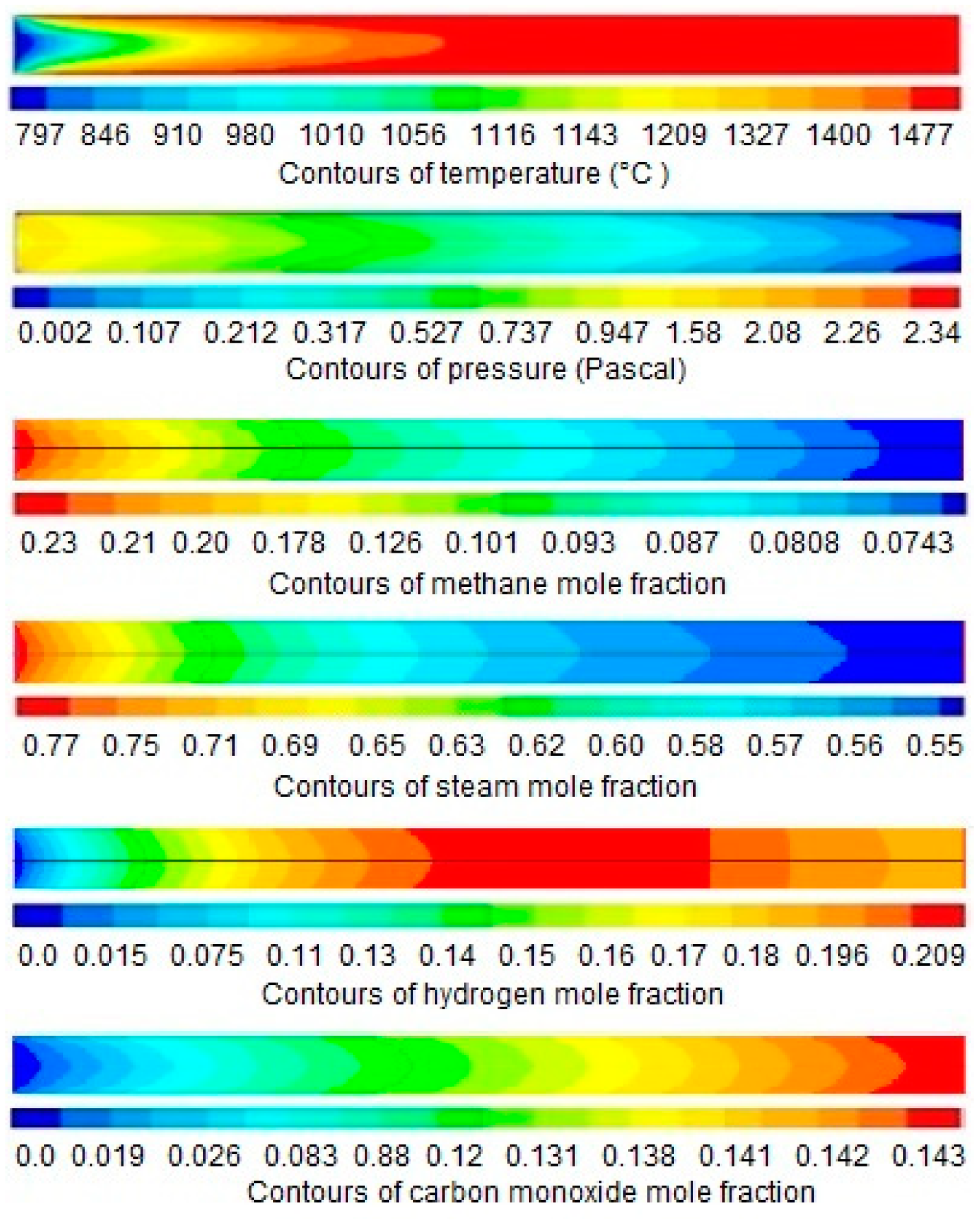
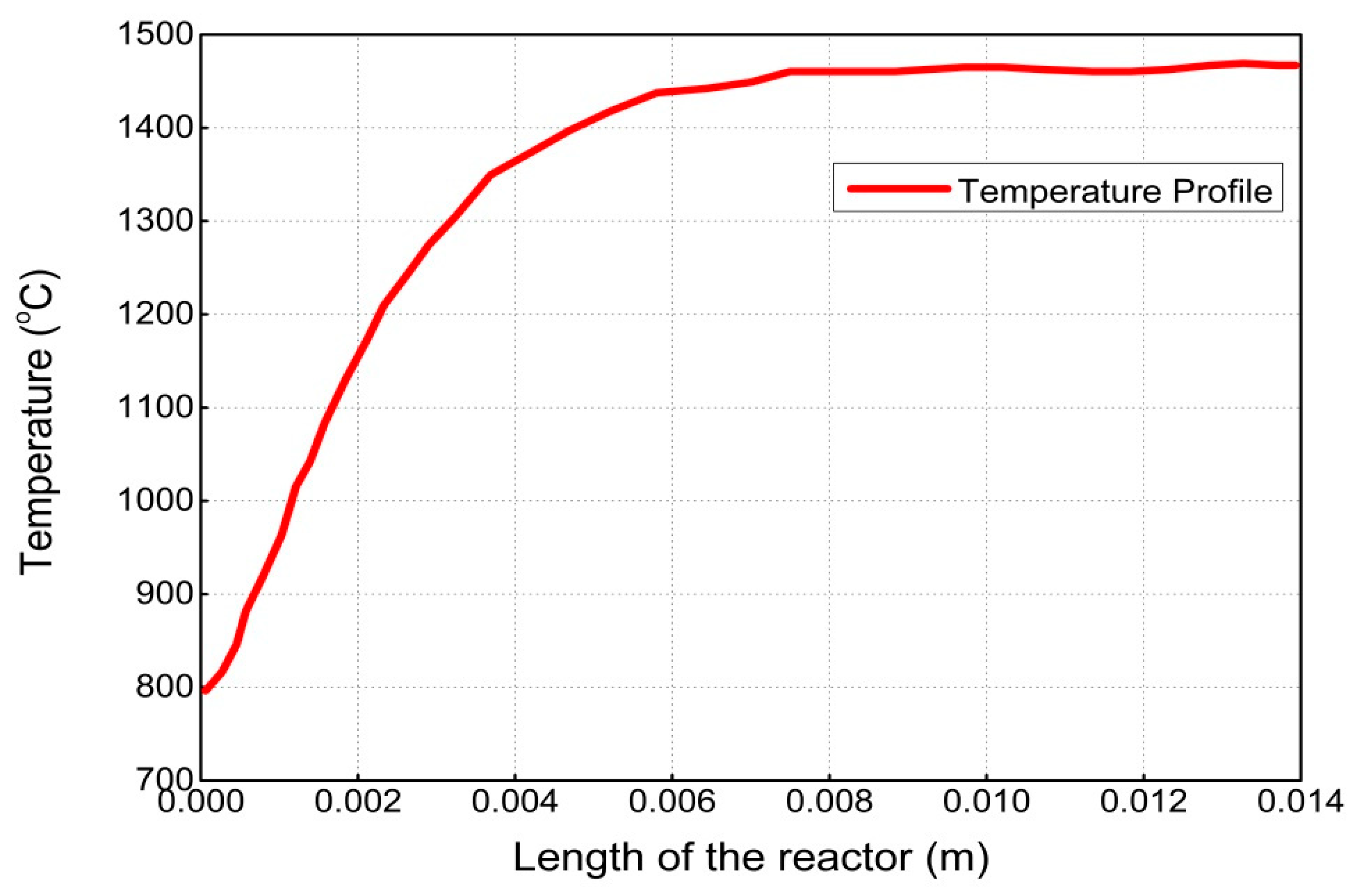
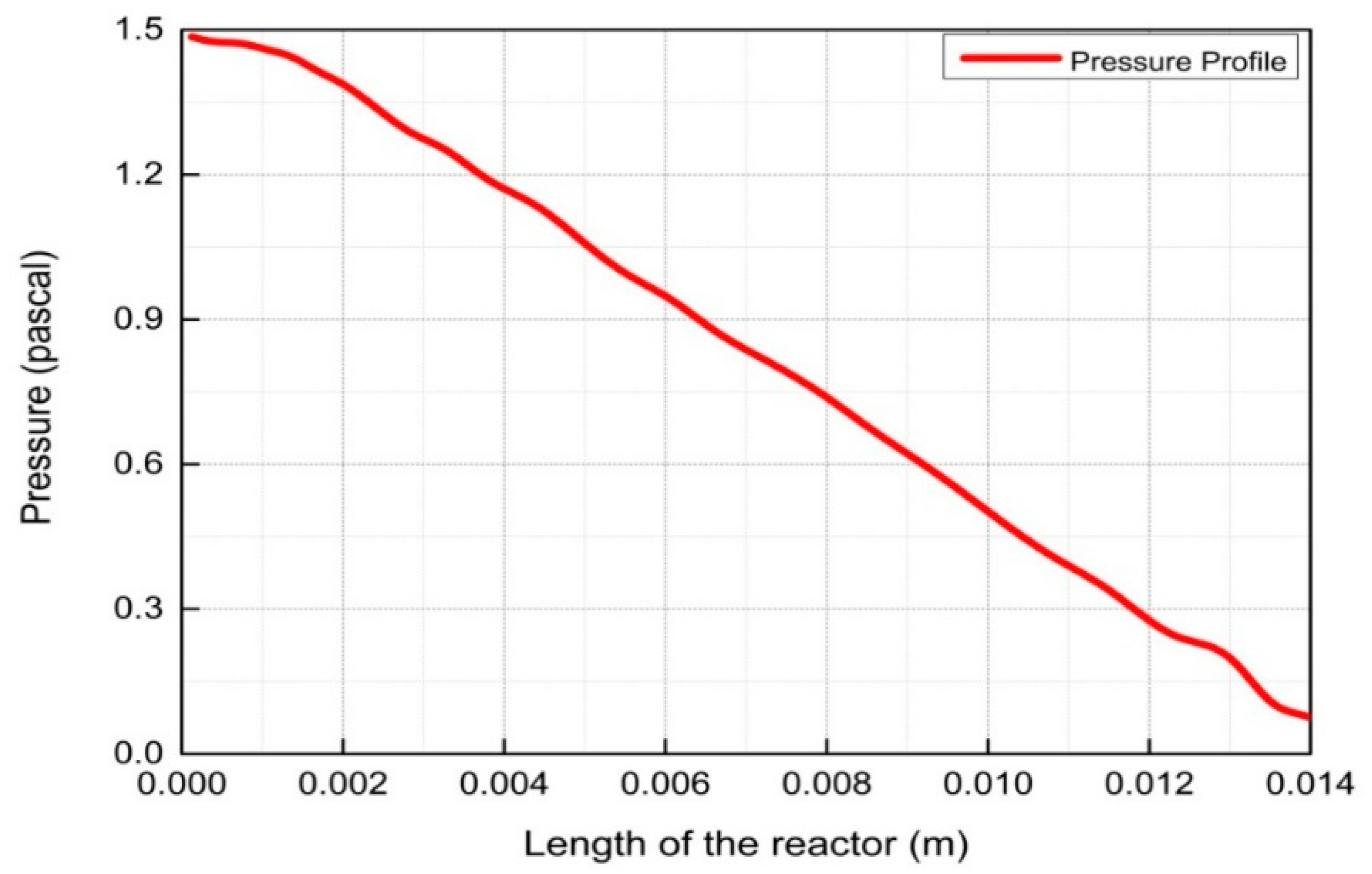
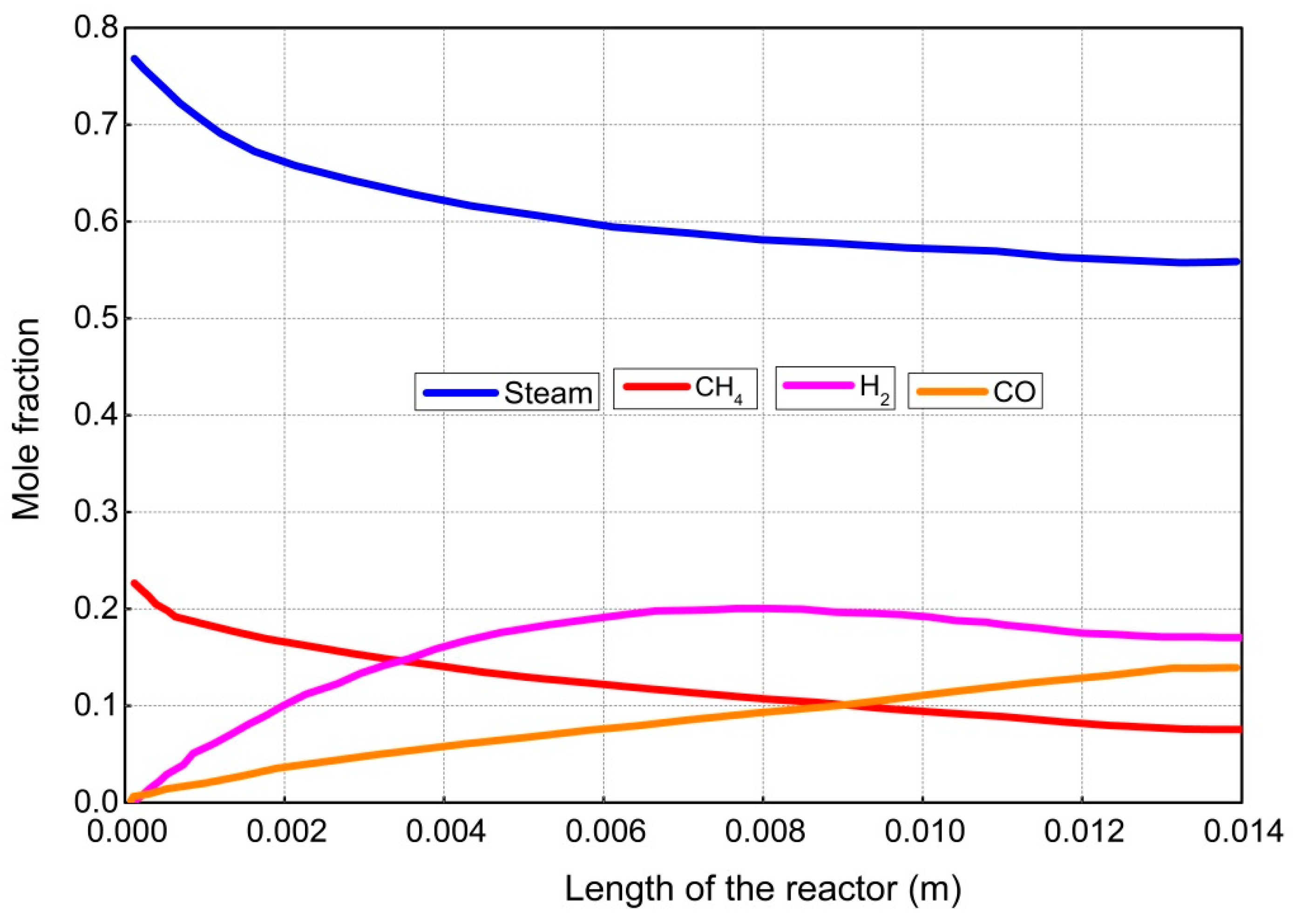
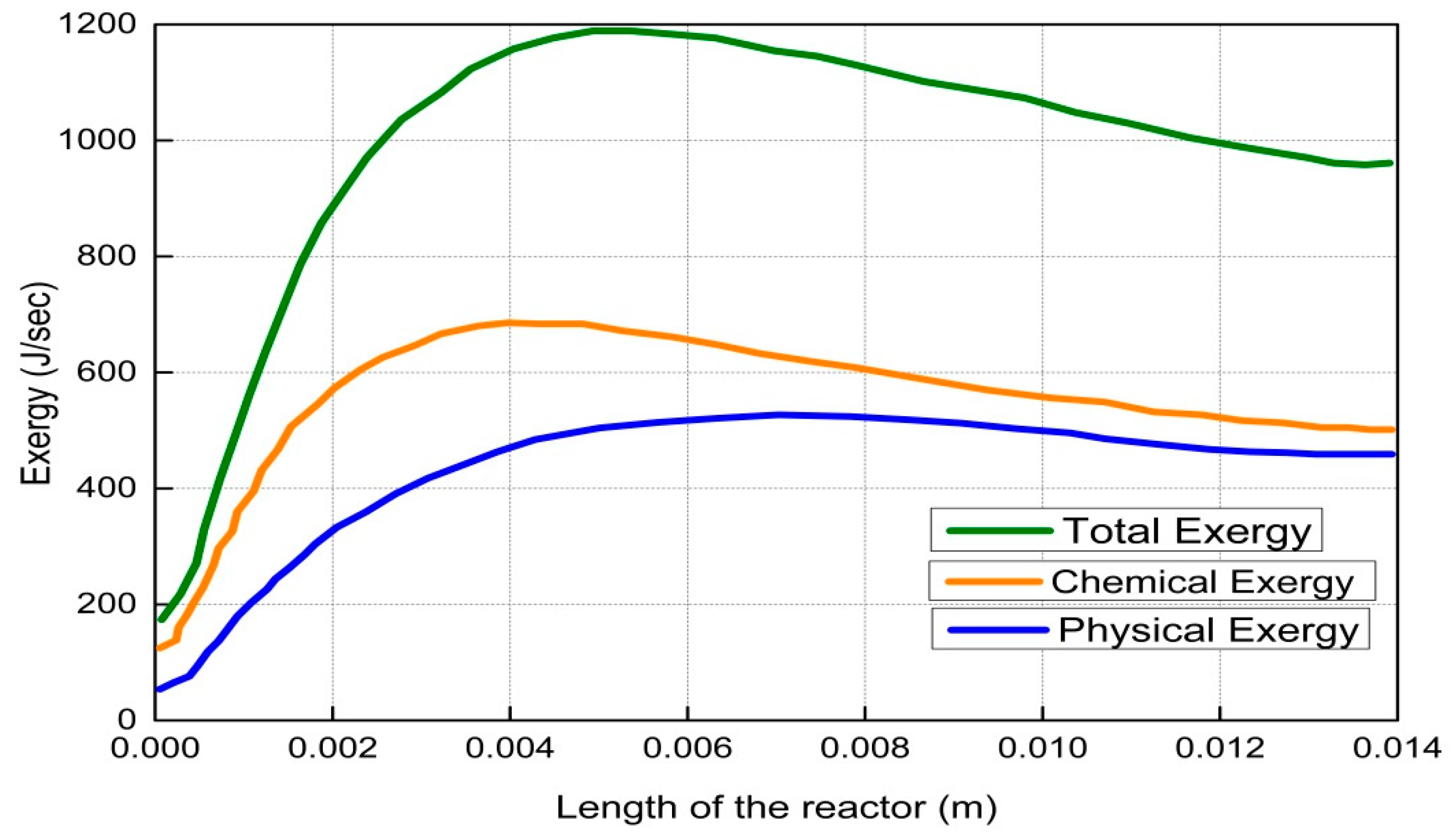
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CFD | computational fluid dynamics |
| SMR | steam methane reforming |
| PSA | pressure swing adsorption |
| Eph | molar physical exergy |
| Emix | molar mixing exergy |
| Ech | molar chemical exergy |
| molar Gibbs function | |
| R | Ideal gas constant |
| specific heat constant | |
| dissipation energy per unit volume | |
| mass fraction | |
| diffusion coefficient | |
| mass flux of component i | |
| production rate | |
| forward rate coefficient | |
| pre-exponential factor of the reaction r | |
| temperature exponent | |
| activation energy of the reaction r | |
| surface site density | |
| molar mass of i-th species | |
| Rh | Rhodium catalyst |
References
- Zhai, X.; Ding, S.; Cheng, Y.; Jin, Y.; Cheng, Y. CFD simulation with detailed chemistry of steam reforming of methane for hydrogen production in an integrated micro-reactor. Int. J. Hydrogen Energy 2010, 35, 5383–5392. [Google Scholar] [CrossRef]
- Irani, M.; Alizadehdakhel, A.; Pour, A.N.; Hoseini, N.; Adinehnia, M. CFD modeling of hydrogen production using steam reforming of methane in monolith reactors: Surface or volume-base reaction model? Int. J. Hydrogen Energy 2011, 36, 15602–15610. [Google Scholar]
- Saeidi, S.; Fazlollahi, F.; Najari, S.; Iranshahi, D.; Klemeš, J.J.; Baxter, L.L. Hydrogen production: Perspectives, separation with special emphasis on kinetics of WGS reaction: A state-of-the-art review. J. Ind. Eng. Chem. 2017, 49, 1–25. [Google Scholar] [CrossRef]
- Baharudin, L.; Watson, M.J. Monolithic substrate support catalyst design considerations for steam methane reforming operation. Rev. Chem. Eng. 2018, 34, 481–501. [Google Scholar] [CrossRef]
- Granlund, M.Z.; Görke, O.; Pfeifer, P.; Pettersson, L.J. Comparison between a micro reactor with multiple air inlets and a monolith reactor for oxidative steam reforming of diesel. Int. J. Hydrogen Energy 2014, 39, 18037–18045. [Google Scholar] [CrossRef]
- Bhat, S.A.; Sadhukhan, J. Process intensification aspects for steam methane reforming: An overview. AIChE J. 2009, 55, 408–422. [Google Scholar] [CrossRef]
- Chen, J.; Yan, L.; Song, W.; Xu, D. Effect of heat and mass transfer on the combustion stability in catalytic micro-combustors. Appl. Therm. Eng. 2018, 131, 750–765. [Google Scholar] [CrossRef]
- Yu, X.; Tu, S.T.; Wang, Z.; Qi, Y. Development of a microchannel reactor concerning steam reforming of methanol. Chem. Eng. J. 2006, 116, 123–132. [Google Scholar] [CrossRef]
- Theampetch, A.; Chaiwang, W.; Jermkwan, N.; Narataruksa, P.; Sornchamni, T.; Prapainainar, C. Design of Microreactor Flow Channel for Fischer Tropsch Synthesis Using Computational Fluid Dynamic. Energy Procedia 2016, 100, 439–447. [Google Scholar] [CrossRef][Green Version]
- Kansha, Y.; Kotani, Y.; Aziz, M.; Kishimoto, A.; Tsutsumi, A. Evaluation of a self-heat recuperative thermal process based on thermodynamic irreversibility and exergy. J. Chem. Eng. Jpn. 2012, 12we084. [Google Scholar] [CrossRef]
- Hosseini, S.E.; Wahid, M.A. Enhancement of exergy efficiency in combustion systems using flameless mode. Energy Convers. Manag. 2014, 86, 1154–1163. [Google Scholar] [CrossRef]
- An, H.; Li, A.; Sasmito, A.P.; Kurnia, J.C.; Jangam, S.V.; Mujumdar, A.S. Computational fluid dynamics (CFD) analysis of micro-reactor performance: Effect of various configurations. Chem. Eng. Sci. 2012, 75, 85–95. [Google Scholar] [CrossRef]
- Kashid, M.N.; Agar, D.W.; Turek, S. CFD modeling of mass transfer with and without chemical reaction in the liquid–liquid slug flow microreactor. Chem. Eng. Sci. 2007, 62, 5102–5109. [Google Scholar] [CrossRef]
- Tzanetis, K.; Martavaltzi, C.; Lemonidou, A. Comparative exergy analysis of sorption enhanced and conventional methane steam reforming. Int. J. Hydrogen Energy 2012, 37, 16308–16320. [Google Scholar] [CrossRef]
- Simpson, A.P.; Lutz, A.E. Exergy analysis of hydrogen production via steam methane reforming. Int. J. Hydrogen Energy 2007, 32, 4811–4820. [Google Scholar] [CrossRef]
- Boulenouar, M.; Ouadha, A. CFD-Exergy analysis of the flow in a supersonic steam ejector. J. Phys. Conf. Ser. 2015. [Google Scholar] [CrossRef]
- Mustafa, J.; Ahmad, I.; Ahsan, M.; Kano, M. Computational fluid dynamics based model development and exergy analysis of naphtha reforming reactors. Int. J. Exergy 2017, 24, 344–363. [Google Scholar] [CrossRef]
- Alabi, K.; von Spakovskyρ, M.; Ladeinde, F.; Moorhouse, D.; Camberos, J. A comparison of empirical and CFD-based exergy modeling for the airframe subsystem of aircraft design. In Proceedings of the 25th International Congress of the Aeronautical Sciences, Hamburg, Germany, 3–8 September 2006. [Google Scholar]
- Gunjo, D.G.; Mahanta, P.; Robi, P.S. Exergy and energy analysis of a novel type solar collector under steady state condition: Experimental and CFD analysis. Renew. Energy 2017, 114, 655–669. [Google Scholar] [CrossRef]
- Debnath, P.; Pandey, K. Exergetic efficiency analysis of hydrogen–air detonation in pulse detonation combustor using computational fluid dynamics. Int. J. Spray Combust. Dyn. 2017, 9, 44–54. [Google Scholar] [CrossRef]
- Erguvan, M.; MacPhee, D. Energy and Exergy Analyses of Tube Banks in Waste Heat Recovery Applications. Energies 2018, 11, 2094. [Google Scholar] [CrossRef]
- Alabi, K.; Ladeinde, F. Utilizing CFD-based exergy calculations in the design/optimization of a complete aircraft system. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2007; p. 1130. [Google Scholar]
- Ao, Y.-A.; Gao, X.-Q.; Shen, L.; Wang, Y.-R.; Feng, G.-H. Exergy analysis of exhaust-gas of burning liquefied-gas in a Chinese kitchen. In Proceedings of the 2009 International Conference on Energy and Environment Technology, Guilin, China, 16–18 October 2009; pp. 40–43. [Google Scholar]
- Farmahini-Farahani, M. Investigation of four geometrical parameters on thermal stratification of cold water tanks by exergy analysis. Int. J. Exergy 2012, 10, 332–345. [Google Scholar] [CrossRef]
- Lao, L.; Aguirre, A.; Tran, A.; Wu, Z.; Durand, H.; Christofides, P.D. CFD modeling and control of a steam methane reforming reactor. Chem. Eng. Sci. 2016, 148, 78–92. [Google Scholar] [CrossRef]
- Hajjaji, N.; Pons, M.N.; Houas, A.; Renaudin, V. Exergy analysis: An efficient tool for understanding and improving hydrogen production via the steam methane reforming process. Energy Policy 2012, 42, 392–399. [Google Scholar] [CrossRef]
- Palma, V.; Miccio, M.; Ricca, A.; Meloni, E.; Ciambelli, P. Monolithic catalysts for methane steam reforming intensification: Experimental and numerical investigations. Fuel 2014, 138, 80–90. [Google Scholar] [CrossRef]
- Sato, N. Chemical Energy and Exergy: An Introduction to Chemical Thermodynamics for Engineers; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Rosen, M.A. Exergy as a tool for sustainability. In Proceedings of the 3rd IASME/WSEAS International Conference on Energy & Environment, Cambridge, UK, 23–25 February 2008; pp. 90–98. [Google Scholar]
- Moran, M.J.; Shapiro, H.N.; Boettner, D.D.; Bailey, M.B. Fundamentals of Engineering Thermodynamics; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Hinderink, A.; Kerkhof, F.; Lie, A.; Arons, J.D.S.; Van Der Kooi, H. Exergy analysis with a flowsheeting simulator—I. Theory; calculating exergies of material streams. Chem. Eng. Sci. 1996, 51, 4693–4700. [Google Scholar] [CrossRef]
- Querol, E.; Gonzalez-Regueral, B.; Perez-Benedito, J.L. Exergy concept and determination. In Practical Approach to Exergy and Thermoeconomic Analyses of Industrial Processes; Springer: Berlin, Germany, 2013; pp. 9–28. [Google Scholar]
- Deutschmann, O.; Schmidt, L.D. Two-dimensional modeling of partial oxidation of methane on rhodium in a short contact time reactor. Symp. (Int.) Combust. 1998, 27, 2283–2291. [Google Scholar] [CrossRef]
- Chen, J.; Yan, L.; Song, W.; Xu, D. Methane steam reforming thermally coupled with catalytic combustion in catalytic microreactors for hydrogen production. Int. J. Hydrogen Energy 2017, 42, 664–680. [Google Scholar] [CrossRef]
- Menon, K.G.; Patnaikuni, V.S. CFD simulation of fuel reactor for chemical looping combustion of Indian coal. Fuel 2017, 203, 90–101. [Google Scholar] [CrossRef]
- Cao, C.; Zhang, N.; Chen, X.; Cheng, Y. A comparative study of Rh and Ni coated microchannel reactor for steam methane reforming using CFD with detailed chemistry. Chem. Eng. Sci. 2015, 137, 276–286. [Google Scholar] [CrossRef]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method; Pearson Education: London, UK, 2007. [Google Scholar]
- Karakaya, C.; Maier, L.; Deutschmann, O. Surface reaction kinetics of the oxidation and reforming of CH4 over Rh/Al2O3 catalysts. Int. J. Chem. Kinet. 2016, 48, 144–160. [Google Scholar] [CrossRef]
- Thormann, J.; Maier, L.; Pfeifer, P.; Kunz, U.; Deutschmann, O.; Schubert, K. Steam reforming of hexadecane over a Rh/CeO2 catalyst in microchannels: Experimental and numerical investigation. Int. J. Hydrogen Energy 2009, 34, 5108–5120. [Google Scholar] [CrossRef]
- Mundhwa, M.; Thurgood, C.P. Numerical study of methane steam reforming and methane combustion over the segmented and continuously coated layers of catalysts in a plate reactor. Fuel Process. Technol. 2017, 158, 57–72. [Google Scholar] [CrossRef]
- Deutschmann, O.; Schwiedemoch, R.; Maier, L.I.; Chatterjee, D. Natural gas conversion in monolithic catalysts: Interaction of chemical reactions and transport phenomena. In Studies in Surface Science and Catalysis; Elsevier: Amsterdam, The Netherlands, 2001; Volume 136, pp. 251–258. [Google Scholar]
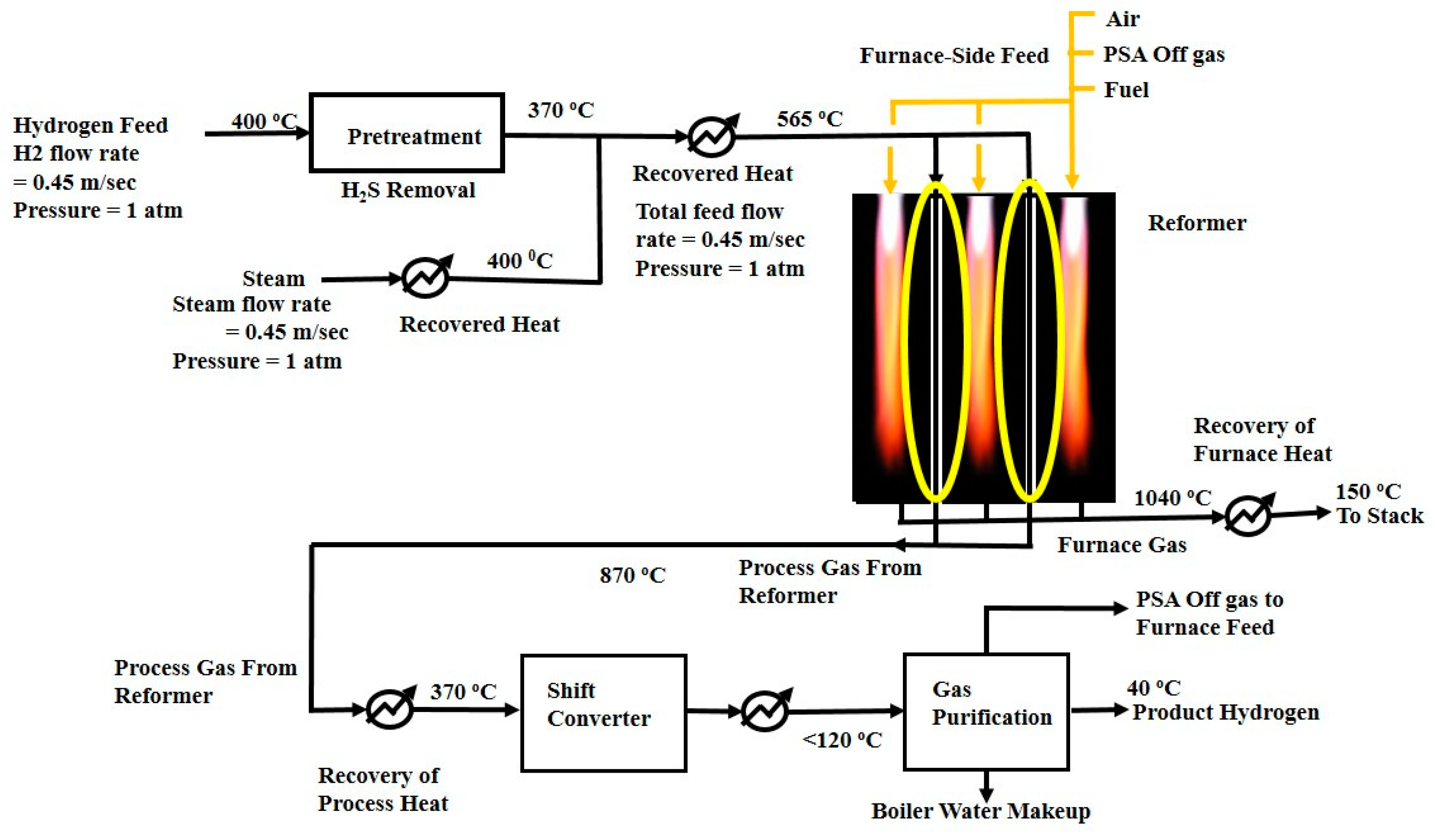
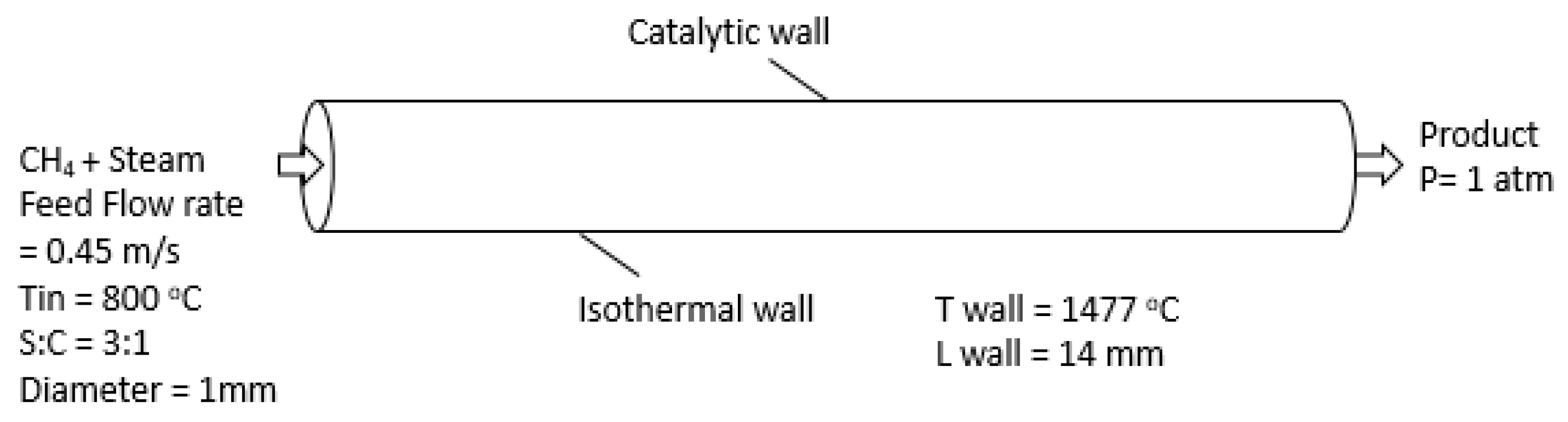
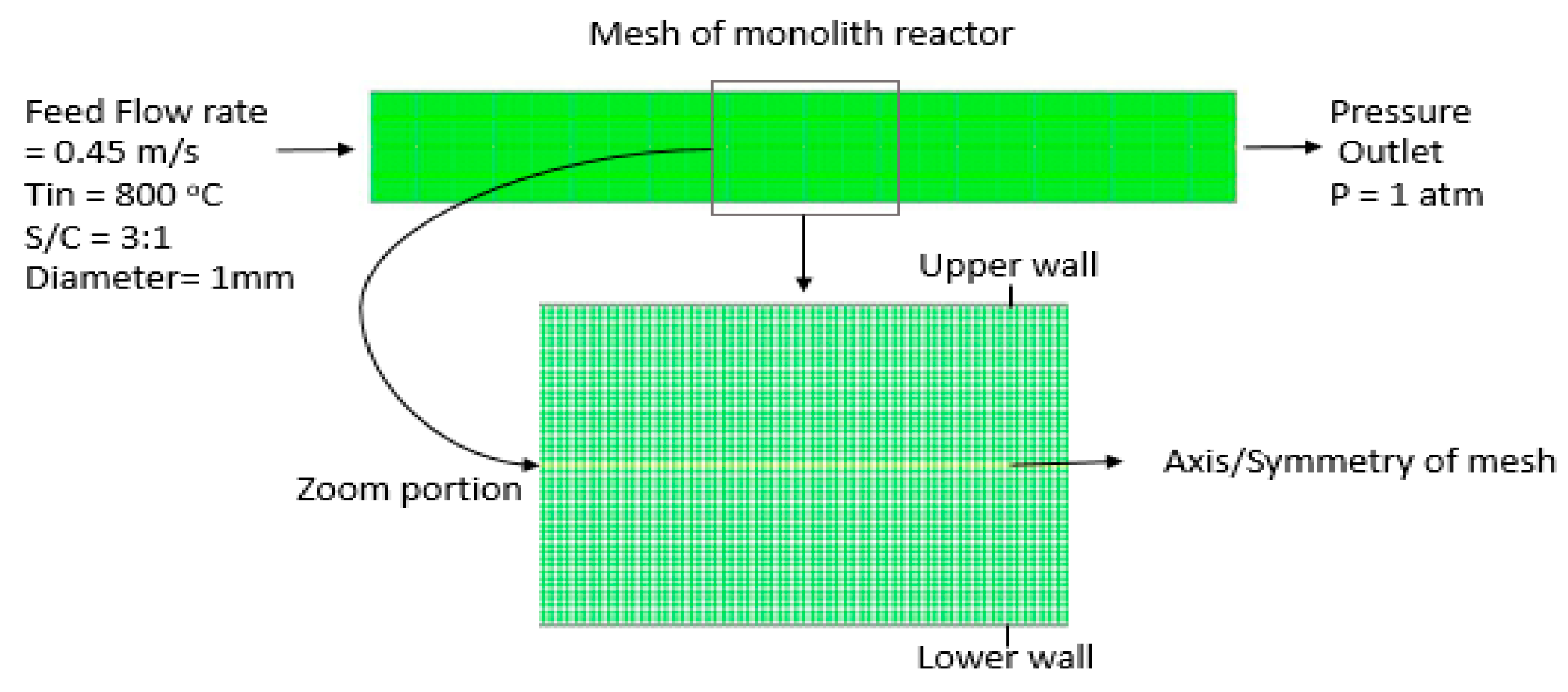


| Parameters | Symbol | Value |
|---|---|---|
| Channel length | L | 14 mm |
| Channel diameter | D | 1 mm |
| Inlet temperature | Tin | 800 °C |
| Isothermal wall temperature | Tw | 1477 °C |
| Pressure | P | 1 atm |
| Ratio of steam to methane | S/C | 3:1 |
| Inlet velocity | Vin | 0.45m/s |
| Number of catalyst active sites (catalyst density) | Γ | 2.7 × 10−9 mol/cm2 |
| Properties of Mesh | Values |
|---|---|
| Orthogonal quality (minimum) | 1.0 |
| Ortho skew (maximum) | 0.0 |
| Aspect ratio (maximum) | 1.4 |
| The number of nodes | 7525 |
| The number of cells | 7200 |
| Minimum volume (m3) | 2.4 × 10−13 |
| Maximum volume (m3) | 2.3 × 10−11 |
| Total volume (m3) | 4.2 × 10−8 |
| Minimum face area (m2) | 4.1 × 10−5 |
| Maximum face area (m2) | 4.5 × 10−5 |
| Serial No. | Reactions | Akr (mol, cm, s, K) | Ear [KJ/mol] | |
|---|---|---|---|---|
| 1. | H2 + 2Rh(s)→2H(s) | 0.01 | 0.0 | |
| 2. | 2H(s)→H2 + 2Rh(s) | 3.0 × 1021 | 77.8 | |
| 3. | O2 + 2Rh(s)→2O(s) | |||
| 4. | 2O(s)→O2 + 2Rh(s) | 1.33 × 1022 | 355.2 | |
| 5. | CH4 + Rh(s)→CH4(s) | 8.0 × 10−3 | 0.0 | |
| 6. | CH4(s)→CH4 + Rh(s) | 2.0 × 1014 | 25.1 | |
| 7. | H2O + Rh(s)→H2O(s) | 0.1 | 0.0 | |
| 8. | H2O(s)→H2O + Rh(s) | 6.0 × 1013 | 45 | |
| 9. | CO2 + Rh(s)→CO2(s) | 1.0 × 10−5 | 0.0 | |
| 10. | CO2(s)→CO2 + Rh(s) | 3.0 × 108 | 21.7 | |
| 11. | CO + Rh(s)→CO(s) | 5 × 10−1 | 0.0 | |
| 12. | CO(s)→CO + Rh(s) | 1.0 × 1013 | 133.4 | |
| 13. | H(s) + O(s)→OH(s) + Rh(s) | 5.0 × 1022 | 83.7 | |
| 14. | OH(s) + Rh(s)→ H(s) + O(s) | 3.0 × 1020 | 37.7 | |
| 15. | H(s) + OH(s)→H2O(s) + Rh(s) | 3.0 × 1020 | 33.5 | |
| 16. | H2O(s) + Rh(s)→ H(s) + OH(s) | 5.0 × 1022 | 106.4 | |
| 17. | 2OH(s)→H2O(s) + O(s) | 3.0 × 1021 | 100.8 | |
| 18. | H2O(s) + O(s)→ 2OH(s) | 3.0 × 1021 | 171.8 | |
| 19. | C(s) + O(s)→CO(s) + Rh(s) | 5.0 × 1023 | 97.9 | |
| 20. | CO(s) + Rh(s)→C(s) + O(s) | 3.7 × 1021 | 169.0 | |
| 21. | CO(s) + O(s)→CO2(s) + Rh(s) | 1.0 × 1019 | 121.6 | |
| 22. | CO2 + Rh(s)→ CO(s) + O(s) | 5.0 × 1021 | 115.3 | |
| 23. | CO(s) + H(s)→HCO(s) + Rh(s) | 5.0 × 1019 | 108.9 | |
| 24. | HCO(s) + Rh(s)→ CO(s) + H(s) | 3.7 × 1021 | 0.0 | |
| 25. | HCO(s) + Rh(s)→CH(s) + O(s) | 8.0 × 1023 | 59.5 | |
| 26. | CH(s) + O(s)→ HCO(s) + Rh(s) | 3.7 × 1021 | 167.5 | |
| 27. | CH4(s) + Rh(s)→CH3 + H(s) | 5.5 × 1020 | 61.0 | |
| 28. | CH3 + H(s)→ CH4(s) + Rh(s) | 3.7 × 1021 | 51.0 | |
| 29. | CH3(s) + Rh(s)→CH2(s) + H(s) | 3.7 × 1021 | 103.0 | |
| 30. | CH2(s) + H(s)→ CH3(s) + Rh(s) | 3.7 × 1021 | 44.0 | |
| 31. | CH2(s) + Rh(s)→CH(s) + Rh(s) | 3.7 × 1034 | 100.0 | |
| 32. | CH(s) + Rh(s)→ CH2(s) + Rh(s) | 3.7 × 1034 | 68.0 | |
| 33. | CH(s) + Rh(s)→C(s) + H(s) | 3.7 × 1021 | 21.0 | |
| 34. | C(s) + H(s)→ CH(s) + Rh(s) | 3.7 × 1021 | 172.8 | |
| 35. | CH4(s) + O(s)→CH3(s) + OH(s) | 1.7 × 1024 | 80.3 | |
| 36. | CH3(s) + OH(s)→CH4(s) + O(s) | 3.7 × 1021 | 24.3 | |
| 37. | CH3(s) + O(s)→CH2(s) + OH(s) | 3.7 × 1024 | 120.3 | |
| 38. | CH2(s) + OH(s)→CH3(s) + O(s) | 3.7 × 1021 | 15.1 | |
| 39. | CH2(s) + O(s)→CH(s) + OH(s) | 3.7 × 1024 | 114.5 | |
| 40. | CH(s) + OH(s)→CH2(s) + O(s) | 3.7 × 1021 | 36.8 | |
| 41. | CH(s) + O(s)→C(s) + OH(s) | 3.7 × 1021 | 30.1 | |
| 42. | C(s) + OH(s)→CH(s) + O(s) | 3.7 × 1021 | 136.0 | |
| 43. | CO(s) + H(s)→C(s) + OH(s) | 3.7 × 1021 | 142.0 | |
| 44. | C(s) + OH(s)→CO(s) + H(s) | 3.7 × 1020 | 25.5 |
| Parameters | Literature Data [36] | Proposed Model Data |
|---|---|---|
| Feed temperature | 800 °C | 800 °C |
| Wall temperature | 900 °C | 1477 °C |
| Pressure | 1 atm | 1 atm |
| Steam to methane ratio | 3:1 | 3:1 |
| Inlet velocity | 0.45 m/s | 0.45m/s |
| Length | 6.0 × 10−2 m | 1.4 × 10−2 m |
| Surface area | 1.88 × 10−4 m2 | 4.4 × 10−5 m2 |
| Heat requirement | 22.05 kW | 7.7 kW |
| Conversion | 60 % | 67.4 % |
| Catalyst requirement per length | 5.076 × 10−9 moles | 1.18 × 10−9 moles |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahman, Z.u.; Ahmad, I.; Kano, M.; Mustafa, J. Model Development and Exergy Analysis of a Microreactor for the Steam Methane Reforming Process in a CFD Environment. Entropy 2019, 21, 399. https://doi.org/10.3390/e21040399
Rahman Zu, Ahmad I, Kano M, Mustafa J. Model Development and Exergy Analysis of a Microreactor for the Steam Methane Reforming Process in a CFD Environment. Entropy. 2019; 21(4):399. https://doi.org/10.3390/e21040399
Chicago/Turabian StyleRahman, Zia ur, Iftikhar Ahmad, Manabu Kano, and Jawad Mustafa. 2019. "Model Development and Exergy Analysis of a Microreactor for the Steam Methane Reforming Process in a CFD Environment" Entropy 21, no. 4: 399. https://doi.org/10.3390/e21040399
APA StyleRahman, Z. u., Ahmad, I., Kano, M., & Mustafa, J. (2019). Model Development and Exergy Analysis of a Microreactor for the Steam Methane Reforming Process in a CFD Environment. Entropy, 21(4), 399. https://doi.org/10.3390/e21040399






