Mesoscopic Simulation of the (2 + 1)-Dimensional Wave Equation with Nonlinear Damping and Source Terms Using the Lattice Boltzmann BGK Model
Abstract
1. Introduction
2. Lattice Boltzmann BGK Model
3. Numerical Simulation
- (1)
- The relative error norm (-error)
- (2)
- The max error norm (-error)
- (3)
- The global relative error norm (GRE-error)
- (4)
- The root mean square error norm (RMS-error)
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Abdou, M.A.; Soliman, A.A. Variational iteration method for solving Burger’s and coupled Burger’s equations. J. Comput. Appl. Math. 2005, 181, 245–251. [Google Scholar] [CrossRef]
- Ӧzpınar, F. Applying discrete homotopy analysis method for solving fractional partial differential equations. Entropy 2018, 20, 332. [Google Scholar]
- Petrila, T.; Trif, D. Introduction to Numberical Solutions for Ordinary and Partial Differential Equations. In Basics of Fluid Mechanics and Introduction to Computational Fluid Dynamics; Springer: Boston, MA, USA, 2005; pp. 197–246. [Google Scholar]
- Chang, C.W.; Liu, C.S. An implicit Lie-group iterative scheme for solving the nonlinear Klein-Gordon and sine-Gordon equations. Appl. Math. Model. 2016, 40, 1157–1167. [Google Scholar] [CrossRef]
- Dehghan, M.; Shokri, A. A meshless method for numerical solution of a linear hyperbolic equation with variable coefficients in two space dimensions. Numer. Methods Part. Differ. Equ. 2009, 25, 494–506. [Google Scholar] [CrossRef]
- Liu, W.J.; Sun, J.B.; Wu, B.Y. Space-time spectral method for the two-dimensional generalized sine-Gordon equation. J. Math. Anal. Appl. 2015, 427, 787–804. [Google Scholar] [CrossRef]
- Ding, H.F.; Zhang, Y.X. A new fourth-order compact finite difference scheme for the two-dimensional second-order hyperbolic equation. J. Comput. Appl. Math. 2009, 230, 626–632. [Google Scholar] [CrossRef]
- Shi, D.Y.; Pei, L.F. Nonconforming quadrilateral finite element method for a class of nonlinear sine-Gordon equations. Appl. Math. Comput. 2013, 219, 9447–9460. [Google Scholar] [CrossRef]
- Benzi, R.; Succi, S.; Vergasola, M. The lattice Boltzmann equation: Theory and applications. Phys. Rep. 1992, 222, 145–197. [Google Scholar] [CrossRef]
- Chen, S.Y.; Doolen, G.D. Lattice Boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef]
- Xu, A.G.; Zhang, G.C.; Ying, Y.J.; Wang, C. Complex fields in heterogeneous materials under shock: Modeling, simulation and analysis. Sci. China Phys. Mech. Astron. 2016, 59, 650501. [Google Scholar] [CrossRef]
- Li, Q.; Luo, K.H.; Kang, Q.J.; He, Y.L.; Chen, Q.; Liu, Q. Lattice Boltzmann methods for multiphase flow and phase-change heat transfer. Prog. Energy Combust. Sci. 2016, 52, 62–105. [Google Scholar] [CrossRef]
- Christensen, A.; Graham, S. Multiscale lattice Boltzmann modeling of phonon transport in crystalline semiconductor materials. Numer. Heat Transf. B 2010, 57, 89–109. [Google Scholar] [CrossRef]
- Li, Q.; Luo, K.H.; Gao, Y.J.; He, Y.L. Additional interfacial force in lattice Boltzmann models for incompressible multiphase flows. Phys. Rev. E 2012, 85, 026704. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Shu, C.; Teo, C.J. Thermal lattice Boltzmann flux solver and its application for simulation of incompressible thermal flows. Comput. Fluids 2014, 94, 98–111. [Google Scholar] [CrossRef]
- Wang, Y.; Shu, C.; Huang, H.B.; Teo, C.J. Multiphase lattice Boltzmann flux solver for incompressible multiphase flows with large density ratio. J. Comput. Phys. 2015, 280, 404–423. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, L.M.; Shu, C. From lattice Boltzmann method to lattice Boltzmann flux solver. Entropy 2015, 17, 7713–7735. [Google Scholar] [CrossRef]
- Wei, Y.K.; Wang, Z.D.; Qian, Y.H. A numerical study on entropy generation in two-dimensional Rayleigh-Bénard convection at different Prandtl number. Entropy 2017, 19, 443. [Google Scholar] [CrossRef]
- Wei, Y.K.; Wang, Z.D.; Qian, Y.H.; Guo, W.J. Study on bifurcation and dual solutions in natural convection in a horizontal annulus with rotating inner cylinder using thermal immersed boundary-lattice Boltzmann method. Entropy 2018, 20, 733. [Google Scholar] [CrossRef]
- Yang, X.Y.; He, H.Z.; Xu, J.; Wei, Y.K.; Zhang, H. Entropy generation rates in two-dimensional Rayleigh-Taylor turbulence mixing. Entropy 2018, 20, 738. [Google Scholar] [CrossRef]
- Wei, Y.K.; Dou, H.S.; Qian, Y.H.; Wang, Z.D. A novel two-dimensional coupled lattice Boltzmann model for incompressible flow in application of turbulence Rayleigh-Taylor instability. Comput. Fluids 2017, 156, 97–102. [Google Scholar] [CrossRef]
- Wei, Y.K.; Yang, H.; Dou, H.S.; Lin, Z.; Wang, Z.D.; Qian, Y.H. A novel two-dimensional coupled lattice Boltzmann model for thermal incompressible flows. Appl. Math. Comput. 2018, 339, 556–567. [Google Scholar] [CrossRef]
- Yuan, H.Z.; Niu, X.D.; Shu, S.; Li, M.J.; Yamaguchi, H. A momentum exchange-based immersed boundary-lattice Boltzmann method for simulating a flexible filament in an incompressible flow. Comput. Math. Appl. 2014, 67, 1039–1056. [Google Scholar] [CrossRef]
- Yuan, H.Z.; Wang, Y.; Shu, C. An adaptive mesh refinement-multiphase lattice Boltzmann flux solver for simulation of complex binary fluid flows. Phys. Fluids 2017, 29, 123604. [Google Scholar] [CrossRef]
- Yuan, H.Z.; Chen, Z.; Shu, C.; Wang, Y.; Niu, X.D.; Shu, S. A free energy-based surface tension force model for simulation of multiphase flows by level-set method. J. Comput. Phys. 2017, 345, 404–426. [Google Scholar] [CrossRef]
- Xu, A.G.; Lin, C.D.; Zhang, G.C.; Li, Y.J. Multiple-relaxation-time lattice Boltzmann kinetic model for combustion. Phys. Rev. E 2015, 91, 043306. [Google Scholar] [CrossRef] [PubMed]
- Gan, Y.B.; Xu, A.G.; Zhang, G.C.; Succi, S. Discrete Boltzmann modeling of multiphase flows: Hydrodynamic and thermodynamic non-equilibrium effects. Soft Matter 2015, 11, 5336–5345. [Google Scholar] [CrossRef] [PubMed]
- Gan, Y.B.; Xu, A.G.; Zhang, G.C.; Zhang, Y.D.; Succi, S. Discrete Boltzmann trans-scale modeling of high-speed compressible flows. Phys. Rev. E 2018, 97, 053312. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.D.; Xu, A.G.; Zhang, G.C.; Zhu, C.M.; Lin, C.D. Kinetic modeling of detonation and effects of negative temperature coefficient. Combust Flame 2016, 173, 483–492. [Google Scholar] [CrossRef]
- Zhang, Y.D.; Xu, A.G.; Zhang, G.C.; Chen, Z.H.; Wang, P. Discrete ellipsoidal statistical BGK model and Burnett equations. Front. Phys. 2018, 13, 135101. [Google Scholar] [CrossRef]
- Zhang, Y.D.; Xu, A.G.; Zhang, G.C.; Gan, Y.B.; Chen, Z.H.; Succi, S. Entropy production in thermal phase separation: A kinetic-theory approach. Soft Matter 2019, 15, 2245–2259. [Google Scholar] [CrossRef]
- Xu, A.G.; Zhang, G.C.; Zhang, Y.D.; Wang, P.; Ying, Y.J. Discrete Boltzmann model for implosion- and explosion-related compressible flow with spherical symmetry. Front. Phys. 2018, 13, 135102. [Google Scholar] [CrossRef]
- Gan, Y.B.; Xu, A.G.; Zhang, G.C.; Lin, C.D.; Lai, H.L.; Liu, Z.P. Nonequilibrium and morphological characterizations of Kelvin-Helmholtz instability in compressible flows. Front. Phys. 2019, 14, 43602. [Google Scholar] [CrossRef]
- Lin, C.D.; Xu, A.G.; Zhang, G.C.; Li, Y.J. Double-distribution-function discrete Boltzmann model for combustion. Combust Flame 2016, 164, 137–151. [Google Scholar] [CrossRef]
- Lin, C.D.; Xu, A.G.; Zhang, G.C.; Luo, K.H.; Li, Y.J. Discrete Boltzmann modeling of Rayleigh-Taylor instability in two-component compressible flows. Phys. Rev. E 2017, 96, 053305. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.D.; Luo, K.H. MRT discrete Boltzmann method for compressible exothermic reactive flows. Combust Flame 2018, 166, 176–183. [Google Scholar] [CrossRef]
- Lai, H.L.; Xu, A.G.; Zhang, G.C.; Gan, Y.B.; Ying, Y.J.; Succi, S. Nonequilibrium thermohydrodynamic effects on the Rayleigh-Taylor instability in compressible flows. Phys. Rev. E 2016, 94, 023106. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.Y.; Sun, D.K.; Zhang, Y.F.; Zhu, M.F. Numerical modeling of condensate droplet on superhydrophobic nanoarrays using the lattice Boltzmann method. Chin. Phys. B 2016, 25, 066401. [Google Scholar] [CrossRef]
- Sun, D.K.; Chai, Z.H.; Li, Q.; Lin, G. A lattice Boltzmann-cellular automaton study on dendrite growth with melt convection in solidification of ternary alloys. Chin. Phys. B 2018, 27, 088105. [Google Scholar] [CrossRef]
- Li, Q.; Kang, Q.J.; Francois, M.M.; He, Y.L.; Luo, K.H. Lattice Boltzmann modeling of boiling heat transfer: The boiling curve and the effects of wettability. Int. J. Heat Mass Transf. 2015, 85, 787–796. [Google Scholar] [CrossRef]
- Gao, Y.; Le, L.H.; Shi, B.C. Numerical solution of Burgers’ equation by lattice Boltzmann method. Appl. Math. Comput. 2013, 219, 7685–7692. [Google Scholar] [CrossRef]
- Lai, H.L.; Ma, C.F. A new lattice Boltzmann model for solving the coupled viscous Burgers’ equation. Physica A 2014, 395, 445–457. [Google Scholar] [CrossRef]
- Wang, H.M. Solitary wave of the Korteweg-de Vries equation based on lattice Boltzmann model with three conservation laws. Adv. Space Res. 2017, 59, 283–292. [Google Scholar] [CrossRef]
- Wang, H.M.; Yan, G.W. Lattice Boltzmann model for the interaction of (2 + 1)-dimensional solitons in generalized Gross-Pitaevskii equation. Appl. Math. Model. 2016, 40, 5139–5152. [Google Scholar] [CrossRef]
- Shi, B.C.; Guo, Z.L. Lattice Boltzmann model for nonlinear convection-diffusion equations. Phys. Rev. E 2009, 79, 016701. [Google Scholar] [CrossRef]
- Chai, Z.H.; He, N.Z.; Guo, Z.L.; Shi, B.C. Lattice Boltzmann model for high-order nonlinear partial differential equations. Phys. Rev. E 2018, 97, 013304. [Google Scholar] [CrossRef] [PubMed]
- Chai, Z.H.; Zhao, T.S. Lattice Boltzmann model for the convection-diffusion equation. Phys. Rev. E 2013, 87, 063309. [Google Scholar] [CrossRef]
- Yoshida, H.; Nagaoka, M. Lattice Boltzmann method for the convection-diffusion equation in curvilinear coordinate systems. J. Comput. Phys. 2014, 257, 884–900. [Google Scholar] [CrossRef]
- Wang, L.; Shi, B.C.; Chai, Z.H. Regularized lattice Boltzmann model for a class of convection-diffusion equations. Phys. Rev. E 2015, 92, 043311. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Chai, Z.H.; Shi, B.C. Regularized lattice Boltzmann simulation of double-diffusive convection of power-law nanofluids in rectangular enclosures. Int. J. Heat Mass Transf. 2016, 102, 381–395. [Google Scholar] [CrossRef]
- Chai, Z.H.; Shi, B.C.; Guo, Z.L. A multiple-relaxation-time lattice Boltzmann model for general nonlinear anisotropic convection-diffusion equations. J. Sci. Comput. 2016, 69, 355–390. [Google Scholar] [CrossRef]
- Lai, H.L.; Ma, C.F. Lattice Boltzmann method for the generalized Kuramoto-Sivashinsky equation. Physica A 2009, 388, 1405–1412. [Google Scholar] [CrossRef]
- Yan, G.W. A lattice Boltzmann equation for waves. J. Comput. Phys. 2000, 161, 61–69. [Google Scholar]
- Lai, H.L.; Ma, C.F. Lattice Boltzmann model for generalized nonlinear wave equations. Phys. Rev. E 2011, 84, 046708. [Google Scholar] [CrossRef]
- Shi, B.C.; Guo, Z.L. Lattice Boltzmann model for the one-dimensional nonlinear Dirac equation. Phys. Rev. E 2009, 79, 066704. [Google Scholar] [CrossRef]
- Chai, Z.H.; Shi, B.C. A novel lattice Boltzmann model for the Poisson equation. Appl. Math. Model. 2008, 32, 2050–2058. [Google Scholar] [CrossRef]
- Guo, Z.L.; Zheng, C.G.; Shi, B.C. An extrapolation method for boundary conditions in lattice Boltzmann method. Phys. Fluids 2002, 14, 2007–2010. [Google Scholar] [CrossRef]
- Sheng, Q.; Khaliq, A.Q.M.; Voss, D.A. Numerical simulation of two-dimensional sine-Gordon solitons via a split cosine scheme. Math. Comput. Simul. 2005, 68, 355–373. [Google Scholar] [CrossRef]
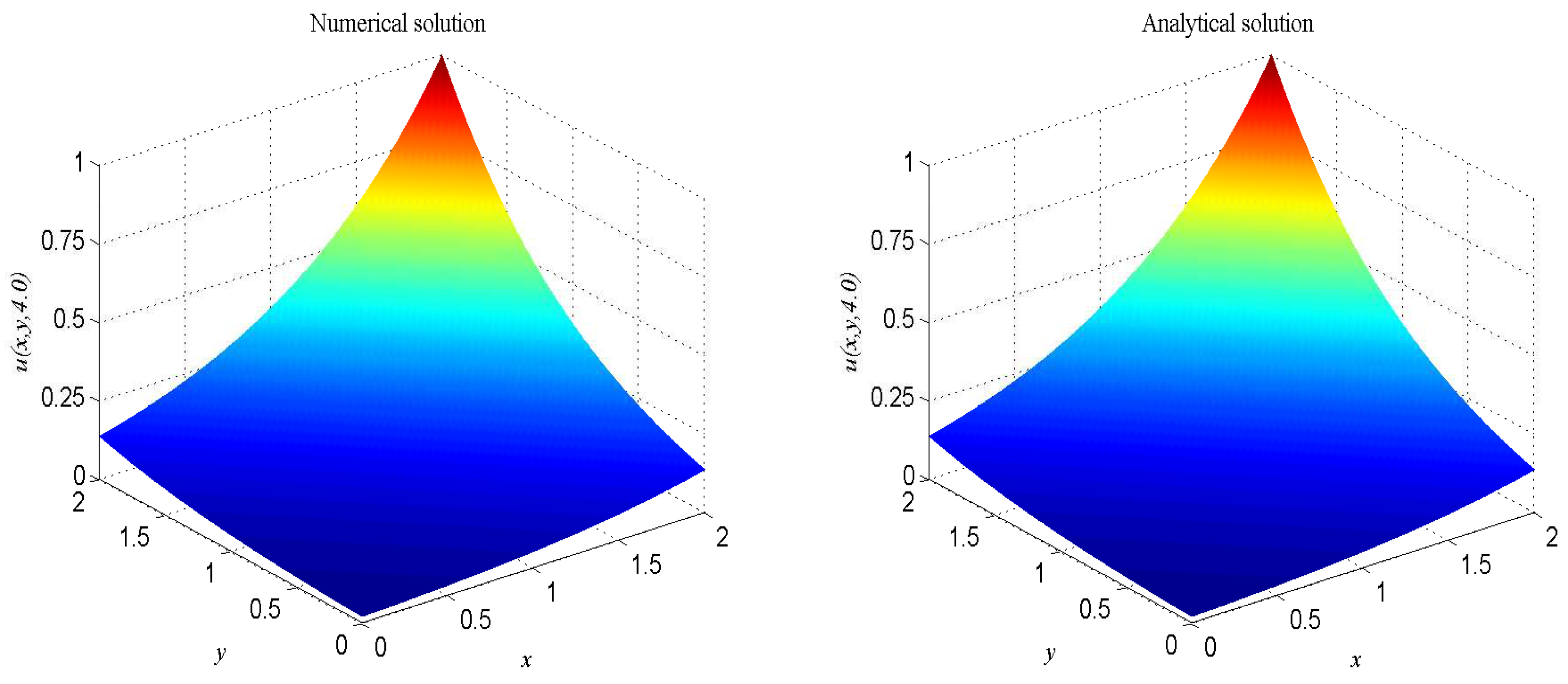
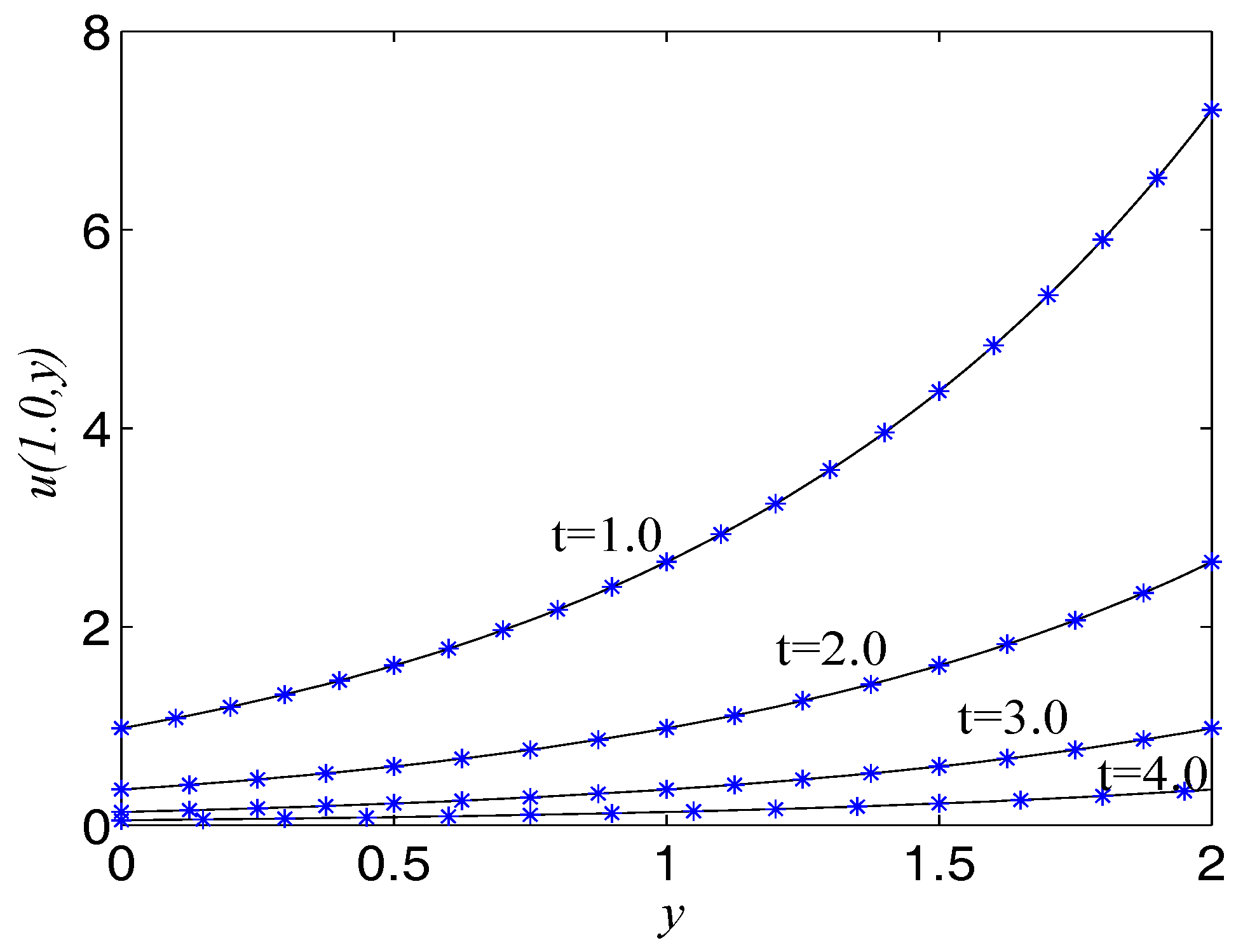
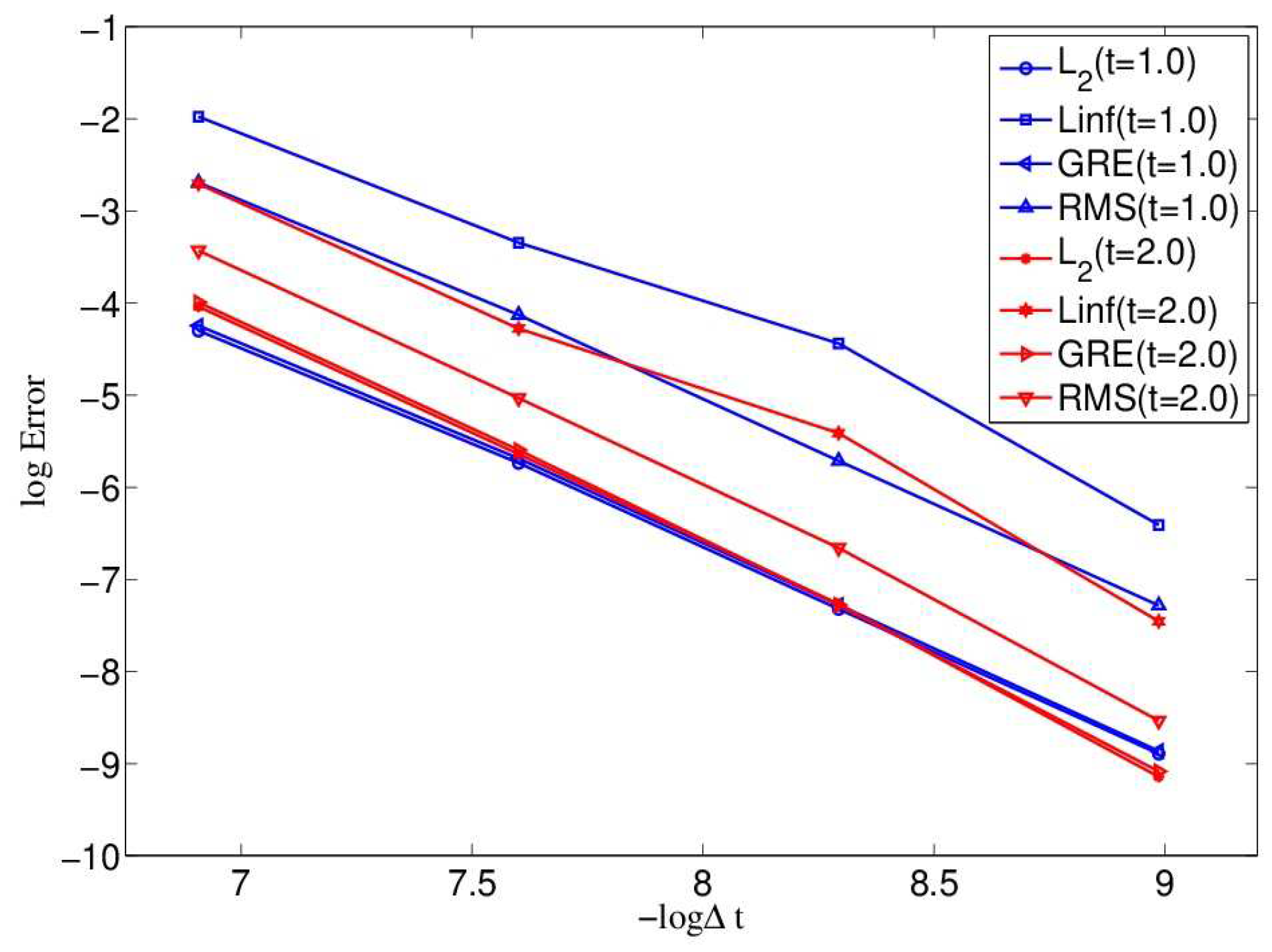
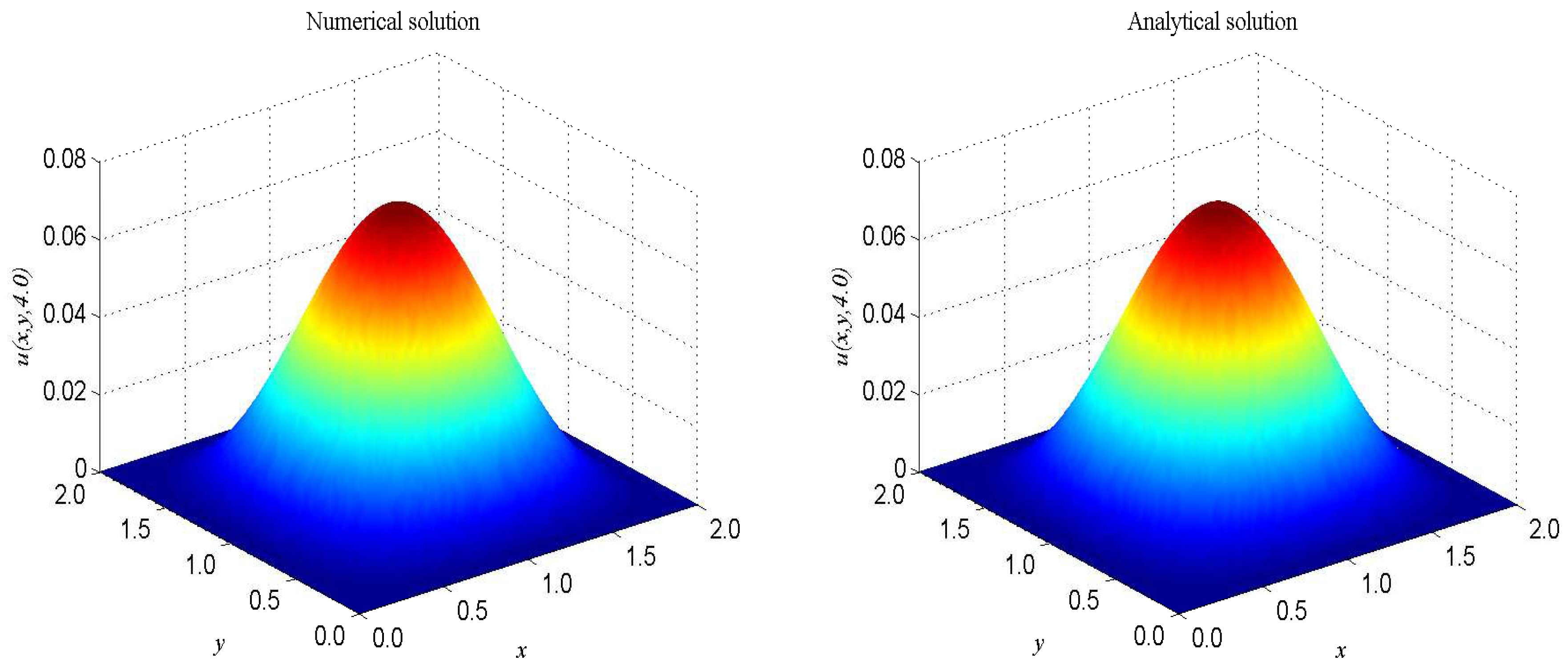
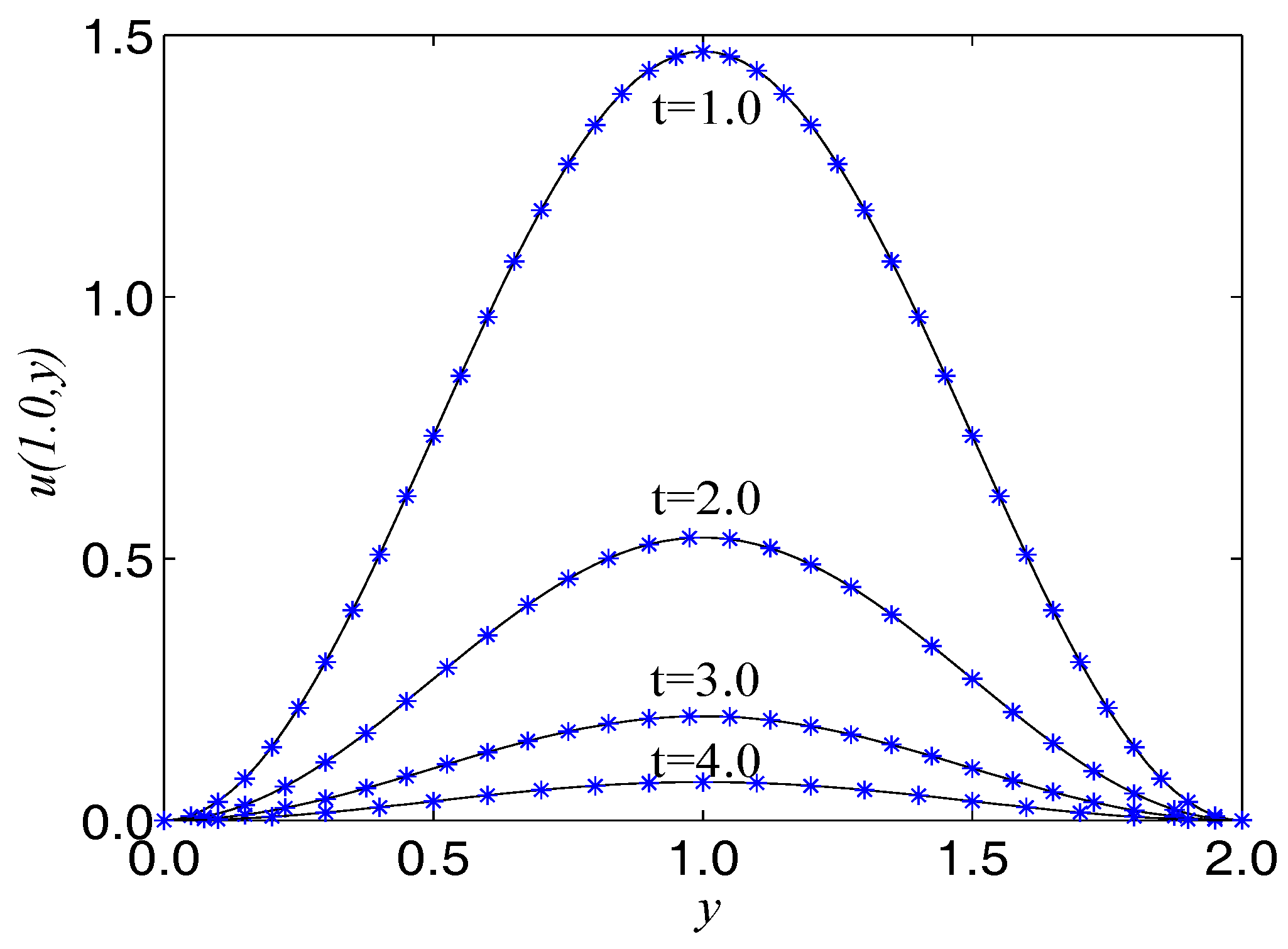
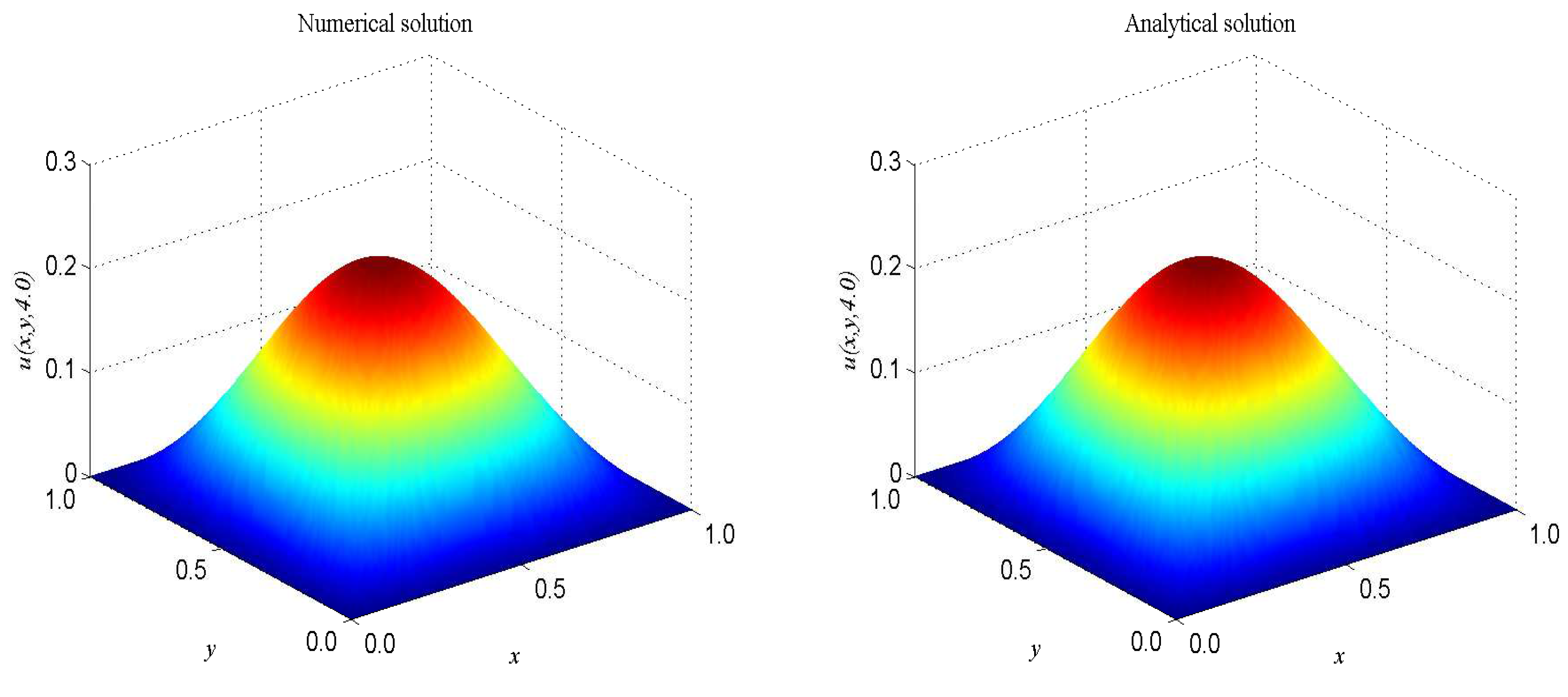
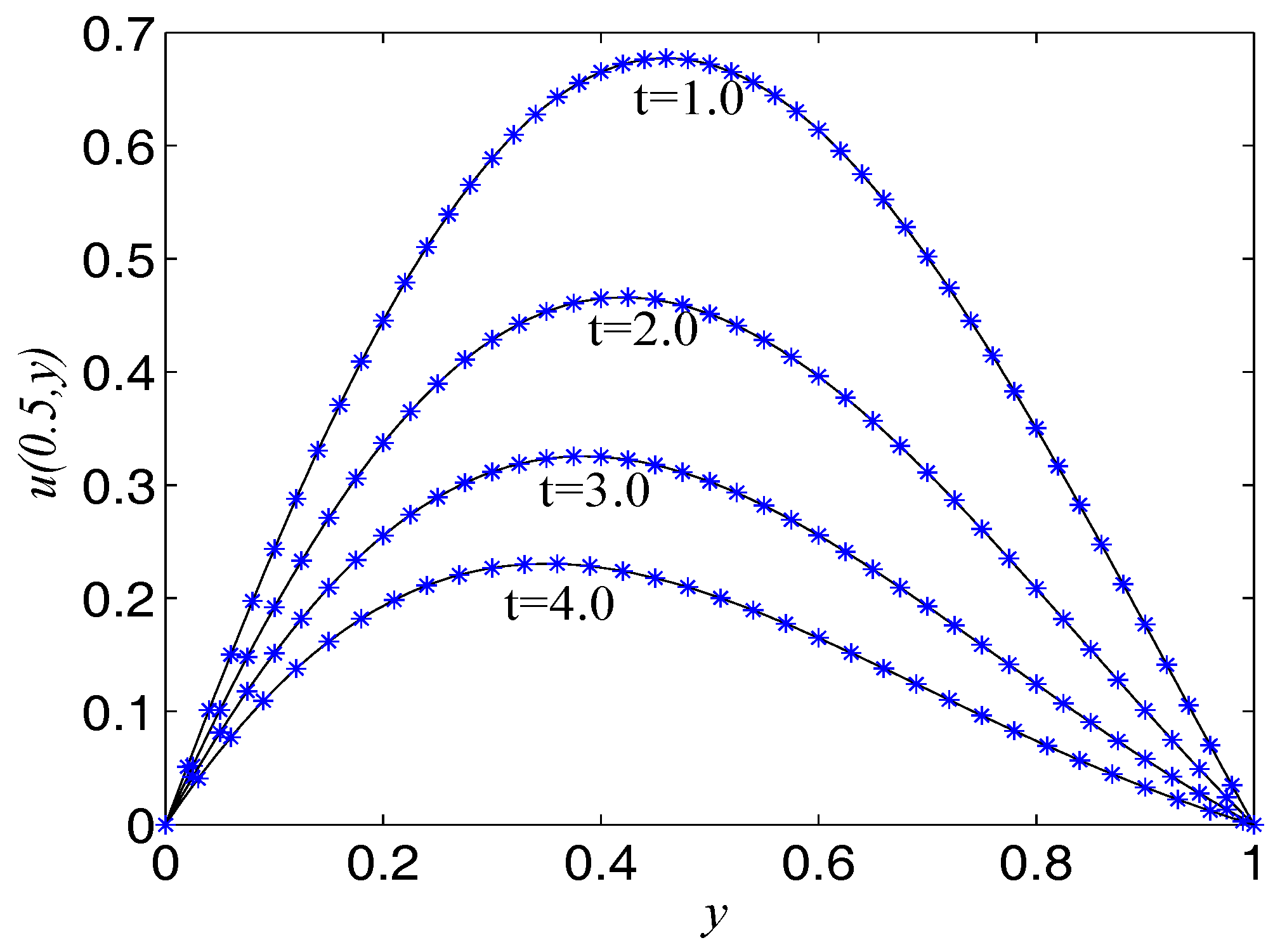
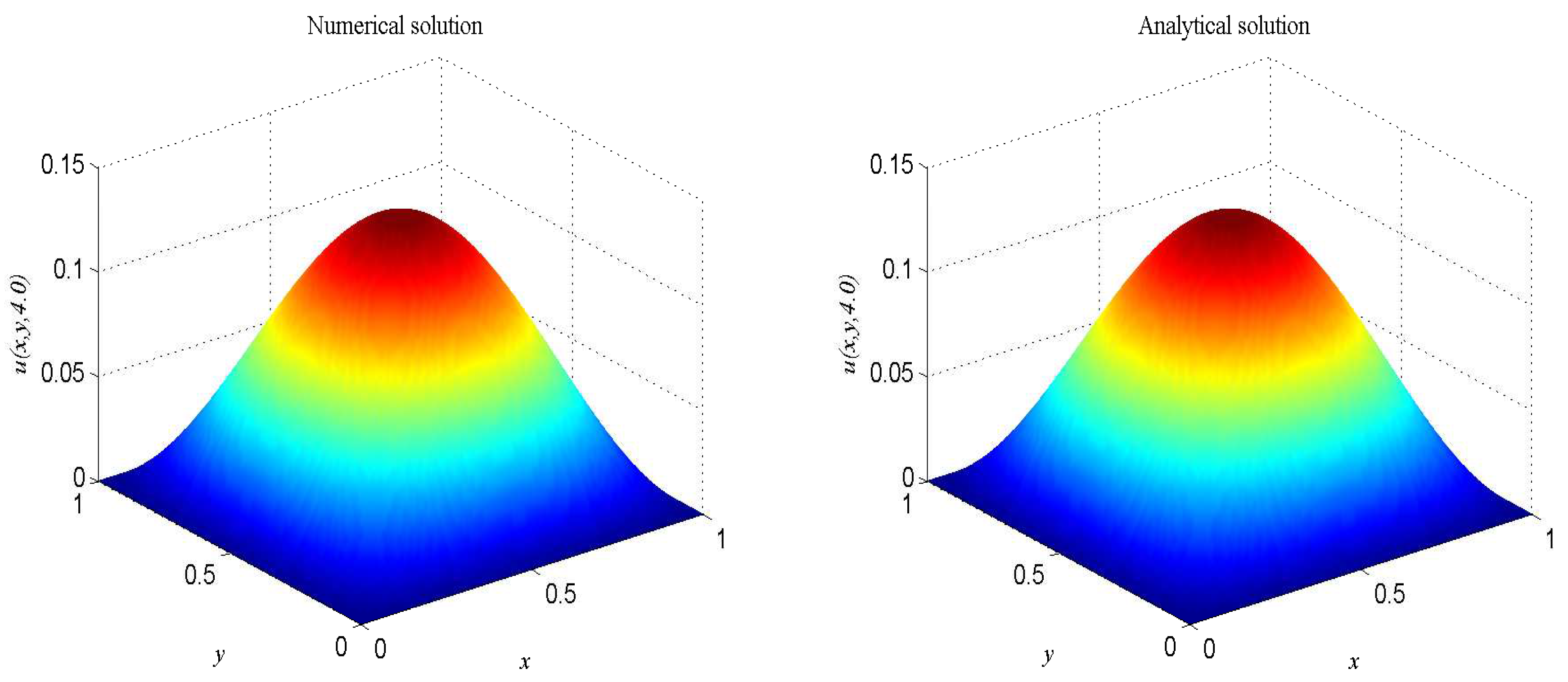
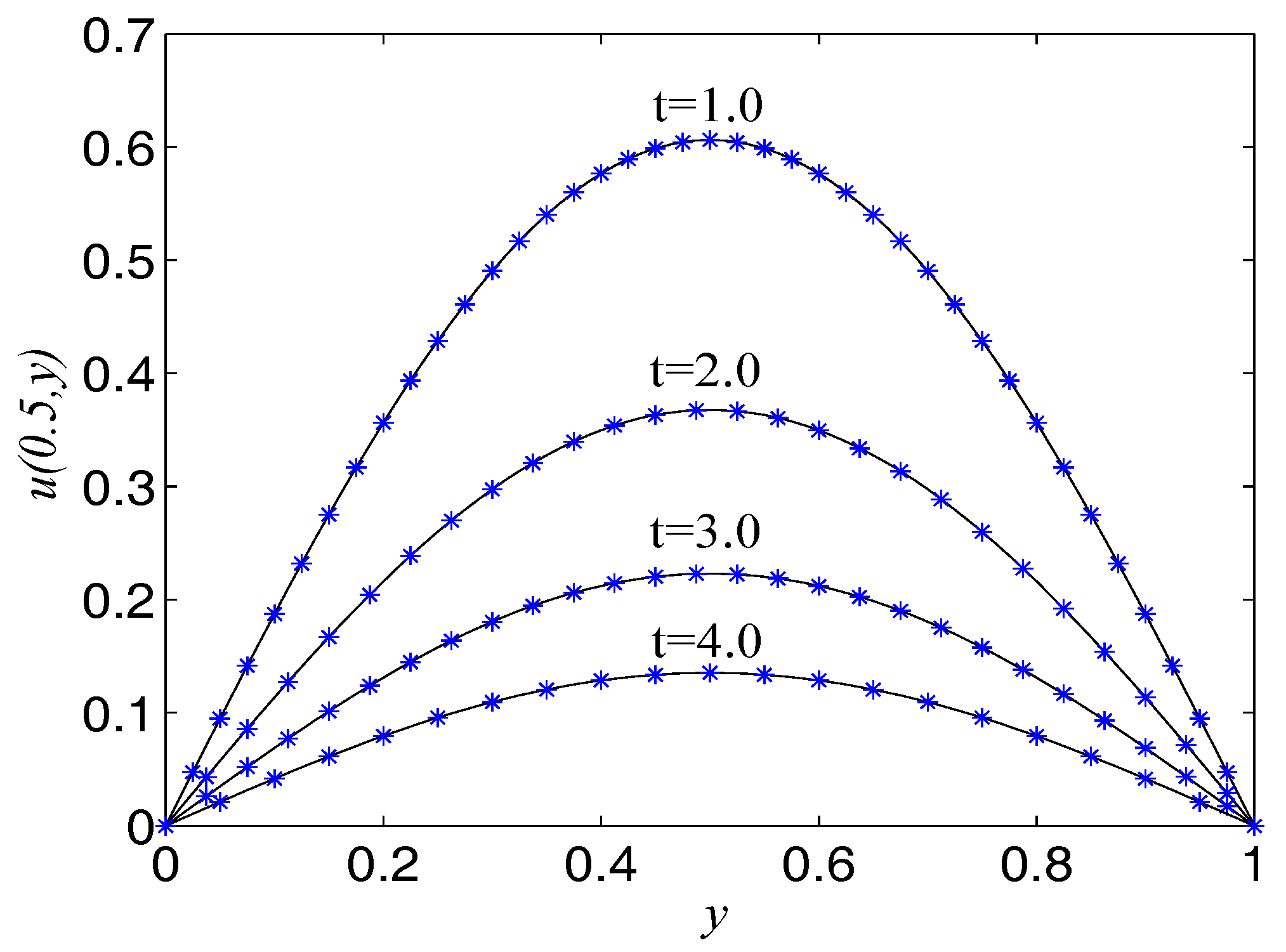
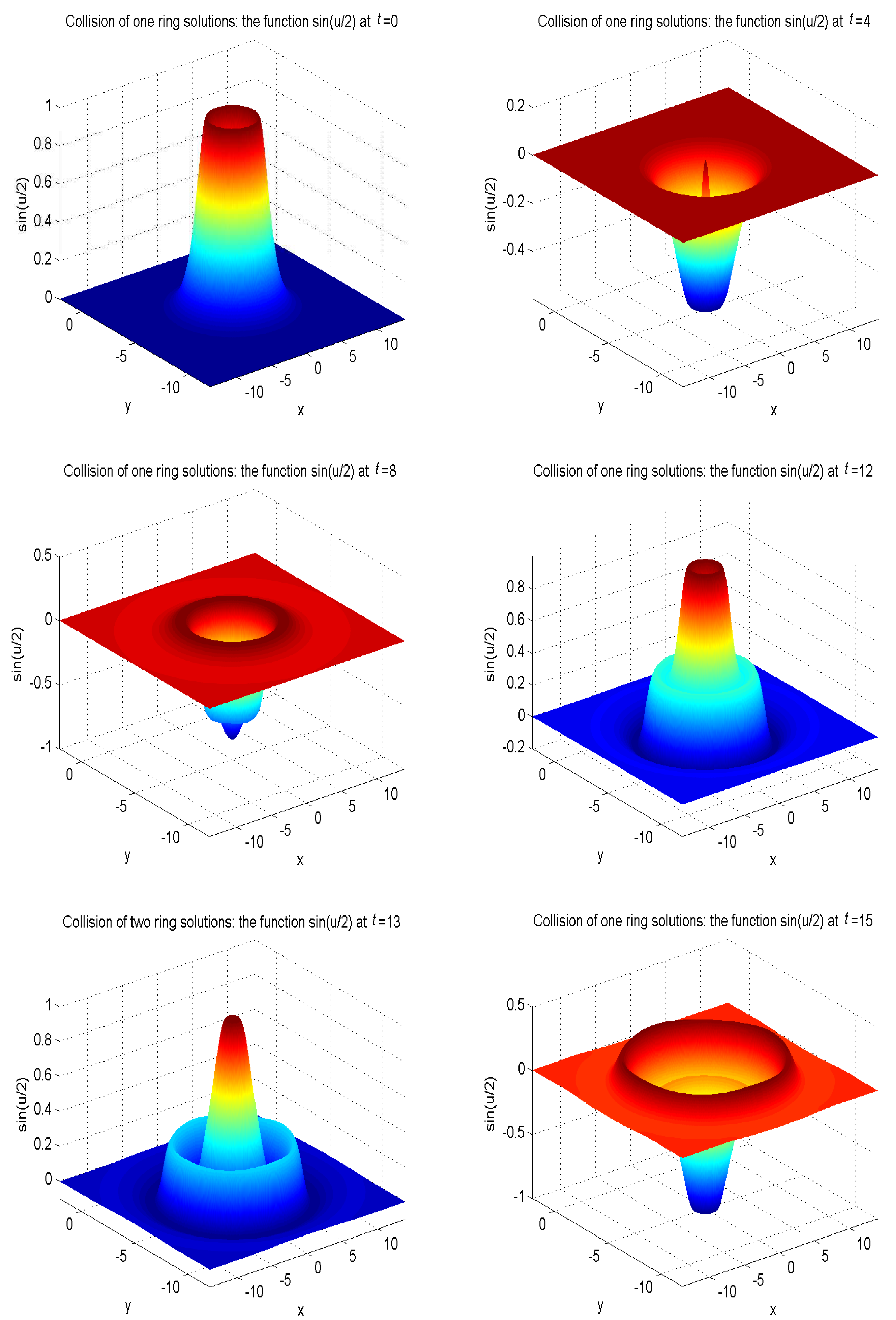
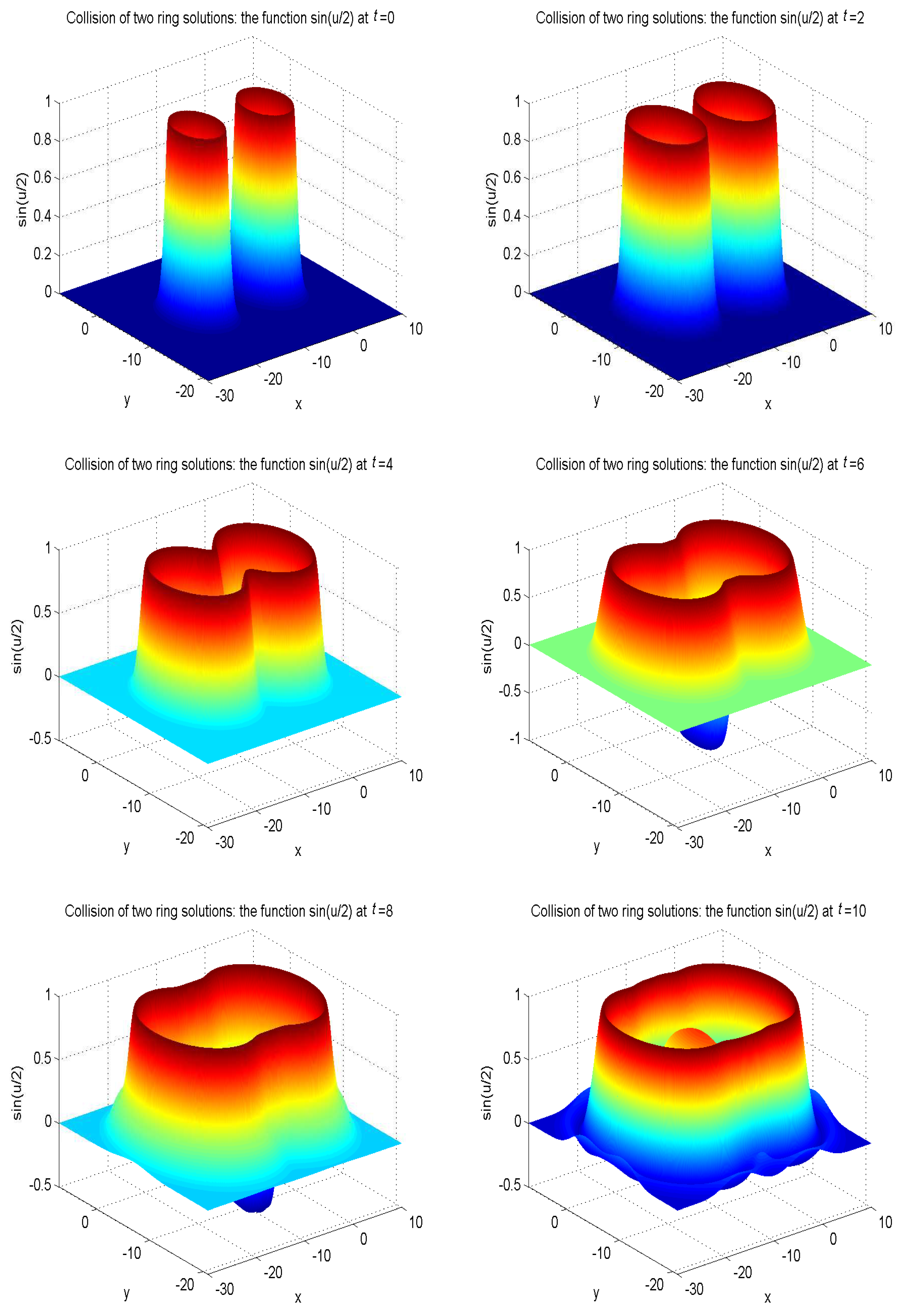
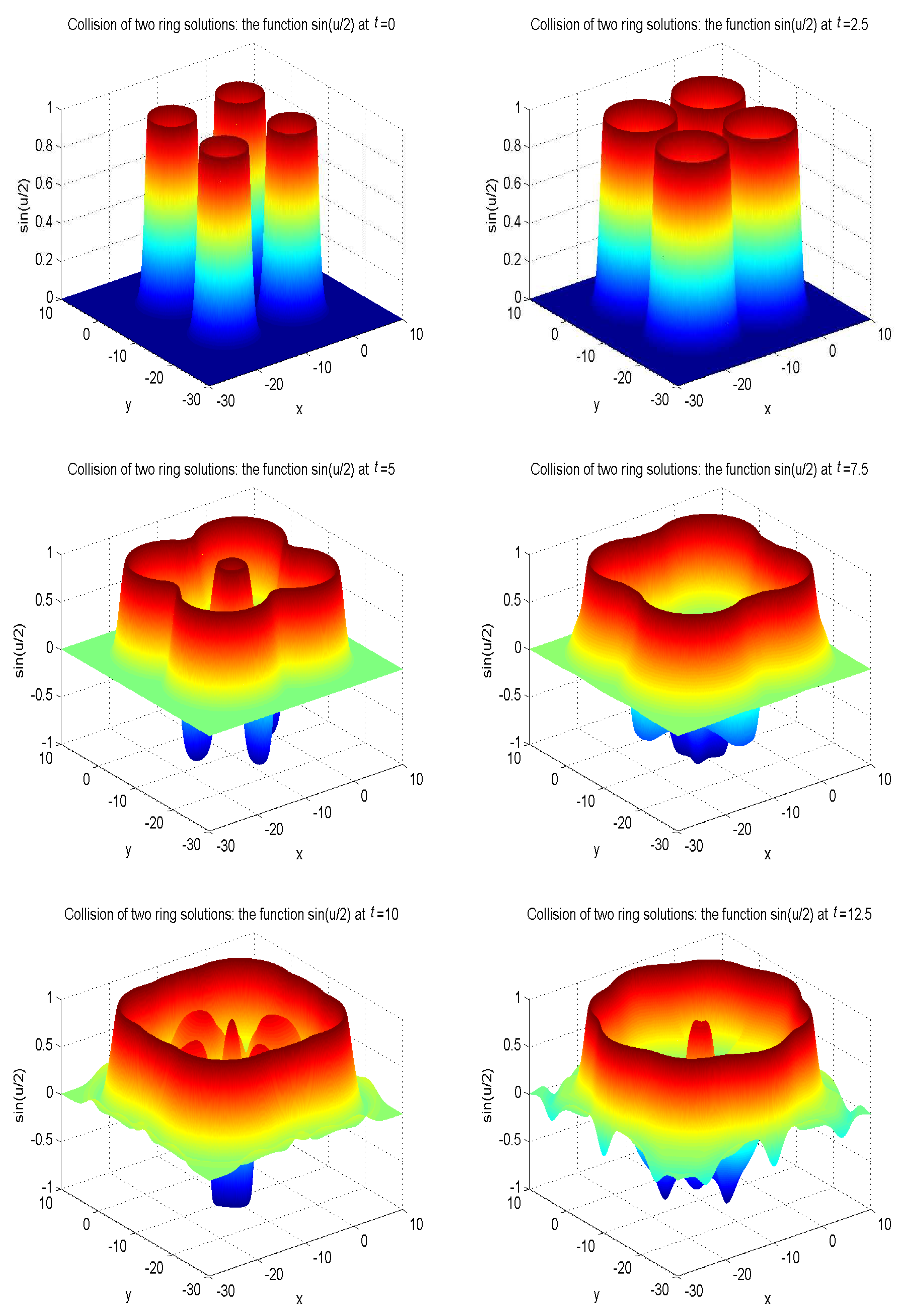
| t | 1.0 | 2.0 | 3.0 | 4.0 |
|---|---|---|---|---|
| t | 1.0 | 2.0 | 3.0 | 4.0 |
|---|---|---|---|---|
| t | 1.0 | 2.0 | 3.0 | 4.0 |
|---|---|---|---|---|
| t | 1.0 | 2.0 | 3.0 | 4.0 |
|---|---|---|---|---|
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, D.; Lai, H.; Shi, B. Mesoscopic Simulation of the (2 + 1)-Dimensional Wave Equation with Nonlinear Damping and Source Terms Using the Lattice Boltzmann BGK Model. Entropy 2019, 21, 390. https://doi.org/10.3390/e21040390
Li D, Lai H, Shi B. Mesoscopic Simulation of the (2 + 1)-Dimensional Wave Equation with Nonlinear Damping and Source Terms Using the Lattice Boltzmann BGK Model. Entropy. 2019; 21(4):390. https://doi.org/10.3390/e21040390
Chicago/Turabian StyleLi, Demei, Huilin Lai, and Baochang Shi. 2019. "Mesoscopic Simulation of the (2 + 1)-Dimensional Wave Equation with Nonlinear Damping and Source Terms Using the Lattice Boltzmann BGK Model" Entropy 21, no. 4: 390. https://doi.org/10.3390/e21040390
APA StyleLi, D., Lai, H., & Shi, B. (2019). Mesoscopic Simulation of the (2 + 1)-Dimensional Wave Equation with Nonlinear Damping and Source Terms Using the Lattice Boltzmann BGK Model. Entropy, 21(4), 390. https://doi.org/10.3390/e21040390




