Measuring Software Modularity Based on Software Networks
Abstract
1. Introduction
- We characterize software modularity as a whole. The existing metrics usually only characterized some modularity-related attributes—either coupling or cohesion. They cannot take both the coupling and cohesion into consideration to character software modularity. In this work, we use software networks to represent software, and apply the metric modularity in complex network research to character software modularity. Thus, we can characterize software modularity as a whole.
- The proposed metric modularity considers the coupling strength between software elements which has been neglected by the existing metrics. Our proposed software network, FCN, is a weighted software network. The weight on the edges denotes the coupling strength between software elements. The calculation of modularity considers the weight on the edge. Thus, our metric is more reasonable since it conforms to the reality of a specific piece of software.
- The proposed modularity is validated theoretically using widely accepted evaluation criteria, and empirically using open source Java software systems. The data set and software used to compute software modularity are available for download [15] (see in Supplementary Materials).
2. Related Work
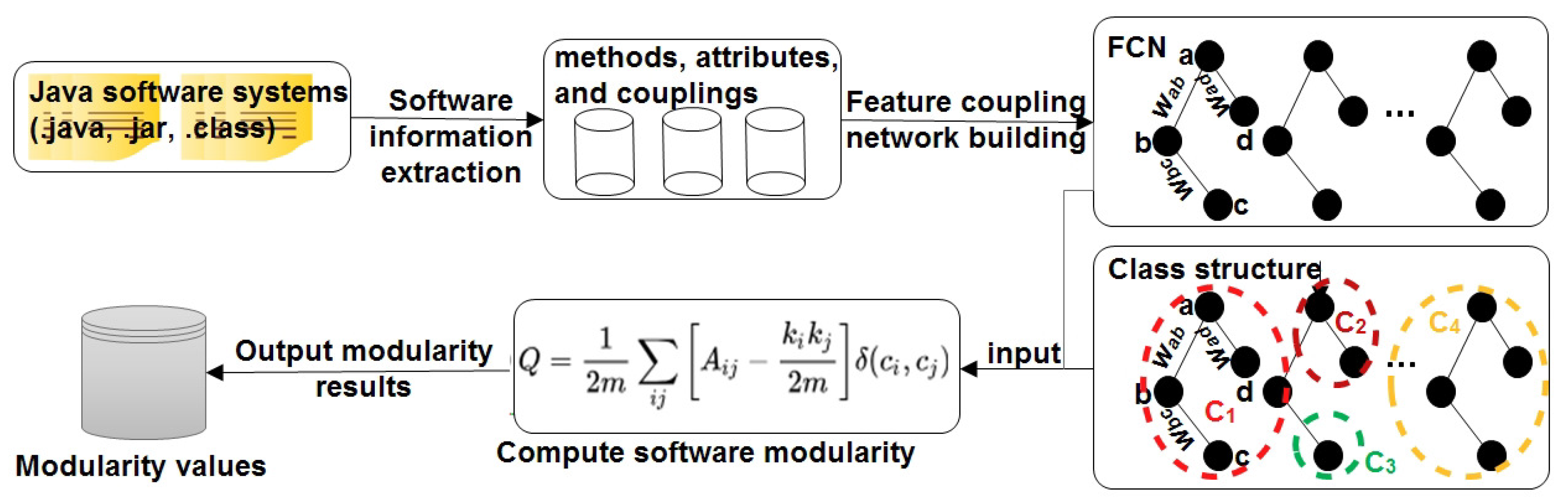
3. The Proposed Approach
3.1. Software Information Extraction
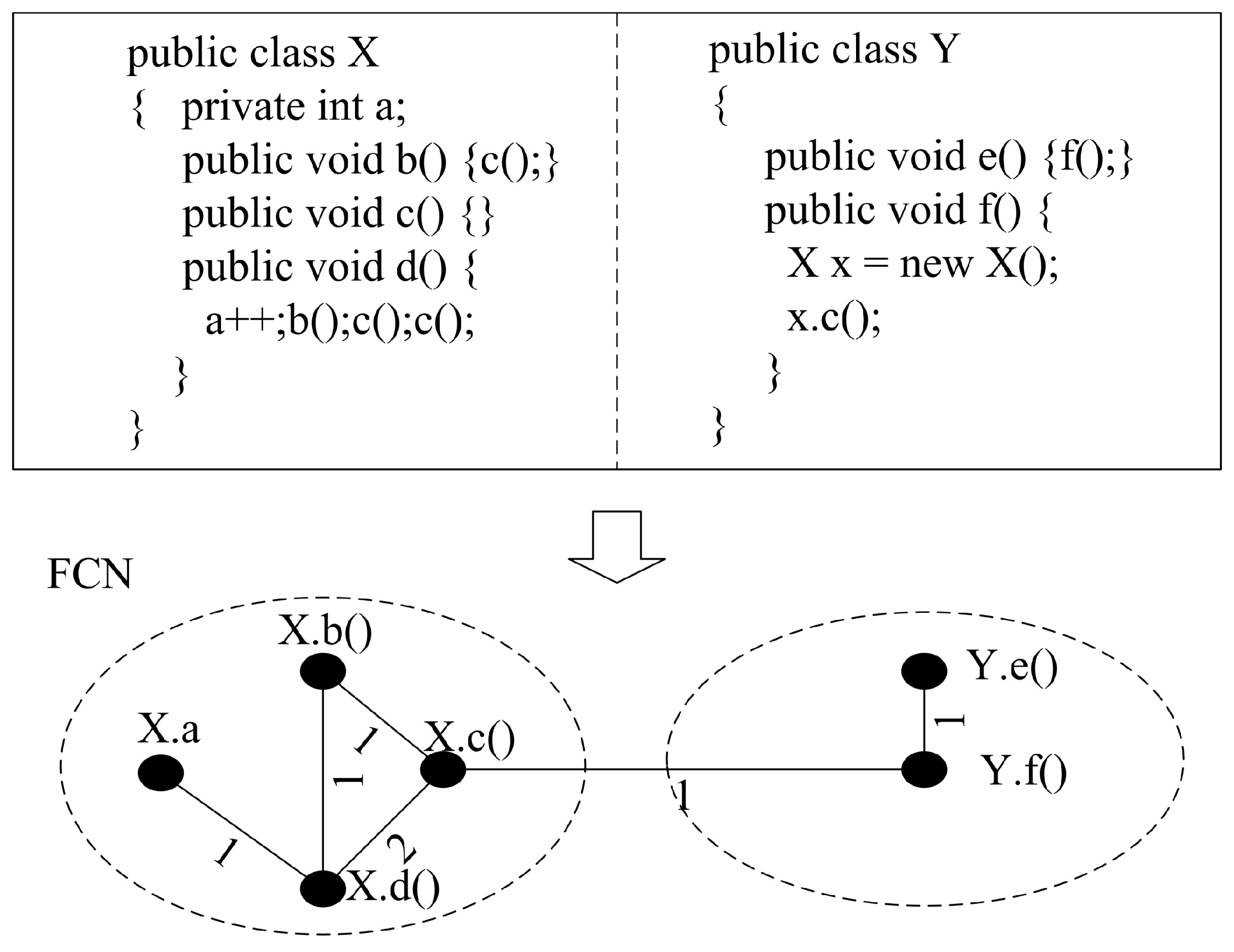
3.2. Feature Coupling Network
3.3. Software Modularity
3.4. Pseudo-Code of the Algorithm to Compute Q
| Algorithm 1 Pseudo-code of the algorithm to compute Q |
| Input: |
| FCN, (number of nodes in FCN), and A ( in FCN). |
| Output: |
| Print the Q. |
|
4. Evaluations
4.1. Research Questions
- RQ1: Does Q satisfy Weyuker’s nine properties? Q is a metric used to measure software modularity and also can be classified into the category of complexity metrics. Weyuker’s nine properties are widely used and famous criteria to validate the usefulness of software complex metrics. We wish to know whether our Q also satisfies Weyuker’s nine properties.
- RQ2: What about the Q values obtained in different software systems? Different software systems may have different Q values. For interests, we wish to examine the Q values obtained in different software systems.
- RQ3: Can Q tell the software using design patterns from two function-equivalent software systems? Using design patterns in software development is regarded as an effective way to improve software quality. However, design pattern implementations may suffer from some of the typical problems and heavily affect the software modularity. As an effective metric, Q should have the ability to reflect such a degradation in software modularity. Thus, we wish to know whether our Q has the ability to tell the software using design pattern from two function-equivalent software systems (one uses design patterns, and the other not).
- RQ4: Is Q scalable to large software systems? In practise, a software metric will be applied to software systems with different sizes. Thus, we wish to know whether Q can be applied to larger software systems.
4.2. Answers to Research Questions
4.2.1. RQ1: Does Q Satisfy Weyuker’s Nine Properties?
4.2.2. RQ2: What about the Q Values Obtained in Different Software Systems?
4.2.3. RQ3: Can Q Tell the Software Using Design Patterns from Two Function-Equivalent Software Systems?
4.2.4. RQ4: Is Q Scalable to Large Software Systems?
- (i)
- Extracting structural information from the source code of software systems.
- (ii)
- Building FCNs for software systems.
- (iii)
- Computing the software modularity according to Equation (2).
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Pressman, R.S. Software Engineering: A Practitioner’s Approach; McGraw-Hill: New York, NY, USA, 1992. [Google Scholar]
- Sullivan, K.J.; Griswold, W.G.; Cai, Y.F.; Hallen, B. The structure and value of modularity in software design. In Proceedings of the 8th European Software Engineering Conference and 9th ACM SIGSOFT International Symposium on Foundations of Software Engineering (ESEC/FSE-9), Vienna, Austria, 10–14 September 2001; pp. 99–108. [Google Scholar]
- Fenton, N.E.; Pfleeger, S.L. Software Metrics: A Rigorous and Practical Approach, 2nd ed.; International Thomson Computer Press: London, UK, 1996. [Google Scholar]
- Sarkar, S.; Kak, A.C.; Rama, G.M. Metrics for measuring the quality of modularization of large-scale object-oriented software. IEEE Trans. Softw. Eng. 2008, 34, 700–720. [Google Scholar] [CrossRef]
- Myers, C.R. Software systems as complex networks: Structure, function, and evolvability of software collaboration graphs. Phys. Rev. E 2003, 68, 046116. [Google Scholar] [CrossRef]
- Potanin, A.; Noble, J.; Frean, M.; Biddle, R. Scale-free geometry in OO programs. Commun. ACM 2005, 48, 99–103. [Google Scholar] [CrossRef]
- Concas, G.; Marchesi, M.; Pinna, S.; Serra, N. Power-laws in a large object-oriented software system. IEEE Trans. Softw. Eng. 2007, 33, 687–708. [Google Scholar] [CrossRef]
- Pan, W.F.; Ming, H.; Chang, C.K; Yang, Z.J.; Kim, D.-K. ElementRank: Ranking Java Software Classes and Packages using Multilayer Complex Network-Based Approach. IEEE Trans. Softw. Eng. 2019. [Google Scholar] [CrossRef]
- Canfora, G.; Cerulo, L.; Cimitile, M.; Penta, M.D. How changes affect software entropy: An empirical study. Empir. Softw. Eng. 2014, 19, 1–38. [Google Scholar] [CrossRef]
- Li, H.; Hao, L.Y.; Chen, R. Multi-level formation of complex software systems. Entropy 2016, 18, 178. [Google Scholar] [CrossRef]
- Pan, W.F.; Li, B.; Ma, Y.T.; Liu, J. Class structure refactoring of object-oriented softwares using community detection in dependency networks. Front. Comput. Sci. 2009, 3, 396–404. [Google Scholar] [CrossRef]
- Pan, W.F.; Song, B.B.; Li, K.S.; Zhang, K.J. Identifying key classes in object-oriented software using generalized k-core decomposition. Future Gener. Comput. Syst. 2018, 81, 188–202. [Google Scholar] [CrossRef]
- Pan, W.F.; Li, B.; Ma, Y.T.; Liu, J. Test case prioritization based on complex software networks. Acta Electron. Sin. 2012, 40, 2456–2465. [Google Scholar]
- Weyuker, E.J. Evaluating software complexity measures. IEEE Trans. Softw. Eng. 1988, 14, 1357–1365. [Google Scholar] [CrossRef]
- Apple Inc. Available online: https://www.icloud.com/iclouddrive/0zRViWdWuiQkYTueyNbCIB49A#2018modularity (accessed on 23 March 2019).
- Chidamber, S.R.; Kemerer, C.F. A metrics suite for object-oriented design. IEEE Trans. Softw. Eng. 1994, 20, 476–493. [Google Scholar] [CrossRef]
- Eder, J.; Kappel, G.; Schre, M. Coupling and cohesion in object-oriented systems. In Proceedings of the Conference on Information and Knowledge; ACM Press: New York, NY, USA, 1992. [Google Scholar]
- Ott, L.M.; Bieman, J.M. Program slices as an abstraction for cohesion measurement. Inf. Softw. Technol. 1998, 40, 691–699. [Google Scholar] [CrossRef]
- Bieman, J.M.; Kang, B.K. Cohesion and reuse in an objectoriented system. In Proceedings of the Symposium on Software Reusability (SSR 1995), Seattle, WA, USA, 29–30 April 1995; pp. 259–262. [Google Scholar]
- Bansiya, J.; Davis, C. A hierarchical model for objectoriented design quality assessment. IEEE Trans. Softw. Eng. 2002, 28, 4–17. [Google Scholar] [CrossRef]
- Briand, L.C.; Morasca, S.; Basili, V.R. Defining and validating measures for object-based high-level design. IEEE Trans. Softw. Eng. 1999, 25, 722–743. [Google Scholar] [CrossRef]
- Morris, K. Metrics for Object-Oriented Software Development Environments. Master’s Thesis, Sloan School of Management, MIT, Cambridge, MA, USA, 1989. [Google Scholar]
- Patel, S.; Chu, W.C.; Baxter, R. A measure for composite module cohesion. In Proceedings of the 14th International Conference on Software Engineering, Melbourne, Australia, 11–15 May 1992; pp. 38–48. [Google Scholar]
- Martin, R. Agile Software Development, Principles, Patterns, and Practices; Prentice-Hall: New York, NY, USA, 2002. [Google Scholar]
- Lee, Y.S.; Liang, B.S. Measuring the coupling and cohesion of an object-oriented program based on information flow. In Proceedings of the International Conference on Software Quality, Maribor, Slovenia, 6–8 November 1995; pp. 81–90. [Google Scholar]
- Jenkins, S.; Kirk, S.R. Software architecture graphs as complex networks: A novel parttion scheme to measure stability and evolution. Inf. Sci. 2007, 177, 2587–2601. [Google Scholar] [CrossRef]
- Qu, Y.; Guan, X.H.; Zheng, Q.H.; Liu, T.; Wang, L.D.; Hou, Y.Q.; Yang, Z.J. Exploring community structure of software call graph and its applications in class cohesion measurement. J. Syst. Softw. 2015, 108, 193–210. [Google Scholar] [CrossRef]
- Gu, A.H.; Zhou, X.F.; Li, Z.H.; Li, Q.F.; Li, L. Measuring Object-Oriented Class Cohesion Based on Complex Networks. Arab. J. Sci. Eng. 2017, 42, 3551–3561. [Google Scholar] [CrossRef]
- Zhang, J.; Wu, J.J.; Xia, Y.X.; Ye, F.H. Measuring cohesion of software systems using weighted directed complex networks. In Proceedings of the 2018 IEEE International Symposium on Circuits and Systems (ISCAS 2018), Florence, Italy, 27–30 May 2018; pp. 1–5. [Google Scholar]
- Pan, W.F.; Li, B.; Jiang, B.; Liu, K. RECODE: Software package refactoring via community detection in bipartite software networks. Adv. Complex Syst. 2014, 17, 1450006. [Google Scholar] [CrossRef]
- Mancoridis, S.; Mitchell, B.S.; Rorres, C.; Chen, Y.; Gansner, E.R. Using automatic clustering to produce high-level system organizations of source code. In Proceedings of the Sixth International Workshop on Program Comprehension (IWPC 1998), Ischia, Italy, 26 June 1998; pp. 45–53. [Google Scholar]
- Tucker, A.; Swift, S.; Liu, X. Variable grouping multivariate time series via correlation. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2001, 31, 235–245. [Google Scholar] [CrossRef]
- Newman, M.E.J. Fast algorithm for detecting community structure in networks. Phys. Rev. 2004, 69, 066133. [Google Scholar] [CrossRef]
- Cherniavsky, J.C.; Smith, C.H. On Weyuker’s axioms for software complexity measures. IEEE Trans. Softw. Eng. 1991, 17, 636–638. [Google Scholar] [CrossRef]
- Gursaran; Roy, G. On the applicability of Weyuker Property 9 to object-oriented structural inheritance complexity metrics. IEEE Trans. Softw. Eng. 2001, 27, 381–384. [Google Scholar] [CrossRef]
- Harrison, W. An entropy-based measure of software complexity. IEEE Trans. Softw. Eng. 1992, 18, 1025–1029. [Google Scholar] [CrossRef]
- Tsantalis, N.; Chatzigeorgous, E.; Stephanides, G.; Halkidis, S.T. Design pattern detection using similarity scoring. IEEE Trans. Softw. Eng. 2006, 32, 896–909. [Google Scholar] [CrossRef]
- Monteiro, M.P.; Gomes, J. Implementing design patterns in Object Teams. Softw. Pract. Exp. 2013, 43, 1519–1551. [Google Scholar] [CrossRef]


| Systems | Domain | Directory | KLOC | URLs |
|---|---|---|---|---|
| jmeter-3.0 | testing | src/core | 37.951 | https://jmeter.apache.org/ |
| jfreechart-1.0.19 | tool | source | 97.880 | http://www.jfree.org/ |
| ant-1.6.1 | parsers | src/main | 81.515 | https://ant.apache.org/ |
| struts-2.5.2 | middleware | src/core | 48.347 | https://struts.apache.org/ |
| freemind-1.0.1 | data visualization | src | 45.049 | http://freemind.sourceforge.net/ |
| bcel-6.0 | programming language | src | 29.206 | https://commons.apache.org/ |
| mybatis-3 | middleware | src | 20.385 | http://www.mybatis.org |
| colt-1.2.0 | sdk | src | 34.709 | https://dst.lbl.gov/ACSSoftware/ |
| jbullet-2.72.2.4 | middleware | com | 22.297 | http://jbullet.advel.cz/ |
| junit4-r4.12 | testing | src | 9.296 | https://junit.org/junit4/ |
| jxtaim-0.1i | communications | src | 12.423 | http://jxtaim.sourceforge.net/ |
| commons-email-1.4 | communications | src | 2.705 | https://commons.apache.org/ |
| Systems | Q | ||
|---|---|---|---|
| jmeter-3.0 | 3339 | 2342 | 0.4292 |
| jfreechart-1.0.19 | 11,946 | 9967 | 0.2429 |
| ant-1.6.1 | 11,858 | 14,437 | 0.3589 |
| struts-2.5.2 | 5089 | 3301 | 0.5099 |
| freemind-1.0.1 | 6620 | 8742 | 0.4062 |
| bcel-6.0 | 3984 | 3667 | 0.3113 |
| mybatis-3 | 3193 | 3131 | 0.3131 |
| colt-1.2.0 | 4735 | 6497 | 0.4650 |
| jbullet-2.72.2.4 | 3288 | 4065 | 0.3603 |
| junit4-r4.12 | 1576 | 1406 | 0.3277 |
| jxtaim-0.1i | 1531 | 1429 | 0.3039 |
| commons-email-1.4 | 375 | 256 | 0.3422 |
| Design Pattern | Version | LOC | Q | ||
|---|---|---|---|---|---|
| Builder | before | 130 | 11 | 8 | 0.2656 |
| after | 161 | 29 | 19 | 0.2041 | |
| Composite | before | 59 | 10 | 9 | −0.0787 |
| after | 60 | 11 | 8 | −0.1194 | |
| Decorator | before | 34 | 13 | 6 | −0.1667 |
| after | 39 | 15 | 5 | −0.1800 | |
| Iterator | before | 112 | 4 | 1 | 0 |
| after | 174 | 12 | 7 | −0.0078 | |
| State | before | 61 | 5 | 4 | 0.1550 |
| after | 83 | 11 | 5 | 0.1200 |
| Step | jmeter | jfreechart | ant | struts | freemind | bcel | mybatis |
| i | 6 s | 35 s | 30 s | 8 s | 15 s | 11 s | 5 s |
| ii | 0 s | 0 s | 0 s | 0 s | 0 s | 0 s | 0 s |
| iii | 0 s | 0 s | 0 s | 0 s | 0 s | 0 s | 0 s |
| Step | colt | jbullet | junit4 | jxtaim | commons-email | ||
| i | 13 s | 7 s | 2 s | 2 s | 0 s | ||
| ii | 0 s | 0 s | 0 s | 0 s | 0 s | ||
| iii | 0 s | 0 s | 0 s | 0 s | 0 s |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiang, Y.; Pan, W.; Jiang, H.; Zhu, Y.; Li, H. Measuring Software Modularity Based on Software Networks. Entropy 2019, 21, 344. https://doi.org/10.3390/e21040344
Xiang Y, Pan W, Jiang H, Zhu Y, Li H. Measuring Software Modularity Based on Software Networks. Entropy. 2019; 21(4):344. https://doi.org/10.3390/e21040344
Chicago/Turabian StyleXiang, Yiming, Weifeng Pan, Haibo Jiang, Yunfang Zhu, and Hao Li. 2019. "Measuring Software Modularity Based on Software Networks" Entropy 21, no. 4: 344. https://doi.org/10.3390/e21040344
APA StyleXiang, Y., Pan, W., Jiang, H., Zhu, Y., & Li, H. (2019). Measuring Software Modularity Based on Software Networks. Entropy, 21(4), 344. https://doi.org/10.3390/e21040344





