A New Extension of the Generalized Half Logistic Distribution with Applications to Real Data
Abstract
1. Introduction
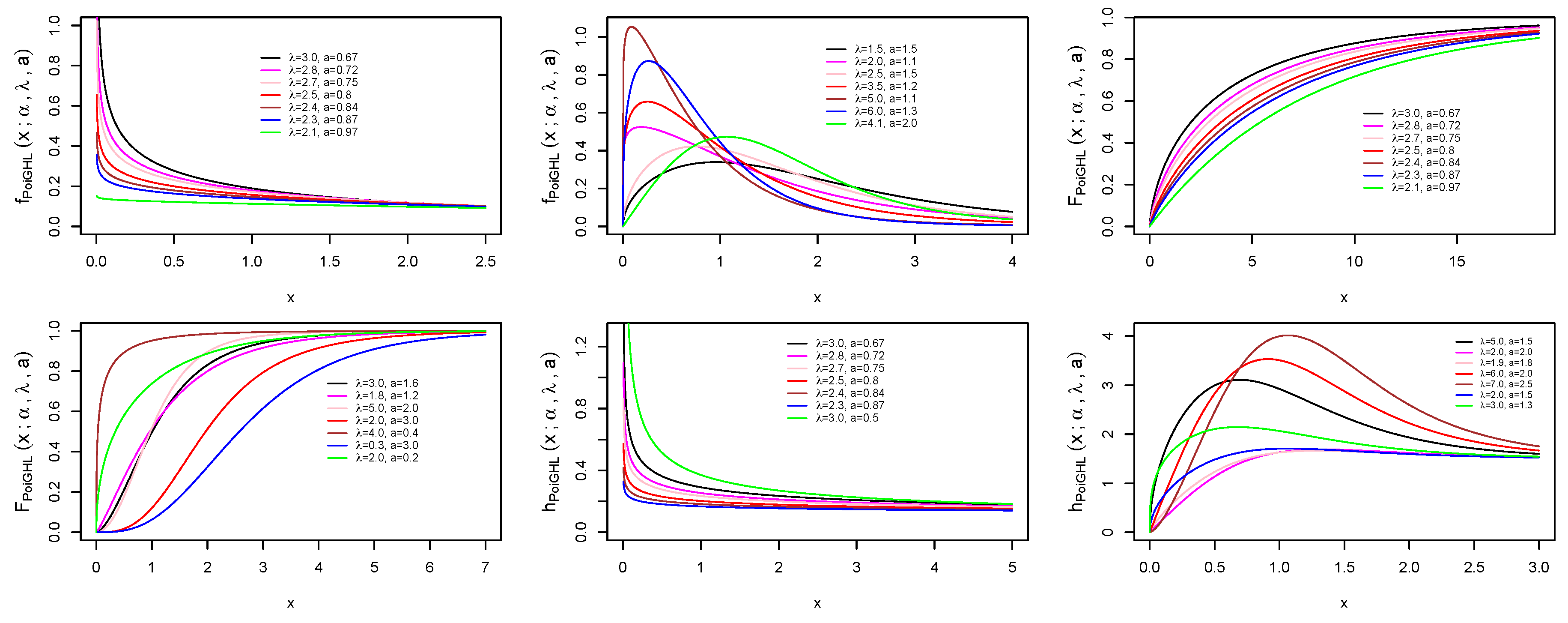
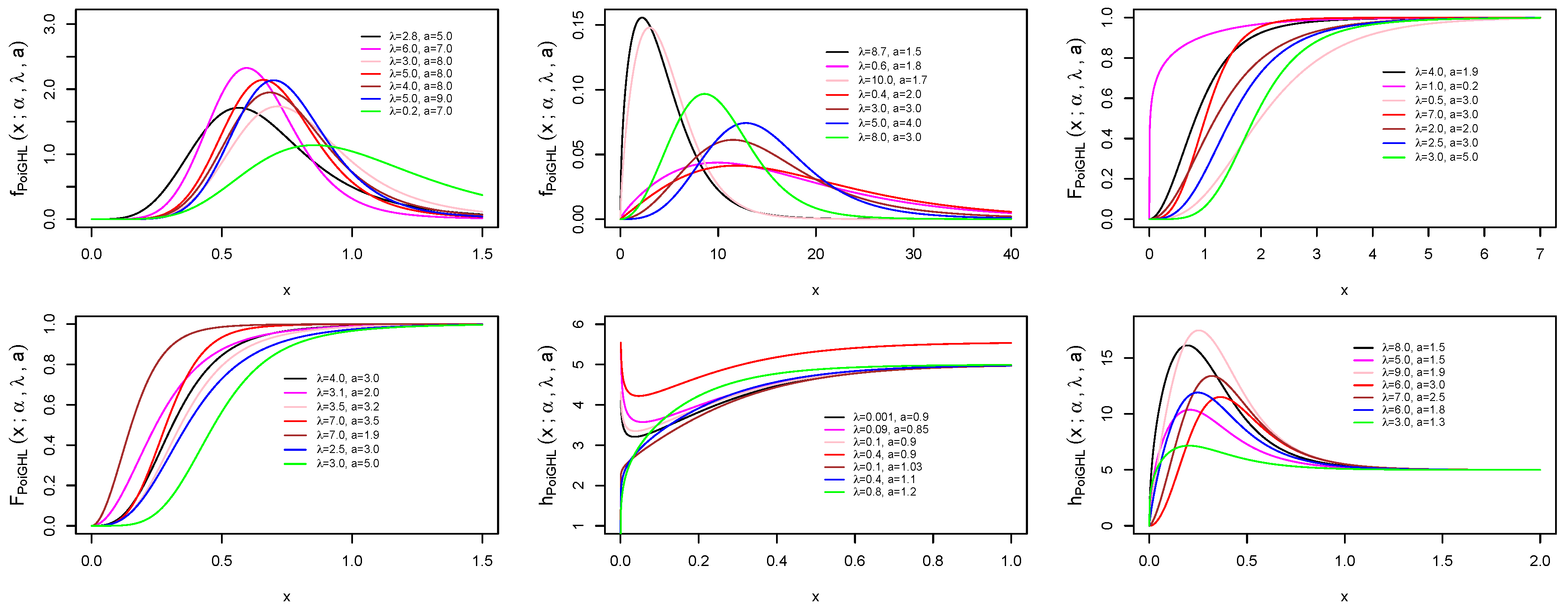
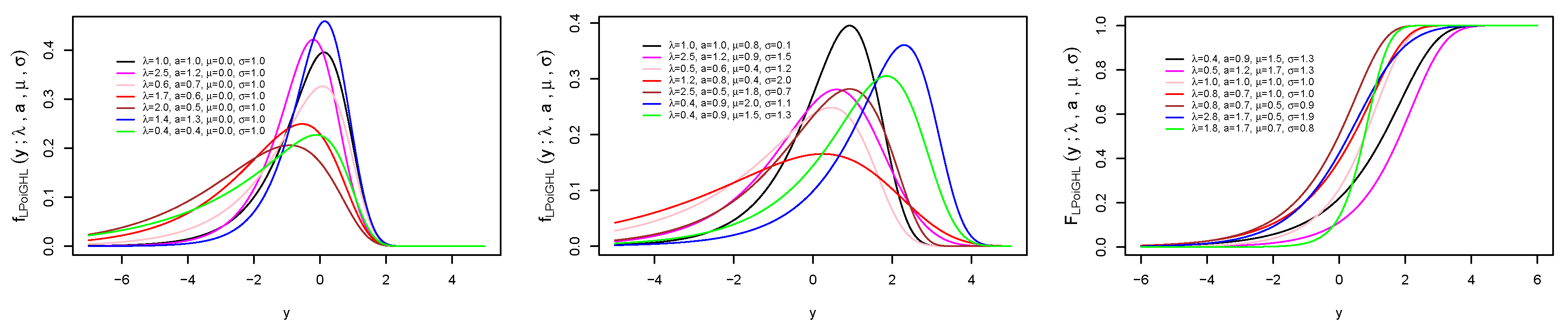
2. The PoiGHL Model and Properties
2.1. Quantiles
Quantile Series Expansion
2.2. Moments, Mean Deviations, Bonferroni and Lorenz Curves
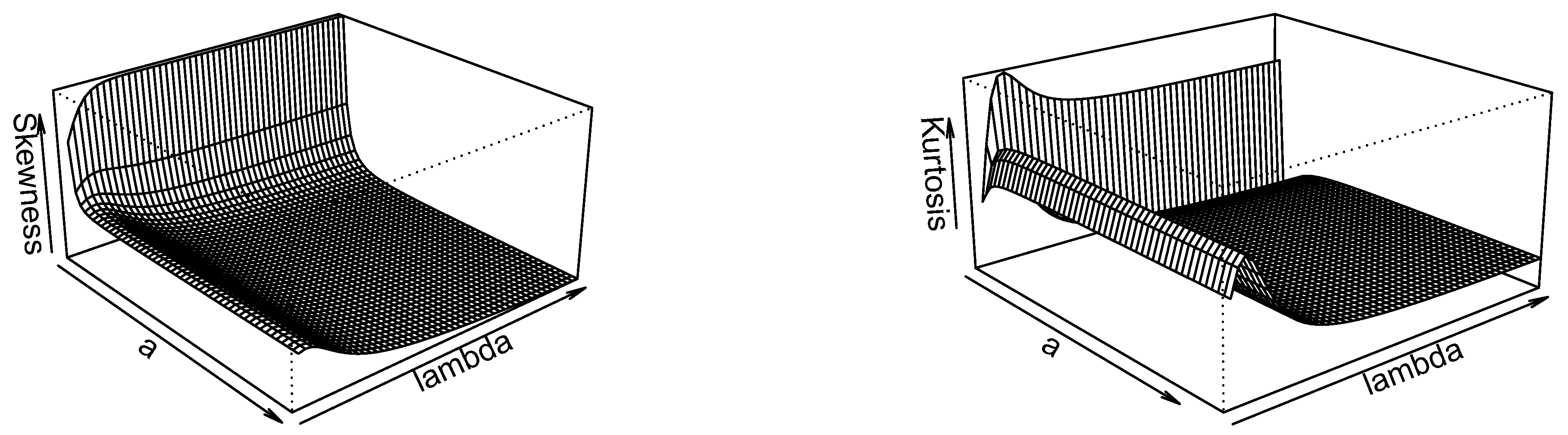
2.2.1. Moments
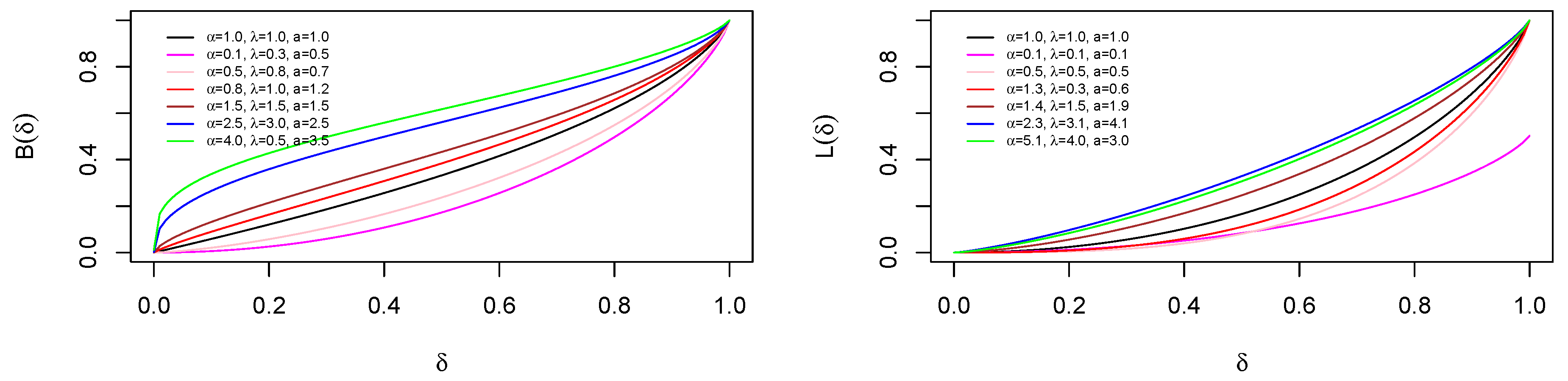
2.2.2. Mean Deviations, Bonferroni and Lorenz Curves
2.3. Moments of Residual Life
2.4. Order Statistics
2.5. Probability Weighted Moments
2.6. Log-PoiGHL Distribution
Some Related Distributions
3. Entropies and Kullback-Leibler Divergence
3.1. Shannon and Renyi Entropies
3.2. Kullback-Leibler Divergence
4. Characterization of PoiGHL Sub Model by Truncated Moments
5. Estimation and Inference
5.1. Simulation Study
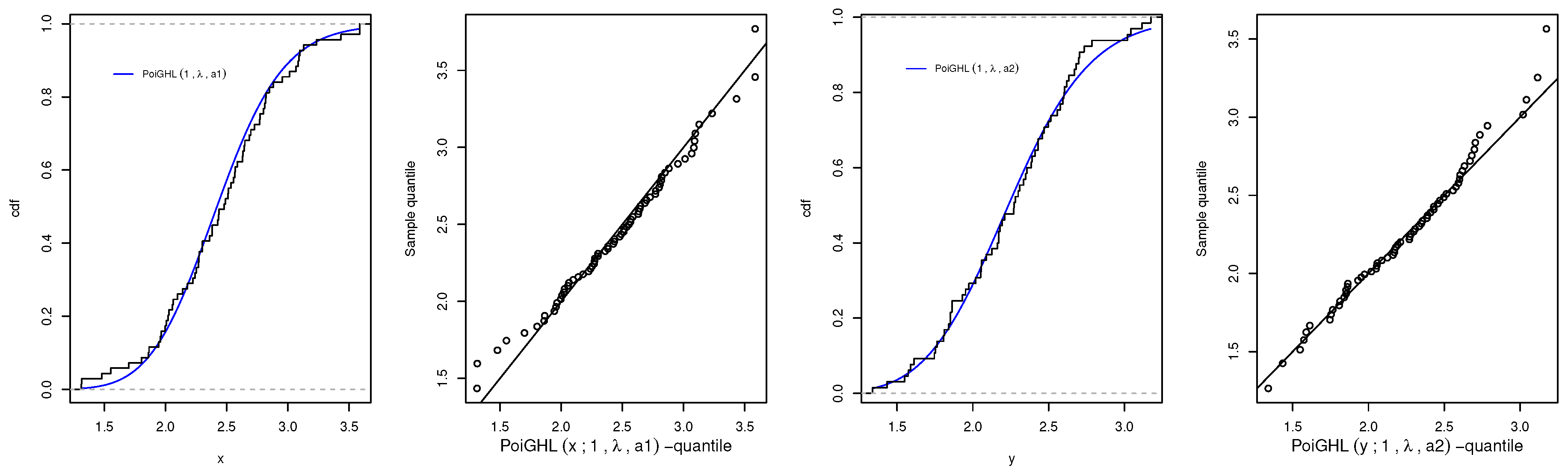
6. Stress-Strength Reliabilty Analysis
6.1. Estimation of R with a Common Parameter
6.1.1. MLE and Asymptotic Confidence Interval of R
6.1.2. Simulation Results
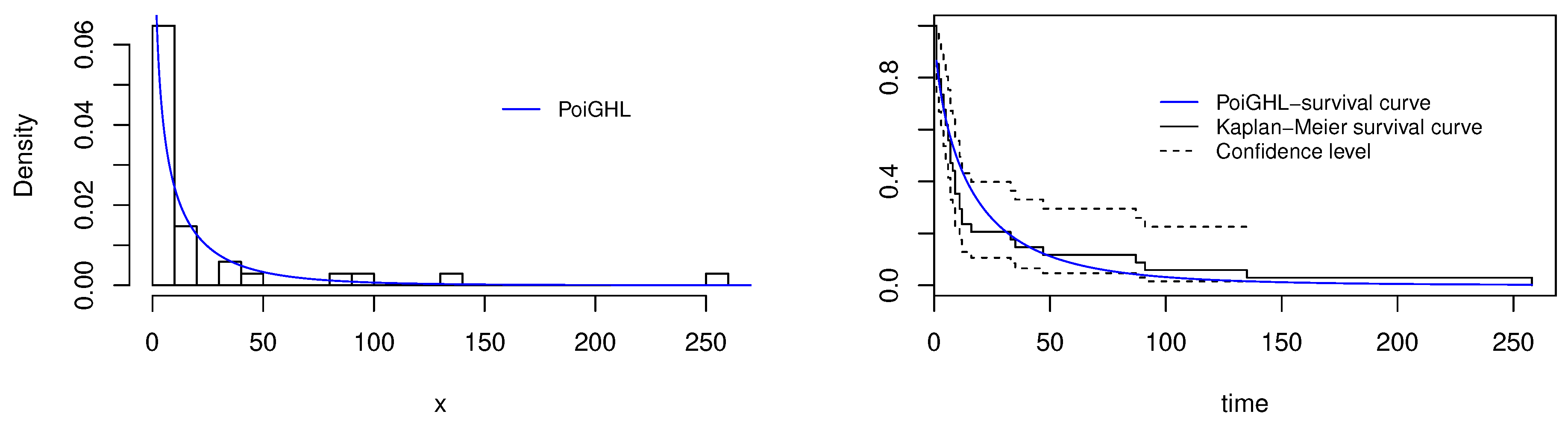
7. Real Data Applications
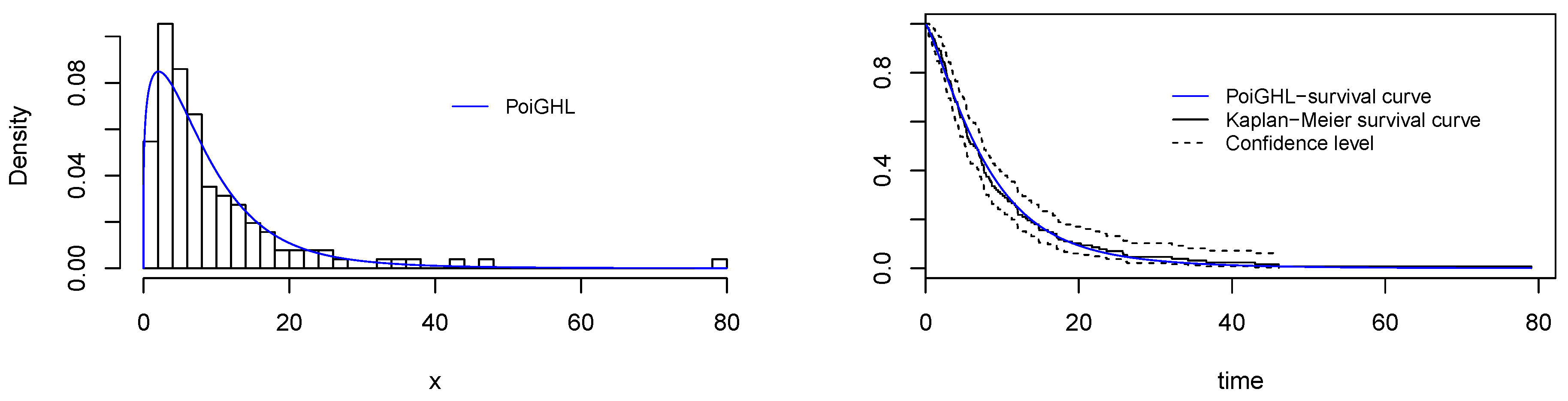
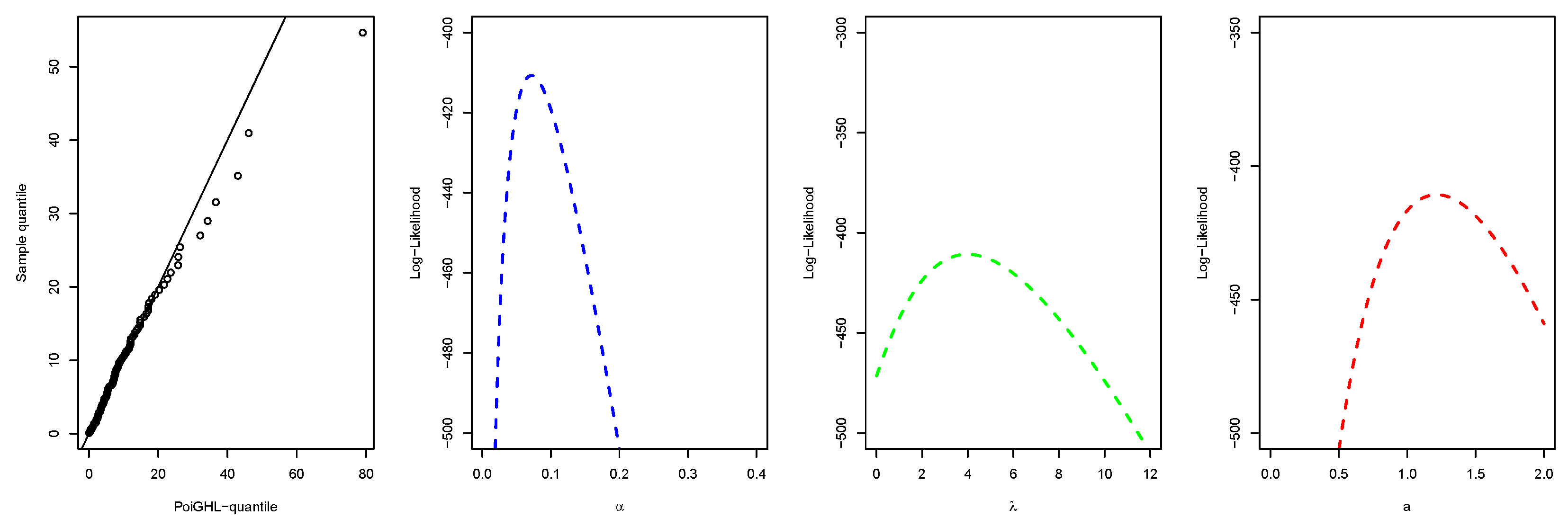
7.1. Application I
- Mc-Donald half-logistic (McHL) [42] with cdf defined by,.
- Beta half-logistic (BHL) [43],
- Kumaraswamy half-logistic (KwHL) [44],
- Type I half-logistic Burr X (TIHLBx) [45],
- Poisson odd generalize exponential-half logistic (POGE-HL) [11],
- Generalized half logistic poisson (GHLP) [46],
- Power half logistic (PwHL) [15], .
- Olapade half logistic (OHL) [16], .
- Poisson half logistic (PHL) [13], .
- Exponentiated generalized standardized half logistic (EGSHL) [47],
- Half logistic (HL)
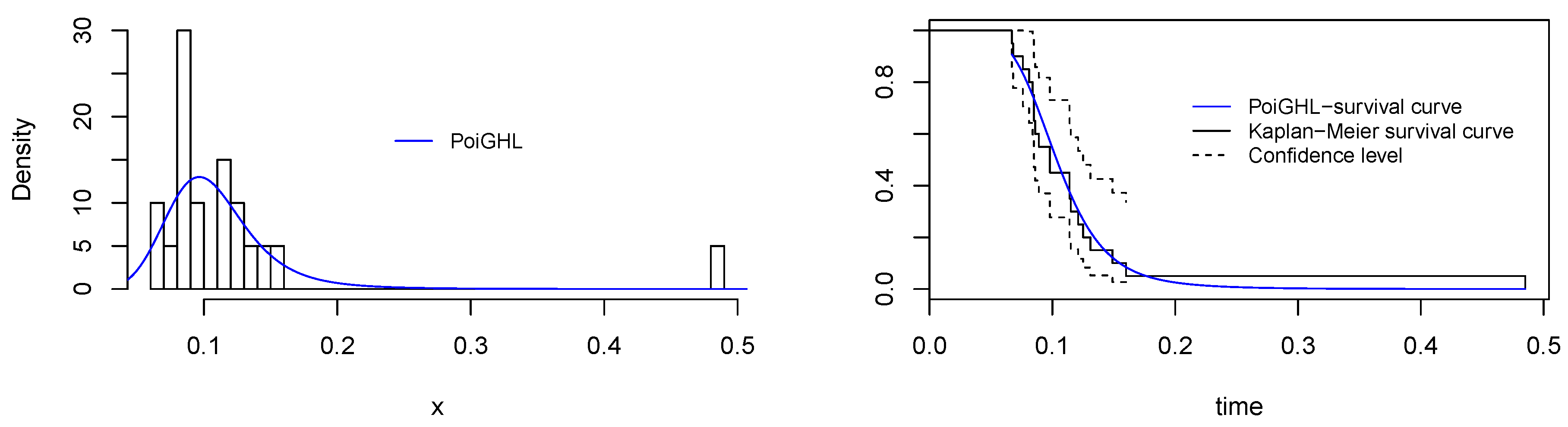
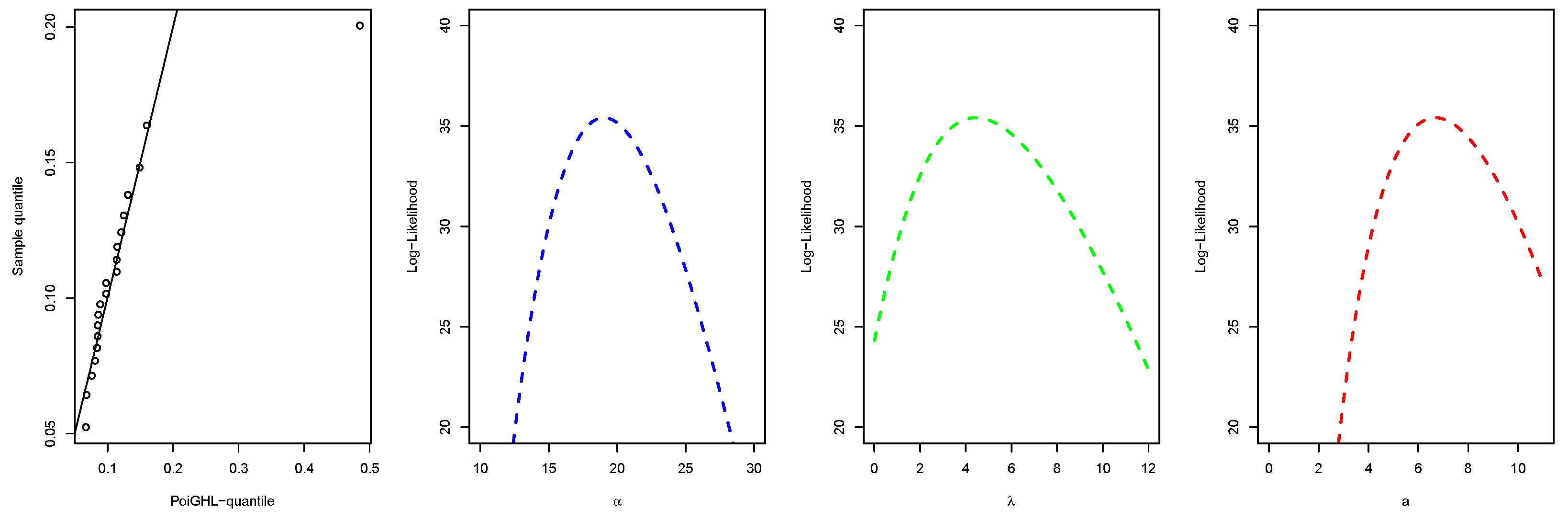
7.2. Application II
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Proofs of Theorems 2 and 3
Appendix A.1. Proof of Theorem 2
Appendix A.2. Proof of Theorem 3
Appendix B. The Elements of Information Matrix
Appendix C. Element of Information Matrix for the Estimators of R, Computations of the uij and , and
Appendix C.1. Element of Information Matrix for the Estimators of R
Appendix C.2. Computations of the uij
Appendix C.3. Computations of , and
References
- Kuş, C. A New Lifetime Distribution. Comput. Stat. Data Anal. 2007, 51, 4497–4509. [Google Scholar] [CrossRef]
- Silva, R.B.; Cordeiro, G.M. The Burr XII power series distributions: A new compounding family. Braz. J. Probab. Stat. 2015, 29, 565–589. [Google Scholar] [CrossRef]
- Adamidis, K.; Loukas, S. A lifetime distribution with decreasing failure rate. Stat. Probab. Lett. 1998, 39, 35–42. [Google Scholar] [CrossRef]
- Cancho, V.G.; Louzada-Neto, F.; Barriga, G.D.C. The Poisson-exponential lifetime distribution. Comput. Stat. Data Anal. 2011, 55, 677–686. [Google Scholar] [CrossRef]
- Mahmoudi, E.; Jafari, A.A. Generalized Exponential-power Series Distributions. Comput. Stat. Data Anal. 2012, 56, 4047–4066. [Google Scholar] [CrossRef]
- Mahmoudi, E.; Jafari, A.A. The compound class of linear failure rate-power series distributions: Model, properties, and applications. Commun. Stat. Simul. Comput. 2017, 46, 1414–1440. [Google Scholar] [CrossRef]
- Mahmoudi, E.; Sepahdar, A. Exponentiated Weibull–Poisson distribution: Model, properties and applications. Math. Comput. Simul. 2013, 92, 76–97. [Google Scholar] [CrossRef]
- Mahmoudi, E.; Sepahdar, A.; Lemonte, A. Exponentiated Weibull-logarithmic Distribution: Model, Properties and Applications. arXiv, 2014; arXiv:1402.5264. [Google Scholar]
- Mahmoudi, E.; Shiran, M. Exponentiated weibull power series distributions and its applications. arXiv, 2012; arXiv:1212.5613. [Google Scholar]
- Muhammad, M. The Complementary Exponentiated BurrXII Poisson Distribution: Model, properties and application. J. Stat. Appl. Probab. 2017, 6, 33–48. [Google Scholar] [CrossRef]
- Muhammad, M. Poisson-odd generalized exponential family of distributions: Theory and applications. Hacet. J. Math. Stat. 2018, 47, 1652–1670. [Google Scholar] [CrossRef]
- Muhamma, M.; Yahaya, M.A. The half logistic-Poisson distribution. Asian J. Math. Appl. 2017, 2017, 1–15. [Google Scholar]
- Abdel-Hamid, A.H. Properties, estimations and predictions for a Poisson-half-logistic distribution based on progressively type-II censored samples. Appl. Math. Model. 2016, 40, 7164–7181. [Google Scholar] [CrossRef]
- Kantam, R.; Ramakrishna, V.; Ravikumar, M. Estimation and testing in type I generalized half logistic distribution. J. Mod. Appl. Stat. Methods 2013, 12, 22. [Google Scholar] [CrossRef]
- Krishnarani, S.D. On a Power Transformation of Half-Logistic Distribution. J. Probab. Stat. 2016. [Google Scholar] [CrossRef]
- Olapade, A.K.A. The Type I Generalized Half Logistic Distribution. J. Iran. Stat. Soc. 2014, 13, 69–82. [Google Scholar]
- Seo, J.; Kang, S. Notes on the exponentiated half logistic distribution. Appl. Math. Model. 2015, 39, 6491–6500. [Google Scholar] [CrossRef]
- Bowley, A.L. Elements of Statistics; PS King & son: London, UK, 1920; Volume 2. [Google Scholar]
- Moors, J. A quantile alternative for kurtosis. J. R. Stat. Soc. Ser. D Stat. 1988, 37, 25–32. [Google Scholar] [CrossRef]
- Jeffrey, A.; Zwillinger, D. Preface to the Seventh Edition. In Table of Integrals, Series, and Products, 7th ed.; Jeffrey, A., Zwillinger, D., Gradshteyn, I., Ryzhik, I., Eds.; Academic Press: Boston, MA, USA, 2007. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Landwehr, J.M.; Matalas, N.C.; Wallis, J.R. Probability weighted moments: Definition and relation to parameters of several distributions expressable in inverse form. Water Resour. Res. 1979, 15, 1049–1054. [Google Scholar] [CrossRef]
- Hosking, J.R.M. The Theory of Probability Weighted Moments; Technical Report RC 12210; IBM Thomas J. Watson Research Center: Yorktown Heights, NY, USA, 1986. [Google Scholar]
- Hosking, J.R.; Wallis, J.R.; Wood, E.F. Estimation of the Generalized Extreme-Value Distribution by the Method of Probability-Weighted Moments. Technometrics 1985, 27, 251–261. [Google Scholar] [CrossRef]
- Gomes, A.E.; da Silva, C.Q.; Cordeiro, G.M.; Ortega, E.M.M. The beta Burr III model for lifetime data. Braz. J. Probab. Stat. 2013, 27, 502–543. [Google Scholar] [CrossRef]
- Morais, A.L.; Barreto-Souza, W. A compound class of Weibull and power series distributions. Comput. Stat. Data Anal. 2011, 55, 1410–1425. [Google Scholar] [CrossRef]
- Lu, W.; Shi, D. A new compounding life distribution: The Weibull–Poisson distribution. J. Appl. Stat. 2012, 39, 21–38. [Google Scholar] [CrossRef]
- Ristić, M.M.; Nadarajah, S. A new lifetime distribution. J. Stat. Comput. Simul. 2014, 84, 135–150. [Google Scholar] [CrossRef]
- Nasiru, S.; Atem, M.; Nantomah, K. Poisson Exponentiated Erlang-Truncated Exponential Distribution. J. Stat. Appl. Probab. 2018, 7, 245–261. [Google Scholar] [CrossRef]
- Jafari, A.A.; Tahmasebi, S. Gompertz-power series distributions. Commun. Stat. Theory Methods 2016, 45, 3761–3781. [Google Scholar] [CrossRef]
- Gupta, R.C.; Kirmani, S.N.U.A. Some Characterization of Distributions by Functions of Failure Rate and Mean Residual Life. Commun. Stat. Theory Methods 2004, 33, 3115–3131. [Google Scholar] [CrossRef]
- Laurent, A.G. On Characterization of Some Distributions by Truncation Properties. J. Am. Stat. Assoc. 1974, 69, 823–827. [Google Scholar] [CrossRef]
- Gupta, P.L.; Gupta, R.C. On the moments of residual life in reliability and some characterization results. Commun. Stat. Theory Methods 1983, 12, 449–461. [Google Scholar] [CrossRef]
- Ahsanullah, M.; Ghitany, M.E.; Al-Mutairi, D.K. Characterization of Lindley distribution by truncated moments. Commun. Stat. Theory Methods 2017, 46, 6222–6227. [Google Scholar] [CrossRef]
- Muhammad, M. A Generalization of the BurrXII-Poisson Distribution and its Applications. J. Stat. Appl. Probab. 2016, 5, 29–41. [Google Scholar] [CrossRef]
- Muhammad, M. A New Lifetime Model with a Bounded Support. Asian Res. J. Math. 2017, 7, 1–11. [Google Scholar] [CrossRef]
- Rezaei, S.; Tahmasbi, R.; Mahmoodi, M. Estimation of P [Y< X] for generalized Pareto distribution. J. Stat. Plan. Inference 2010, 140, 480–494. [Google Scholar]
- Raqab, M.Z.; Madi, M.T.; Kundu, D. Estimation of P (Y< X) for the three-parameter generalized exponential distribution. Commun. Stat. Theory Methods 2008, 37, 2854–2864. [Google Scholar]
- Nadarajah, S. Reliability for Logistic distributions. Elektron. Modelirovanie 2004, 26, 65–82. [Google Scholar]
- Nadarajah, S. Reliability for Laplace distributions. Math. Probl. Eng. 2004, 2004, 169–183. [Google Scholar] [CrossRef]
- Gross, J.; Ligges, U. Package ‘nortest’. Five Omnibus Tests for Testing the Composite Hypothesis of Normality. 2015. Available online: https://cran.r-project.org/web/packages/nortest/index.html (accessed on 28 March 2019).
- Su, S. GLDEX. Package: This Package Fits RS and FMKL Generalised Lambda…. 2016. Available online: https://rdrr.io/cran/GLDEX/ (accessed on 28 March 2019).
- Oliveira, J.; Santos, J.; Xavier, C.; Trindade, D.; Cordeiro, G.M. The McDonald half-logistic distribution: Theory and practice. Commun. Stat. Theory Methods 2016, 45, 2005–2022. [Google Scholar] [CrossRef]
- Jose, J.K.; Manoharan, M. Beta half logistic distribution—A new probability model for lifetime data. J. Stat. Manag. Syst. 2016, 19, 587–604. [Google Scholar] [CrossRef]
- Usman, R.; Haq, M.; Talib, J. Kumaraswamy Half-Logistic Distribution: Properties and Applications. J. Stat. Appl. Probab. 2017, 6, 597–609. [Google Scholar] [CrossRef]
- Shrahili, M.; Elbata, I.; Muhammad, M. The type I half-logistic Burr X distribution: Theory and practice. J. Nonlinear Sci. Appl. 2019, 12, 262–277. [Google Scholar] [CrossRef][Green Version]
- Muhammad, M. Generalized Half Logistic Poisson Distributions. Commun. Stat. Appl. Methods 2017, 24, 353–365. [Google Scholar] [CrossRef]
- Andrade, T.; Cordeiro, G.; Bourguignon, M.; Gomes-Silva, F. The Exponentiated Generalized Standardized Half-logistic Distribution. Int. J. Stat. Probab. 2017, 6, 1–42. [Google Scholar] [CrossRef]
- Lee, E.T.; Wang, J. Statistical Methods for Survival Data Analysis, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2003; Volume 476. [Google Scholar]
- Murthy, D.N.P.; Xie, M.; Jiang, R. Weibull Models; Wiley series in probability and statistics; Wiley: Hoboken, NJ, USA, 2004. [Google Scholar]
- Rausand, M.; Hoyland, A. System Reliability Theory: Models, Statistical Methods, and Applications, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Asgharzadeh, A.; Bakouch, H.S.; Esmaeili, L. Pareto Poisson–Lindley distribution with applications. J. Appl. Stat. 2013, 40, 1717–1734. [Google Scholar] [CrossRef]
- Badar, M.G.; Priest, A.M. Statistical aspects of fibre and bundle strength in hybrid composites. In Progress in Science and Engineering Composites; Hayashi, T., Kawata, K., Umekawa, S., Eds.; ICCM-IV: Tokyo, Japan, 1982; pp. 1129–1136. [Google Scholar]
- Al-Mutairi, D.K.; Ghitany, M.E.; Kundu, D. Inferences on stress-strength reliability from weighted Lindley distributions. Commun. Stat. Theory Methods 2015, 44, 4096–4113. [Google Scholar] [CrossRef]

| a | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.1 | 0.1 | 0.0152 | 2.1791 | 38.9293 | 1143.69 | 45579.83 | 2278781 | 136790766 | 34.18098 | 2.6830 | 4.5532 | 31.3715 | 3.2156 | 2.1778 |
| 0.3 | 0.3 | 0.4 | 0.9775 | 2.2510 | 14.7363 | 148.925 | 2005.103 | 33625.3 | 674865.9 | 9.6695 | 1.3815 | 2.4020 | 11.0717 | 2.2255 | 1.9835 |
| 0.4 | 0.5 | 0.5 | 0.9719 | 1.8872 | 9.3310 | 70.7262 | 713.707 | 8971.80 | 135005.1 | 5.7694 | 1.2728 | 2.2616 | 10.2491 | 1.7407 | 1.5831 |
| 0.5 | 0.7 | 0.6 | 0.9375 | 1.6356 | 6.4782 | 39.1585 | 315.337 | 3166.367 | 38084.38 | 3.8031 | 1.1924 | 2.1738 | 9.7942 | 1.4224 | 1.3104 |
| 0.9 | 0.8 | 0.8 | 0.7386 | 1.0948 | 2.4910 | 8.4379 | 37.8400 | 211.216 | 1411.52 | 1.2923 | 1.0383 | 1.9611 | 8.6776 | 0.8419 | 0.7928 |
| 1.0 | 1.2 | 1.3 | 0.9794 | 1.2504 | 2.6615 | 8.1081 | 32.4804 | 162.124 | 970.999 | 1.0979 | 0.8380 | 1.7685 | 7.9311 | 0.7810 | 0.7496 |
| 1.5 | 1.4 | 1.6 | 0.7455 | 0.9136 | 1.3203 | 2.6749 | 7.0962 | 23.4803 | 93.4016 | 0.4856 | 0.7628 | 1.7179 | 7.8155 | 0.5191 | 0.5007 |
| 1.9 | 1.8 | 2.0 | 0.6476 | 0.7682 | 0.8729 | 1.3640 | 2.7913 | 7.1688 | 22.2753 | 0.2828 | 0.6923 | 1.7226 | 8.0760 | 0.3938 | 0.3812 |
| 2.9 | 2.8 | 3.5 | 0.5397 | 0.5996 | 0.4573 | 0.4440 | 0.5505 | 0.8637 | 1.6734 | 0.0978 | 0.5215 | 1.7199 | 8.8174 | 0.2290 | 0.2235 |
| 4.0 | 5.0 | 4.5 | 0.3818 | 0.4056 | 0.1923 | 0.1080 | 0.0743 | 0.0653 | 0.0752 | 0.0278 | 0.4111 | 1.6112 | 9.9278 | 0.1229 | 0.1213 |
| 4.8 | 5.9 | 5.5 | 0.343 | 0.3582 | 0.1441 | 0.0657 | 0.0348 | 0.0225 | 0.0188 | 0.0158 | 0.3509 | 1.3886 | 9.1031 | 0.0938 | 0.0930 |
| 8.0 | 9.0 | 15 | 0.3078 | 0.3114 | 0.1006 | 0.0337 | 0.0117 | 0.0043 | 0.0016 | 0.0036 | 0.1919 | 0.6331 | 5.2352 | 0.0463 | 0.0462 |
| 10 | 19 | 25 | 0.2716 | 0.2718 | 0.0751 | 0.0211 | 0.0060 | 0.0017 | 0.0005 | 0.0010 | 0.1299 | 0.0577 | 3.1648 | 0.0280 | 0.0280 |
| a | a | a | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.01 | 0.01 | 0.05 | −10.7912 | 1.7 | 1.8 | 1.75 | 1.0116 | 4.1 | 4.3 | 4.2 | 2.0155 |
| 0.1 | 0.1 | 0.1 | −3.9721 | 1.8 | 1.9 | 1.8 | 1.0458 | 4.3 | 4.5 | 4.3 | 2.1516 |
| 0.2 | 0.2 | 0.2 | −0.3430 | 2.0 | 2.0 | 2.0 | 1.0856 | 4.5 | 4.8 | 4.9 | 2.1980 |
| 0.5 | 0.6 | 0.4 | 0.6704 | 2.5 | 2.5 | 2.5 | 1.2474 | 5.0 | 6.0 | 7.0 | 2.2810 |
| 0.6 | 0.7 | 0.5 | 0.8521 | 2.7 | 2.8 | 2.9 | 1.2786 | 7.0 | 8.0 | 8.5 | 3.7662 |
| 0.7 | 0.9 | 0.8 | 1.0452 | 3.1 | 2.9 | 3.0 | 1.5198 | 8.0 | 9.5 | 10 | 4.4776 |
| 0.9 | 0.9 | 0.9 | 1.0032 | 3.4 | 3.1 | 3.4 | 1.6384 | 18 | 13 | 15 | 13.2729 |
| 1.0 | 1.0 | 1.0 | 0.9930 | 3.6 | 3.5 | 3.6 | 1.7517 | 19 | 15 | 18 | 14.0397 |
| 1.2 | 1.3 | 1.5 | 0.9005 | 3.9 | 3.8 | 3.9 | 1.9155 | 20 | 25 | 21 | 14.8347 |
| 1.5 | 1.6 | 1.7 | 0.9375 | 4.0 | 4.2 | 4.1 | 1.9585 | 30 | 35 | 40 | 23.7911 |
| 0.1 | 4.9083 | 3.5180 | 3.2903 | 2.5368 | 2.2091 | 1.8922 | 1.5776 | 1.1016 | −0.6298 | −1.6882 |
| 0.4 | 3.9700 | 2.5734 | 2.3386 | 1.6470 | 1.7067 | 1.3694 | 1.0423 | 0.5108 | −1.3035 | −2.2009 |
| 0.5 | 3.8503 | 2.4527 | 2.2168 | 1.5383 | 1.1741 | 0.8047 | 0.4574 | -0.1326 | −1.7326 | −2.5517 |
| 0.7 | 3.6868 | 2.2881 | 2.0506 | 1.3928 | 1.0197 | 0.6407 | 0.2880 | -0.3072 | −1.8409 | −2.6551 |
| 0.9 | 3.5773 | 2.1781 | 1.9401 | 1.2977 | 0.9186 | 0.5340 | 0.1014 | -0.4155 | −1.9135 | −2.7256 |
| 1.1 | 3.4971 | 2.0980 | 1.8597 | 1.2296 | 0.8461 | 0.4581 | -0.0018 | -0.4901 | −1.9668 | −2.7778 |
| 1.5 | 3.3844 | 1.9864 | 1.7487 | 1.1367 | 0.7475 | 0.3559 | -0.0822 | -0.5882 | −2.0417 | −2.8514 |
| 2.0 | 3.2906 | 1.8950 | 1.6589 | 1.0626 | 0.6694 | 0.2758 | -0.2476 | -0.6641 | −2.1033 | −2.9122 |
| 4.5 | 3.0647 | 1.6889 | 1.4643 | 0.9059 | 0.5057 | 0.1101 | -0.3001 | -0.8210 | −2.2397 | −3.0474 |
| 15 | 2.6944 | 1.4645 | 1.3387 | 0.7740 | 0.3701 | -0.0258 | -0.3831 | -0.9518 | −2.3606 | −3.1678 |
| Sample Size | Actual Values | Estimated Values | Standard Deviations | Bias | Mean Square Error | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 30 | 0.3 | 0.1 | 0.5 | 0.2930 | 0.7526 | 0.5822 | 0.0916 | 1.0682 | 0.1461 | -0.0070 | 0.6526 | 0.0822 | 0.0084 | 1.5667 | 0.0281 |
| 0.5 | 0.3 | 0.1 | 0.5721 | 0.4093 | 0.1125 | 0.2925 | 0.6730 | 0.0239 | 0.0721 | 0.1093 | 0.0125 | 0.0907 | 0.4649 | 0.0007 | |
| 0.1 | 0.8 | 0.6 | 0.1037 | 1.1375 | 0.6374 | 0.0364 | 1.6721 | 0.1497 | 0.0037 | 0.3375 | 0.0374 | 0.0013 | 2.9094 | 0.0238 | |
| 1.5 | 0.5 | 2.0 | 1.5008 | 0.8681 | 2.1868 | 0.3431 | 1.1441 | 0.6001 | 0.0008 | 0.3680 | 0.1868 | 0.1178 | 1.4444 | 0.3949 | |
| 0.2 | 2.0 | 0.2 | 0.3145 | 1.8311 | 0.1970 | 0.4751 | 1.6644 | 0.0510 | 0.1145 | −0.1689 | −0.0030 | 0.2388 | 2.7984 | 0.0026 | |
| 1.0 | 1.0 | 1.0 | 1.0260 | 1.1293 | 1.0201 | 0.3494 | 1.2945 | 0.2767 | 0.0260 | 0.1293 | 0.0202 | 0.1228 | 1.6924 | 0.0770 | |
| 0.1 | 2.5 | 0.8 | 0.1334 | 1.8896 | 0.7911 | 0.0580 | 1.6869 | 0.1676 | 0.0334 | −0.6104 | −0.0089 | 0.0045 | 3.2178 | 0.0282 | |
| 0.1 | 2.3 | 0.87 | 0.1286 | 1.7516 | 0.8644 | 0.0517 | 1.5180 | 0.1894 | 0.0286 | −0.5484 | −0.0057 | 0.0035 | 2.6050 | 0.0359 | |
| 1.3 | 1.1 | 1.5 | 1.3943 | 1.1345 | 1.5909 | 0.3892 | 1.2700 | 0.4059 | 0.0943 | 0.0345 | 0.0909 | 0.1604 | 1.6139 | 0.1730 | |
| 50 | 0.3 | 0.1 | 0.5 | 0.2892 | 0.6294 | 0.5612 | 0.0713 | 0.9262 | 0.1138 | −0.0108 | 0.5294 | 0.0612 | 0.0052 | 1.1380 | 0.0167 |
| 0.5 | 0.3 | 0.1 | 0.5247 | 0.2621 | 0.1064 | 0.1275 | 0.4667 | 0.0161 | 0.0248 | −0.0379 | 0.0064 | 0.0169 | 0.2192 | 0.0003 | |
| 0.1 | 0.8 | 0.6 | 0.1005 | 1.0509 | 0.6231 | 0.0288 | 1.1500 | 0.01196 | 0.0005 | 0.2509 | 0.0231 | 0.0008 | 1.3854 | 0.0148 | |
| 1.5 | 0.5 | 2.0 | 1.4437 | 0.7400 | 1.9299 | 0.2799 | 1.1384 | 0.4897 | −0.0563 | 0.2400 | −0.0702 | 0.0815 | 1.3535 | 0.2447 | |
| 0.2 | 2.0 | 0.2 | 0.2501 | 1.7826 | 0.1928 | 0.1759 | 1.2446 | 0.0458 | 0.0501 | −0.2174 | −0.0072 | 0.0335 | 1.5961 | 0.0025 | |
| 1.0 | 1.0 | 1.0 | 0.9985 | 1.1944 | 1.0062 | 0.2930 | 1.3341 | 0.2067 | −0.0015 | 0.1944 | 0.0062 | 0.0858 | 1.8175 | 0.0428 | |
| 0.1 | 2.5 | 0.8 | 0.1219 | 2.0981 | 0.7828 | 0.0477 | 1.4728 | 0.1315 | 0.0219 | −0.4019 | −0.0172 | 0.0028 | 2.3305 | 0.0178 | |
| 0.1 | 2.3 | 0.87 | 0.1187 | 1.9504 | 0.8547 | 0.0432 | 1.4612 | 0.1455 | 0.019 | 0.3496 | −0.0150 | 0.0022 | 2.2570 | 0.0214 | |
| 1.3 | 1.1 | 1.5 | 1.3308 | 1.2346 | 1.5304 | 0.3369 | 1.2361 | 0.2903 | 0.0308 | 0.0346 | 0.0304 | 0.1145 | 1.6030 | 0.0852 | |
| 100 | 0.3 | 0.1 | 0.5 | 0.2895 | 0.4806 | 0.5405 | 0.0513 | 0.7105 | 0.0815 | −0.0105 | 0.3806 | 0.0405 | 0.0028 | 0.6496 | 0.0083 |
| 0.5 | 0.3 | 0.1 | 0.5033 | 0.3269 | 0.1015 | 0.0303 | 0.1670 | 0.0070 | 0.0036 | 0.0269 | 0.0015 | ||||
| 0.1 | 0.8 | 0.6 | 0.0994 | 0.9789 | 0.6123 | 0.0222 | 1.0996 | 0.0911 | −0.0007 | 0.1789 | 0.0122 | 0.0005 | 1.2410 | 0.0085 | |
| 1.5 | 0.5 | 2.0 | 1.4293 | 0.6856 | 1.8640 | 0.2415 | 1.1216 | 0.4095 | −0.0708 | 0.1856 | −0.1360 | 0.0633 | 1.2924 | 0.1861 | |
| 0.2 | 2.0 | 0.2 | 0.1996 | 1.7591 | 0.1865 | 0.1066 | 1.0954 | 0.0450 | −0.0004 | −0.2410 | −0.0135 | 0.0114 | 1.2579 | 0.0022 | |
| 1.0 | 1.0 | 1.0 | 0.9889 | 1.2083 | 1.0038 | 0.2360 | 1.2935 | 0.1459 | −0.0111 | 0.2083 | 0.0038 | 0.0558 | 1.7163 | 0.02129 | |
| 0.1 | 2.5 | 0.8 | 0.1115 | 2.3604 | 0.7848 | 0.0384 | 1.4364 | 0.0975 | 0.0115 | −0.1396 | −0.0152 | 0.0016 | 2.0826 | 0.0097 | |
| 0.1 | 2.3 | 0.87 | 0.1096 | 2.1827 | 0.8531 | 0.0354 | 1.4344 | 0.1080 | 0.0096 | −0.1173 | −0.0169 | 0.0014 | 2.0711 | 0.0120 | |
| 1.3 | 1.1 | 1.5 | 1.2967 | 1.2688 | 1.4863 | 0.2938 | 1.2132 | 0.2031 | 0.0034 | 0.0314 | −0.0137 | 0.0863 | 1.5436 | 0.0415 | |
| 150 | 0.3 | 0.1 | 0.5 | 0.2914 | 0.3870 | 0.5303 | 0.0409 | 0.5374 | 0.0664 | −0.0086 | 0.2870 | 0.0303 | 0.0017 | 0.3711 | 0.0053 |
| 0.5 | 0.3 | 0.1 | 0.5006 | 0.3066 | 0.1004 | 0.0119 | 0.0791 | 0.0033 | 0.0007 | 0.0066 | 0.0004 | ||||
| 0.1 | 0.8 | 0.6 | 0.0994 | 0.9245 | 0.6074 | 0.0191 | 0.8763 | 0.0779 | −0.0006 | 0.1245 | 0.0074 | 0.0004 | 0.7834 | 0.0061 | |
| 1.5 | 0.5 | 2.0 | 1.4334 | 0.6147 | 1.8281 | 0.2198 | 1.0580 | 0.3939 | −0.0667 | 0.1147 | −0.1719 | 0.0527 | 1.1324 | 0.1847 | |
| 0.2 | 2.0 | 0.2 | 0.1803 | 1.6778 | 0.1807 | 0.0907 | 1.0959 | 0.0476 | −0.0197 | −0.3223 | −0.0193 | 0.0086 | 1.2048 | 0.0026 | |
| 1.0 | 1.0 | 1.0 | 0.9805 | 1.2255 | 1.0027 | 0.2153 | 1.2483 | 0.1251 | −0.0195 | 0.2255 | 0.0027 | 0.0467 | 1.6090 | 0.0157 | |
| 0.1 | 2.5 | 0.8 | 0.1070 | 2.4901 | 0.7878 | 0.0344 | 1.4110 | 0.0794 | 0.0070 | -0.0099 | −0.0122 | 0.0012 | 1.9907 | 0.0065 | |
| 0.1 | 2.3 | 0.87 | 0.1059 | 2.3018 | 0.8557 | 0.0321 | 1.4126 | 0.0890 | 0.0059 | 0.0018 | −0.0143 | 0.0011 | 1.9952 | 0.0081 | |
| 1.3 | 1.1 | 1.5 | 1.2825 | 1.3056 | 1.4850 | 0.2729 | 1.2032 | 0.1710 | −0.0175 | 0.0528 | −0.0151 | 0.0748 | 1.4061 | 0.0295 | |
| 200 | 0.1 | 0.3 | 0.5 | 0.2926 | 0.3463 | 0.5257 | 0.0357 | 0.4722 | 0.0581 | −0.0074 | 0.2463 | 0.0257 | 0.0013 | 0.2836 | 0.0040 |
| 0.5 | 0.3 | 0.1 | 0.5002 | 0.3009 | 0.1001 | 0.0065 | 0.0230 | 0.0013 | |||||||
| 0.1 | 0.8 | 0.6 | 0.0999 | 0.8651 | 0.6034 | 0.0163 | 0.7471 | 0.0710 | −0.0001 | 0.0651 | 0.0034 | 0.0003 | 0.5624 | 0.0051 | |
| 1.5 | 0.5 | 2.0 | 1.4406 | 0.5526 | 1.8095 | 0.2070 | 0.9963 | 0.3866 | −0.595 | 0.0526 | −0.1905 | 0.0464 | 0.9952 | 0.1838 | |
| 0.2 | 2. | 0.2 | 0.1677 | 1.5567 | 0.1740 | 0.0834 | 1.1169 | 0.0500 | −0.0323 | −0.4433 | -0.0260 | 0.0080 | 1.2039 | 0.0022 | |
| 1.0 | 1.0 | 1.0 | 0.9805 | 1.2255 | 1.0027 | 0.2153 | 1.2483 | 0.1251 | −0.0195 | 0.2255 | 0.0027 | 0.0467 | 1.6090 | 0.0157 | |
| 0.1 | 2.5 | 0.8 | 0.1048 | 2.5536 | 0.7899 | 0.0317 | 1.3723 | 0.0695 | 0.0048 | 0.0536 | −0.0101 | 0.0010 | 1.8859 | 0.0049 | |
| 0.1 | 2.3 | 0.87 | 0.1033 | 2.3845 | 0.8583 | 0.0298 | 1.3826 | 0.0778 | 0.0033 | 0.0845 | −0.0117 | 0.0009 | 1.9323 | 0.0062 | |
| 1.3 | 1.1 | 1.5 | 1.2779 | 1.3112 | 1.4871 | 0.2589 | 1.2010 | 0.1519 | −0.0221 | 0.0511 | −0.0129 | 0.0675 | 1.4030 | 0.0232 | |
| 300 | 0.1 | 0.3 | 0.5 | 0.2937 | 0.2869 | 0.5190 | 0.0286 | 0.3793 | 0.0471 | −0.0063 | 0.1869 | 0.0190 | 0.0009 | 0.1788 | 0.0026 |
| 0.5 | 0.3 | 0.1 | 0.5001 | 0.3001 | 0.1000 | 0.0024 | 0.0067 | 0.005 | |||||||
| 0.1 | 0.8 | 0.6 | 0.997 | 0.8449 | 0.6018 | 0.01365 | 0.6169 | 0.0602 | −0.0003 | 0.0449 | 0.0018 | 0.0002 | 0.3825 | 0.0036 | |
| 1.5 | 0.5 | 2.0 | 1.4461 | 0.4892 | 1.7794 | 0.1903 | 0.9318 | 0.3850 | −0.0539 | −0.0108 | −2206 | 0.0391 | 0.8684 | 0.1831 | |
| 0.2 | 2.0 | 0.2 | 0.2153 | 1.3274 | 0.2002 | 0.481 | 0.9477 | 0.0014 | 0.0153 | −0.0726 | 0.0002 | 0.0025 | 1.2010 | 0.0002 | |
| 1.0 | 1.0 | 1.0 | 0.9901 | 1.1144 | 0.9978 | 0.1063 | 0.9928 | 0.0932 | −0.0099 | 0.1144 | −0.0022 | 0.0277 | 0.9986 | 0.0087 | |
| 1.2 | 2.5 | 0.8 | 0.1028 | 2.5891 | 0.7915 | 0.0281 | 1.3050 | 0.0571 | 0.0028 | 0.0891 | −0.0085 | 0.0008 | 1.7107 | 0.0033 | |
| 0.1 | 2.3 | 0.87 | 0.1014 | 2.4315 | 0.8609 | 0.0266 | 1.3086 | 0.0635 | 0.0014 | 0.1315 | −0.0091 | 0.0007 | 1.7296 | 0.0041 | |
| 1.3 | 1.1 | 1.5 | 1.2776 | 1.2838 | 1.4869 | 0.2352 | 1.1806 | 0.1268 | −0.0224 | 0.1038 | −0.0131 | 0.0558 | 1.3275 | 0.0162 | |
| (n, m) | R | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (20, 20) | 1.5 | 2.5 | 3.0 | 1.5734 | 2.6242 | 3.3101 | 0.3135 | 0.3155 | −0.0018 | 0.0057 | 0.0449 | 0.8672 |
| 1.5 | 0.5 | 1.9 | 1.6094 | 0.5387 | 2.1903 | 0.8040 | 0.8070 | 0.0030 | 0.0035 | 0.0230 | 0.5945 | |
| 0.9 | 0.5 | 2.0 | 0.9652 | 0.5362 | 2.3130 | 0.6841 | 0.6878 | 0.0036 | 0.0055 | 0.0446 | 0.8276 | |
| 0.8 | 1.7 | 2.5 | 0.8479 | 1.8004 | 2.7912 | 0.2565 | 0.2544 | −0.0022 | 0.0047 | 0.0743 | 1.0682 | |
| 0.7 | 0.8 | 0.9 | 0.7808 | 0.8890 | 1.2374 | 0.4626 | 0.4636 | − | 0.0068 | 1.2532 | 4.3884 | |
| 1.7 | 2.8 | 3.5 | 1.7932 | 2.9562 | 3.8935 | 0.3081 | 0.3056 | −0.0025 | 0.0057 | 0.0374 | 0.7581 | |
| 3.7 | 3.0 | 4.0 | 2.8006 | 2.3522 | 2.8152 | 0.5892 | 0.5577 | −0.0316 | 0.0073 | 0.0518 | 0.8923 | |
| (30, 20) | 1.5 | 2.5 | 3.0 | 1.5614 | 2.6288 | 3.2709 | 0.3153 | 0.3119 | −0.0035 | 0.0048 | 0.0392 | 0.7759 |
| 1.5 | 0.5 | 1.9 | 1.6137 | 0.5371 | 2.0804 | 0.8040 | 0.8051 | 0.0011 | 0.0034 | 0.0196 | 0.5480 | |
| 0.9 | 0.5 | 2.0 | 0.9469 | 0.5313 | 2.2317 | 0.6841 | 0.6852 | 0.0011 | 0.0045 | 0.0254 | 0.6254 | |
| 0.8 | 1.7 | 2.5 | 0.8371 | 1.7927 | 2.7557 | 0.2565 | 0.2529 | −0.0036 | 0.0038 | 0.0372 | 0.7565 | |
| 0.7 | 0.8 | 0.9 | 0.7580 | 0.8779 | 1.1530 | 0.4626 | 0.4600 | −0.0026 | 0.0055 | 0.8146 | 3.5379 | |
| 1.7 | 2.8 | 3.5 | 1.7736 | 2.9562 | 3.8935 | 0.3081 | 0.3061 | −0.0021 | 0.0048 | 0.0339 | 0.7214 | |
| 3.7 | 3.0 | 4.0 | 3.0946 | 2.6644 | 3.3268 | 0.5892 | 0.5526 | −0.0366 | 0.0082 | 0.0336 | 0.7187 | |
| (30, 40) | 1.5 | 2.5 | 3.0 | 1.5230 | 2.5219 | 3.0900 | 0.3153 | 0.3177 | 0.0023 | 0.0039 | 0.0364 | 0.7481 |
| 1.5 | 0.5 | 1.9 | 1.5792 | 0.5356 | 2.0192 | 0.8040 | 0.8015 | −0.0025 | 0.0029 | 0.0099 | 0.3910 | |
| 0.9 | 0.5 | 2.0 | 0.9371 | 0.5190 | 2.1635 | 0.6841 | 0.6861 | 0.0019 | 0.0032 | 0.0049 | 0.2750 | |
| 0.8 | 1.7 | 2.5 | 0.8294 | 1.7507 | 2.6559 | 0.2565 | 0.2565 | − | 0.0027 | 0.0245 | 0.6131 | |
| 0.7 | 0.8 | 0.9 | 0.7284 | 0.8319 | 1.0114 | 0.4626 | 0.4624 | −0.0002 | 0.0025 | 0.0357 | 0.7411 | |
| 1.7 | 2.8 | 3.5 | 1.7553 | 2.8778 | 3.7114 | 0.3081 | 0.3080 | −0.0002 | 0.0034 | 0.0290 | 0.6670 | |
| 3.7 | 3.0 | 4.0 | 3.7540 | 3.0374 | 4.1474 | 0.5892 | 0.5898 | 0.0006 | 0.0041 | 0.0189 | 0.5387 | |
| (50, 50) | 1.5 | 2.5 | 3.0 | 1.5341 | 2.5532 | 3.1299 | 0.3153 | 0.3149 | −0.0005 | 0.0022 | 0.0159 | 0.4957 |
| 1.5 | 0.5 | 1.9 | 1.5640 | 0.5178 | 1.9527 | 0.8040 | 0.8038 | −0.0002 | 0.0019 | 0.0042 | 0.2543 | |
| 0.9 | 0.5 | 2.0 | 0.9237 | 0.5130 | 2.1048 | 0.6841 | 0.6853 | 0.0012 | 0.0022 | 0.0016 | 0.1541 | |
| 0.8 | 1.7 | 2.5 | 0.8212 | 1.7449 | 2.6221 | 0.2565 | 0.2552 | −0.0013 | 0.0018 | 0.0098 | 0.3883 | |
| 0.7 | 0.8 | 0.9 | 0.7458 | 0.8512 | 1.0814 | 0.4626 | 0.4615 | −0.0011 | 0.0038 | 0.0303 | 0.6825 | |
| 1.7 | 2.8 | 3.5 | 1.7370 | 2.8558 | 3.6418 | 0.3081 | 0.3076 | −0.0005 | 0.0023 | 0.0119 | 0.4270 | |
| 3.7 | 3.0 | 4.0 | 3.7245 | 3.0374 | 4.0996 | 0.5892 | 0.5858 | −0.0035 | 0.0034 | 0.0155 | 0.4885 |
| Model | a | b | c | L | AIC | BIC | CAIC | KS | AD | CvM | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PoiGHL | 0.0718 | - | - | 3.9829 | 1.2157 | - | - | -410.72 | 827.43 | 835.99 | 827.62 | 0.0485 | 0.3528 | 0.0603 |
| (0.9243) | (0.4609) | (0.3721) | ||||||||||||
| McHL | 0.3582 | - | - | - | 0.3586 | 0.3329 | 3.4083 | −412.37 | 832.75 | 844.16 | 833.07 | 0.0623 | 0.5438 | 0.0895 |
| (0.7029) | (0.1594) | (0.1546) | ||||||||||||
| BHL | - | - | - | 1.1110 | 39.3700 | - | −414.19 | 834.38 | 842.94 | 834.58 | 0.0779 | 0.8202 | 0.1372 | |
| (0.4190) | (0.0332) | (0.0347) | ||||||||||||
| KwHL | 0.3759 | - | - | - | 1.0149 | 0.3362 | - | −413.57 | 833.15 | 841.70 | 833.34 | 0.0833 | 0.7050 | 0.1179 |
| (0.3379) | (0.0642) | (0.0633) | ||||||||||||
| THLBx | - | 0.4373 | 81.6600 | - | - | - | −415.48 | 836.96 | 845.52 | 837.15 | 0.0768 | 1.0172 | 0.1730 | |
| (0.4365) | (0.0108) | (0.0117) | ||||||||||||
| GHL | 0.1440 | - | - | - | 0.9527 | - | - | −416.64 | 837.27 | 842.9755 | 837.37 | 0.0949 | 1.2663 | 0.2163 |
| (0.1994) | (0.0026) | (0.0033) | ||||||||||||
| PHL | 0.1479 | - | - | - | - | - | −416.73 | 837.45 | 843.16 | 837.55 | 0.0989 | 1.2406 | 0.2119 | |
| (0.1631) | (0.0030) | (0.0037) | ||||||||||||
| PwHL | 0.8880 | 0.2015 | - | - | - | - | - | −415.10 | 834.19 | 839.90 | 834.29 | 0.0765 | 0.9722 | 0.1654 |
| (0.4420) | (0.0140) | (0.0147) | ||||||||||||
| HLP | 0.0313 | - | - | 7.1580 | - | - | - | −413.33 | 830.66 | 836.37 | 830.76 | 0.0930 | 0.4559 | 0.0763 |
| (0.2188) | (0.2632) | (0.2297) | ||||||||||||
| HL | 0.1479 | - | - | - | - | - | - | −416.73 | 835.45 | 838.30 | 835.48 | 0.0989 | 1.2406 | 0.2119 |
| (0.1631) | (0.0030) | (0.0037) |
| Model | a | b | L | AIC | BIC | CAIC | KS | AD | CvM | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PoiGHL | 19.0226 | - | - | 4.4492 | 6.6818 | - | 35.41 | −64.82 | −61.84 | −63.32 | 0.1370 | 0.7601 | 0.1040 |
| (0.7990) | (0.0399) | (0.0914) | |||||||||||
| POGE-HL | 40.9400 | 10.3810 | - | 1.3350 | - | - | 32.92 | −59.84 | −56.86 | −58.34 | 0.1497 | 1.2059 | 0.1718 |
| (0.7247) | (0.0029) | (0.0109) | |||||||||||
| TIHLBx | 0.4710 | - | 0.6786 | 64.1814 | - | - | 26.06 | −46.11 | −43.12 | −44.61 | 0.2876 | 2.3938 | 0.3965 |
| (0.0587) | () | () | |||||||||||
| BHL | 0.5680 | - | - | - | 3.8541 | 106.9291 | 29.50 | −53.01 | −50.02 | −51.51 | 0.2338 | 1.9006 | 0.2987 |
| (0.1911) | () | (0.00028) | |||||||||||
| EGSHL | - | - | - | - | 50.2194 | 11.4110 | 32.24 | −60.47 | −58.48 | −59.77 | 0.1719 | 1.3311 | 0.1941 |
| (0.5391) | (0.0014) | (0.0056) | |||||||||||
| HLP | 1.0000 | - | - | 16.5311 | - | - | 22.13 | −40.26 | −38.27 | −39.56 | 0.4251 | 1.7893 | 0.2776 |
| (0.00085) | () | (0.0005) | |||||||||||
| GHL | 29.1899 | - | - | - | 8.2315 | - | 32.64 | −61.289 | −59.30 | −60.58 | 0.1607 | 1.2237 | 0.1757 |
| (0.6236) | (0.0026) | (0.0097) | |||||||||||
| PHL | 12.4294 | - | - | - | - | 24.34 | −44.69 | −42.69 | −43.98 | 0.3939 | 1.9953 | 0.3164 | |
| (0.0026) | () | (0.00018) | |||||||||||
| OGHL | 24.7668 | 0.4163 | - | - | - | - | 24.97 | −45.95 | −43.95 | −45.24 | 0.3780 | 1.7672 | 0.2734 |
| (0.0045) | (0.0001) | (0.00057) | |||||||||||
| HL | 12.4291 | - | - | - | - | - | 24.34 | −46.69 | −45.69 | −46.46 | 0.3939 | 1.9913 | 0.3164 |
| (0.00026) | ) | (0.00018) |
| Model | a | b | c | ℓ | AIC | BIC | CAIC | KS | AD | CvM | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
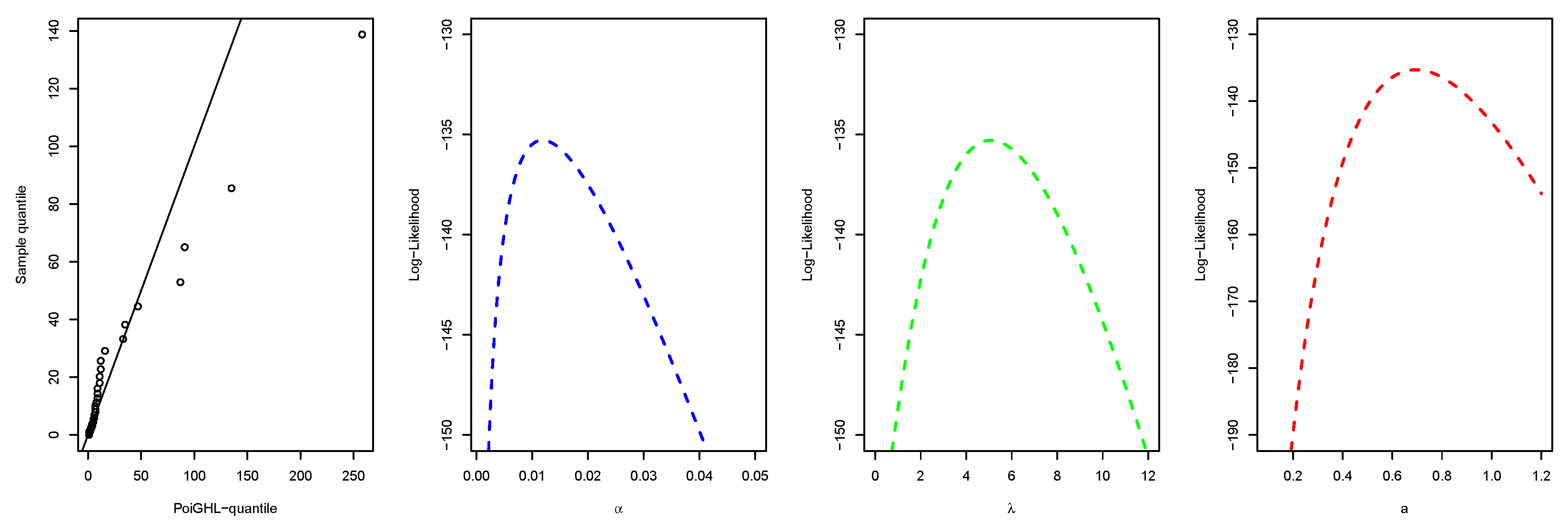
| PoiGHL | 0.119 | - | - | 5.0802 | 0.6944 | - | - | −135.29 | 276.57 | 281.15 | 277.37 | 0.2065 | 1.4015 | 0.2490 |
| (0.0950) | (0.0011) | (0.0012) | ||||||||||||
| McHL | o.1193 | - | - | - | 1.5867 | 0.3148 | 0.2119 | −144.71 | 297.42 | 303.52 | 298.80 | 0.3342 | 2.8523 | 0.5377 |
| (0.0007) | () | () | ||||||||||||
| TIHLBx | - | 0.2642 | 40.6600 | - | - | - | −136.66 | 279.32 | 283.90 | 280.12 | 0.2075 | 1.5922 | 0.2866 | |
| (0.0923) | (0.00035) | (0.00043) | ||||||||||||
| KwHL | 0.1172 | - | - | - | 0.4077 | 0.3117 | - | −144.41 | 294.83 | 299.41 | 295.63 | 0.3539 | 2.7622 | 0.5196 |
| (0.0003) | () | () | ||||||||||||
| BHL | 0.1109 | - | - | - | 0.3087 | 0.3239 | - | −144.93 | 295.85 | 300.43 | 296.65 | 0.2291 | 2.9305 | 0.5535 |
| (0.0474) | () | () | ||||||||||||
| GHLP | 0.0176 | - | - | 4.2976 | 0.6561 | - | - | −137.03 | 280.06 | 284.64 | 280.86 | 0.2449 | 1.7197 | 0.3109 |
| (0.0279) | (0.00016) | (0.00022) | ||||||||||||
| EGSHL | - | - | - | - | 0.0238 | 0.4836 | - | −137.45 | 278.90 | 281.96 | 279.29 | 0.2672 | 1.7163 | 0.31176 |
| (0.0124) | (0.00017) | (0.0022) | ||||||||||||
| HLP | 0.0156 | - | - | 6.6167 | - | - | - | −139.27 | 282.53 | 285.58 | 282.92 | 0.3004 | 1.6233 | 0.2902 |
| (0.0032) | (0.0003) | (0.0004) | ||||||||||||
| GHL | 0.0275 | - | - | - | 0.4346 | - | - | −141.46 | 286.93 | 289.98 | 287.31 | 0.3094 | 2.4062 | 0.4473 |
| (0.0022) | () | () | ||||||||||||
| PHL | 0.0048 | - | - | - | - | - | −151.80 | 307.60 | 310.65 | 307.99 | 0.4748 | 2.4034 | 0.4471 | |
| () | () | () | ||||||||||||
| OGH | 0.0496 | 0.9976 | - | - | - | - | - | −151.80 | 307.60 | 310.65 | 307.99 | 0.4758 | 2.4053 | 0.4471 |
| () | () | () | ||||||||||||
| HL | 0.0496 | - | - | - | - | - | - | −151.80 | 305.60 | 307.12 | 305.72 | 0.4759 | 2.4034 | 0.4471 |
| () | () | () |
| , HLP vs. , PoiGHL | |||
|---|---|---|---|
| First Data | Second Data | Third Data | |
| LR-statistic | 5.22 | 26.56 | 7.96 |
| p-value | 0.0223 | 0.0048 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muhammad, M.; Liu, L. A New Extension of the Generalized Half Logistic Distribution with Applications to Real Data. Entropy 2019, 21, 339. https://doi.org/10.3390/e21040339
Muhammad M, Liu L. A New Extension of the Generalized Half Logistic Distribution with Applications to Real Data. Entropy. 2019; 21(4):339. https://doi.org/10.3390/e21040339
Chicago/Turabian StyleMuhammad, Mustapha, and Lixia Liu. 2019. "A New Extension of the Generalized Half Logistic Distribution with Applications to Real Data" Entropy 21, no. 4: 339. https://doi.org/10.3390/e21040339
APA StyleMuhammad, M., & Liu, L. (2019). A New Extension of the Generalized Half Logistic Distribution with Applications to Real Data. Entropy, 21(4), 339. https://doi.org/10.3390/e21040339




