Simultaneous Classical Communication and Quantum Key Distribution Based on Plug-and-Play Configuration with an Optical Amplifier
Abstract
:1. Introduction
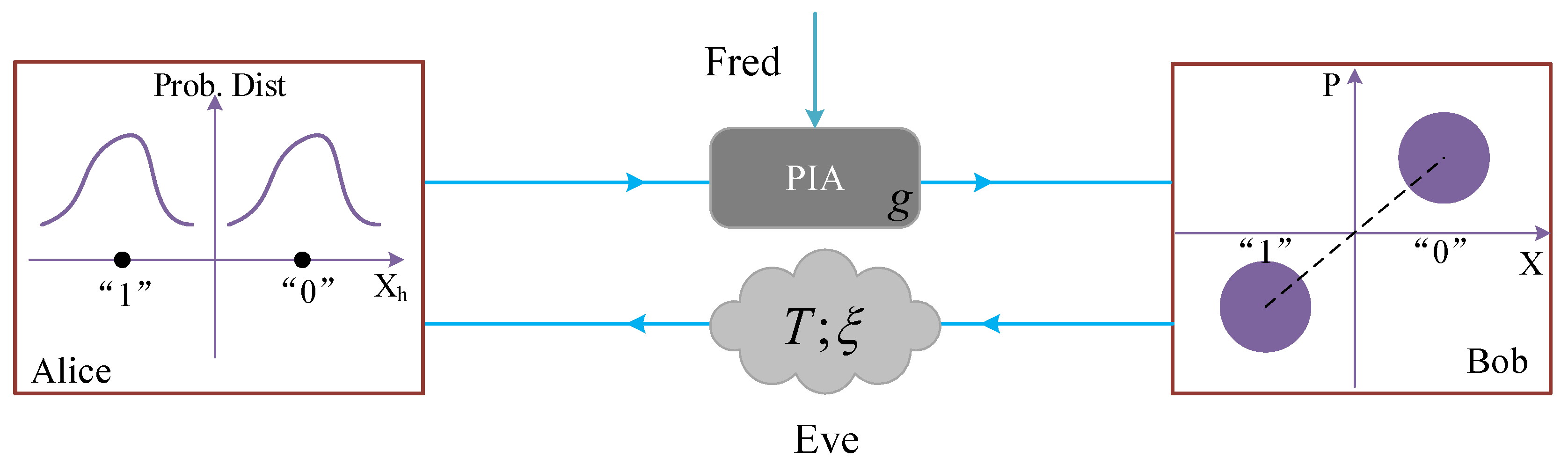
2. Protocol Description
2.1. The Plug-and-Play DPMCS Protocol
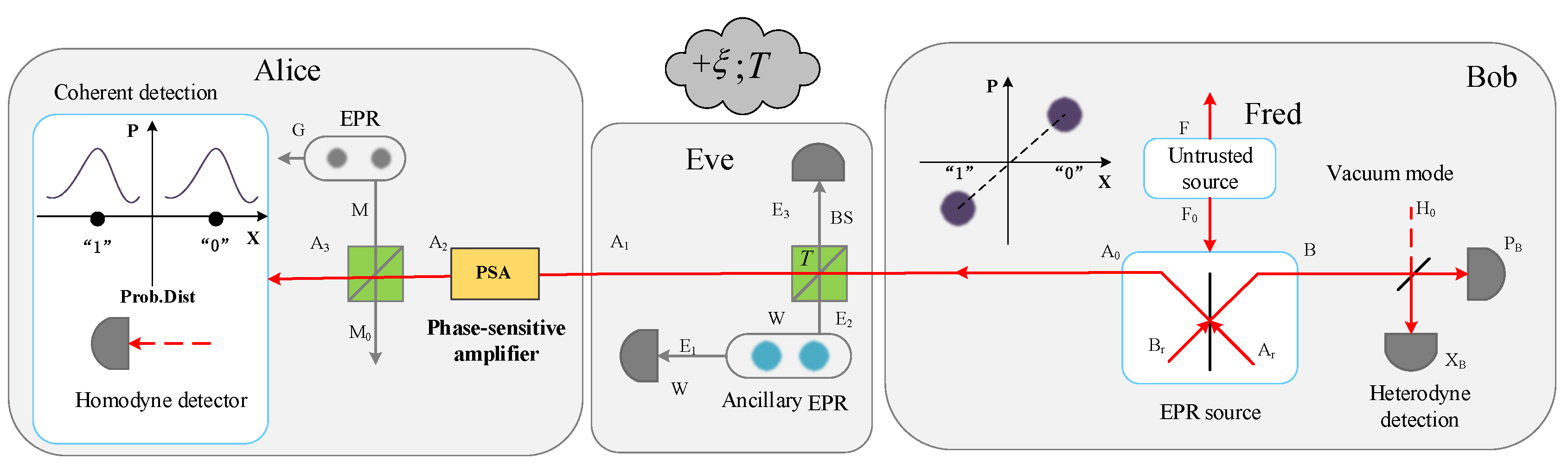
2.2. SCCQ Protocol Based on Plug-and-Play Configuration
2.3. Addition of an Optical Amplifier
3. Performance Analysis and Discussion
3.1. Noise Model of SCCQ Protocol Based on Plug-and-Play Configuration
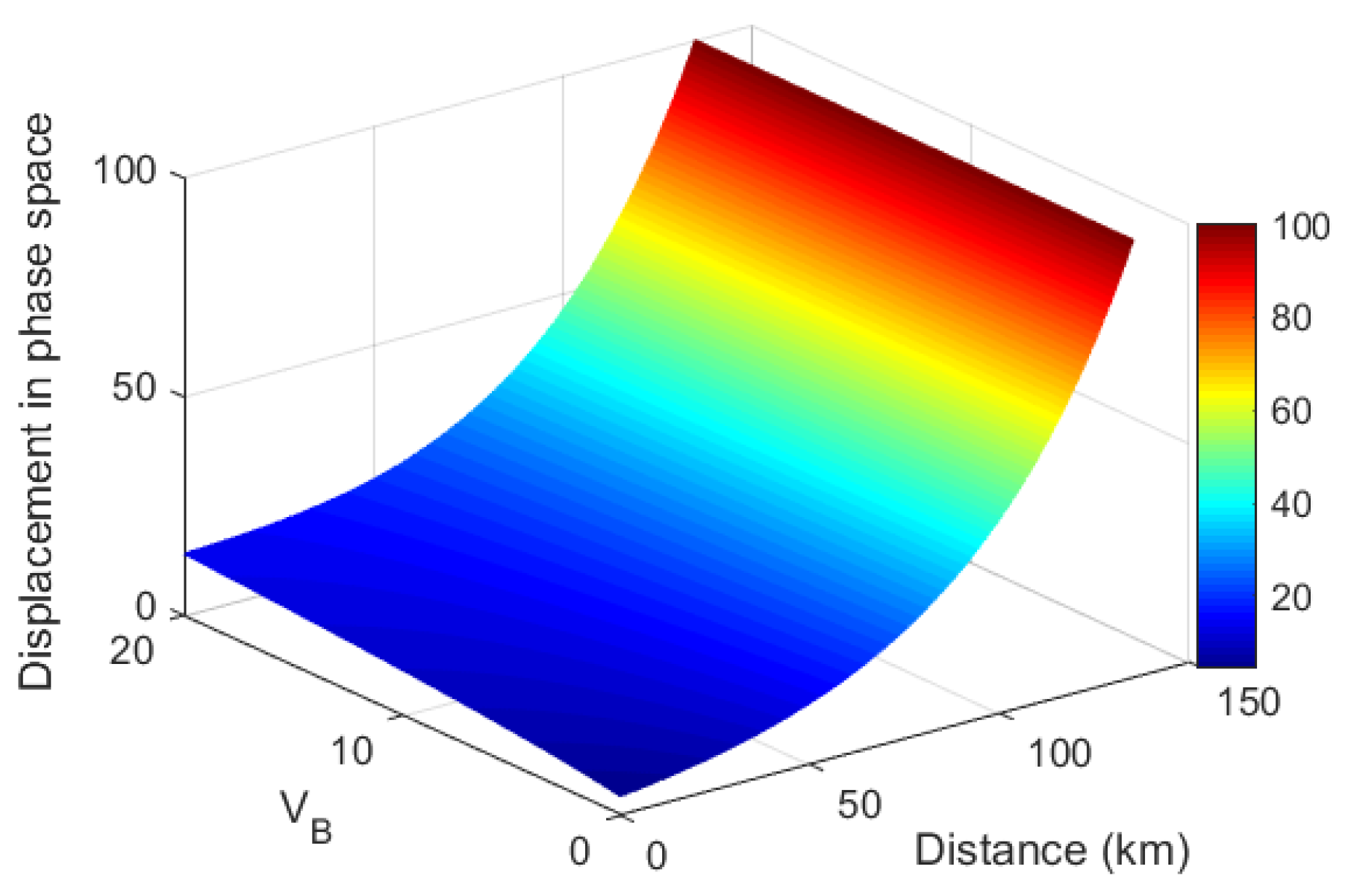
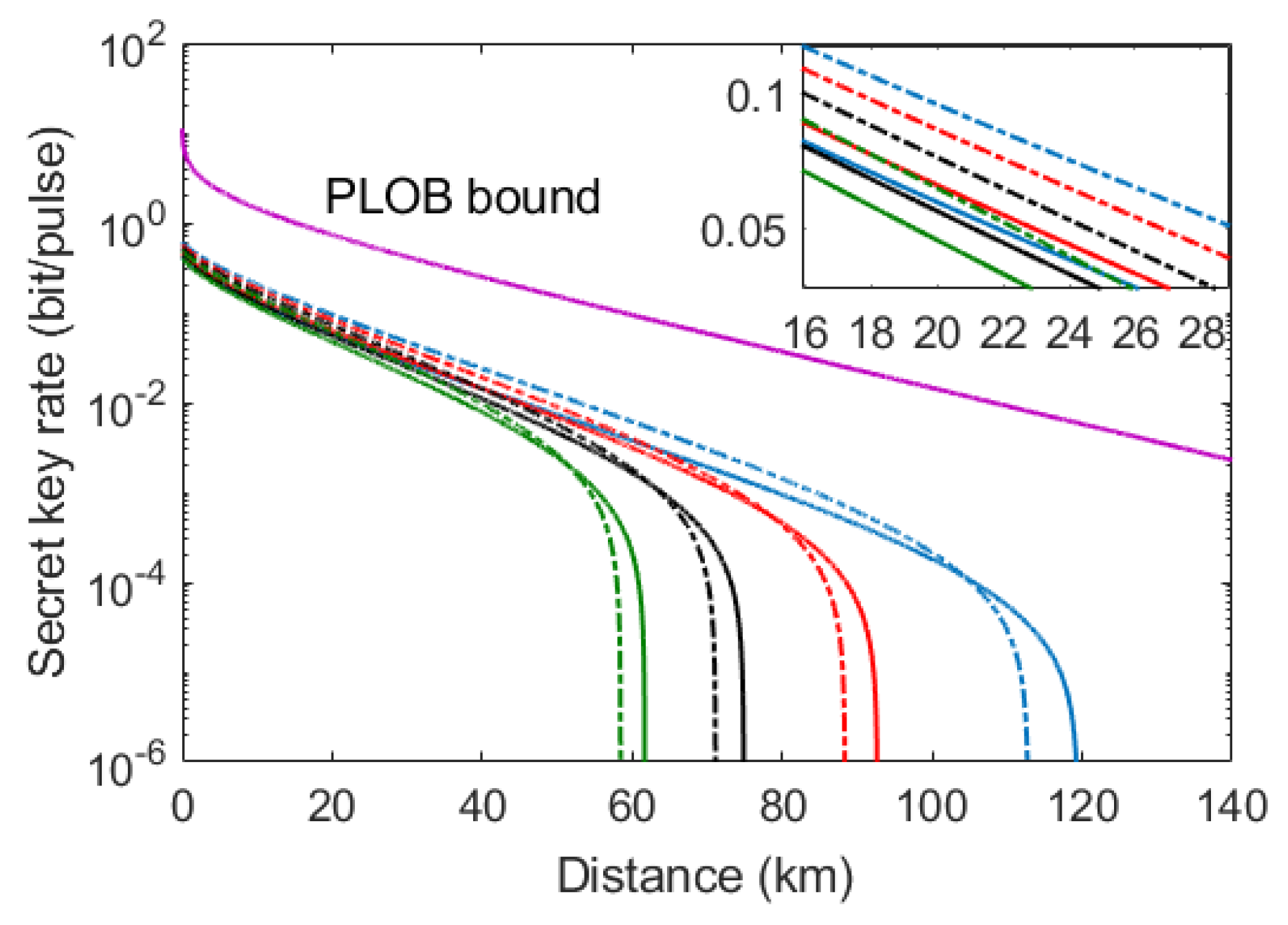
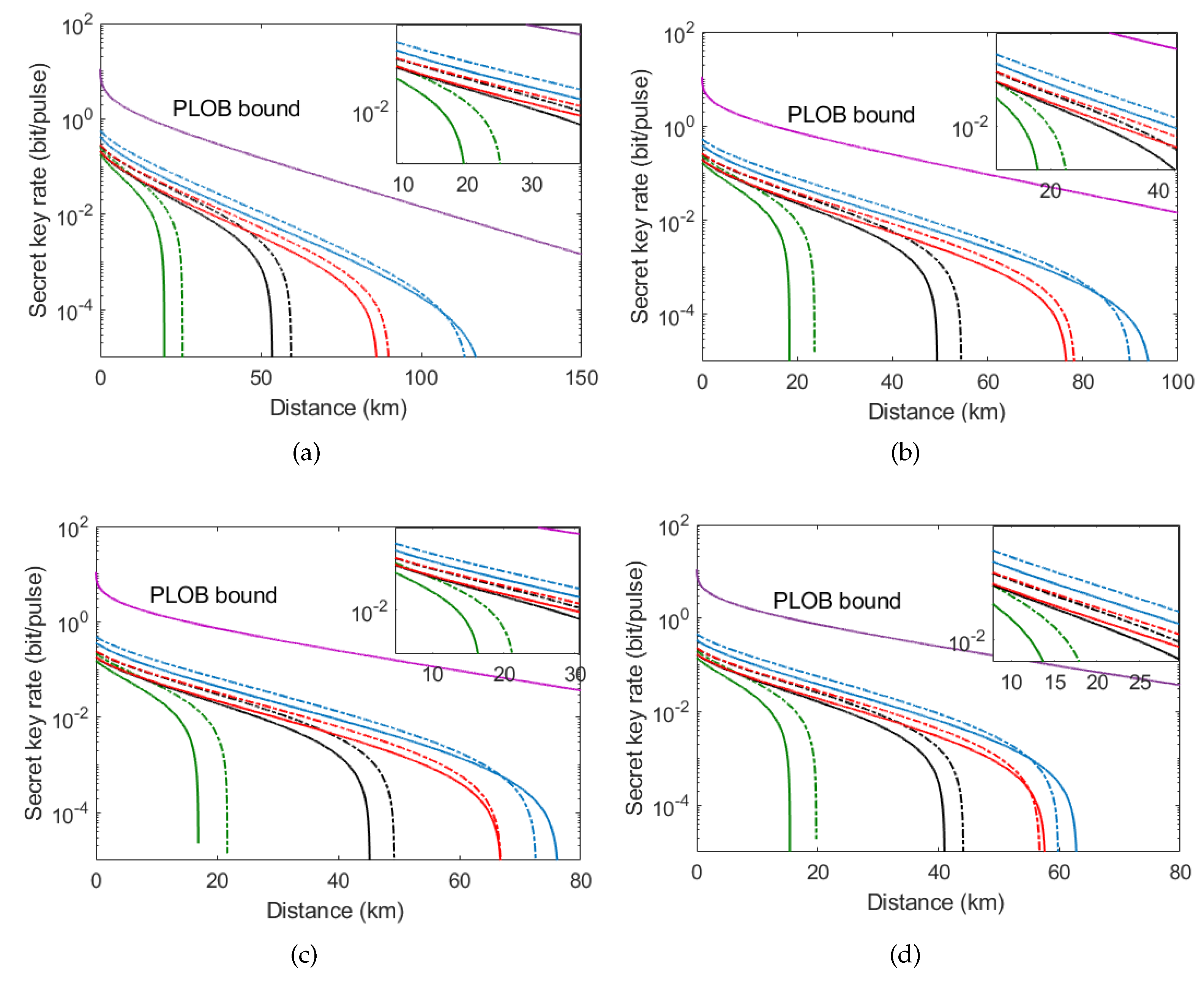
3.2. Simulation Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Parameter Optimization
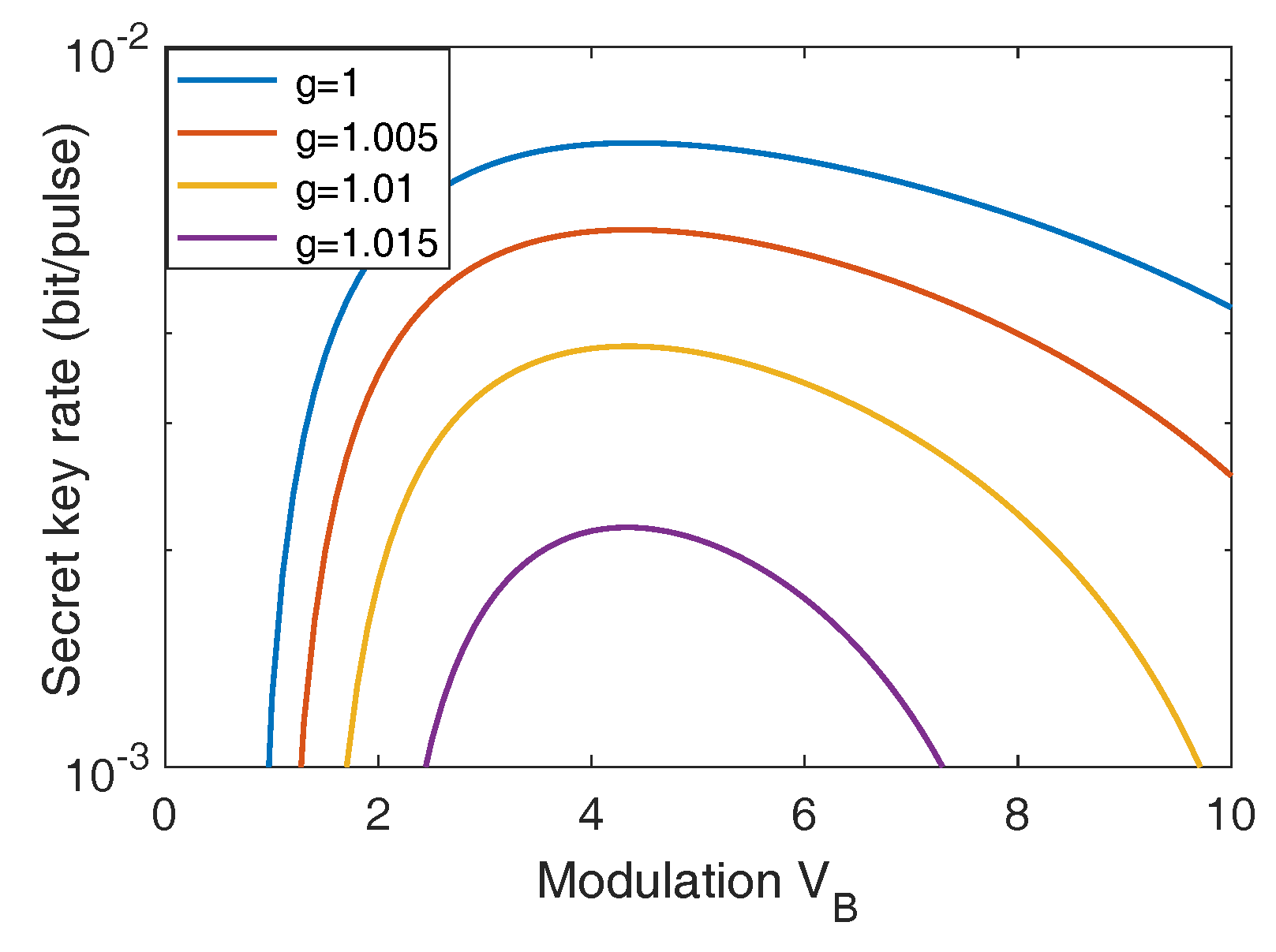
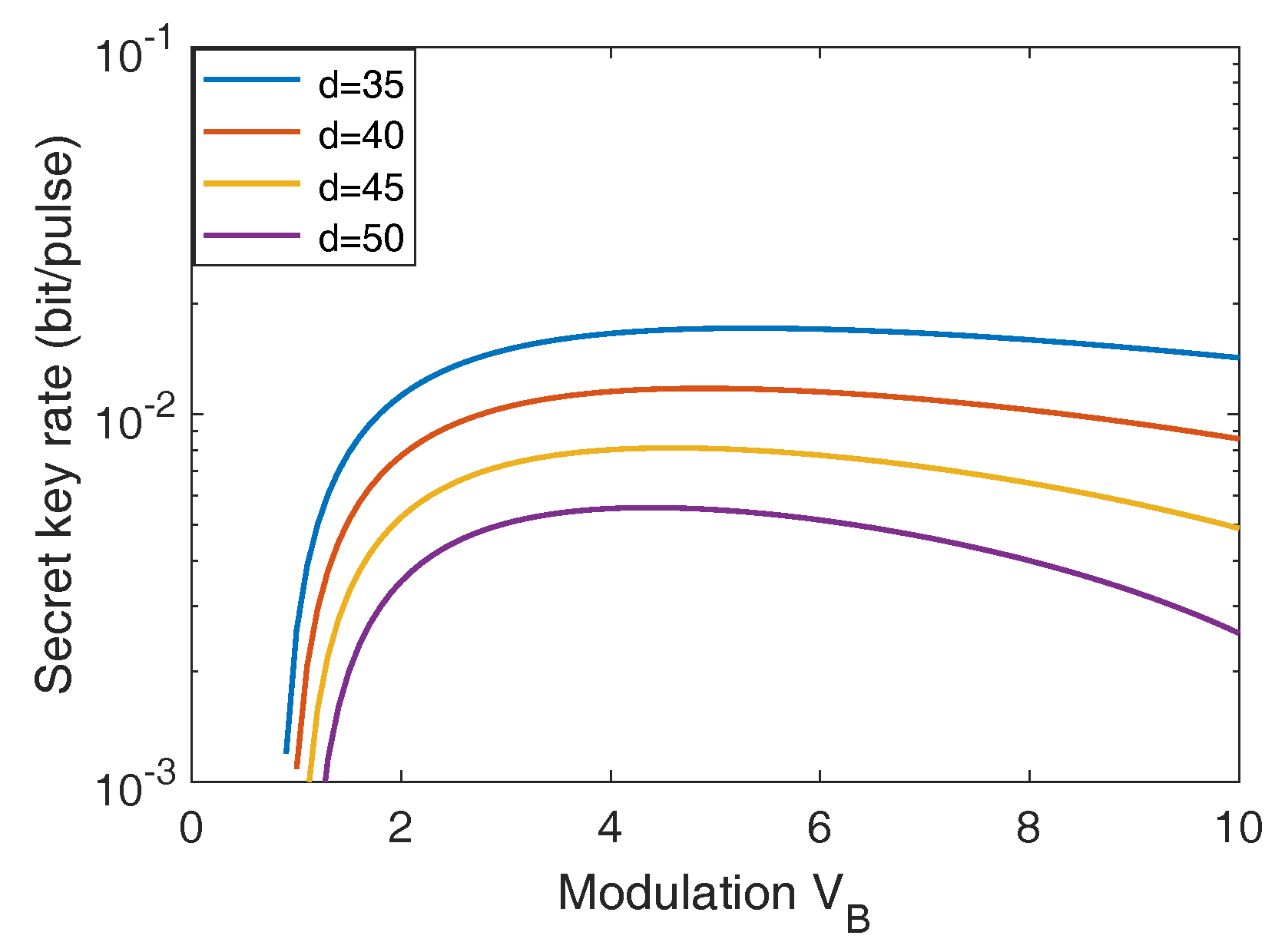
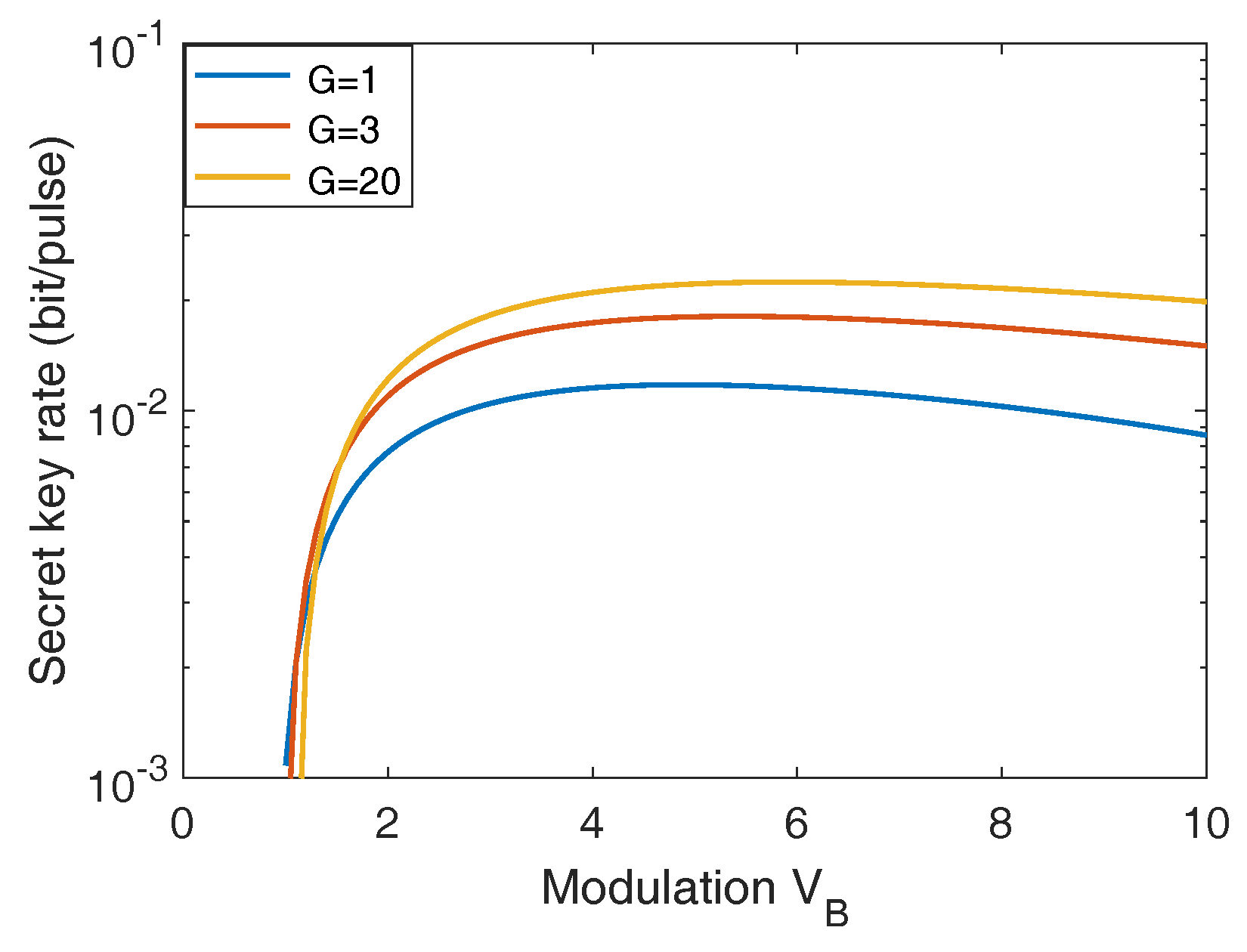
Appendix B. Calculation of Asymptotic Secret Key Rate
Appendix C. Secret Key Rate in the Finite-Size Scenario
References
- Gisin, N.; Ribordy, G.; Tittel, W.; Zbinden, H. Quantum cryptography. Rev. Mod. Phys. 2002, 74, 145. [Google Scholar] [CrossRef]
- Lo, H.-K.; Curty, M.; Tamaki, K. Secure Quantum Key Distribution. Nat. Photon. 2014, 8, 595. [Google Scholar] [CrossRef]
- Scarani, V.; Bechmann-Pasquinucci, H.; Cerf, N.J.; Dušek, M.; Lütkenhaus, N.; Peev, M. The Security of Practical Quantum Key Distribution. Rev. Mod. Phys. 2009, 81, 1301. [Google Scholar] [CrossRef]
- Weedbrook, C.; Pirandola, S.; García-Patrón, R.; Cerf, N.J.; Ralph, T.C.; Shapiro, J.H.; Lloyd, S. Gaussian quantum information. Rev. Mod. Phys. 2012, 84, 621. [Google Scholar] [CrossRef]
- Shor, P.W.; Preskill, J. Simple proof of security of the BB84 quantum key distribution protocol. Phys. Rev. Lett. 2000, 85, 441. [Google Scholar] [CrossRef]
- Lo, H.K.; Chau, H.F. Unconditional security of quantum key distribution over arbitrarily long distances. Science 1999, 283, 2050. [Google Scholar] [CrossRef] [PubMed]
- Takeda, S.; Fuwa, M.; Van, L.P.; Furusawa, A. Entanglement Swapping between Discrete and Continuous Variables. Phys. Rev. Lett. 2015, 114, 100501. [Google Scholar] [CrossRef]
- Huang, D.; Lin, D.; Wang, C.; Liu, W.Q.; Peng, J.Y.; Fang, S.H.; Huang, P.; Zeng, G.H. Continuous-variable quantum key distribution with 1 Mbps secure key rate. Opt. Express 2015, 23, 17511. [Google Scholar] [CrossRef] [PubMed]
- Pirandola, S.; Ottaviani, C.; Spedalieri, G.; Weedbrook, C.; Braunstein, S.L.; Lloyd, S.; Gehring, T.; Jacobsen, C.S.; Andersen, U.L. High-rate measurement-device-independent quantum cryptography. Nat. Photon. 2015, 9, 397. [Google Scholar] [CrossRef]
- Huang, D.; Huang, P.; Li, H.; Wang, T.; Zhou, Y.; Zeng, G. Field demonstration of a continuous-variable quantum key distribution network. Opt. Lett. 2016, 41, 3511. [Google Scholar] [CrossRef]
- Grosshans, F.; Van, A.G.; Wenger, J.; Brouri, R.; Cerf, N.J.; Grangier, P. Quantum key distribution using gaussian-modulated coherent states. Nature 2003, 421, 238. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.D.; Liao, Q.; Huang, D.; Wu, X.H.; Guo, Y. Balancing four-state continuous-variable quantum key distribution with linear optics cloning machine. Chin. Phys. B 2017, 26, 110304. [Google Scholar] [CrossRef]
- Grosshans, F.; Grangier, P. Continuous variable quantum cryptography using coherent states. Phys. Rev. Lett. 2002, 88, 057902. [Google Scholar] [CrossRef]
- Huang, P.; Fang, J.; Zeng, G. State-discrimination attack on discretely modulated continuous-variable quantum key distribution. Phys. Rev. A 2014, 89, 042330. [Google Scholar] [CrossRef]
- Guo, Y.; Liao, Q.; Wang, Y.J.; Huang, D.; Huang, P.; Zeng, G.H. Performance improvement of continuous-variable quantum key distribution with an entangled source in the middle via photon subtraction. Phys. Rev. A 2017, 95, 032304. [Google Scholar] [CrossRef]
- Huang, D.; Huang, P.; Lin, D.; Zeng, G. Long-distance continuous-variable quantum key distribution by controlling excess noise. Sci. Rep. 2016, 6, 19201. [Google Scholar] [CrossRef]
- Jouguet, P.; Kunz-Jacques, S.; Leverrier, A. Long-distance continuous-variable quantum key distribution with a Gaussian modulation. Phys. Rev. A 2011, 84, 062317. [Google Scholar] [CrossRef]
- Milicevic, M.; Chen, F.; Zhang, L.; Gulak, P.G. Quasi-cyclic multi-edge LDPC codes for long-distance quantum cryptography. NPJ Quantum Inf. 2018, 4, 21. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, Y.; Yu, S.; Guo, H. High speed error correction for continuous-variable quantum key distribution with multi-edge type LDPC code. Sci. Rep. 2018, 8, 10543. [Google Scholar] [CrossRef] [PubMed]
- Kikuchi, K. Fundamentals of coherent optical fiber communications. J. Lightwave Technol. 2016, 34, 157. [Google Scholar] [CrossRef]
- Qi, B. Simultaneous classical communication and quantum key distribution using continuous variables. Phys. Rev. A 2016, 94, 042340. [Google Scholar] [CrossRef]
- Qi, B.; Lim, C.C.W. Noise analysis of simultaneous quantum key distribution and classical communication scheme using a true local oscillator. Phys. Rev. Appl. 2018, 9, 054008. [Google Scholar] [CrossRef]
- Huang, D.; Huang, P.; Lin, D.-K.; Wang, C.; Zeng, G.-H. High-speed continuous-variable quantum key distribution without sending a local oscillator. Opt. Lett. 2015, 40, 3695. [Google Scholar] [CrossRef] [PubMed]
- Qi, B.; Lougovski, P.; Pooser, R.; Grice, W.; Bobrek, M. Generating the Local Oscillator Locally in Continuous-Variable Quantum Key Distribution Based on Coherent Detection. Phys. Rev. X 2015, 5, 041009. [Google Scholar] [CrossRef]
- Soh, D.B.S.; Brif, C.; Coles, P.J.; Lütkenhaus, N.; Camacho, R.M.; Urayama, J.; Sarovar, M. Self-Referenced Continuous-Variable Quantum Key Distribution Protocol. Phys. Rev. X 2015, 5, 041010. [Google Scholar] [CrossRef]
- Huang, D.; Huang, P.; Wang, T.; Li, H.S.; Zhou, Y.M.; Zeng, G.H. Continuous-variable quantum key distribution based on a plug-and-play dual-phase-modulated coherent-states protocol. Phys. Rev. A 2016, 94, 032305. [Google Scholar] [CrossRef]
- Fossier, S.; Diamanti, E.; Debuisschert, T.; Tualle-Brouri, R.; Grangier, P. Improvement of continuous-variable quantum key distribution systems by using optical preamplifiers. J. Phys. B 2009, 42, 114014. [Google Scholar] [CrossRef]
- Zhang, H.; Fang, J.; He, G. Improving the performance of the four-state continuous-variable quantum key distribution by using optical amplifiers. Phys. Rev. A 2012, 86, 022338. [Google Scholar] [CrossRef]
- Guo, Y.; Li, R.J.; Liao, Q.; Zhou, J.; Huang, D. Performance improvement of eight-state continuous-variable quantum key distribution with an optical amplifiers. Phys. Lett. A 2017, 382, 372–381. [Google Scholar] [CrossRef]
- Subacius, D.; Zavriyev, A.; Trifonov, A. Backscattering limitation for fiber-optic quantum key distribution systems. Appl. Phys. Lett. 2005, 86, 011103. [Google Scholar] [CrossRef]
- Pirandola, S.; Laurenza, R.; Ottaviani, C.; Banchi, L. Fundamental limits of repeaterless quantum communications. Nat. Commun. 2017, 8, 15043. [Google Scholar] [CrossRef] [PubMed]
- Renner, R.; Cirac, J.I. de Finetti representation theorem for infinite-dimensional quantum systems and applications to quantum cryptography. Phys. Rev. Lett. 2009, 102, 110504. [Google Scholar] [CrossRef] [PubMed]
- Leverrier, A.; Grosshans, F.; Grangier, P. Finite-size analysis of continuous-variable quantum key distribution. Phys. Rev. A 2010, 81, 062343. [Google Scholar] [CrossRef]
- Furrer, F.; Franz, T.; Berta, M.; Leverrier, A.; Scholz, V.B.; Tomamichel, M.; Werner, R.F. Continuous variable quantum key distribution: finite-key analysis of composable security against coherent attacks. Phys. Rev. Lett. 2012, 109, 100502. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, X.; Wang, Y.; Liao, Q.; Zhong, H.; Guo, Y. Simultaneous Classical Communication and Quantum Key Distribution Based on Plug-and-Play Configuration with an Optical Amplifier. Entropy 2019, 21, 333. https://doi.org/10.3390/e21040333
Wu X, Wang Y, Liao Q, Zhong H, Guo Y. Simultaneous Classical Communication and Quantum Key Distribution Based on Plug-and-Play Configuration with an Optical Amplifier. Entropy. 2019; 21(4):333. https://doi.org/10.3390/e21040333
Chicago/Turabian StyleWu, Xiaodong, Yijun Wang, Qin Liao, Hai Zhong, and Ying Guo. 2019. "Simultaneous Classical Communication and Quantum Key Distribution Based on Plug-and-Play Configuration with an Optical Amplifier" Entropy 21, no. 4: 333. https://doi.org/10.3390/e21040333
APA StyleWu, X., Wang, Y., Liao, Q., Zhong, H., & Guo, Y. (2019). Simultaneous Classical Communication and Quantum Key Distribution Based on Plug-and-Play Configuration with an Optical Amplifier. Entropy, 21(4), 333. https://doi.org/10.3390/e21040333




