Brain Network Modeling Based on Mutual Information and Graph Theory for Predicting the Connection Mechanism in the Progression of Alzheimer’s Disease
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Acquisition and Participants Selection
2.2. Data Preprocessing
2.3. Construction of Real Brain Network
2.4. Synthetic Brain Network Modeling
2.4.1. Network Modeling Steps
- Initialization: At the beginning of modeling, all participants in groups of NC, MCI and AD were preprocessed and the corresponding inter-regional correlation matrices , , were obtained, where , and represent the number of participants in NC, MCI, and AD, respectively. We calculated the average correlation matrix of each group, and each average correlation matrix was threshold with the same to construct the corresponding real brain networks, i.e., for NC, for MCI and for AD. The real brain network in each group consisted of a constant number of nodes, . The connection number of , and were represented by , and , respectively. In current work, we studied the evolution process of AD networks from two stages, i.e., the stage from NC to MCI and the stage from NC to AD. By comparing the elements in the binary graphs , and , we obtained a constant number of connections that need to be added; another constant number of connections that need to be deleted in the stage from NC to MCI; and connections to be added and connections to be deleted from NC to AD. Here, and because a declining number of connections was found when comparing and with (). It is worth mentioning that we call the real brain network of NC the initial network in our modeling, and call and the real target brain networks (TN).
- Connection probabilities calculation: After initialization, we calculated the connection probabilities of any node pairs in according to the proposed connection probabilities models, i.e., ECM and MINM introduced in the following subsection. Then, we sorted each node pair in line with its connection probability. The node pair with the largest connection probability and the node pair with the smallest connection probability were recorded, respectively.
- Evolution: Our model started to evolve from the initial graph . In each iteration, a random number was generated to decide whether to add or delete one connection in . The node pair with the largest connection probability will establish a link if its two nodes disconnected with each other. Meanwhile, the node pair with the smallest connection probability would cut off its link if there were a connection between its two nodes. It should be noted that each node must have a connection to ensure the connectivity of the synthetic network. Therefore, a new pair of nodes must be chosen according to the sorted connection probabilities, if either node’s connection number in the node pair is equal to 1 when deleting the link between them. We upgraded connection set in at the end of this step.
- End of the modeling: Our model ran the above steps of connection probabilities calculation and evolution round by round. The simulation did not proceed to the end, if connections were established and connections were deleted successfully for in the stage from NC to MCI; or connections were established and connections were deleted in the stage from NC to AD. Finally, we obtained two synthetic networks with the same connection size as and , respectively.
2.4.2. Connection Probabilities Models
- Connection probability of ECM: The more common neighbors (CN) that node u and node v have, the higher topological similarity to one another [48]. The number of common neighbors between node u and node v can be described bywhere and represent the set of neighboring nodes of node u and node v, respectively. Scaling by the Euclidean distance similarity between two brain regions, the ECN connection probability between node u and node v, i.e., the probability that u prefers to build the connection with v, is given by
- Connection probability of MINM: Given a pair of node , whose common neighbors can be represented by , the connection probability of MINM between them can be given bywhere is the topological similarity between node u and node v, which represents the topology-based mutual information between them. is the Euclidean distance similarity, which is similar with ECM. can be given bywhere denotes the conditional self-information of an event that there is a connection between node u and node v, whose common neighbors are known as . From Equation (6), we can know that the smaller is, the higher topological similarity is, and this indicates that a larger probability for node u and node v to establish one connection between them.
2.5. Evaluation of Synthetic Networks
3. Results
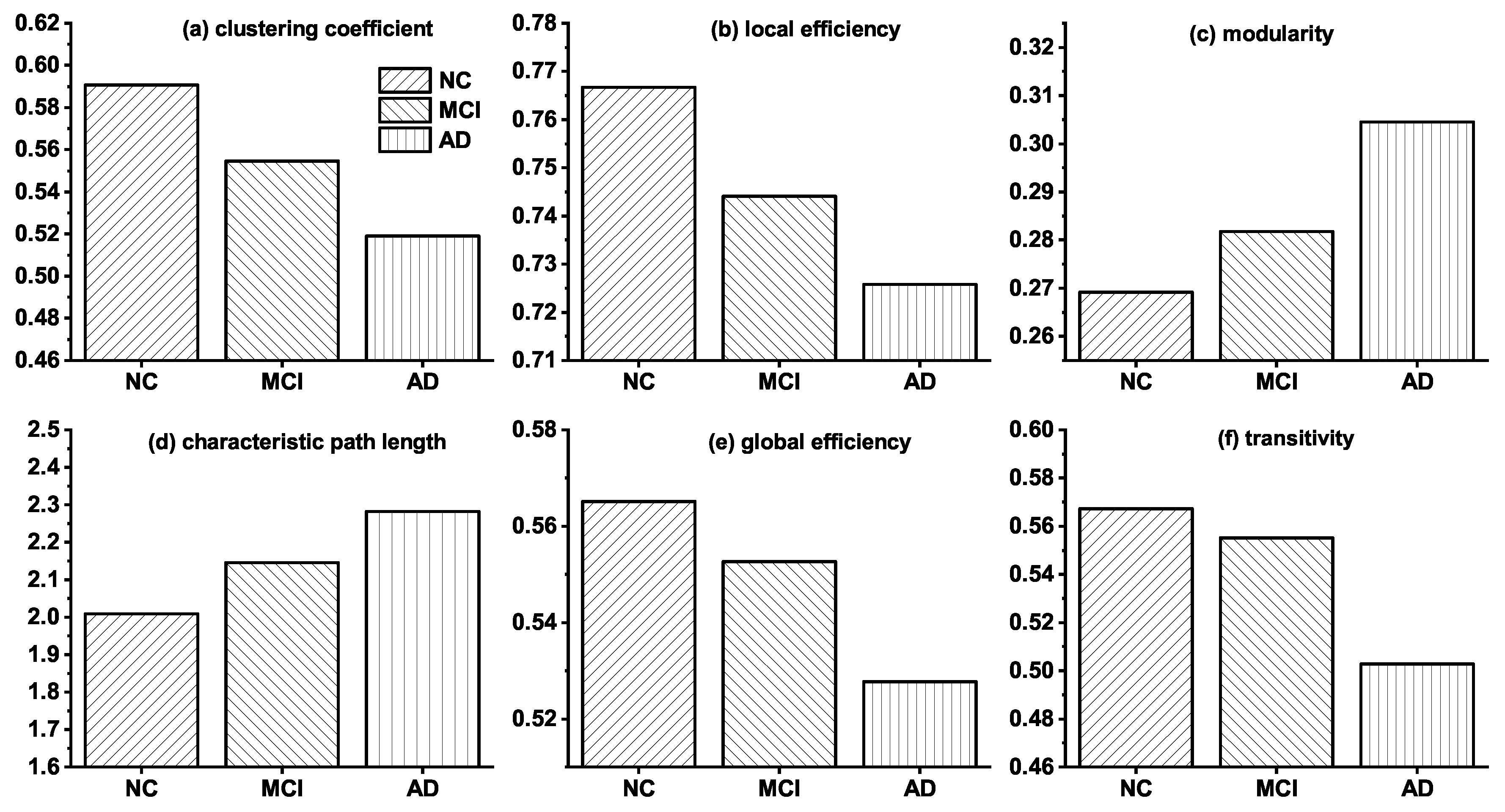
3.1. Topological Differences in Brain Networks of NC, MCI and AD
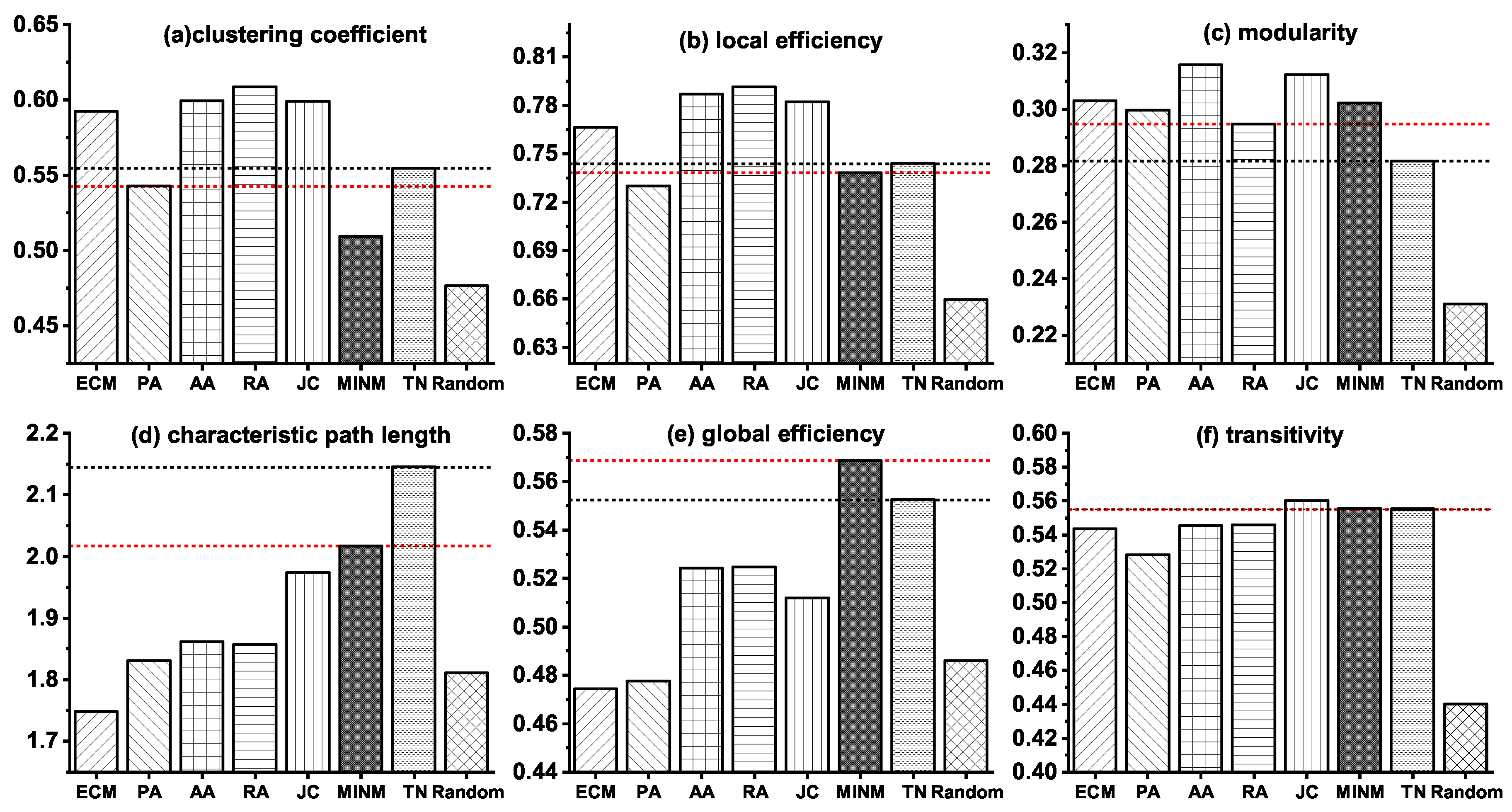
3.2. Network Modeling of the Stage from NC to MCI
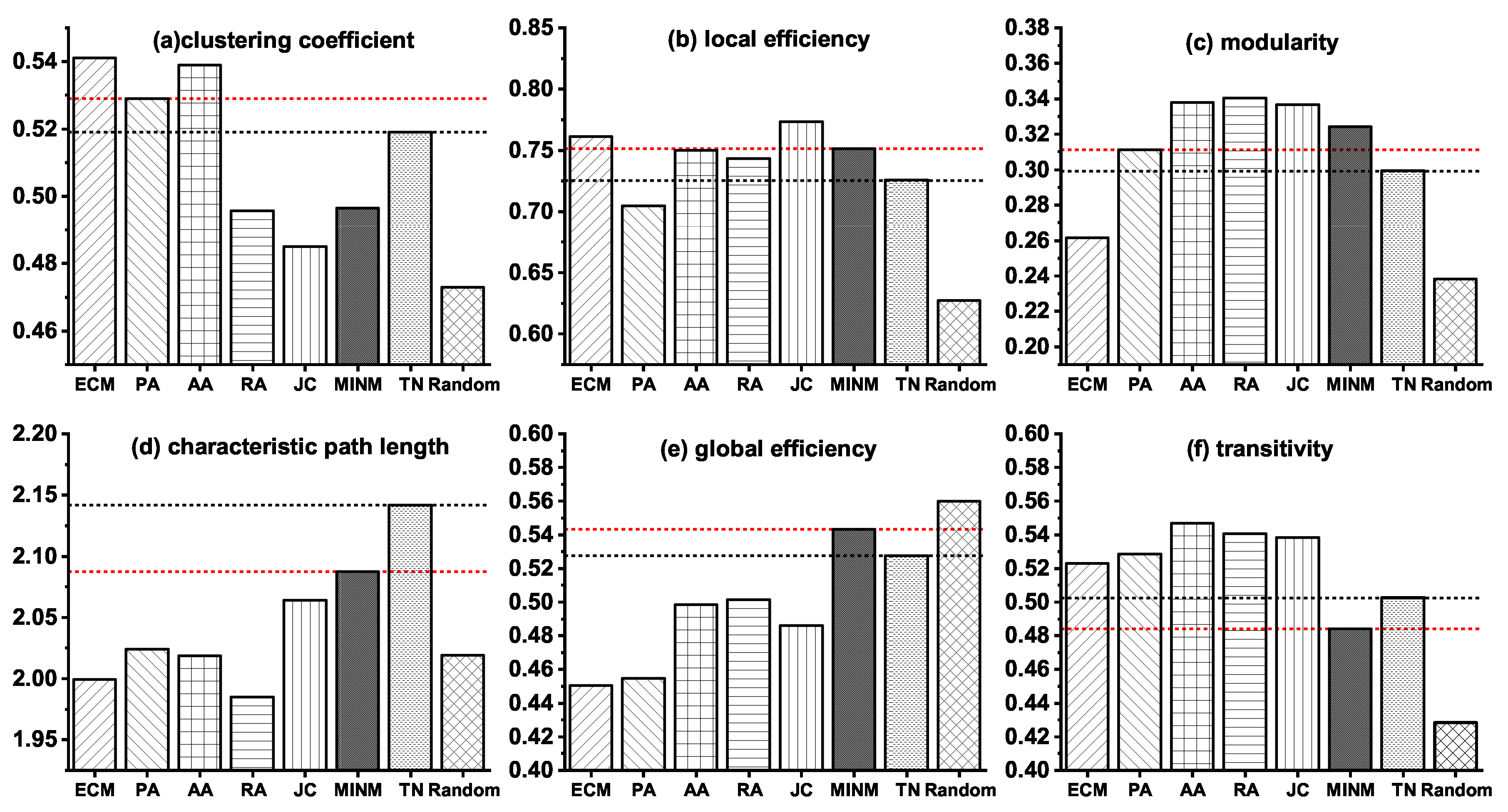
3.3. Network Modeling of the Stage from NC to AD
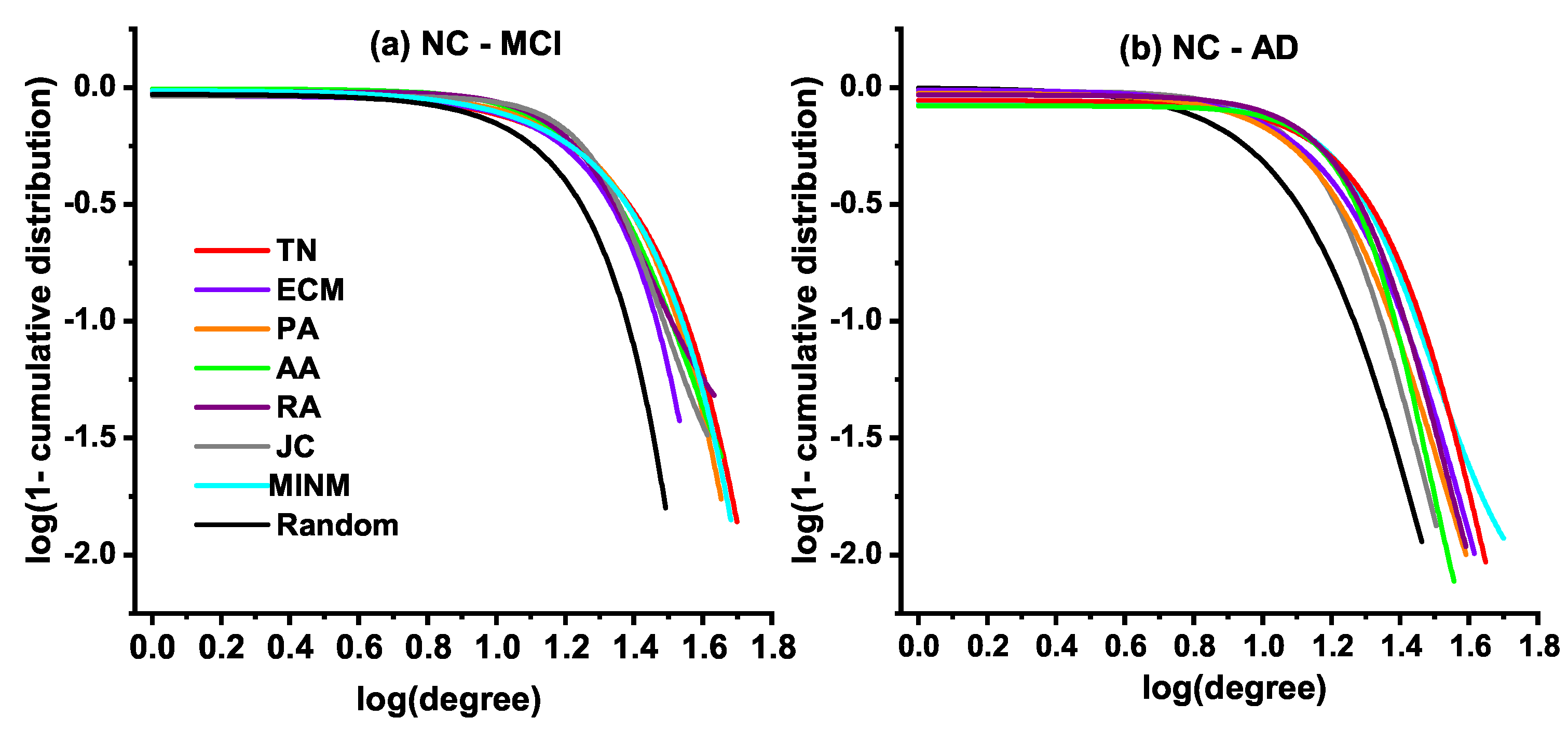
3.4. Degree Distribution
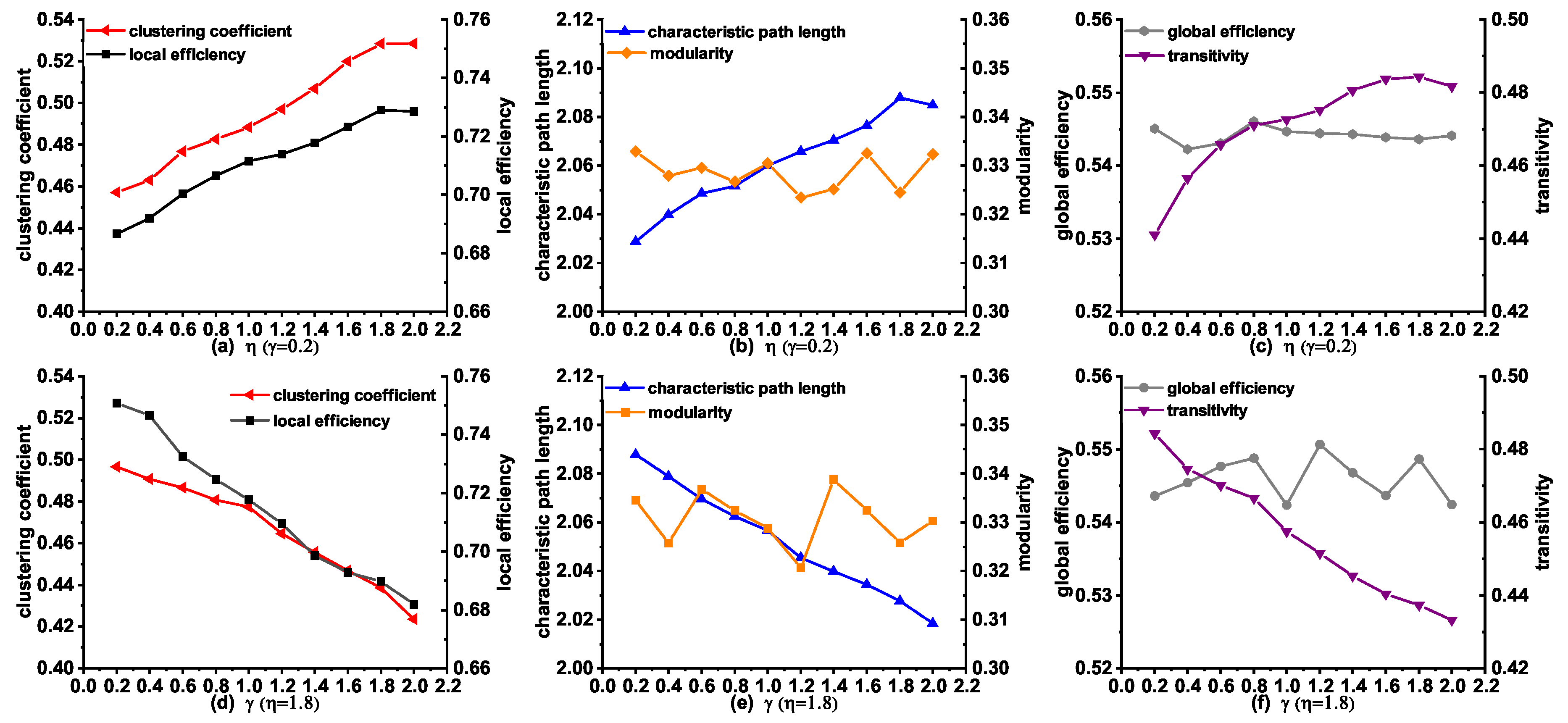
3.5. Topological Properties of the Synthetic Networks Generated by MINM with Different and
3.6. Connections Deleted in the Early Stage from NC to AD
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Alzheimer’s Association. 2018 Alzheimer’s disease facts and figures. Alzheimers Dement. 2018, 14, 367–429. [Google Scholar] [CrossRef]
- Zhang, Z.Q.; Liu, Y.; Zhou, B.; Zheng, J.L.; Yao, H.X.; An, N.Y.; Wang, P.; Guo, Y.E.; Dai, H.T.; Wang, L.N.; et al. Altered functional connectivity of the marginal division in Alzheimer’s disease. Curr. Alzheimer Res. 2014, 11, 145–155. [Google Scholar] [CrossRef] [PubMed]
- Jessen, F.; Amariglio, R.E.; van Boxtel, M.; Breteler, M.; Ceccaldi, M.; Chételat, G.; Dubois, B.; Dufouil, C.; Ellis, K.A.; van der Flier, W.M.; et al. A conceptual framework for research on subjective cognitive decline in preclinical Alzheimer’s disease. Alzheimers Dement. 2014, 10, 844–852. [Google Scholar] [CrossRef] [PubMed]
- Cai, S.P.; Chong, T.; Peng, Y.L.; Shen, W.Y.; Li, J.; von Deneen, K.M.; Huang, L.Y. Altered functional brain networks in amnestic mild cognitive impairment: a resting-state fMRI study. Brain Imaging Behav. 2017, 11, 619–631. [Google Scholar] [CrossRef] [PubMed]
- He, Y.; Chen, Z.; Evans, A. Structural insights into aberrant topological patterns of large-scale cortical networks in Alzheimer’s disease. J. Neurosci. 2008, 28, 4756–4766. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Wang, M.; Zhu, W.Z.; Qin, Y.Y.; Huang, Y.; Chen, X. Simulating the evolution of functional brain networks in Alzheimer’s disease: exploring disease dynamics from the perspective of global activity. Sci. Rep. 2016, 6, 34156. [Google Scholar] [CrossRef]
- Li, Y.P.; Qin, Y.; Chen, X.; Li, W. Exploring the functional brain network of Alzheimer’s disease: based on the computational experiment. PLoS ONE 2013, 8, e73186. [Google Scholar] [CrossRef] [PubMed]
- Bullmore, E.; Sporns, O. Complex brain networks: graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci. 2009, 10, 186–198. [Google Scholar] [CrossRef] [PubMed]
- Bullmore, E.; Sporns, O. The economy of brain network organization. Nat. Rev. Neurosci. 2012, 13, 336–349. [Google Scholar] [CrossRef]
- Avena-Koenigsberger, A.; Misic, B.; Sporns, O. Communication dynamics in complex brain networks. Nat. Rev. Neurosci. 2018, 19, 17–33. [Google Scholar] [CrossRef] [PubMed]
- Bassett, D.S.; Sporns, O. Network neuroscience. Nat. Neurosci. 2017, 20, 353–364. [Google Scholar] [CrossRef] [PubMed]
- Zuo, X.N.; He, Y.; Betzel, R.F.; Colcombe, S.; Sporns, O.; Milham, M.P. Human connectomics across the life span. Trends Cogn. Sci. 2017, 21, 32–45. [Google Scholar] [CrossRef]
- He, Y.; Evans, A. Graph theoretical modeling of brain connectivity. Curr. Opin. Neurol. 2010, 23, 341–350. [Google Scholar] [CrossRef] [PubMed]
- Barban, F.; Mancini, M.; Cercignani, M.; Adriano, F.; Perri, R.; Annicchiarico, R.; Carlesimo, G.A.; Ricci, C.; Lombardi, M.G.; Teodonno, V. A pilot study on brain plasticity of functional connectivity modulated by cognitive training in mild Alzheimer’s disease and mild cognitive impairment. Brain Sci. 2017, 7, 50. [Google Scholar] [CrossRef] [PubMed]
- Vecchio, F.; Miraglia, F.; Piludu, F.; Granata, G.; Romanello, R.; Caulo, M.; Onofrj, V.; Bramanti, P.; Colosimo, C.; Rossini, P.M. “Small World” architecture in brain connectivity and hippocampal volume in Alzheimer’s disease: a study via graph theory from EEG data. Brain Imaging Behav. 2017, 11, 473–485. [Google Scholar] [CrossRef] [PubMed]
- Si, S.Z.; Wang, J.F.; Yu, C.; Zhao, H. Energy-efficient and Fault-tolerant Evolution Models based on Link Prediction for Large-scale Wireless Sensor Networks. IEEE Access 2018, 6, 73341–73356. [Google Scholar] [CrossRef]
- Liu, X.; Wang, J.F.; Jing, W.; de Jong, M.; Tummers, J.S.; Zhao, H. Evolution of the Internet AS-level topology: From nodes and edges to components. Chin. Phys. B 2018, 27, 120501. [Google Scholar] [CrossRef]
- Jalili, M.; Orouskhani, Y.; Asgari, M.; Alipourfard, N.; Perc, M. Link prediction in multiplex online social networks. R. Soc. Open Sci. 2017, 4, 160863. [Google Scholar] [CrossRef]
- Cannistraci, C.V.; Alanis-Lobato, G.; Ravasi, T. From link-prediction in brain connectomes and protein interactomes to the local-community-paradigm in complex networks. Sci. Rep. 2013, 3, 1613. [Google Scholar] [CrossRef]
- Newman, M.; Barabasi, A.L.; Watts, D.J. The Structure and Dynamics of Networks; Princeton University Press: Princeton, UK, 2011; ISBN 9780691113579. [Google Scholar]
- Ma, C.; Zhou, T.; Zhang, H.F. Playing the role of weak clique property in link prediction: A friend recommendation model. Sci. Rep. 2016, 6, 30098. [Google Scholar] [CrossRef]
- Wang, P.; Xu, B.W.; Wu, Y.R.; Zhou, X.Y. Link prediction in social networks: the state-of-the-art. Sci. China Inf. Sci. 2015, 58, 1–38. [Google Scholar] [CrossRef]
- Zhu, L.; Deng, S.P.; You, Z.H.; Huang, D.S. Identifying spurious interactions in the protein-protein interaction networks using local similarity preserving embedding. IEEE-ACM Trans. Comput. Biol. Bioinform. (TCBB) 2017, 14, 345–352. [Google Scholar] [CrossRef] [PubMed]
- Pan, L.; Zhou, T.; Lv, L.; Hu, C.K. Predicting missing links and identifying spurious links via likelihood analysis. Sci. Rep. 2016, 6, 22955. [Google Scholar] [CrossRef]
- Guimera, R.; Sales-Pardo, M. Missing and spurious interactions and the reconstruction of complex networks. Proc. Natl. Acad. Sci. USA 2009, 106, 22073–22078. [Google Scholar] [CrossRef] [PubMed]
- Vértes, P.E.; Alexander-Bloch, A.F.; Gogtay, N.; Giedd, J.N.; Rapoport, J.L.; Bullmore, E.T. Simple models of human brain functional networks. Proc. Natl. Acad. Sci. USA 2012, 109, 5868–5873. [Google Scholar] [CrossRef] [PubMed]
- Betzel, R.F.; Avena-Koenigsberger, A.; Goñi, J.; He, Y.; de Reus, M.A.; Griffa, A.; Vértes, P.E.; Mišic, B.; Thiran, J.P.; Hagmann, P. Generative models of the human connectome. Neuroimage 2016, 124, 1054–1064. [Google Scholar] [CrossRef]
- Bassett, D.S.; Zurn, P.; Gold, J.I. On the nature and use of models in network neuroscience. Nat. Rev. Neurosci. 2018, 19, 566–578. [Google Scholar] [CrossRef] [PubMed]
- Cabral, J.; Kringelbach, M.L.; Deco, G. Exploring the network dynamics underlying brain activity during rest. Prog. Neurobiol. 2014, 114, 102–131. [Google Scholar] [CrossRef] [PubMed]
- Zhao, T.D.; Xu, Y.H.; He, Y. Graph theoretical modeling of baby brain networks. NeuroImage 2018, 185, 711–727. [Google Scholar] [CrossRef]
- Sporns, O. Contributions and challenges for network models in cognitive neuroscience. Nat. Neurosci. 2014, 17, 652–660. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Gibson, J. Entropy Power, Autoregressive Models, and Mutual Information. Entropy 2018, 20, 750. [Google Scholar] [CrossRef]
- Wang, Z.; Alahmadi, A.; Zhu, D.; Li, T.T. Brain functional connectivity analysis using mutual information. In Proceedings of the 2015 IEEE Global Conference of Signal and Information Processing (GlobalSIP), Orlando, FL, USA, 14–16 December 2015; pp. 542–546. [Google Scholar]
- Ruiz-Gómez, S.J.; Gómez, C.; Poza, J.; Gutiérrez-Tobal, G.C.; Tola-Arribas, M.A.; Cano, M.; Hornero, R. Automated multiclass classification of spontaneous EEG activity in Alzheimer’s Disease and mild cognitive impairment. Entropy 2018, 20, 35. [Google Scholar] [CrossRef]
- Sayood, K. Information Theory and Cognition: A Review. Entropy 2018, 20, 706. [Google Scholar] [CrossRef]
- Jeong, J.; Gore, J.C.; Peterson, B.S. Mutual information analysis of the EEG in patients with Alzheimer’s disease. Clin. Neurophysiol. 2001, 112, 827–835. [Google Scholar] [CrossRef]
- Garn, H.; Waser, M.; Deistler, M.; Benke, T.; Dal-Bianco, P.; Ransmayr, G.; Schmidt, H.; Sanin, G.; Santer, P.; Caravias, G.; et al. Electroencephalographic Complexity Markers Explain Neuropsychological Test Scores in Alzheimer’s Disease. In Proceedings of the 2014 IEEE-EMBS International Conference on Biomedical and Health Informatics (BHI), Valencia, Spain, 1–4 June 2014; pp. 496–499. [Google Scholar]
- Arevalo-Rodriguez, I.; Smailagic, N.; i Figuls, M.R.; Ciapponi, A.; Sanchez-Perez, E.; Giannakou, A.; Pedraza, O.L.; Cosp, X.B.; Cullum, S. Mini-Mental State Examination (MMSE) for the detection of Alzheimer’s disease and other dementias in people with mild cognitive impairment (MCI). Cochrane Database Syst. Rev. 2015, 3, CD010783. [Google Scholar]
- Coronel, C.; Garn, H.; Waser, M.; Deistler, M.; Benke, T.; Dal-Bianco, P.; Ransmayr, G.; Seiler, S.; Grossegger, D.; Schmidt, R. Quantitative EEG markers of entropy and auto mutual information in relation to MMSE scores of probable Alzheimer’s disease patients. Entropy 2017, 19, 130. [Google Scholar] [CrossRef]
- Hsu, W.C.; Denq, C.; Chen, S.S. A diagnostic methodology for Alzheimer’s disease. J. Clin. Bioinf. 2013, 3, 9–21. [Google Scholar] [CrossRef]
- Blokh, D.; Stambler, I. The application of information theory for the research of aging and aging-related diseases. Prog. Neurobiol. 2017, 157, 158–173. [Google Scholar] [CrossRef]
- Sulaimany, S.; Khansari, M.; Zarrineh, P.; Daianu, M.; Jahanshad, N.; Thompsonc, P.M.; Masoudi-Nejad, A. Predicting brain network changes in Alzheimer’s disease with link prediction algorithms. Mol. Biosyst. 2017, 13, 725–735. [Google Scholar] [CrossRef]
- Supekar, K.; Menon, V.; Rubin, D.; Musen, M.; Greicius, M.D. Network analysis of intrinsic functional brain connectivity in Alzheimer’s disease. PLoS Comput. Biol. 2008, 4, e1000100. [Google Scholar] [CrossRef] [PubMed]
- Yan, C.G.; Zang, Y.F. DPARSF: A MATLAB toolbox for “pipeline” data analysis of resting-state fMRI. Front. Syst. Neurosci. 2010, 4, 13–19. [Google Scholar] [CrossRef] [PubMed]
- Penny, W.D.; Friston, K.J.; Ashburner, J.T.; Kiebel, S.J.; Nichols, T.E. Statistical Parametric Mapping: The Analysis of Functional Brain Images; Academic Press: London, UK, 2011; ISBN 9780123725608. [Google Scholar]
- Tzourio-Mazoyer, N.; Landeau, B.; Papathanassiou, D.; Crivello, F.; Etard, O.; Delcroix, N.; Mazoyer, B.; Joliot, M. Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain. Neuroimage 2002, 15, 273–289. [Google Scholar] [CrossRef] [PubMed]
- Liben-Nowell, D.; Kleinberg, J. The link-prediction problem for social networks. J. Am. Soc. Inf. Sci. Technol. 2007, 58, 1019–1031. [Google Scholar] [CrossRef]
- Newman, M.E.J. Clustering and preferential attachment in growing networks. Phys. Rev. E 2001, 64, 025102. [Google Scholar] [CrossRef] [PubMed]
- Lü, L.Y.; Zhou, T. Link prediction in complex networks: A survey. Physica A 2011, 390, 1150–1170. [Google Scholar] [CrossRef]
- Adamic, L.A.; Adar, E. Friends and neighbors on the web. Soc. Netw. 2003, 25, 211–230. [Google Scholar] [CrossRef]
- Zhou, T.; Lü, L.Y.; Zhang, Y.C. Predicting missing links via local information. Eur. Phys. J. B 2009, 71, 623–630. [Google Scholar] [CrossRef]
| NC | MCI | AD | |
|---|---|---|---|
| Number | 62 | 45 | 40 |
| Gender (Male/Female) | 27/35 | 20/25 | 21/19 |
| Age | 73.95 ± 4.83 | 74.38 ± 4.92 | 74.86 ± 5.52 |
| MMSE score | 28.72 ± 1.06 | 27.68 ± 1.86 | 22.36 ± 2.77 |
| CDR score | 0.00 ± 0.00 | 0.51 ± 0.17 | 0.93 ± 0.16 |
| Property Name | Symbol | Description |
|---|---|---|
| Clustering coefficient | C | It is a measure of the number of triangles in a graph. |
| Local efficiency | Eloc | It is a measure to quantify the efficiency of local information transmission. |
| Global efficiency | Eglob | It is a measure to quantify the efficiency of global information transmission. |
| Characteristic path length | L | L is the average shortest path length between all node pairs in the network. |
| Modularity | M | It is used to detect the strength of the division of a network into communities. |
| Transitivity | T | It measures the probability that the adjacent nodes of a node are connected. |
| Degree | k | It indicates the number of links connecting with a node. |
| Models | Abbreviation | Mathematical |
|---|---|---|
| Preferential Attachment [49] | PA | |
| Jaccard [50] | JC | |
| Adamic–Adar [51] | AA | |
| Resource Allocation [52] | RA |
| Models | SI | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| ECM | 0.2 | 1.6 | 0.0687 | 0.0302 | 0.0713 | 0.1851 | 0.1413 | 0.0205 | 1.9339 |
| PA | 0.2 | 1.8 | 0.0213 | 0.0187 | 0.0639 | 0.1464 | 0.1356 | 0.0480 | 2.4010 |
| AA | 0.2 | 1.4 | 0.0811 | 0.0578 | 0.1210 | 0.1324 | 0.0514 | 0.0173 | 2.1692 |
| RA | 0.4 | 2.0 | 0.0975 | 0.0638 | 0.0465 | 0.1345 | 0.0502 | 0.0164 | 2.4358 |
| JC | 0.2 | 0.2 | 0.0844 | 0.0515 | 0.1082 | 0.0861 | 0.0789 | 0.0126 | 2.3714 |
| MINM | 0.4 | 2.0 | 0.0816 | 0.0077 | 0.0727 | 0.0598 | 0.0292 | 0.0010 | 3.9683 |
| Random | – | – | 0.1406 | 0.1132 | 0.1796 | 0.1558 | 0.1204 | 0.2068 | 1.0912 |
| Models | SI | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| CN | 0.4 | 1.2 | 0.0426 | 0.0491 | 0.1263 | 0.0665 | 0.1460 | 0.0419 | 2.1169 |
| PA | 0.2 | 1.6 | 0.0194 | 0.0289 | 0.0395 | 0.0551 | 0.1377 | 0.0515 | 3.0111 |
| AA | 0.2 | 1.6 | 0.0386 | 0.0339 | 0.1291 | 0.0576 | 0.0551 | 0.0881 | 2.4851 |
| RA | 0.2 | 2.0 | 0.0448 | 0.0245 | 0.1370 | 0.0732 | 0.0496 | 0.0758 | 2.4697 |
| JC | 0.4 | 0.4 | 0.0653 | 0.0661 | 0.1249 | 0.0364 | 0.0786 | 0.0709 | 2.2614 |
| MINM | 0.2 | 1.8 | 0.0432 | 0.0358 | 0.0835 | 0.0253 | 0.0303 | 0.0368 | 3.9231 |
| Random | – | – | 0.0888 | 0.1355 | 0.2304 | 0.0534 | 0.0611 | 0.1476 | 1.3951 |
| Deleted Connections Number = 10 | Deleted Connections Number = 20 | Deleted Connections Number = 30 |
|---|---|---|
| (85,2) (53,4) | (54,7) (53,2) | (51,10) (54,23) |
| (77,12) (85,4) | (51,14) (49,26) | (51,23) (54,24) |
| (51,4) (86,85) | (52,7) (54,3) | (50,7) (49,14) |
| (51,8) (51,2) | (53,14) (51,24) | (53,24) (54,13) |
| (53,8) (85,8) | (49,8) (49,10) | (49,24) (52,9) |
| Deleted Connections Number | C | M | L | T | ||
|---|---|---|---|---|---|---|
| 0 | 0.5906 | 0.7667 | 0.2691 | 2.0082 | 0.5651 | 0.5672 |
| 10 | 0.5829 | 0.7626 | 0.2723 | 2.0109 | 0.5639 | 0.5492 |
| 20 | 0.5784 | 0.7626 | 0.2760 | 2.0254 | 0.5616 | 0.5459 |
| 30 | 0.5764 | 0.7626 | 0.2772 | 2.0397 | 0.5575 | 0.5438 |
| AD | 0.5190 | 0.7258 | 0.3045 | 2.2821 | 0.5277 | 0.5027 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Si, S.; Wang, B.; Liu, X.; Yu, C.; Ding, C.; Zhao, H. Brain Network Modeling Based on Mutual Information and Graph Theory for Predicting the Connection Mechanism in the Progression of Alzheimer’s Disease. Entropy 2019, 21, 300. https://doi.org/10.3390/e21030300
Si S, Wang B, Liu X, Yu C, Ding C, Zhao H. Brain Network Modeling Based on Mutual Information and Graph Theory for Predicting the Connection Mechanism in the Progression of Alzheimer’s Disease. Entropy. 2019; 21(3):300. https://doi.org/10.3390/e21030300
Chicago/Turabian StyleSi, Shuaizong, Bin Wang, Xiao Liu, Chong Yu, Chao Ding, and Hai Zhao. 2019. "Brain Network Modeling Based on Mutual Information and Graph Theory for Predicting the Connection Mechanism in the Progression of Alzheimer’s Disease" Entropy 21, no. 3: 300. https://doi.org/10.3390/e21030300
APA StyleSi, S., Wang, B., Liu, X., Yu, C., Ding, C., & Zhao, H. (2019). Brain Network Modeling Based on Mutual Information and Graph Theory for Predicting the Connection Mechanism in the Progression of Alzheimer’s Disease. Entropy, 21(3), 300. https://doi.org/10.3390/e21030300





