Extinction Analysis of Stochastic Predator–Prey System with Stage Structure and Crowley–Martin Functional Response
Abstract
1. Introduction
2. Preliminaries
3. Existence and Uniqueness of Global Positive Solution
4. Stochastically Ultimate Boundedness
5. Stochastic Extinction
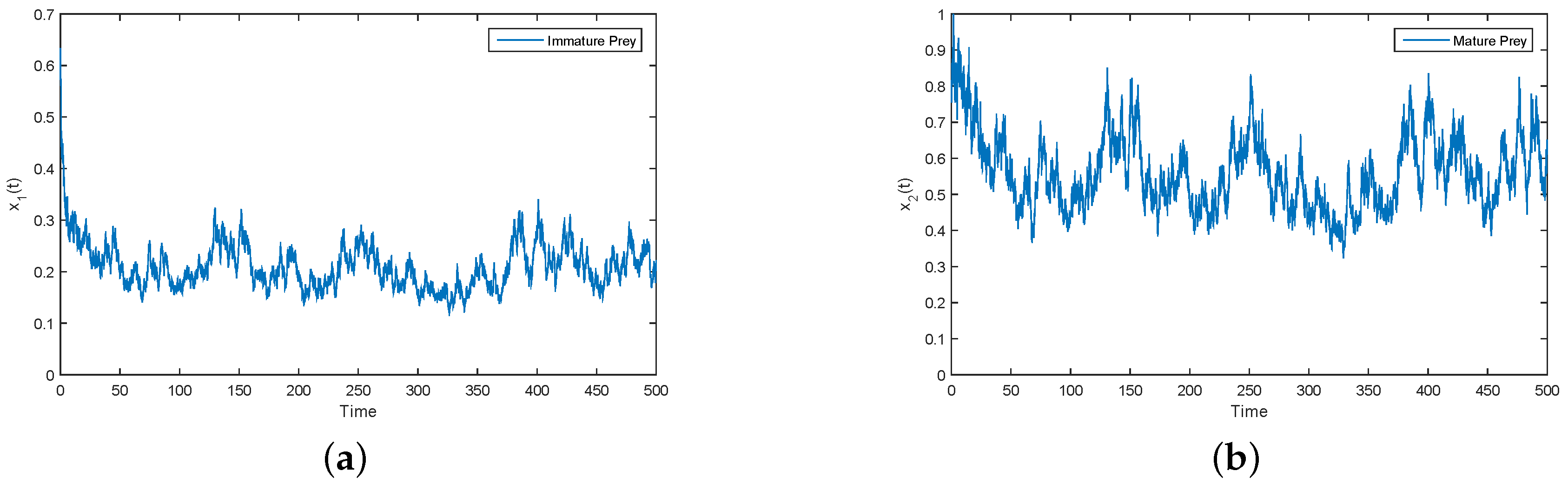
6. Numerical Simulations
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lotka, A. Elements of Mathematical Biology; Dover Publications: New York, NY, USA, 1956. [Google Scholar]
- Mukherjee, D. Persistence and bifurcation analysis on a predator-prey system of Holling type. Esaim Math. Model. Numer. Anal. 2003, 37, 339–344. [Google Scholar] [CrossRef]
- Liu, Z.J.; Zhong, S.M. Permanence and extinction analysis for a delayed periodic predator-prey system with Holling type II response function and diffusion. Appl. Math. Comput. 2010, 216, 3002–3015. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, H.; Fu, M. Hopf bifurcation in a predator-prey system with Holling type III functional response and time delays. J. Appl. Math. Comput. 2014, 44, 337–356. [Google Scholar] [CrossRef]
- Sklaski, G.T.; Gilliam, J.F. Functional responses with predator interference: Viable alternative to Holling type II model. Ecology 2001, 82, 3083–3092. [Google Scholar] [CrossRef]
- Wang, K.; Zhu, Y.L. Permanence and global asymptotic stability of a delayed predator-prey model with Hassell-Varley type functional response. Bull. Iran. Math. Soc. 2013, 94, 1–14. [Google Scholar]
- Cui, J.; Takeuchi, Y. Permanence, extinction and periodic solution of predator-prey system with Beddington-DeAngelis functional response. J. Math. Anal. Appl. 2006, 317, 464–474. [Google Scholar] [CrossRef]
- Lahrouz, A.; Settati, A.; Mandal, P.S. Dynamics of a switching diffusion modified Leslie-Gower predator-prey system with Beddington-DeAngelis functional response. Nonlinear Dyn. 2016, 85, 853–870. [Google Scholar] [CrossRef]
- Tripathi, J.P.; Abbas, S.; Thakur, M. Dynamical analysis of a prey-predator model with Beddington-DeAngelis type function response incorporating a prey refuge. Nonlinear Dyn. 2015, 80, 177–196. [Google Scholar] [CrossRef]
- Tripathi, J.P.; Tyagi, S.; Abbas, S. Global analysis of a delayed density dependent predator–prey model with Crowley-Martin functional response. Commun. Nonlinear Sci. Numer. Simul. 2016, 30, 45–69. [Google Scholar] [CrossRef]
- Upadhyay, R.K.; Naji, R.K. Dynamics of a three species food chain model with Crowley–Martin type functional response. Chaos Solitons Fractals 2009, 42, 1337–1346. [Google Scholar] [CrossRef]
- Wang, W.; Chen, L. A predator-prey system with stage-structure for predator. Comput. Math. Appl. 1997, 33, 83–91. [Google Scholar] [CrossRef]
- Chen, Y.; Song, C. Stability and Hopf bifurcation analysis in a prey-predator system with stage-structure for prey and time delay. Chaos Solitons Fractals 2008, 38, 1104–1114. [Google Scholar] [CrossRef]
- Huang, C.Y.; Zhao, M.; Zhao, L.C. Permanence of periodic predator-prey system with two predators and stage structure for prey. Nonlinear Anal. Real World Appl. 2014, 2018, 503–514. [Google Scholar] [CrossRef]
- Yang, W.; Li, X.; Bai, Z. Permanence of periodic Holling type-IV predator-prey system with stage structure for prey. Math. Comput. Model. 2008, 48, 677–684. [Google Scholar] [CrossRef]
- Meng, X.Y.; Huo, H.F.; Xiang, H.; Yin, Q.Y. Stability in a predator–prey model with Crowley-Martin function and stage structure for prey. Appl. Math. Comput. 2014, 232, 810–819. [Google Scholar] [CrossRef]
- Sun, X.K.; Huo, H.F.; Xiang, H. Bifurcation and stability analysis in predator-prey model with a stage-structure for predator. Nonlinear Dyn. 2009, 58, 497–513. [Google Scholar] [CrossRef]
- Xu, R. Global dynamics of a predator-prey model with time delay and stage structure for the prey. Nonlinear Anal. Real World Appl. 2011, 12, 2151–2162. [Google Scholar] [CrossRef]
- Lu, Y.; Pawelek, K.A.; Liu, S. A stage-structured predator-prey model with predation over juvenile prey. Appl. Math. Comput. 2017, 297, 115–130. [Google Scholar] [CrossRef]
- Yang, L.; Zhong, S.M. Global stability of a stage-structured predator-prey model with stochastic perturbation. Discret. Dyn. Nat. Soc. 2014, 2014, 1–8. [Google Scholar] [CrossRef]
- Liu, M.; Wang, K. Global stability of stage-structured predator–prey models with Beddington-DeAngelis functional response. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 3792–3797. [Google Scholar] [CrossRef]
- Zhao, S.; Song, M. A stochastic predator-prey system with stage structure for predator. Abstr. Appl. Anal. 2014, 2014, 1–7. [Google Scholar] [CrossRef]
- Liu, Q.; Jiang, D.Q.; Hayat, T.; Alsaedi, A. Dynamics of a stochastic predator-prey model with stage structure for predator and Holling type II functional response. J. Nonlinear Sci. 2018, 28, 1151–1187. [Google Scholar] [CrossRef]
- Chen, F.D.; You, M.S. Permanence, extinction and periodic solution of the predator-prey system with Beddington-DeAngelis functional response and stage structure for prey. Nonlinear Anal.-Real World Appl. 2008, 9, 207–221. [Google Scholar] [CrossRef]
- Liu, X.Q.; Zhong, S.M.; Tian, B.D.; Zheng, F.X. Asymptotic properties of a stochastic predator-prey model with Crowley-Martin functional response. J. Appl. Math. Comput. 2013, 43, 479–490. [Google Scholar] [CrossRef]
- Mao, X.R. Stochastic Differential Equations and Applications; Horwood Publishing: Chichester, UK, 1997. [Google Scholar]
- May, R.M. Stability and Complexity in Model Ecosystems; Princeton University Press: Princeton, NJ, USA, 2001; Volume 6, p. 779. [Google Scholar]
- Li, X.Y.; Gray, A.; Jiang, D.Q.; Mao, X.R. Sufficient and necessary conditions of stochastic permanence and extinction for stochastic logistic populations under regime switching. J. Math. Anal. Appl. 2011, 376, 11–28. [Google Scholar] [CrossRef]
- Higham, D.J. An algorithmic introduction to numerical simulation of stochastic differential equations. SIAM Rev. 2001, 43, 525–546. [Google Scholar] [CrossRef]
- Liu, Q.; Jiang, D.Q.; Hayat, T.; Ahmad, B. Stationary distribution and extinction of a stochastic predator–prey model with additional food and nonlinear perturbation. Appl. Math. Computat. 2018, 320, 226–239. [Google Scholar] [CrossRef]
- Liu, M.; Bai, C.Z. On a stochastic delayed predator-prey model with Lévy jumps. Appl. Math. Computat. 2014, 228, 563–570. [Google Scholar] [CrossRef]
- Aguirre, P.; Eduardo, G.O.; Torres, S. Stochastic predator-prey model with Allee effect on prey. Nonlinear Anal. Real World Appl 2013, 14, 768–779. [Google Scholar] [CrossRef]
- Ali, E.; Asif, M.; Ajbar, A.H. Study of chaotic behavior in predator–prey interactions in a chemostat. Ecol. Model. 2013, 259, 10–15. [Google Scholar] [CrossRef]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, C.; Ren, G.; Yu, Y. Extinction Analysis of Stochastic Predator–Prey System with Stage Structure and Crowley–Martin Functional Response. Entropy 2019, 21, 252. https://doi.org/10.3390/e21030252
Xu C, Ren G, Yu Y. Extinction Analysis of Stochastic Predator–Prey System with Stage Structure and Crowley–Martin Functional Response. Entropy. 2019; 21(3):252. https://doi.org/10.3390/e21030252
Chicago/Turabian StyleXu, Conghui, Guojian Ren, and Yongguang Yu. 2019. "Extinction Analysis of Stochastic Predator–Prey System with Stage Structure and Crowley–Martin Functional Response" Entropy 21, no. 3: 252. https://doi.org/10.3390/e21030252
APA StyleXu, C., Ren, G., & Yu, Y. (2019). Extinction Analysis of Stochastic Predator–Prey System with Stage Structure and Crowley–Martin Functional Response. Entropy, 21(3), 252. https://doi.org/10.3390/e21030252





