Amplitude Constrained MIMO Channels: Properties of Optimal Input Distributions and Bounds on the Capacity †
Abstract
:1. Introduction
1.1. Contributions and Paper Organization
1.2. Notation
2. Problem Statement
- (i)
- per-antenna amplitude constraints, i.e., for some given ; and
- (ii)
- -dimensional amplitude constraint, i.e., for some given .
3. Properties of an Optimal Input Distribution
3.1. Necessary and Sufficient Conditions for Optimality
- is unique and symmetric if is left invertible [18].
3.2. General Structure of Capacity-Achieving Input Distributions
- Towards a contradiction, it is assumed that the set of points of increase is infinite.
- The assumption in Step 1 is then used to establish a certain property of the function on the input space . For example, by showing that has an analytic continuation to . Then, by means of the Identity Theorem of complex analysis and the Bolzano–Weierstrass Theorem [25], Smith was able to show that must be constant.
- By using either the Fourier or Laplace transform of together with the property of established in Step 2, a new a property of the channel output distribution is established. For example, Smith was able to show that must be constant.
- A conclusion out of Step 3 is used to reach a contradiction. The contradiction implies that must be finite. For example, to reach a contradiction, Smith was using the fact that the channel output distribution results from a convolution with a Gaussian probability density, which cannot be constant.
- (i)
- is an open set.
- (ii)
- is a set of positive Lebesgue measure.
- is unique.
- is symmetric.
- is discrete with the number of mass points being of the order .
- contains probability mass points at .
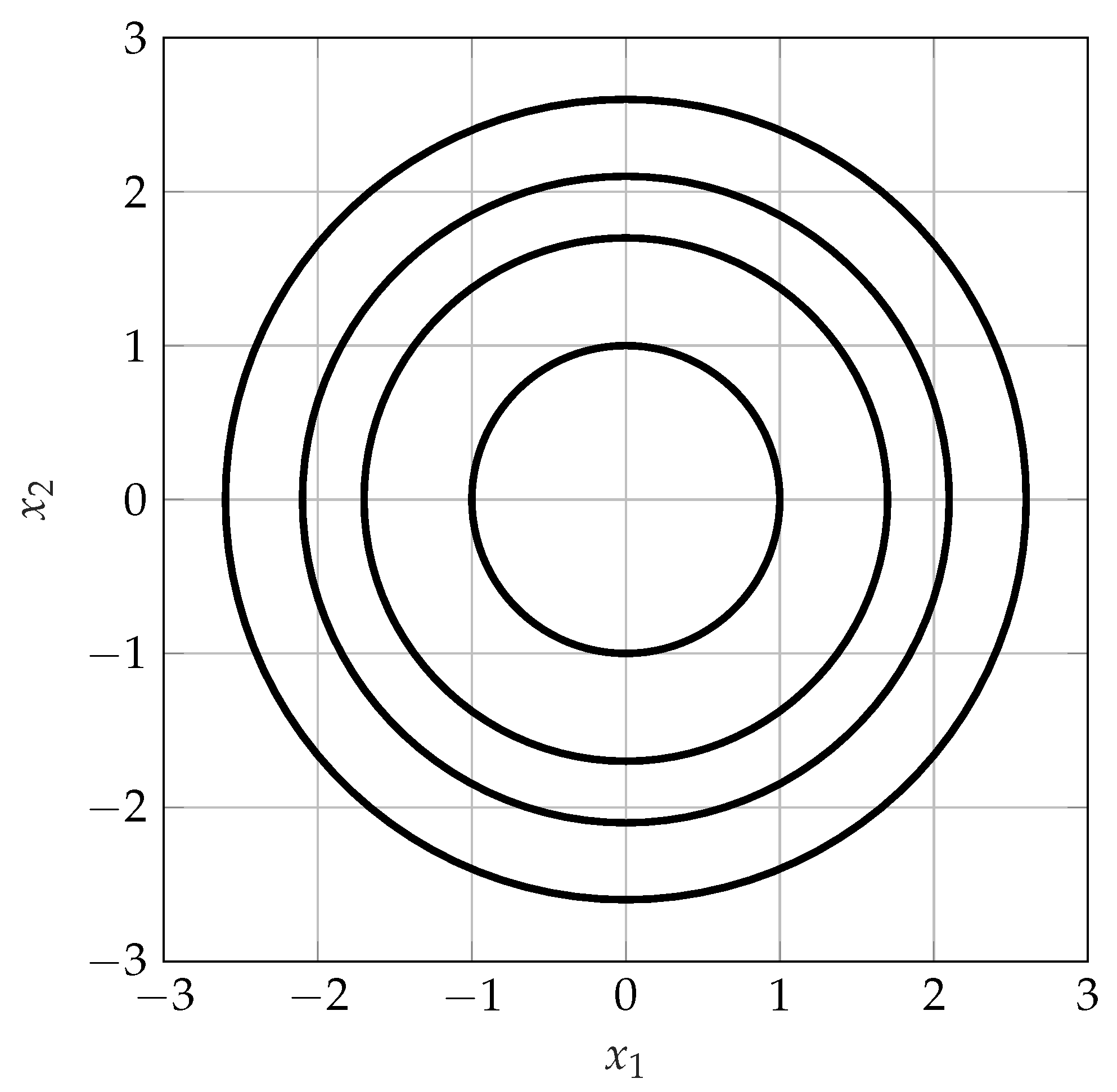
3.3. Properties of Capacity-Achieving Input Distributions in the Small (But Not Vanishing) Amplitude Regime
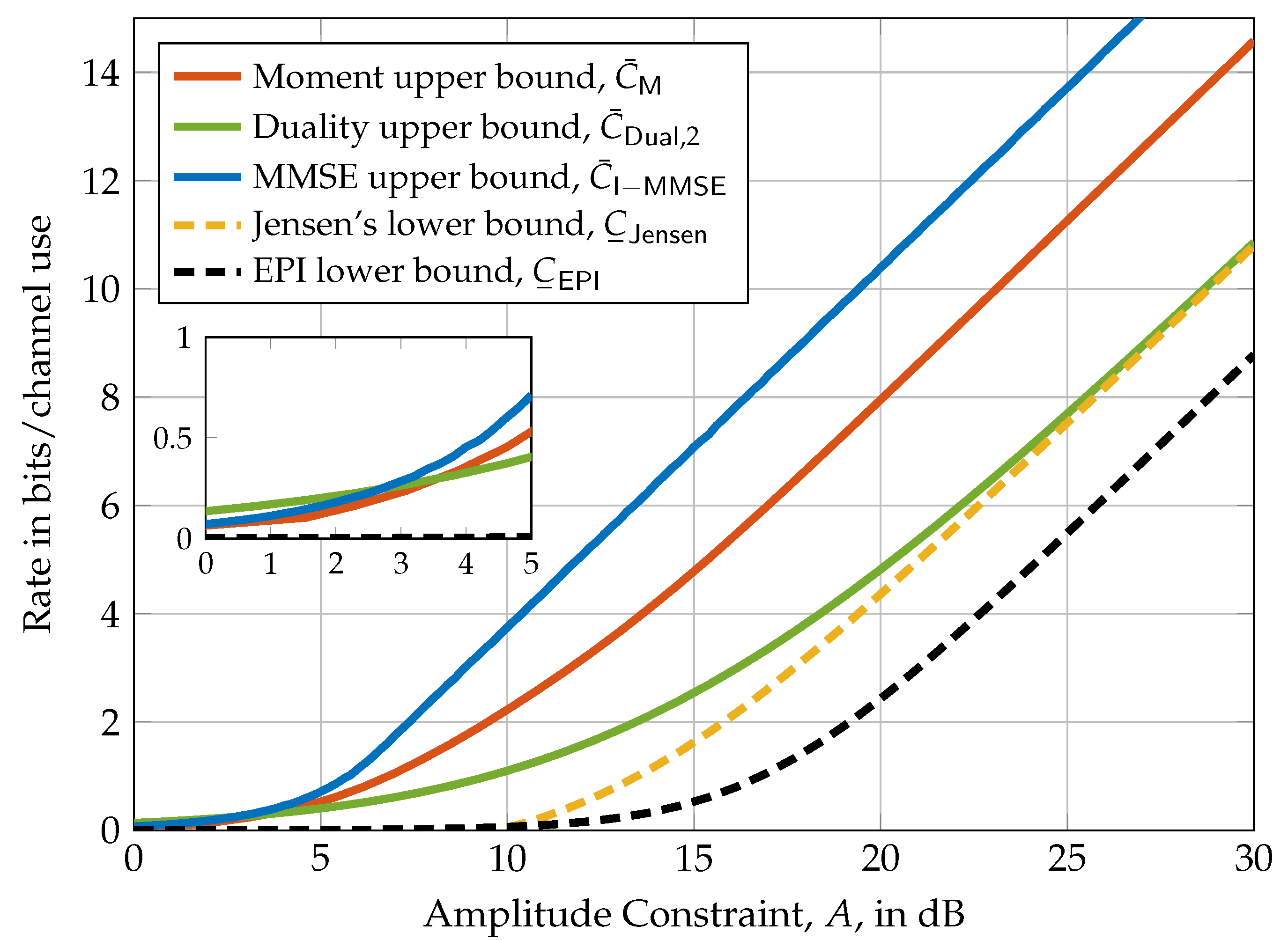
4. Upper and Lower Bounds on the Capacity
4.1. Upper Bounds
4.2. Lower Bounds
5. Invertible Channel Matrices
5.1. Diagonal Channel Matrices
5.2. Gap to the Capacity
6. Arbitrary Channel Matrices
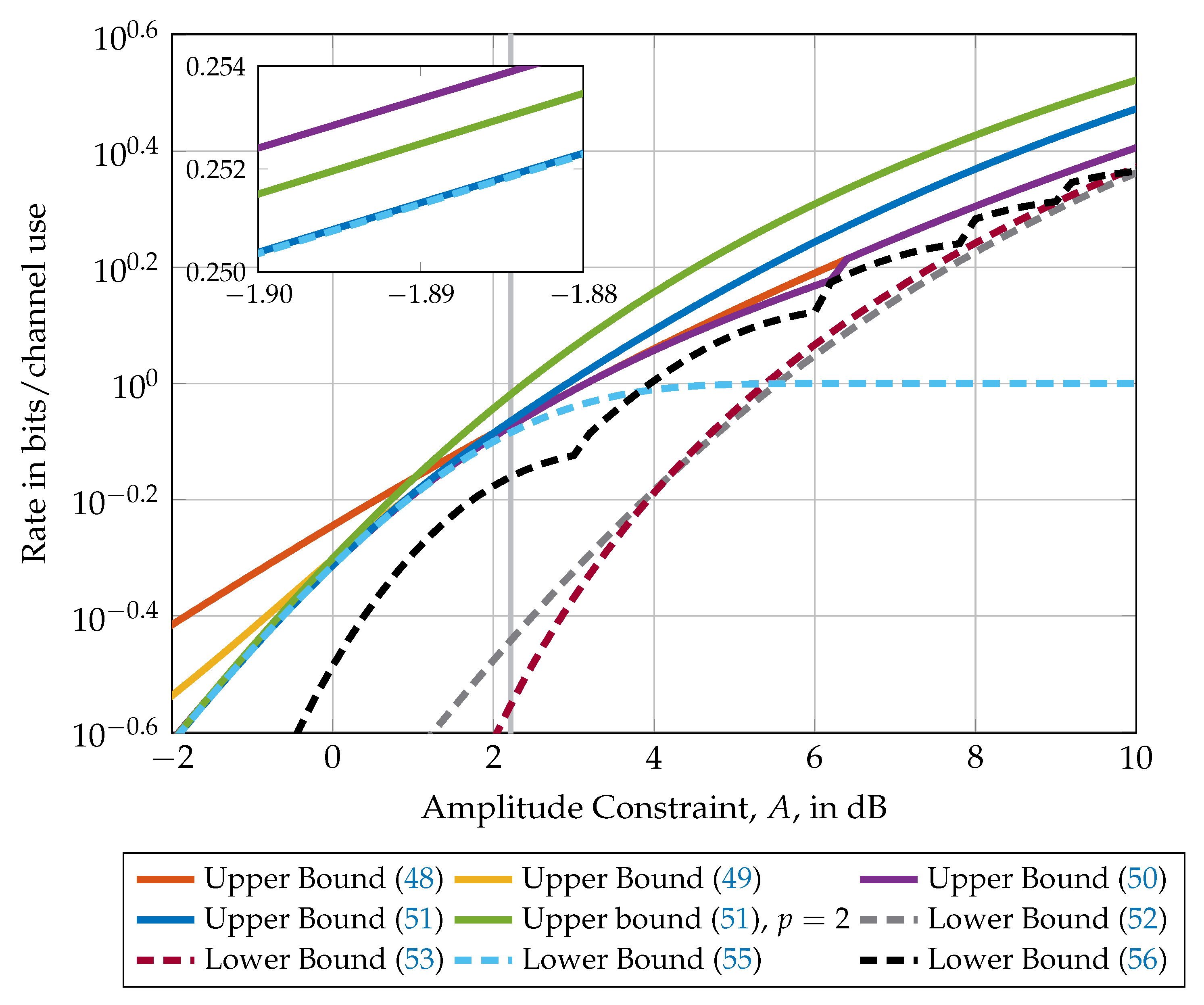
7. The SISO Case
7.1. Upper and Lower Bounds
7.2. High and Low Amplitude Asymptotics
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Telatar, I.E. Capacity of multi-antenna Gaussian channels. Eur. Trans. Telecommun. 1999, 10, 585–595. [Google Scholar] [CrossRef]
- Shannon, C. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27. [Google Scholar] [CrossRef]
- Smith, J.G. The information capacity of amplitude-and variance-constrained scalar Gaussian channels. Inf. Control 1971, 18, 203–219. [Google Scholar] [CrossRef]
- Shamai (Shitz), S.; Bar-David, I. The capacity of average and peak-power-limited quadrature Gaussian channels. IEEE Trans. Inf. Theory 1995, 41, 1060–1071. [Google Scholar] [CrossRef]
- Rassouli, B.; Clerckx, B. On the capacity of vector Gaussian channels with bounded inputs. IEEE Trans. Inf. Theory 2016, 62, 6884–6903. [Google Scholar] [CrossRef]
- Sharma, N.; Shamai (Shitz), S. Transition points in the capacity-achieving distribution for the peak-power limited AWGN and free-space optical intensity channels. Probl. Inf. Transm. 2010, 46, 283–299. [Google Scholar] [CrossRef]
- McKellips, A.L. Simple tight bounds on capacity for the peak-limited discrete-time channel. In Proceedings of the 2004 IEEE International Symposium on Information Theory (ISIT), Chicago, IL, USA, 27 June–2 July 2004; p. 348. [Google Scholar]
- Thangaraj, A.; Kramer, G.; Böcherer, G. Capacity Bounds for Discrete-Time, Amplitude-Constrained, Additive White Gaussian Noise Channels. Available online: https://arxiv.org/abs/1511.08742 (accessed on 15 February 2019).
- Rassouli, B.; Clerckx, B. An Upper Bound for the Capacity of Amplitude-Constrained Scalar AWGN Channel. IEEE Commun. Lett. 2016, 20, 1924–1926. [Google Scholar] [CrossRef]
- ElMoslimany, A.; Duman, T.M. On the Capacity of Multiple-Antenna Systems and Parallel Gaussian Channels With Amplitude-Limited Inputs. IEEE Trans. Commun. 2016, 64, 2888–2899. [Google Scholar] [CrossRef]
- Dytso, A.; Goldenbaum, M.; Poor, H.V.; Shamai (Shitz), S. A Generalized Ozarow-Wyner Capacity Bound with Applications. In Proceedings of the 2017 IEEE International Symposium on Information Theory (ISIT), Aachen, Germany, 25–30 June 2017; pp. 1058–1062. [Google Scholar]
- Dytso, A.; Goldenbaum, M.; Shamai (Shitz), S.; Poor, H.V. Upper and Lower Bounds on the Capacity of Amplitude-Constrained MIMO Channels. In Proceedings of the 2017 IEEE Global Communications Conference (GLOBECOM), Singapore, 4–8 December 2017; pp. 1–6. [Google Scholar]
- Cao, P.L.; Oechtering, T.J. Optimal transmit strategy for MIMO channels with joint sum and per-antenna power constraints. In Proceedings of the 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017. [Google Scholar]
- Loyka, S. The Capacity of Gaussian MIMO Channels Under Total and Per-Antenna Power Constraints. IEEE Trans. Commun. 2017, 65, 1035–1043. [Google Scholar] [CrossRef]
- Loyka, S. On the Capacity of Gaussian MIMO Channels under the Joint Power Constraints. Available online: https://arxiv.org/abs/1809.00056 (accessed on 15 February 2019).
- Tuninetti, D. On the capacity of the AWGN MIMO channel under per-antenna power constraints. In Proceedings of the 2014 IEEE International Conference on Communications (ICC), Sydney, NSW, Australia, 10–14 June 2014; pp. 2153–2157. [Google Scholar]
- Vu, M. MISO capacity with per-antenna power constraint. IEEE Trans. Commun. 2011, 59, 1268–1274. [Google Scholar] [CrossRef]
- Chan, T.H.; Hranilovic, S.; Kschischang, F.R. Capacity-achieving probability measure for conditionally Gaussian channels with bounded inputs. IEEE Trans. Inf. Theory 2005, 51, 2073–2088. [Google Scholar] [CrossRef]
- Csiszar, I.; Körner, J. Information Theory: Coding Theorems for Discrete Memoryless Systems; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Abou-Faycal, I.C.; Trott, M.D.; Shamai, S. The capacity of discrete-time memoryless Rayleigh-fading channels. IEEE Trans. Inf. Theory 2001, 47, 1290–1301. [Google Scholar] [CrossRef]
- Fahs, J.; Abou-Faycal, I. On properties of the support of capacity-achieving distributions for additive noise channel models with input cost constraints. IEEE Trans. Inf. Theory 2018, 64, 1178–1198. [Google Scholar] [CrossRef]
- Gursoy, M.C.; Poor, H.V.; Verdú, S. The noncoherent Rician fading channel-part I: Structure of the capacity-achieving input. IEEE Trans. Wireless Commun. 2015, 4, 2193–2206. [Google Scholar] [CrossRef]
- Katz, M.; Shamai, S. On the capacity-achieving distribution of the discrete-time noncoherent and partially coherent AWGN channels. IEEE Trans. Inf. Theory 2004, 50, 2257–2270. [Google Scholar] [CrossRef]
- Ozel, O.; Ekrem, E.; Ulukus, S. Gaussian wiretap channel with amplitude and variance constraints. IEEE Trans. Inf. Theory 2015, 61, 5553–5563. [Google Scholar] [CrossRef]
- Bak, J.; Newman, D.J. Complex Analysis; Springer Science & Business Media: Berlin, Germany, 2010. [Google Scholar]
- Witsenhausen, H.S. Some Aspects of Convexity Useful in Information Theory. IEEE Trans. Inf. Theory 1980, 26, 265–271. [Google Scholar] [CrossRef]
- Krantz, S.G.; Parks, H.R. A Primer of Real Analytic Functions; Springer Science & Business Media: New York, NY, USA, 2002. [Google Scholar]
- Dytso, A.; Yagli, S.; Poor, H.V.; Shamai (Shitz), S. Capacity Achieving Distribution for the Amplitude Constrained Additive Gaussian Channel: An Upper Bound on the Number of Mass Points. Available online: https://arxiv.org/abs/1901.03264 (accessed on 15 February 2019).
- Ransford, T. Potential Theory in the Complex Plane; London Mathematical Society Student Texts; Cambridge University Press: Cambridge, UK, 1995; Volume 28. [Google Scholar]
- Hatsell, C.; Nolte, L. Some geometric properties of the likelihood ratio (Corresp.). IEEE Trans. Inf. Theory 1971, 17, 616–618. [Google Scholar] [CrossRef]
- Dytso, A.; Poor, H.V.; Shamai (Shitz), S. On the Capacity of the Peak Power Constrained Vector Gaussian Channel: An Estimation Theoretic Perspective. Available online: https://arxiv.org/abs/1804.08524 (accessed on 15 February 2019).
- Dytso, A.; Goldenbaum, M.; Poor, H.V.; Shamai (Shitz), S. When are Discrete Channel Inputs Optimal?—Optimization Techniques and Some New Results. In Proceedings of the 2018 Annual Conference on Information Sciences and Systems (CISS), Princeton, NJ, USA, 21–23 March 2018; pp. 1–6. [Google Scholar]
- Guo, D.; Shamai, S.; Verdú, S. Mutual information and minimum mean-square error in Gaussian channels. IEEE Trans. Inf. Theory 2005, 51, 1261–1282. [Google Scholar] [CrossRef]
- Dytso, A.; Tuninetti, D.; Devroye, N. Interference as Noise: Friend or Foe? IEEE Trans. Inf. Theory 2016, 62, 3561–3596. [Google Scholar] [CrossRef]
- Resnick, S.I. A Probability Path; Springer Science & Business Media: New York, NY, USA, 2013. [Google Scholar]
- Dytso, A.; Bustin, R.; Tuninetti, D.; Devroye, N.; Shamai (Shitz), S.; Poor, H.V. On the Minimum Mean p-th Error in Gaussian Noise Channels and its Applications. IEEE Trans. Inf. Theory 2018, 64, 2012–2037. [Google Scholar] [CrossRef]
- Lozano, A.; Tulino, A.M.; Verdú, S. Optimum power allocation for parallel Gaussian channels with arbitrary input distributions. IEEE Trans. Inf. Theory 2006, 52, 3033–3051. [Google Scholar] [CrossRef]
- Pérez-Cruz, F.; Rodrigues, M.R.; Verdú, S. MIMO Gaussian channels with arbitrary inputs: Optimal precoding and power allocation. IEEE Trans. Inf. Theory 2010, 56, 1070–1084. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th dover printing ed.; Dover Publications: New York, NY, USA, 1964. [Google Scholar]
- Winkelbauer, A. Moments and Absolute Moments of the Normal Distribution. Available online: https://arxiv.org/abs/1209.4340 (accessed on 15 February 2019).
- Guo, D.; Wu, Y.; Shamai, S.; Verdú, S. Estimation in Gaussian Noise: Properties of the Minimum Mean-Square Error. IEEE Trans. Inf. Theory 2011, 57, 2371–2385. [Google Scholar]
- Moser, S.M.; Mylonakis, M.; Wang, L.; Wigger, M. Asymptotic Capacity Results for MIMO Wireless Optical Communication. In Proceedings of the 2017 IEEE International Symposium on Information Theory (ISIT), Aachen, Germany, 25–30 June 2017; pp. 536–540. [Google Scholar]
- Dytso, A.; Egan, M.; Perlaza, S.; Poor, H.V.; Shamai (Shitz), S. Optimal Inputs for Some Classes of Degraded Wiretap Channels. In Proceedings of the 2018 IEEE Information Theory Workshop (ITW), Guangzhou, China, 25–29 November 2018; pp. 1–5. [Google Scholar]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dytso, A.; Goldenbaum, M.; Poor, H.V.; Shamai, S. Amplitude Constrained MIMO Channels: Properties of Optimal Input Distributions and Bounds on the Capacity. Entropy 2019, 21, 200. https://doi.org/10.3390/e21020200
Dytso A, Goldenbaum M, Poor HV, Shamai S. Amplitude Constrained MIMO Channels: Properties of Optimal Input Distributions and Bounds on the Capacity. Entropy. 2019; 21(2):200. https://doi.org/10.3390/e21020200
Chicago/Turabian StyleDytso, Alex, Mario Goldenbaum, H. Vincent Poor, and Shlomo Shamai (Shitz). 2019. "Amplitude Constrained MIMO Channels: Properties of Optimal Input Distributions and Bounds on the Capacity" Entropy 21, no. 2: 200. https://doi.org/10.3390/e21020200
APA StyleDytso, A., Goldenbaum, M., Poor, H. V., & Shamai, S. (2019). Amplitude Constrained MIMO Channels: Properties of Optimal Input Distributions and Bounds on the Capacity. Entropy, 21(2), 200. https://doi.org/10.3390/e21020200





.png)
