Progress in Carnot and Chambadal Modeling of Thermomechanical Engine by Considering Entropy Production and Heat Transfer Entropy
Abstract
1. Introduction
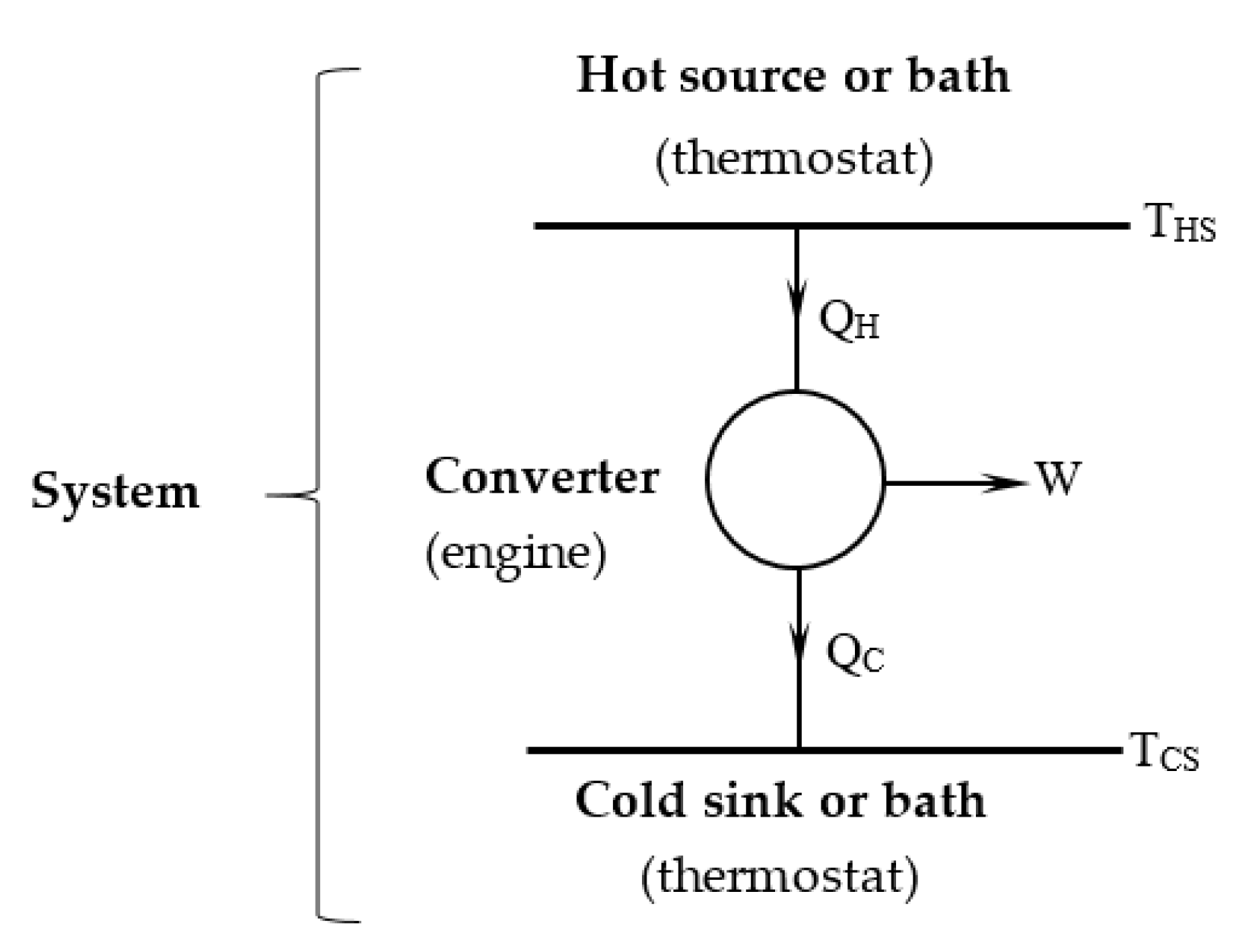
2. The Endo-Irreversible Carnot Engine
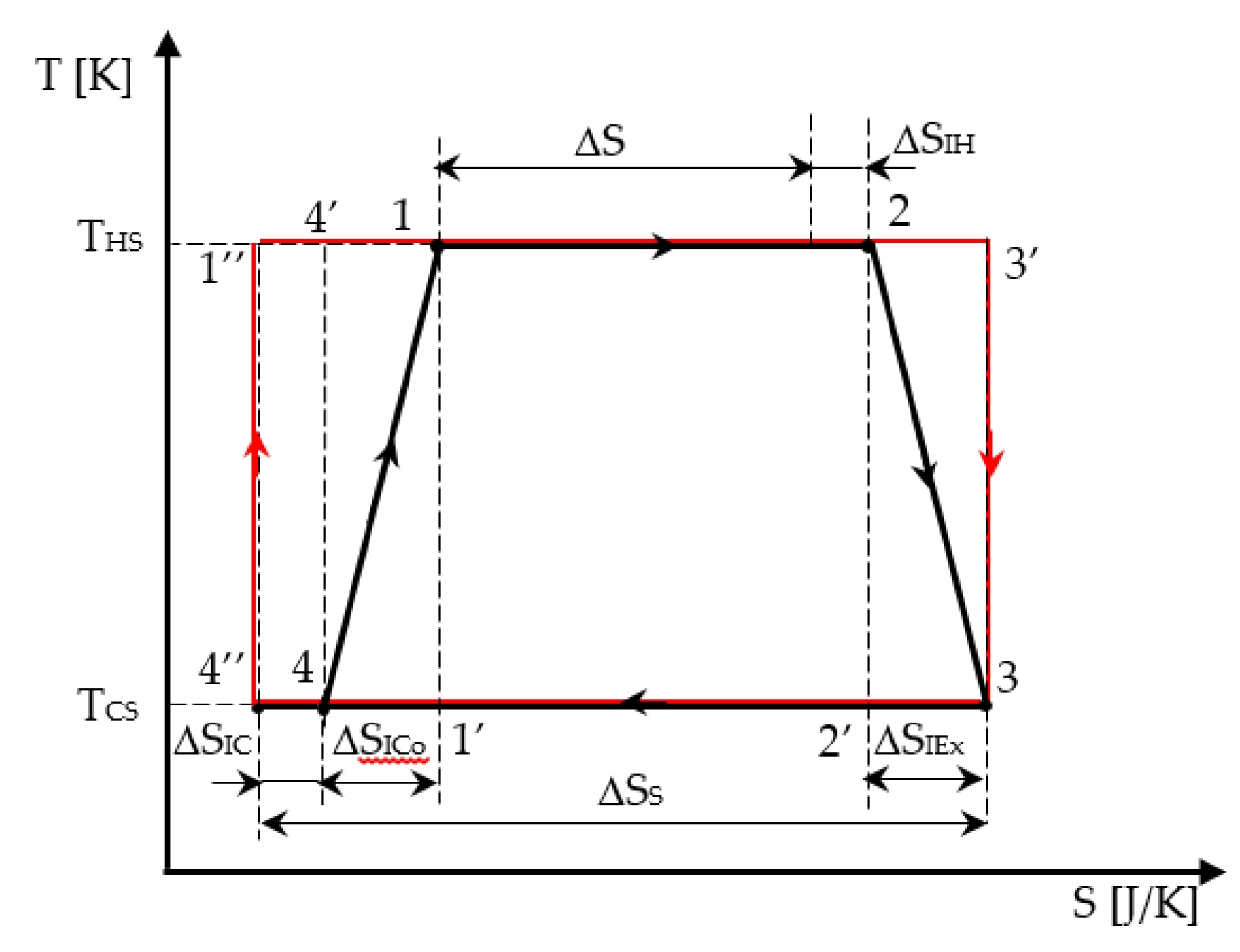
2.1. Cycle Representation in T-S Diagram
- ΔSIEx, production of entropy during the adiabatic expansion;
- ΔSICo, production of entropy during the adiabatic compression; and
- ΔSIC, production of entropy on the cold isotherm, as shown in Figure 2.
2.2. Analytical Model
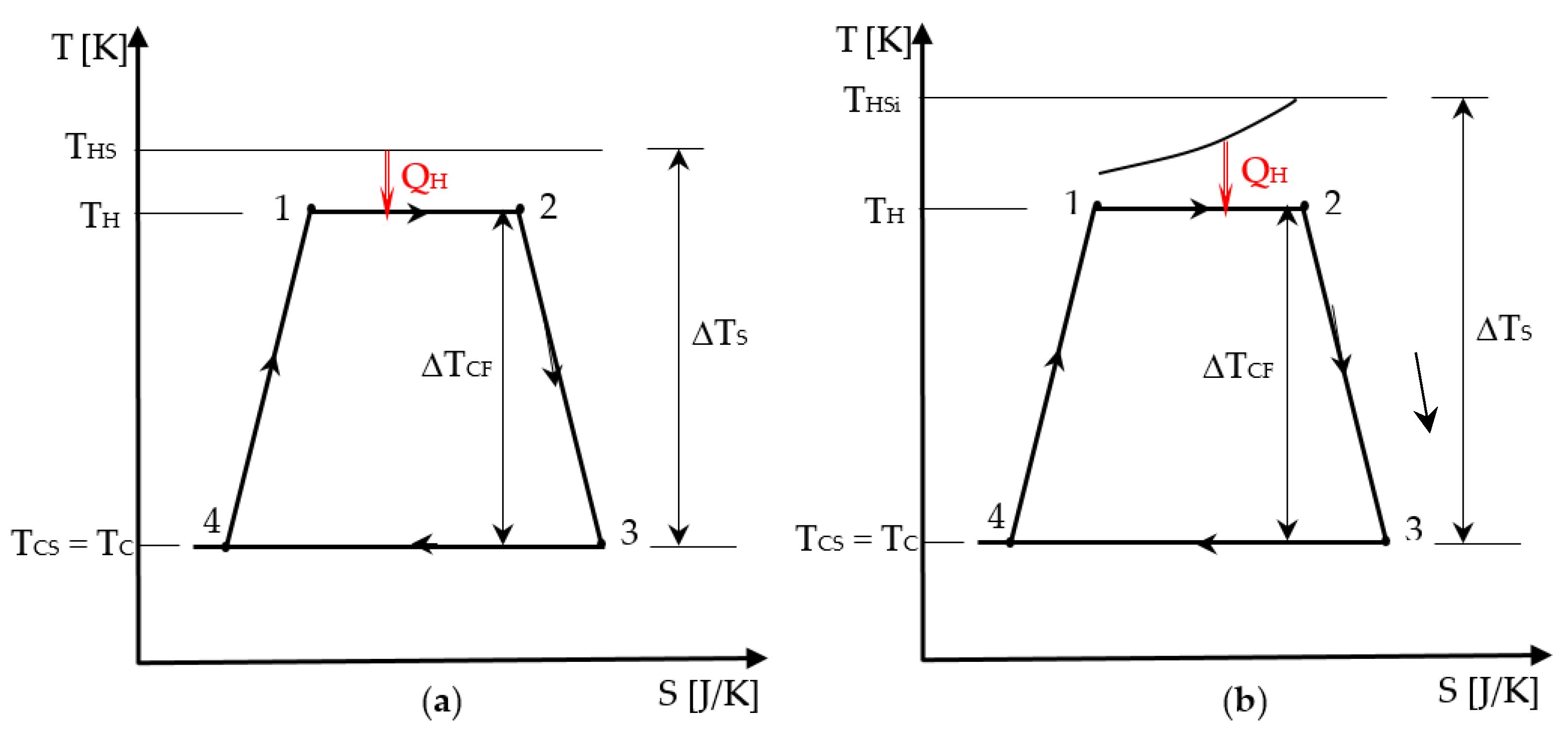
3. The Chambadal Engine
3.1. Optimization Approach for the Entropic Ratio Model
- (i)
- IH is a constant parameter.
- (ii)
3.2. Optimization Approach for the Entropic Production Model
- (i)
- ΔSI is a constant parameter.
- (ii)
- A linear dependence of ΔSI on the temperature difference ΔTT = TH – TCS is considered.
- the first, an intensive one: ;
- the second, an extensive one: .
3.3. Quasi-Chambadal Model with Added Heat Transfer Entropy Constraint and Production of Entropy
- (i)
- the presence of the Novikov’s irreversibility degree [9], that is expressed by:
- (ii)
- when ΔSI is a constant parameter, one finds similarly:
- (iii)
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
| Symbols | |
| A | heat transfer area, [m2] |
| cp | specific heat at constant pressure, [J/(kg K)] |
| heat capacity rate, [W/K] | |
| d | Novikov’s irreversibility degree, [-] |
| ECOP | ecological coefficient of performance, [-] |
| G | finite physical dimension, [J/K] |
| K | heat transfer conductance, [W/K] |
| I | entropic ratio, [-] |
| NTU | number of heat transfer units, [-] |
| Q | heat, [J] |
| heat transfer rate, [W] | |
| S | entropy, [J/K] |
| T | temperature, [K] |
| U | overall heat transfer coefficient, [W/(m2 K)] |
| W | mechanical work, [J] |
| Greek Symbols | |
| ε | effectiveness, [-] |
| η | efficiency, [-] |
| Subscripts | |
| C | relative to the cycled fluid at the cold source |
| Co | relative to compression |
| CS | cold source or sink |
| Ex | relative to expansion |
| H | relative to the cycled fluid at the hot source |
| HS | hot source |
| HSi | hot source |
| I | irreversibility of the converter |
| IS | irreversibility of the system (source-converter-sink) |
| S | source or sink, relative to temperature difference of source and sink |
| T | total, relative to extreme temperature difference of the cycled fluid |
| 0 | ambient |
References
- Carnot, S. Réflexion sur la Puissance Motrice du feu; Bachelier: Paris, France, 1824. (In French) [Google Scholar]
- Carnot, S. Principes Fondamentaux de L’équilibre et du Mouvement; Wentworth Press: Paris, France, 2018. (In French) [Google Scholar]
- Andresen, B.; Berry, R.S.; Ondrechen, M.I. Thermodynamics for processes in finite time. Acc. Chem. Res. 1984, 17, 266–271. [Google Scholar] [CrossRef]
- Ibrahim, O.M.; Klein, S.A.; Mitchell, J.W. Optimum heat power cycles for specified boundary conditions. J. Eng. Gas Turb. Power 1991, 113, 514–521. [Google Scholar]
- Feidt, M. Thermodynamique Optimale en Dimensions Physiques Finies; Hermes: Paris, France, 2013. (In French) [Google Scholar]
- Sánchez Salas, N.; Velasco, S.; Calvo Hernández, A. Unified working regime of irreversible Carnot-like heat engines with nonlinear heat transfer laws. Energy Convers. Manag. 2002, 43, 2341–2348. [Google Scholar] [CrossRef]
- Chen, L.; Xia, S.; Sun, F. Maximum power output of multistage irreversible heat engines under a generalized heat transfer law by using dynamic programming. Sci. Iran. 2013, 20, 301–312. [Google Scholar]
- Feidt, M.; Costea, M.; Petrescu, S.; Stanciu, C. Nonlinear Thermodynamic analysis and optimization of a Carnot engine cycle. Entropy 2016, 18, 243. [Google Scholar] [CrossRef]
- Zhan, Y.-B.; Ma, P.-C.; Zhu, X.-Q. Ecological optimization for a generalized irreversible Carnot engine with an universal heat transfer law. Procedia Environ. Sci. 2011, 11 Pt B, 945–952. [Google Scholar] [CrossRef][Green Version]
- Stanciu, C.; Feidt, M.; Costea, M.; Stanciu, D. Optimization and entropy production: Application to Carnot-like refrigeration machines. Entropy 2018, 20, 953. [Google Scholar] [CrossRef]
- Park, H.; Kim, M.S. Performance analysis of sequential Carnot cycles with finite heat sources and heat sinks and its application in organic Rankine cycles. Energy 2016, 99, 1–9. [Google Scholar] [CrossRef]
- Feidt, M.; Costea, M.; Petre, C.; Petrescu, S. Optimization of direct Carnot cycle. Appl. Therm. Eng. 2007, 27, 829–839. [Google Scholar] [CrossRef]
- Feidt, M. Optimal Thermodynamics—New upperbounds. Entropy 2009, 11, 529–547. [Google Scholar] [CrossRef]
- Kodal, A.; Sahin, B.; Yilmaz, T. A comparative performance analysis of irreversible Carnot heat engines under maximum power density and maximum power conditions. Energy Convers. Manag. 2000, 41, 235–248. [Google Scholar] [CrossRef]
- Feidt, M. Thermodynamique et Optimisation Énergétique des Systèmes et Procédés, 1st ed.; Lavoisier TEC et DOC: Paris, France, 1987. (In French) [Google Scholar]
- Vaudrey, A.; Lanzetta, F.; Feidt, M.H.B. Reitlinger and the origin of efficiency at maximum power formula for heat engines. J. Non-Equil. Thermodyn. 2014, 39, 199–203. [Google Scholar] [CrossRef]
- Dong, Y.; El-Bakkali, A.; Feidt, M.; Descombes, G.; Périlhon, C. Association of finite-dimension thermodynamics and bond-graph approach for modeling on irreversible heat engine. Entropy 2012, 14, 642–653. [Google Scholar] [CrossRef]
- Sieniutycz, S.; Jeżowski, J. Energy Optimization in Process Systems and Fuel Cells, 3rd ed.; Elsevier: London, UK, 2018. [Google Scholar]
- Long, R.; Liu, W. Ecological optimization for general heat engine. Phys. A Stat. Mech. Appl. 2015, 434, 232–239. [Google Scholar] [CrossRef]
- Yu, J.; Zhou, Y.; Liu, Y. Performance optimization of an irreversible Carnot refrigerator with finite mass flow rate. Int. J. Refrig. 2011, 34, 567–572. [Google Scholar]
- Feidt, M.; Le Saos, K.; Costea, M.; Petrescu, S. Optimal allocation of HEX inventory associated with fixed power output or fixed heat transfer rate input. Int. J. Thermodyn. 2002, 5, 25–36. [Google Scholar]
- Feidt, M.; Costea, M. From Finite Time to Finite Dimensions Thermodynamics: The Carnot engine and Onsager’s relations revisited. J. Non-Equil. Thermodyn. 2018, 43, 151–161. [Google Scholar] [CrossRef]
- Blaise, M.; Feidt, M.; Maillet, D. Influence of the working fluid properties on optimized power of an irreversible finite dimensions Carnot engine. Energy Convers. Manag. 2018, 163, 444–456. [Google Scholar] [CrossRef]
- Feidt, M. Thermodynamics applied to reverse cycle machines, a review. Int. J. Refrig. 2010, 33, 1327–1342. [Google Scholar] [CrossRef]
- Feidt, M. Thermodynamics of energy systems and processes: A review and perspectives. J. Appl. Fluid Mech. 2012, 5, 85–98. [Google Scholar]
- Han, Y.; Wang, D.; Zhang, C.; Zhu, Y. The entransy degeneration and entransy loss equations for the generalized irreversible Carnot engine system. Int. J. Heat Mass Transf. 2017, 106, 895–907. [Google Scholar] [CrossRef]
- Feidt, M. Finite Physical Dimensions Optimal Thermodynamics 1—Fundamentals; ISTE Press—Elsevier: London, UK, 2017; pp. 75–97. [Google Scholar]
- Bhattacharyya, S.; Blank, D.A. Power optimized work limit for internally irreversible reciprocating engines. Int. J. Mech. Sci. 2000, 42, 1357–1368. [Google Scholar] [CrossRef]
- Chambadal, P. Les Centrales Nucléaires; Armand Colin: Paris, France, 1957. (In French) [Google Scholar]
- Curzon, F.L.; Ahlborn, B. Efficiency of a Carnot engine at maximum power output. Am. J. Phys. 1975, 43, 22–24. [Google Scholar] [CrossRef]
- Wang, J.; He, J. Efficiency at maximum power output of an irreversible Carnot-like cycle with internally dissipative friction. Phys. Rev. 2012, E86, 051112. [Google Scholar] [CrossRef] [PubMed]
- Novikov, I.I. The efficiency of atomic power stations. At. Energy 1957, 3, 409–412. [Google Scholar] [CrossRef]
- Esposito, M.; Kawai, R.; Lindenberg, K.; Van den Broeck, C. Efficiency at maximum power of low dissipation Carnot engines. Phys. Rev. Lett. 2010, 105, 150603. [Google Scholar] [CrossRef]
- Holubec, V.; Ryabov, A. Cycling tames power fluctuations near optimum efficiency. Phys. Rev. Lett. 2018, 121, 120601. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feidt, M.; Costea, M. Progress in Carnot and Chambadal Modeling of Thermomechanical Engine by Considering Entropy Production and Heat Transfer Entropy. Entropy 2019, 21, 1232. https://doi.org/10.3390/e21121232
Feidt M, Costea M. Progress in Carnot and Chambadal Modeling of Thermomechanical Engine by Considering Entropy Production and Heat Transfer Entropy. Entropy. 2019; 21(12):1232. https://doi.org/10.3390/e21121232
Chicago/Turabian StyleFeidt, Michel, and Monica Costea. 2019. "Progress in Carnot and Chambadal Modeling of Thermomechanical Engine by Considering Entropy Production and Heat Transfer Entropy" Entropy 21, no. 12: 1232. https://doi.org/10.3390/e21121232
APA StyleFeidt, M., & Costea, M. (2019). Progress in Carnot and Chambadal Modeling of Thermomechanical Engine by Considering Entropy Production and Heat Transfer Entropy. Entropy, 21(12), 1232. https://doi.org/10.3390/e21121232




