Abstract
Massive open online courses (MOOCs), which have been deemed a revolutionary teaching mode, are increasingly being used in higher education. However, there remain deficiencies in understanding the relationship between online behavior of students and their performance, and in verifying how well a student comprehends learning material. Therefore, we propose a method for predicting student performance and mastery of knowledge points in MOOCs based on assignment-related online behavior; this allows for those providing academic support to intervene and improve learning outcomes of students facing difficulties. The proposed method was developed while using data from 1528 participants in a C Programming course, from which we extracted assignment-related features. We first applied a multi-task multi-layer long short-term memory-based student performance predicting method with cross-entropy as the loss function to predict students’ overall performance and mastery of each knowledge point. Our method incorporates the attention mechanism, which might better reflect students’ learning behavior and performance. Our method achieves an accuracy of 92.52% for predicting students’ performance and a recall rate of 94.68%. Students’ actions, such as submission times and plagiarism, were related to their performance in the MOOC, and the results demonstrate that our method predicts the overall performance and knowledge points that students cannot master well.
1. Introduction
Massive open online courses (MOOCs) are being increasingly used in higher education. When compared with traditional classes, MOOCs can provide many teaching resources with rich content [1], including online discussion forums, interactive simulations, and so on [2]. Furthermore, students can access MOOCs whenever and wherever they want, which can enhance students’ learning interest and initiative [3,4,5].
Previous researchers have demonstrated that MOOCs have positive effects on teaching and learning [6]. However, the mode makes instructors unable to easily perceive the status of students’ learning different from face-to-face interaction of traditional teaching mode. Currently, instructors check the completion of assignments or examinations [7], or the existence and extent of procrastination behavior [8] of students to predict student performance. However, assignment or examination completion and procrastination behavior do not fully reflect students’ learning achievement [9].
The learning process is also an important factor in influencing student performance. Therefore, we fully consider the temporal features in the learning process and present a study that is aimed at predicting overall performance and student deficiency in mastering knowledge points based on certain assignment-related online behavior in MOOCs. We extract assignment behavior-related features, which include temporal individual features that are related to individual assignments, temporal grouping features related to grouped assignments of certain knowledge point, and comprehensive features that are related to all assignments. We propose a model that is based on multi-task learning and long short-term memory (LSTM). In addition, we construct a main task for predicting students’ performance and an auxiliary task to predict students’ mastery of knowledge points.
The contributions of this paper are as follows:
- We propose a multi-task learning framework that is based on a multi-layer LSTM network to predict whether the students will pass the final exam as well as their mastery of knowledge points. Our framework combined multi-task prediction and comprehensive prediction with attention mechanism, which can mix multi-dimension knowledge and improve the prediction accuracy.
- We present an attention-based multi task LSTM neural network method that incorporates a shared parameters layer. The multi task architecture with shared parameters can avoid overfitting and improve the prediction. The LSTM neural network with attention mechanism adjusts the importance of temporal individual features, temporal grouping features, and it could reflect students’ learning behaviors well.
- The results demonstrate that our method is superior to other existing multi-task-based LSTM methods. Our framework can predict students’ performance with 92.52% accuracy and students’ mastery of knowledge points with 99.58% accuracy on the experimental dataset.
2. Related Work
2.1. Prediction in MOOCs
The use of MOOCs can improve students’ academic performance, and researchers have turned their attention to this field [10,11,12]. Conijn, Van, and Cuijpers [13] investigated the relationship among students’ final exam grade, activity frequencies, specific course item frequencies, and the order of activities. They demonstrated that students who spend more time on learning perform better, but no convincing correlation was found between the sequence of activities and student performance. Meier, Xu, Atan, and van der Schaar [14] proposed a method for improving the teaching effects of traditional classes and MOOCs. They suggest that assessment methods, such as MOOC quizzes, could provide a timely prediction of students’ performance, allowing for appropriate interventions to be made by instructors.
Studying different student behavior patterns can lead to improvements in the effects of teaching. Kahan, Soffer, and Nachmias [15] identified seven participant patterns, including Tasters, Downloaders, Disengagers, Offline Engagers, Online Engagers, Moderately Social Engagers, and Social Engagers, to support the idea that different behavior in MOOCs affects the certification rate. Moreover, Rodrigues, Ramos, Silva, and Gomes [16] identified the participation patterns of students in MOOCs by using educational data mining technologies. Their analysis guided the design of adaptive strategies and helped to improve the learning experience. Furthermore, Brinton, Buccapatnam, Chiang, and Poor [17] studied video viewing behavior and tested the performance among middle school students in MOOCs. They found that some of these behaviors were significantly associated with the accuracy of first-attempt responses to test questions.
In terms of cheating in MOOCs, some students cheat because MOOCs are online and it is difficult to detect cheating in online environments. Northcutt, Ho, and Chuang [18] described a spoofing strategy that used a Copying Answers while using Multiple Existences Online (CAMEO) strategy to replicate the answer using a ‘harvester’ account to provide a solution to an evaluation problem and then submit the correct answer while using a separate ‘master’ account. Alexandron, Ruipérez, Chen, Muñoz, and Pritchard [19] demonstrated academic dishonesty involving the use of multiple accounts in MOOCs to obtain authorization solutions. In their study, they were able to determine the prevalence of CAMEO, study its detailed characteristics, and infer the motivation for using it.
2.2. Multitask Learning
Multi-task learning is a method of machine learning that uses the shared network to carry out multiple tasks at the same time to achieve a better learning effect. Multi-task learning is widely used in biology, education, and machine learning. The two most commonly used ways to perform multi-task learning are typically hard or soft parameter sharing of hidden layers [20]. Hard parameter sharing is the most commonly used approach for multi-task learning; it shares the hidden layers between all of the tasks while keeping several task-specific output layers. Hard parameter sharing can greatly reduce the risk of overfitting. Baxter [21] demonstrated that the risk of shared parameter overfitting is order N, where N is the number of tasks, when compared with the traditional deep learning method. For soft parameter sharing, each task has its own model with its own parameters. The distance between the parameters is regularized to make the parameters more similar [22,23].
In recent work, researchers have paid more attention to joint learning, weighting losses, and learning with auxiliary tasks. For joint learning, Hashimoto, Xiong, Tsuruoka, and Socher [24] proposed a hierarchical architecture that consisted of several natural language processing (NLP) tasks. For the weighting losses, Kendall, Gal, and Cipolla [25] took the approach of adjusting each task’s relative weight in the loss function based on maximizing the Gaussian likelihood with task-dependent uncertainty. Regarding auxiliary tasks, there remains the need to find suitable auxiliary tasks to improve the performance of multi-Task learning. Zhang, Luo, Loy, and Tang [26] used head pose estimation and facial attribute inference as the auxiliary tasks for facial landmark detection.
Multi-Task learning is a method for improving the generalization effect by using the domain information that is contained in training signals of related tasks as inductive bias. Multi-Task learning can improve the generalization effect by learning tasks in parallel [27] while using a shared representation.
2.3. LSTM
A LSTM neural network [28] is an improved recurrent neural network. It solves the problem of gradient explosion and gradient disappearance of a recurrent neural network, and it can transmit information in a long sequence. LSTM can control the transmission, storage, and forgetting of information through an input gate, output gate, and forgetting gate [29]. LSTM is widely used in action recognition [30], semantic analysis [31], and trajectory prediction [32,33]. Alahi [32] proposed a LSTM model to learn human movements and predict their future trajectories. In contrast with traditional approaches, they demonstrated that their method outperforms state-of-the-art methods on several public datasets. They analyzed the trajectories predicted to demonstrate motion behavior.
Song [30] proposed a spatial and temporal attention model for exploring features for human action recognition and detection. They built a recurrent neural network with long short-term memory units and focused on the discriminative joints of skeletons. The experimental results demonstrate that their proposed model is effective for both action recognition and action detection.
3. Method
3.1. Framework
This paper proposes a multi-task-based model for predicting students’ performance and mastery of knowledge points. We extract the temporal features, including temporal individual features, temporal grouping features, and comprehensive features. Temporal individual features are extracted from all of the assignments as a sequence that reflects the learning processes of students. Temporal grouping features are a sequence extracted from specific assignments related to certain knowledge points, and they reflect students’ mastery of specific knowledge points. Comprehensive features are vectors extracted from all the assignments to reflect the overall learning state of students. Thus, we use temporal individual features to predict students’ performance in the main task, temporal grouping features to predict students’ mastery of knowledge points in auxiliary tasks, and comprehensive features to predict students’ overall performance. We adjust the importance among temporal individual features, temporal grouping features, and comprehensive features while using an attention mechanism to improve the prediction performance.
This framework includes four parts, i.e., shared-parameters layer, multi-task prediction, comprehensive prediction, and attention mechanism, for predicting students’ performance and mastery of knowledge points, as shown in Figure 1. [X0, X1, …, Xt] is the temporal individual feature sequence, Xk is a vector extracted from assignments completed in the kth week, and Xk is also the kth input of the shared parameters layer for the main task. [Y0, Y1, ….., Yt] is the temporal grouping feature sequence, Yk is a vector extracted from assignments completed in the kth week related to specific knowledge points, and Yk is also the kth input of the shared parameters layer for auxiliary task.
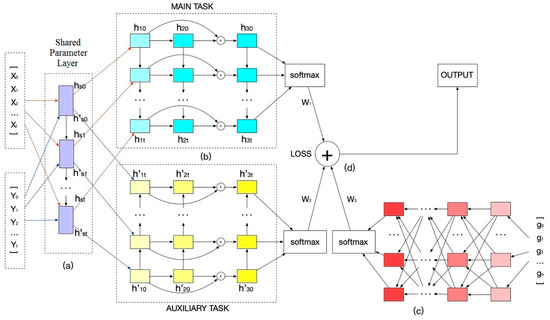
Figure 1.
Proposed framework. (a) Shared parameters layer, (b) multi-task part with multi-layer LSTM. (c) multi-layer perceptron (MLP) using comprehensive features, and (d) attention mechanism.
In Figure 1a, a shared parameters layer is then placed, and the two feature sequences share the same parameters when they are trained in the shared parameters layer. The shared parameters layer help to discover hidden information and avoid over-fitting.
The multi-task module in Figure 1b includes the main task of predicting students’ performance and the auxiliary task of predicting students’ mastery of knowledge points. The multi-task method can mix multi-dimension knowledge and use the idea of transfer learning to improve the prediction accuracy.
In Figure 1c, we add an MLP model to focus on comprehensive features for comprehensive prediction. Here, g is the comprehensive feature vector that is extracted from all of the assignments completed by the student. It helps to improve the accuracy of prediction by adding comprehensive information that cannot be reflected by temporal features.
The combined loss from the MLP and multi-task with attention mechanism that is shown in Figure 1d could utilize the effective information in the temporal individual features, temporal grouping features, and comprehensive features. Attention mechanism will pay greater attention to important information, give higher weight, and improve the accuracy of prediction.
3.2. Multi-Task Learning
In this part, we propose a multi-task learning method that includes a main and auxiliary task to predict students’ performance and mastery of knowledge points. In the main task, we predict the students who will fail the final exam. In the auxiliary task, we predict students’ mastery of knowledge points. The main and auxiliary task both have the same architectures.
3.2.1. Fully-Connected Multi-Layer LSTM Neural Network
We construct a fully-connected multi-layer LSTM neural network in the main and auxiliary tasks. It helps to enhance the importance of critical information. The input of each layer comes not only from the output of the upper layer, but also from the weighted input of all the previous layers, unlike a traditional multi-layer LSTM neural network.
Both tasks are fully-connected neural networks. For the traditional multi-layer LSTM neural network, as shown in Formula (1), the input Int of the next layer is the output hn-1,t of the former layer, while n is the layer number and t is LSTM unit number.
For our fully-connected multi-layer LSTM, the input of the first layer of the LSTM comes from the shared parameters layer, the input I2,t of the second layer comes from the output h1,t of the first layer, and the input I3.t of the third layer comes from the outputs h1,t of the first and h2,t of the second layers. The input of each layer comes from the weighted sum of the output of all the previous layers, as shown in Formula (2).
3.2.2. Shared Parameters Layer
The shared parameters layer is a traditional LSTM neural network, and it is built, such that the inputs X and Y share the same network parameters (see Figure 1a). Subsequent to training by the shared parameters layer, the outputs of the LSTM neural network are used as the inputs of the main and auxiliary tasks. The shared parameters layer can avoid over-fitting and mix information regarding multiple tasks for improving the accuracy of prediction.
For the input X, hsk is the output of the feature sequence in the kth LSTM unit of the shared parameters layer, and it is also the kth input of the main task. For the input Y, h’sk is the output of the feature sequence in the kth LSTM unit of the shared parameters layer, and it is also the kth input of the auxiliary task. The outputs hsk and h’sk from the shared parameters layer with the input sequence Xk and Yk will be the inputs of the main and auxiliary tasks, respectively.
Figure 2 shows the shared parameters layer, and we take the input X as an example.
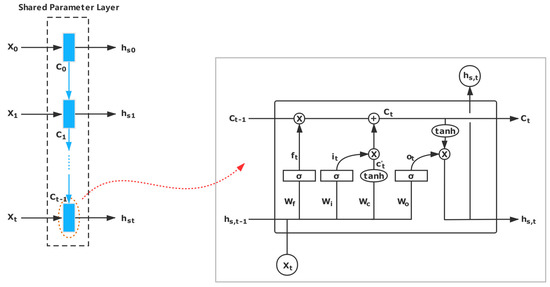
Figure 2.
Shared parameters layer. For the inputs X and Y, they share the same network parameters by the shared parameters layer. In this figure, we take the input X as example.
For the input X, the output ht is calculated while using the following equations.
In these equations, denotes the hidden states, and stands for element-wise multiplication. is the sigmoid function, and Wf, bf, Wi, bi, Wo, bo, Wc, and bc are the parameters in the LSTM unit. Furthermore, we represent [Wf, Wi, Wo, Wc] as W and [bf, bi, bo, bc] as B.
During the entire training process, the main and auxiliary tasks share the relevant parameters (W, B) of the layer network, as shown in Formula (10):
3.2.3. Attention Mechanism
We can predict students’ performance while using the learning process and the overall learning state. In this section, we use the attention mechanism to adjust the weights of the learning process and the overall learning state to achieve better prediction.
Temporal attention focuses on the effects of temporal features, including temporal individual features and temporal grouping features, on students’ performance. The LSTM neural network is an improved neural network algorithm that can deal with temporal features for prediction, and solve the problems of gradient disappearance and gradient explosion.
Comprehensive attention focuses on the impact of students’ overall learning status on their performance. The existence of the forget gate causes the loss of some important information, although LSTM solves the problem of long-term dependence in feature sequences. We add an MLP neural network in Figure 1d using comprehensive features to supplement the prediction results that were obtained using temporal features to better reflect students’ behavior and predict students’ performance.
3.3. Loss Function with Cross Entropy
3.3.1. Loss Function
Cross-entropy is a concept in information theory [34,35,36,37,38] and it is used to express the similarity of two probability distributions. The smaller the value of cross-entropy is, the closer the two probability distributions are. We use cross-entropy as a loss function for training the neural network. In our method, we use the ensemble loss from the multitask multi-layer LSTM neural network and the MLP, as shown in Figure 1b,c, respectively.
As shown in Formula (11), we use attention-based loss for the loss of MLP in Figure 1c. In this formula, g is the input of MLP, wg is the weight of the loss, LM is the cross entropy loss of MLP, and GL is the attentional loss of MLP.
The Loss LM(g) can be calculated by Formula (12). q is the actual probability distribution for a sample and p is the output probability distribution from the MLP. S is number of samples and x is the position in the probability distribution.
For a sample g in the MLP neural network of n classification, we can transform the output [z1, z2,…, zn] into the probability distribution p while using the softmax function, as shown in Formulas (13) and (14). The actual classification of the sample can be transformed into the probability distribution q as q = [0, 0... 1, 0... 0], where 1 represents correct classification of the sample and 0 represents misclassification.
As shown in Formulas (15) and (16), we use attention-based loss of multi task in Figure 1b, where task loss (TL) is the ensemble loss of multiple tasks and TL(c) is the loss of task c.
Furthermore, is the weight of task c, M is the number of LSTM units in one layer, is the weight of kth unit in the last layer of task c for classification, xc is the input of the shared parameters layer in task c, and LL(k, xc, ) is the loss of kth unit in the last layer of LSTM. LL can be calculated similarly as Formula (12).
We define an attention-based loss function to coalesce classification errors from all tasks. Comprehensive attention focuses on comprehensive features in the MLP model, while temporal attention focuses on temporal individual features and the temporal grouping features in the LSTM model. We adjust our attention by a mixed loss function and multiple weights.
For our method, the combined loss CL is shown as Formula (17):
where T is the number of tasks.
3.3.2. Training
As shown in Figure 1d, the ensemble loss is composed of the losses of the two neural networks in Figure 1b and the losses of the neural networks in Figure 1c. We introduce the training process for parameters with ensemble cross entropy loss of the neural network while taking the MLP neural network as an example.
As described in the preceding section, [z1, z2, …, zn] is the output of the MLP neural network for a sample, p is the probability distribution that is outputted by the neural network, and q is the actual probability distribution. We first deduce the derivative of with respect to , as shown by Formula (18) (refer to Formula (13)).
Subsequently, we deduce the derivative of ensemble loss CL with respect to . When we derive the output of a neural network with total loss, it is independent of the other neural networks. The process is shown in Formula (19).
After the above deduction, we can use the gradient descent method to reduce the overall loss and train all of the parameters. In addition, can also be learned by minimizing the ensemble loss (CL) by training all the records. Experiments demonstrate that the share network for related tasks can improve the performance of the network.
4. Experiment
4.1. Data
For this study, we chose a C programming MOOC course offered by a university from February 2012 to June 2012. A total of 1528 students took the course. These students are sophomores and their average age is 19. This course is a compulsory course for all students, and the exam of this course is rather difficult, as not all students are expert in programming. The number of students who score more than 70 is 448 and who score more than 60 is 650 in the final exam. In this course, there were 69 programming assignments, and it lasted for 14 weeks. For each student, X and Y in Figure 1 are feature sequences of 14 lengths as the course lasts 14 weeks. The students were required to complete the assignments, and the grades for all of the assignments were converted into a portion of the final grade. The final grade for the course comprised the final exam and assignment grades. The data cannot be disclosed due to confidentiality agreement.
Table A1 represents the data from one programming assignment in which the students write a program that determines whether the three line segments can form a triangle. It is difficult to pass all the test cases by submitting the assignment only once, as several difficult hidden test cases exist in some complex assignments. We found that some of the students who had submitted and passed all of the test cases at once had copied the assignment from other students who had already completed it. Figure A1 shows some related log files to elucidate the structure of the log in the database. We extracted 34 features from the logs of the assignments; Table A2 lists a few of the features and their corresponding meanings.
Figure 3 illustrates the relationship between the final grades and the completion duration. Students with grades between 85 and 90 rarely accomplish their assignments in 300 s, while students with grades between 20 and 25 complete several assignments in 300 s; this reveals that the completion of the assignments in a very short time period might indicate plagiarism. As programming assignments have special requirements for the output format, few students submit it after finishing their assignments in other places.
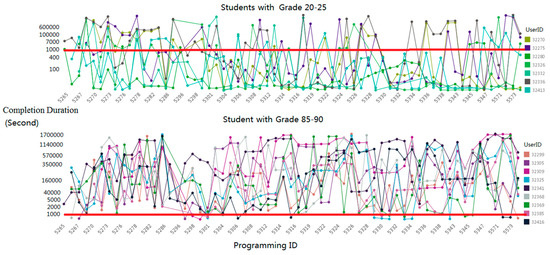
Figure 3.
Relationship between completion duration and grade.
Figure 4 reveals the relationship between the average score and average submission order. Submission order refers to the order in which students submit their assignments. The submission order of the student who first submits his assignment is 1, and the submission order of the student who second submits his assignment is 2. Students with an average submission order between 0 and 200 for all assignments have an average score of 74.52, and students with an average submission order between 1400 and 1528 for all assignments have an average score of 32.23, as shown in Figure 4. Although the submission order does not completely determine students’ score, we can find that the submission order has a great relationship with students’ score. The average submission order reflects students’ learning initiative and motivation; students who submit earlier have higher learning initiative and may get a higher score.
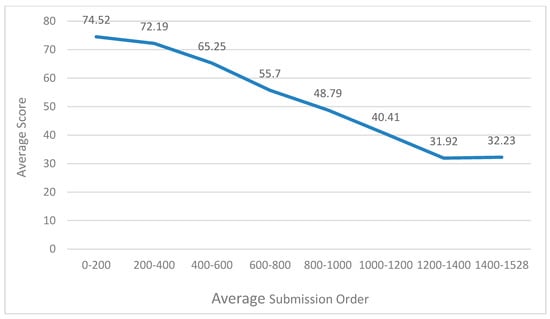
Figure 4.
Relationship knowledge between average score and average submission order.
We divided the assignment into groups according to the points and extracted the grouping features to predict the corresponding knowledge points’ mastery. We manually labeled the programming assignments and divided the programming assignments into 10 groups based on knowledge points. Table 1 summarizes the details.

Table 1.
Programming assignments grouped by knowledge points.
Of the 69 assignments, 13 were related to drawing a figure, 14 to a calculation, and eight to recursive questions. In the follow-up experiments, we paid attention to the mastery of these three knowledge points. We can predict students’ scores for the three knowledge points in the final examination while using students’ behavior in these 35 assignments of drawing a figure, calculation, and recursive questions.
4.2. Baselines
We experimented with standard naïve Bayes (NB), standard logistic regression (LR), standard multi-layer perceptron (MLP), LSTM [28], M-F-LSTM [39], M-S-LSTM [40], and our method.
LSTM [28] is an improved recurrent neural network that can transmit information in a long sequence and solve the problem of gradient explosion and disappearance.
M-F-LSTM [39] is a fully-connected multi-layer LSTM among neural network layers. It has better performance in terms of delivering key information and forgetting unimportant information when compared to the standard LSTM neural networks.
M-S-LSTM [40] is a multi-task neural network with a shared layer. Different tasks share the same parameters in the shared layer; furthermore, it can mix multi-domain knowledge to improve the prediction accuracy and avoid over-fitting.
4.3. Evaluation Metrics
We can predict their achievement and mastery of knowledge points while using the data of students’ behavior. For the prediction of achievement, we label their grades on a 70-point scale in the final exam. We selected three knowledge points with a total score of 30 in the final exam and labeled them with a threshold score of 21 for the prediction of knowledge points. We use behaviors related to all assignments to predict the student achievement and corresponding assignments to predict the mastery of knowledge point.
We use accuracy, recall, and cross-validation scores to evaluate the performance of the algorithm. In the prediction process, we use 80% of the data for training, and the remaining 20% for prediction. Furthermore, we use five-fold cross validation to calculate the cross validation score. We take the average value of the experimental results for five times, and use the variance estimation to measure the stability of the algorithm of the results.
4.4. Experimental Details
We use the tensor flow framework and GPU for training the neural network. In the training process, there are 14 LSTM units in each layer for the main task, auxiliary task, and shared layers. For the main task and auxiliary task, the layer number is 3. We set weight_decay to 1e-5, hidden_size to 32, drop_out to 0.9, and batch_size to 256. After iterative training, we get the parameter values of each module, among which w1 = 0.571, w2 = 0.286, and w3 = 0.143. It means that the main task of temporal attention occupies the largest weight subsequent to training, the auxiliary task of temporal attention occupies the medium weight, and comprehensive attention occupies the smallest weight.
4.5. Result
In this subsection, we predict the performance of students while using temporal features as the main task separately and detect the mastery of knowledge points using grouping temporal features as the auxiliary task separately. We then test our multi-task framework while using individual temporal, grouping temporal, and comprehensive features. In the main task, we predict whether the student will pass the final exam or not; in the auxiliary task, we predict whether the student will attain a 60% score for the corresponding knowledge points. The experimental results are as follows:
Table 2 lists the results that predict using features whether a student would pass the final exam:

Table 2.
Separate predictions of performance.
We then separately predict the mastery of knowledge points using grouping temporal features. In this programming course, the programming tests in the final exam comprise a calculation, drawing figures, and recursive questions, with a top score of 30. We extract features from the logs of these labeled programming tests. We use these logs to predict the students’ programming grade in the final examination. Table 3 summarizes the results and indicates that we could use grouping temporal features to predict the performance of corresponding knowledge points; furthermore, we could find the weaknesses of the students.

Table 3.
Separate predictions of the mastery of knowledge points.
We use the proposed method to predict both the main and auxiliary tasks by performing 100,000 iterations. Figure 5 shows the process of iteration. The losses converge after 100,000 iterations.
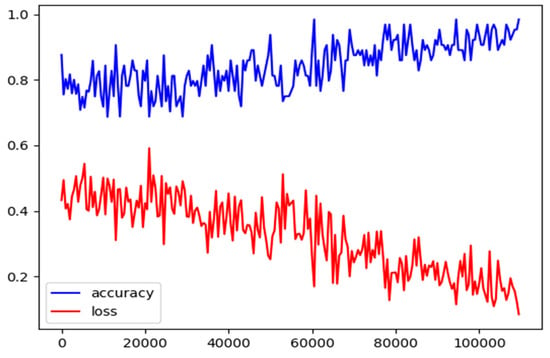
Figure 5.
Variations of loss and accuracy of the proposed method with iterations.
In our experiments, since LSTM and M-F-LSTM are single task framework, they only predict students’ performance and mastery of knowledge points, respectively. While our algorithm and M-S-LSTM are multi task algorithms, they predict students’ performance and mastery of knowledge points in the same framework. The results demonstrate that the proposed method can predict the students’ mastery of knowledge points and can achieve better performance when combined with the selected temporal features in the multi task framework, as shown in Table 4. Among these methods when predicting students’ mastery of knowledge points, the F1 Score of LSTM, M-F-LSTM, M-S-LSTM, and our method are 0.8956, 0.9792, 0.9912, and 0.9936, respectively, and the multi-task methods (M-S-LSTM and our method) have gained better performance in predicting students’ mastery of knowledge points. The ranges of LSTM, M-F-LSTM, M-S-LSTM, and our method at 95% confidence interval (CI) of F1 Score while predicting student performance are 0.0082, 0.0063, 0.0082, and 0.0031, respectively, and fully-connected LSTM based methods (M-F-LSTM and our method) have gained a lower range of the 95% CI of F1 Score.

Table 4.
The experimental results on student performance and mastery of knowledge point prediction.
These results reveal that the multi task framework with different features can get good prediction results, and fully-connected LSTM based methods have low range of the CI.
5. Conclusions
In this study, we identified influential online assignment behaviors by building a classification model that can predict students’ final exam performance and mastery of each knowledge point in MOOCs. We presented a multi-task multi-layer LSTM-based student performance prediction method while using the cross-entropy loss function to predict the overall performance of students and their mastery of each knowledge point based on the selected features. A shared parameters layer is placed to avoid over-fitting and improve the accuracy of prediction. Subsequently, attention mechanism is used to adjust the weights of the learning process and the overall learning state to achieve better prediction. Our method performs better and achieves an accuracy of 92.52% in predicting students’ performance and a recall rate of 94.68% when compared with LSTM, M-F-LSTM, and M-S-LSTM. This work contributes to understanding the relationship between students’ online behavior and performance and it has the potential to maximize the effectiveness of tutors and help students in need. Another advantage of this work is that it can predict knowledge points that students will have trouble learning, which can enable tutors to provide more targeted help to students. In the future, we will do further research on the contents of assignments completed by students.
Author Contributions
Conceptualization, S.Q. and B.W.; methodology, S.Q.; software, B.W.; validation, B.W.; formal analysis, S.Q.; investigation, S.Q.; resources, S.Q.; data curation, K.Z.; writing—original draft preparation, S.Q., X.Z.; writing—review and editing, K.L.; visualization, X.Z.; supervision, S.Q.; project administration, S.Q.; funding acquisition, K.L.
Funding
This research was funded by Key Program of the National Natural Science Foundation of China, grant number 71834001.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
The assignment contains seven test cases. The first four are known to students, and the last three are hidden from them. After the student submits the assignment they have programmed, the MOOC platform will compile the assignment, enter the test inputs and judge whether the outputs of the students’ assignment are consistent with the expected outputs of the respective test cases. If it is consistent, the student will pass the test case.
Questions:
Give the length of three line segments and judge whether they can form a triangle.
Input:
The length of segment a, b and c.
Output:
Whether they can form a triangle.
Figure A1 shows some related log files, in which mdl_programming stores the contents of assignments including name, introduction, start time, end time, and other information. Mdl_programming_submits stores information regarding every assignment submitted by the students, including completion time (when students submit their assignment), content, compiled information, and test results. Mdl_programming_result stores the final result of the assignment for each student. Mdl_log stores students’ behavior on the MOOC platform including browsing assignments, watching videos, visiting time on each page, and so on.
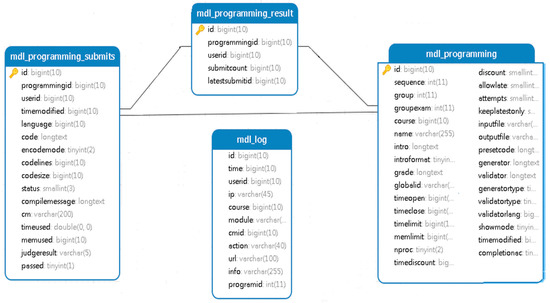
Figure A1.
Logs from MOOC platform.
We extracted 34 features from the logs of the assignments; a few features and their corresponding meanings are listed in Table A2. Owing to the particularity of programming assignments, to ensure that the programming assignment can pass all the test cases, students may submit the programming assignment several times. Submission times is the number of times that the students submit their assignments. Completion time refers to the time when a student has submitted an assignment. The submission order refers to the ranking of one student’s completion time in relation to that of all other students. Completion duration is time between when a student first views the assignment to when they finally submit it. If a student’s completion duration for an assignment is under 300 s, it is considered as a quick submission. As it is almost impossible to complete the assignments within 300 s owing to the difficulty of the assignments, quick submission means that the student is likely to have copied the assignment from others. The number of quick submissions by students reflects the degree of their cheating.

Table A1.
Test Cases.
Table A1.
Test Cases.
| ID | Public | Test Input | Test Output | Time Limitation | Memory Limitation | Weight |
|---|---|---|---|---|---|---|
| 1 | Yes | 3, 4, 5 | Yes | 1 s | 0KB | 1 |
| 2 | Yes | 1, 4, 6 | No | 1 s | 0KB | 1 |
| 3 | Yes | −1, 2, 3 | Error Input | 1 s | 0KB | 1 |
| 4 | Yes | 3, 6, 6 | Yes | 1 s | 0KB | 1 |
| 5 | No | 3, 3, 3 | Yes | 1 s | 0KB | 1 |
| 6 | No | −5, 7, 9 | Error Input | 1 s | 0KB | 1 |
| 7 | No | 1, 4, 9 | No | 1 s | 0KB | 1 |

Table A2.
Features.
Table A2.
Features.
| Feature | Meaning |
|---|---|
| Average First Submission Order | Order of submitting one assignment to the website for the first-time |
| Average Submission Times | Average value of submission times for all assignments |
| Average Completion Duration | Average value of completion duration for all assignments |
| One-Time Pass Number | Number passing all cases for one submission in all assignments |
| Quick Submission Times | Quick submission times of all assignments |
| Completion time | The time when a student submitted an assignment |
References
- Smith, M. Opening education. Science 2009, 323, 89–93. [Google Scholar] [CrossRef] [PubMed]
- d’Oliveira, C.; Carson, S.; James, K.; Lazarus, J. MIT OpenCourseWare: Unlocking knowledge, empowering minds. Science 2010, 329, 525–526. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Peter, B.J.; Fronmueller, M.P. MOOCs and the future of higher education. J. Higher Ed. Theory Pract. 2013, 34, 36–43. [Google Scholar]
- Christensen, G.; Steinmetz, A.; Alcorn, B.; Bennett, A.; Woods, D.; Emanuel, E. The MOOC phenomenon: Who takes massive open online courses and why? SSRN Electron. J. 2014. [Google Scholar] [CrossRef]
- Ho, A.; Ho, A.; Reich, J.; Nesterko, S.; Seaton, D.; Mullaney, T.; Waldo, J.; Chuang, I. HarvardX and MITx: The first year of open online courses, fall 2012-summer 2013. SSRN Electron. J. 2014. [Google Scholar] [CrossRef]
- Martin, F. Will massive open online courses change how we teach? Commun. ACM 2012, 55, 26–28. [Google Scholar] [CrossRef]
- Romero, C.; Ventura, S.; García, E. Data mining in course management systems: Moodle case study and tutorial. Comput. Ed. 2008, 51, 368–384. [Google Scholar] [CrossRef]
- Cerezo, R.; Sánchez-Santillán, M.; Paule-Ruiz, M.; Núñez, J. Students’ LMS interaction patterns and their relationship with achievement: A case study in higher education. Comput. Ed. 2016, 96, 42–54. [Google Scholar] [CrossRef]
- Wayne, B.; Janie, G.; Suzanne, C. Implementing technology to prevent online cheating: A case study at a small southern regional university (SSRU). MERLOT J. Online Learn. Teach. 2009, 2, 230–238. [Google Scholar]
- Pang, Y.; Song, M.; Jin, Y.; Zhang, Y. Survey of MOOC related research. In Proceedings of the International Conference on Database Systems for Advanced Applications, Hanoi, Vietnam, 20–23 April 2015; pp. 181–189. [Google Scholar]
- Romero, C.; Ventura, S. Educational data science in massive open online courses. Wiley Interdiscip. Rev Data Min. Knowl. Discov. 2016, 7, e1187. [Google Scholar] [CrossRef]
- Qu, S.; Li, K.; Zhang, S.; Wang, Y. Predicting Achievement of Students in Smart Campus. IEEE Access 2018, 6, 60264–60273. [Google Scholar] [CrossRef]
- Conijn, R.; Van den Beemt, A.; Cuijpers, P. Predicting student performance in a blended MOOC. J. Comput. Assist. Learn. 2018, 34, 615–628. [Google Scholar] [CrossRef]
- Meier, Y.; Xu, J.; Atan, O.; Schaar, M. Personalized grade prediction: A data mining approach. In Proceedings of the 2015 IEEE International Conference on Data Mining, Atlantic City, NJ, USA, 14–17 November 2015. [Google Scholar]
- Kahan, T.; Soffer, T.; Nachmias, R. Types of participant behavior in a massive open online course. Int. Rev. Res. Open Distribut. Learn. 2017, 18. [Google Scholar] [CrossRef]
- Rodrigues, R.L.; Ramos, J.L.C.; Silva, J.C.S.; Gomes, A.S. Discovery engagement patterns MOOCs through cluster analysis. IEEE Lat. Am. Trans. 2016, 14, 4129–4135. [Google Scholar] [CrossRef]
- Brinton, C.; Buccapatnam, S.; Chiang, M.; Poor, H. Mining MOOC clickstreams: Video-watching behavior vs. in-video quiz performance. IEEE Trans. Signal Proc. 2016, 64, 3677–3692. [Google Scholar] [CrossRef]
- Northcutt, C.; Ho, A.; Chuang, I. Detecting and preventing “multiple-account” cheating in massive open online courses. Comput. Ed. 2016, 100, 71–80. [Google Scholar] [CrossRef]
- Alexandron, G.; Ruipérez-Valiente, J.; Chen, Z.; Muñoz-Merino, P.; Pritchard, D. Copying@Scale: Using harvesting accounts for collecting correct answers in a MOOC. Comput. Ed. 2017, 108, 96–114. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, Q. An overview of multi-task learning. Natl. Sci. Rev. 2017, 5, 30–43. [Google Scholar] [CrossRef]
- Baxter, J. A Bayesian/information theoretic model of learning to learn via multiple task sampling. Mach. Learn. 1997, 28, 7–39. [Google Scholar] [CrossRef]
- Duong, L.; Cohn, T.; Bird, S.; Cook, P. Low Resource Dependency Parsing: Cross-lingual Parameter Sharing in a Neural Network Parser. In Proceedings of the 53rd Annual Meeting of the Association for Computational Linguistics and the 7th International Joint Conference on Natural Language Processing (Volume 2: Short Papers), Beijing, China, 26–31 July 2015. [Google Scholar]
- Yang, Y.; Hospedales, T. Trace Norm Regularised Deep Multi-Task Learning. arXiv 2016, arXiv:1606.04038. [Google Scholar]
- Hashimoto, K.; Xiong, C.; Tsuruoka, Y.; Socher, R. A joint many-task model: Growing a neural network for multiple NLP tasks. In Proceedings of the 2017 Conference on Empirical Methods in Natural Language Processing, Copenhagen, Denmark, 9–11 September 2017. [Google Scholar]
- Kendall, A.; Gal, Y.; Cipolla, R. Multi-task learning using uncertainty to weigh losses for scene geometry and semantics. In Proceedings of the 2018 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7482–7491. [Google Scholar]
- Zhang, Z.; Luo, P.; Loy, C.; Tang, X. Facial landmark detection by deep multi-task learning. In Proceedings of the Computer Vision—ECCV 2014, Zurich, Switzerland, 6–12 September 2014; pp. 94–108. [Google Scholar]
- Caruana, R. Multitask learning. Mach. Learn. 1997, 28, 41–75. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to forget: Continual prediction with LSTM. Neural Comput. 2000, 12, 2451–2471. [Google Scholar] [CrossRef] [PubMed]
- Song, S.; Lan, C.; Xing, J.; Zeng, W.; Liu, J. Spatio-temporal attention-based LSTM networks for 3D action recognition and detection. IEEE Trarns. Image Proc. 2018, 99, 3459–3471. [Google Scholar] [CrossRef] [PubMed]
- Trigeorgis, G.; Ringeval, F.; Brueckner, R.; Marchi, E.; Nicolaou, M.A.; Schuller, B.; Zafeiriou, S. Adieu features? End-to-end speech emotion recognition using a deep convolutional recurrent network. In Proceedings of the 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20–25 March 2016; pp. 5200–5204. [Google Scholar]
- Alahi, A.; Goel, K.; Ramanathan, V.; Robicquet, A.; Fei-Fei, L.; Savarese, S. Social lstm: Human trajectory prediction in crowded spaces. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 961–971. [Google Scholar]
- Huang, Z.; Xia, J.; Li, F.; Li, Z.; Li, Q. A Peak Traffic Congestion Prediction Method Based on Bus Driving Time. Entropy 2019, 21, 709. [Google Scholar] [CrossRef]
- Duch, W.; Wieczorek, T.; Biesiada, J.; Blachnik, M. Comparison of Feature Ranking Methods Based on Information Entropy. In Proceedings of the 2004 IEEE International Joint Conference on Neural Networks (IEEE Cat. No. 04CH37541), Budapest, Hungary, 25–29 July 2004; Volume 2, pp. 1415–1419. [Google Scholar]
- Hu, Q.; Guo, M.; Yu, D.; Liu, J. Information entropy for ordinal classification. Sci. China Inf. Sci. 2010, 53, 1188–1200. [Google Scholar] [CrossRef]
- Robinson, D.W. Entropy and uncertainty. Entropy 2008, 10, 493–506. [Google Scholar] [CrossRef]
- Rubinstein, R. The Cross-Entropy Method for Combinatorial and Continuous Optimization. Methodol. Comput. Appl. Probab. 1999, 1, 127–190. [Google Scholar] [CrossRef]
- Almgren, K.; Krishna, M.; Aljanobi, F.; Lee, J. AD or Non-AD: A Deep Learning Approach to Detect Advertisements from Magazines. Entropy 2018, 20, 982. [Google Scholar] [CrossRef]
- Wang, C.; Yang, H.; Meinel, C. Image captioning with deep bidirectional LSTMs and multi-task learning. ACM Trans. Multimed. Comput. Commun. Appl. 2018, 14, 40. [Google Scholar] [CrossRef]
- Dong, X.; Chowdhury, S.; Qian, L.; Li, X.; Guan, Y.; Yang, J.; Yu, Q. Deep learning for named entity recognition on Chinese electronic medical records: Combining deep transfer learning with multitask bi-directional LSTM RNN. PLoS ONE 2019, 14, e0216046. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).