Towards Generation of Cat States in Trapped Ions Set-Ups via FAQUAD Protocols and Dynamical Decoupling
Abstract
1. Introduction
2. Local Adiabatic and FAQUAD Protocols
3. Uniform All-To-All Interactions
3.1. Closed System Scenario
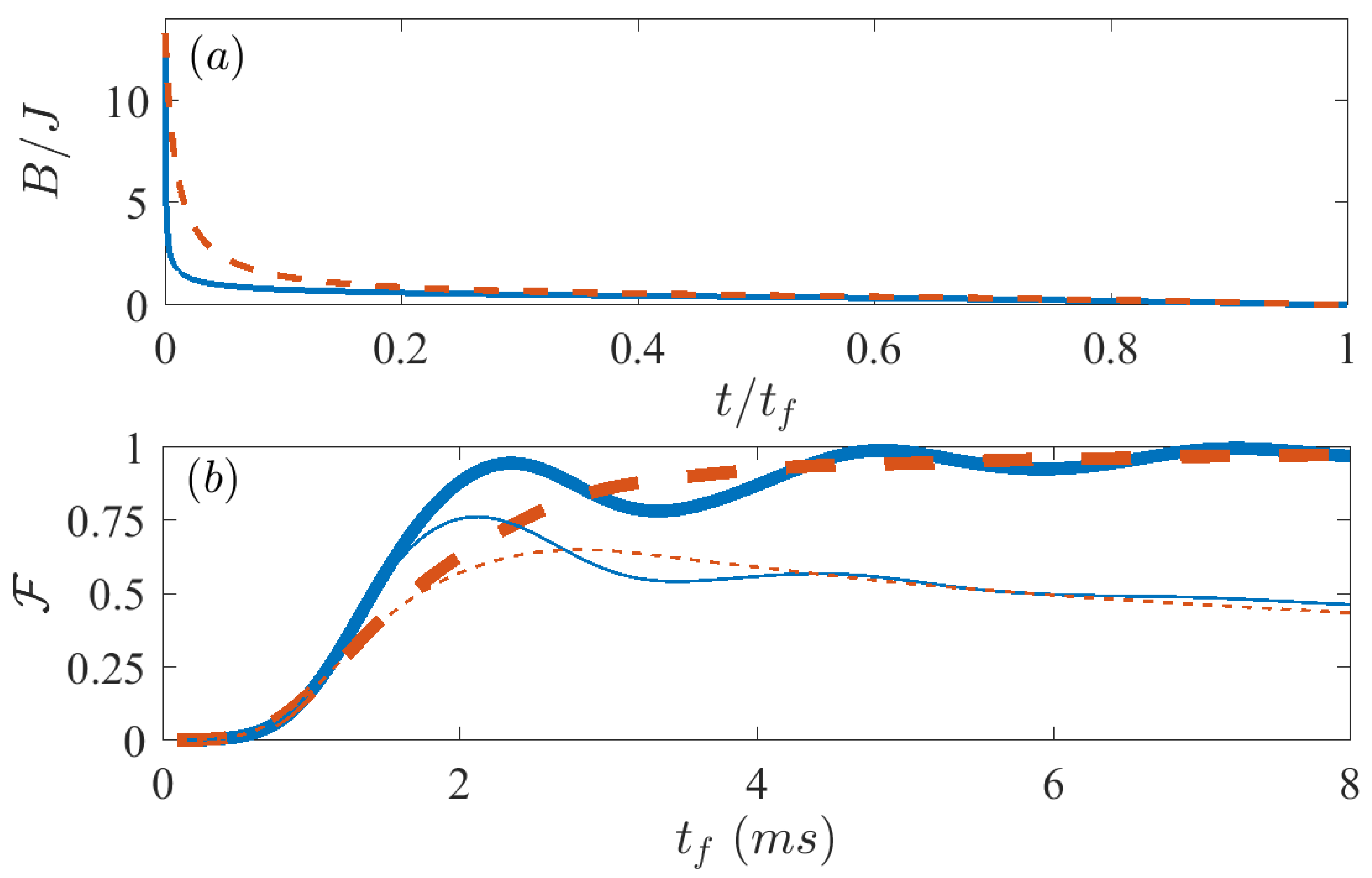
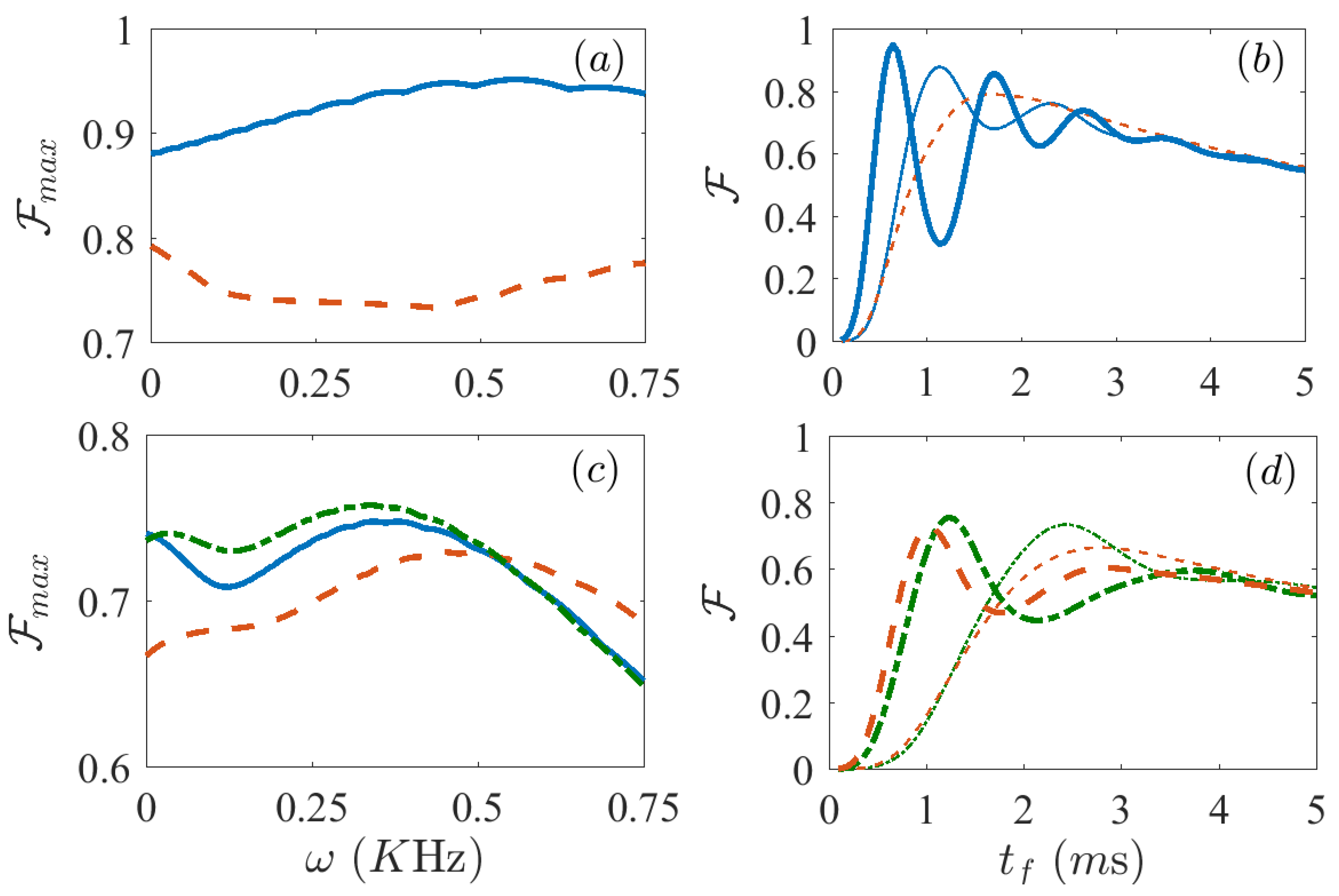
3.2. Performance of the Unitary Protocols in the Open System Scenario
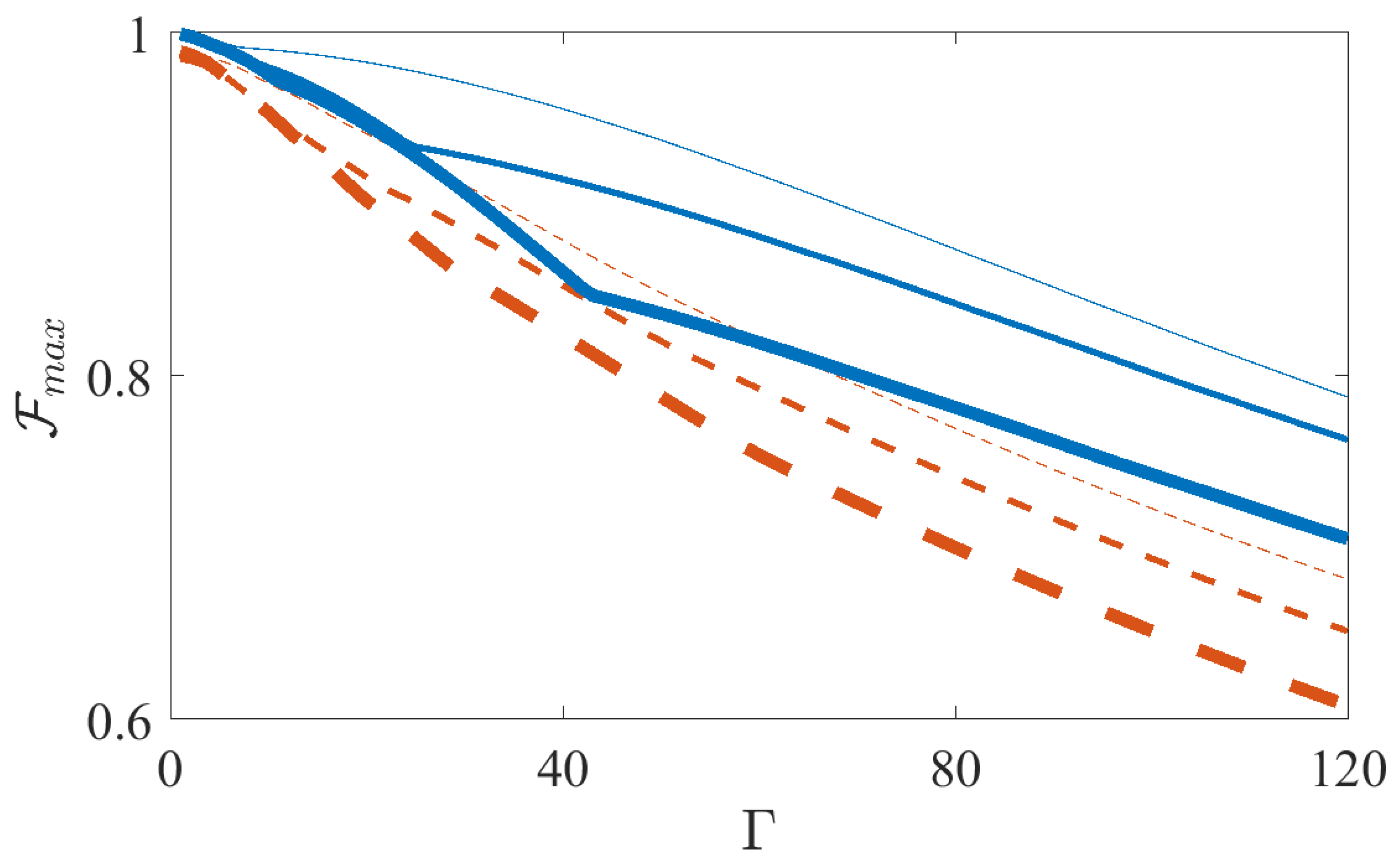
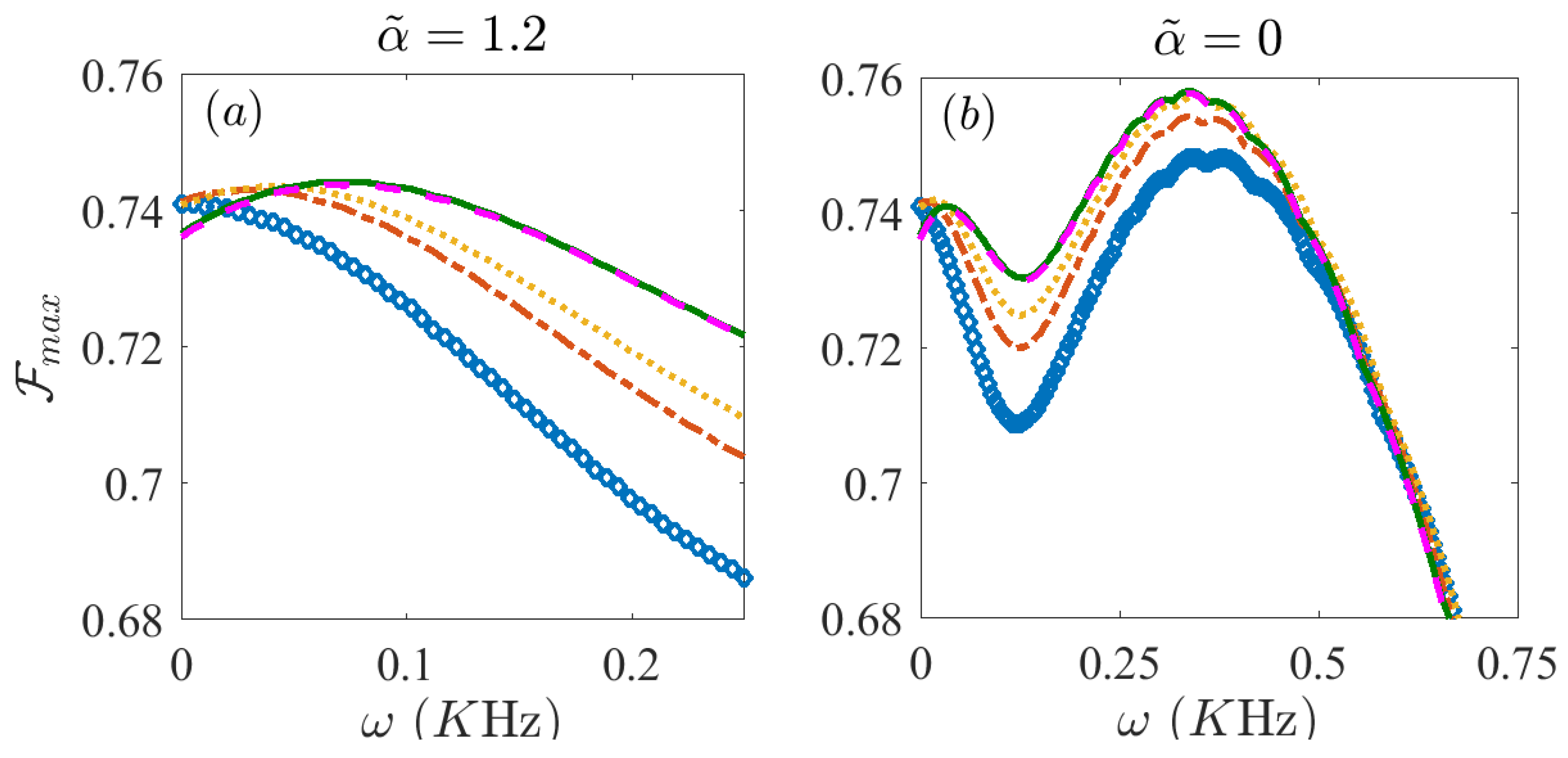
3.3. Dynamical Decoupling of the Dephasing
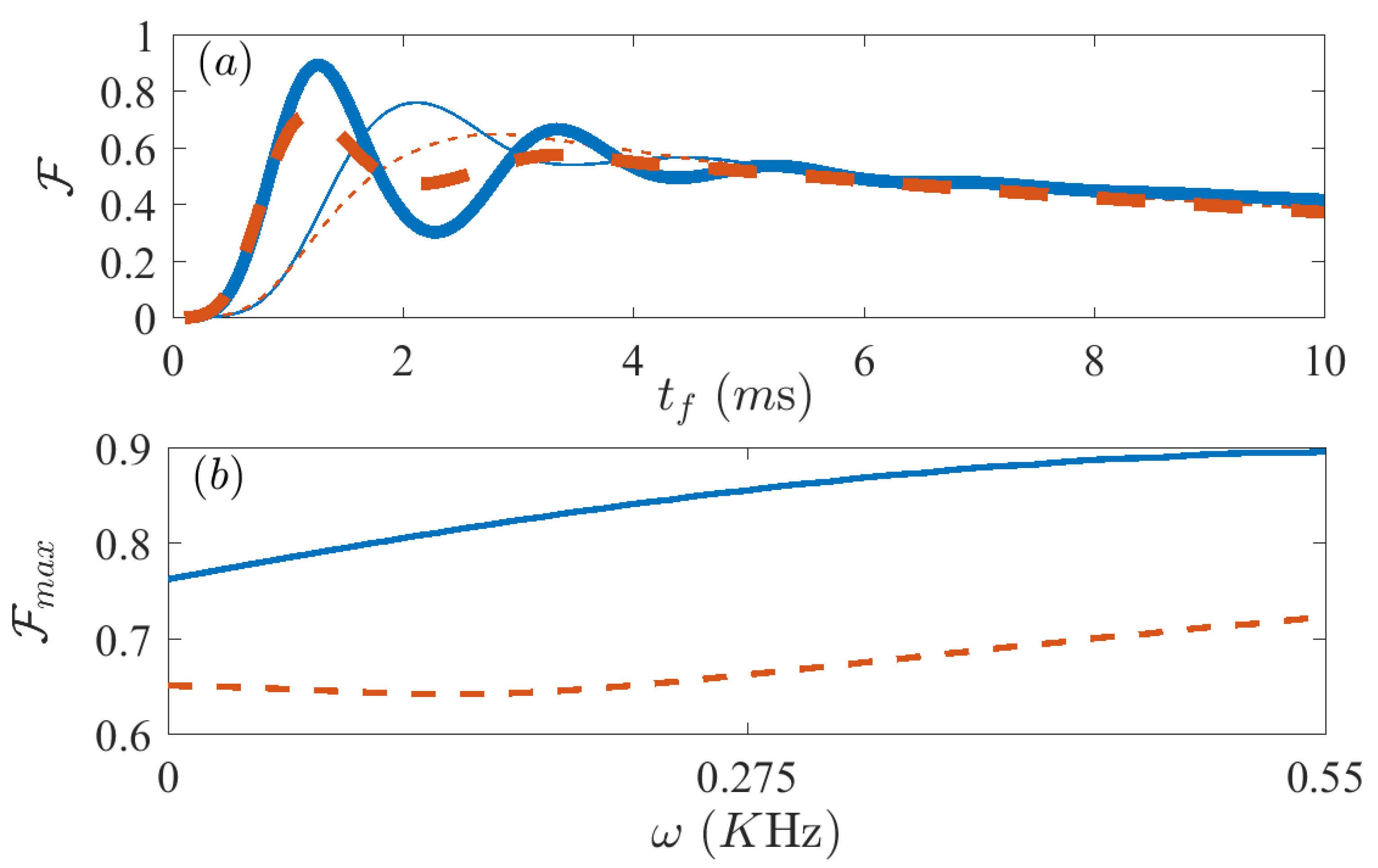
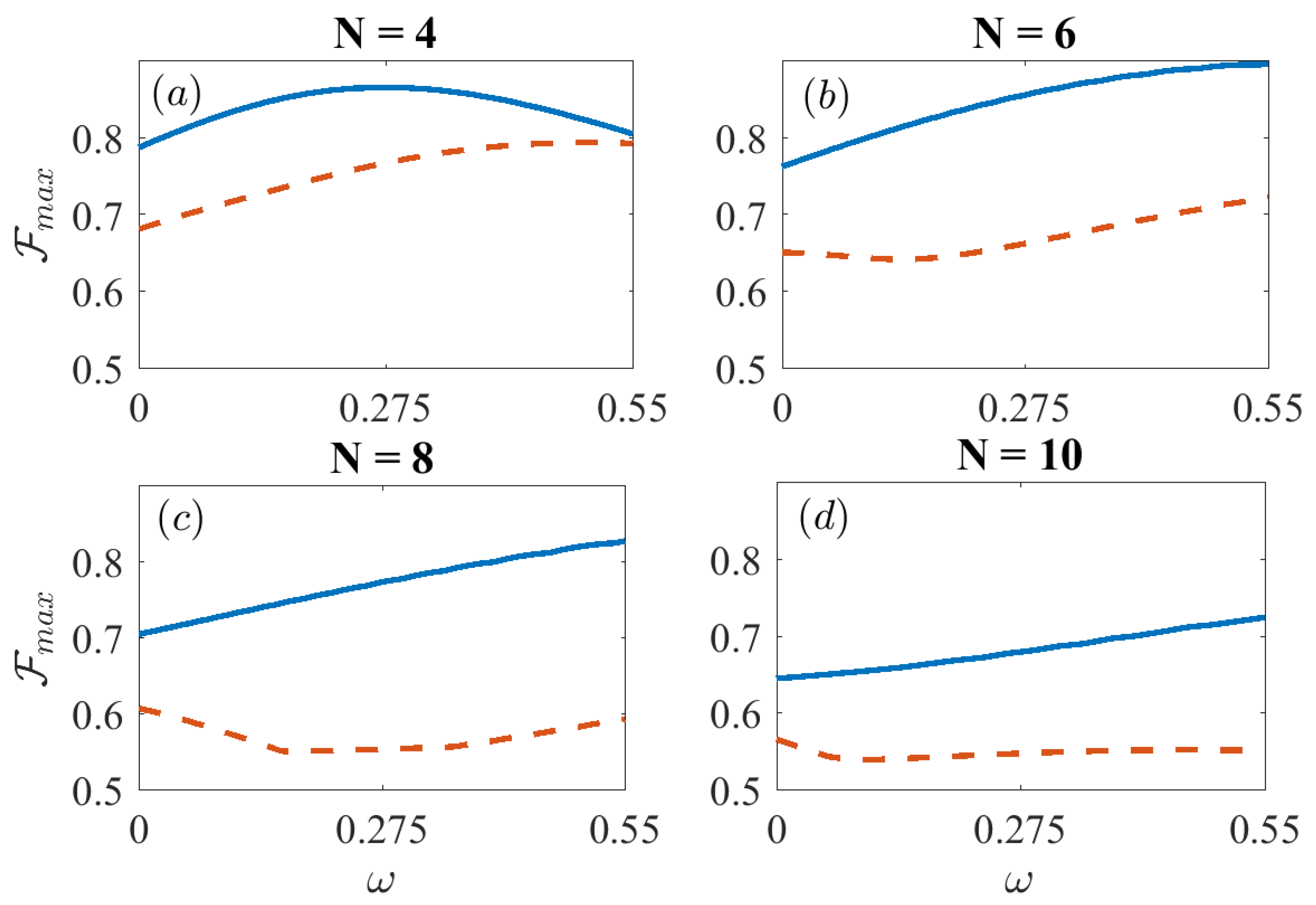
4. Power-Law Interactions
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References and Note
- Leibfried, D.; Knill, E.; Seidelin, S.; Britton, J.; Blakestad, R.B.; Chiaverini, J.; Hume, D.B.; Itano, W.M.; Jost, J.D.; Langer, C.; et al. Creation of a six-atom “Schrödinger cat” state. Nature 2005, 438, 639. [Google Scholar] [CrossRef] [PubMed]
- Gilchrist, A.; Nemoto, K.; Munro, W.J.; Ralph, T.C.; Glancy, S.; Braunstein, S.L.; Milburn, G.J. Schrödinger cats and their power for quantum information processing. J. Opt. B Quantum Semiclassical Opt. 2004, 6, S828–S833. [Google Scholar] [CrossRef]
- Giovannetti, V.; Lloyd, S.; Maccone, L. Quantum-Enhanced Measurements: Beating the Standard Quantum Limit. Science 2004, 306, 1330. [Google Scholar] [CrossRef] [PubMed]
- Strobel, H.; Muessel, W.; Linnemann, D.; Zibold, T.; Hume, D.B.; Pezzè, L.; Smerzi, A.; Oberthaler, M.K. Fisher information and entanglement of non-Gaussian spin states. Science 2014, 345, 424. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, M.A. Cluster-state quantum computation. Rep. Math. Phys. 2006, 57, 147. [Google Scholar] [CrossRef]
- Leroux, I.D.; Schleier-Smith, M.H.; Vuletić, V. Implementation of Cavity Squeezing of a Collective Atomic Spin. Phys. Rev. Lett. 2010, 104, 073602. [Google Scholar] [CrossRef]
- Ritsch, H.; Domokos, P.; Brennecke, F.; Esslinger, T. Cold atoms in cavity-generated dynamical optical potentials. Rev. Mod. Phys. 2013, 85, 553–601. [Google Scholar] [CrossRef]
- Porras, D.; Cirac, J.I. Effective Quantum Spin Systems with Trapped Ions. Phys. Rev. Lett. 2004, 92, 207901. [Google Scholar] [CrossRef]
- Kim, K.; Chang, M.S.; Islam, R.; Korenblit, S.; Duan, L.M.; Monroe, C. Entanglement and Tunable Spin-Spin Couplings between Trapped Ions Using Multiple Transverse Modes. Phys. Rev. Lett. 2009, 103, 120502. [Google Scholar] [CrossRef]
- Islam, R.; Edwards, E.E.; Kim, K.; Korenblit, S.; Noh, C.; Carmichael, H.; Lin, G.D.; Duan, L.M.; Joseph Wang, C.C.; Freericks, J.K.; et al. Onset of a quantum phase transition with a trapped ion quantum simulator. Nat. Commun. 2011, 2, 377. [Google Scholar] [CrossRef]
- Islam, R.; Senko, C.; Campbell, W.C.; Korenblit, S.; Smith, J.; Lee, A.; Edwards, E.E.; Wang, C.C.J.; Freericks, J.K.; Monroe, C. Emergence and Frustration of Magnetism with Variable-Range Interactions in a Quantum Simulator. Science 2013, 340, 583–587. [Google Scholar] [CrossRef] [PubMed]
- Safavi-Naini, A.; Lewis-Swan, R.J.; Bohnet, J.G.; Gärttner, M.; Gilmore, K.A.; Jordan, J.E.; Cohn, J.; Freericks, J.K.; Rey, A.M.; Bollinger, J.J. Verification of a Many-Ion Simulator of the Dicke Model Through Slow Quenches across a Phase Transition. Phys. Rev. Lett. 2018, 121, 040503. [Google Scholar] [CrossRef] [PubMed]
- Richerme, P.; Senko, C.; Smith, J.; Lee, A.; Korenblit, S.; Monroe, C. Experimental performance of a quantum simulator: Optimizing adiabatic evolution and identifying many-body ground states. Phys. Rev. A 2013, 88, 012334. [Google Scholar] [CrossRef]
- Torrontegui, E.; Ibáñez, S.; Martínez-Garaot, S.; Modugno, M.; del Campo, A.; Guéry-Odelin, D.; Ruschhaupt, A.; Chen, X.; Muga, J.G. Shortcuts to Adiabaticity. In Advances in Atomic, Molecular, and Optical Physics; Arimondo, E., Berman, P.R., Lin, C.C., Eds.; Academic Press: Amsterdam, The Netherlands, 2013; Chapter 2; Volume 62, pp. 117–169. [Google Scholar] [CrossRef]
- Guéry-Odelin, D.; Ruschhaupt, A.; Kiely, A.; Torrontegui, E.; Martínez-Garaot, S.; Muga, J.G. Shortcuts to adiabaticity: Concepts, methods, and applications. Rev. Mod. Phys. 2019, 91, 045001. [Google Scholar] [CrossRef]
- Martínez-Garaot, S.; Ruschhaupt, A.; Gillet, J.; Busch, T.; Muga, J.G. Fast quasiadiabatic dynamics. Phys. Rev. A 2015, 92, 043406. [Google Scholar] [CrossRef]
- Viola, L.; Lloyd, S. Dynamical suppression of decoherence in two-state quantum systems. Phys. Rev. A 1998, 58, 2733–2744. [Google Scholar] [CrossRef]
- Viola, L.; Knill, E.; Lloyd, S. Dynamical Decoupling of Open Quantum Systems. Phys. Rev. Lett. 1999, 82, 2417–2421. [Google Scholar] [CrossRef]
- Bohnet, J.G.; Sawyer, B.C.; Britton, J.W.; Wall, M.L.; Rey, A.M.; Foss-Feig, M.; Bollinger, J.J. Quantum spin dynamics and entanglement generation with hundreds of trapped ions. Science 2016, 352, 1297–1301. [Google Scholar] [CrossRef]
- Demirplak, M.; Rice, S.A. Adiabatic Population Transfer with Control Fields. J. Phys. Chem. A 2003, 107, 9937–9945. [Google Scholar] [CrossRef]
- Setiawan, I.; Eka Gunara, B.; Masuda, S.; Nakamura, K. Fast forward of the adiabatic spin dynamics of entangled states. Phys. Rev. A 2017, 96, 052106. [Google Scholar] [CrossRef]
- Hatomura, T. Shortcuts to Adiabaticity in the Infinite-Range Ising Model by Mean-Field Counter-Diabatic Driving. J. Phys. Soc. Jpn. 2017, 86, 094002. [Google Scholar] [CrossRef][Green Version]
- Campbell, S.; De Chiara, G.; Paternostro, M.; Palma, G.M.; Fazio, R. Shortcut to Adiabaticity in the Lipkin-Meshkov-Glick Model. Phys. Rev. Lett. 2015, 114, 177206. [Google Scholar] [CrossRef] [PubMed]
- Doria, P.; Calarco, T.; Montangero, S. Optimal Control Technique for Many-Body Quantum Dynamics. Phys. Rev. Lett. 2011, 106, 190501. [Google Scholar] [CrossRef] [PubMed]
- Cohn, J.; Safavi-Naini, A.; Lewis-Swan, R.J.; Bohnet, J.G.; Gärttner, M.; Gilmore, K.A.; Jordan, J.E.; Rey, A.M.; Bollinger, J.J.; Freericks, J.K. Bang-bang shortcut to adiabaticity in the Dicke model as realized in a Penning trap experiment. New J. Phys. 2018, 20, 055013. [Google Scholar] [CrossRef]
- Takahashi, K. Transitionless quantum driving for spin systems. Phys. Rev. E 2013, 87, 062117. [Google Scholar] [CrossRef]
- Dann, R.; Tobalina, A.; Kosloff, R. Shortcut to Equilibration of an Open Quantum System. Phys. Rev. Lett. 2019, 122, 250402. [Google Scholar] [CrossRef]
- Dupays, L.; Egusquiza, I.L.; del Campo, A.; Chenu, A. Shortcuts in open quantum systems: Superadiabatic control of an open quantum oscillator. arXiv 2019, arXiv:1910.12088. [Google Scholar]
- Dicke, R.H. Coherence in Spontaneous Radiation Processes. Phys. Rev. 1954, 93, 99–110. [Google Scholar] [CrossRef]
- Garraway, B.M. The Dicke model in quantum optics: Dicke model revisited. Philos. Trans. R. Soc. A 2011, 369, 1137. [Google Scholar] [CrossRef]
- Wall, M.L.; Safavi-Naini, A.; Rey, A.M. Boson-mediated quantum spin simulators in transverse fields: XY model and spin-boson entanglement. Phys. Rev. A 2017, 95, 013602. [Google Scholar] [CrossRef]
- Lindblad, G. Completely positive dynamical semigroups of N-level systems. J. Math. Phys. 1976, 48, 119. [Google Scholar] [CrossRef]
- Gorini, V.; Kossakowski, A.; Sudarshan, E. Completely positive dynamical semigroups of N-level systems. J. Math. Phys. 1976, 17, 821. [Google Scholar] [CrossRef]
- We run simulations for up to FAQUAD-5, but the fidelities for protocols taking more meaningful transitions into account did not, in this case, significantly improve the results for the simple FAQUAD, therefore, for clarity of exposition, we only display the results for FAQUAD and LA.
- Sun, Z.; Zhou, L.; Xiao, G.; Poletti, D.; Gong, J. Finite-time Landau-Zener processes and counterdiabatic driving in open systems: Beyond Born, Markov, and rotating-wave approximations. Phys. Rev. A 2016, 93, 012121. [Google Scholar] [CrossRef]
- Fogarty, T.; Deffner, S.; Busch, T.; Campbell, S. Orthogonality Catastrophe as a Consequence of the Quantum Speed Limit. arXiv 2019, arXiv:1910.10728. [Google Scholar]
- Levy, A.; Kiely, A.; Muga, J.G.; Kosloff, R.; Torrontegui, E. Noise resistant quantum control using dynamical invariants. New J. Phys. 2018, 20, 025006. [Google Scholar] [CrossRef]
- Vacanti, G.; Fazio, R.; Montangero, S.; Palma, G.M.; Paternostro, M.; Vedral, V. Transitionless quantum driving in open quantum systems. New J. Phys. 2014, 16, 053017. [Google Scholar] [CrossRef]
- Santos, A.C.; Sarandy, M.S. Generalized shortcuts to adiabaticity and enhanced robustness against decoherence. J. Phys. A Math. Theor. 2017, 51, 025301. [Google Scholar] [CrossRef]
- National Supercomputing Centre, Singapore. Available online: www.nscc.sg (accessed on 28 October 2019).
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Palmero, M.; Simón, M.Á.; Poletti, D. Towards Generation of Cat States in Trapped Ions Set-Ups via FAQUAD Protocols and Dynamical Decoupling. Entropy 2019, 21, 1207. https://doi.org/10.3390/e21121207
Palmero M, Simón MÁ, Poletti D. Towards Generation of Cat States in Trapped Ions Set-Ups via FAQUAD Protocols and Dynamical Decoupling. Entropy. 2019; 21(12):1207. https://doi.org/10.3390/e21121207
Chicago/Turabian StylePalmero, Mikel, Miguel Ángel Simón, and Dario Poletti. 2019. "Towards Generation of Cat States in Trapped Ions Set-Ups via FAQUAD Protocols and Dynamical Decoupling" Entropy 21, no. 12: 1207. https://doi.org/10.3390/e21121207
APA StylePalmero, M., Simón, M. Á., & Poletti, D. (2019). Towards Generation of Cat States in Trapped Ions Set-Ups via FAQUAD Protocols and Dynamical Decoupling. Entropy, 21(12), 1207. https://doi.org/10.3390/e21121207





