The Eigenvalue Complexity of Sequences in the Real Domain
Abstract
1. Introduction
2. Eigenvalue for Real Number Sequences
2.1. Eigenvalue for Binary Sequences
- (1)
- The tuple xk−1xk…xN−1 does not belong to the vocabulary of a proper prefix of yN.
- (2)
- The tuple xkxk+1…xN−1 belongs to the vocabulary of a proper prefix of yN.
2.2. Eigenvalue of Sequences in the Real Domain
3. Two Examples
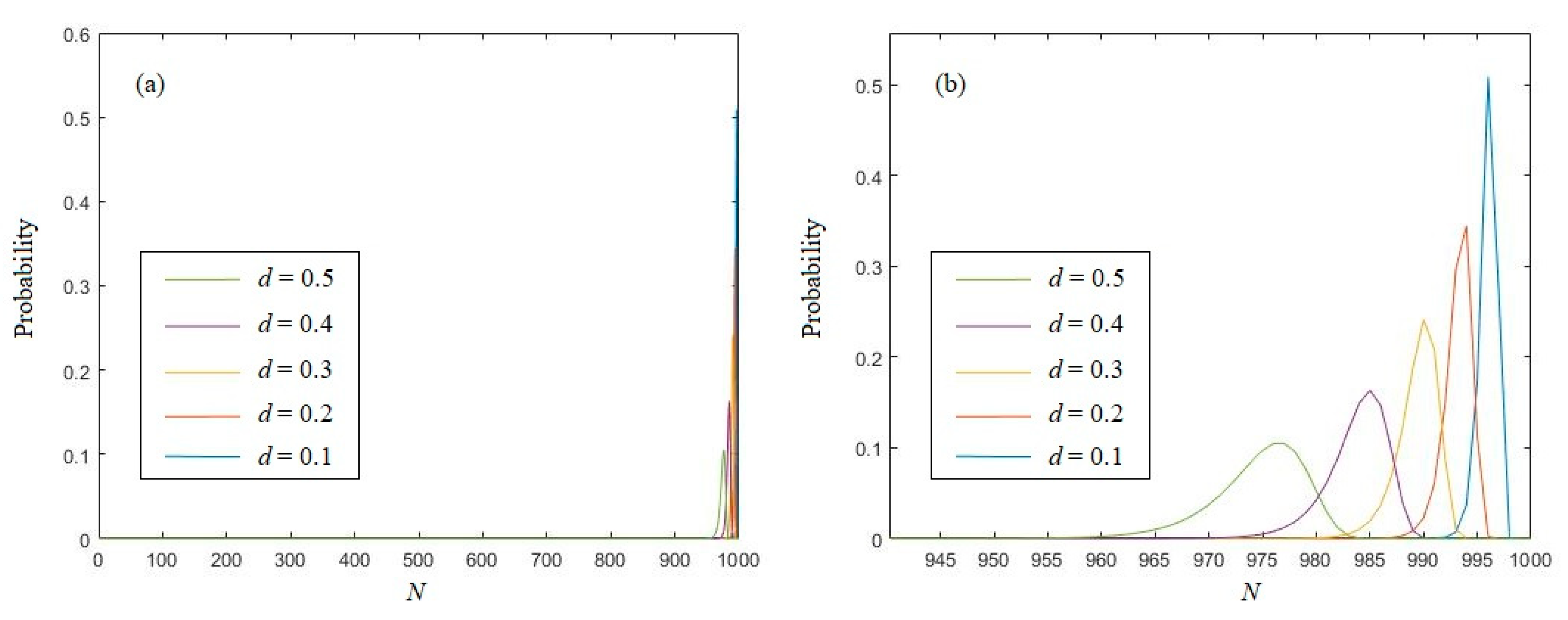
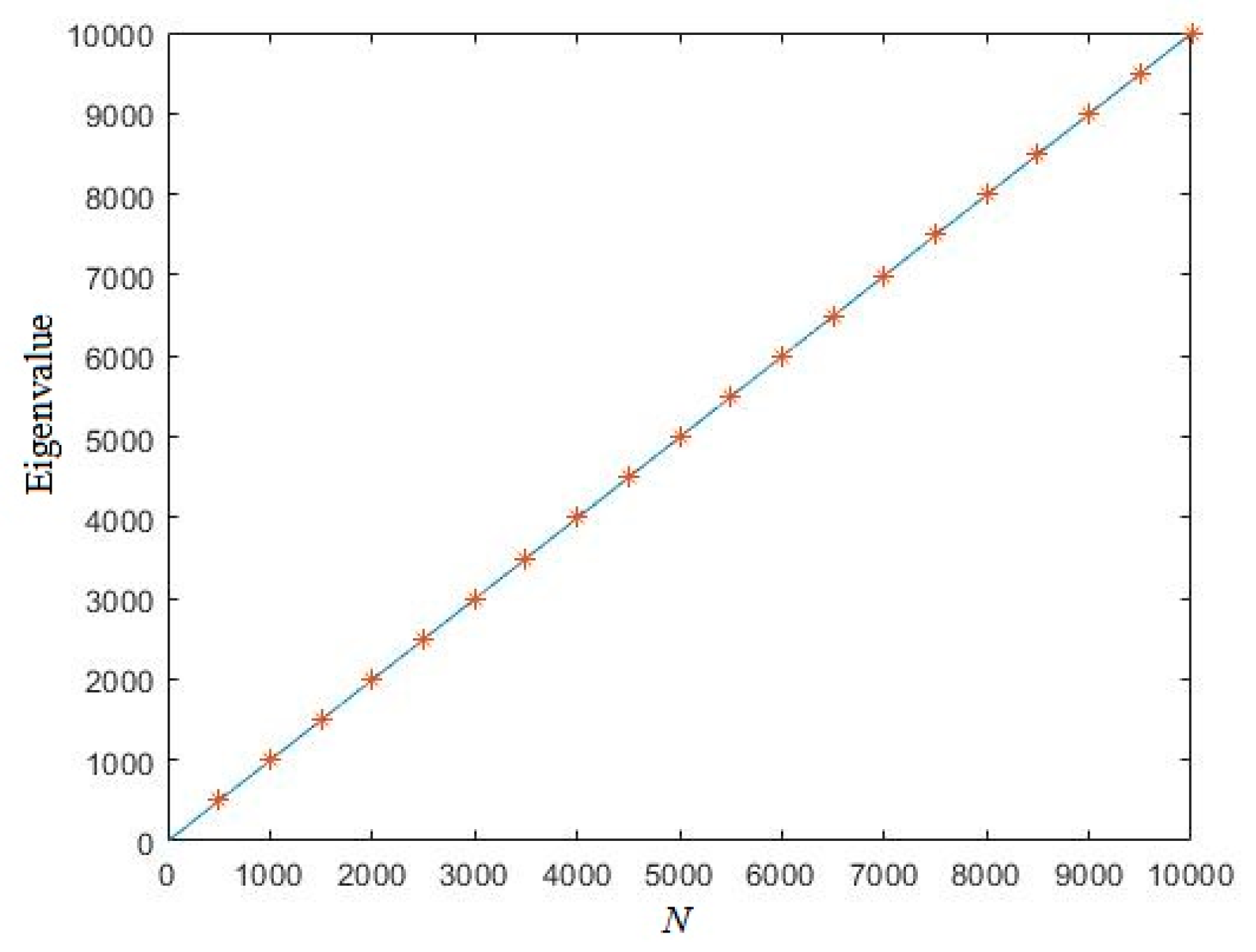
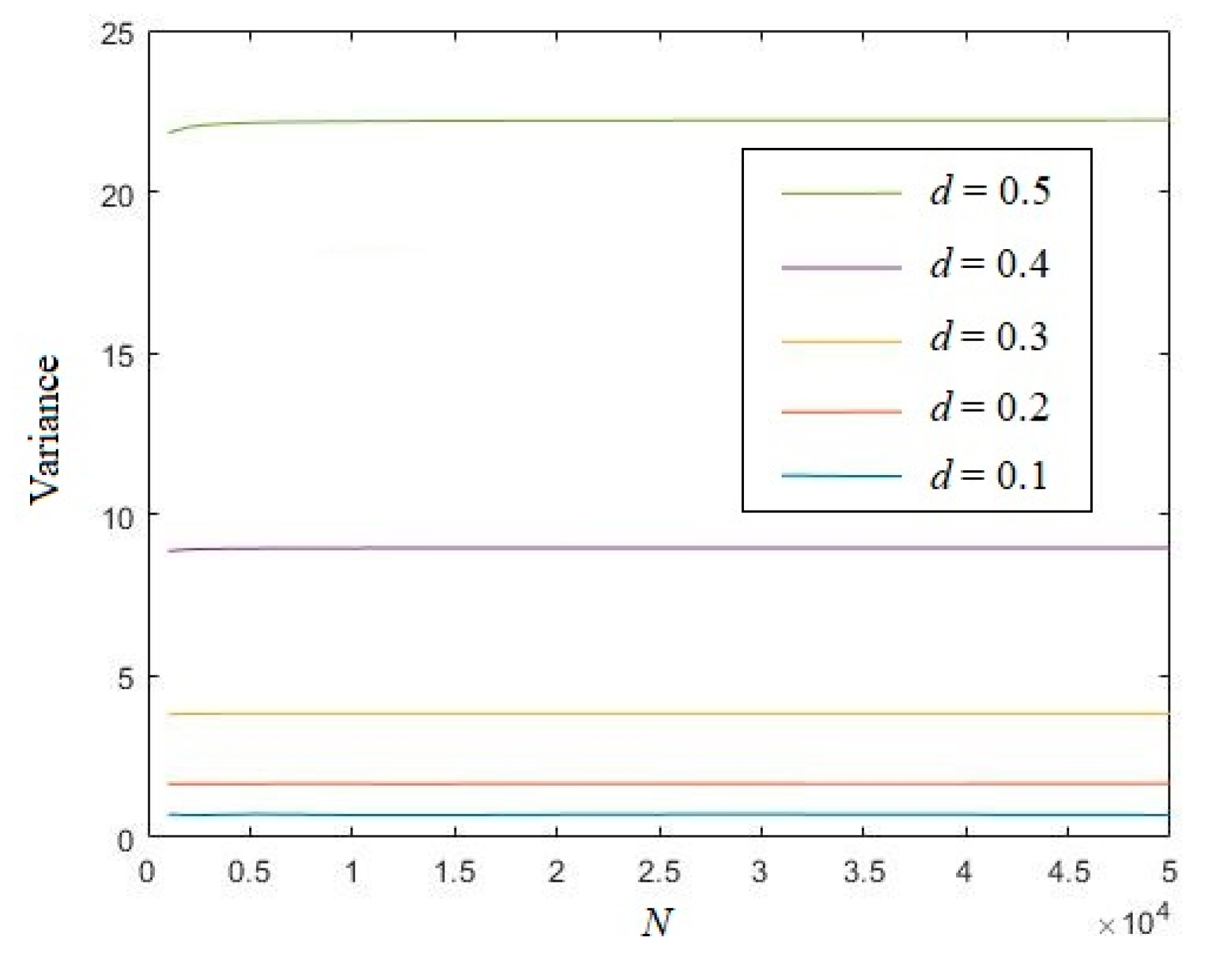
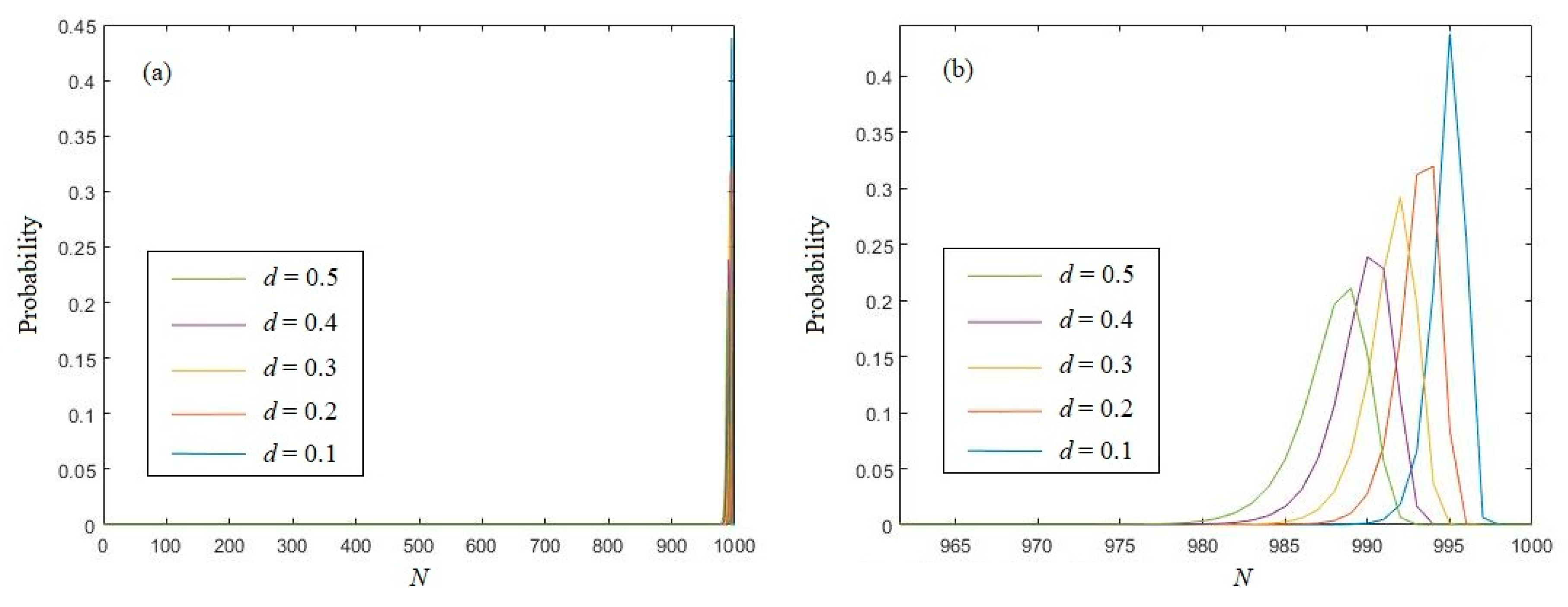
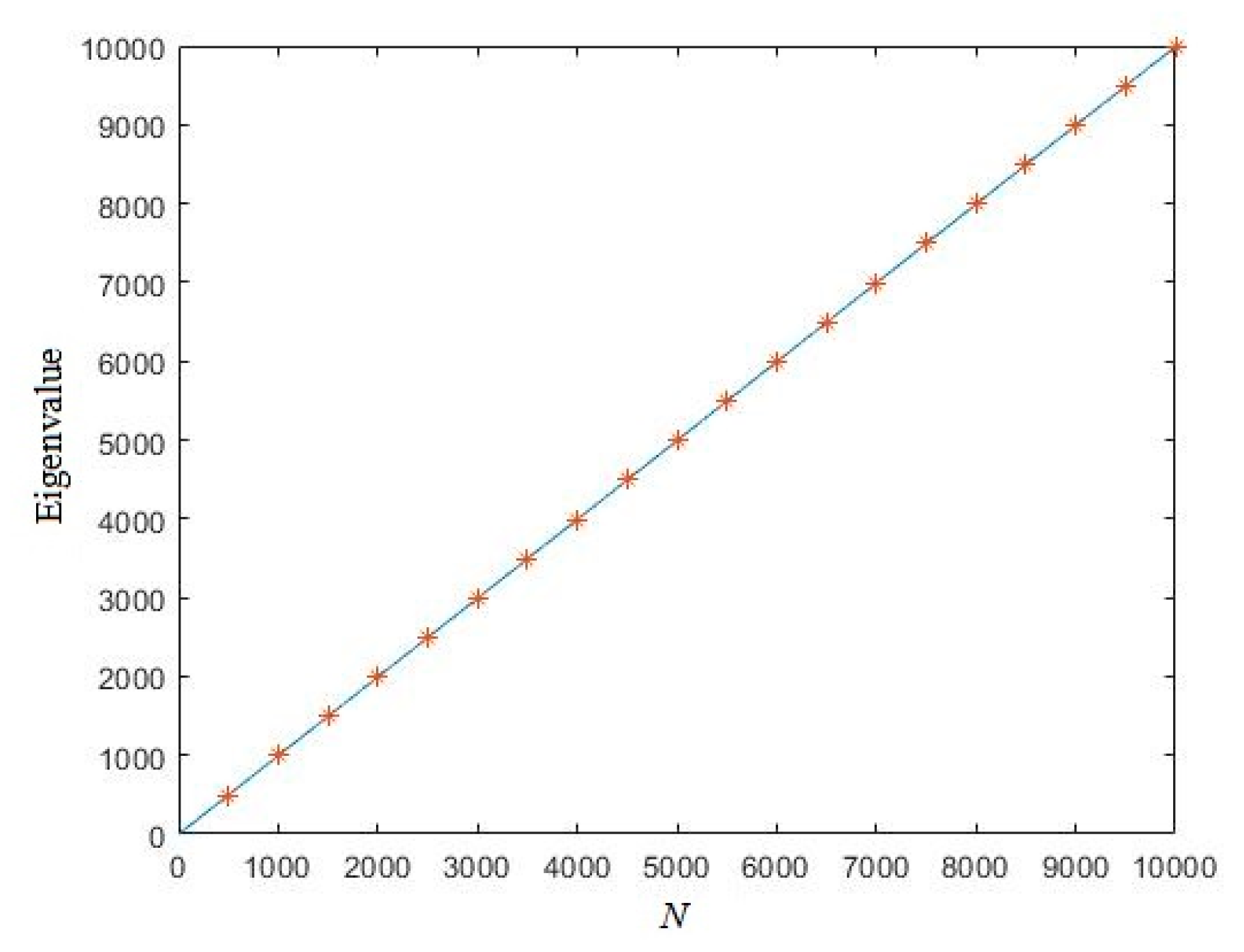
3.1. Eigenvalue of Uniformly Distributed Random Sequence
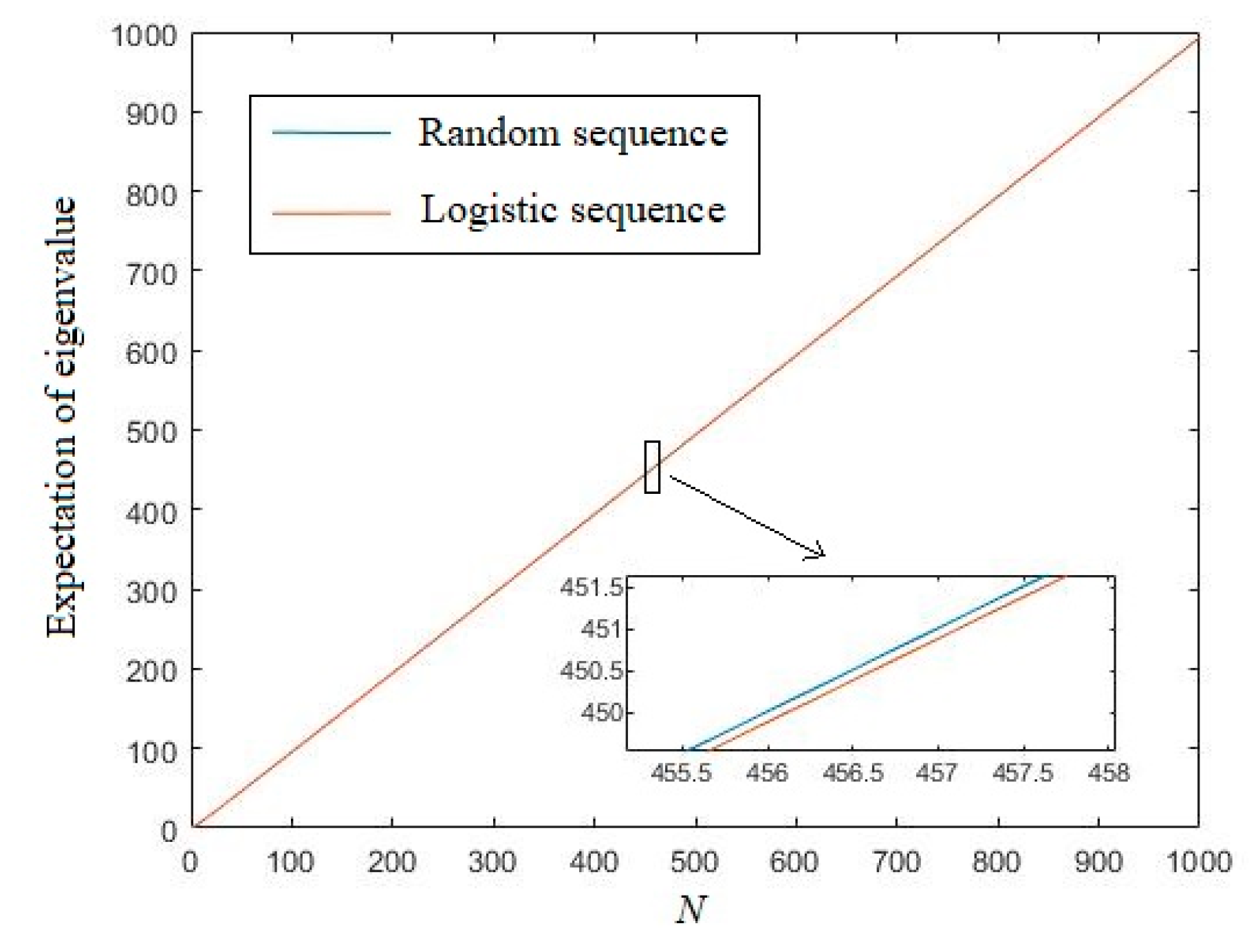
3.2. Eigenvalue of Logistic Chaotic Sequence
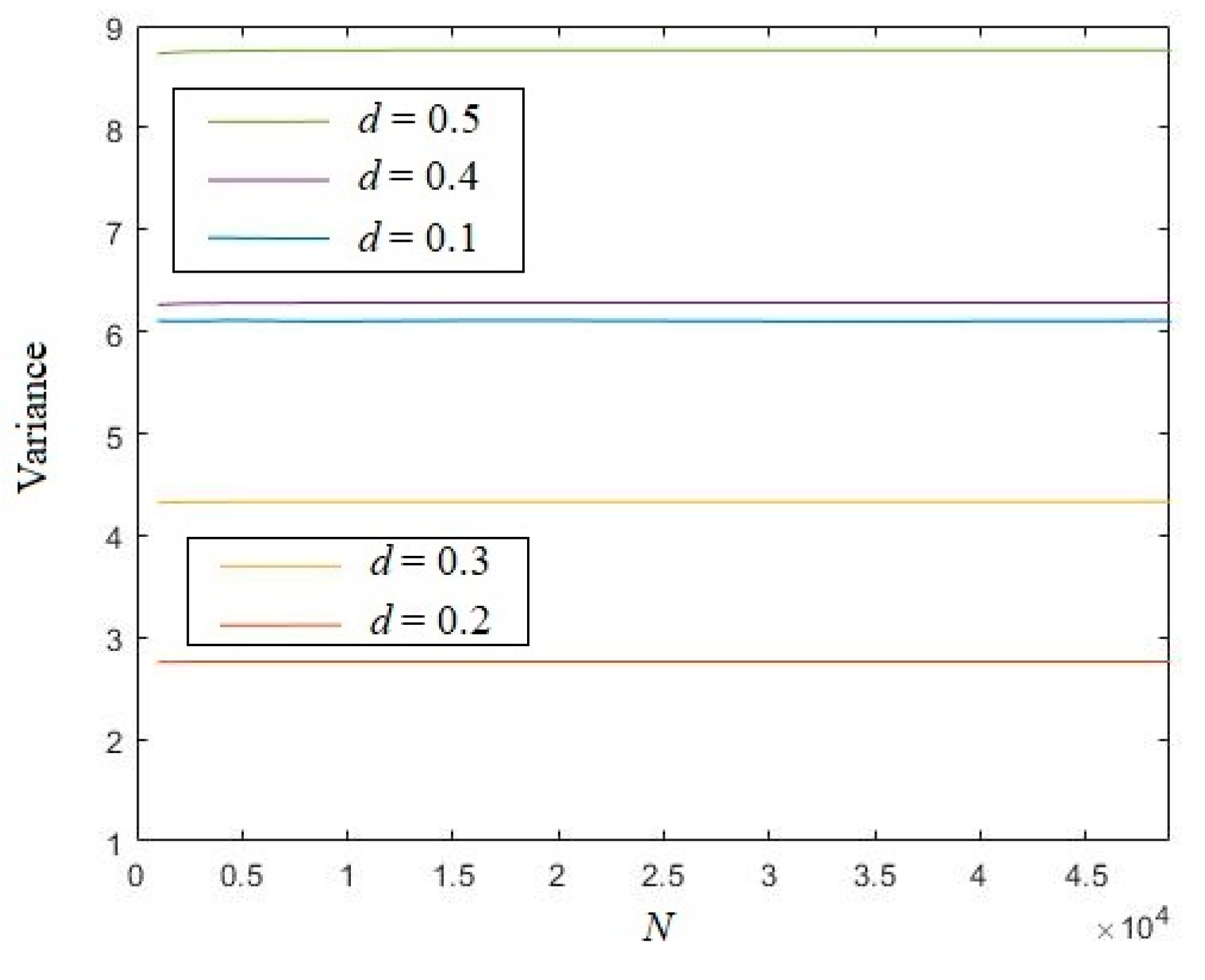
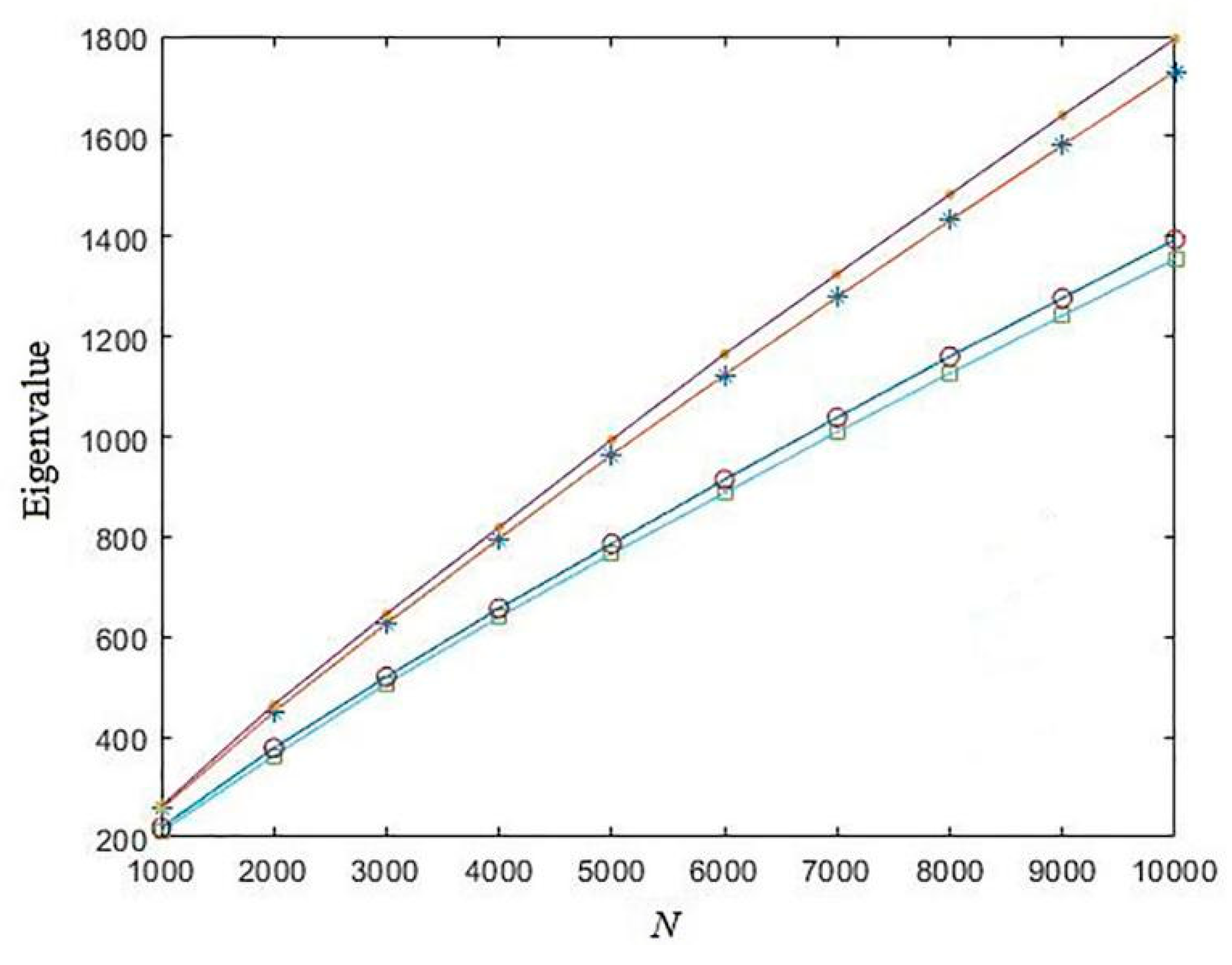
4. Measure the Complexity of Chaotic Sequences
- Chebyshev mapChebyshev map can be written aswhere xi∈(−1, 1) is the state variable, a is the control coefficient. The Chebyshev map will be chaotic since a≧2. In this test, we always set a = 3.
- Sine mapSine map can be mathematically described aswhere r∈(0, 1] is the control parameter. In this test, we set r = 2 to make the Sine map chaotic.
- Tent mapTent map is a kind of piece-wise function, which can be described aswhere p∈(0, 1) is the control parameter. Particularly, when p = 0.5, the generated sequence will quickly fall into a short cycle. Therefore, we always set p = 0.49 in this test.
- Logistic mapThe Logistic map has already been described in Equation (17), which we omitted here to avoid redundancy.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Massey, J.L.; Serconek, S. A Fourier transform approach to the linear complexity of nonlinearly filtered sequences. In Annual International Cryptology Conference; Springer: Berlin/Heidelberg, Germany, 1994; pp. 332–340. [Google Scholar]
- Kolokotronis, N.; Kalouptsidis, N. On the linear complexity of nonlinearly filtered PN-sequences. IEEE Trans. Inf. Theory 2003, 49, 3047–3059. [Google Scholar] [CrossRef]
- Limniotis, K.; Kolokotronis, N.; Kalouptsidis, N. New results on the linear complexity of binary sequences. In 2006 IEEE International Symposium on Information Theory; IEEE: New York, NY, USA, 2006; pp. 2003–2007. [Google Scholar]
- Erdmann, D.; Murphy, S. An approximate distribution for the maximum order complexity. Des. Codes. Cryptogr. 1997, 10, 325–339. [Google Scholar] [CrossRef]
- Rizomiliotis, P. Constructing periodic binary sequences of maximum nonlinear span. IEEE Trans. Inf. Theory 2006, 52, 4257–4261. [Google Scholar] [CrossRef]
- Rizomiliotis, P.; Kolokotronis, N.; Kalouptsidis, N. On the quadratic span of binary sequences. IEEE Trans. Inf. Theory 2005, 51, 1840–1848. [Google Scholar] [CrossRef]
- Lempel, A.; Ziv, J. On the complexity of finite sequences. IEEE Trans. Inf. Theory 1976, 22, 75–81. [Google Scholar] [CrossRef]
- Limniotis, K.; Kolokotronis, N.; Kalouptsidis, N. On the nonlinear complexity and Lempel-Ziv complexity of finite length sequences. IEEE Trans. Inf. Theory 2007, 53, 4293–4302. [Google Scholar] [CrossRef]
- Liu, L.; Miao, S.; Hu, H.; Deng, Y. On the Eigenvlaue and Shannon’s Entropy of Finite Length Random Sequences. Complexity 2015, 21, 154–161. [Google Scholar] [CrossRef]
- Liu, L.; Miao, S.; Liu, B. On nonlinear complexity and Shannon’s entropy of finite length random sequences. Entropy 2015, 17, 1936–1945. [Google Scholar] [CrossRef]
- Tosun, P.; Abásolo, D.; Stenson, G.; Winsky-Sommerer, R. Characterisation of the effects of sleep deprivation on the electroencephalogram using permutation Lempel-Ziv complexity, a non-linear analysis tool. Entropy 2017, 19, 673. [Google Scholar] [CrossRef]
- Peng, J.; Zeng, X.; Sun, Z. Finite length sequences with large nonlinear complexity. Adv. Math. Commun. 2018, 12, 215–230. [Google Scholar] [CrossRef]
- Li, P.; Wang, Y.C.; Wang, A.B.; Wang, B.J. Fast and tunable all-optical physical random number generator based on direct quantization of chaotic self-pulsations in two-section. IEEE J. Sel. Top. Quantum Electron. 2013, 19, 0600208. [Google Scholar]
- Li, R.; Liu, Q.; Liu, L. Novel image encryption algorithm based on improved logistic map. IET Image Process. 2019, 13, 125–134. [Google Scholar] [CrossRef]
- Huang, X.; Liu, L.; Li, X.; Yu, M.; Wu, Z. A new pseudorandom bit generator based on mixing three-dimensional Chen chaotic system with a chaotic tactics. Complexity 2019, 2019, 6567198. [Google Scholar] [CrossRef]
- Kanso, A.; Smaoui, N. Logistic chaotic maps for binary numbers generations. Chaos Solitons Fract. 2009, 40, 2557–2568. [Google Scholar] [CrossRef]
- Larger, L.; Dudley, J.M. Optoelectronic chaos. Nature 2010, 465, 41–42. [Google Scholar] [CrossRef] [PubMed]
- Bahi, J.M.; Fang, X.; Guyeux, C.; Wang, Q. On the design of a family of CI pseudo-random number generators. In Proceedings of the 2011 7th International Conference on Wireless Communications, Networking and Mobile Computing, Wuhan, China, 23–25 September 2011; pp. 1–4. [Google Scholar]
- Masuda, N.; Aihara, K. Cryptosystems with discretized chaotic maps. IEEE Trans Circuits Syst. I 2002, 49, 28–40. [Google Scholar] [CrossRef]
- Li, P.; Wang, Y.C.; Wang, A.B.; Yang, L.Z.; Zhang, M.J.; Zhang, J.Z. Direct generation of all-optical random numbers from optical pulse amplitude chaos. Opt. Express 2012, 20, 4297–4308. [Google Scholar] [CrossRef] [PubMed]
- Kocarev, L. Chaos-based cryptography: A brief overview. IEEE Circ. Syst. Mag. 2001, 1, 6–21. [Google Scholar] [CrossRef]
- Liu, L.; Miao, S.; Hu, H.; Cheng, M. N-phase Logistic chaotic sequence and its application for image encryption. IET Signal Process. 2016, 10, 1096–1104. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Xiang, H.; Li, R.; Hu, H. The Eigenvalue Complexity of Sequences in the Real Domain. Entropy 2019, 21, 1194. https://doi.org/10.3390/e21121194
Liu L, Xiang H, Li R, Hu H. The Eigenvalue Complexity of Sequences in the Real Domain. Entropy. 2019; 21(12):1194. https://doi.org/10.3390/e21121194
Chicago/Turabian StyleLiu, Lingfeng, Hongyue Xiang, Renzhi Li, and Hanping Hu. 2019. "The Eigenvalue Complexity of Sequences in the Real Domain" Entropy 21, no. 12: 1194. https://doi.org/10.3390/e21121194
APA StyleLiu, L., Xiang, H., Li, R., & Hu, H. (2019). The Eigenvalue Complexity of Sequences in the Real Domain. Entropy, 21(12), 1194. https://doi.org/10.3390/e21121194





