Information Flow between Bitcoin and Other Investment Assets
Abstract
1. Introduction
2. Materials and Methods
2.1. Data
2.2. Granger Causality
2.3. Transfer Entropy
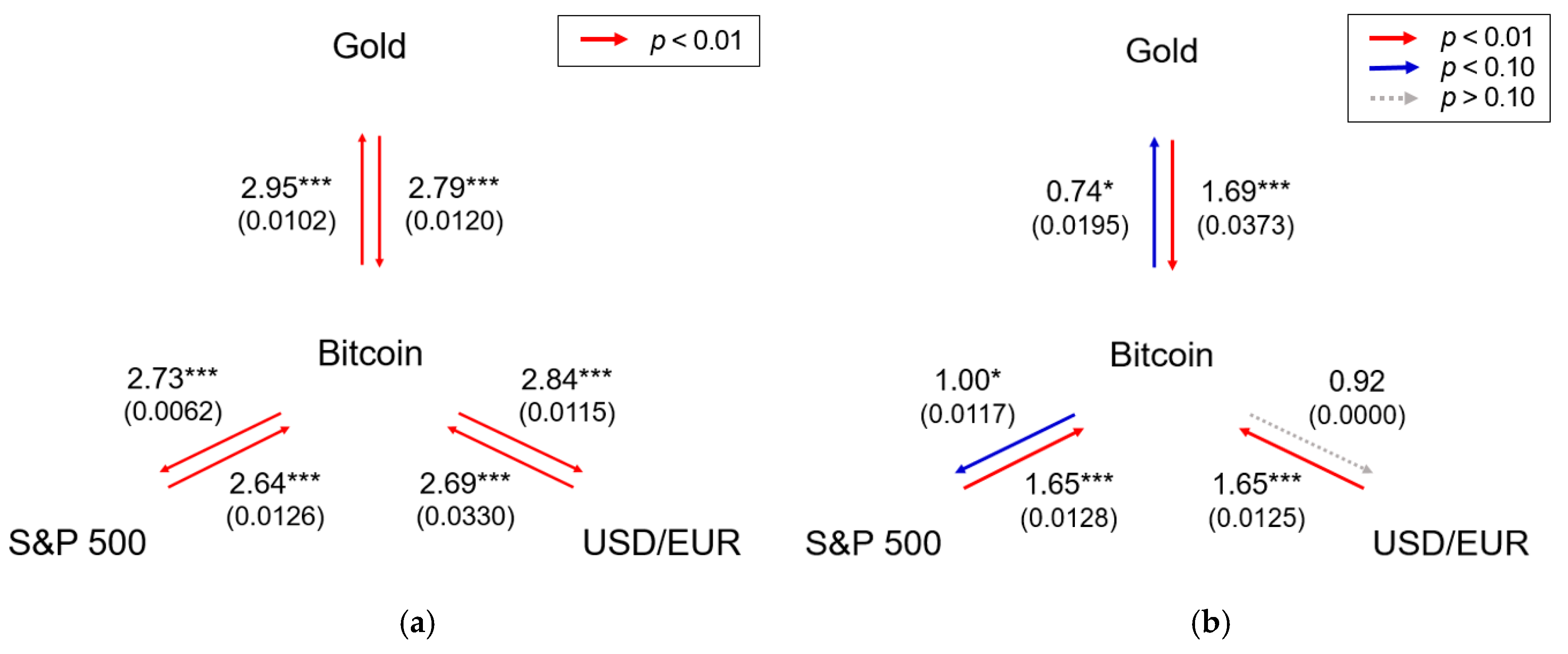
3. Results
3.1. Granger Causality Test
3.2. Normality Test
3.3. Transfer Entropy
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Böhme, R.; Christin, N.; Edelman, B.; Moore, T. Bitcoin: Economics, technology, and governance. J. Econ. Perspect. 2015, 29, 213–238. [Google Scholar] [CrossRef]
- Kim, T. On the transaction cost of Bitcoin. Financ. Res. Lett. 2017, 23, 300–305. [Google Scholar] [CrossRef]
- Chu, J.; Chan, S.; Nadarajah, S.; Osterrieder, J. GARCH modelling of cryptocurrencies. J. Risk Financ. Manag. 2017, 10, 17. [Google Scholar] [CrossRef]
- Guesmi, K.; Saadi, S.; Abid, I.; Ftiti, Z. Portfolio diversification with virtual currency: Evidence from bitcoin. Int. Rev. Financ. Anal. 2019, 63, 431–437. [Google Scholar] [CrossRef]
- Baur, D.G.; Dimpfl, T.; Kuck, K. Bitcoin, gold and the US dollar–A replication and extension. Financ. Res. Lett. 2018, 25, 103–110. [Google Scholar] [CrossRef]
- Klein, T.; Thu, H.P.; Walther, T. Bitcoin is not the new gold–A comparison of volatility, correlation, and portfolio performance. Int. Rev. Financ. Anal. 2018, 59, 105–116. [Google Scholar] [CrossRef]
- Yermack, D. Is Bitcoin a Real Currency? An Economic Appraisal. In Handbook of Digital Currency; Lee, K.C.D., Ed.; Academic Press: Cambridge, MA, USA, 2015; pp. 31–43. [Google Scholar]
- Erdas, M.L.; Caglar, A.E. Analysis of the relationships between Bitcoin and exchange rate, commodities and global indexes by asymmetric causality test. East. J. Eur. Stud. 2018, 9, 27–45. [Google Scholar]
- Corelli, A. Cryptocurrencies and exchange rates: A relationship and causality analysis. Risks 2018, 6, 111. [Google Scholar] [CrossRef]
- Corbet, S.; Meegan, A.; Larkin, C.; Lucey, B.; Yarovaya, L. Exploring the dynamic relationships between cryptocurrencies and other financial assets. Econ. Lett. 2018, 165, 28–34. [Google Scholar] [CrossRef]
- Drożdż, S.; Minati, L.; Oświęcimka, P.; Stanuszek, M.; Wątorek, M. Signatures of the cryptocurrency market decoupling from the Forex. Future Internet 2019, 11, 154. [Google Scholar] [CrossRef]
- Chakravarty, S.; Gulen, H.; Mayhew, S. Informed trading in stock and option markets. J. Financ. 2004, 59, 1235–1257. [Google Scholar] [CrossRef]
- Chen, W.P.; Chung, H. Has the introduction of S&P 500 ETF options led to improvements in price discovery of SPDRs? J. Futures Mark. 2012, 32, 683–711. [Google Scholar] [CrossRef]
- Ahn, K.; Bi, Y.; Sohn, S. Price discovery among SSE 50 Index-based spot, futures, and options markets. J. Futures Mark. 2019, 39, 238–259. [Google Scholar] [CrossRef]
- Kristoufek, L. What are the main drivers of the Bitcoin price? Evidence from wavelet coherence analysis. PloS ONE 2015, 10, 3923. [Google Scholar] [CrossRef]
- Bakshi, G.; Kapadia, N.; Madan, D. Stock return characteristics, skewness law, and the differential pricing of individual equity option. Rev. Financ. Stud. 2003, 16, 101–143. [Google Scholar] [CrossRef]
- Wiener, N. The theory of prediction. In Modern Mathematics for the Engineer, 1st ed.; Beckenbach, E.F., Ed.; McGraw-Hill: New York, NY, USA, 1956; Volume 1, pp. 165–190. [Google Scholar]
- Granger, C.W. Investigating causal relations by econometric models and cross-spectral methods. Econom. J. Econom. Soc. 1969, 37, 424–438. [Google Scholar] [CrossRef]
- Akaike, H. Fitting autoregressive models for prediction. Ann. Inst. Stat. Math. 1969, 21, 243–247. [Google Scholar] [CrossRef]
- Hannan, E.J.; Quinn, B.G. The determination of the order of an autoregression. J. R. Stat. Soc. Ser. B 1979, 41, 190–195. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Multimodel inference: Understanding AIC and BIC in model selection. Sociol. Methods Res. 2004, 33, 261–304. [Google Scholar] [CrossRef]
- Schreiber, T. Measuring information transfer. Phys. Rev. Lett. 2000, 85, 461–464. [Google Scholar] [CrossRef]
- Larson, H.J. Introduction to Probability Theory and Statistical Inference, 2nd ed.; John Wiley and Sons: New York, NY, USA, 1974. [Google Scholar]
- Scott, D.W. On optimal and data-based histograms. Biometrika 1979, 66, 605–610. [Google Scholar] [CrossRef]
- Freedman, D.; Diaconis, P. On the histogram as a density estimator: L2 theory. Probab. Theory Relat. Fields 1981, 57, 453–476. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Ruiz, M.D.C.; Guillamón, A.; Gabaldón, A. A new approach to measure volatility in energy markets. Entropy 2012, 14, 74–91. [Google Scholar] [CrossRef]
- Ahn, K.; Lee, D.; Sohn, S.; Yang, B. Stock market uncertainty and economic fundamentals: An entropy-based approach. Quant. Financ. 2019, 19, 1151–1163. [Google Scholar] [CrossRef]
- Liang, X. The Liang-Kleeman information flow: Theory and applications. Entropy 2013, 15, 327–360. [Google Scholar] [CrossRef]
- Marschinski, R.; Kantz, H. Analysing the information flow between financial time series. Eur. Phys. J. B 2002, 30, 275–281. [Google Scholar] [CrossRef]
- Dimpfl, T.; Peter, F.J. Using transfer entropy to measure information flows between financial markets. Stud. Nonlinear Dyn. Econom. 2013, 17, 85–102. [Google Scholar] [CrossRef]
- Sandoval, L., Jr. Structure of a global network of financial companies based on transfer entropy. Entropy 2014, 16, 4443–4482. [Google Scholar] [CrossRef]
- Risso, W.A. Chapter 8: Symbolic Time Series Analysis and its Application in Social Sciences. In Time Series Analysis and Applications; Mohamudally, N., Ed.; InTech: Croatia, Balkans, 2018; pp. 107–125. [Google Scholar] [CrossRef][Green Version]
- Horowitz, J.L. Bootstrap methods for Markov processes. Econometrica 2003, 71, 1049–1082. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Wei, Y.M. The crude oil market and the gold market: Evidence for cointegration, causality and price discovery. Resour. Policy 2010, 35, 168–177. [Google Scholar] [CrossRef]
- Ajayi, R.A.; Friedman, J.; Mehdian, S.M. On the relationship between stock returns and exchange rates: Tests of Granger causality. Glob. Financ. J. 1998, 9, 241–251. [Google Scholar] [CrossRef]
- Rehman, M.U.; Apergis, N. Determining the predictive power between cryptocurrencies and real time commodity futures: Evidence from quantile causality tests. Resour. Policy 2019, 61, 603–616. [Google Scholar] [CrossRef]
- Gencaga, D.; Knuth, K.H.; Rossow, W.B. A recipe for the estimation of information flow in a dynamical system. Entropy 2015, 17, 438–470. [Google Scholar] [CrossRef]
- Razak, F.A.; Jensen, H.J. Quantifying ‘causality’ in complex systems: Understanding transfer entropy. PLoS ONE 2014, 9, 9462. [Google Scholar] [CrossRef]
- Staniek, M.; Lehnertz, K. Symbolic Transfer Entropy. Phys. Rev. Lett. 2008, 100, 8101. [Google Scholar] [CrossRef]
- Mantegna, R.N.; Stanley, H.E. An Introduction to Econophysics: Correlations and Complexity in Finance, 1st ed.; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Kwon, O.; Yang, J.S. Information flow between stock indices. Europhys. Lett. 2008, 82, 8003. [Google Scholar] [CrossRef]
- Pele, D.T.; Mazurencu-Marinescu-Pele, M. Using high-frequency entropy to forecast Bitcoin’s daily Value at Risk. Entropy 2019, 21, 102. [Google Scholar] [CrossRef]
- Drożdż, S.; Gȩbarowski, R.; Minati, L.; Oświȩcimka, P.; Wa̧torek, M. Bitcoin market route to maturity? Evidence from return fluctuations, temporal correlations and multiscaling effects. Chaos 2018, 28, 6517. [Google Scholar] [CrossRef]
| Min. | Max. | Mean | Std. | Skewness | Kurtosis | |
|---|---|---|---|---|---|---|
| Bitcoin | ||||||
| S&P 500 | ||||||
| Gold | ||||||
| USD/EUR |
| Null Hypothesis (H0) | F-Statistics (p = 1) |
|---|---|
| Gold ↛ Bitcoin Bitcoin ↛ Gold | 0.04 2.83 * |
| S&P 500 ↛ Bitcoin Bitcoin ↛ S&P 500 | 2.88 * 3.24 * |
| USD/EUR ↛ Bitcoin Bitcoin ↛ USD/EUR | 0.84 0.08 |
| Jarque–Bera | Skewness | Kurtosis | |
|---|---|---|---|
| *** | * | *** | |
| *** | *** | *** | |
| *** | *** | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jang, S.M.; Yi, E.; Kim, W.C.; Ahn, K. Information Flow between Bitcoin and Other Investment Assets. Entropy 2019, 21, 1116. https://doi.org/10.3390/e21111116
Jang SM, Yi E, Kim WC, Ahn K. Information Flow between Bitcoin and Other Investment Assets. Entropy. 2019; 21(11):1116. https://doi.org/10.3390/e21111116
Chicago/Turabian StyleJang, Sung Min, Eojin Yi, Woo Chang Kim, and Kwangwon Ahn. 2019. "Information Flow between Bitcoin and Other Investment Assets" Entropy 21, no. 11: 1116. https://doi.org/10.3390/e21111116
APA StyleJang, S. M., Yi, E., Kim, W. C., & Ahn, K. (2019). Information Flow between Bitcoin and Other Investment Assets. Entropy, 21(11), 1116. https://doi.org/10.3390/e21111116






