Application of Spherical-Radial Cubature Bayesian Filtering and Smoothing in Bearings Only Passive Target Tracking
Abstract
:1. Introduction
2. Passive Target Tracking System Model
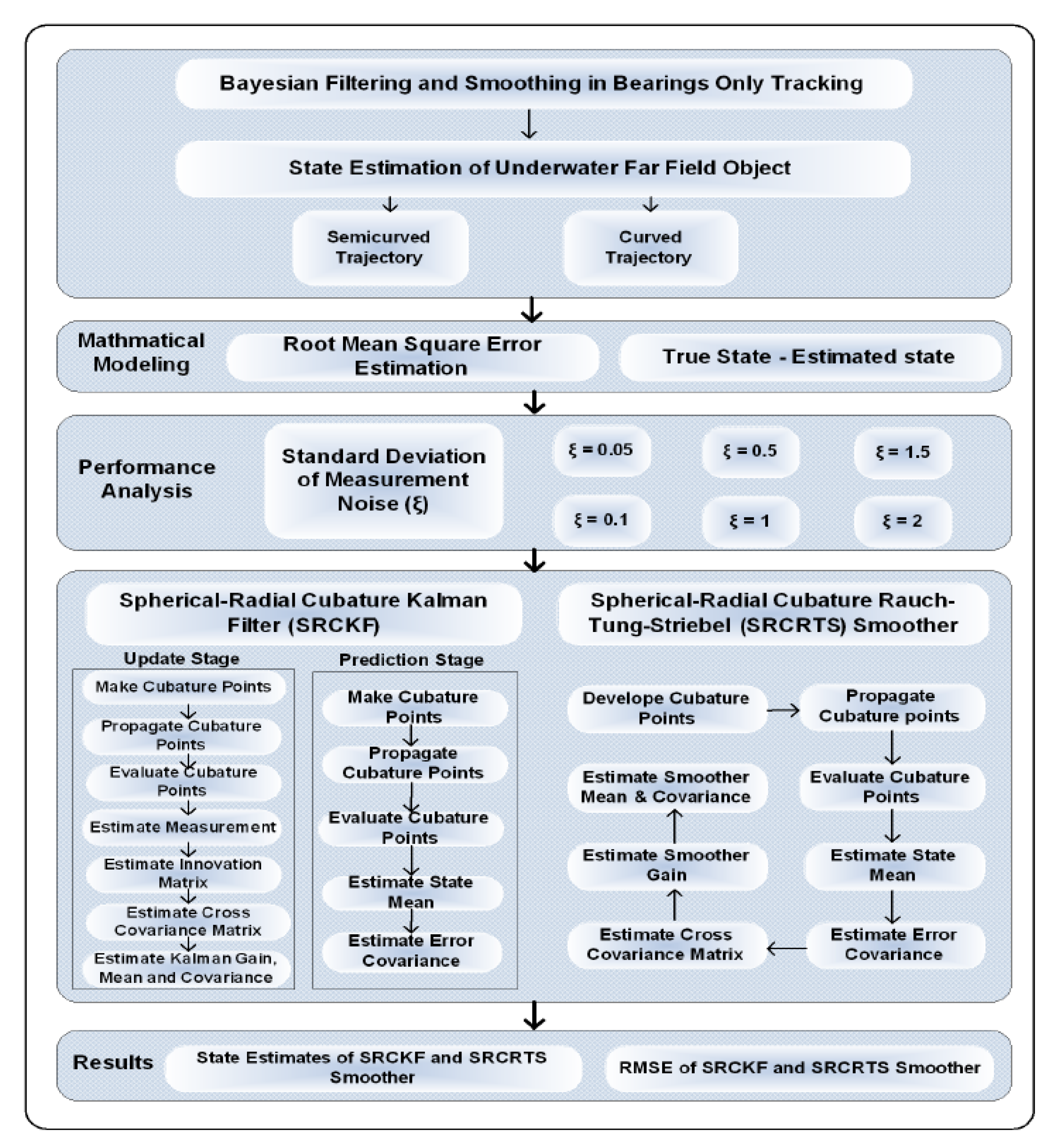
3. Bayesian Filtering and Smoothing Algorithms
3.1. Spherical-Radial Cubature Kalman Filter
- Prediction Phase:
- 1.
- Pick cubature points , while = 1,…,2 from the interchange of the size unit sphere and Cartesian coordinates. Adjust these points by shown as:
- 2.
- Transmit the cubature points in a state-space dynamic model. The lower triangular Cholesky factor is shown in a square root matrix as:
- 3.
- Then, assess the cubature points with the dynamic model function as:
- 4.
- The predicted state mean is computed as:
- 5.
- The predicted error covariance is calculated as:
- Update Phase:
- 1.
- In the first step of the measurement update phase, again develop cubature points , where = 1,…,2 from the relationship of the length unit sphere and the x–y axes. Calibrate them by .
- 2.
- Circulate the cubature points in state equation of dynamic model as:
- 3.
- Classify these cubature points owing to the state equation of the measurement model function as:
- 4.
- Predicted measurement is approximated as:
- 5.
- Then, the innovation covariance matrix is computed as:
- 6.
- The cross-covariance matrix is estimated as:
- 7.
- In the final step gain of the filter, state mean and state covariance terms are calculated as:
3.2. Spherical-Radial Cubature Rauch–Tung–Striebel Smoother
- 1.
- Make cubature points , while = 1,…,2 from the junction of the size unit sphere and the Cartesian coordinates. Regulate cubature points by shown as:
- 2.
- Cubature points are circulated in state space equation as:
- 3.
- Then, cubature points are checked with the dynamic model function as:
- 4.
- Predict state mean as:
- 5.
- Predict error covariance as:
- 6.
- Cross-covariance matrix is computed as:
- 7.
- Smoother gain is computed together with the smoother state mean and covariance as:
4. Simulation and Results
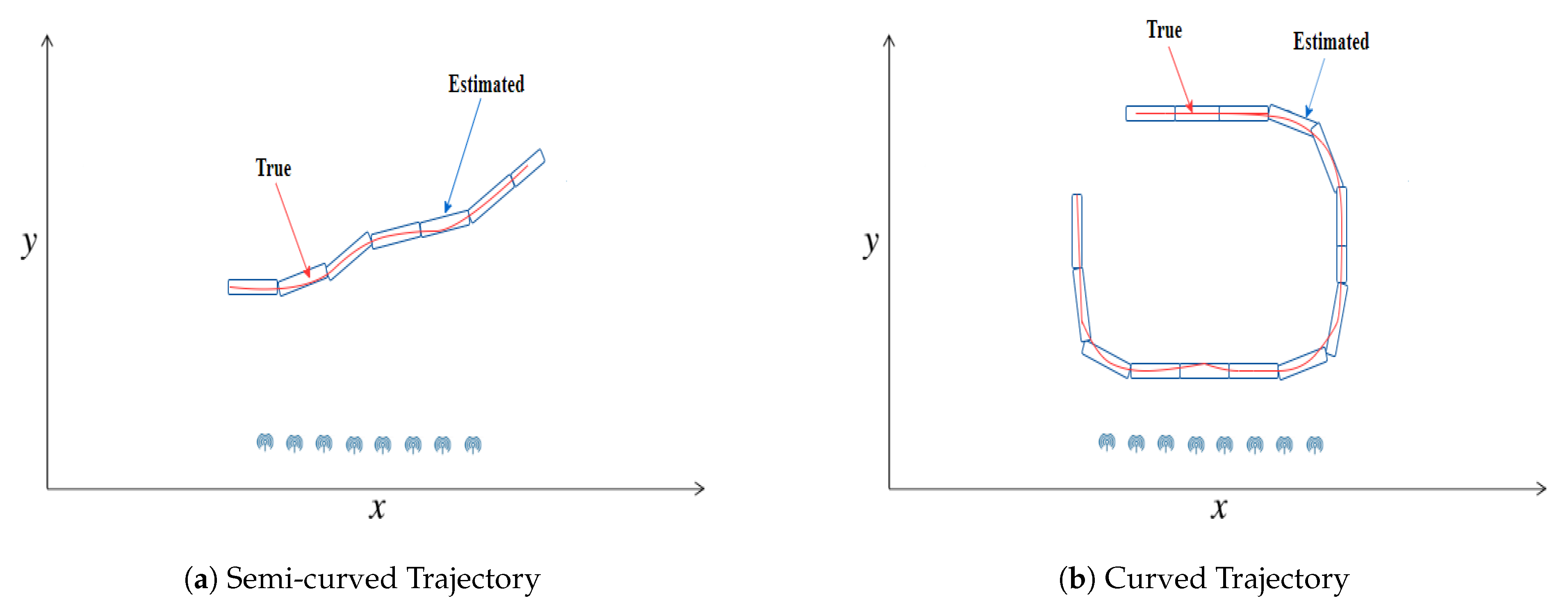
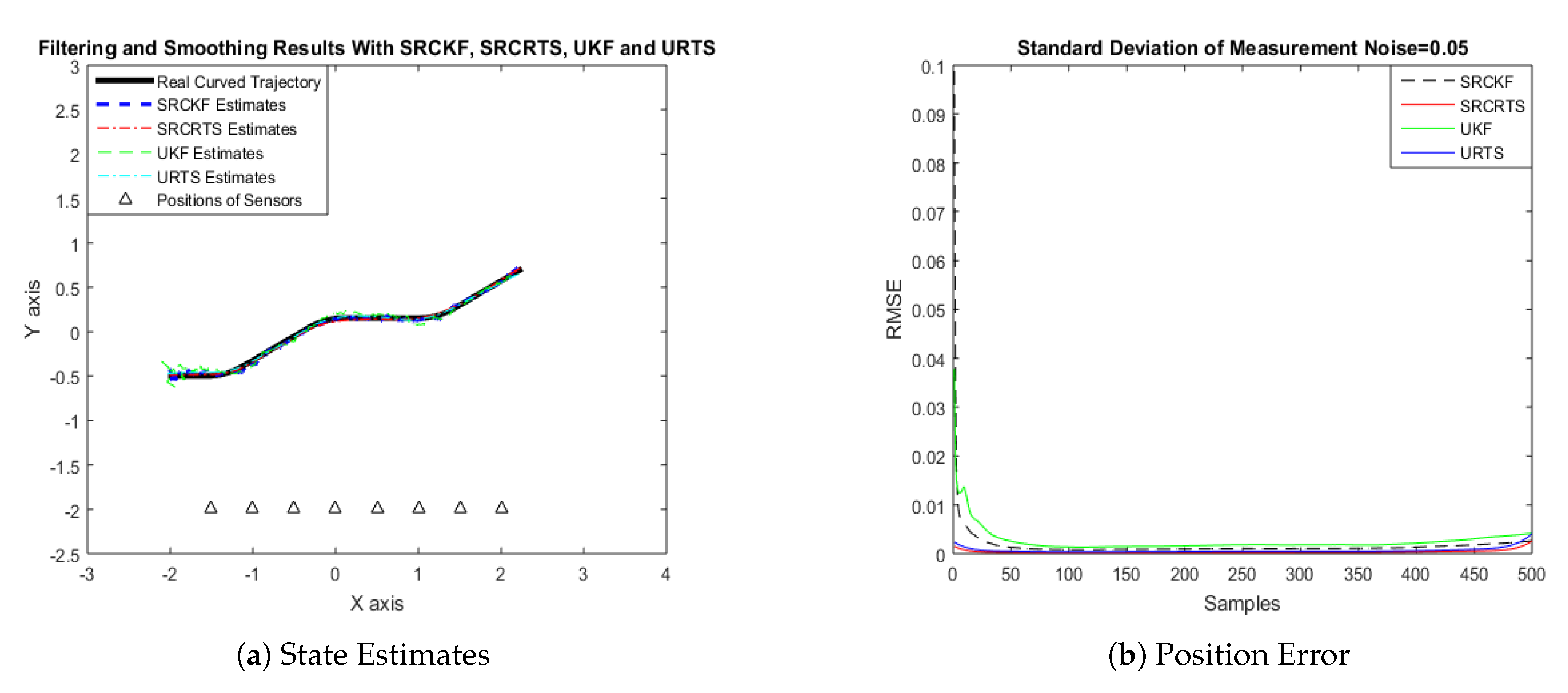
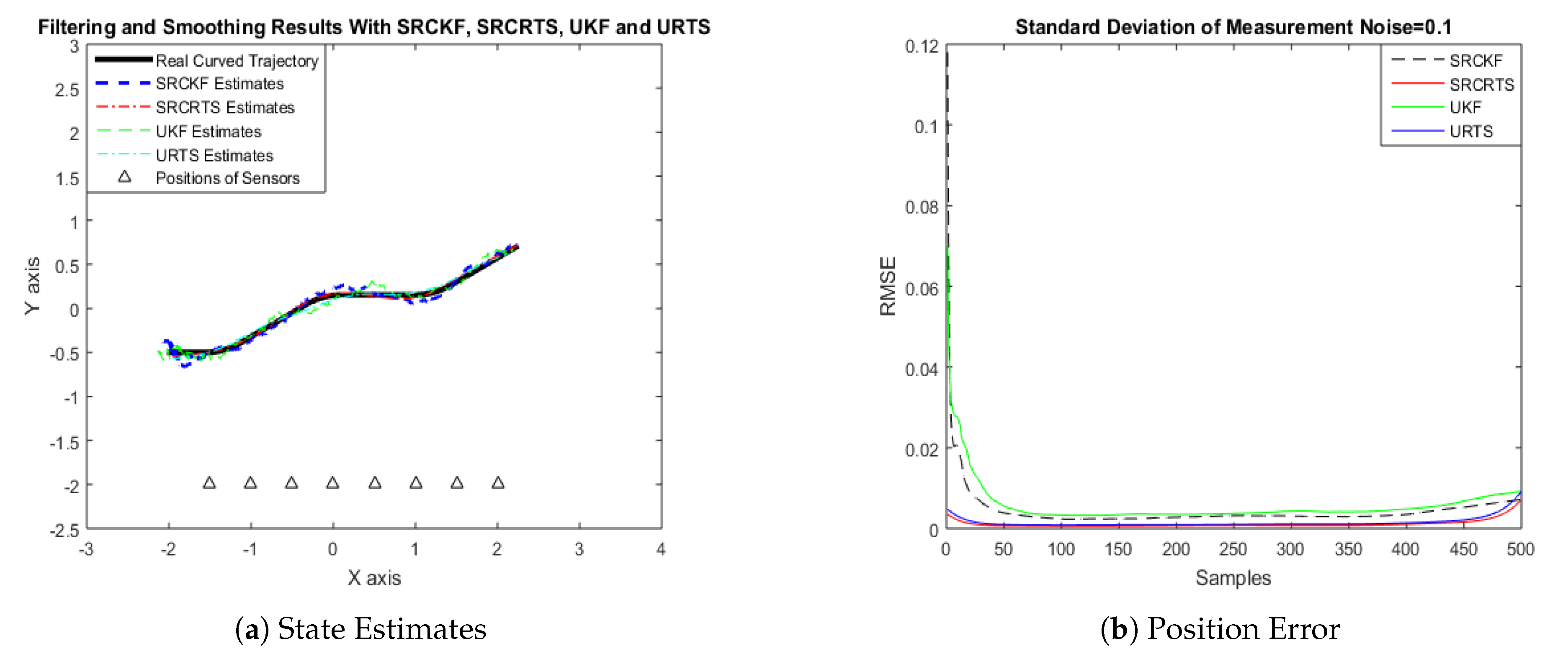
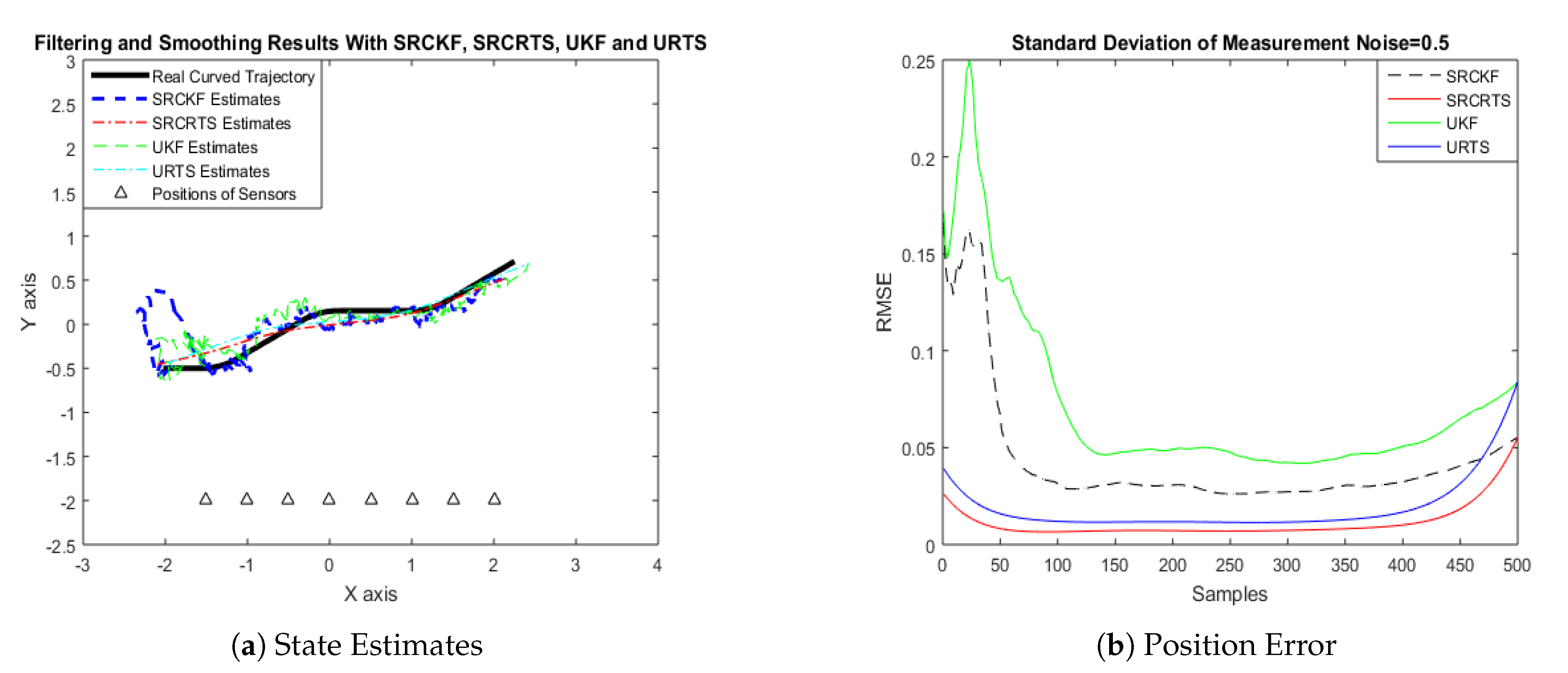
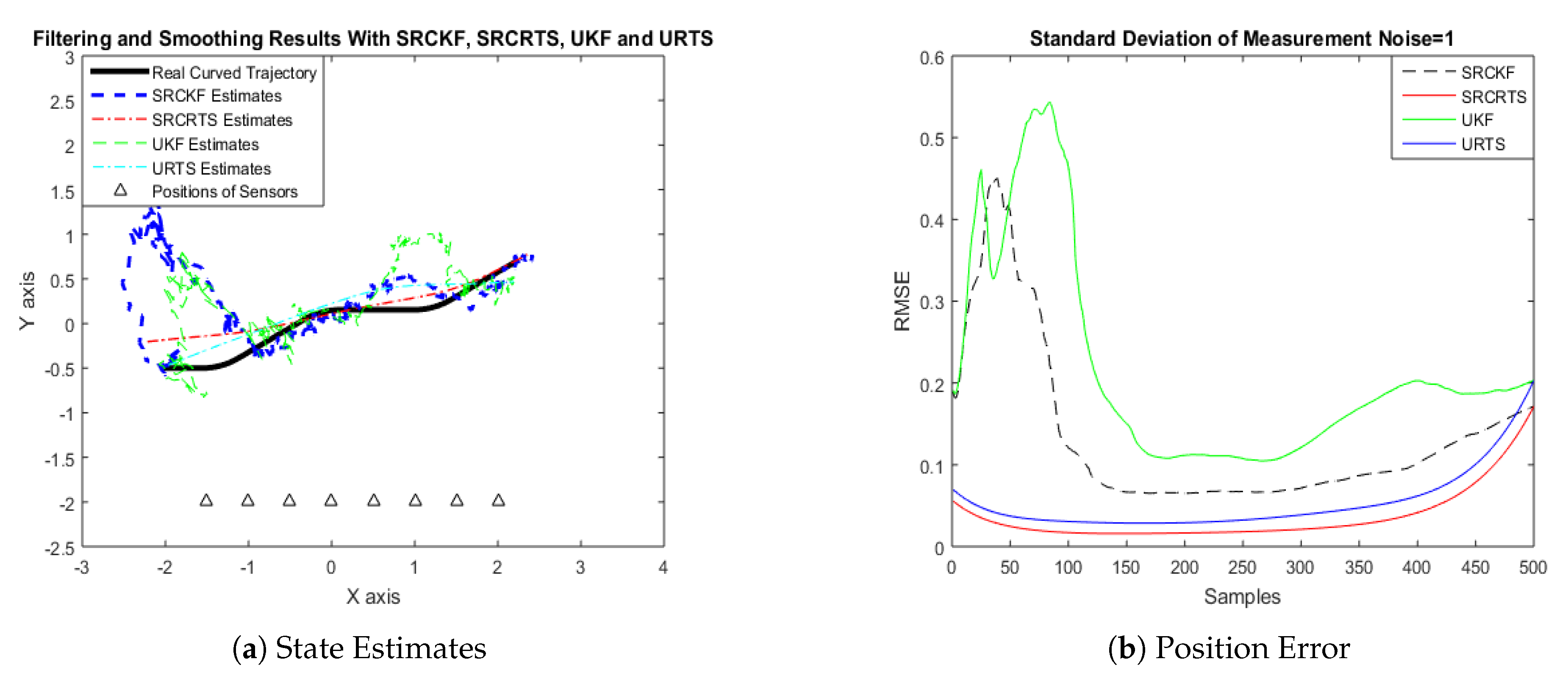
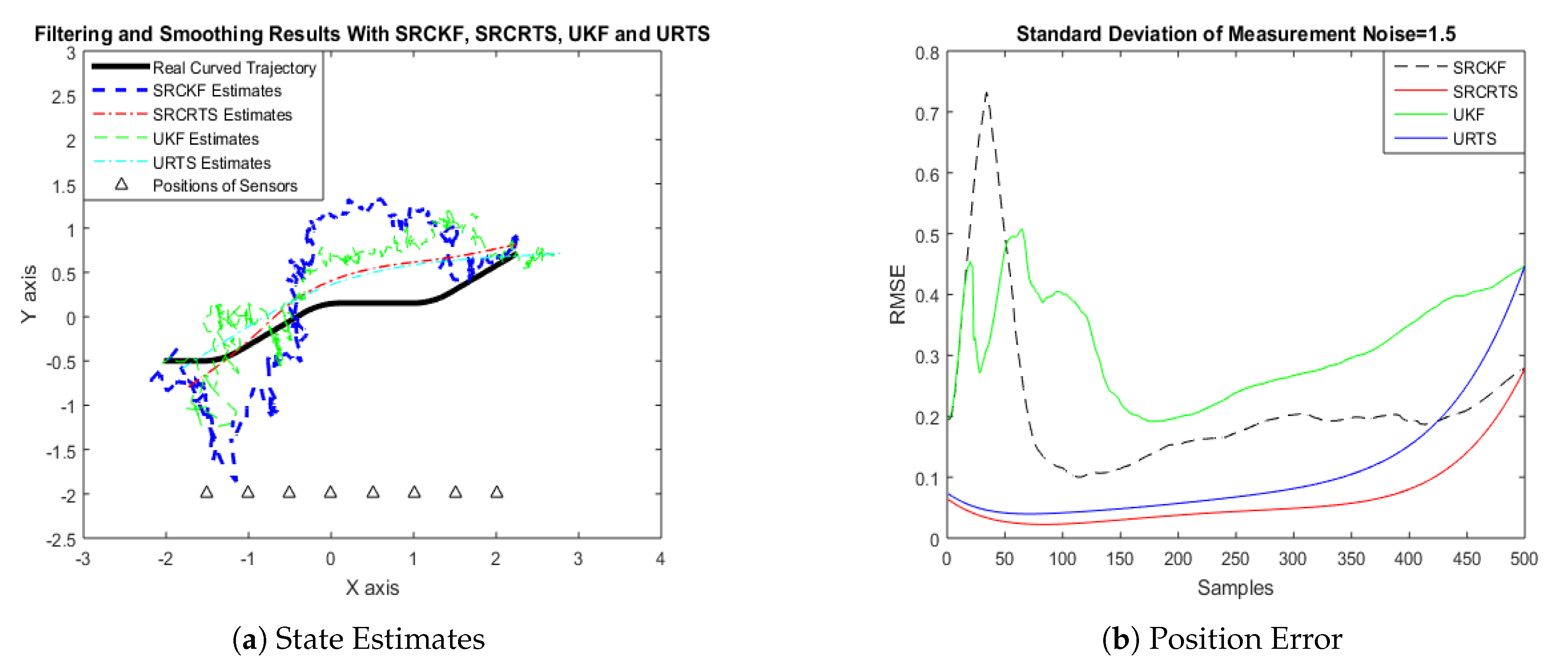
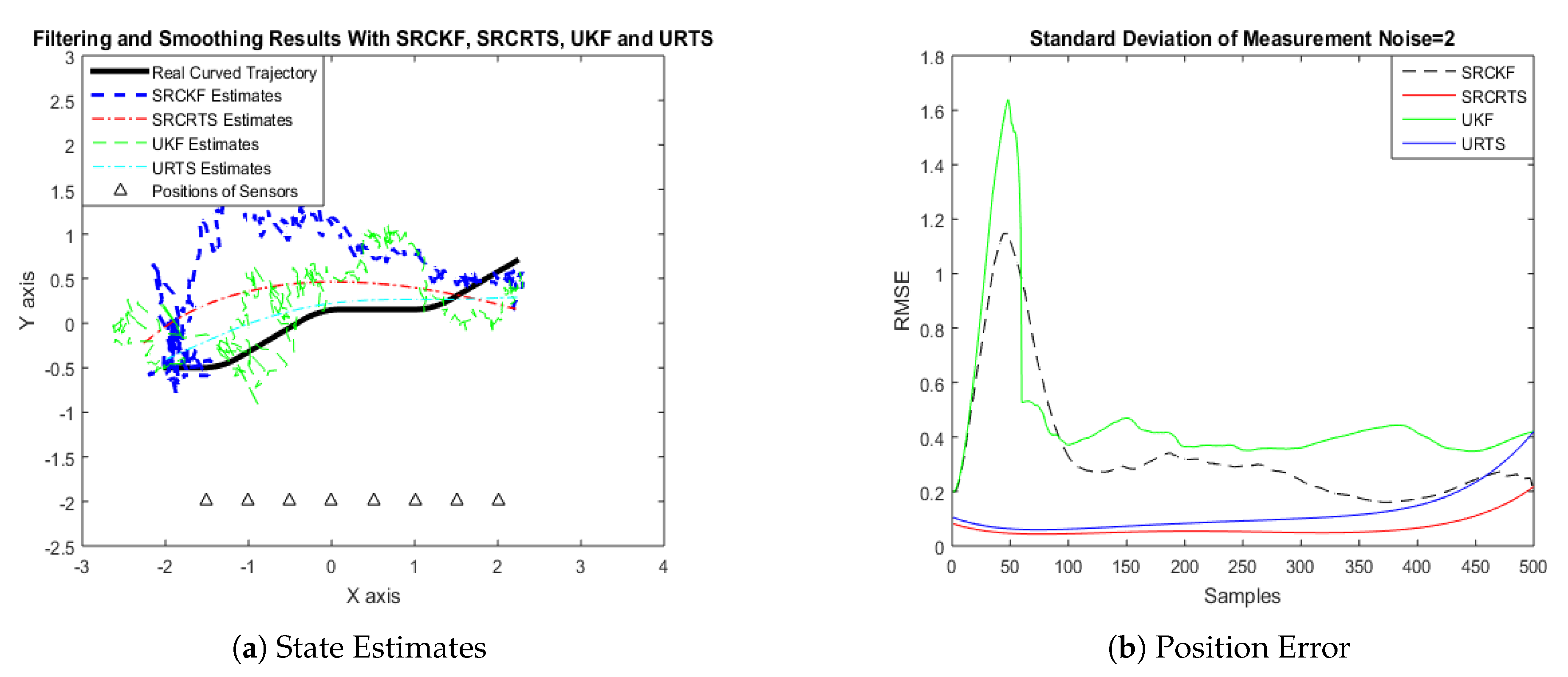
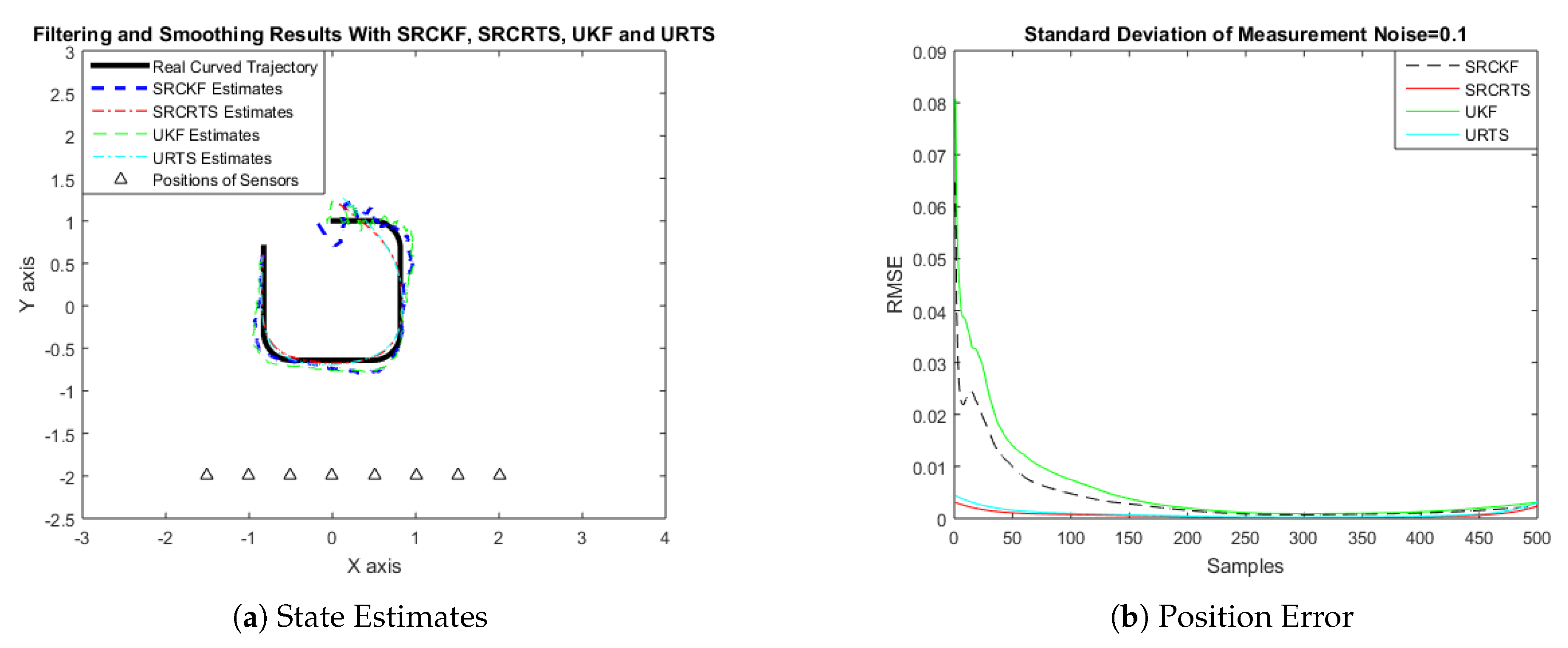
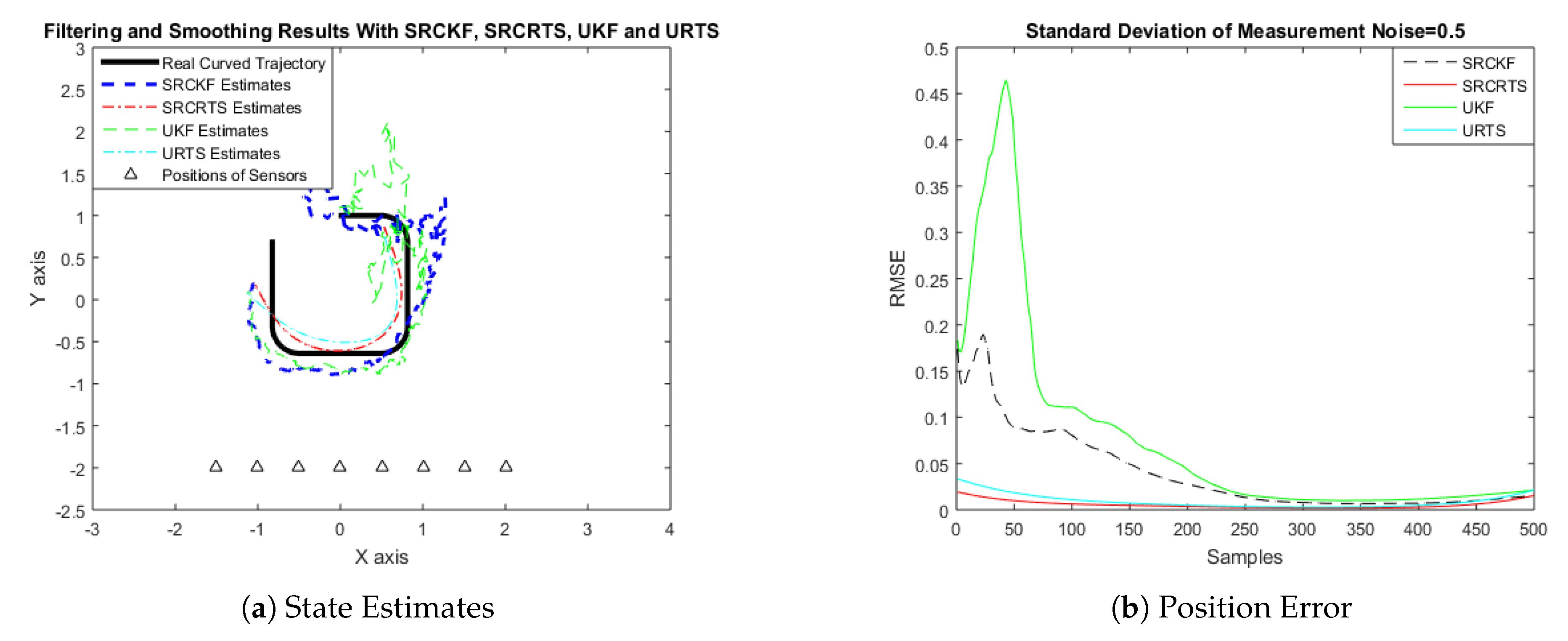
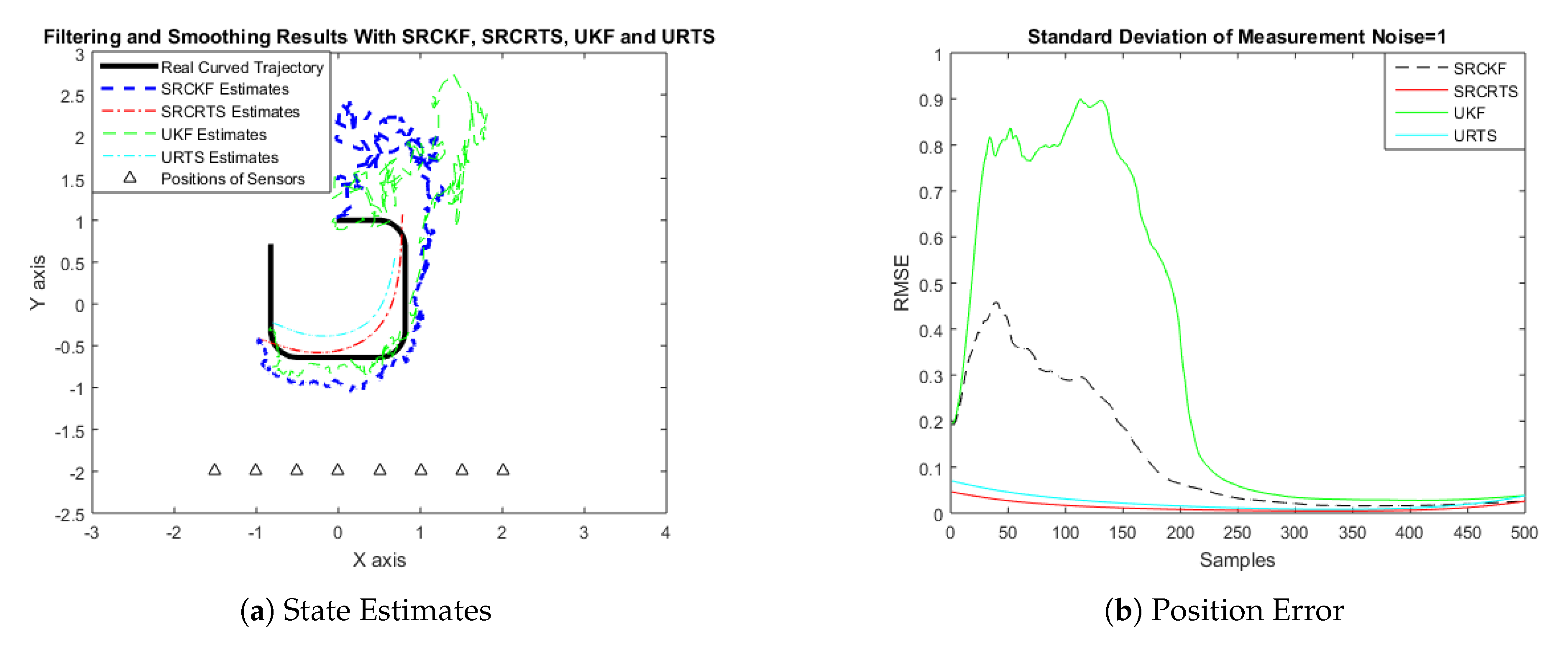
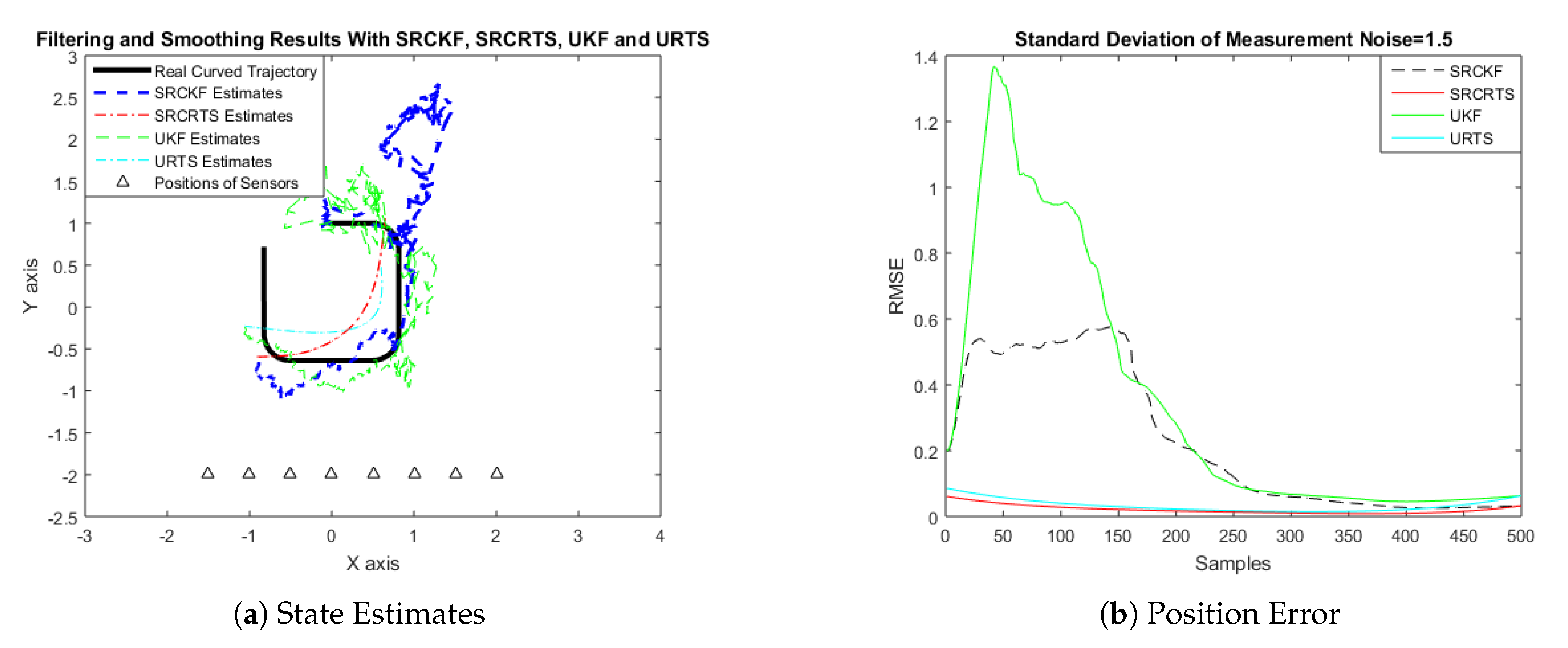
4.1. State Estimation of Semi-Curved Trajectory with Respect to Standard Deviation of Measurement Noise
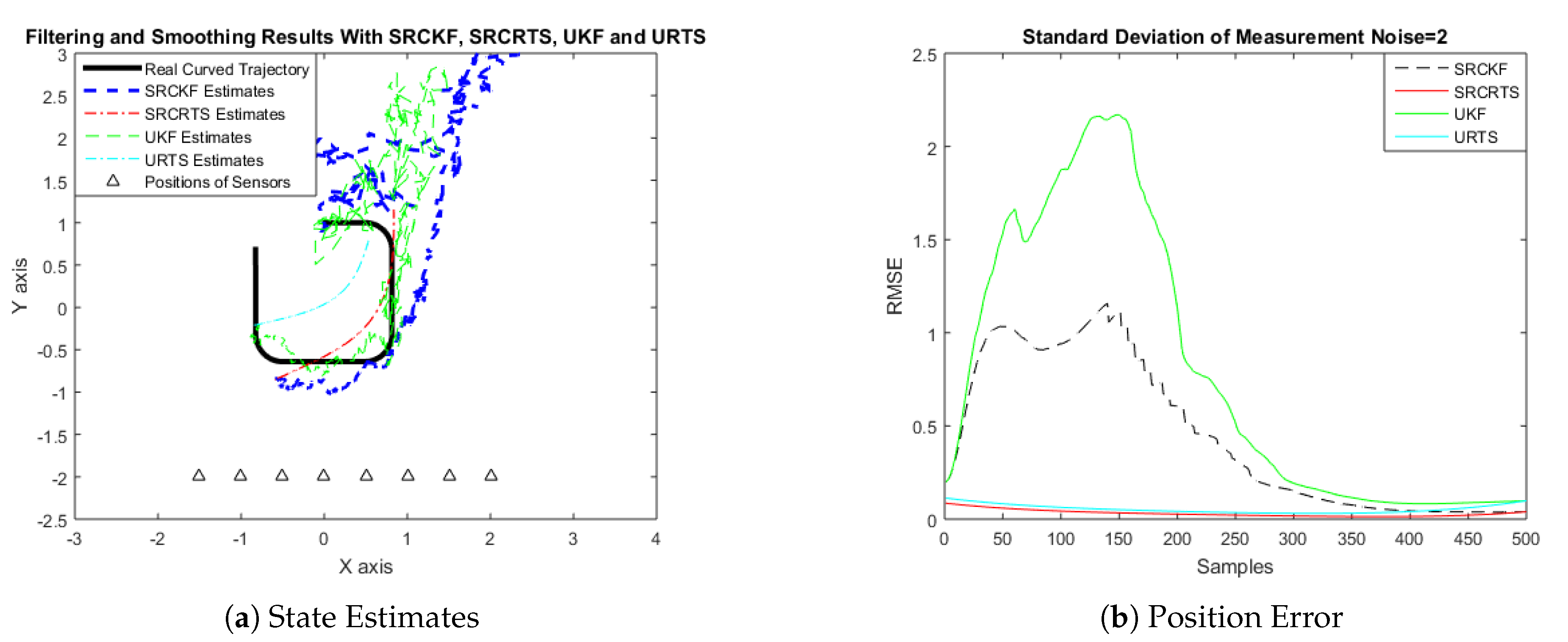
4.2. State Estimation of a Curved Trajectory with Respect to the Standard Deviation of Measurement Noise
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Luo, J.; Han, Y.; Fan, L. Underwater acoustic target tracking: A review. Sensors 2018, 18, 112. [Google Scholar] [CrossRef]
- Pesonen, H.; Piché, R. Novel cubature Kalman filters based on mixed degrees. In Proceedings of the 2015 Sixth International Conference on Intelligent Control and Information Processing (ICICIP), Wuhan, China, 26–28 November 2015; pp. 220–224. [Google Scholar]
- Duník, J.; Straka, O.; Šimandl, M. Stochastic integration filter. IEEE Trans. Autom. Control 2013, 58, 1561–1566. [Google Scholar] [CrossRef]
- Jia, B.; Xin, M.; Cheng, Y. High-degree cubature Kalman filter. Automatica 2013, 49, 510–518. [Google Scholar] [CrossRef]
- Arasaratnam, I.; Haykin, S. Cubature Kalman filters. IEEE Trans. Autom. Control 2009, 54, 1254–1269. [Google Scholar] [CrossRef]
- Pesonen, H.; Piché, R. Cubature-based Kalman filters for positioning. In Proceedings of the 2010 7th Workshop on Positioning, Navigation and Communication, Dresden, Germany, 11–12 March 2010; pp. 45–49. [Google Scholar]
- Li, Y.; Cheng, Y.; Li, X.; Wang, H.; Hua, X.; Qin, Y. Bayesian Nonlinear Filtering via Information Geometric Optimization. Entropy 2017, 19, 655. [Google Scholar] [CrossRef]
- Wang, S.; Feng, J.; Chi, K.T. Spherical simplex-radial cubature Kalman filter. IEEE Signal Process. Lett. 2013, 21, 43–46. [Google Scholar] [CrossRef]
- Jia, B.; Xin, M.; Cheng, Y. Relations between sparse-grid quadrature rule and spherical-radial cubature rule in nonlinear Gaussian estimation. IEEE Trans. Autom. Control 2014, 60, 199–204. [Google Scholar] [CrossRef]
- Ristic, B.; Arulampalam, S.; Gordon, N. Beyond the Kalman Filter: Particle Filters for Tracking Applications; Artech House: London, UK, 2004. [Google Scholar]
- Karlsson, R.; Gustafsson, F. Recursive Bayesian estimation: Bearings-only applications. Proc.-Radar Sonar Navig. 2005, 152, 305–313. [Google Scholar] [CrossRef]
- Zhang, H.; de Saporta, B.; Dufour, F.; Laneuville, D.; Nègre, A. Stochastic control of observer trajectories in passive tracking with acoustic signal propagation optimisation. IET Radar Sonar Navig. 2017, 12, 112–120. [Google Scholar] [CrossRef]
- Alexandri, T.; Diamant, R. A reverse bearings only target motion analysis (BO-TMA) for improving AUV navigation accuracy. In Proceedings of the 2016 13th Workshop on Positioning, Navigation and Communications (WPNC), Bremen, Germany, 19–20 October 2016; pp. 1–5. [Google Scholar]
- Ullah, I.; Qureshi, M.; Khan, U.; Memon, S.; Shi, Y.; Peng, D. Multisensor-Based Target-Tracking Algorithm with Out-of-Sequence-Measurements in Cluttered Environments. Sensors 2018, 18, 4043. [Google Scholar] [CrossRef]
- Saeidi, G.; Moniri, M.R. Bearings-Only Tracking of Manoeuvring Targets Using Multiple Model Variable Rate Particle Filter with Differential Evolution. Asia Pac. J. Energy Environ. 2014, 1, 200–214. [Google Scholar] [CrossRef]
- He, R.; Chen, S.; Wu, H.; Xu, H.; Chen, K.; Liu, J. Adaptive Covariance Feedback Cubature Kalman Filtering for Continuous-Discrete Bearings-Only Tracking System. IEEE Access 2018, 7, 2686–2694. [Google Scholar] [CrossRef]
- Leung, H.; Zhu, Z.; Ding, Z. An aperiodic phenomenon of the extended Kalman filter in filtering noisy chaotic signals. IEEE Trans. Signal Process. 2000, 48, 1807–1810. [Google Scholar] [CrossRef]
- Julier, S.J.; Uhlmann, J.K. Unscented filtering and nonlinear estimation. Proc. IEEE 2004, 92, 401–422. [Google Scholar] [CrossRef]
- Gustafsson, F.; Hendeby, G. Some relations between extended and unscented Kalman filters. IEEE Trans. Signal Process. 2011, 60, 545–555. [Google Scholar] [CrossRef]
- Arasaratnam, I.; Haykin, S.; Elliott, R.J. Discrete-time nonlinear filtering algorithms using Gauss–Hermite quadrature. Proc. IEEE 2007, 95, 953–977. [Google Scholar] [CrossRef]
- Zarei, J.; Shokri, E.; Karimi, H.R. Convergence analysis of cubature Kalman filter. In Proceedings of the 2014 European Control Conference (ECC), Strasbourg, France, 24–27 June 2014; pp. 1367–1372. [Google Scholar]
- Zhang, X.; Teng, Y. A new derivation of the cubature Kalman filters. Asian J. Control 2014, 16, 1501–1510. [Google Scholar] [CrossRef]
- Hu, C.; Lin, H.; Li, Z.; He, B.; Liu, G. Kullback–Leibler divergence based distributed cubature Kalman filter and its application in cooperative space object tracking. Entropy 2018, 20, 116. [Google Scholar] [CrossRef]
- Ito, K. Gaussian filter for nonlinear filtering problems. In Proceedings of the 39th IEEE Conference on Decision and Control, Sydney, Australia, 12–15 December 2000; Volume 2, pp. 1218–1223. [Google Scholar]
- Jia, B.; Xin, M.; Cheng, Y. Sparse-grid quadrature nonlinear filtering. Automatica 2012, 48, 327–341. [Google Scholar] [CrossRef]
- Leong, P.H.; Arulampalam, S.; Lamahewa, T.A.; Abhayapala, T.D. A Gaussian-sum based cubature Kalman filter for bearings-only tracking. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 1161–1176. [Google Scholar] [CrossRef]
- Kulikov, G.Y.; Kulikova, M.V. Accurate continuous–discrete unscented Kalman filtering for estimation of nonlinear continuous-time stochastic models in radar tracking. Signal Process. 2017, 139, 25–35. [Google Scholar] [CrossRef]
- Li, X.; Zhao, C.; Yu, J.; Wei, W. Underwater Bearing-Only and Bearing-Doppler Target Tracking Based on Square Root Unscented Kalman Filter. Entropy 2019, 21, 740. [Google Scholar] [CrossRef]
- Hu, K.; Wang, P.; Zhou, I.-K.; Zeng, H.; Fang, V. Weak Target Tracking Based on Improved Particle Filter Algorithm. In Proceedings of the 2018 IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2018), Valencia, Spain, 22–27 July 2018; pp. 2769–2772. [Google Scholar]
- Radhakrishnan, R.; Bhaumik, S.; Tomar, N.K. Continuous-discrete shifted Rayleigh filter for underwater passive bearings-only target tracking. In Proceedings of the 2017 11th Asian Control Conference (ASCC), Gold Coast, Australia, 17–20 December 2017; pp. 795–800. [Google Scholar]
- Xu, Y.; Xu, K.; Wan, J.; Xiong, Z.; Li, Y. Research on Particle Filter Tracking Method Based on Kalman Filter. In Proceedings of the 2018 2nd IEEE Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Xi’an, China, 25–27 May 2018; pp. 1564–1568. [Google Scholar]
- Singh, A.K.; Kumar, K.; Swati; Bhaumik, S. Cubature and Quadrature Based Continuous-Discrete Filters for Maneuvering Target Tracking. In Proceedings of the 2018 21st International Conference on Information Fusion (FUSION), Cambridge, UK, 10–13 July 2018; pp. 1–8. [Google Scholar]
- Radhakrishnan, R.; Singh, AK.; Bhaumik, S.; Tomar, N.K. Quadrature filters for underwater passive bearings-only target tracking. In Proceedings of the 2015 Sensor Signal Processing for Defence (SSPD), Edinburgh, UK, 9–10 September 2015; pp. 1–5. [Google Scholar]
- Cui, N.; Hong, L.; Layne, J.R. A comparison of nonlinear filtering approaches with an application to ground target tracking. Signal Process. 2005, 85, 1469–1492. [Google Scholar] [CrossRef]
- Katkuri, J.R.; Jilkov, V.P.; Li, X.R. A comparative study of nonlinear filters for target tracking in mixed coordinates. In Proceedings of the 2010 42nd Southeastern Symposium on System Theory (SSST), Tyler, TX, USA, 7–9 March 2010; pp. 202–207. [Google Scholar]
- Li, Y.; Zhao, Z. Passive Tracking of Underwater Targets Using Dual Observation Stations. In Proceedings of the 2019 16th International Bhurban Conference on Applied Sciences and Technology (IBCAST), Islamabad, Pakistan, 8–12 January 2019; pp. 867–872. [Google Scholar]
- Han, B.; Huang, H.; Lei, L.; Huang, C.; Zhang, Z. An Improved IMM Algorithm Based on STSRCKF for Maneuvering Target Tracking. IEEE Access 2019, 7, 57795–57804. [Google Scholar] [CrossRef]
- Masoumi-Ganjgah, F.; Fatemi-Mofrad, R.; Ghadimi, N. Target tracking with fast adaptive revisit time based on steady state IMM filter. Digital Signal Process. 2017, 69, 154–161. [Google Scholar] [CrossRef]
- Vasuhi, S.; Vaidehi, V. Target tracking using interactive multiple model for wireless sensor network. Inf. Fusion 2016, 27, 41–53. [Google Scholar] [CrossRef]
- Jia, B.; Blasch, E.; Pham, K.D.; Shen, D.; Wang, Z.; Tian, X.; Chen, G. Space object tracking and maneuver detection via interacting multiple model cubature Kalman filters. In Proceedings of the 2015 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2015; pp. 1–8. [Google Scholar]
- Li, Y.; Chen, X.; Yu, J.; Yang, X.; Yang, H. The Data-Driven Optimization Method and Its Application in Feature Extraction of Ship-Radiated Noise with Sample Entropy. Energies 2019, 12, 359. [Google Scholar] [CrossRef]
- Li, Y.; Chen, X.; Yu, J.; Yang, X. TA Fusion Frequency Feature Extraction Method for Underwater Acoustic Signal Based on Variational Mode Decomposition, Duffing Chaotic Oscillator and a Kind of Permutation Entropy. Electronics 2019, 8, 61. [Google Scholar] [CrossRef]
- Wiener, N. The Extrapolation, Interpolation and Smoothing of Stationary Time Series; John Wiley & Sons, Inc.: New York, NY, USA, 1949. [Google Scholar]
- Rauch, H.E.; Striebel, C.T.; Tung, F. Maximum likelihood estimates of linear dynamic systems. AIAA J. 1965, 3, 1445–1450. [Google Scholar] [CrossRef]
- Sarkka, S.; Hartikainen, J. On Gaussian optimal smoothing of nonlinear state space models. IEEE Trans. Autom. Control 2010, 55, 1938–1941. [Google Scholar] [CrossRef]
- Wang, Y. Position estimation using extended kalman filter and RTS-smoother in a GPS receiver. In Proceedings of the 2012 5th International Congress on Image and Signal Processing, Chongqing, China, 16–18 October 2012; pp. 1718–1721. [Google Scholar]
- Belinska, V.; Kluga, A.; Kluga, J. Application of Rauch-Tung and Striebel smoother algorithm for accuracy improvement. In Proceedings of the 13th Biennial Baltic Electronics Conference (BEC), Tallinn, Estonia, 3–5 October 2012. [Google Scholar]
- Chan, W.-L.; Hsiao, F.-B. Implementation of the rauch-tung-striebel smoother for sensor compatibility correction of a fixed-wing unmanned air vehicle. Sensors 2011, 11, 3738–3764. [Google Scholar] [CrossRef]
- Bar-Shalom, Y.; Li, X.-R.; Kirubarajan, T. Estimation with Applications to Tracking and Navigation; A Wiley-Interscience Publication: Hoboken, NJ, USA, 2001. [Google Scholar]
- Chaudhary, N.I.; Raja, M.A.Z.; Aslam, M.S.; Ahmed, N. Novel generalization of Volterra LMS algorithm to fractional order with application to system identification. Neural Comput. Appl. 2018, 29, 41–58. [Google Scholar] [CrossRef]
- Chaudhary, N.I.; Aslam, M.S.; Raja, M.A.Z. Modified Volterra LMS algorithm to fractional order for identification of Hammerstein nonlinear system. IET Signal Process. 2017, 11, 975–985. [Google Scholar] [CrossRef]
- Aslam, M.S.; Chaudhary, N.I.; Raja, M.A.Z. A sliding-window approximation-based fractional adaptive strategy for Hammerstein nonlinear ARMAX systems. Nonlinear Dyn. 2017, 87, 519–533. [Google Scholar] [CrossRef]
- Chaudhary, N.I.; Aslam khan, Z.; Zubair, S.; Raja, M.A.Z.; Dedovic, N. Normalized fractional adaptive methods for nonlinear control autoregressive systems. Appl. Math. Model. 2019, 66, 457–471. [Google Scholar] [CrossRef]

| Parameters | Values |
|---|---|
| Initial location of target in coordinates | = |
| Location of array elements | (,) |
| Number of antennas | j = 8 |
| Spectral intensity of process noise | = 0.1 |
| Covariance of measurement noise | = = rad |
| Initial state covariance of cubature filter | = diag([0.1 0.1 … 10]) |
| Time duration | dt = 0.01 |
| Number of steps for target trajectory | 1 |
| Number of samples | 500 |
| Space between array elements | 0.5 |
| Noise (rad) | SRCKF RMSE (m) | SRCRTS RMSE (m) | UKF RMSE (m) | URTS RMSE (m) |
|---|---|---|---|---|
| = 0.05 | 0.0410 | 0.0195 | 0.0510 | 0.0255 |
| = 0.1 | 0.0675 | 0.0334 | 0.0762 | 0.0388 |
| = 0.5 | 0.2084 | 0.1063 | 0.2689 | 0.1367 |
| = 1 | 0.3661 | 0.1897 | 0.4632 | 0.2296 |
| = 1.5 | 0.4645 | 0.2531 | 0.5632 | 0.3290 |
| = 2 | 0.6254 | 0.2717 | 0.6841 | 0.3478 |
| Noise (rad) | SRCKF RMSE (m) | SRCRTS RMSE (m) | UKF RMSE (m) | URTS RMSE (m) |
|---|---|---|---|---|
| = 0.05 | 0.0351 | 0.0146 | 0.0479 | 0.0191 |
| = 0.1 | 0.0625 | 0.0249 | 0.0752 | 0.0292 |
| = 0.5 | 0.1984 | 0.0743 | 0.2756 | 0.0948 |
| = 1 | 0.3487 | 0.1138 | 0.5601 | 0.1488 |
| = 1.5 | 0.4776 | 0.1436 | 0.5912 | 0.1798 |
| = 2 | 0.6640 | 0.1755 | 0.8835 | 0.2318 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, W.; Li, Y.; Chen, Z.; Raja, M.A.Z.; Ahmed, N.; Chen, X. Application of Spherical-Radial Cubature Bayesian Filtering and Smoothing in Bearings Only Passive Target Tracking. Entropy 2019, 21, 1088. https://doi.org/10.3390/e21111088
Ali W, Li Y, Chen Z, Raja MAZ, Ahmed N, Chen X. Application of Spherical-Radial Cubature Bayesian Filtering and Smoothing in Bearings Only Passive Target Tracking. Entropy. 2019; 21(11):1088. https://doi.org/10.3390/e21111088
Chicago/Turabian StyleAli, Wasiq, Yaan Li, Zhe Chen, Muhammad Asif Zahoor Raja, Nauman Ahmed, and Xiao Chen. 2019. "Application of Spherical-Radial Cubature Bayesian Filtering and Smoothing in Bearings Only Passive Target Tracking" Entropy 21, no. 11: 1088. https://doi.org/10.3390/e21111088
APA StyleAli, W., Li, Y., Chen, Z., Raja, M. A. Z., Ahmed, N., & Chen, X. (2019). Application of Spherical-Radial Cubature Bayesian Filtering and Smoothing in Bearings Only Passive Target Tracking. Entropy, 21(11), 1088. https://doi.org/10.3390/e21111088






