The methodology implemented for the comparative study of causality measures aiming at evaluating the measures and ranking them as to their accuracy in identifying correctly the underlying coupling network is presented here. The methodology includes the causality measures compared in the study, the techniques for the identification of network connections from each measure, the statistical evaluation of the accuracy of each measure in identifying the original coupling network, and the formation of an appropriate score index for the overall performance of each measure. Finally, the synthetic systems used in the simulation study are presented.
2.1. Causality Measures
First, it is noted that in this comparative study correlation or in general symmetric measures of
X and
Y are not considered. Many such measures were initially included in the study, e.g., many phase-based measures such as phase locking value (PLV) [
67], phase lag index (PLI) [
68] and weighted phase lag index (wPLI) [
69], rho index (RHO) [
70], phase slope index (PSI) [
31], and mean phase coherence (MPC) [
71]. However, their evaluation in the designed framework is not possible as the identification of the exact directed connections of the original coupling network is quantified to assess the measure performance.
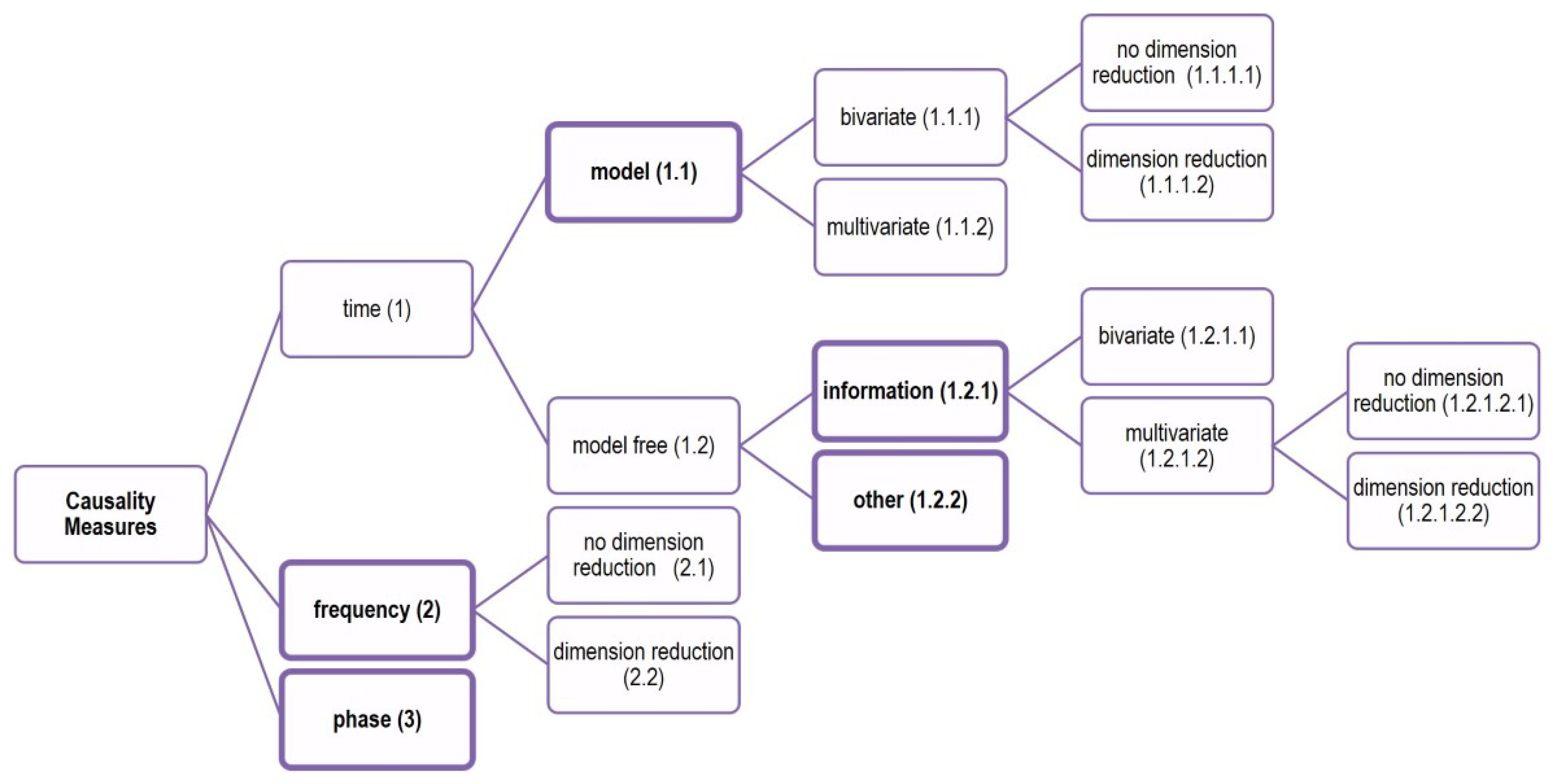
Causality measures can be divided in three categories as to the domain of data representation they are defined in: time, frequency, and phase (see
Figure 1).
The measures in time domain dominate and they are further divided in model-based and model-free measures. Many of the model-free measures are based on information theory measures and the other model-free measures on the time domain are referred to as “other” measures. Thus, five main classes of causality measures are considered in this study: model-based measures, information measures, frequency measures, phase measures, and other measures that cannot be defined in terms of the other four classes. The measures organized in these five classes and included in the comparative study are briefly discussed below, and they are listed in
Table 1, with reference and code number denoting the type of measure (the class, bivariate or multivariate and with our without dimension reduction).
The first class of model-based measures regards measures that implement the original concept of Granger causality, the bivariate measure of Granger causality index (GCI) [
3] (only
X and
Y variables are considered), and the multivariate measures of the conditional Granger causality index (CGCI) [
22] and the partial Granger causality (PGCI) [
72] (also the other observed variables denoted
Z are included). All these measures require the fit of a vector autoregressive model (VAR), on the two or more variables. The order
p of VAR denoting the lagged variables of each variable contained in the model can be estimated by an information criterion such as the Akaike information criterion (AIC) and the Bayesian Information Criterion (BIC), which often does not provide optimal lags, e.g., see the simulation study in [
83] and citations therein, and the so-called
p-hacking (in the sense of
p-value) in terms of VAR models for Granger causality in [
84]. To overcome the use of order estimation criteria, here we use a couple of predefined appropriate orders
p for each system (see
Table 1). In the presence of many observed variables, dimension reduction in VAR has been proposed, and here we use the one developed from our team, the restricted conditional Granger causality index (RCGCI) [
43]. Thus, for this class of measures, there are bivariate and multivariate measures, and multivariate measures that apply dimension reduction, as noted in the sketched division of causality measures in
Figure 1. These are all linear measures and besides this constraint they have been widely used in applications. Other nonlinear extensions are not considered in this study for two reasons: either they were very computationally intensive, such as the cross predictions of local state space models [
14], or they were too complicated so that discrepancies to the original methods may occur [
19,
20].
The information measures of the second class have also been popular in diverse applications recently due to their general form, as they do not require any specific model, they are inherently nonlinear measures and can be applied to both deterministic systems and stochastic processes of any type, e.g., oscillating flows and discrete maps of any dimension. The main measure they rely on is the mutual information (MI), and more precisely the conditional mutual information (CMI). There have been several forms for causality measures based on MI and CMI in the literature, e.g., see the coarse-grained mutual information in [
85], but the prevailing one is the transfer entropy (TE), originally defined for two variables [
27]. The multivariate version, termed partial transfer entropy (PTE) was later proposed together with different estimates of the entropies involved in the definition of PTE, bins [
86], correlation sums [
87], and nearest neighbors [
73]. Here, we consider the nearest neighbor estimate for both TE and PTE, found to be the most appropriate for high dimensions. Equivalent forms to TE and PTE are defined for the ranks of the embedding vectors rather than the observations directly. We consider the bivariate measures of symbolic transfer entropy (STE) [
74] and transfer entropy on rank vectors (TERV) [
76], and the multivariate measures of partial symbolic transfer entropy (PSTE) [
75] and partial transfer entropy on rank vectors (PTERV) [
77]. The idea of dimension reduction was implemented in TE first, applying a scheme for a sparse non-uniform embedding of both
X and
Y, termed mutual information on mixed embedding (MIME) [
29]. This bivariate measure was later extended to the multivariate measure of partial MIME (PMIME) [
42]. Only the PMIME is included in the study simply due to the computational cost, and it is noted that by construction the measure gives zero for insignificant causal effects, so it does not require binarization when networks of binary connections have to be derived (the positive values are simply set to one).
All the methods in the third class of frequency measures rely on the estimation of the VAR model, either on only the two variables
X and
Y or on all the observed variables (we consider only the latter case here). Geweke’s spectral Granger causality (GGC) is the early measure implementing the concept of Grangre causality in the frequency domain [
21,
80], included in the study. Another older such measure included in the study is the direct transfer function (DTF) [
23], which, although it is a multivariate measure, it does not discriminate direct from indirect causal effects. For this, an improvement is proposed and used also in this study, termed direct directed transfer function (dDTF) [
79]. We also consider the partial directed coherence (PDC) [
24] and the improved version of generalized partial directed coherence (GPDC) [
78], which have been particularly popular in EEG analysis. When applied to EEG, the measures are defined in terms of frequency bands of physiological relevance (
,
,
,
,
, going from low to high frequencies), and the same proportional split of the frequency range is followed here (as if the sampling frequency was 100 Hz). Finally, we consider a dimension reduction of VAR in the GPDC measure called restricted GPDC (RGPDC), recently proposed from our team [
81].
As mentioned above the class of phase measures contains a good number of measures used in connectivity analysis, mainly in neuroscience dealing with oscillating signals such as EEG, but most of these measures are symmetric and thus out of the scope of the current study. In the evaluation of the causality measures, we consider the bivariate measure of phase directionality index (DPI) [
30], which is a measure of synchronization designed for oscillating time series. Information measures have also been implemented in the phases, e.g., see [
88], but not considered here.
Another class of measures used mainly in neuroscience regards inter-dependence measures based on neighborhoods in the reconstructed state space of each of the two variables
X and
Y. A series of such measures have been proposed after the first work in [
25], using also ranks of the reconstructed vectors [
89], the latter making the measure computationally very slow. The convergent cross mapping is developed under the same approach [
90], and the same yields for the measure of mean conditional recurrence (MCR) [
26]. It is noted that all these measures are bivariate and they are expected to suffer from estimating indirect connections in the estimated causality network. The MCR is included as a representative of the state space bivariate measures in the class of other measures. In this class, we include also event synchronization measures [
82], and specifically the direct event delay (DED) that is a directional bivariate measure, considered as causality measure and included in the study.
For the information measures where the estimation of entropies in high dimensions is hard, the comparison of the multivariate measures that do not include dimension reduction to these including dimension reduction would be unfair when high-dimensional systems are considered. To address this, in the calculation of a multivariate information measure not making use of dimension reduction, we choose to restrict the set of the conditioning variables
Z in the estimated causal effect
to only the three more relevant variables. In the simulations, we consider the number of observed variables (equal to the subsystems being coupled) to be
and
, while, for
, all the remaining variables are considered in
Z; for
, only three of the remaining 23 variables are selected. The criterion of selection is the mutual information of the remaining variables to the driving variable
X, which is common for the selection of variables [
38].
2.2. Identification of Original Network Connections
We suppose that a dynamical system is formed by the coupling of K subsystems, and we observe one variable from each subsystem, so that a multivariate time series of dimension K is derived. The coupling structure of the original system can be displayed as a network of K nodes where the connections are determined by the system equations. Formally, in the graph-theoretical framework, a network is represented by a graph , where V is the set of K nodes, and E is the set of the connections among the nodes of V. The original coupling network is given as a graph of directed binary connections, where the connection from node i to node j is assigned with a value being one or zero, depending whether variables of the subsystem i are present in the equation determining the variables of the subsystem j. The components , , form the adjacency matrix A that defines the network.
The computation of any causality measure presented in
Section 2.1 on all the directed pairs
of the
K observed variables gives a weight matrix
R (assuming only positive values of the measure, so that a transformation of the measure can be applied if necessary). Thus, the pairwise causality matrix
R with entries
defines a network of weighted connections, assigning the weighted directed connection
from each node
i to each node
j.
In applications, often binary networks are sought to better represent the estimated structure of the underlying system. Here, we are interested to compare how the causality measure retrieves the original directed coupling structure, and therefore we want to transform the weighted network to a binary network. Commonly, the weighted matrix R is transformed into an adjacency matrix A by suitable thresholding, keeping in the graph only connections with weights higher than some threshold (and setting their weights to one) and removing the weaker connections (setting their weights to zero). For each causality measure, an appropriate threshold criterion is sought to determine the significant values of the measure that correspond to connections in the binary network. We consider three approaches for thresholding that have been used in the literature:
Rigorous thresholding is provided by an appropriate significance test for the causality measure
. For all considered causality measures in this study, we expect the causality measure to lie at the zero level if there is no causal effect and be positive if it is, so that the test is one-sided. Thus, the null and alternative hypotheses are respectively:
Parametric significance tests have been developed only for the linear causality measures, and for consistency we apply the randomization significance test to all causality measures, making use of the simple technique of time-shifted surrogates. Specifically, we generate
M resampled (surrogates) time series for the driving variable
X, each by shifting cyclically the original observations of
X by a random step
w. For the original time series of the driving variable
denoted
, the surrogate time series is
. In this way, we destroy any form of coupling of
and any other variable
, so that
is consistent to
, but it preserves the dynamics and the marginal distribution of
. The test statistic is the causality measure
, and it takes the value
on the original time series pair and the values
on each of the
M resampled time series pairs. The rank of
in the ordered list of
values
, denoted
, defines the
p-value of the randomization test as
[
91]. If
is at the right tail of the empirical distribution formed by
, then the H
is rejected, which suggests that
, where
is the significance level of the test determining the tail. For a multivariate time series of
K variables,
significance tests in total are performed for each causality measure, indicating that multiple tests are performed on the same dataset. This is a known issue in statistics and corrections for multiple testing can be further be applied, such as the false discovery rate [
92]. Here, we refrain from using such a correction and rather use three different significance levels
. We opted for this as the same setting is applied for all causality measures.
The second thresholding criterion is given by the desired density of the binary network. In the simulation study, we know the density of the original network, denoted by the number of connections . We consider five different values for the density of the estimated causality binary network given in multiples of as .
The third thresholding criterion is simply given by a predefined magnitude threshold on the causality measure. Here, we select an appropriate threshold separately for each causality measure and each coupling strength for the same system, where indicates the corresponding density. Having 10 realizations for each scenario (system and coupling strength), the is the average of the thresholds found for the given density in the 10 realizations.
2.3. Performance Indices for Statistical Evaluation of Methods Accuracy
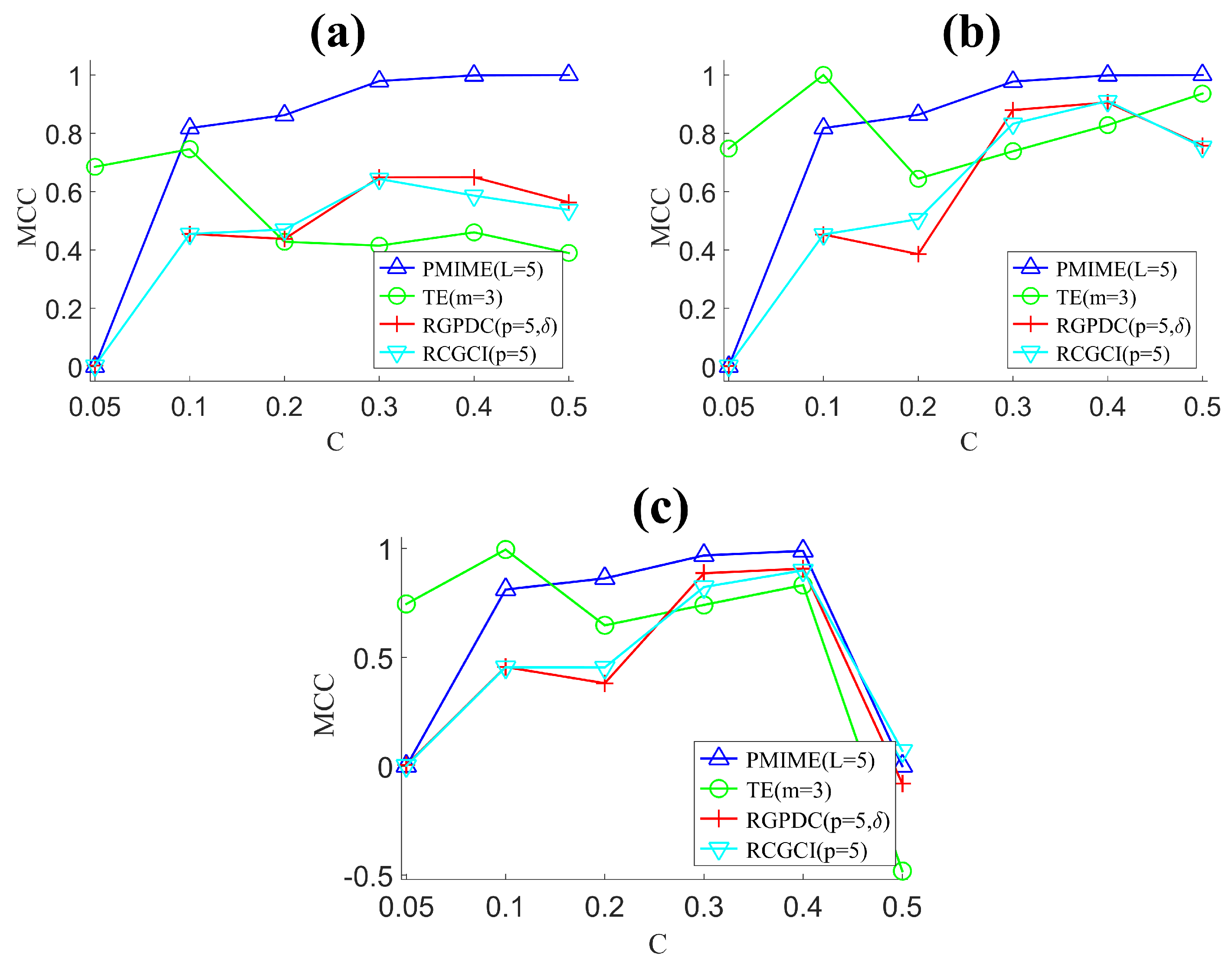
For a system of K variables, there are ordered pairs of variables to estimate causality. In the simulations of known systems, we know the true coupling pairs and thus we can compute performance indices to rate the causality measures as for their overall matching of the original connections in the network. Here, we consider the performance indices of specificity, sensitivity, Matthews correlation coefficient, F-measure, and Hamming distance.
The sensitivity is the proportion of the true causal effects (true positives, TP) correctly identified as such, given as sens = TP/(TP + FN), where FN (false negatives) denotes the number of pairs having true causal effects but have gone undetected. The specificity is the proportion of the pairs correctly not identified as having causal effects (true negatives, TN), given as spec = TN/(TN + FP), where FP (false positives) denotes the number of pairs found falsely to have causal effects. An ideal causality measure would give values of sensitivity and specificity at one. To weigh sensitivity and specificity collectively, we consider the Matthews correlation coefficient (MCC) [
93] given as
MCC ranges from −1 to 1. If MCC = 1, there is perfect identification of the pairs of true and no causality, if MCC = −1, there is total disagreement and pairs of no causality are identified as pairs of causality and vice versa, whereas MCC at the zero level indicates random assignment of pairs to causal and non-causal effects.
Similarly, we consider the F-measure that combines precision and sensitivity. The precision, called also positive predictive value, is the number of detected true causal effects divided by the total number of detected casual effects, given as prec = TP/(TP + FP), and the F-measure (FM) is defined as
which ranges from 0 to 1. If FM = 1, there is perfect identification of the pairs of true causality, whereas, if FM = 0, no true coupling is detected.
The Hamming distance (HD) is the sum of false positives (FP) and false negatives (FN), HD = FP + FN. Thus, HD gets non-negative integer values bounded below by zero (perfect identification) and above by if all pairs are misclassified.
2.4. Score Index
In
Section 2.3, we presented five performance indices to evaluate in different ways the match of the original network and the estimated network from each causality measure. Furthermore, we want to quantify this match for different settings, which involve different systems and different scenarios for each system regarding the number of variables
K, the system free parameter, the time series length
n and the coupling strength
C, where applicable (to be presented below in
Section 2.5). For this, we rely on the index MCC, and, for each scenario of a different system, we rank the causality measures according to their average MCC (across 10 realizations generated per scenario). For equal MCC, ordinal ranking (called also “1234” ranking) is adopted [
94]. Specifically, the order of measures of equal MCC is decided from distinct ordinal numbers given at random to each measure of equal MCC value. Next, we derive the average rank of a causality measure
i for all different coupling strengths
C of a system
j,
, as the average of the ranks of the causality measure
i in all coupling strengths tested for the system
j. A score
of the causality measure
i for the system
j is then derived by normalization of the average rank
over the number
N of all measures so as to scale between zero and one,
, where one is for the best measure ranked at top. The overall score of the causality measure
i over all systems,
, is simply given by the average
over all systems, including the two different
K values for systems S1, S2 and S3, the two values for the system parameter
and
A for systems S2 and S3, respectively, and the two time series lengths
n for system S1. The systems are presented in the next section.
2.5. Synthetic Systems
For the comparative study, we use four systems with different properties: the coupled Hénon maps as an example of discrete-time chaotic coupled system [
42], the coupled Mackey–Glass system as an example of continuous-time chaotic coupled system but of high complexity [
42,
95], the so-called neural mass model as an example of a continuous-time stochastic system used as an EEG model [
96,
97], and the vector autoregressive model (VAR) as suggested in [
98], used as an example of a discrete-time linear stochastic process. The four systems are briefly presented below:
S1: The system of coupled Hénon maps is a system of coupled chaotic maps defined as
where
K denotes the number of variables and
C is the coupling strength. We consider the system for
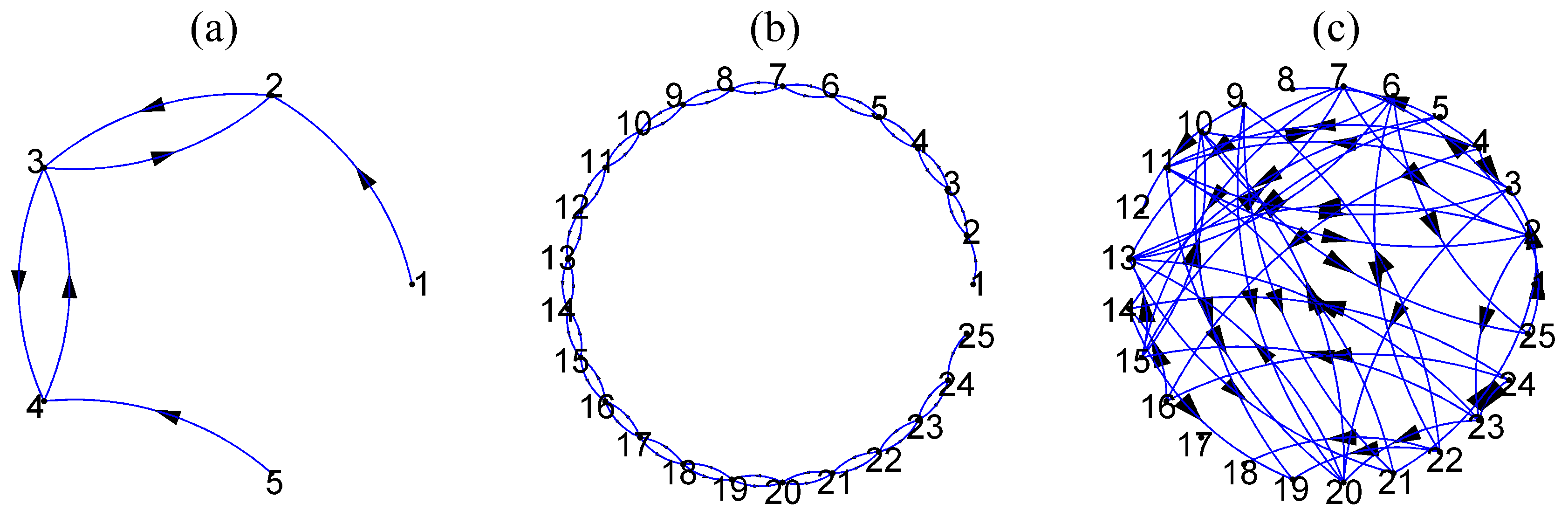
and
and the corresponding coupling network is shown in
Figure 2a,b, respectively.
Multivariate time series of size
K are generated, and we use short and long time series of length
and
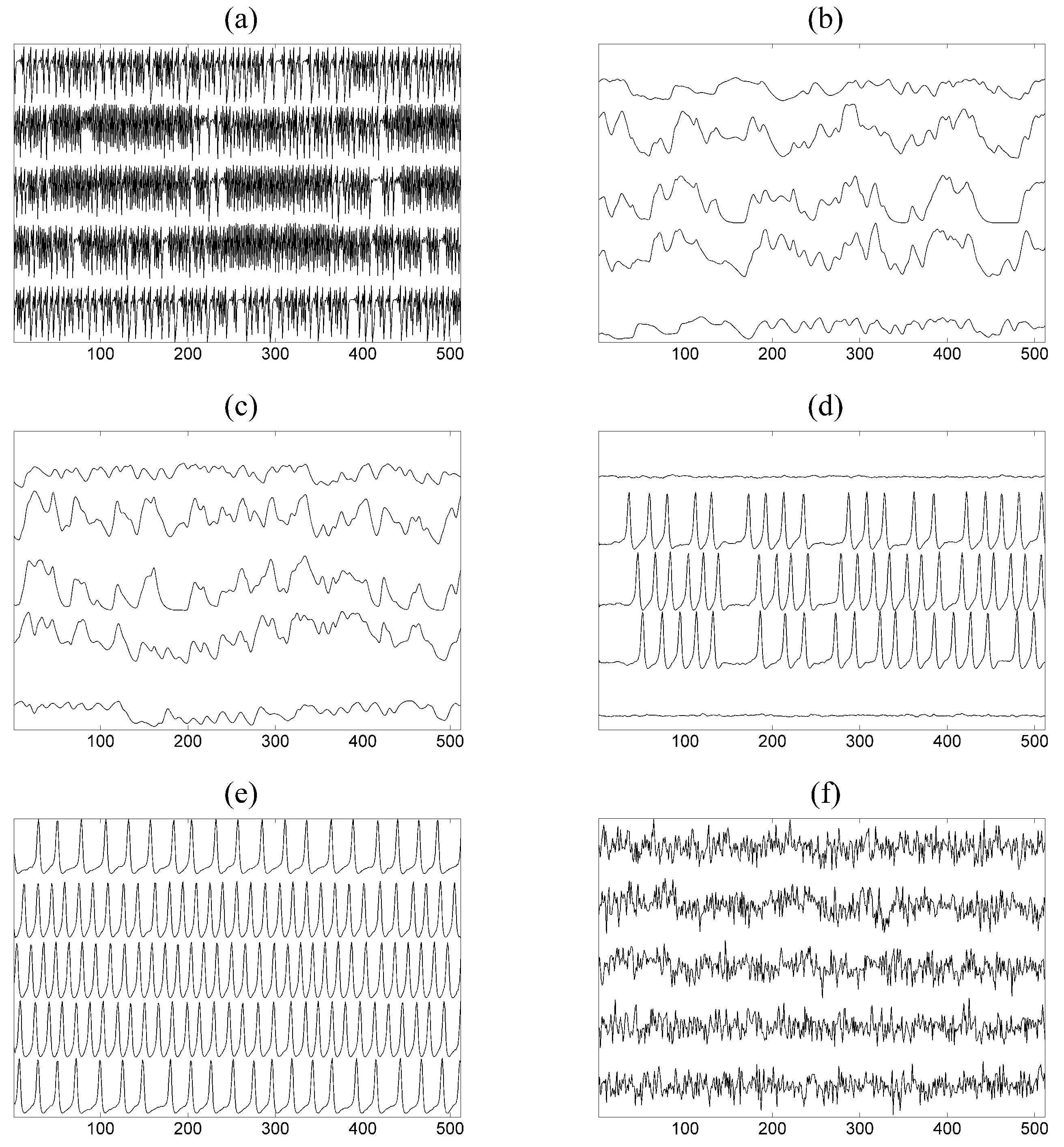
, respectively. An exemplary time series for
is given in
Figure 3a.
S2: The system of coupled Mackey–Glass is a system of coupled identical delayed differential equations defined as
where
K is the number of subsystems coupled to each other,
is the coupling strength, and
is the lag parameter. We set
and
for
zero or
C according to the ring coupling structure shown in
Figure 2a,b for
and
, respectively. For details on the solution of the delay differential equations and the generation of the time series, see [
42]. Two scenarios are considered regarding the inherent complexity of each of the
K subsystems given by
and
, regarding high complexity (correlation dimension is about 7.0 [
99]) and even higher complexity (not aware of any specific study for this regime), respectively. Exemplary time series for each
and
are given in
Figure 3b,c. The time series used in the study have length
.
S3: The neural mass model is a system of coupled differential equations with a stochastic term that produces time series similar to EEG simulating different states of brain activity, e.g., normal and epileptic. It is defined as
where
j denotes each of the
K subsystems representing the neuron population defined by eight interacting variables and the population (subsystem) interacts with other populations through variable
with coupling strength
. We set
and
for
zero or
C according to the ring coupling structure shown in
Figure 2a,b for
and
, respectively. The term
represents a random influence from neighboring or distant populations,
A is an excitation parameter and
B,
a,
b,
,
–
other parameters (see [
96] for more details). The function
S is the sigmoid function
, where
r is the steepness of the sigmoid and
,
are other parameters explained in [
96]. From each population
, we consider only the first variable
and obtain the multivariate time series of
K variables. The value of the excitation parameter
A affects the form of the output signals combined with the coupling strength level, ranging from similar to normal brain activity with no spikes to almost periodic with many spikes similar to epileptic brain activity. We consider two values for this parameter, one for low excitation with
and one for high excitation with
. Exemplary time series for each
A and
are given in
Figure 3d,e. The time series used in the study have length
.
S4: The VAR process on
variables and order
as suggested in [
98] is used as a representative of a high-dimensional linear stochastic process. Initially, 4% of the coefficients (total coefficients 1875) of VAR(3) selected randomly are set to 0.9 and the rest are zero and the positive coefficients are reduced iteratively until the stationarity condition is fulfilled. The autoregressive terms of lag one are set to one. The true couplings are 8% of a total of 600 possible ordered couplings. An exemplary coupling network of random type is shown in
Figure 2c. The time series length is set to
and an exemplary time series of only five of the
variables of the VAR(3) process is shown in
Figure 3f.
For S1, S2, and S3, the coupling strength
C, fixed for all couplings, is varied to study a wide range of coupling levels from zero coupling to very strong coupling. Specifically, for S1 and S2,
, and for S3
. For S4, only one case of coupling strength is considered, given by the magnitude
of all non-zero coefficients, for which the stationarity of VAR(3) process is reached. For each system and scenario of different coupling strength, 10 multivariate time series (realizations) are generated to obtain statistically valid results. The evaluation is performed as described in
Section 2.4.