Comparison of Two Efficient Methods for Calculating Partition Functions
Abstract
1. Introduction
2. Methods
2.1. Nested Sampling
2.2. Direct Integral Approach
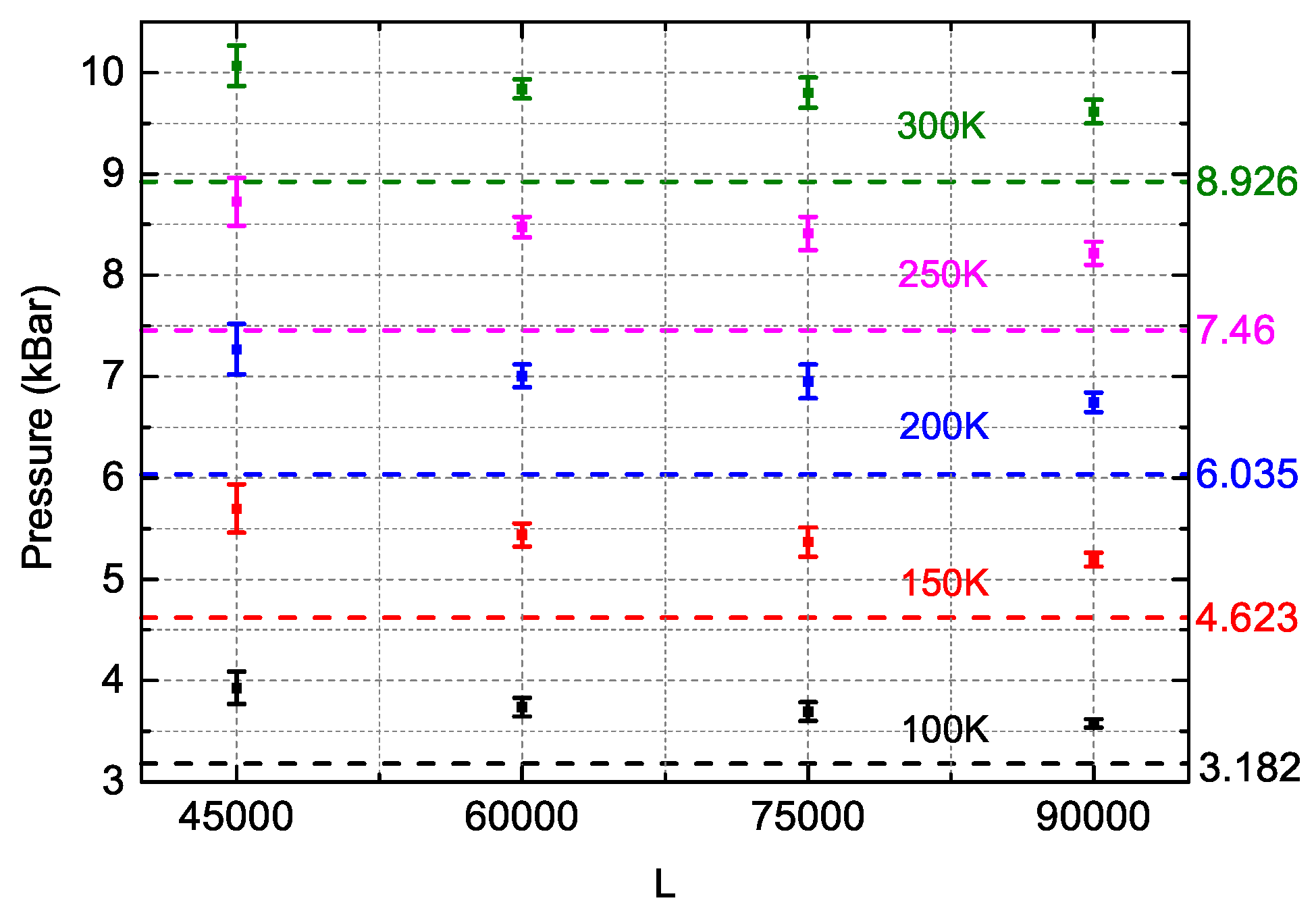
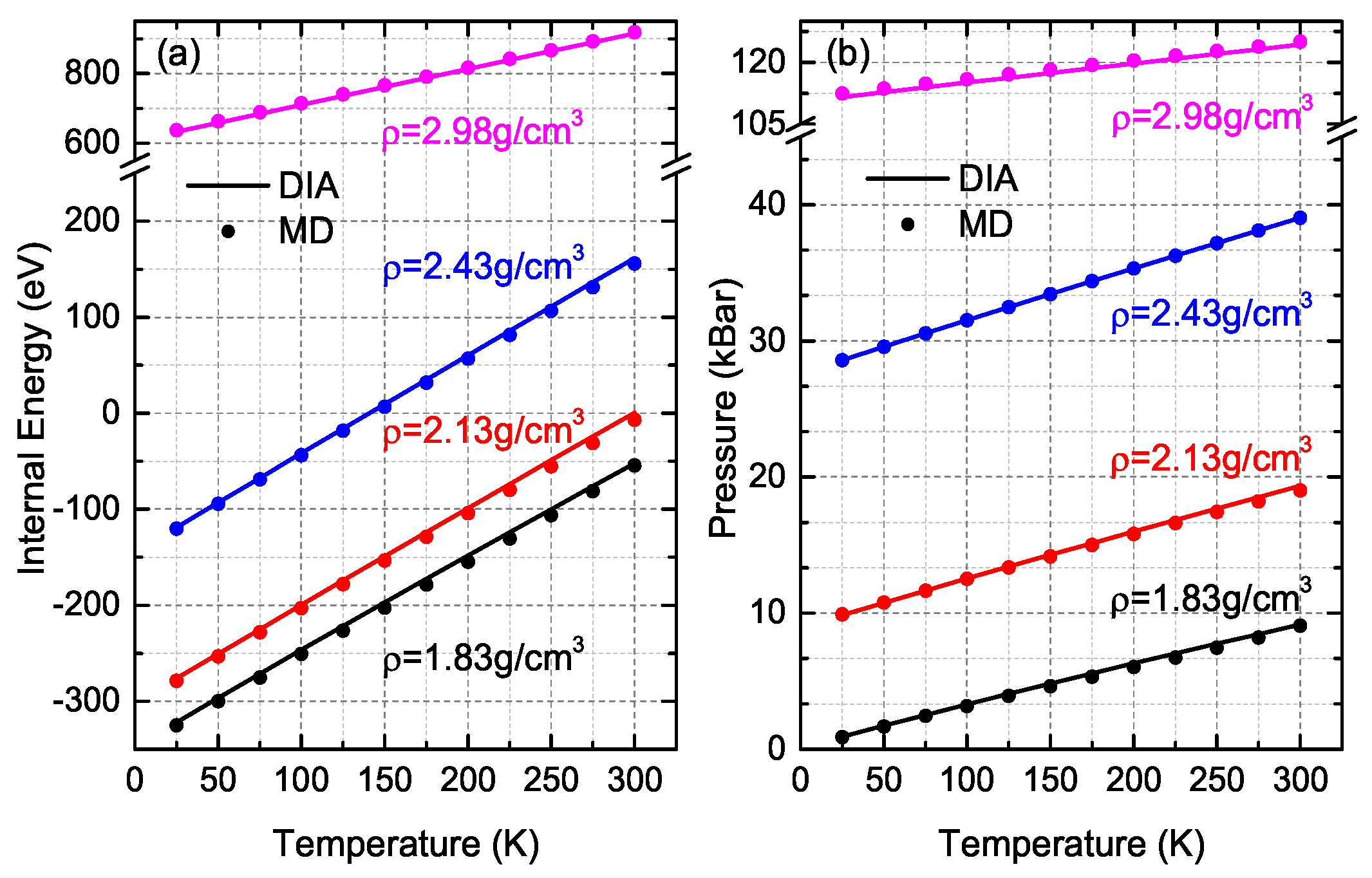
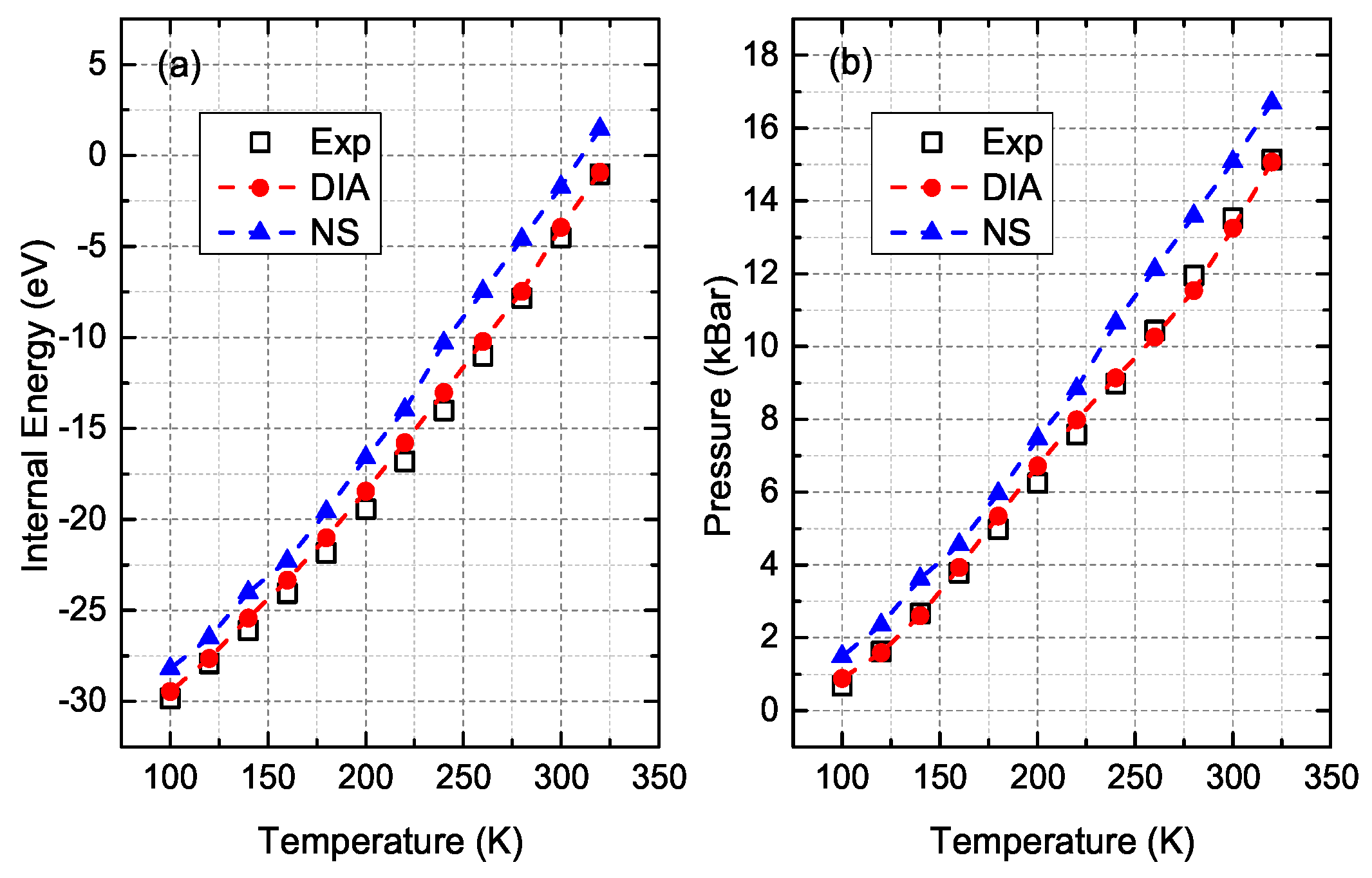
3. Comparisons and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References and Notes
- Baldock, R.J.; Pártay, L.B.; Bartók, A.P.; Payne, M.C.; Csányi, G. Determining pressure-temperature phase diagrams of materials. Phys. Rev. B 2016, 93, 174108. [Google Scholar] [CrossRef]
- Hansen, J.P.; Verlet, L. Phase transitions of the Lennard-Jones system. Phys. Rev. 1969, 184, 151. [Google Scholar] [CrossRef]
- Gadomski, A. Polymorphic phase transitions in systems evolving in a two-dimensional discrete space. Phys. Rev. E 1999, 60, 1252–1261. [Google Scholar] [CrossRef] [PubMed]
- Burkoff, N.S.; Várnai, C.; Wells, S.A.; Wild, D.L. Exploring the energy landscapes of protein folding simulations with Bayesian computation. Biophys. J. 2012, 102, 878–886. [Google Scholar] [CrossRef]
- Chipot, C.; Pohorille, A. Free Energy Calculations: Theory and Applications in Chemistry and Biology; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007; Volume 86. [Google Scholar]
- Ushcats, M.V.; Bulavin, L.A.; Sysoev, V.M.; Bardik, V.Y.; Alekseev, A.N. Statistical theory of condensation— Advances and challenges. J. Mol. Liq. 2016, 224, 694–712. [Google Scholar] [CrossRef]
- Singh, S.; Chopra, M.; de Pablo, J.J. Density of states–based molecular simulations. Annu. Rev. Chem. Biomol. Eng. 2012, 3, 369–394. [Google Scholar] [CrossRef]
- Mastny, E.A.; de Pablo, J.J. Direct calculation of solid-liquid equilibria from density-of-states Monte Carlo simulations. J. Chem. Phys. 2005, 122, 124109. [Google Scholar] [CrossRef]
- Mitchell, M.J.; McCammon, J.A. Free energy difference calculations by thermodynamic integration: Difficulties in obtaining a precise value. J. Comput. Chem. 1991, 12, 271–275. [Google Scholar] [CrossRef]
- Bussi, G.; Laio, A.; Parrinello, M. Equilibrium free energies from nonequilibrium metadynamics. Phys. Rev. Lett. 2006, 96, 090601. [Google Scholar] [CrossRef]
- Hansmann, U.H. Parallel tempering algorithm for conformational studies of biological molecules. Chem. Phys. Lett. 1997, 281, 140–150. [Google Scholar] [CrossRef]
- Wang, F.; Landau, D. Efficient, multiple-range random walk algorithm to calculate the density of states. Phys. Rev. Lett. 2001, 86, 2050. [Google Scholar] [CrossRef]
- Li, J.T.; Ning, B.Y.; Zhuang, J.; Ning, X.J. Rapidly calculating the partition function of macroscopic systems. Chin. Phys. B 2016, 26, 030501. [Google Scholar] [CrossRef]
- Skilling, J. Nested Sampling. AIP Conf. Proc. 2004, 735, 395–405. [Google Scholar]
- Skilling, J. Nested sampling for general Bayesian computation. Bayesian Anal. 2006, 1, 833–859. [Google Scholar] [CrossRef]
- Pártay, L.B.; Bartók, A.P.; Csányi, G. Efficient sampling of atomic configurational spaces. J. Phys. Chem. B 2010, 114, 10502–10512. [Google Scholar] [CrossRef] [PubMed]
- Do, H.; Hirst, J.D.; Wheatley, R.J. Calculation of partition functions and free energies of a binary mixture using the energy partitioning method: Application to carbon dioxide and methane. J. Phys. Chem. B 2012, 116, 4535–4542. [Google Scholar] [CrossRef] [PubMed]
- Do, H.; Wheatley, R.J. Density of states partitioning method for calculating the free energy of solids. J. Chem. Theory Comput. 2012, 9, 165–171. [Google Scholar] [CrossRef]
- Brewer, B.J.; Pártay, L.B.; Csányi, G. Diffusive nested sampling. Stat. Comput. 2011, 21, 649–656. [Google Scholar] [CrossRef]
- Nielsen, S.O. Nested sampling in the canonical ensemble: Direct calculation of the partition function from NVT trajectories. J. Chem. Phys. 2013, 139, 124104. [Google Scholar] [CrossRef]
- Wilson, B.A.; Gelb, L.D.; Nielsen, S.O. Nested sampling of isobaric phase space for the direct evaluation of the isothermal-isobaric partition function of atomic systems. J. Chem. Phys. 2015, 143, 154108. [Google Scholar] [CrossRef]
- Do, H.; Hirst, J.D.; Wheatley, R.J. Rapid calculation of partition functions and free energies of fluids. J. Chem. Phys. 2011, 135, 174105. [Google Scholar] [CrossRef] [PubMed]
- Bolhuis, P.G.; Csányi, G. Nested Transition Path Sampling. Phys. Rev. Lett. 2018, 120, 250601. [Google Scholar] [CrossRef] [PubMed]
- Baldock, R.J.; Bernstein, N.; Salerno, K.M.; Pártay, L.B.; Csányi, G. Constant-pressure nested sampling with atomistic dynamics. Phys. Rev. E 2017, 96, 043311. [Google Scholar] [CrossRef] [PubMed]
- Martiniani, S.; Stevenson, J.D.; Wales, D.J.; Frenkel, D. Superposition enhanced nested sampling. Phys. Rev. X 2014, 4, 031034. [Google Scholar] [CrossRef]
- Ning, B.Y.; Gong, L.C.; Weng, T.C.; Ning, X.J. Solution to partition function for macroscopic condensed matters—The key problem of statistical physics. arXiv 2019, arXiv:1901.08233. [Google Scholar]
- Liu, Y.P.; Ning, B.Y.; Gong, L.C.; Weng, T.C.; Ning, X.J. A New Model to Predict Optimum Conditions for Growth of 2D Materials on a Substrate. Nanomaterials 2019, 9, 978. [Google Scholar] [CrossRef]
- Andersen, H.C. Molecular dynamics simulations at constant pressure and/or temperature. J. Chem. Phys. 1980, 72, 2384–2393. [Google Scholar] [CrossRef]
- Nosé, S. A molecular dynamics method for simulations in the canonical ensemble. Mol. Phys. 1984, 52, 255–268. [Google Scholar] [CrossRef]
- Hoover, W.G. Constant-pressure equations of motion. Phys. Rev. A 1986, 34, 2499. [Google Scholar] [CrossRef]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Oxford University Press: Oxford, UK, 1989. [Google Scholar]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Evans, D.J.; Holian, B.L. The nose–hoover thermostat. J. Chem. Phys. 1985, 83, 4069–4074. [Google Scholar] [CrossRef]
- Louwerse, M.J.; Baerends, E.J. Calculation of pressure in case of periodic boundary conditions. Chem. Phys. Lett. 2006, 421, 138–141. [Google Scholar] [CrossRef]
- Thompson, A.P.; Plimpton, S.J.; Mattson, W. General formulation of pressure and stress tensor for arbitrary many-body interaction potentials under periodic boundary conditions. J. Chem. Phys. 2009, 131, 154107. [Google Scholar] [CrossRef] [PubMed]
- For several given conditions, the relative differences of both DIA and NS between MD simulations are quite large, which might be due to the large fluctuations of MD simulations. For instance, at (N = 400, ρ = 2.13 g/cm3, T = 300 K), the RDEs of DIA and NS are 107.59% and 455.18% respectively while the fluctuations of MD simulations of internal energy at this condition is 23.2% with the EMD = −0.92 eV (EDIA = 0.07 eV and ENS = 3.27 eV). For an accurate analysis, as a result, we excluded the data of which the MD fluctuations are over 20%.
- Crawford, R.; Lewis, W.; Daniels, W. Thermodynamics of solid argon at high temperatures. J. Phys. C Solid State Phys. 1976, 9, 1381. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, L.-C.; Ning, B.-Y.; Weng, T.-C.; Ning, X.-J. Comparison of Two Efficient Methods for Calculating Partition Functions. Entropy 2019, 21, 1050. https://doi.org/10.3390/e21111050
Gong L-C, Ning B-Y, Weng T-C, Ning X-J. Comparison of Two Efficient Methods for Calculating Partition Functions. Entropy. 2019; 21(11):1050. https://doi.org/10.3390/e21111050
Chicago/Turabian StyleGong, Le-Cheng, Bo-Yuan Ning, Tsu-Chien Weng, and Xi-Jing Ning. 2019. "Comparison of Two Efficient Methods for Calculating Partition Functions" Entropy 21, no. 11: 1050. https://doi.org/10.3390/e21111050
APA StyleGong, L.-C., Ning, B.-Y., Weng, T.-C., & Ning, X.-J. (2019). Comparison of Two Efficient Methods for Calculating Partition Functions. Entropy, 21(11), 1050. https://doi.org/10.3390/e21111050




