Bandwidth-Limited and Noisy Pulse Sequences for Single Qubit Operations in Semiconductor Spin Qubits
Abstract
1. Introduction
2. Results
2.1. and with Bandwidth-Limited Pulses
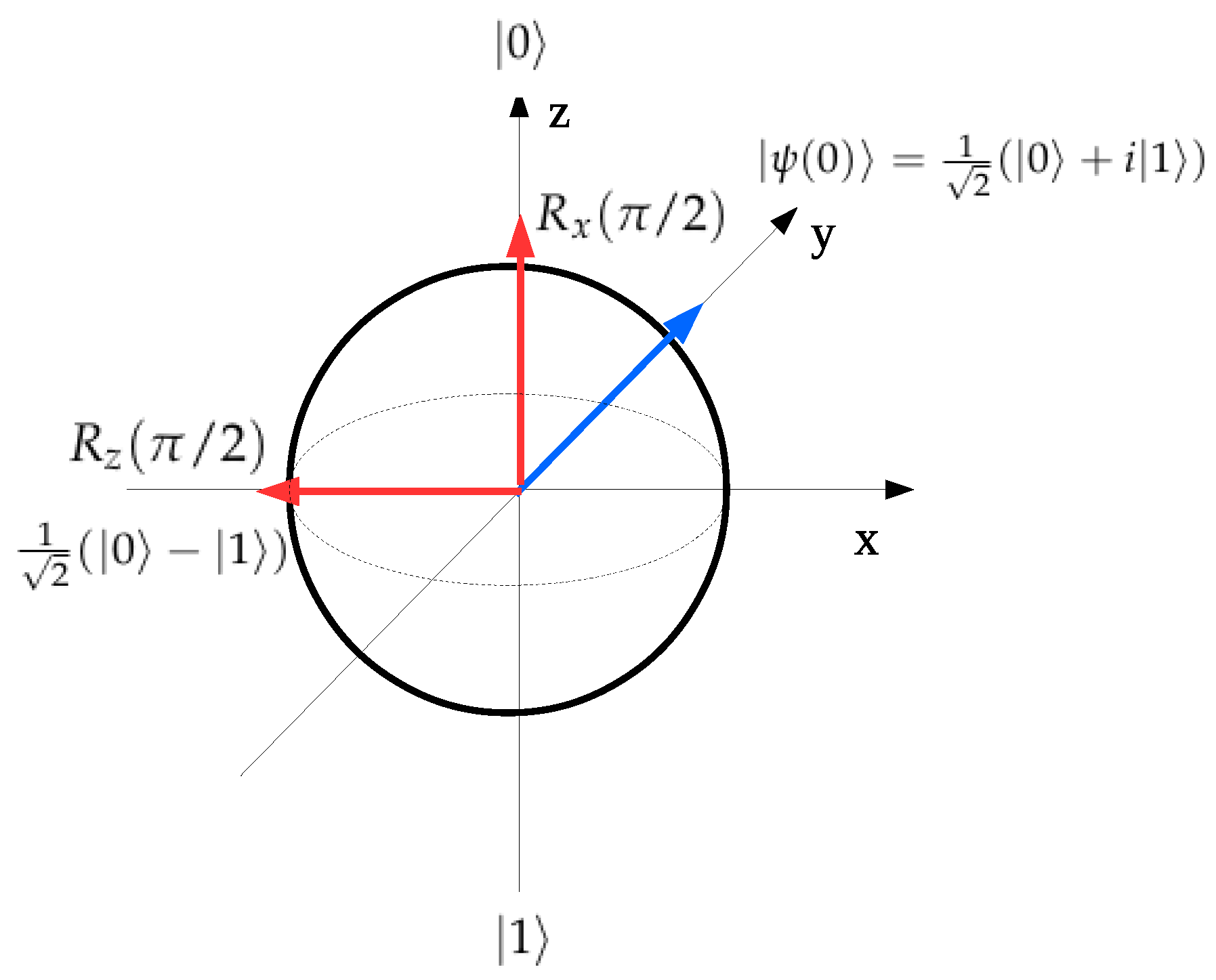
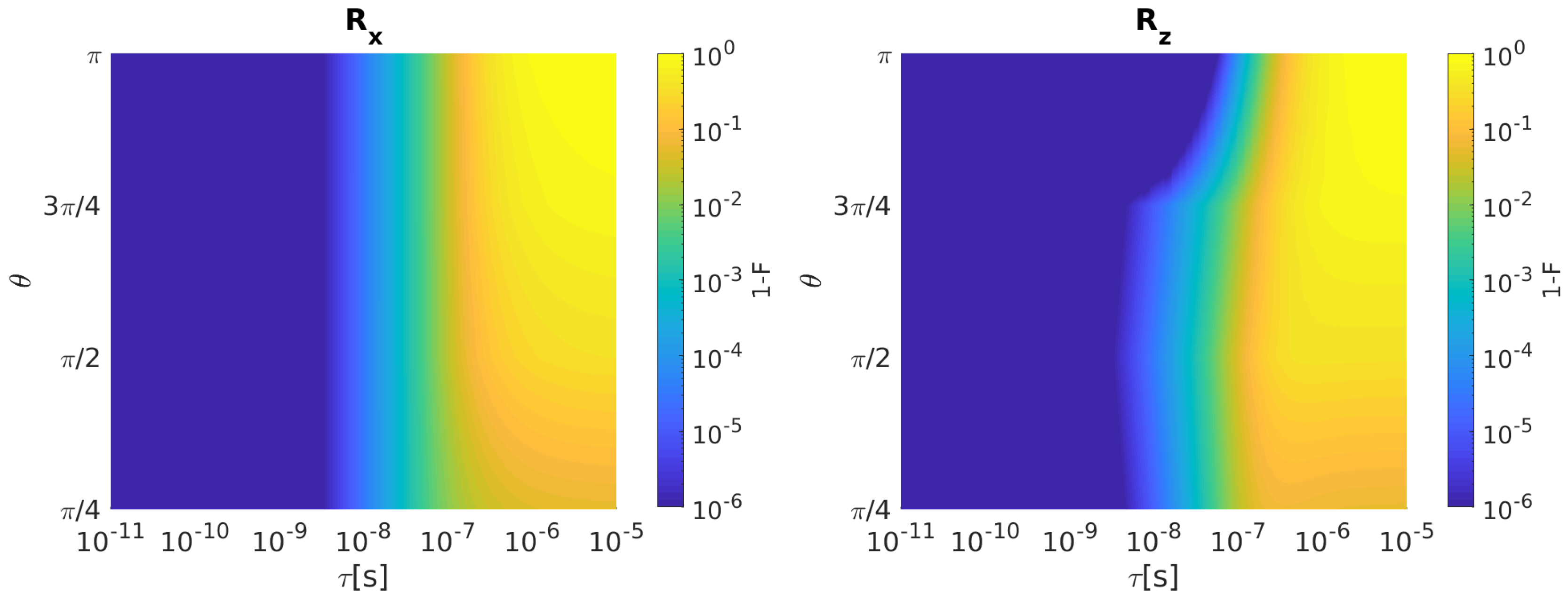
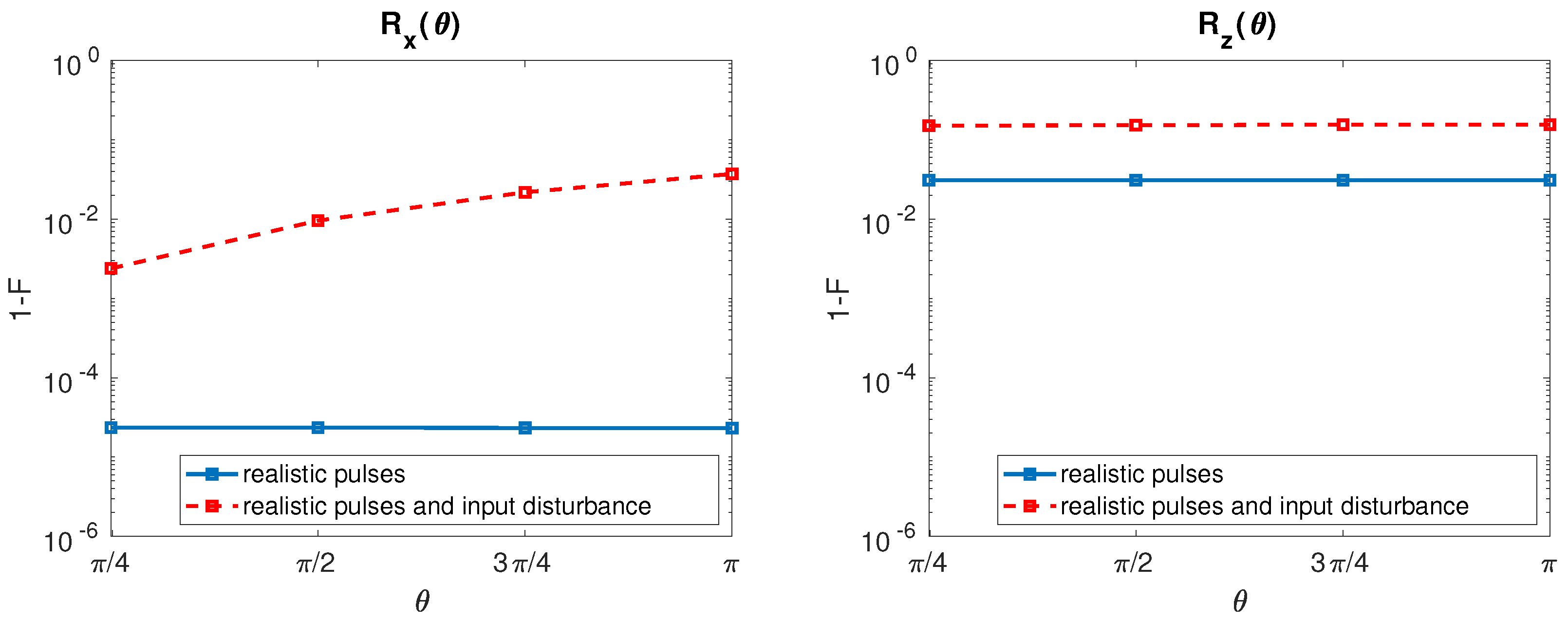
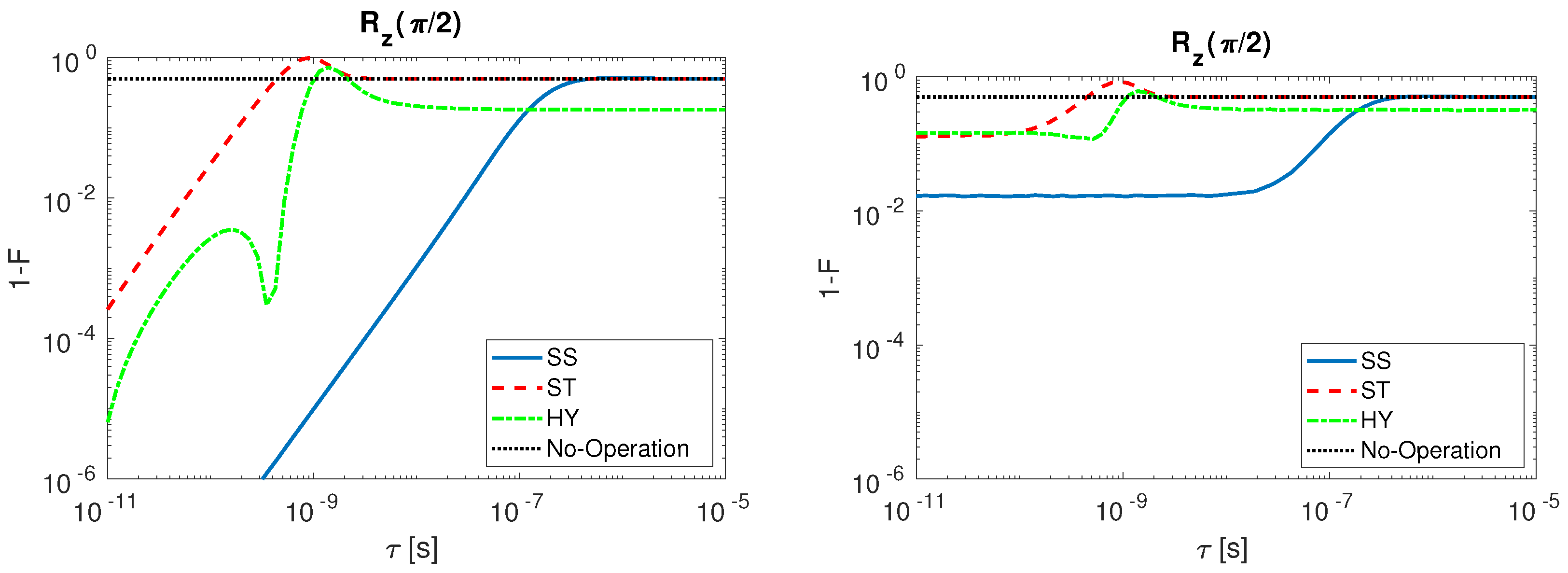
2.1.1. Single Spin Qubit
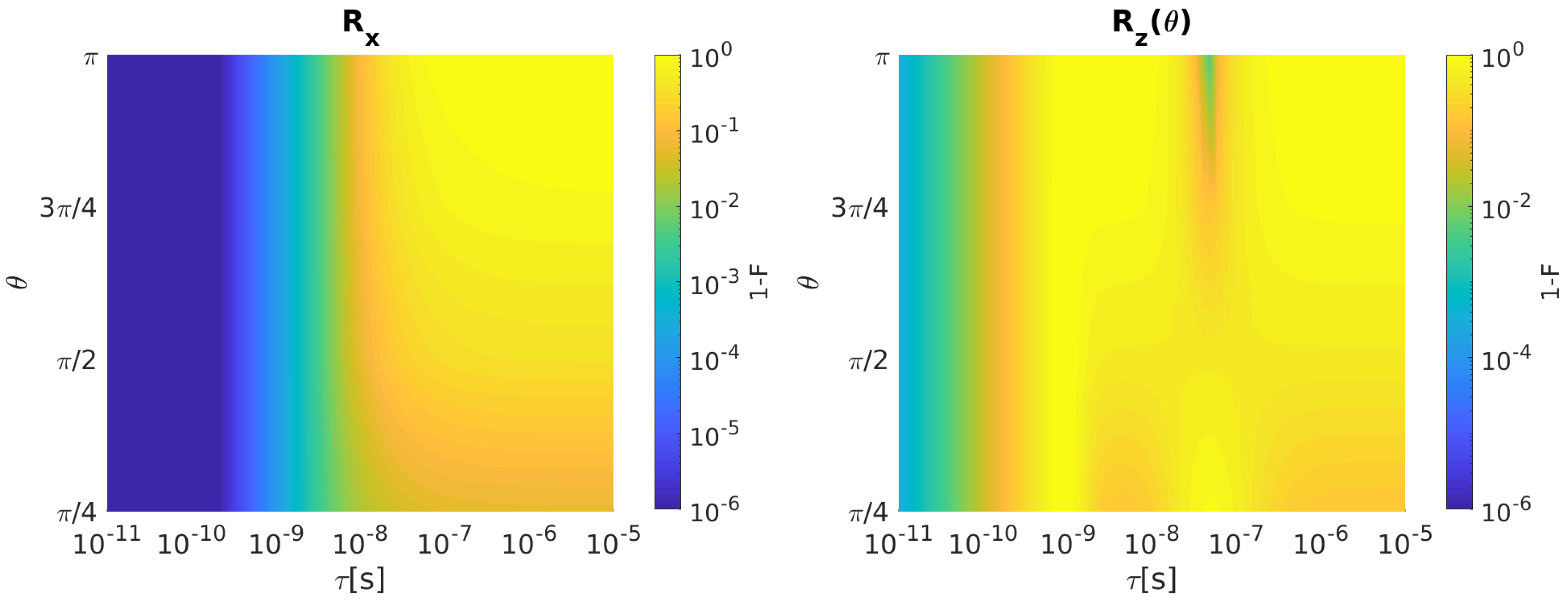
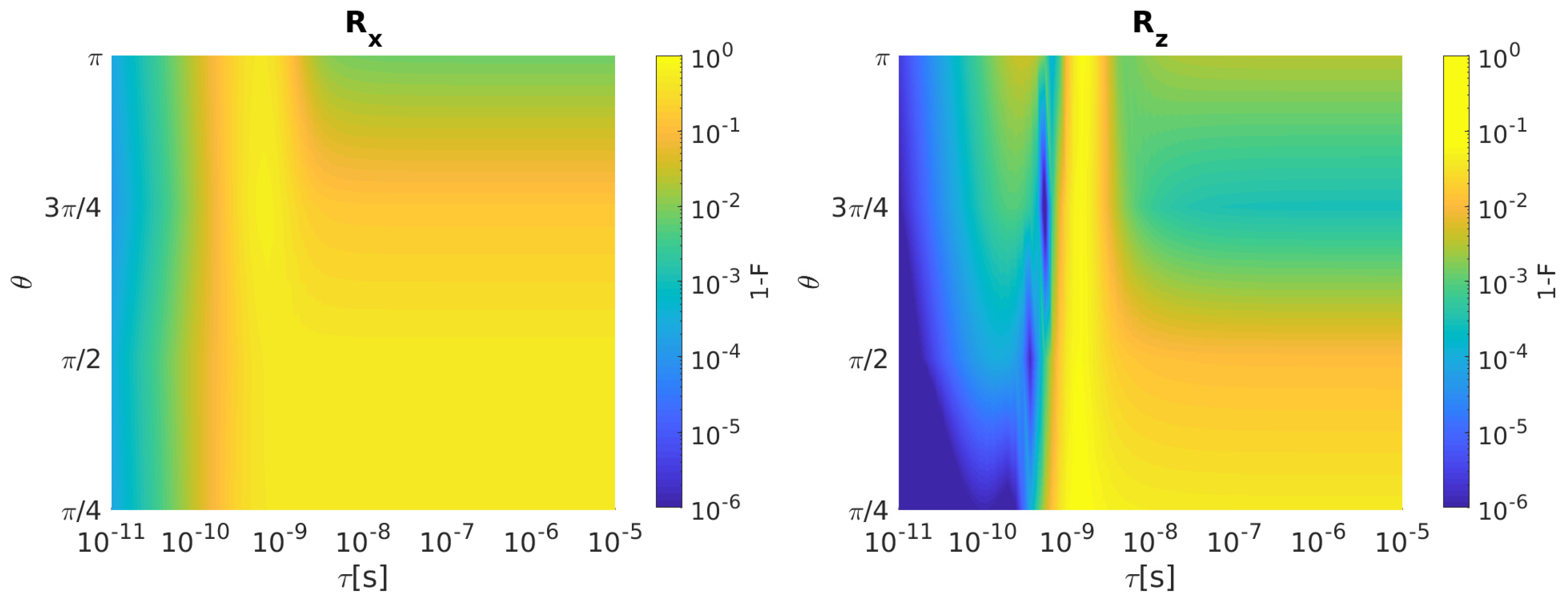
2.1.2. Singlet–Triplet Qubit
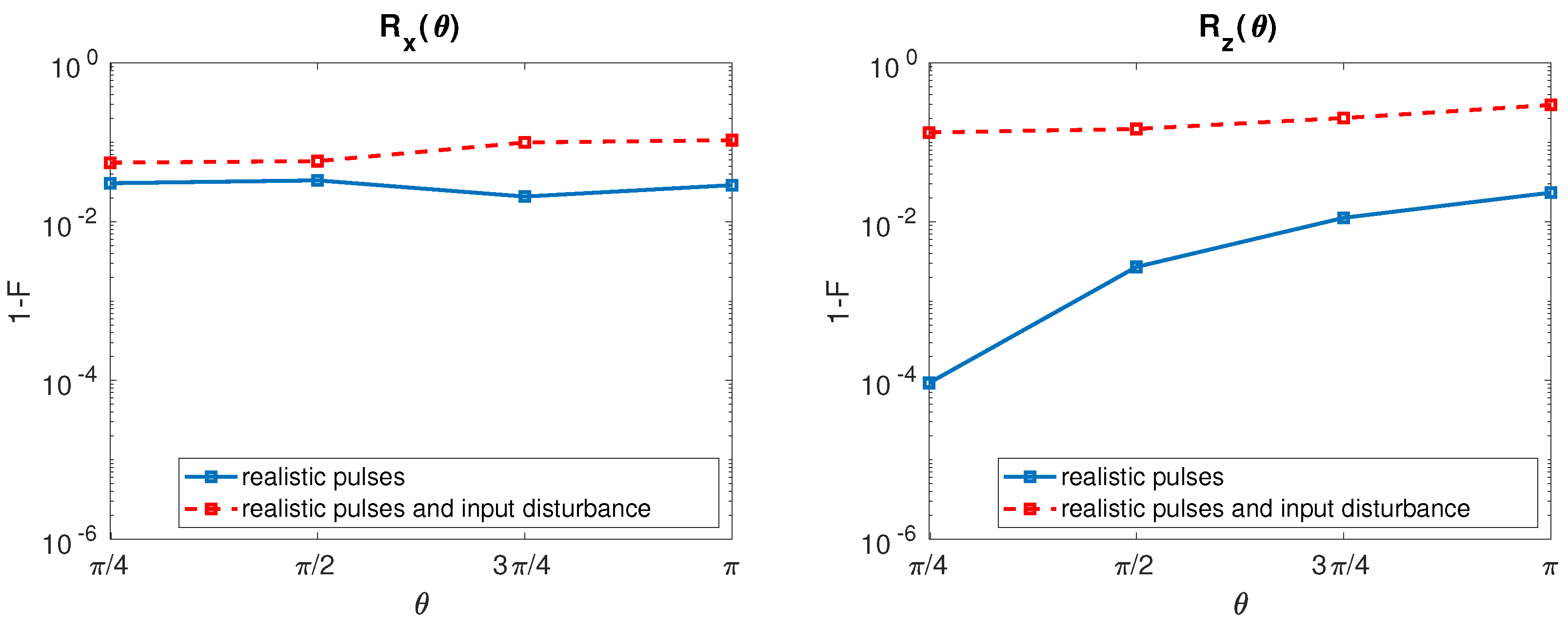
2.1.3. Hybrid Qubit
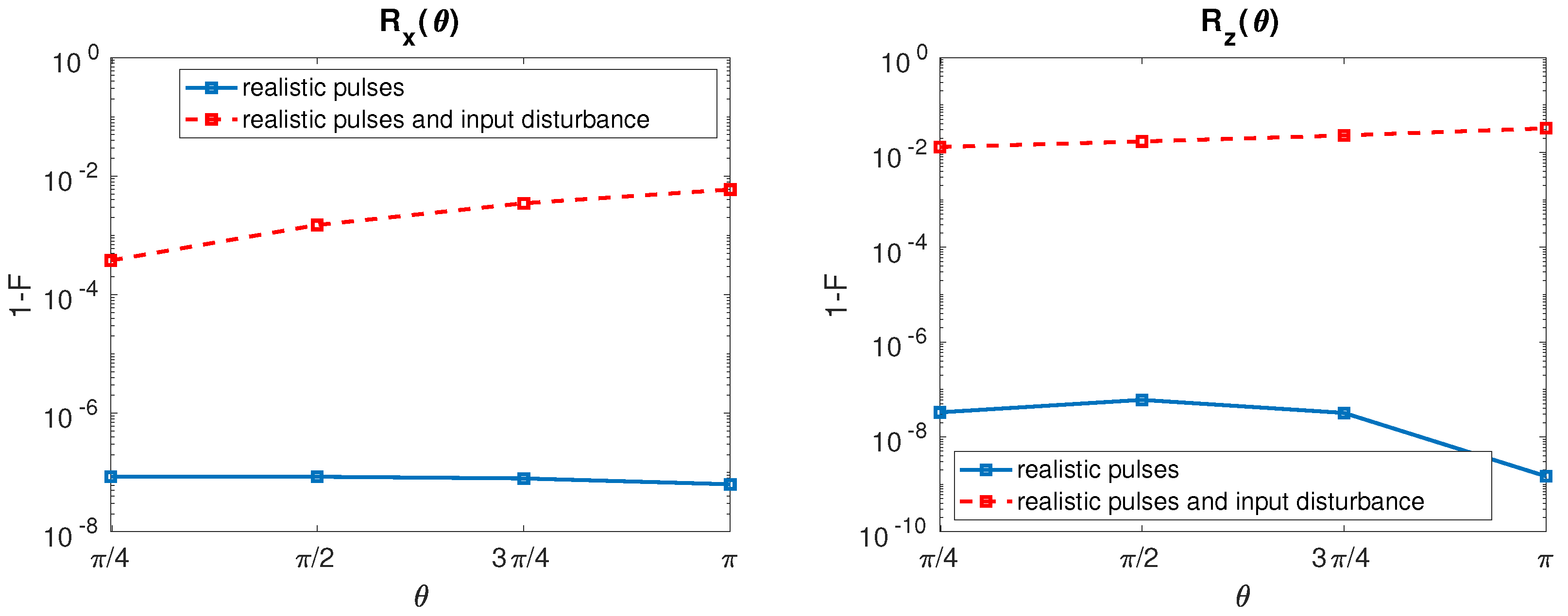
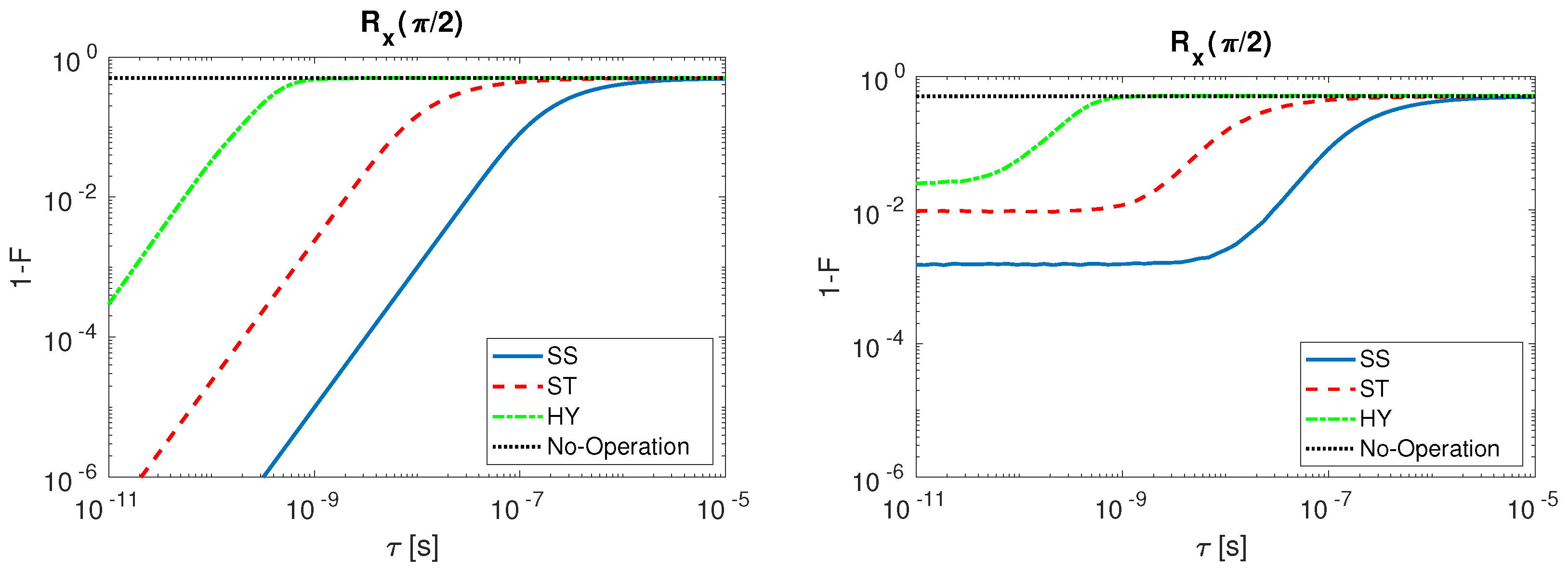
2.2. Fidelity Comparison
3. Discussion
4. Methods
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| QD | Quantum Dot |
| SS | Single Spin |
| ST | Singlet–Triplet |
| HY | Hybrid |
Appendix A. Analytical Gate Sequences
| Qubit | ||
|---|---|---|
| SS | ||
| ST | with n integer | |
| HY | with , and | with and |
References
- Hanson, R.; Kouwenhoven, L.P.; Petta, J.R.; Tarucha, S.; Vandersypen, L.M.K. Spins in few-electron quantum dots. Rev. Mod. Phys. 2007, 79, 1217. [Google Scholar] [CrossRef]
- Vandersypen, L.M.K.; Bluhm, H.; Clarke, J.S.; Dzurak, A.S.; Ishihara, R.; Morello, A.; Reilly, D.J.; Schreiber, L.R.; Veldhorst, M. Interfacing spin qubits in quantum dots and donors—Hot, dense, and coherent. NPJ Quantum Inf. 2017, 3, 34. [Google Scholar] [CrossRef]
- Russ, M.; Burkard, G. Three-electron spin qubits. J. Phys. Condens. Matter 2017, 29, 393001. [Google Scholar] [CrossRef] [PubMed]
- Rotta, D.; Sebastiano, F.; Charbon, E.; Prati, E. Quantum information density scaling and qubit operation time constraints of CMOS silicon-based quantum computer architectures. NPJ Quantum Inf. 2017, 3, 26. [Google Scholar] [CrossRef]
- Loss, D.; DiVincenzo, D.P. Quantum computation with quantum dots. Phys. Rev. A 1998, 57, 120. [Google Scholar] [CrossRef]
- Veldhorst, M.; Hwang, J.C.C.; Yang, C.H.; Leenstra, A.W.; de Ronde, B.; Dehollain, J.P.; Muhonen, T.J.; Hudson, F.E.; Itoh, K.M.; Morello, A.; et al. An addressable quantum dot qubit with fault-tolerant control-fidelity. Nat. Nanotechnol. 2014, 9, 981–985. [Google Scholar] [CrossRef]
- Kawakami, E.; Scarlino, P.; Ward, D.R.; Braakman, F.R.; Savage, D.E.; Lagally, M.G.; Friesen, M.; Coppersmith, S.N.; Eriksson, M.A.; Vandersypen, L.M.K. Electrical control of a long-lived spin qubit in a Si/SiGe quantum dot. Nat. Nanotechnol. 2014, 9, 666–670. [Google Scholar] [CrossRef]
- Kane, B.E. A silicon-based nuclear spin quantum computer. Nature 1998, 393, 133. [Google Scholar] [CrossRef]
- Pla, J.; Tan, K.; Dehollain, J.; Lim, W.; Morton, J.; Jamieson, D.; Dzurak, A.; Morello, A. A single-atom electron spin qubit in silicon. Nature 2012, 489, 541. [Google Scholar] [CrossRef]
- Pla, J.J.; Tan, K.Y.; Dehollain, J.P.; Lim, W.H.; Morton, J.J.L.; Zwanenburg, F.A.; Jamieson, D.N.; Dzurak, A.S.; Morello, A. High-fidelity readout and control of a nuclear spin qubit in silicon. Nature 2013, 334, 496. [Google Scholar] [CrossRef]
- Pica, G.; Lovett, B.W.; Bhatt, R.N.; Schenkel, T.; Lyon, S.A. Surface code architecture for donors and dots in silicon with imprecise and nonuniform qubit couplings. Phys. Rev. B 2016, 93, 035306. [Google Scholar] [CrossRef]
- Harvey-Collard, P.; Jacobson, N.T.; Rudolph, M.; Dominguez, J.; Eyck, G.A.T.; Wendt, J.R.; Pluym, T.; Gamble, J.K.; Lilly, M.P.; Pioro-Ladrière, M.; et al. Coherent coupling between a quantum dot and a donor in silicon. Nat. Commun. 2017, 8, 1029. [Google Scholar] [CrossRef] [PubMed]
- Morton, J.J.L.; McCamey, D.R.; Eriksson, M.A.; Lyon, S.A. Embracing the quantum limit in silicon computing. Nature 2011, 479, 345–353. [Google Scholar] [CrossRef] [PubMed]
- Levy, J. Universal Quantum Computation with Spin-1/2 Pairs and Heisenberg Exchange. Phys. Rev. Lett. 2002, 89, 147902. [Google Scholar] [CrossRef] [PubMed]
- Shi, Z.; Simmons, C.B.; Prance, J.R.; Gamble, J.K.; Koh, T.S.; Shim, Y.P.; Hu, X.; Savage, D.E.; Lagally, M.G.; Eriksson, M.A.; et al. Fast Hybrid Silicon Double-Quantum-Dot Qubit. Phys. Rev. Lett. 2012, 108, 140503. [Google Scholar] [CrossRef]
- Ferraro, E.; De Michielis, M.; Mazzeo, G.; Fanciulli, M.; Prati, E. Effective Hamiltonian for the hybrid double quantum dot qubit. Quantum Inf. Process. 2014, 13, 1155–1173. [Google Scholar] [CrossRef]
- Ferraro, E.; De Michielis, M.; Fanciulli, M.; Prati, E. Effective Hamiltonian for two interacting double-dot exchange-only qubits and their controlled-NOT operations. Quantum Inf. Process. 2015, 14, 47–65. [Google Scholar] [CrossRef][Green Version]
- Ferraro, E.; Fanciulli, M.; De Michielis, M. Gate fidelity comparison in semiconducting spin qubit implementations affected by control noises. J. Phys. Commun. 2018, 2, 115022. [Google Scholar] [CrossRef]
- Keysight, T. Keysight Technologies E8257D PSG Microwave Analog Signal Generator. 2017. Available online: https://www.keysight.com/en/pdx-x202237-pn-E8257D/psg-analog-signal-generator-100-khz-to-67-ghz (accessed on 25 October 2019).
- Wu, X.; Ward, D.R.; Prance, J.R.; Kim, D.; Gamble, J.K.; Mohr, R.T.; Shi, Z.; Savage, D.E.; Lagally, M.G.; Friesen, M.; et al. Two-axis control of a singlet—Triplet qubit with an integrated micromagnet. Proc. Natl. Acad. Sci. USA 2014, 111, 11938–11942. [Google Scholar] [CrossRef]
- De Michielis, M.; Ferraro, E.; Fanciulli, M.; Prati, E. Universal set of quantum gates for double-dot exchange-only spin qubits with intradot coupling. J. Phys. A Math. Theor. 2015, 48, 065304. [Google Scholar] [CrossRef][Green Version]
- Thorgrimsson, B.; Kim, D.; Yang, Y.C.; Smith, L.W.; Simmons, C.B.; Ward, D.R.; Foote, R.H.; Corrigan, J.; Savage, D.E.; Lagally, M.G.; et al. Extending the coherence of a quantum dot hybrid qubit. NPJ Quantum Inf. 2017, 3, 32. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferraro, E.; De Michielis, M. Bandwidth-Limited and Noisy Pulse Sequences for Single Qubit Operations in Semiconductor Spin Qubits. Entropy 2019, 21, 1042. https://doi.org/10.3390/e21111042
Ferraro E, De Michielis M. Bandwidth-Limited and Noisy Pulse Sequences for Single Qubit Operations in Semiconductor Spin Qubits. Entropy. 2019; 21(11):1042. https://doi.org/10.3390/e21111042
Chicago/Turabian StyleFerraro, Elena, and Marco De Michielis. 2019. "Bandwidth-Limited and Noisy Pulse Sequences for Single Qubit Operations in Semiconductor Spin Qubits" Entropy 21, no. 11: 1042. https://doi.org/10.3390/e21111042
APA StyleFerraro, E., & De Michielis, M. (2019). Bandwidth-Limited and Noisy Pulse Sequences for Single Qubit Operations in Semiconductor Spin Qubits. Entropy, 21(11), 1042. https://doi.org/10.3390/e21111042





