Entropy Analysis in Double-Diffusive Convection in Nanofluids through Electro-Osmotically Induced Peristaltic Microchannel
Abstract
1. Introduction
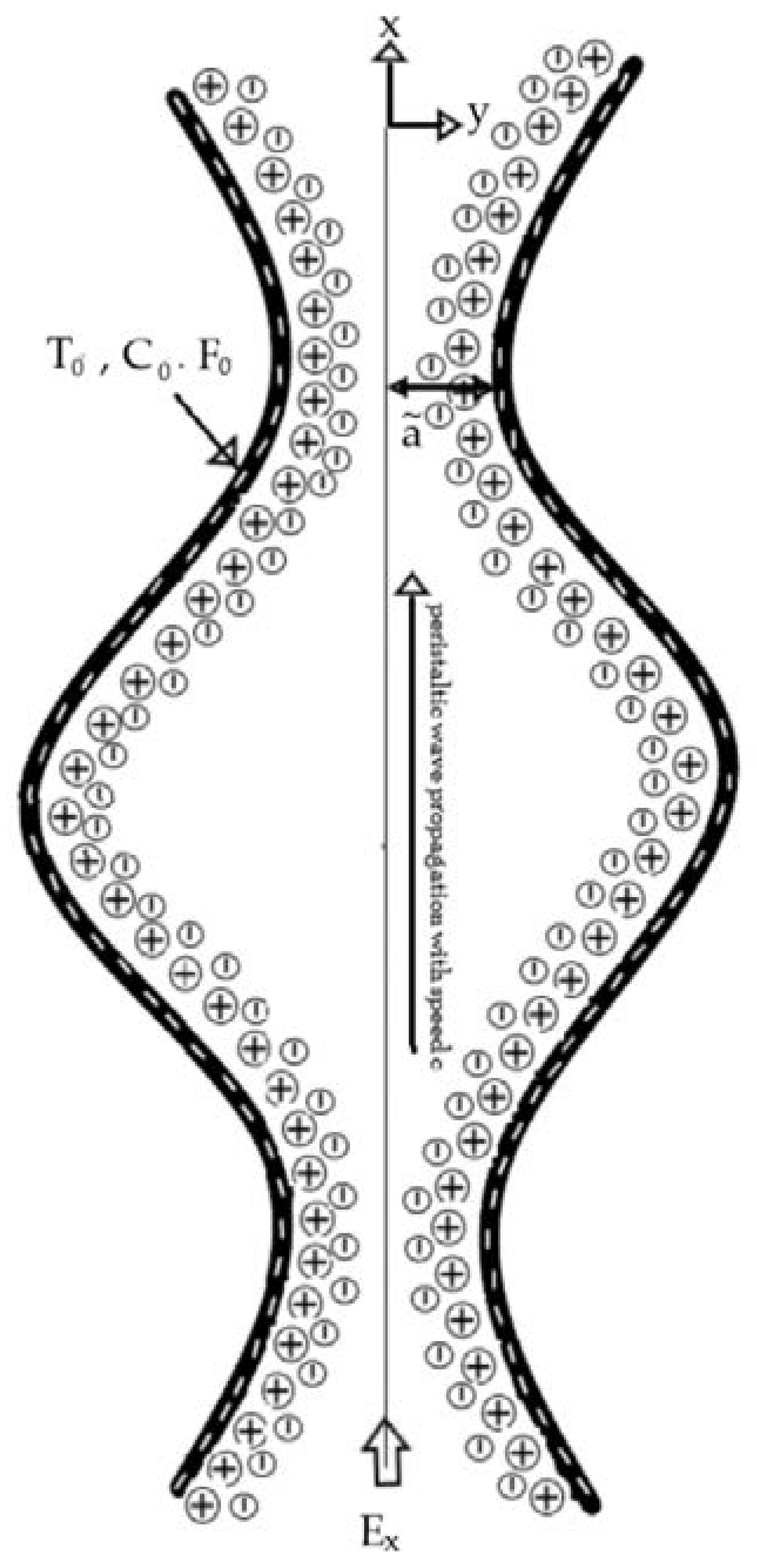
2. Mathematical Formulation
2.1. Flow Regime
2.2. Governing Equations
3. Solution Procedure
Analytical Solution
4. Entropy Generation Analysis
5. Results and Discussion
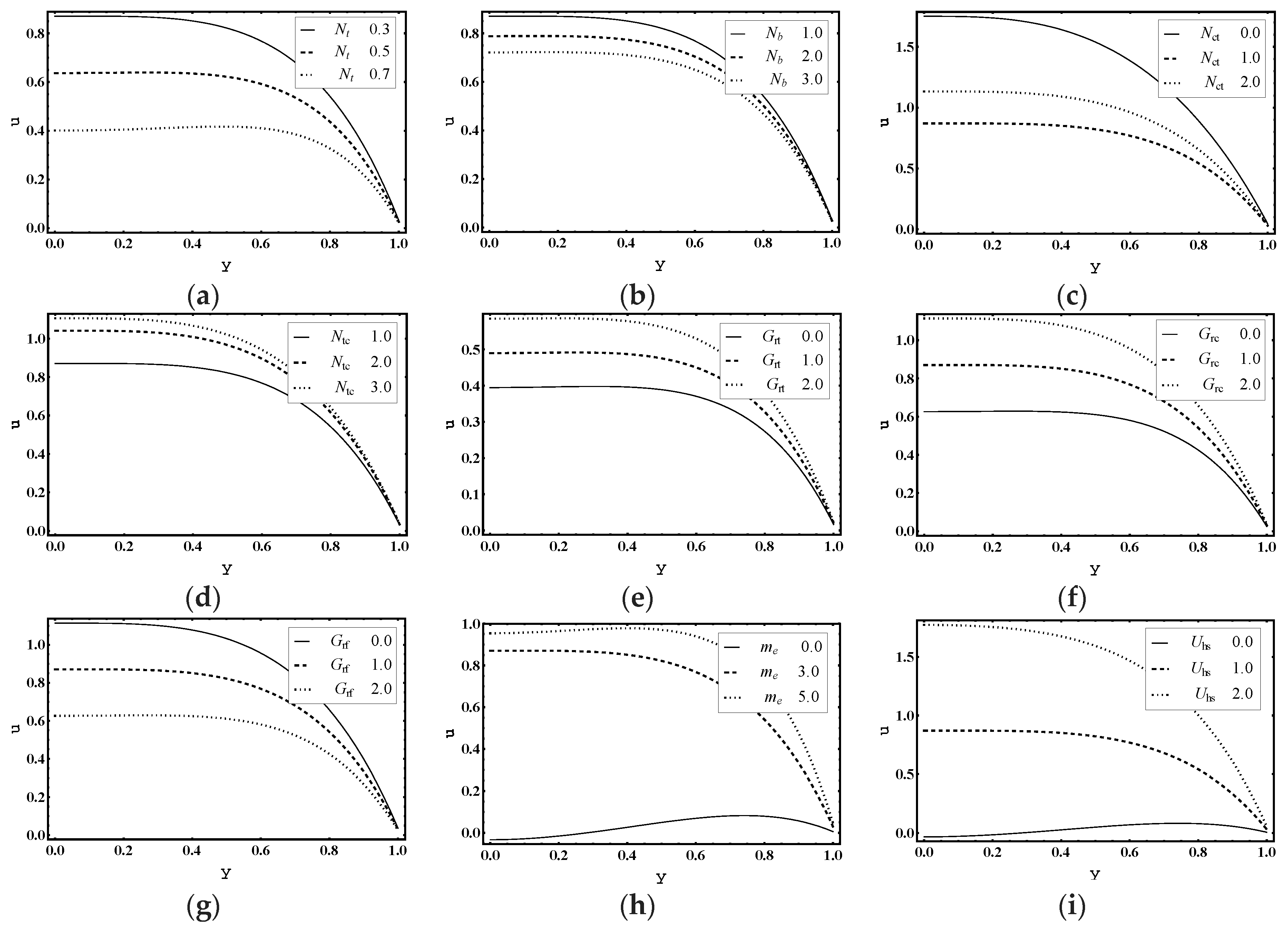
5.1. Flow Characteristics
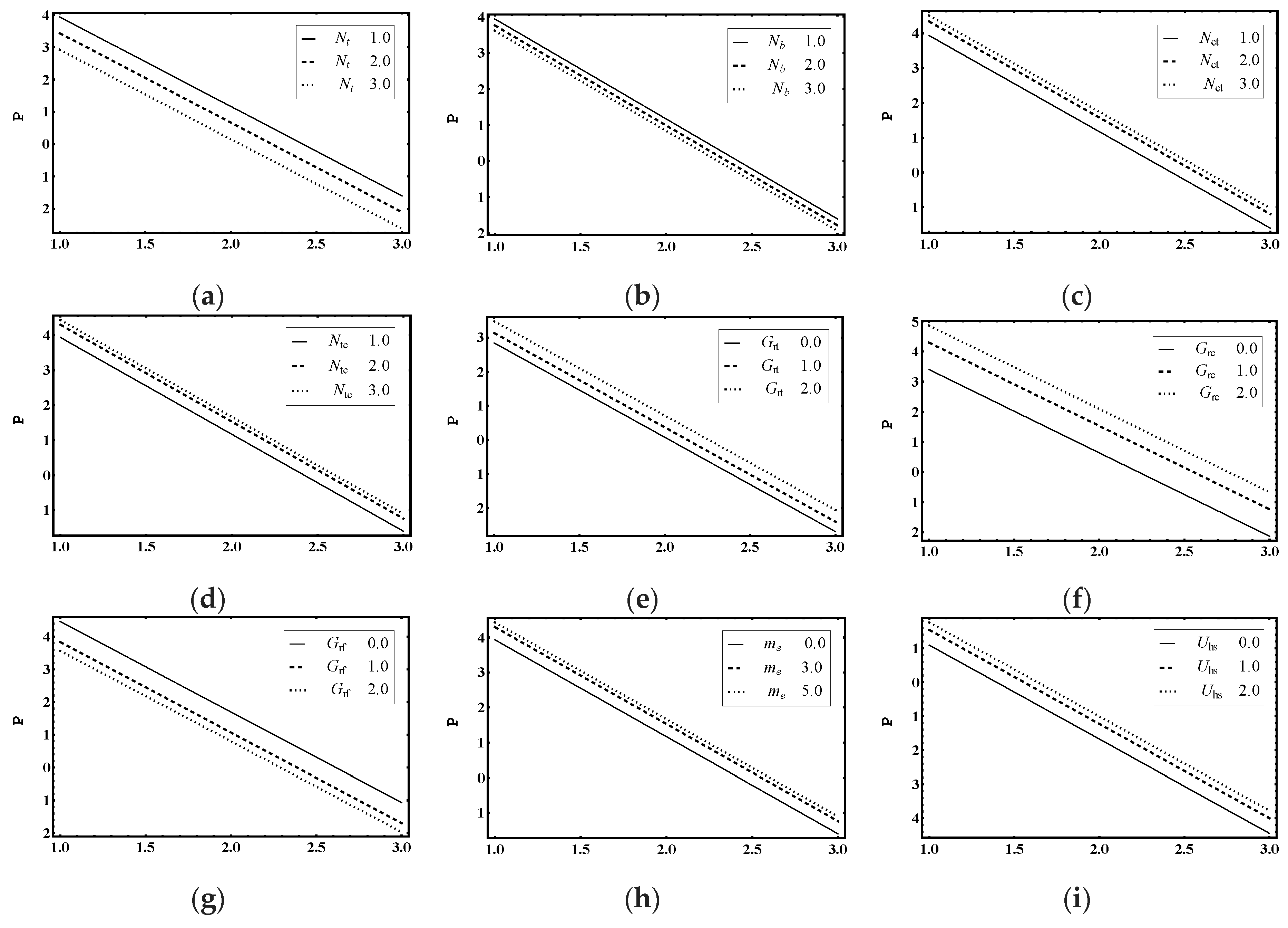
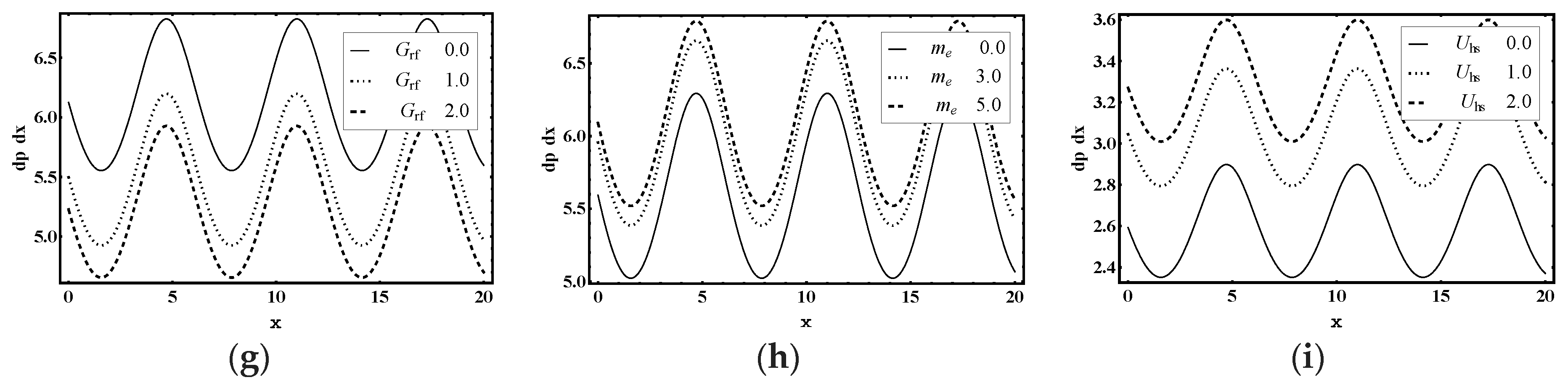
5.2. Pumping Characteristics
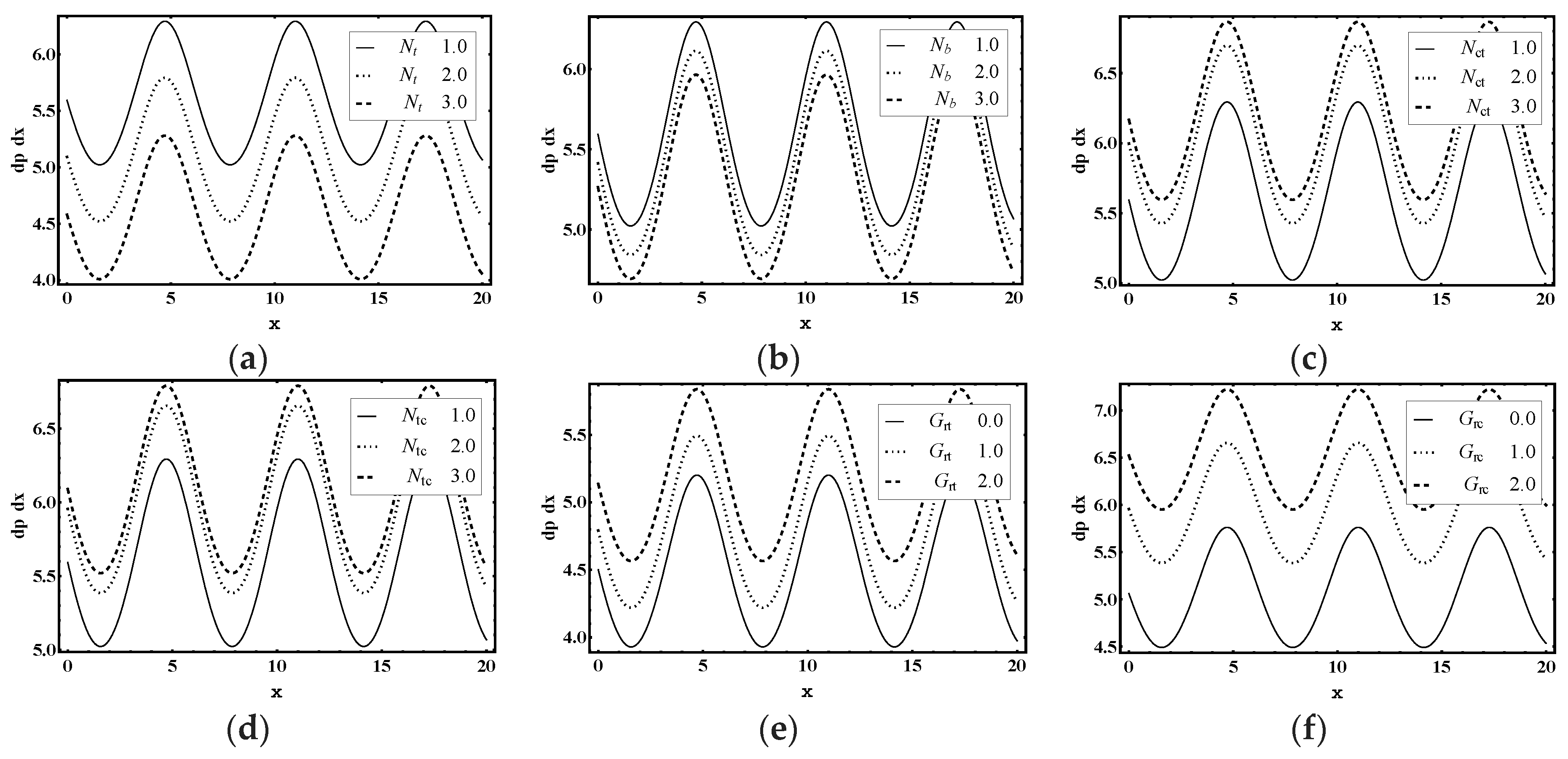
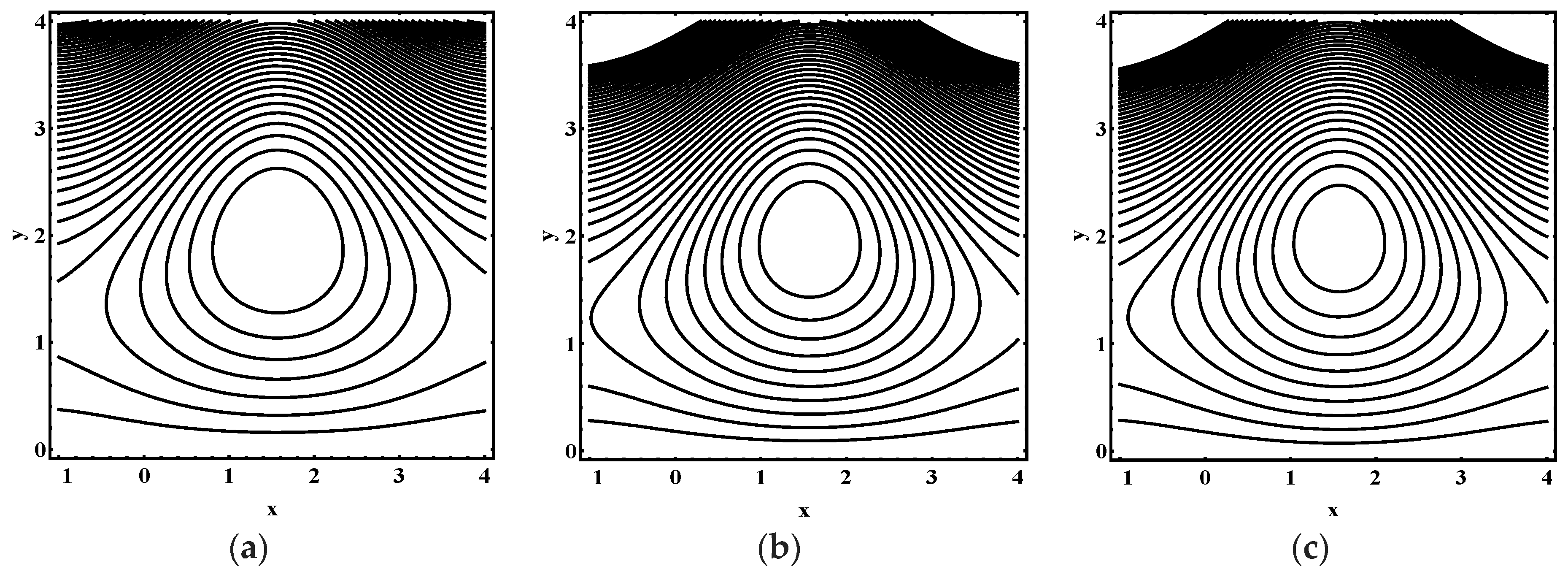
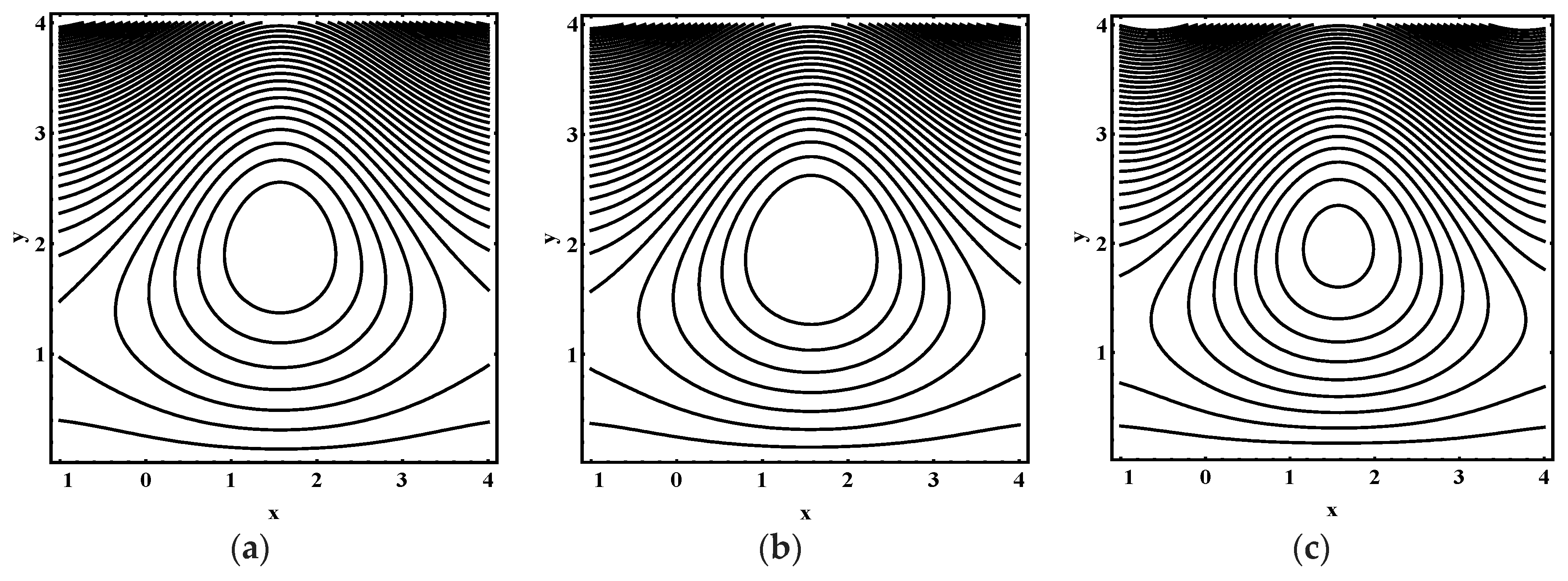
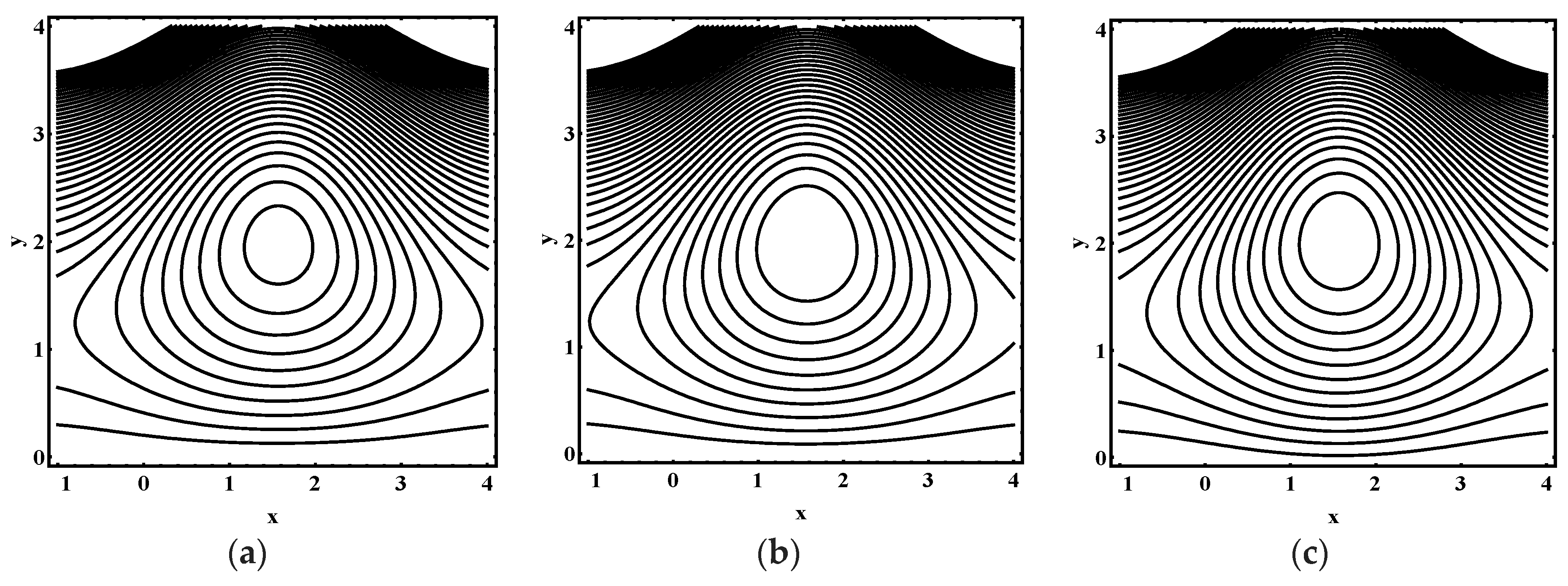
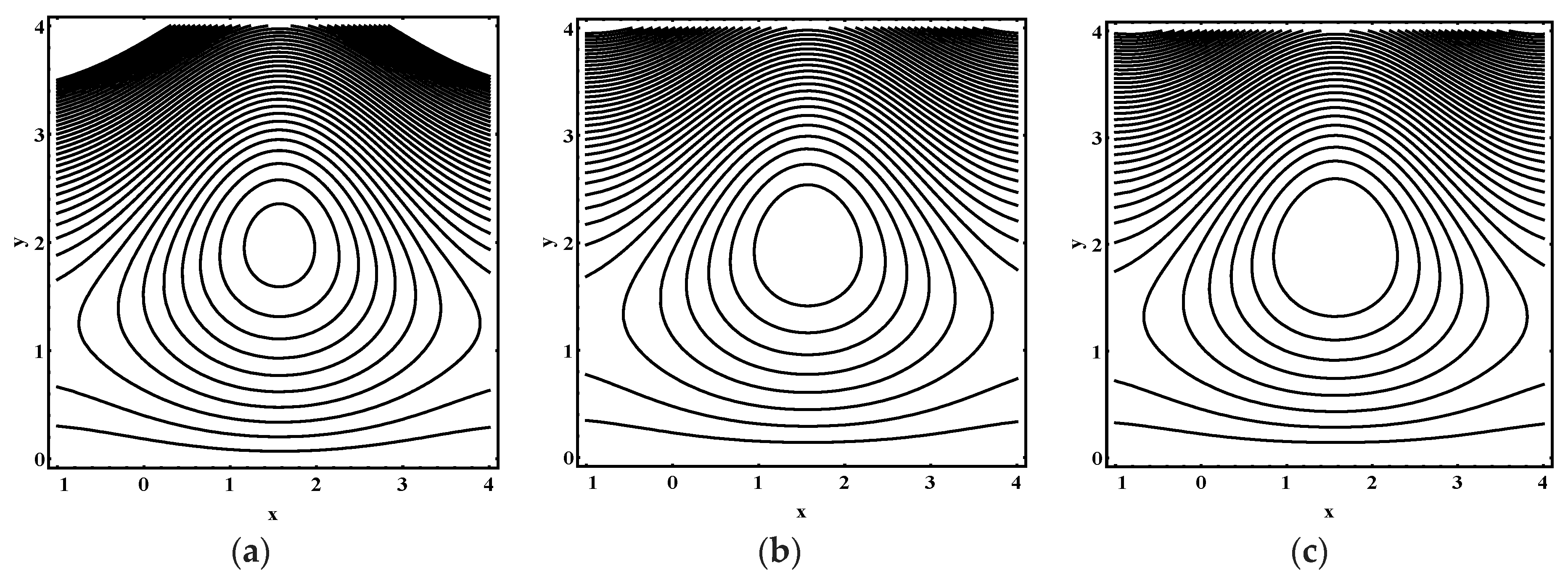
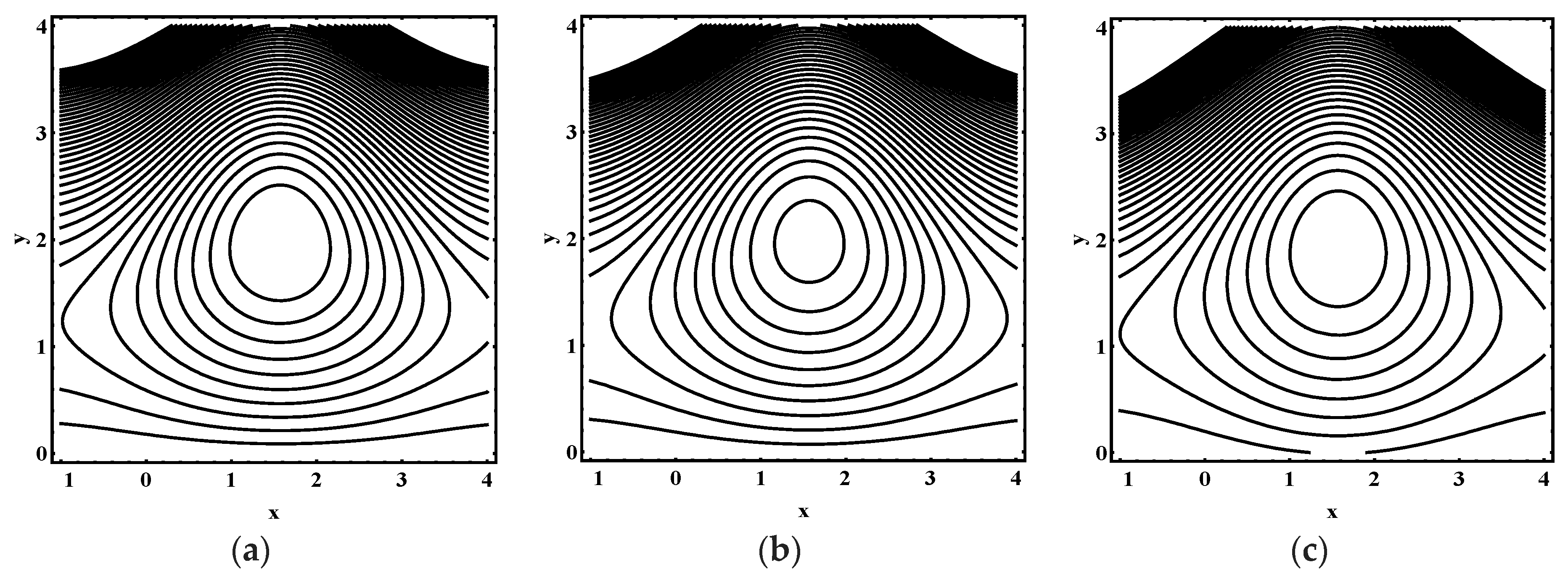
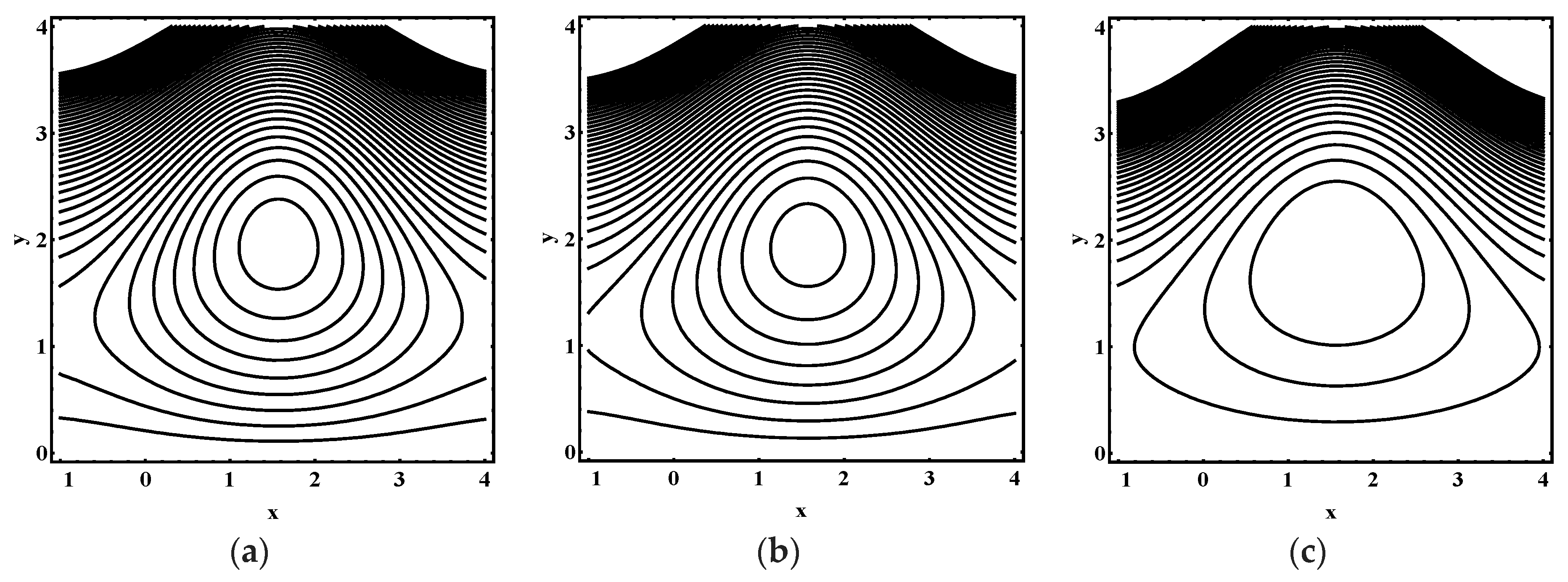
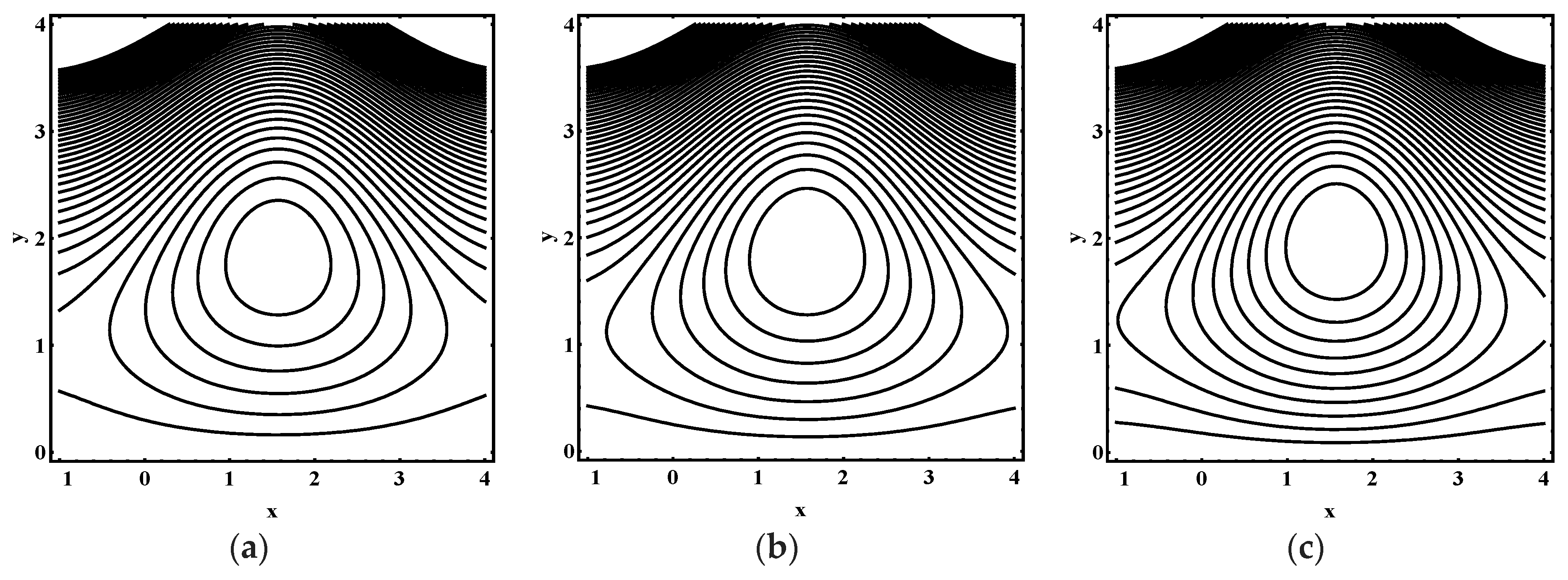
5.3. Trapping Characteristics
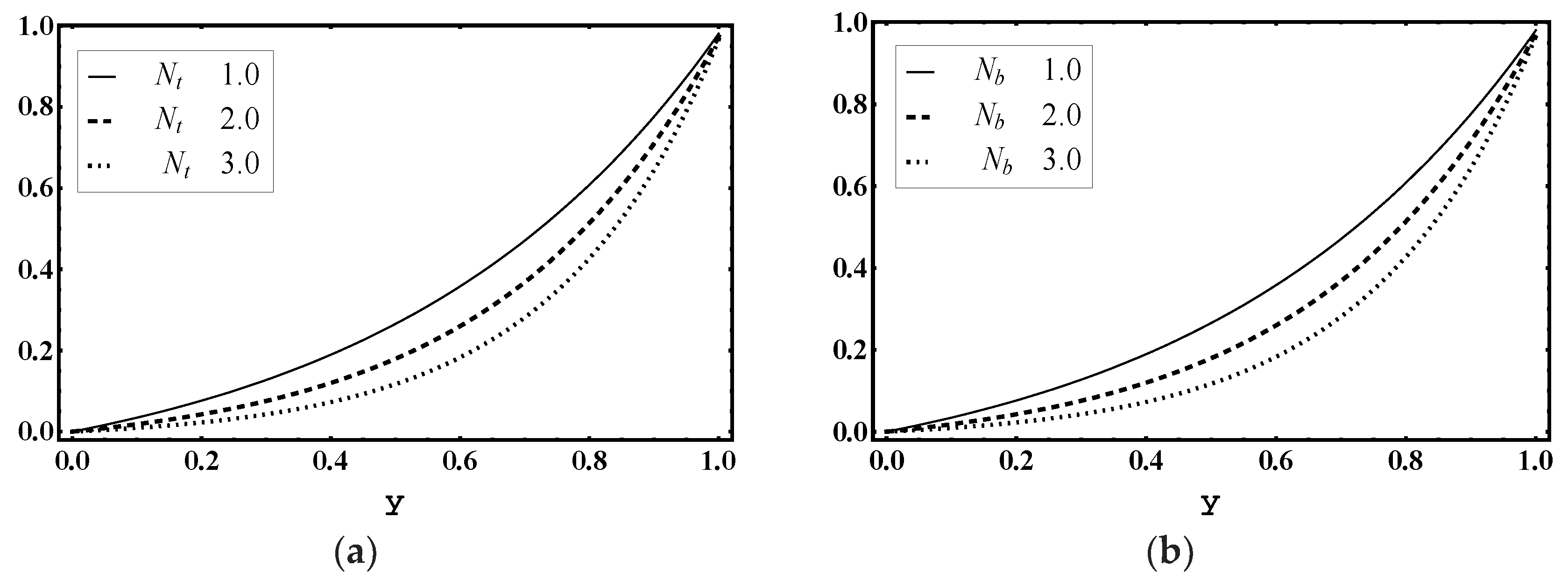
5.4. Temperature Characteristics
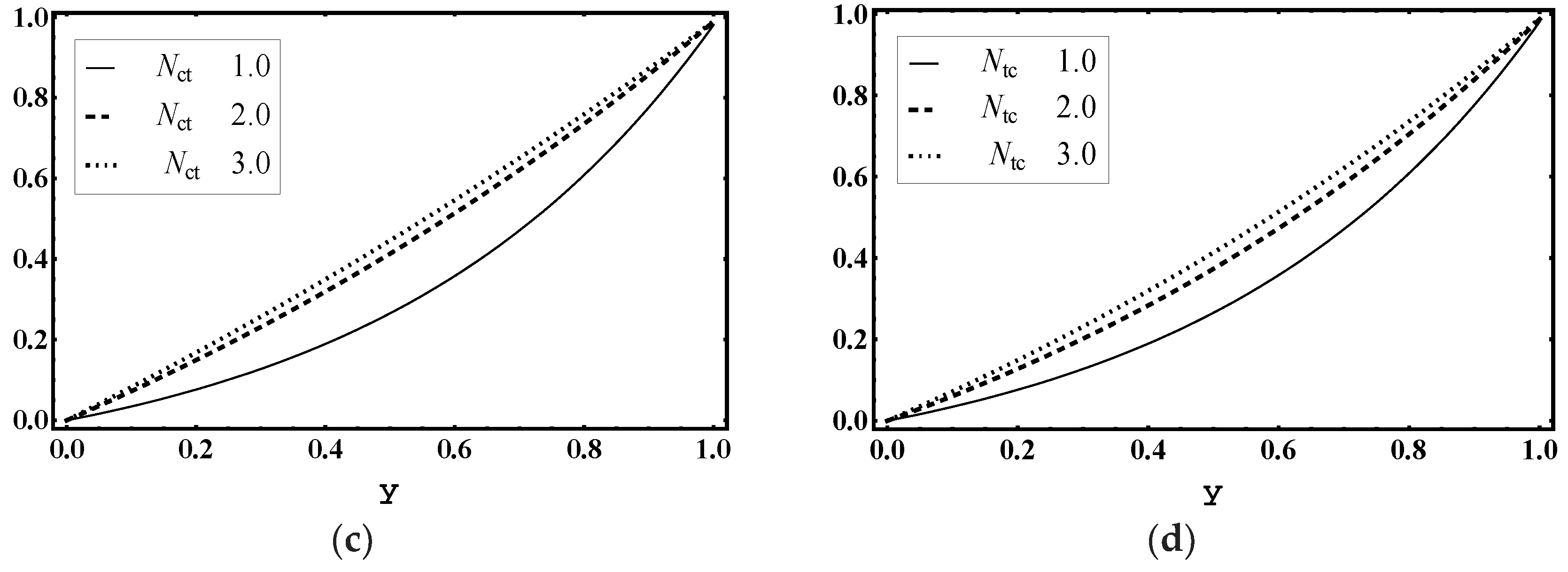
5.5. Concentration Characteristics
5.6. Nanoparticle Volume Fraction Characteristics
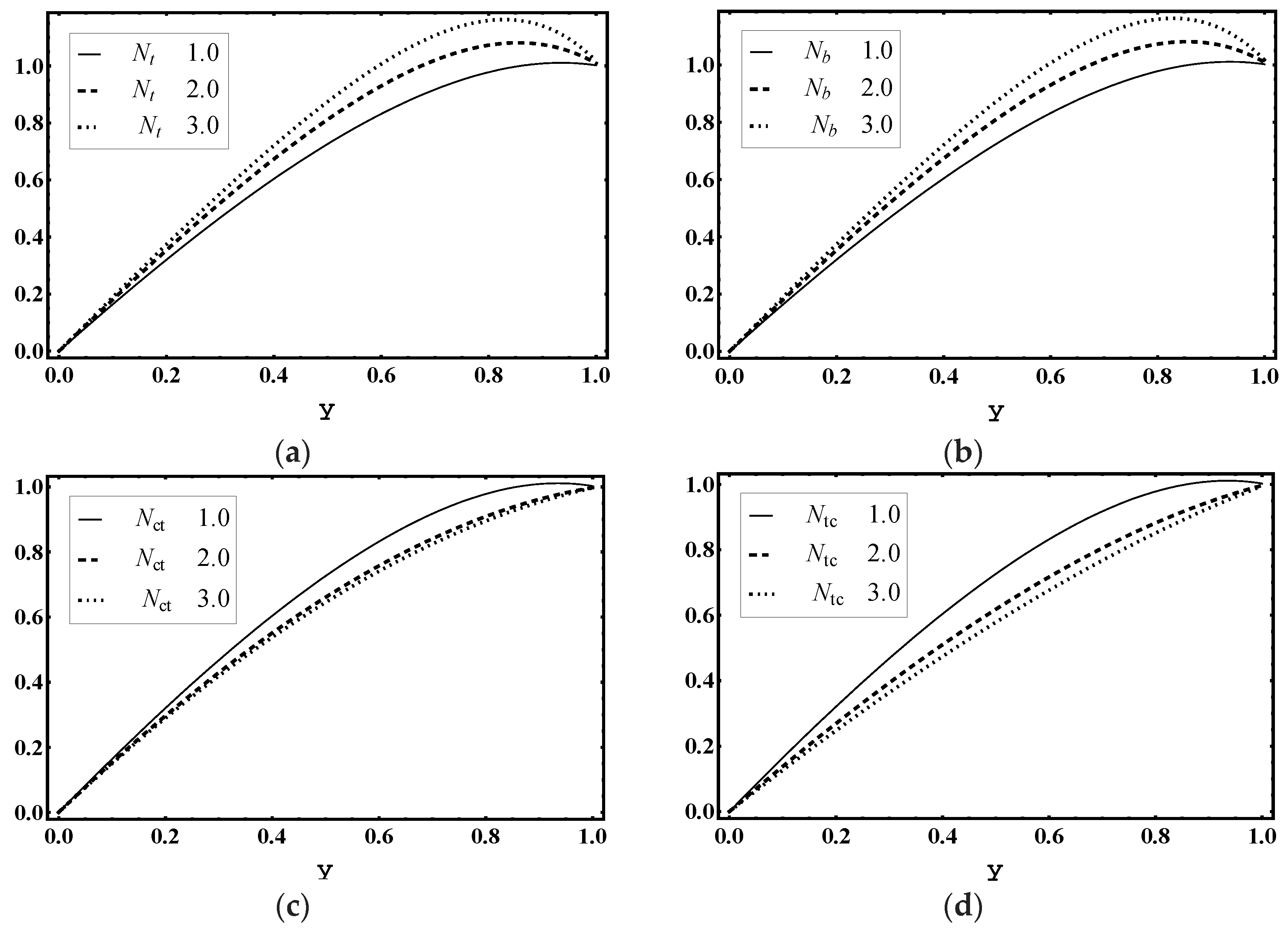
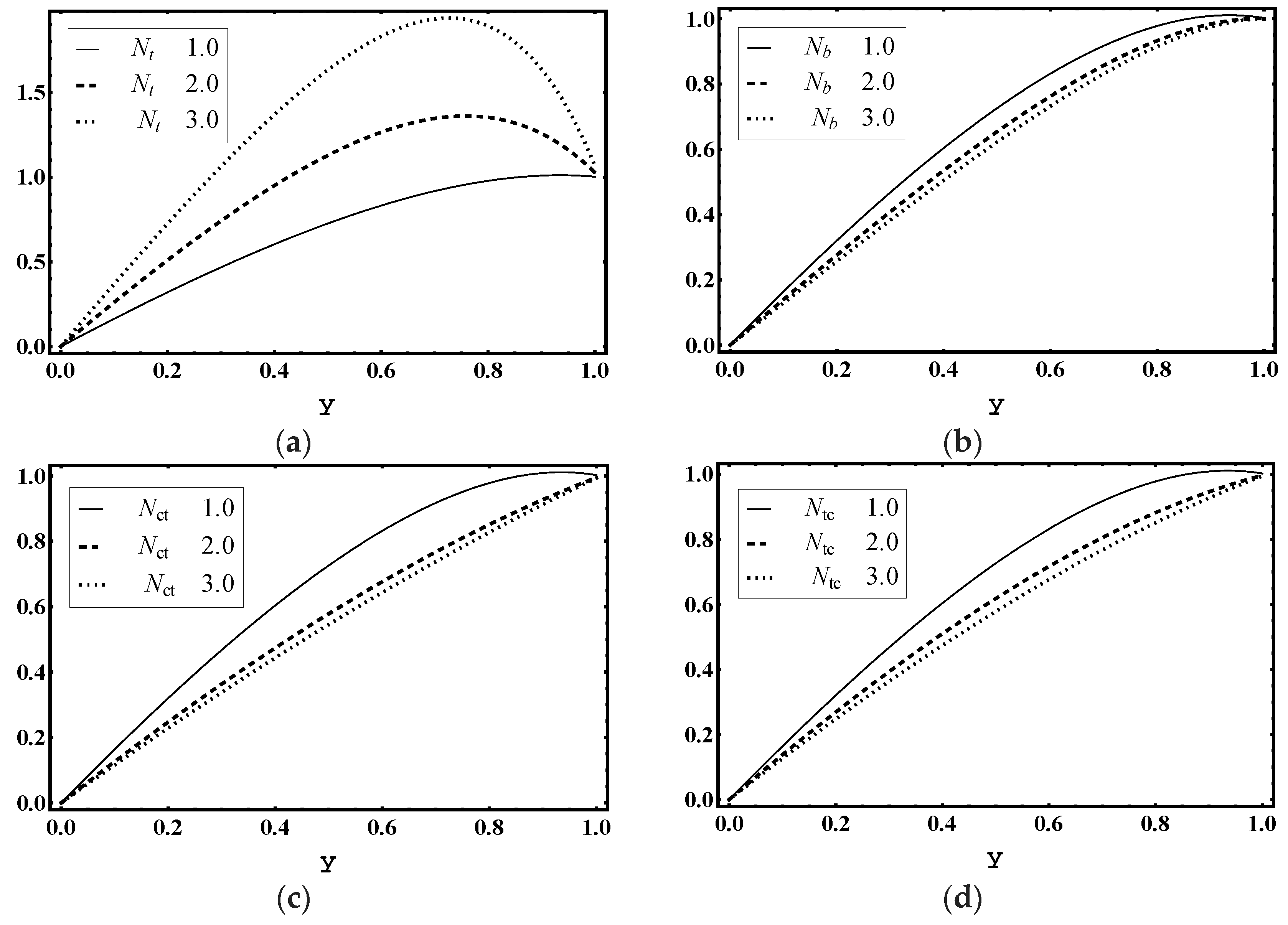
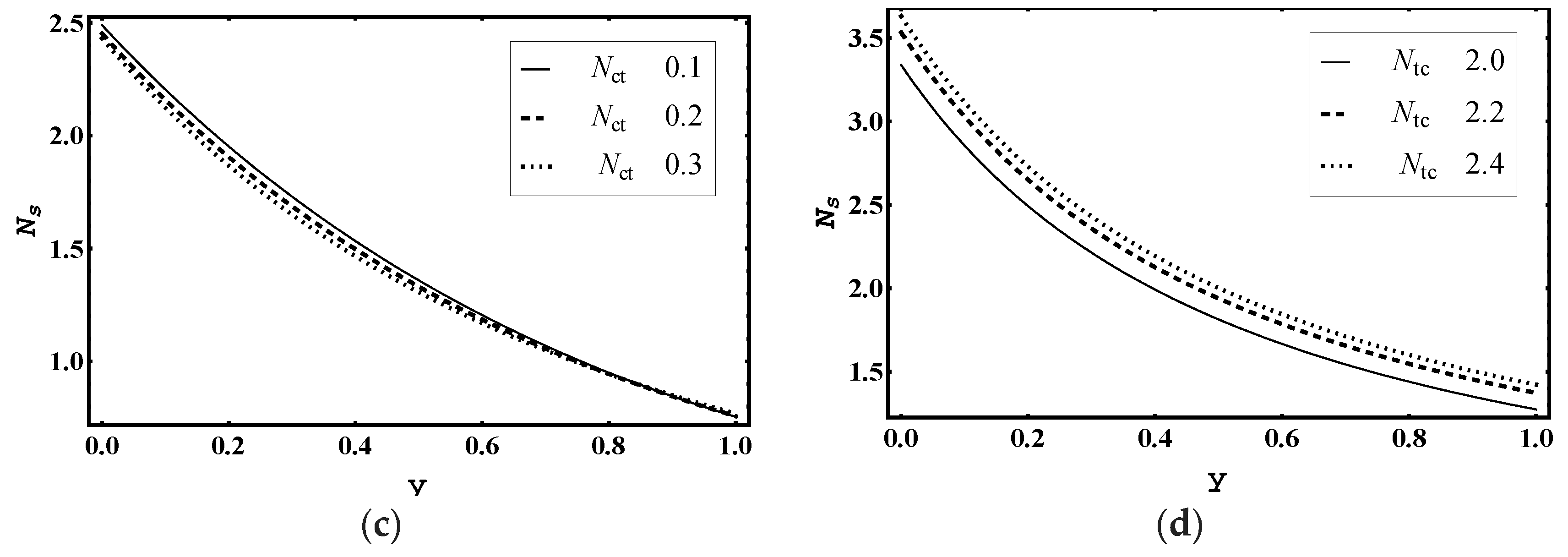
5.7. Entropy Production
5.8. Heat Transfer Coefficient
6. Concluding Remarks
- The magnitude of total entropy generation increased as the thermophoresis parameter and Brownian motion parameter increases.
- Soret parameter and Dufour parameter strongly controlld the temperature profile and Bejan number profile.
- The velocity, pressure difference, pressure rise, temperature and Bejan number profile decreased as thermophoresis parameter and Brownian motion parameter increased.
- Electro-osmotic parameter strongly affected the velocity profile.
- The magnitude of pressure difference and pressure gradient enhances in the pumping region with the increase in Soret parameter, Dufour parameter, thermal Grashof number, solutal Grashof number, nanoparticle Grashof number, electro-osmotic parameter and Helmholtz-Smoluchowski velocity.
- The volume and number of trapped bolus increased as the thermophoresis parameter , Brownian motion parameter, thermal Grashof number and Helmholtz-Smoluchowski velocity increases.
- Heat transfer coefficient, entropy generation number and nanoparticles volume fraction strongly surged with the thermophoresis parameter and the Brownian motion parameter increased.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Half width of channel [L] | |
| Amplitude of wave [] | |
| Bejan number [-] | |
| Wave speed [L/] | |
| Solutal concentration | |
| Solutal concentration for lower wall | |
| Specific heat | |
| Heat capacity of fluid | |
| Brownian diffusion coefficient | |
| Thermophoretic diffusion coefficient | |
| Solutal diffusivity | |
| Soret diffusivity | |
| Dufour diffusivity | |
| Electron charge | |
| Electric field | |
| Dimensionless volume flow rate in fixed frame | |
| Nanoparticle volume fraction | |
| Nanoparticle volume fraction for lower wall | |
| Acceleration due to gravity | |
| Thermal Grashof number [-] | |
| Solutal Grashof number [-] | |
| Nanoparticle Grashof number [-] | |
| Transverse vibration of wall | |
| Boltzmann constant | |
| Thermal conductivity | |
| Electroosmotic parameter [-] | |
| Positive, negative ions | |
| Average number of or ions | |
| Brownian motion parameter [-] | |
| Thermophoresis parameter [-] | |
| Soret parameter [-] | |
| Dufour parameter [-] | |
| Entropy generation number [-] | |
| Dimensionless entropy generation due to heat transfer [-] | |
| Dimensionless entropy generation due to solutal concentration [-] | |
| Pressure field [ML/] | |
| Pressure field [-] | |
| Prandtl number [-] | |
| Peclet number [-] | |
| Reynolds number [-] | |
| Schmidt number [-] | |
| Dimensional time [] | |
| Dimensionless time [-] | |
| Temperature field [K] | |
| Temperature of fluid at lower wall [] | |
| Average temperature [] | |
| Helmholtz-Smoluchowski velocity | |
| Dimensional velocity components in stationary frame [/T] | |
| Non-dimensional velocity components in wave frame [-] | |
| Dimensional coordinates in stationary frame [] | |
| Non-dimensional coordinates in wave frame [-] | |
| Valence of ions | |
| Heat transfer coefficient [-] | |
| Wave number [-] | |
| Volumetric thermal expansion coefficient of fluid [/K] | |
| Volumetric solutal expansion coefficient of fluid [-] | |
| Dimensionless nanoparticle volume fraction [-] | |
| Dielectric permittivity [-] | |
| Amplitude ratio [-] | |
| Non-dimensional volume flow rate [-] | |
| Dimensionless temperature [-] | |
| Wavelength of peristaltic wave [] | |
| Debye length [-] | |
| Fluid viscosity [/] | |
| Nanofluid density at reference temperature [/] | |
| Nanoparticle mass density [/] | |
| Density of fluid [/] | |
| Net ionic charge density [/] | |
| Heat capacity of fluid [/] | |
| Effective heat capacity of nanoparticle [/] | |
| Dimensional electric potential distribution [/] | |
| Non-dimensional electric potential distribution [-] | |
| Dimensional Stream function [/] | |
| Non-dimensional concentration field [-] |
References
- Reuss, F.F. Charge-induced flow. Proc. Imp. Soc. Nat. Mosc. 1809, 3, 327–344. [Google Scholar]
- Patankar, N.A.; Hu, H.H. Numerical simulation of electroosmotic flow. Anal. Chem. 1998, 70, 1870–1881. [Google Scholar] [CrossRef]
- Yang, R.J.; Fu, L.M.; Lin, Y.C. Electroosmotic flow in microchannels. J. Colloid Interface Sci. 2001, 239, 98–105. [Google Scholar] [CrossRef] [PubMed]
- Tang, G.H.; Li, X.F.; He, Y.L.; Tao, W.Q. Electroosmotic flow of non-Newtonian fluid in microchannels. J. Non-Newton. Fluid Mech. 2009, 157, 133–137. [Google Scholar] [CrossRef]
- Miller, S.A.; Young, V.Y.; Martin, C.R. Electroosmotic flow in template-prepared carbon nanotube membranes. J. Am. Chem. Soc. 2001, 123, 12335–12342. [Google Scholar] [CrossRef] [PubMed]
- Shapiro, A.H.; Jaffrin, M.Y.; Weinberg, S.L. Peristaltic pumping with long wavelengths at low Reynolds number. J. Fluid Mech. 1969, 37, 799–825. [Google Scholar] [CrossRef]
- Noreen, S.; Qasim, M. Peristaltic flow with inclined magnetic field and convective boundary conditions. Appl. Bionics Biomech. 2014, 11, 61–67. [Google Scholar] [CrossRef]
- Noreen, S.; Qasim, M. Influence of Hall Current and Viscous Dissipation on Pressure Driven Flow of Pseudoplastic Fluid with Heat Generation: A Mathematical Study. PLoS ONE 2015, 10, e0129588. [Google Scholar] [CrossRef] [PubMed]
- Kefayati, G.R. Magnetic field effect on heat and mass transfer of mixed convection of shear-thinning fluids in a lid-driven enclosure with non-uniform boundary conditions. J. Taiwan Inst. Chem. Eng. 2015, 51, 20–33. [Google Scholar] [CrossRef]
- Noreen, S. Effects of Joule Heating and Convective Boundary Conditions on Magnetohydrodynamic Peristaltic Flow of Couple-Stress Fluid. J. Heat Transf. 2016, 138, 094502. [Google Scholar] [CrossRef]
- Noreen, S. Magneto-thermo hydrodynamic peristaltic flow of Eyring-Powell nanofluid in asymmetric channel. Nonlinear Eng. 2018, 7, 83–90. [Google Scholar] [CrossRef]
- Akbar, N.S.; Nadeem, S. Endoscopic effects on peristaltic flow of a nanofluid. Commun. Theor. Phys. 2011, 56, 761. [Google Scholar] [CrossRef]
- Noreen, S. Mixed convection peristaltic flow of third order nanofluid with an induced magnetic field. PLoS ONE 2013, 8, e78770. [Google Scholar] [CrossRef] [PubMed]
- Tripathi, D.; Bég, O.A. A study on peristaltic flow of nanofluids: Application in drug delivery systems. Int. J. Heat Mass Transf. 2014, 70, 61–70. [Google Scholar] [CrossRef]
- Reddy, M.G.; Reddy, K.V. Influence of Joule heating on MHD peristaltic flow of a nanofluid with compliant walls. Procedia Eng. 2015, 127, 1002–1009. [Google Scholar] [CrossRef]
- Ebaid, A.; Aly, E.H. Additional results for the peristaltic transport of viscous nanofluid in an asymmetric channel with effects of the convective conditions. Natl. Acad. Sci. Lett. 2018, 41, 59–63. [Google Scholar] [CrossRef]
- Shao, Q.; Fahs, M.; Younes, A.; Makradi, A.; Mara, T. A new benchmark reference solution for double-diffusive convection in a heterogeneous porous medium. Numer. Heat Transf. Part B Fundam. 2016, 70, 373–392. [Google Scholar] [CrossRef]
- Huppert, H.E.; Turner, J.S. Double-diffusive convection. J. Fluid Mech. 1981, 106, 299–329. [Google Scholar] [CrossRef]
- Bég, O.A.; Tripathi, D. Mathematica simulation of peristaltic pumping with double-diffusive convection in nanofluids: A bio-nano-engineering model. Proc. Inst. Mech. Eng. Part N J. Nanoeng. Nanosyst. 2011, 225, 99–114. [Google Scholar] [CrossRef]
- Kefayati, G.R. Double-diffusive mixed convection of pseudoplastic fluids in a two-sided lid-driven cavity using FDLBM. J. Taiwan Inst. Chem. Eng. 2014, 45, 2122–2139. [Google Scholar] [CrossRef]
- Rout, B.R.; Parida, S.K.; Pattanayak, H.B. Effect of radiation and chemical reaction on natural convective MHD flow through a porous medium with double diffusion. J. Eng. Thermophys. 2014, 23, 53–65. [Google Scholar] [CrossRef]
- Gaffar, S.A.; Prasad, V.R.; Reddy, E.K.; Beg, O.A. Thermal radiation and heat generation/absorption effects on viscoelastic double-diffusive convection from an isothermal sphere in porous media. Ain Shams Eng. J. 2015, 6, 1009–1030. [Google Scholar] [CrossRef]
- Mohan, C.G.; Satheesh, A. The numerical simulation of double-diffusive mixed convection flow in a lid-driven porous cavity with magnetohydrodynamic effect. Arab. J. Sci. Eng. 2016, 41, 1867–1882. [Google Scholar] [CrossRef]
- Bandopadhyay, A.; Tripathi, D.; Chakraborty, S. Electroosmosis-modulated peristaltic transport in microfluidic channels. Phys. Fluids 2016, 28, 052002. [Google Scholar] [CrossRef]
- Tripathi, D.; Mulchandani, J.; Jhalani, S. Electrokinetic transport in unsteady flow through peristaltic microchannel. AIP Publ. 2016, 1724, 020043. [Google Scholar]
- Tripathi, D.; Yadav, A.; Bég, O.A. Electro-osmotic flow of couple stress fluids in a micro-channel propagated by peristalsis. Eur. Phys. J. Plus 2017, 132, 173. [Google Scholar] [CrossRef]
- Prakash, J.; Tripathi, D. Electroosmotic flow of Williamson ionic nanoliquids in a tapered microfluidic channel in presence of thermal radiation and peristalsis. J. Mol. Liq. 2018, 256, 352–371. [Google Scholar] [CrossRef]
- Tripathi, D.; Yadav, A.; Bég, O.A.; Kumar, R. Study of microvascular non-Newtonian blood flow modulated by electroosmosis. Microvasc. Res. 2018, 117, 28–36. [Google Scholar] [CrossRef]
- Tripathi, D.; Jhorar, R.; Bég, O.A.; Shaw, S. Electroosmosis modulated peristaltic biorheological flow through an asymmetric microchannel: mathematical model. Meccanica 2018, 53, 2079–2090. [Google Scholar] [CrossRef]
- Tripathi, D.; Sharma, A.; Bég, O.A. Joule heating and buoyancy effects in electro-osmotic peristaltic transport of aqueous nanofluids through a microchannel with complex wave propagation. Adv. Powder Technol. 2018, 29, 639–653. [Google Scholar] [CrossRef]
- Waheed, S.; Noreen, S.; Hussanan, A. Study of Heat and Mass Transfer in Electroosmotic Flow of Third Order Fluid through Peristaltic Microchannels. Appl. Sci. 2019, 9, 2164. [Google Scholar] [CrossRef]
- Noreen, S.; Tripathi, D. Heat transfer analysis on electroosmotic flow via peristaltic pumping in non-Darcy porous medium. Therm. Sci. Eng. Prog. 2019, 11, 254–262. [Google Scholar] [CrossRef]
- Noreen, S.; Waheed, S.; Hussanan, A. Peristaltic motion of MHD nanofluid in an asymmetric micro-channel with Joule heating, wall flexibility and different zeta potential. Bound. Value Probl. 2019, 2019, 12. [Google Scholar] [CrossRef]
- Kefayati, G.H.R. Heat transfer and entropy generation of natural convection on non-Newtonian nanofluids in a porous cavity. Powder Technol. 2016, 299, 127–149. [Google Scholar] [CrossRef]
- Kefayati, G.R. Simulation of double diffusive natural convection and entropy generation of power-law fluids in an inclined porous cavity with Soret and Dufour effects (Part II: Entropy generation). Int. J. Heat Mass Transf. 2016, 94, 582–624. [Google Scholar] [CrossRef]
- Kefayati, G.H.R. Simulation of double diffusive MHD (magnetohydrodynamic) natural convection and entropy generation in an open cavity filled with power-law fluids in the presence of Soret and Dufour effects (part II: entropy generation). Energy 2016, 107, 917–959. [Google Scholar] [CrossRef]
- Kefayati, G.R. FDLBM simulation of entropy generation in double diffusive natural convection of power-law fluids in an enclosure with Soret and Dufour effects. Int. J. Heat Mass Transf. 2015, 89, 267–290. [Google Scholar] [CrossRef]
- Ranjit, N.K.; Shit, G.C. Entropy generation on electro-osmotic flow pumping by a uniform peristaltic wave under magnetic environment. Energy 2017, 128, 649–660. [Google Scholar] [CrossRef]
- Bhatti, M.; Sheikholeslami, M.; Zeeshan, A. Entropy analysis on electro-kinetically modulated peristaltic propulsion of magnetized nanofluid flow through a microchannel. Entropy 2017, 19, 481. [Google Scholar] [CrossRef]
- Kefayati, G.H.R. Simulation of natural convection and entropy generation of non-Newtonian nanofluid in a porous cavity using Buongiorno’s mathematical model. Int. J. Heat Mass Transf. 2017, 112, 709–744. [Google Scholar] [CrossRef]
- Kefayati, G.H.R.; Tang, H. Simulation of natural convection and entropy generation of MHD non-Newtonian nanofluid in a cavity using Buongiorno’s mathematical model. Int. J. Hydrogen Energy 2017, 42, 17284–17327. [Google Scholar] [CrossRef]
- Kefayati, G.H.R. Double-diffusive natural convection and entropy generation of Bingham fluid in an inclined cavity. Int. J. Heat Mass Transf. 2018, 116, 762–812. [Google Scholar] [CrossRef]
- Ranjit, N.K.; Shit, G.C. Entropy generation on electromagnetohydrodynamic flow through a porous asymmetric micro-channel. Eur. J. Mech. B/Fluids 2019, 77, 135–147. [Google Scholar] [CrossRef]
- Noreen, S.; Ain, Q.U. Entropy generation analysis on electroosmotic flow in non-Darcy porous medium via peristaltic pumping. J. Therm. Anal. Calorim. 2019, 137, 1991–2006. [Google Scholar] [CrossRef]



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Noreen, S.; Waheed, S.; Hussanan, A.; Lu, D. Entropy Analysis in Double-Diffusive Convection in Nanofluids through Electro-Osmotically Induced Peristaltic Microchannel. Entropy 2019, 21, 986. https://doi.org/10.3390/e21100986
Noreen S, Waheed S, Hussanan A, Lu D. Entropy Analysis in Double-Diffusive Convection in Nanofluids through Electro-Osmotically Induced Peristaltic Microchannel. Entropy. 2019; 21(10):986. https://doi.org/10.3390/e21100986
Chicago/Turabian StyleNoreen, Saima, Sadia Waheed, Abid Hussanan, and Dianchen Lu. 2019. "Entropy Analysis in Double-Diffusive Convection in Nanofluids through Electro-Osmotically Induced Peristaltic Microchannel" Entropy 21, no. 10: 986. https://doi.org/10.3390/e21100986
APA StyleNoreen, S., Waheed, S., Hussanan, A., & Lu, D. (2019). Entropy Analysis in Double-Diffusive Convection in Nanofluids through Electro-Osmotically Induced Peristaltic Microchannel. Entropy, 21(10), 986. https://doi.org/10.3390/e21100986





