Abstract
For Dempster–Shafer evidence theory, how to measure the uncertainty of basic probability assignment (BPA) is still an open question. Deng entropy is one of the methods for measuring the uncertainty of Dempster–Shafer evidence. Recently, some limitations of Deng entropy theory are found. For overcoming these limitations, some modified theories are given based on Deng entropy. However, only one special situation is considered in each theory method. In this paper, a unified form of the belief entropy is proposed on the basis of Deng entropy. In the new proposed method, the scale of the frame of discernment (FOD) and the relative scale of a focal element with reference to FOD are considered. Meanwhile, for an example, some properties of the belief entropy are obtained based on a special situation of a unified form. Some numerical examples are illustrated to show the efficiency and accuracy of the proposed belief entropy.
1. Introduction
Recently, Dempster–Shafer evidence theory [1,2] has been a useful theory for dealing with uncertainty information. It has a wide range of applications and has been extensively studied in many fields, such as decision-making [3,4,5,6], supplier management [7,8,9], pattern recognition [10], risk evaluation [11,12,13], probability density estimation [14], complex network [15,16], and so on. Dempster–Shafer evidence theory is regarded as an extension of the Bayesian theory. The basic probability assignment (BPA) is a fundamental concept in Dempster–Shafer evidence theory. Each BPA represents how strongly the evidence supports one of the elements of the frame. By giving a confidence degree for any subsets of the system, the information of quantitative or qualitative formation is represented by BPA. Meanwhile, some pieces of evidence can be combined into one piece of evidence by the rule of Dempster’s combination. However, there are some open issues in Dempster–Shafer evidence theory. For examples, counterintuitive results may be obtained from some highly conflicting evidence [2,17]. For real applications, a collectively exhaustive and mutually exclusive set in FOD is difficult to be satisfied for real applications [18,19]. Uncertainty modeling is usually discussed when we deal with these open issues. Therefore, how to manage the uncertainty of (BPA) accurately and efficiently is significant and has attracted widespread attention [20,21]. Some methods are proposed for measuring the uncertainty of Dempster–Shafer evidence theory such as Yager’s dissonance measures [22], distance-based measure [23,24], weighted Hartley entropy [25], Klir and Ramer’s discord measure [26] and George and Pal’s conflict measure [27].
Shannon entropy is an effective measure to handle the uncertainty of the system. Although Shannon entropy was first developed to model an uncertain measure of information volume in information theory, it is widely applied for measuring the uncertainty of kinds of systems and processes [28,29]. However, for measuring the uncertainty of Dempster–Shafer evidence theory, Shannon entropy theory can’t be applied because a mass function is a generalized probability, which is assigned on the power set of FOD in Dempster–Shafer evidence theory [30]. In order to address this problem, some modified entropy theories are proposed based on Shannon entropy such as Yager’s dissonance measures, distance-based measure, weighted Hartley entropy [22,24,25,27,31]. However, for some cases, these entropy theories can’t effectively measure the uncertainty of Dempster–Shafer evidence theory [32].
Based on Shannon entropy, a new entropy, known as Deng entropy, has been proposed recently [32]. Deng entropy uses the BPA of the evidence and the cardinality of the element of the BPA as variables to calculate the uncertainty of evidence. That is, Deng entropy considered not only the BPA of the evidence, but also the cardinality of the element of the BPA. Therefore, Deng entropy has successfully solved many practical applications and been applied to many fields [33,34,35]. Meanwhile, Deng entropy can degenerate into the Shannon entropy when the cardinality of elements in BPA is 1. Recently, some limitations of Deng entropy have been found. Deng entropy only considers the BPA of the evidence and the cardinality of the element of the BPA, without the scale of FOD. In fact, the scale of FOD is an important factor for measuring uncertainty of evidence theory [30]. Therefore, some modified methods are proposed for overcoming these limitations of Deng entropy. For examples, Zhou et al. [36], Pan et al. [37] and Cui et al. [38] modified Deng entropy, respectively. In three references, they all consider the scale of FOD and the relative scale between a focal element of FOD with itself. In these references, the relative scale of these is represented from different views, respectively. Therefore, although these methods take into consideration of the scale of FOD and the influence of the intersection between statements on uncertainty, each method only considers one special situation. In this paper, a unified form about belief entropy based on Deng entropy is proposed. The proposed entropy can improve the performance of Deng entropy by considering the scale of the FOD and the relative scale of a focal element with respect to FOD. Meanwhile, the proposed method keeps all the benefits of Deng entropy, and the proposed method can also degenerate into Shannon entropy in the sense of the probability consistency. Some numerical examples are used to illustrate the effectiveness of the proposed entropy.
This paper is organized as follows. In Section 2, some concepts about Dempster–Shafer evidence theory, Shannon entropy, Deng theory and some uncertainty measures in the Dempster–Shafer framework are briefly introduced. In Section 3, the new belief entropy is presented. In Section 4, some numerical examples are given to verify the validity, as well as a comparative study between the new belief entropy and some other uncertainty measures. The conclusions are given in Section 5.
2. Preliminaries
In this section, some methods of uncertainty measurement are briefly introduced, including Dempster–Shafer evidence theory [1,2], Shannon entropy [28], Deng entropy [32] and some other typical uncertainty measures in the Dempster–Shafer framework.
2.1. Dempster–Shafer Evidence Theory
Let X be a set of mutually exclusive and collectively exhaustive events, indicated by
where X is an FOD, and is the power set of X; we have:
A mass function, denoted as BPA, is defined as a mapping of the power set to the interval [0,1]:
where the mass function satisfies the following conditions:
where represents the belief degree to A, namely the degree of evidence supports A.
A BPA can also be represented by its associated belief function (Bel) and plausibility function (Pl), respectively. Bel and Pl are defined as follows: respectively:
In Dempster–Shafer evidence theory, there are two BPAs indicated by and , respectively. They can be combined by Dempster’s rule of combination as follows:
where k is a normalization constant, which represents the degree of conflict between and ; k is defined as follows:
where .
2.2. Shannon Entropy
In information theory, Shannon entropy, is an uncertain measure of information volume in a system or process, which is the quantification of the expected value of the information in a message. Shannon entropy, which is denoted as H, is defined as follows [28]:
where N is the number of basic states, and is the probability of state i. We have . Usually, , which means that the unit of information is bits.
Although Shannon entropy is first developed to model an uncertain measure of information volume in information theory, there are still some limitations for measuring the uncertainty of Dempster–Shafer evidence theory [38]. Therefore, other entropies are given for measuring the uncertainty of Dempster–Shafer evidence theory. In the next section, some uncertainty measures about Dempster–Shafer framework are introduced.
2.3. Some Uncertainty Measures for Dempster–Shafer Framework
X is an FOD. There are focal elements of the mass function of X, which are called A and B, and denotes the cardinality of A. For the Dempster–Shafer method, some definitions of uncertain measures are briefly introduced as follows.
2.3.1. Hohle’s Confusion Measure
Hohle’s confusion measure, denoted as , is defined as follows [26]:
2.3.2. Yager’s Dissonance Measure
Dissonance measure, denoted as , is defined as follows [22]:
2.3.3. Dubois and Prade’s Weighted Hartley Entropy
Dubois and Prad’s weighted Hartley entropy, denoted as , is defined as follows [25]:
2.3.4. Klir and Ramer’s Discord Measure
Another discord measure, denoted as , is defined as follows [26]:
2.3.5. Klir and Parviz’s Strife Measure
Klir and Parviz’s strife measure, denoted as , is defined as follows [39]:
2.3.6. George and Pal’s Conflict Measure
The total conflict measure proposed by George and Pal, denoted as , is defined as follows [27]:
2.4. Deng Entropy and Its Modified Entropy
As a generalization of Shannon entropy, Deng entropy is given as follows:
where X is the FOD, A represents a proposition in mass function m and is the cardinality of proposition A. From the above definition, Deng entropy can be degenerated to the Shannon entropy if and only if the mass value is assigned to singleton elements, which is .
2.4.1. Zhou et al.’s Entropy
Zhou et al. considered the scale of FOD, and defined another belief entropy as follows [30]:
where represents the number of proposition A, and represents the cardinality of X, which is the FOD.
2.4.2. Pan et al.’s Entropy
Inspired by Deng entropy, Pan et al. give an entropy base on the probability interval in Dempster–Shafer evidence theory. Pan et al.’s entropy is given as follows [37]:
2.4.3. Cui et al.’s Entropy
Based on Deng entropy and Zhou et al.’s entropy, a new belief entropy (Cui et al.’s entropy) is defined as follows [38]:
3. The Proposed Method
In the framework of Dempster–Shafer evidence theory, the uncertain information can be modeled not only as a mass function, but also as the source of uncertainty and the number of elements in the FOD. Deng entropy only takes the BPA of the evidence and the cardinality of the element of the BPA into consideration; the relative scale of a focal element with respect to FOD and the scale of FOD are totally ignored. Although these factors are considered in the modified method such as in Refs. [30,37,38], they are not a unified form. In this paper, a new belief entropy, which is called W entropy, is proposed. The mass function, source of uncertainty and the scale of FOD are considered in the proposed method. Meanwhile, a unified form about the scale of FOD and the relative scale of a focal element with reference to FOD is given in the proposed method. W entropy is defined as follows:
where is a constant and , is the function about the cardinality of X. A is a proposition in mass function m, and denotes the cardinality of proposition A. From Equation (19), Deng entropy and its modified entropy are a special case of W entropy. For example, W entropy is the same as Deng entropy when in Equation (19). For Zhou et al.’s entropy (Equation (16)) and Cui et al.’s entropy (Equation (18)), they are , and in W entropy (Equation (19)), respectively. That is, is an indeterminate nonnegative number, and it can take an appropriate number based on the actual example. In fact, compared with Zhou et al.’s entropy and Cui et al.’s entropy, it is more typical to replace with e.
Meanwhile, when the number of conditionals of that increases by the scale of the frame of discernment in Zhou et al.’s entropy and Cui et al.’s entropy, the influence of the number of conditions for the intersection of elements will be greatly reduced for the measurement of the uncertainty of the evidence. Therefore, in this paper, let , and we have W entropy that is denoted as follows:
where is the cardinality of the intersection of A and B, and is the cardinality of the union set of A and B.
4. Numerical Examples
In this section, some examples are used to present the effectiveness and superiority of W entropy based on Equation (20). Firstly, the classical problem of Dempster–Shafer evidence theory is discussed.
In order to solve the high conflict evidence combination problem of D–S evidence, a new method of evidence modification is established and then based on the new entropy in this paper.
Step 1: Through the sensor, we obtain the evidence bodies in different directions and determine their BPA, which are recorded as . They represent different decision schemes and have some influence on the final decision-making scheme.
Step 2: With the new proposed entropy (W entropy), determine the entropy of each piece of evidence, denoted as
Step 3: Intuitively, the more confusing the evidence is, the more uncertain the information that it contains, the accuracy is then lower, and vice versa. Hence, we define the formula of the weight of evidence as follows:
where is the entropy value of the evidence , and is the weight of the evidence . When , the value of the function is equal to 1, and, when the gradually increases, the value of the function approaches zero at an exponential rate.
Step 4: By using a combination of D–S evidence theory, the BPA of the modified evidence is combined by times to obtain the final decision-making scheme.
Example 1: Assume that the FOD is . The results of FOD are presented and listed as follows:
The results of the combination by using the Dempster’s combination rule and the proposed method are shown in Table 1, respectively.

Table 1.
The results of the new proposed entropy with combination rule.
In fact, and means that A and B are strongly supported in the and , respectively. While in the results of a combination using the Dempster’s combination rule. Therefore, from Table 1, the results of Dempster–Shafer evidence theory are counter-intuitive. However, the result () of the proposed method is feasible and resultful.
Secondly, an example is given for comparing the rule of the Deng entropy, Zhou et al.’s entropy and Cui et al.’s entropy, and the proposed method.
Example 2: Assume that the FOD is . The results present a body of evidence (BOE) listed as follows:
The uncertainty of and are used by the Deng entropy, Zhou et al.’s entropy and Cui et al.’s entropy, respectively. The results are as follows:
Deng entropy:
Zhou’s belief entropy:
Cui et al.’s entropy:
From these results, these entropies have the same shortages that couldn’t measure the differences of uncertain degree between two BOEs. Deng entropy and Zhou’s belief entropy only considered the two effects of BPAs and the conditional number of focal elements. Cui et al.’s entropy considers the condition number of the intersection between focal elements of evidence on the basis of Deng entropy. However, when the number of conditions for identifying the frame is large, the influence factor of the number of conditions for the intersection of elements between the evidence will be greatly reduced for the measurement of the uncertainty of the evidence. In other words, in the framework of multi-element recognition, Cui et al.’s entropy and Deng entropy have strong similarity. However, the uncertainty of and is distinguished by the proposed method. According to Equation (20), two BOEs are calculated and shown as follows:
From these results, W entropy not only considered the scale of the FOD and the influence of the intersection between statements on uncertainty in BPA, but also solved the problem of uncertain measurement under the framework of multi-element recognition.
Example 3 [30]: Given a frame of discernment X with 15 elements that are denoted as element 1, element 2, etc. That is, the FOD . A mass function is shown as follows:
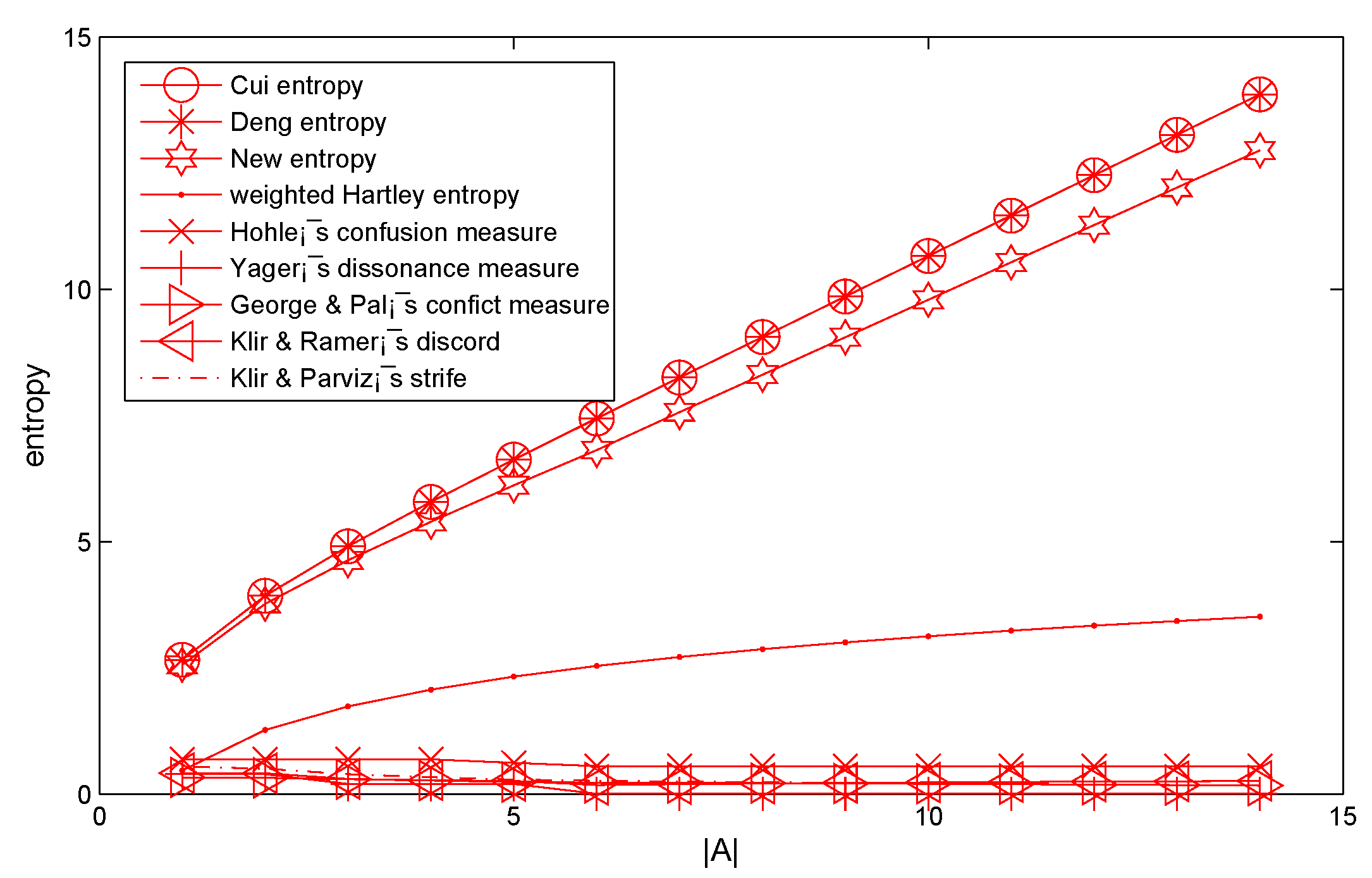
where A is a variable subset, the number of the element of A is changed from element 1 to element 14. When the A changes, Deng entropy, Cui’s entropy and W entropy are calculated and shown in Table 2 and Figure 1, respectively.

Table 2.
Deng entropy, Cui’s entropy and W entropy for A changes.
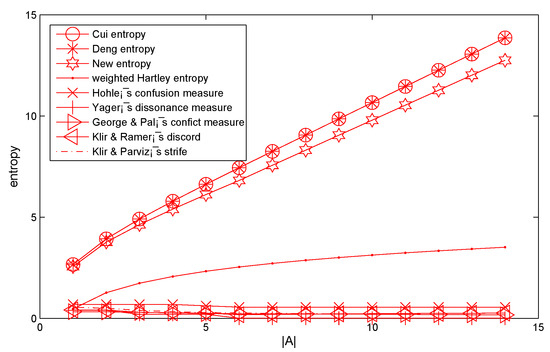
Figure 1.
Comparison between the new entropy and other uncertainty measures based on Example 3.
From Table 2 and Figure 1, the results showed that some other entropies and our proposed method are smaller than Deng entropy and Cui’s entropy. This is reasonable because more information in the BOE is taken into consideration within these entropies and the proposed method. When the frame has fewer elements, the W entropy gets almost the same result as the calculation of Cui’s entropy. In particular, when the mass value (BPA) is assigned only on a singleton element subset and the intersection of focal elements of evidence as empty; W entropy can degenerate to the following equation:
As shown in Table 2 and Figure 1, the uncertain degree measured by Deng entropy, Cui’s entropy and the proposed entropy are obviously increased with the linear increasing of . From Figure 1, Deng entropy and Cui’s entropy almost coincide and can’t distinguish the different uncertain degree of them. The proposed entropy (W entropy) successfully solved the above problems, and ensure it to be more reasonable and effective for uncertainty measure in Dempster–Shafer framework.
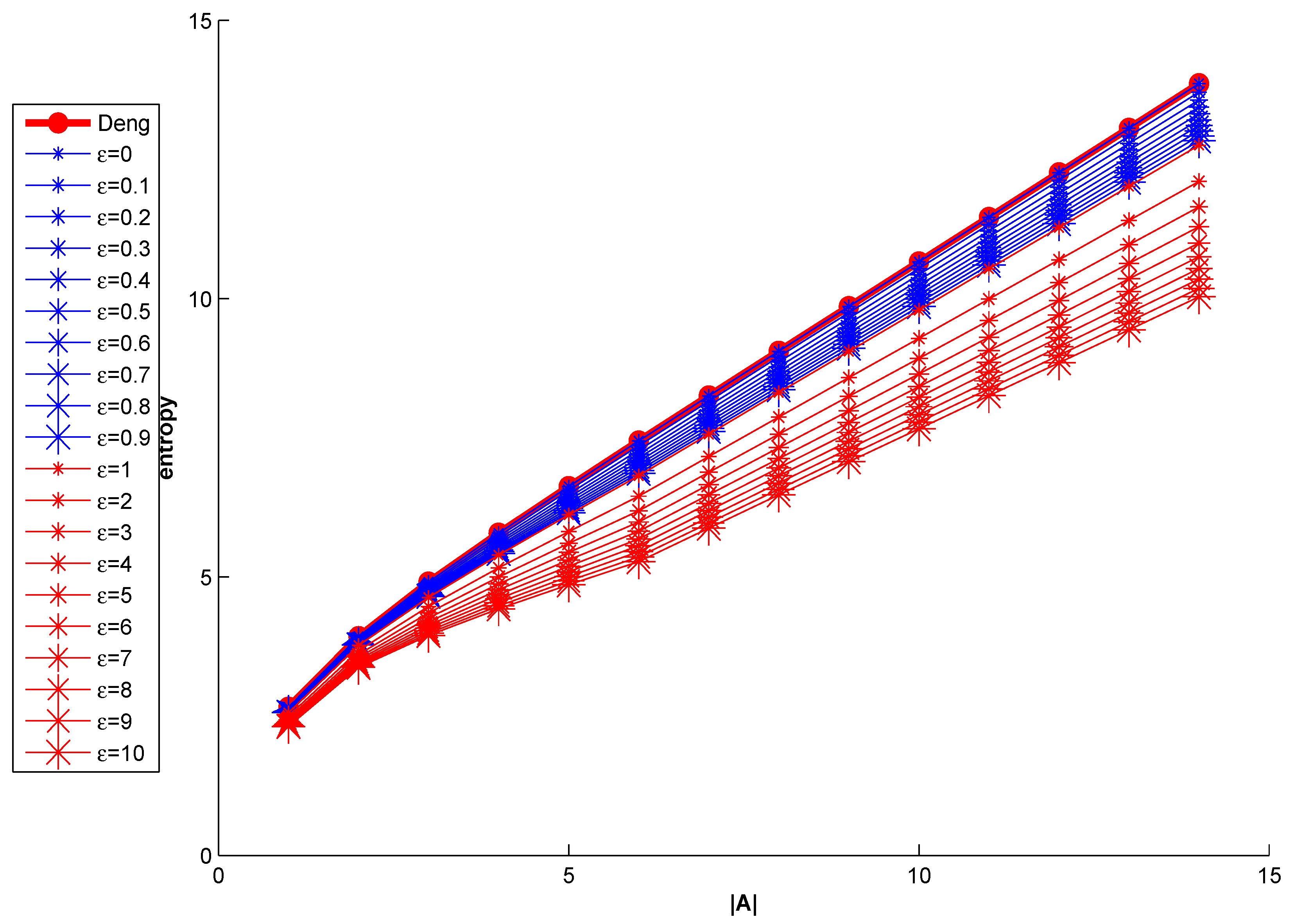
Meanwhile, some models of W entropy are given on the basis of Equation (20). The relationship of the value of W entropy and parameter is shown in Figure 2.
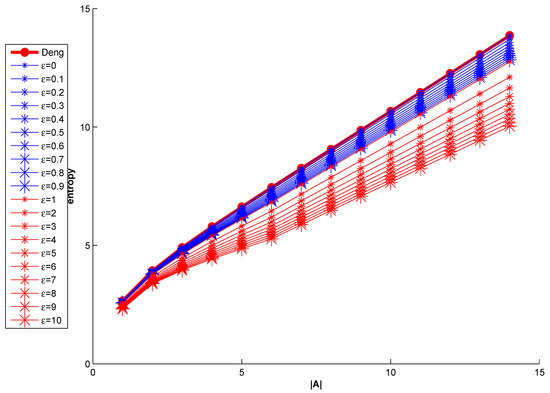
Figure 2.
Based on Equation (20), the relationship of the value of W entropy and parameter .
5. Conclusions
Although Deng entropy is a useful method for measuring the uncertainty of BPA in Dempster–Shafer evidence, there are some limitations. Therefore, some entropy theories were modified based on Deng entropy. However, only one special situation is considered in each theory method. This paper represents a unified form of the belief entropy, which considers the scale of the frame of discernment (FOD) and the influence of the intersection between statements on uncertainty. The previous work about Deng entropy is a special situation of the proposed method. Furthermore, when the mass value (BPA) is assigned only on a singleton element subset and the intersection of focal elements of evidence as empty, W entropy can degenerate to Deng entropy and Shannon Entropy. Some numerical examples illustrate the effectiveness and the superiority of the proposed entropy. The proposed entropy gives a unified form of computational uncertainty, which not only considers the scale of the FOD and the influence of the intersection between statements on uncertainty in BPA, but also solved the problem of uncertain measurement under the framework of multi-element recognition.
Author Contributions
For research articles with several authors, a short paragraph specifying their individual contributions must be provided. The following statements should be used “conceptualization, D.W. (Dan Wang) and D.W. (Daijun Wei); methodology, D.W. (Dan Wang); software, J.G.; validation, D.W. (Dan Wang), J.G. and D.W. (Daijun Wei); formal analysis, D.W. (Dan Wang); investigation, J.G.; resources, D.W. (Daijun Wei); data curation, D.W. (Dan Wang); writing–original draft preparation, D.W. (Dan Wang); writing–review and editing, D.W. (Dan Wang); visualization, D.W. (Dan Wang); supervision, D.W. (Dan Wang); project administration, D.W. (Daijun Wei); funding acquisition, D.W. (Daijun Wei)”.
Funding
The work is partially supported by the National Natural Science Foundation of China (Grant No. 61763009) and the Training Programs of Innovation and Entrepreneurship for Undergraduates of Hubei Minzu University (Grant Nos. S201910517096 and X201910517190).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gordon, J.; Shortliffe, E.H. The Dempster–Shafer theory of evidence. Rule-Based Expert Systems: The MYCIN Experiments of the Stanford Heuristic Programming Project. Available online: https://dl.acm.org/citation.cfm?id=85351 (accessed on 9 October 2019).
- Zadeh, L.A. A simple view of the Dempster–Shafer theory of evidence and its implication for the rule of combination. AI Mag. 1986, 7, 85. [Google Scholar]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision-making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Bell, D.E. Regret in decision-making under uncertainty. Oper. Res. 1982, 30, 961–981. [Google Scholar] [CrossRef]
- Polikar, R. Ensemble based systems in decision-making. IEEE Circuits Syst. Mag. 2006, 6, 21–45. [Google Scholar] [CrossRef]
- Edwards, W. The theory of decision-making. Psychol. Bull. 1954, 51, 380. [Google Scholar] [CrossRef]
- Spekman, R.E.; Kamauff, J.; Spear, J. Towards more effective sourcing and supplier management. Eur. J. Purch. Supply Manag. 1999, 5, 103–116. [Google Scholar] [CrossRef]
- Reuter, C.; Foerstl, K.; Hartmann, E.; Blome, C. Sustainable global supplier management: The role of dynamic capabilities in achieving competitive advantage. J. Supply Chain Manag. 2010, 46, 45–63. [Google Scholar] [CrossRef]
- Choi, T.Y.; Kim, Y. Structural embeddedness and supplier management: A network perspective. J. Supply Chain Manag. 2008, 44, 5–13. [Google Scholar] [CrossRef]
- Hu, M.K. Visual pattern recognition by moment invariants. IRE Trans. Inf. Theory 1962, 8, 179–187. [Google Scholar]
- Brose, M.S.; Rebbeck, T.R.; Calzone, K.A.; Stopfer, J.E.; Nathanson, K.L.; Weber, B.L. Cancer risk estimates for BRCA1 mutation carriers identified in a risk evaluation program. J. Natl. Cancer Inst. 2002, 94, 1365–1372. [Google Scholar] [CrossRef]
- Klinke, A.; Renn, O. A New Approach to Risk Evaluation and Management: Risk-Based, Precaution-Based, and Discourse-Based Strategies 1. Risk Anal. Int. J. 2002, 22, 1071–1094. [Google Scholar] [CrossRef]
- Nashef, S.A.; Roques, F.; Michel, P.; Gauducheau, E.; Lemeshow, S.; Salamon, R.; Group, E.S. European system for cardiac operative risk evaluation (Euro SCORE). Eur. J. Cardiothorac. Surg. 1999, 16, 9–13. [Google Scholar] [CrossRef]
- Epanechnikov, V.A. Non-parametric estimation of a multivariate probability density. Theory Probab. Appl. 1969, 14, 153–158. [Google Scholar] [CrossRef]
- Rubinov, M.; Sporns, O. Complex network measures of brain connectivity: Uses and interpretations. Neuroimage 2010, 52, 1059–1069. [Google Scholar] [CrossRef] [PubMed]
- Sporns, O. The human connectome: a complex network. Ann. N. Y. Acad. Sci. 2011, 1224, 109–125. [Google Scholar] [CrossRef]
- Deng, Y. Generalized evidence theory. Appl. Intell. 2015, 43, 530–543. [Google Scholar] [CrossRef]
- Wanga, N.; Liua, F.; Weia, D. A modified combination rule for D numbers theory. Math. Prob. Eng. 2016, 2016, 1–10. [Google Scholar] [CrossRef]
- Wang, N.; Liu, X.; Wei, D. A Modified D Numbers’ Integration for Multiple Attributes Decision Making. Int. J. Fuzzy Syst. 2017, 20, 1–12. [Google Scholar] [CrossRef]
- Boudraa, A.O.; Bentabet, L.; Salzenstein, F. Dempster–Shafer’s basic probability assignment based on fuzzy membership functions. Electron. Lett. Comput. Vision Image Anal. 2004, 4, 1–10. [Google Scholar] [CrossRef]
- Deng, X.; Liu, Q.; Deng, Y.; Mahadevan, S. An improved method to construct basic probability assignment based on the confusion matrix for classification problem. Inf. Sci. 2016, 340, 250–261. [Google Scholar] [CrossRef]
- Yager, R.R. Entropy and specificity in a mathematical theory of evidence. Int. J. Gen. Syst. 1983, 9, 249–260. [Google Scholar] [CrossRef]
- De Mántaras, R.L. A distance-based attribute selection measure for decision tree induction. Mach. Learn. 1991, 6, 81–92. [Google Scholar] [CrossRef]
- Morgan, B.S. An Alternate Approach to the Development of a Distance-Based Measure of Racial Segregation. Am. J. Sociol. 1983, 88, 1237–1249. [Google Scholar] [CrossRef]
- Tang, Y.; Zhou, D.; Xu, S.; He, Z. A weighted belief entropy-based uncertainty measure for multi-sensor data fusion. Sensors 2017, 17, 928. [Google Scholar] [CrossRef] [PubMed]
- Pal, N.R.; Bezdek, J.C.; Hemasinha, R. Uncertainty measures for evidential reasoning I: A review. Int. J. Approximate Reason. 1992, 7, 165–183. [Google Scholar] [CrossRef]
- George, T.; Pal, N.R. Quantification of conflict in the Dempster–Shafer framework: A new approach. Int. J. Gen. Syst. 1996, 24, 407–423. [Google Scholar] [CrossRef]
- Lin, J. Divergence measures based on the Shannon entropy. IEEE Trans. Inf. Theory 1991, 37, 145–151. [Google Scholar] [CrossRef]
- Rai, A.; Al-Hindi, H. The effects of development process modeling and task uncertainty on development quality performance. Inf. Manag. 2000, 37, 335–346. [Google Scholar] [CrossRef]
- Zhou, D.; Tang, Y.; Jiang, W. A modified belief entropy in dempster-shafer framework. PLoS ONE 2017, 12, e0176832. [Google Scholar] [CrossRef]
- Chen, X.H.; Dempster, A.P.; Liu, J.S. Weighted finite population sampling to maximize entropy. Biometrika 1994, 81, 457–469. [Google Scholar] [CrossRef]
- Deng, Y. Deng entropy. Chaos Solitons Fractals 2016, 91, 549–553. [Google Scholar] [CrossRef]
- Li, Z.; Pradeep, K.G.; Deng, Y.; Raabe, D.; Tasan, C.C. Metastable high-entropy dual-phase alloys overcome the strength-ductility trade-off. Nature 2016, 534, 227. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Xiao, F.; Deng, X.; Fei, L.; Deng, Y. Weighted evidence combination based on distance of evidence and entropy function. Int. J. Distrib. Sens. Netw. 2016, 12, 3218784. [Google Scholar] [CrossRef]
- Abellán, J. Analyzing properties of Deng entropy in the theory of evidence. Chaos Solitons Fractals 2017, 95, 195–199. [Google Scholar] [CrossRef]
- Ng, M.; Fleming, T.; Robinson, M.; Thomson, B.; Graetz, N.; Margono, C.; Mullany, E.C.; Biryukov, S.; Abbafati, C.; Abera, S.F.; et al. Global, regional, and national prevalence of overweight and obesity in children and adults during 1980–2013: A systematic analysis for the Global Burden of Disease Study 2013. Lancet 2014, 384, 766–781. [Google Scholar] [CrossRef]
- Pan, L.; Deng, Y. A new belief entropy to measure uncertainty of basic probability assignments base on belief function and plausibility function. Entropy 2018, 20, 842. [Google Scholar] [CrossRef]
- Cui, H.; Liu, Q.; Zhang, J.; Kang, B. An improved Deng entropy and its application in pattern recognition. IEEE Access 2019, 7, 18283–18292. [Google Scholar] [CrossRef]
- Florea, M.C.; Jousselme, A.L.; Grenier, D.; Bossé, É. An unified approach to the fusion of imperfect data? In Proceedings of SPIE—The International Society for Optical Engineering; SPIE: Bellingham, WA, USA, 2002; pp. 75–85. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).