High Order Split Operators for the Time-Dependent Wavepacket method of Triatomic Reactive Scattering in Hyperspherical Coordinates
Abstract
1. Introduction
2. Theory: Coordinates System, Hamiltonian and Split Operators
2.1. Theory: Mass Scaled Jacobi Coordinate and Initial WavePacket
2.2. Hyperspherical Coordinate for Triatomic Reactive Scattering
2.3. Split Operators
2.3.1. Second Order Split Operator
2.3.2. High Order Split Operator
2.4. Split Operator in the APH Coordinate
3. Results and Discussion
3.1. H + H Reaction
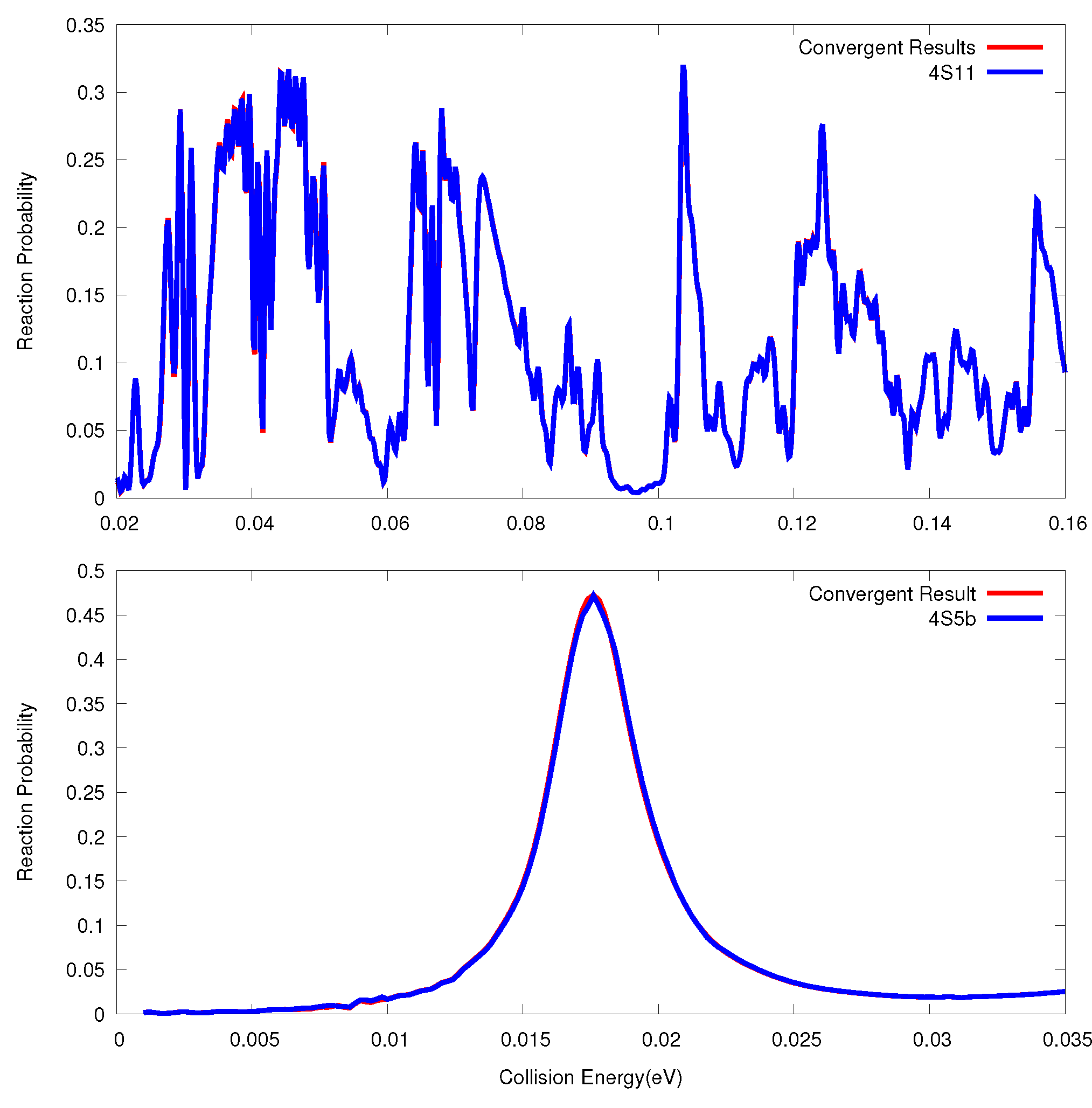
3.2. O + O Reaction
3.3. F + HD→ HF + D Reaction
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kosloff, R. Time-dependent quantum-mechanical methods for molecular dynamics. J. Phys. Chem. 1988, 92, 2087–2100. [Google Scholar] [CrossRef]
- Baumert, T.; Engel, V.; Meier, C.; Gerber, G. High laser field effects in multiphoton ionization of Na2: Experiment and quantum calculations. Chem. Phys. Lett. 1992, 200, 488–494. [Google Scholar] [CrossRef]
- Heitz, M.C.; Durand, G.; Spiegelman, F.; Meier, C. Time-resolved photoelectron spectra as probe of excited state dynamics: A full quantum study of the Na2F cluster. J. Chem. Phys. 2003, 118, 1282. [Google Scholar] [CrossRef]
- Sun, Z.; Lou, N. Autler-Townes Splitting in the Multiphoton Resonance Ionization Spectrum of Molecules Produced by Ultrashort Laser Pulses. Phys. Rev. Lett. 2003, 91, 023002. [Google Scholar] [CrossRef] [PubMed]
- Nyman, G.; Yu, H.G. Quantum theory of bimolecular chemical reactions. Rep. Prog. Phys. 2000, 63, 1001–1059. [Google Scholar] [CrossRef]
- Crawford, J.; Parker, G.A. State-to-state three-atom time-dependent reactive scattering in hyperspherical coordinates. J. Chem. Phys. 2013, 138, 054313. [Google Scholar] [CrossRef] [PubMed]
- Althorpe, S.C. Quantum wavepacket method for state-to-state reactive cross sections. J. Chem. Phys. 2001, 114, 1601. [Google Scholar] [CrossRef]
- Sun, Z.; Xu, X.; Lee, S.Y.; Zhang, D.H. A Reactant-Coordinate-Based Time-Dependent Wave Packet Method for Triatomic State-to-State Reaction Dynamics: Application to the H + O2 Reaction. J. Phys. Chem. A 2009, 113, 4145–4154. [Google Scholar] [CrossRef] [PubMed]
- Pack, R.T.; Packer, G.A. Quantum reactive scattering in three dimensions using hyperspherical (APH) coordinates. Theory. J. Chem. Phys. 1987, 87, 3888. [Google Scholar] [CrossRef]
- Zhao, H.L.; Hu, X.X.; Sun, Z.G. Quantum wavepacket method for state-to-state reactive cross sections in hyperspherical coordinates. J. Chem. Phys. 2018, 149, 174103. [Google Scholar] [CrossRef]
- Zhao, H.L.; Umer, U.; Hu, X.X.; Xie, D.Q.; Sun, Z.G. An interaction-asymptotic region decomposition method for general state-to-state reactive scatterings. J. Chem. Phys. 2019, 150, 134105. [Google Scholar] [CrossRef] [PubMed]
- Kosloff, D.; Kosloff, R. A Fourier method solution for the time-dependent Schrödinger equation as a tool in molecular dynamics. J. Comput. Phys. 1983, 52, 35–53. [Google Scholar] [CrossRef]
- Kosloff, R.; Kosloff, D. Absorbing boundaries for wave propagation problems. J. Comput. Phys. 1986, 63, 363–376. [Google Scholar] [CrossRef]
- Leforestier, C.L.; Bisseling, R.H.; Cerjan, C.; Feit, M.D.; Friesner, R.; Guldberg, A.; Hammerich, A.; Jolicard, G.; Karrlein, W.; Meyer, H.D.; et al. A comparison of different propagation schemes for the time-dependent Schrödinger equation. J. Comput. Phys. 1991, 94, 59–80. [Google Scholar] [CrossRef]
- Fattal, E.; Kosloff, R. Phase space approach for optimizing grid representations: The mapped Fourier method. Phys. Rev. E 1996, 53, 1217. [Google Scholar] [CrossRef]
- Kokoouline, V.; Dulieu, O.; Kosloff, R.; Masnou-Seeuws, F. Mapped Fourier methods for long-range molecules: Application to perturbations in the Rb2(0π+) photoassociation spectrum. J. Chem. Phys. 1999, 110, 9865. [Google Scholar] [CrossRef]
- Harris, D.O.; Engerholm, G.G.; Gwinn, W.D. Calculation of Matrix Elements for One-Dimensional Quantum-Mechanical Problems and the Application to Anharmonic Oscillators. J. Chem. Phys. 1965, 43, 1515. [Google Scholar] [CrossRef]
- Light, J.C.; Carrington, T., Jr. Discrete-variable representations and their utilization. Adv. Chem. Phys. 2000, 114, 263–310. [Google Scholar]
- Ba<i>c</i>˘i<i>c</i>´, Z.; Light, J.C. Theoretical methods for rovibrational states of floppy molecules. Annu. Rev. Phys. Chem. 1989, 40, 469–498. [Google Scholar]
- Light, J.C.; Hamilton, I.P.; Lill, J.V. Generalized discrete variable approximation in quantum mechanics. J. Chem. Phys. 1985, 82, 1400. [Google Scholar] [CrossRef]
- Tal-Ezer, H.; Kosloff, R. An accurate and efficient scheme for propagating the time-dependent Schrödinger equation. J. Chem. Phys. 1984, 81, 3967. [Google Scholar] [CrossRef]
- Feit, M.D.; Fleck, J.A., Jr.; Steiger, A. Solution of the Schrödinger equation by a spectral method. J. Comput. Phys. 1982, 47, 412–433. [Google Scholar] [CrossRef]
- Fleck, J.A., Jr.; Morris, J.R.; Feit, M.D. Time-dependent propagation of high energy laser beams through the atmosphere. Ann. Phys. 1976, 10, 129–160. [Google Scholar]
- Gray, S.K.; Balint-Kurti, G.G. Quantum dynamics with real wave packets, including application to three-dimensional (J = 0) D + H2 —> HD + H reactive scattering. J. Chem. Phys. 1998, 108, 950. [Google Scholar] [CrossRef]
- Chen, R.; Guo, H. The Chebyshev propagator for quantum systems. Comput. Phys. Commun. 1999, 119, 19–31. [Google Scholar] [CrossRef]
- Sun, Z.; Lee, S.Y.; Guo, H.; Zhang, D.H. Comparison of second-order split operator and Chebyshev propagator in wave packet based state-to-state reactive scattering calculations. J. Chem. Phys. 2009, 130, 174102. [Google Scholar] [CrossRef] [PubMed]
- Blanes, S.; Cases, F.; Oteo, J.A.; Ros, J. The Magnus expansion and some of its applications. Phys. Rep. 2009, 450, 151–238. [Google Scholar] [CrossRef]
- Bandrauk, A.D.; Dehghanuan, E.; Lu, H. Complex integration steps in decomposition of quantum exponential evolution operators. Chem. Phys. Lett. 2006, 419, 346–350. [Google Scholar] [CrossRef]
- Bandrauk, A.D.; Shen, H. Exponential split operator methods for solving coupled time-dependent Schrödinger equations. J. Chem. Phys. 1993, 99, 1185. [Google Scholar] [CrossRef]
- Bandrauk, A.D.; Shen, H. High-order split-step exponential methods for solving coupled nonlinear Schrodinger equations. J. Phys. A 1994, 27, 7147–7155. [Google Scholar] [CrossRef]
- Gray, S.K.; Manolopoulos, D.E. Symplectic integrators tailored to the time-dependent Schrödinger equation. J. Chem. Phys. 1996, 104, 7099. [Google Scholar] [CrossRef]
- Bader, P.; Blanes, S.; Fernando, C. Solving the Schrödinger eigenvalue problem by the imaginary time propagation technique using splitting methods with complex coefficients. J. Chem. Phys. 2013, 139, 124117. [Google Scholar] [CrossRef] [PubMed]
- Bandrauk, A.D.; Lu, H.Z. Exponential propagators (integrators) for the time-dependent Schrödinger equation. J. Theor. Comput. Chem. 2013, 12, 1340001. [Google Scholar] [CrossRef]
- Thalhammer, M.; Caliari, M.; Neuhauser, C. High-order time-splitting Hermite and Fourier spectral methods. J. Comput. Phys. 2009, 228, 822–832. [Google Scholar] [CrossRef]
- Antoine, X.; Bao, W.Z.; Besse, C. Computational methods for the dynamics of the nonlinear Schrödinger/Gross–Pitaevskii equations. Comput. Phys. Commun. 2013, 184, 2621–2633. [Google Scholar] [CrossRef]
- Alvermann, A.; Fehske, H.; Littlewood, P.B. Numerical time propagation of quantum systems in radiation fields. New J. Phys. 2012, 14, 105008. [Google Scholar] [CrossRef]
- Alvermann, A.; Fehske, H. High-order commutator-free exponential time-propagation of driven quantum systems. J. Comput. Phys. 2011, 230, 5930–5956. [Google Scholar] [CrossRef]
- Staruch, F.W. Any-order propagation of the nonlinear Schrödinger equation. Phys. Rev. E 2007, 76, 046701. [Google Scholar] [CrossRef]
- Sofroniou, M.; Spaletta, G. Derivation of symmetric composition constants for symmetric integrators. Optim. Methods Softw. 2005, 20, 597–613. [Google Scholar] [CrossRef]
- Schlier, C.; Seiter, A. High-order symplectic integration: An assessment. Comput. Phys. Commun. 2000, 130, 176–189. [Google Scholar] [CrossRef]
- McLachlan, R.I. Error Bounds for Dynamic Responses in Forced Vibration Problem. SIAM J. Sci. Comput. 1995, 15, 1–15. [Google Scholar]
- Omelyan, I.P.; Mrygold, I.M.; Folk, R. Construction of high-order force-gradient algorithms for integration of motion in classical and quantum systems. Phys. Rev. E 2002, 66, 026701. [Google Scholar] [CrossRef] [PubMed]
- Sun, Z.G.; Zhang, D.H.; Yang, W.T. Higher-order split operator schemes for solving the Schrödinger equation in the time-dependent wave packet method: Applications to triatomic reactive scattering calculations. Phys. Chem. Chem. Phys. 2012, 14, 1827–1845. [Google Scholar] [CrossRef] [PubMed]
- Li, W.T.; Zhang, D.H.; Sun, Z.G. Efficient Fourth-Order Split Operator for Solving the Triatomic Reactive Schrödinger Equation in the Time-Dependent Wavepacket Approach. J. Phys. Chem. A 2014, 14, 9801–9810. [Google Scholar] [CrossRef] [PubMed]
- Smith, F.T. A Symmetric Representation for Three-Body Problems. I. Motion in a Plane. J. Math. Phys. 1962, 3, 735. [Google Scholar] [CrossRef]
- Whitten, R.C.; Smith, R.T. Symmetric Representation for Three-Body Problems. II. Motion in Space. J. Math. Phys. 1968, 9, 1103. [Google Scholar] [CrossRef]
- Kuppermann, A. A useful mapping of triatomic potential energy surfaces. Chem. Phys. Lett. 1975, 32, 374–375. [Google Scholar] [CrossRef]
- Johnson, B.R. On hyperspherical coordinates and mapping the internal configurations of a three body system. J. Chem. Phys. 1980, 73, 5051. [Google Scholar] [CrossRef]
- Brink, D.M.; Satchler, G.R. Angular Momentum, 2nd ed.; Clarendon: Oxford, UK, 1968. [Google Scholar]
- Suzuki, M. Fractal decomposition of exponential operators with applications to many-body theories and Monte Carlo simulations. Phys. Lett. A 1990, 146, 319–323. [Google Scholar] [CrossRef]
- Youshida, H. Construction of higher order symplectic integrators. Phys. Lett. A 1990, 150, 262–268. [Google Scholar] [CrossRef]
- Greutz, M.; Gocksch, A. Higher-order hybrid Monte Carlo algorithms. Phys. Rev. Lett. 1989, 63, 9. [Google Scholar]
- McLachlan, R.I.; Quispel, G.R.W. Splitting methods. Acta Numer. 2002, 11, 341–434. [Google Scholar] [CrossRef]
- McLachlan, R.I. Composition methods in the presence of small parameters. BIT Numer. Math. 1995, 35, 258–268. [Google Scholar] [CrossRef]
- Monovasillis, T.; Simos, T.E. Symplectic methods for the numerical integration of the Schrödinger equation. Comput. Mater. Sci. 2007, 38, 526–532. [Google Scholar] [CrossRef]
- Hairer, E.; Wanner, G.; Lubich, C. Geometric Numerical Integration; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Boothroyd, A.I.; Keogh, W.J.; Martin, P.G.; Peterson, M.R. A refined H3 potential energy surface. J. Chem. Phys. 1996, 104, 7139. [Google Scholar] [CrossRef]
- Babikov, D.; Kendrick, B.K.; Walker, P.B.; Pack, R.T. Metastable states of ozone calculated on an accurate potential energy surface. J. Chem. Phys. 2003, 118, 6298. [Google Scholar] [CrossRef]
- Fu, B.; Zhang, D.H. A hierarchical construction scheme for accurate potential energy surface generation: An application to the F + H2 reaction. J. Phys. Chem. 2008, 129, 011103. [Google Scholar] [CrossRef] [PubMed]
- Ren, Z.; Che, L.; Qiu, M.; Wang, X.; Dong, W.; Dai, D.; Wang, X.; Yang, X.; Sun, Z.; Fu, B.; et al. Probing the resonance potential in the F atomreaction with hydrogen deuteride withspectroscopic accuracy. Proc. Natl. Acad. Sci. USA 2008, 105, 12662–12666. [Google Scholar] [CrossRef]
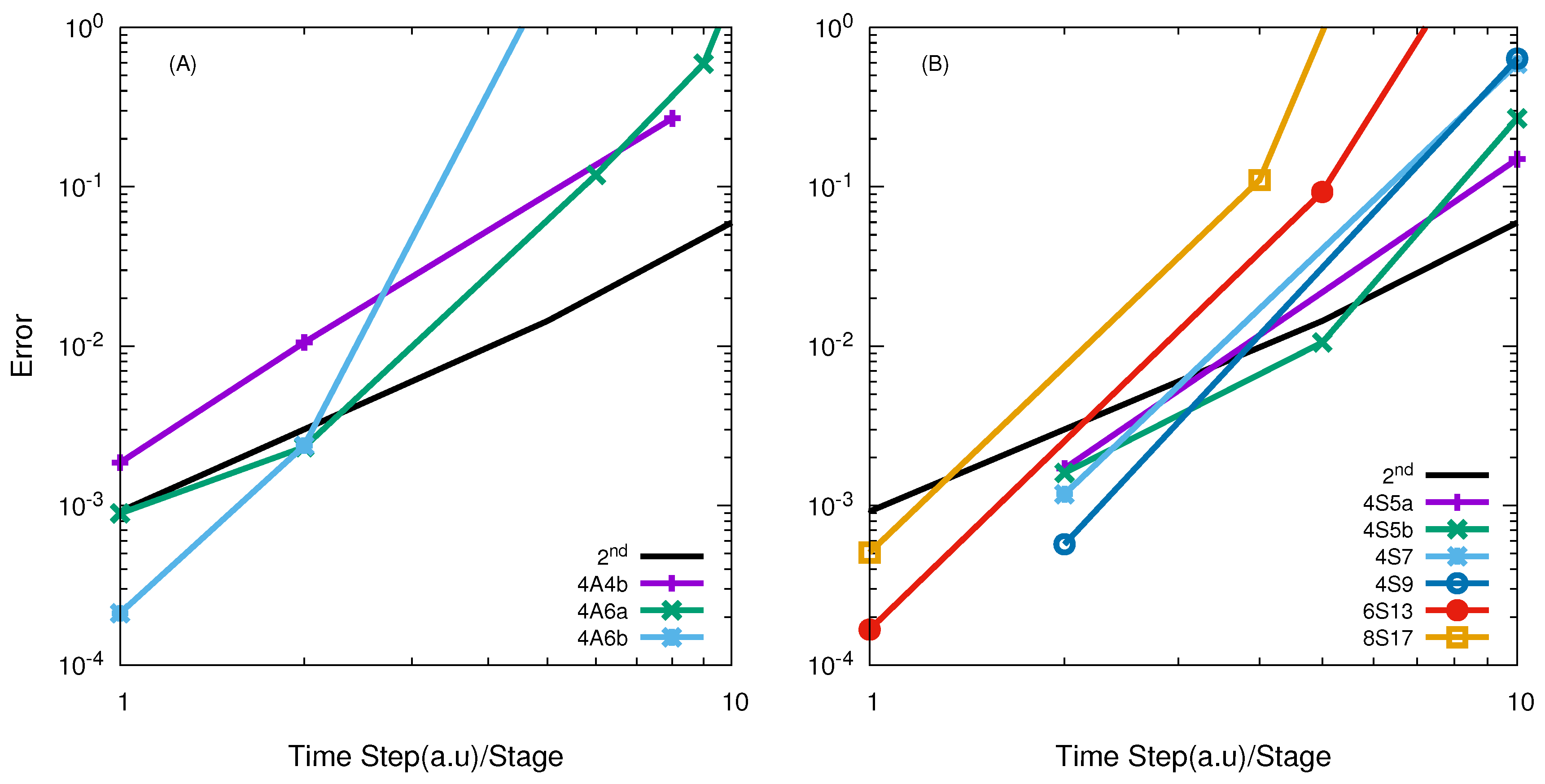
| Reactions | M | Range of Energies |
|---|---|---|
| H + H | 700 | [0.3, 1.0] |
| O + O | 701 | [0.02, 0.16] |
| F + HD | 341 | [0.01, 0.035] |
| Jacobi | APH | Jacobi | APH | |
|---|---|---|---|---|
| Reactions | A Class/Time Step (a.u) | A Class/Time Step (a.u) | S Class/Time Step (a.u) | S Class/Time Step (a.u) |
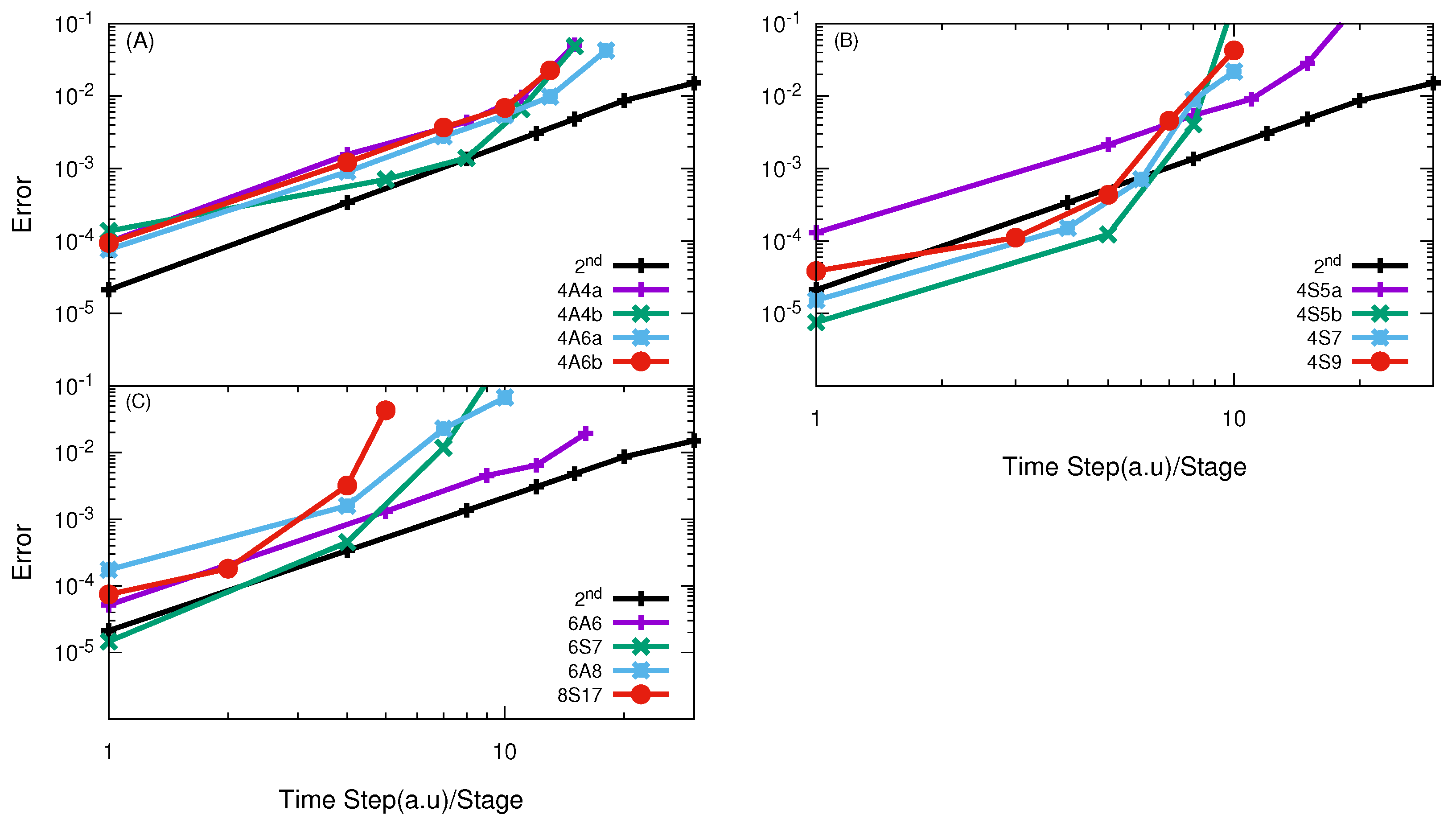
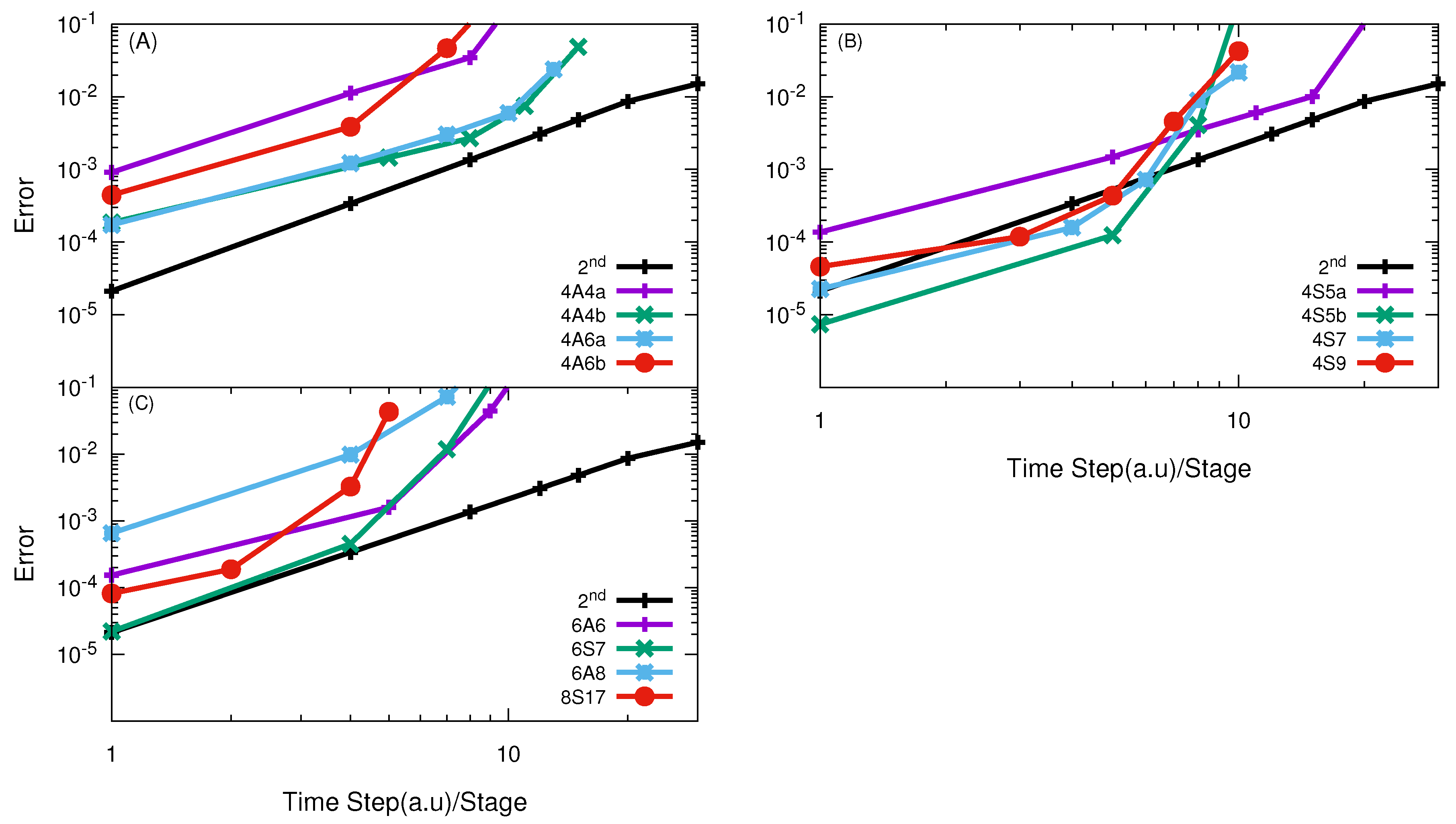
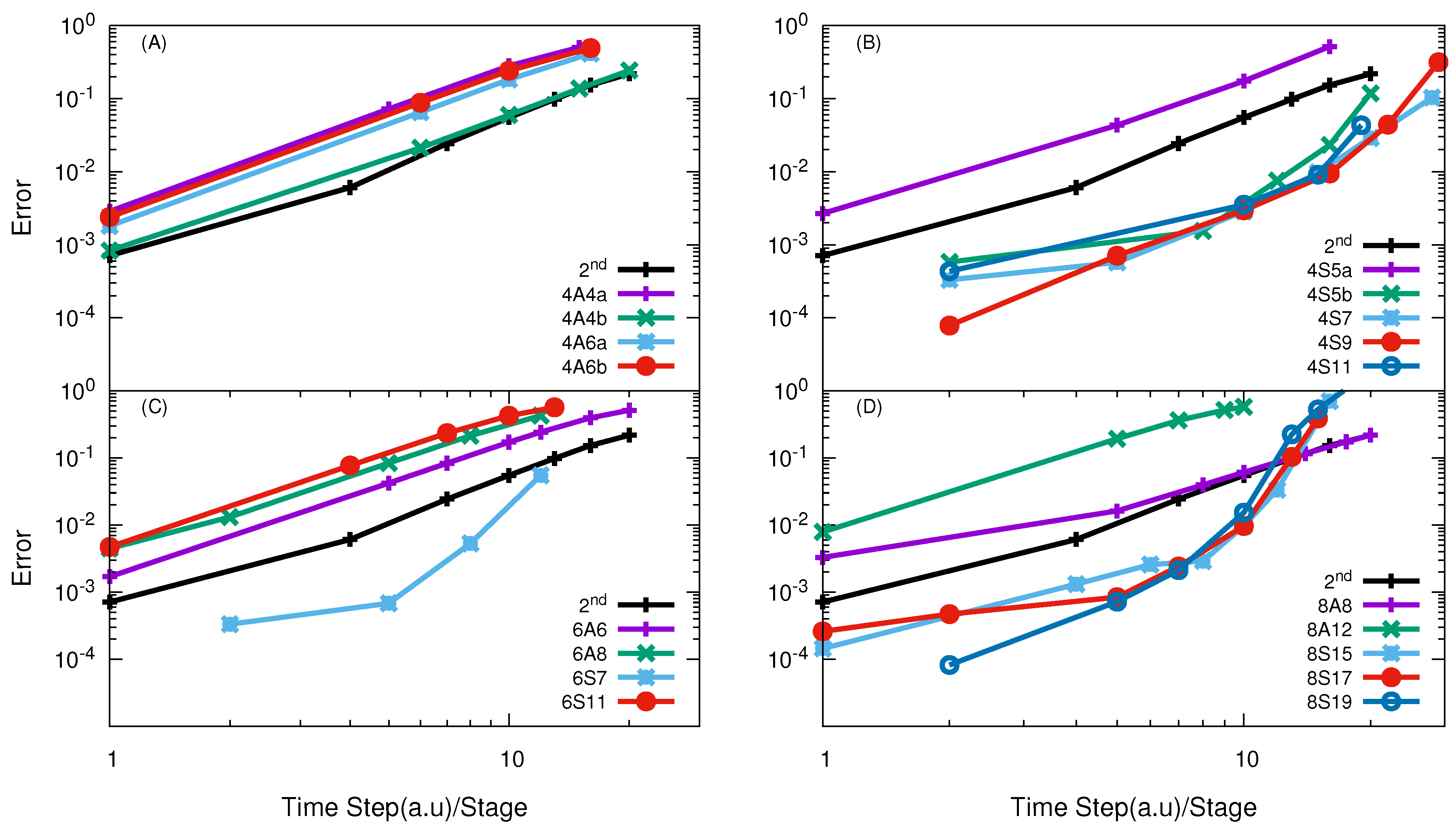
| H + H | 4A4b/5.0, 4A6b/3.3 | 4A4b/11.9, 4A6b/13.1, 6A6/14.91 | 4S5b/4.5 | 4S5a/12.1, 4S5b/8.7 |
| O + O | - | 4A4b/5.25 | - | 4S9/16.41 |
| F + HD | 4A6a/9.0 | 4A6a/4.08 | 4S7, 4S9/5.1 | 4S5b/5.99 |
| Jacobi | APH | Jacobi | APH | |
|---|---|---|---|---|
| Reactions | A Class/Time Step (a.u) | A Class/Time Step (a.u) | S Class/Time Step (a.u) | S Class/Time Step (a.u) |
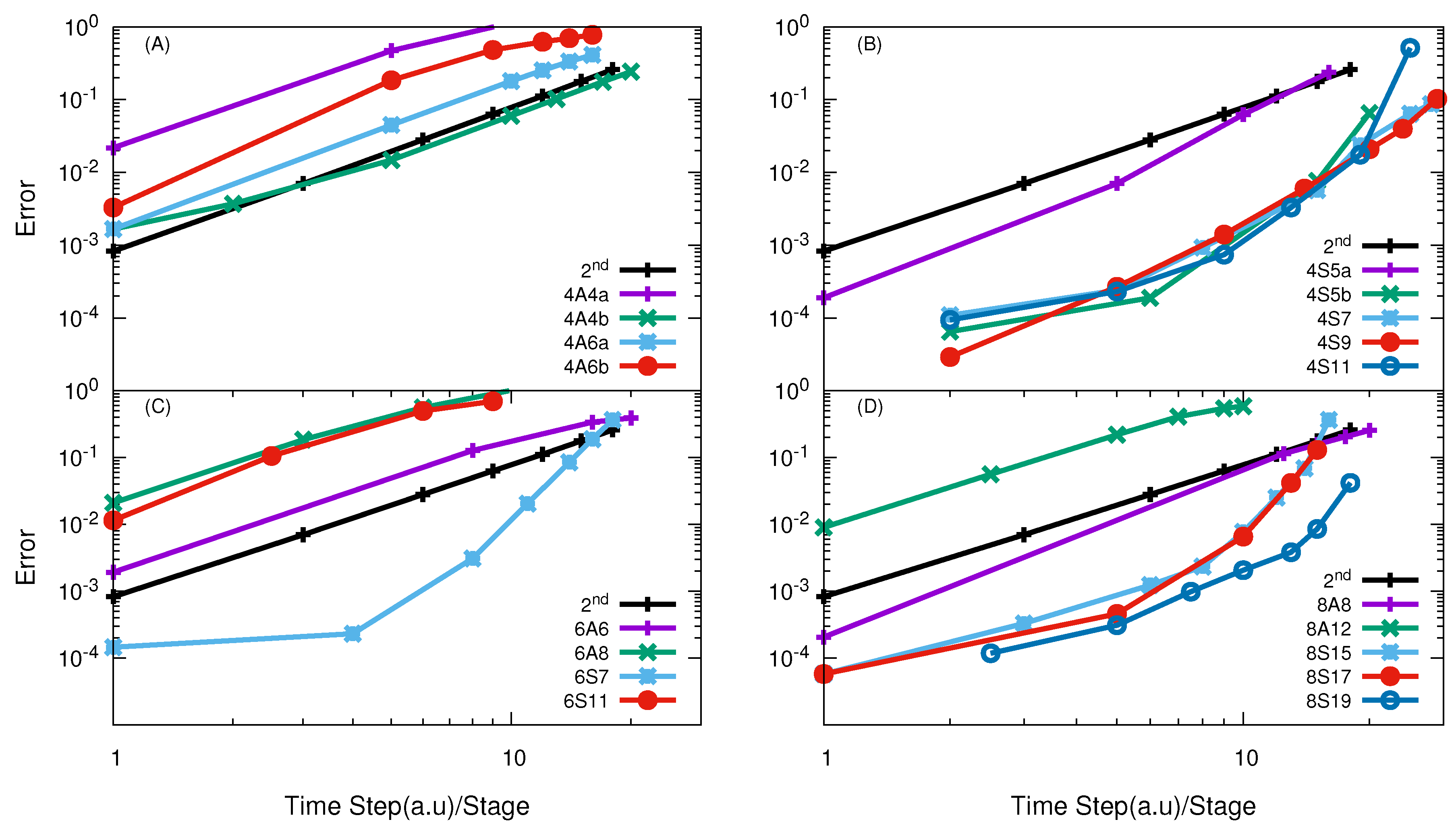
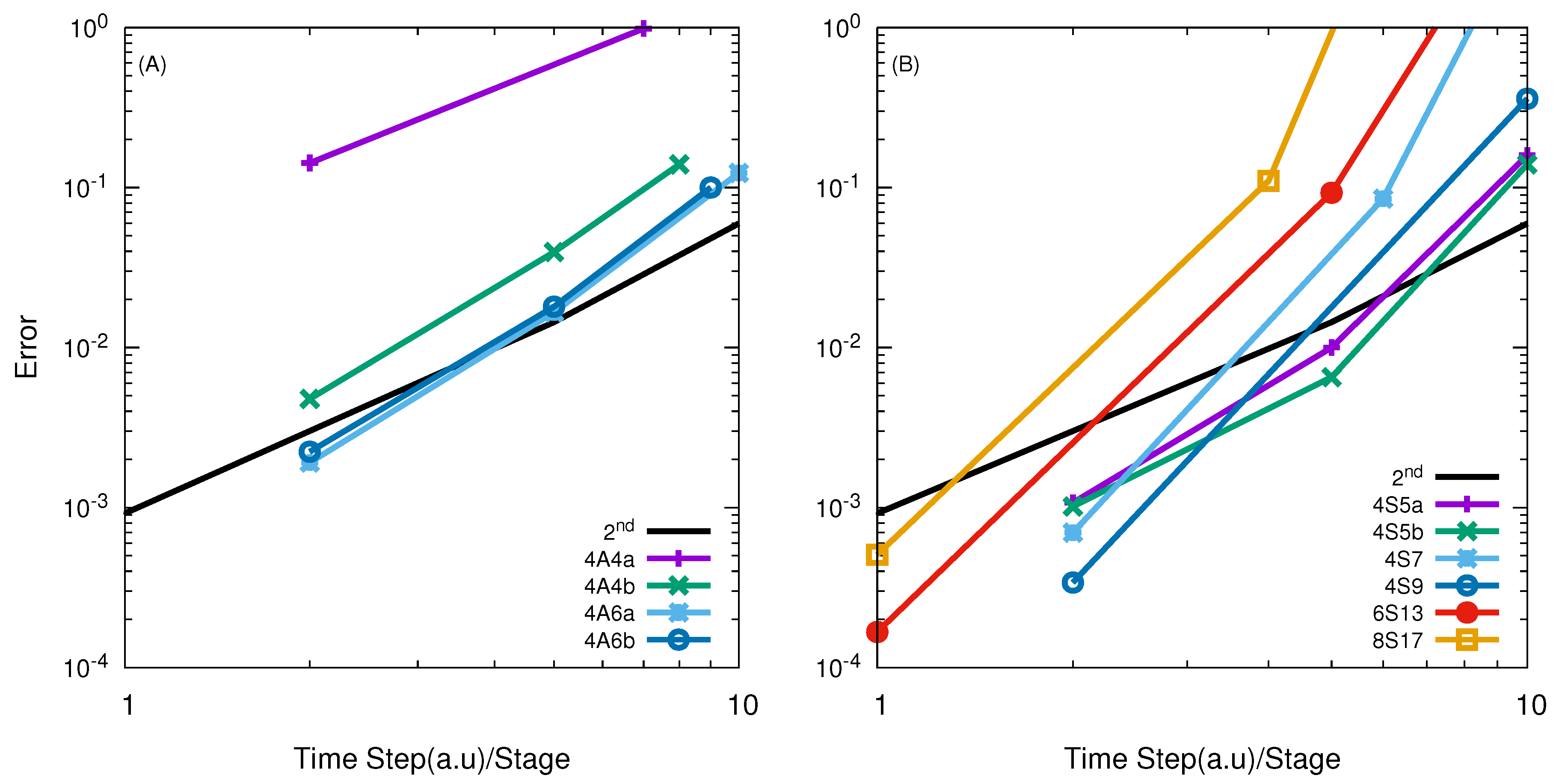
| O + O | 4A6a/20.0 | 4A4b/5.05 | - | 4S11/16.96 |
| F + HD | 6A8/10.0 | 4A6a/3.41 | 4S7/4.5 | 4S5b/5.94 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Umer, U.; Zhao, H.; Usman, S.K.; Sun, Z. High Order Split Operators for the Time-Dependent Wavepacket method of Triatomic Reactive Scattering in Hyperspherical Coordinates. Entropy 2019, 21, 979. https://doi.org/10.3390/e21100979
Umer U, Zhao H, Usman SK, Sun Z. High Order Split Operators for the Time-Dependent Wavepacket method of Triatomic Reactive Scattering in Hyperspherical Coordinates. Entropy. 2019; 21(10):979. https://doi.org/10.3390/e21100979
Chicago/Turabian StyleUmer, Umair, Hailin Zhao, Syed Kazim Usman, and Zhigang Sun. 2019. "High Order Split Operators for the Time-Dependent Wavepacket method of Triatomic Reactive Scattering in Hyperspherical Coordinates" Entropy 21, no. 10: 979. https://doi.org/10.3390/e21100979
APA StyleUmer, U., Zhao, H., Usman, S. K., & Sun, Z. (2019). High Order Split Operators for the Time-Dependent Wavepacket method of Triatomic Reactive Scattering in Hyperspherical Coordinates. Entropy, 21(10), 979. https://doi.org/10.3390/e21100979





