A High Spectral Entropy (SE) Memristive Hidden Chaotic System with Multi-Type Quasi-Periodic and its Circuit
Abstract
1. Introduction
2. A New 5-D Memristive Chaotic System
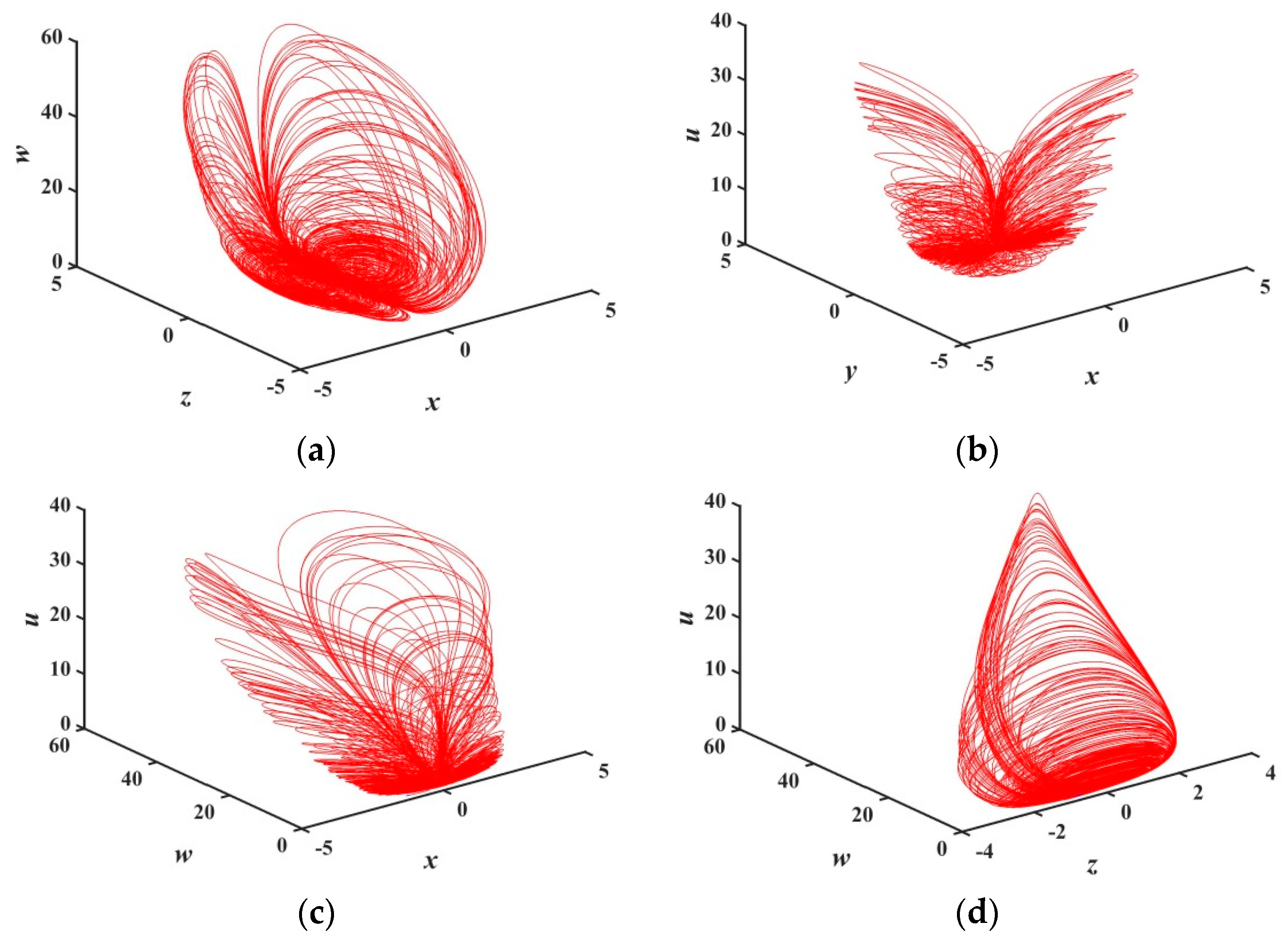
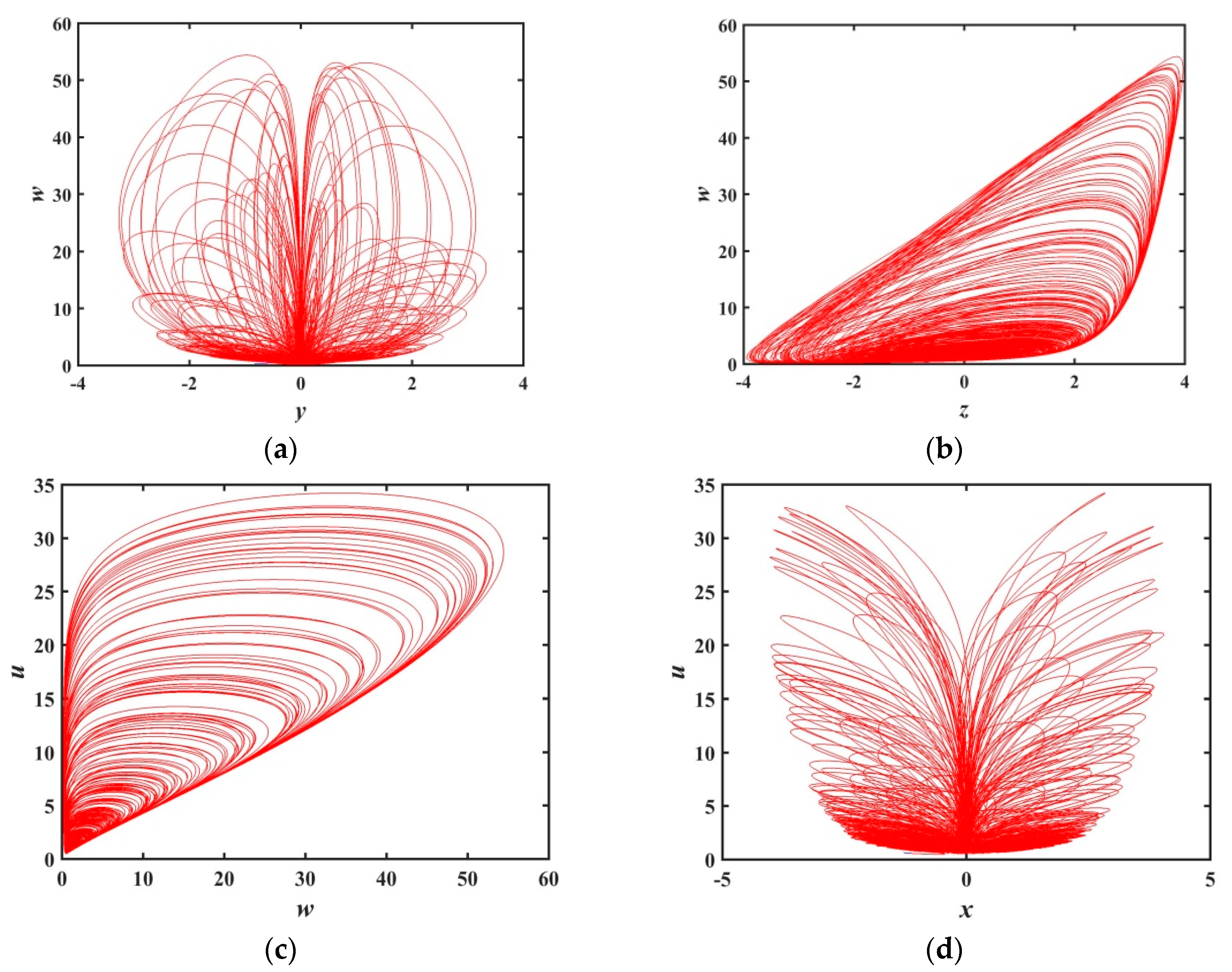
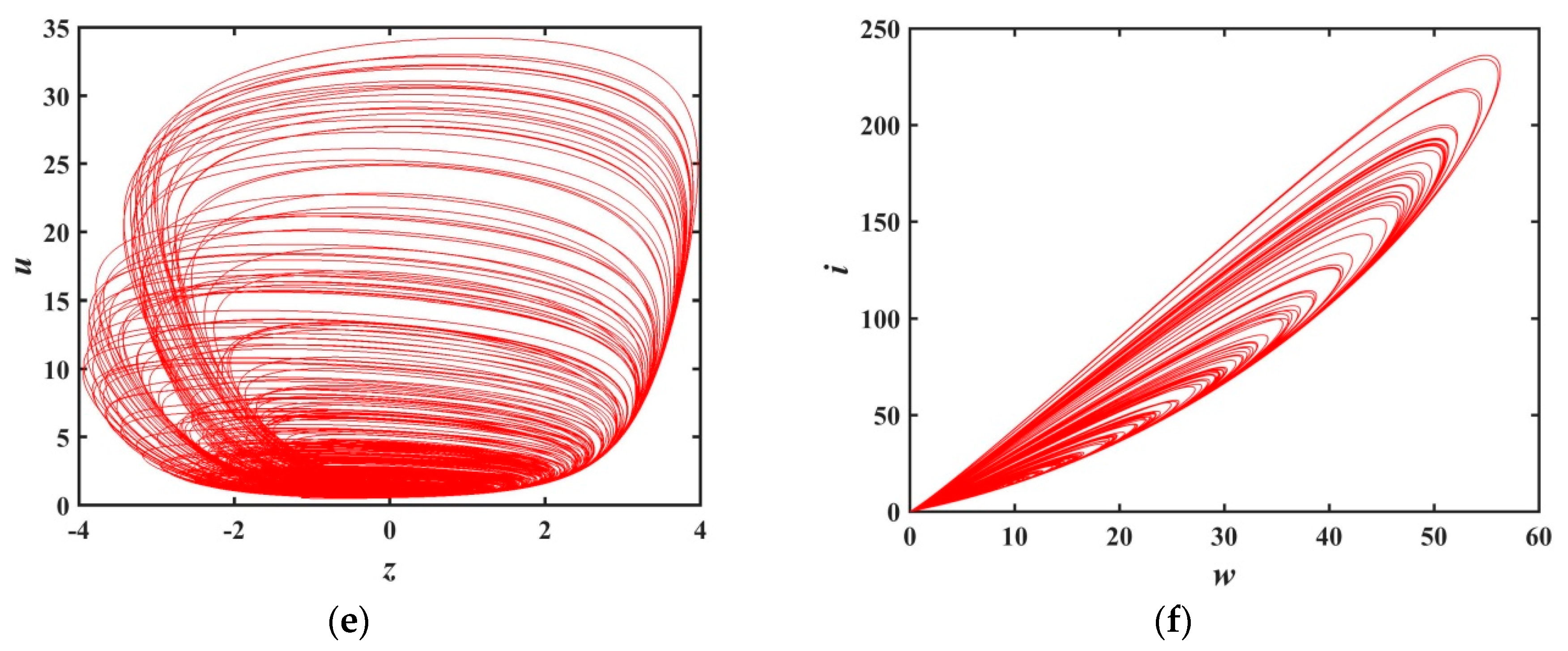
2.1. Description of the New Memristive Chaotic System
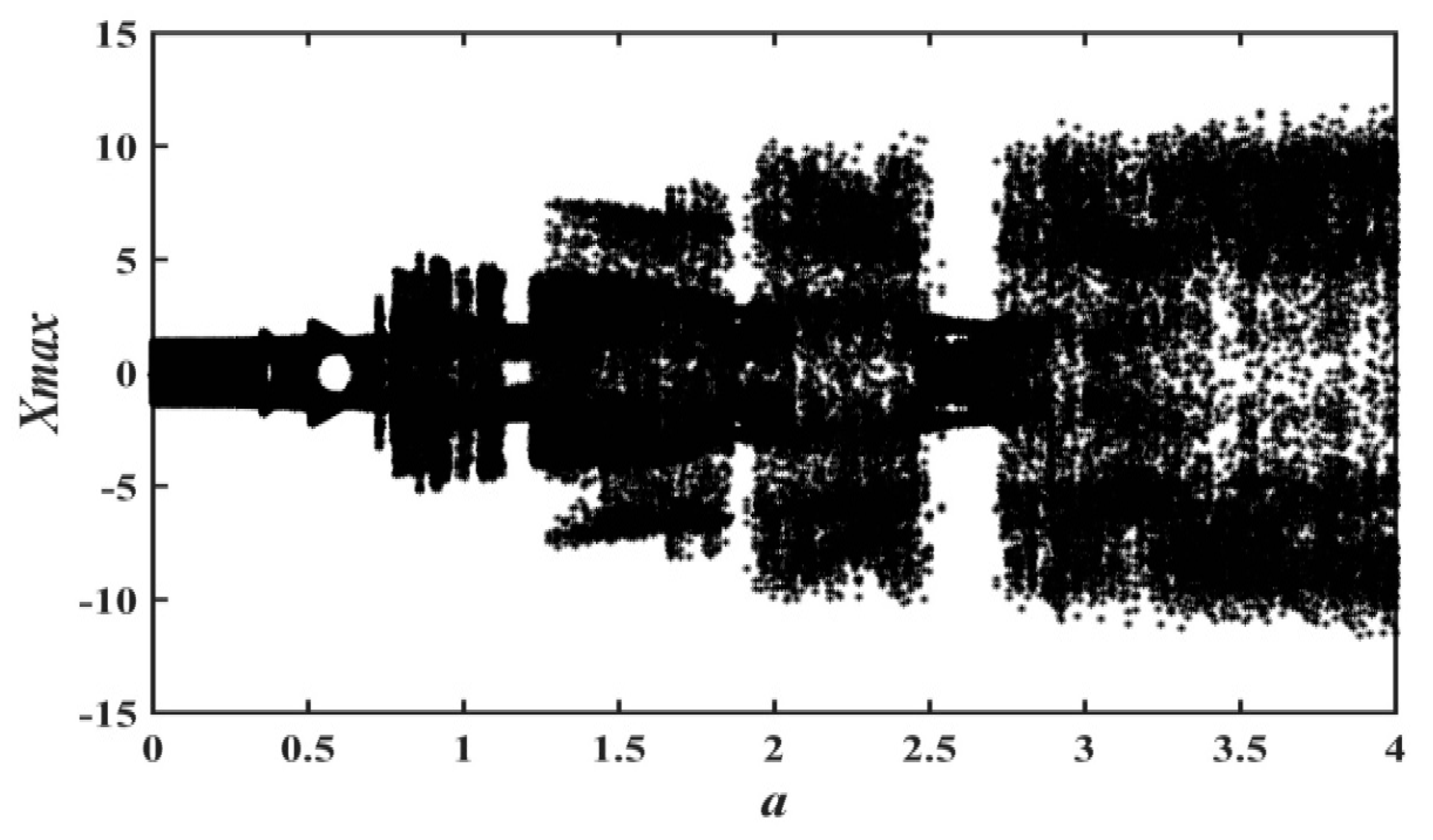
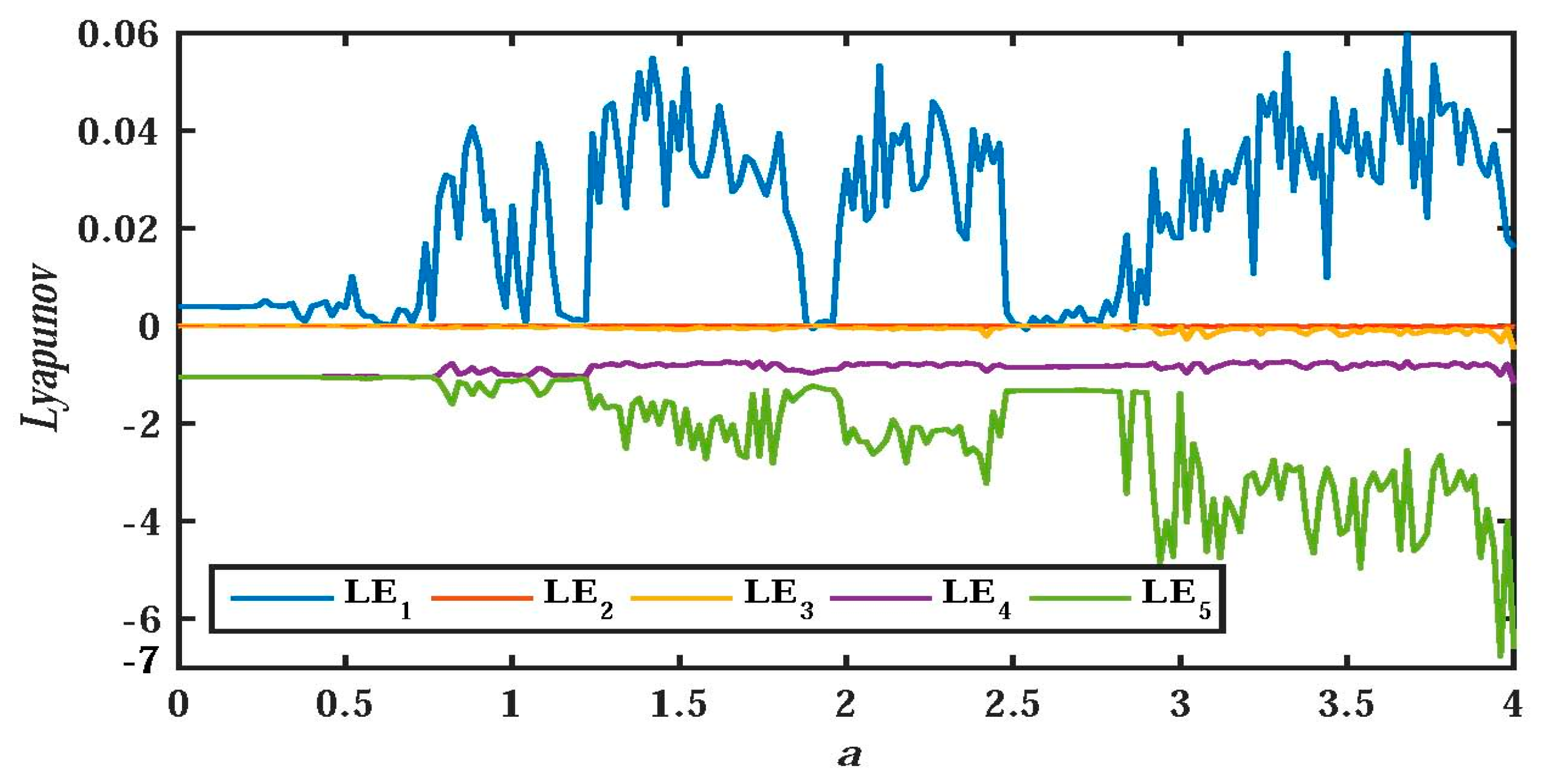
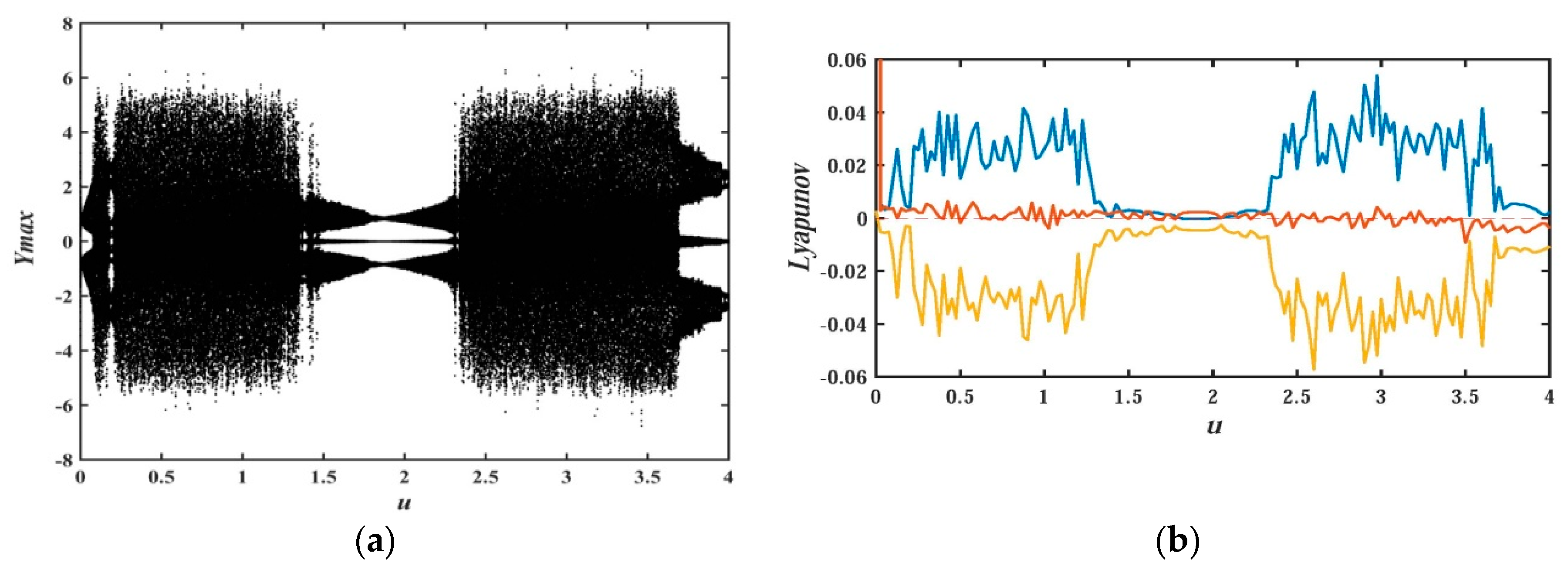
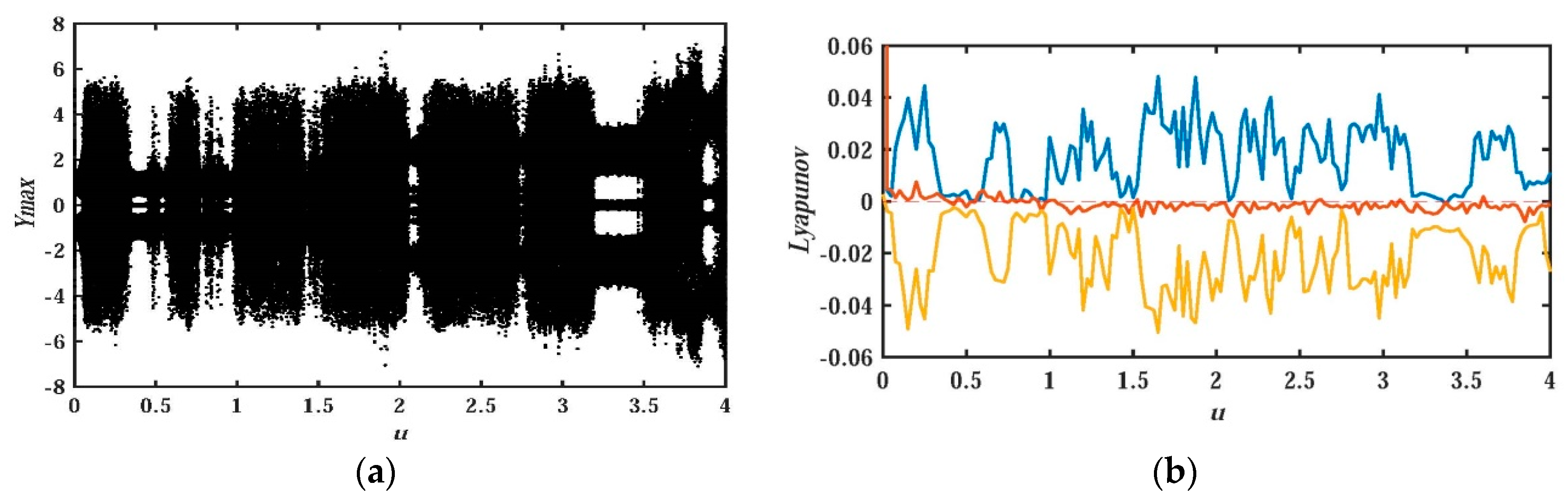
2.2. Bifurcation Diagram with as Varying Parameter
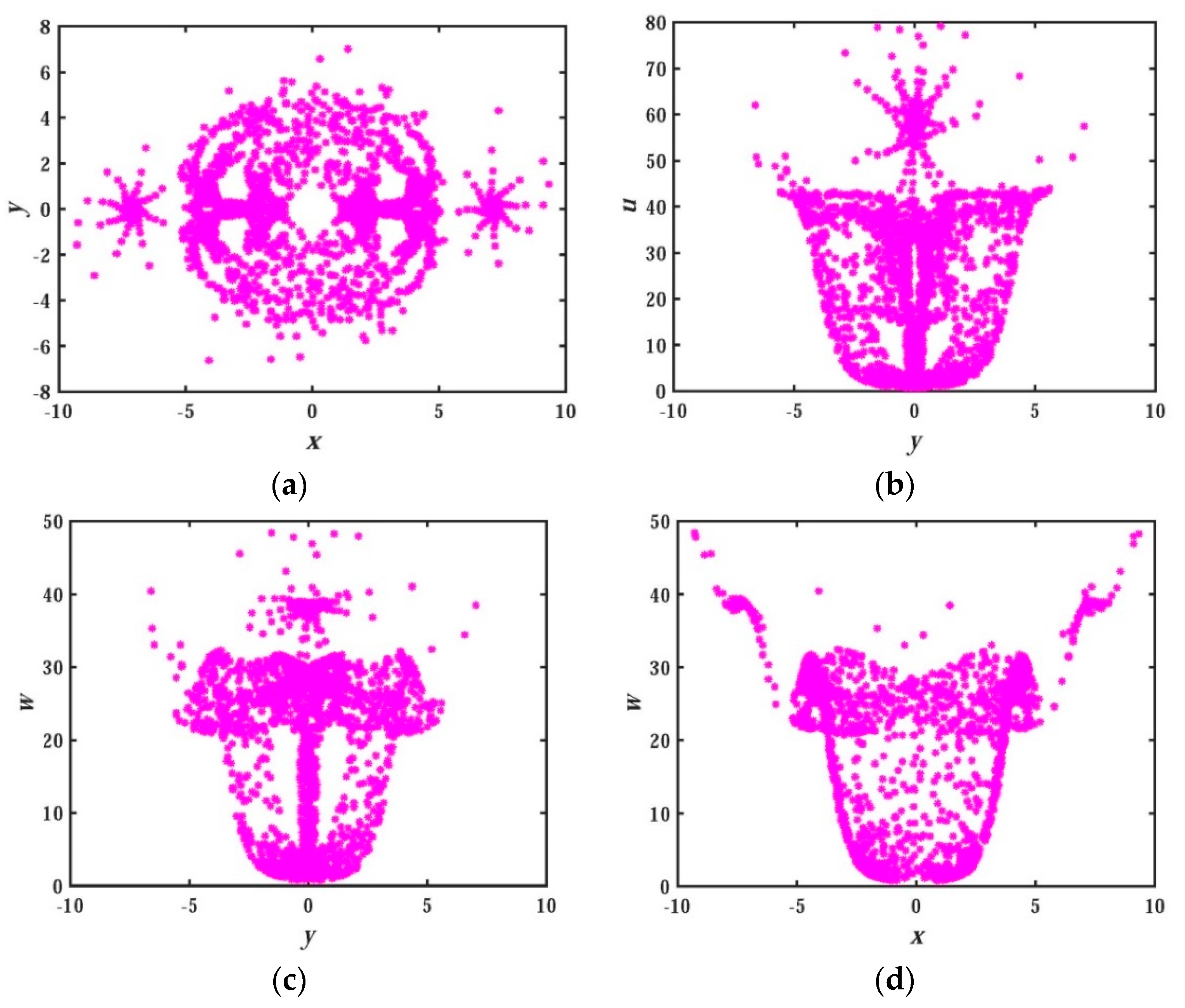
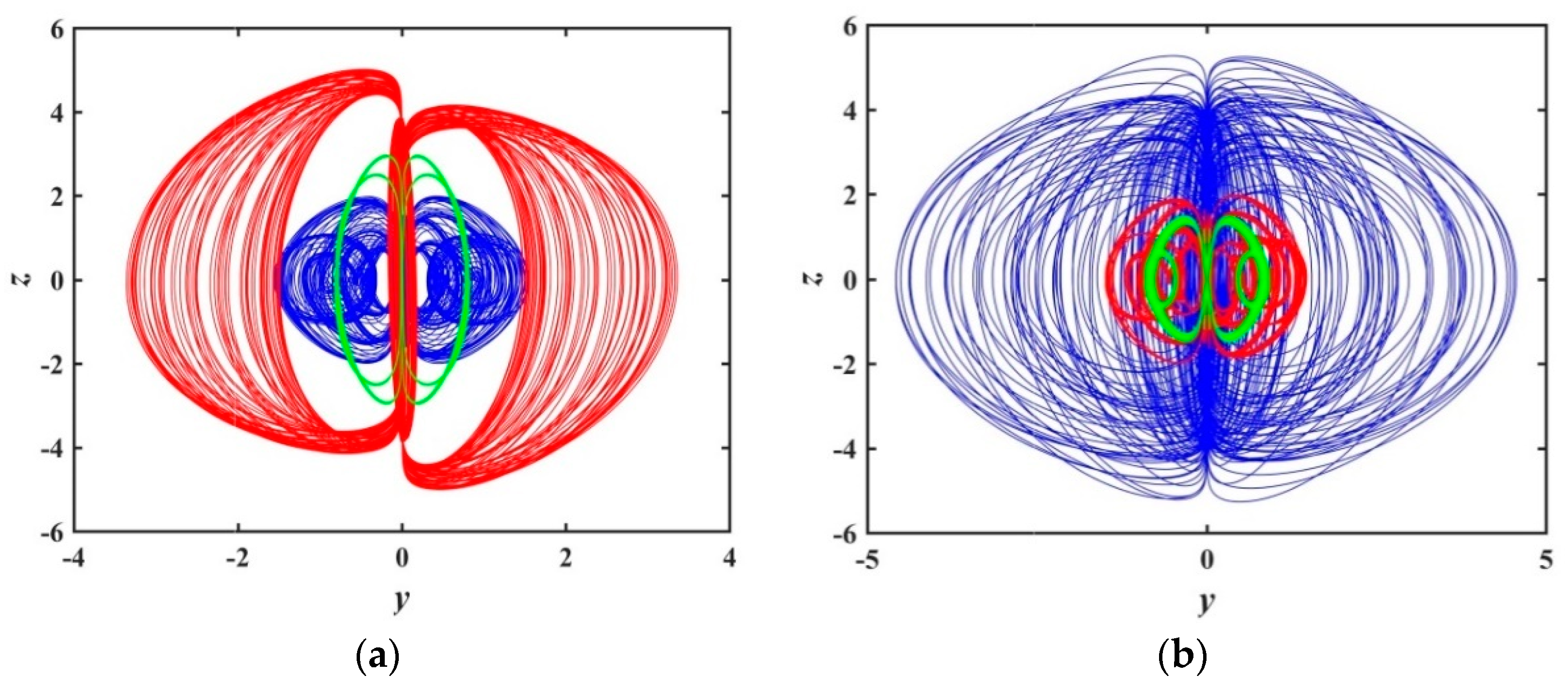
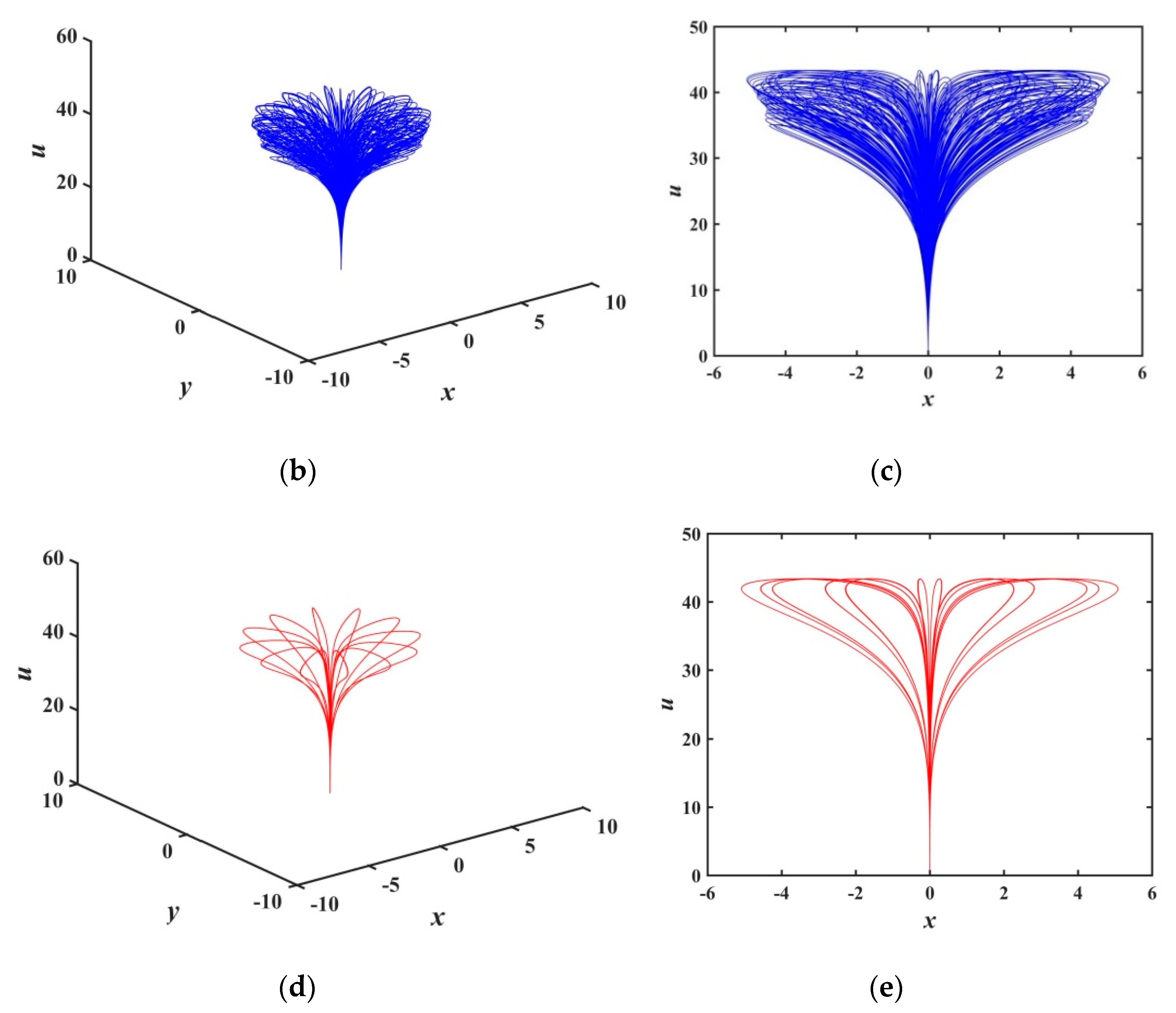
2.3. Analysis of Multi-Stability
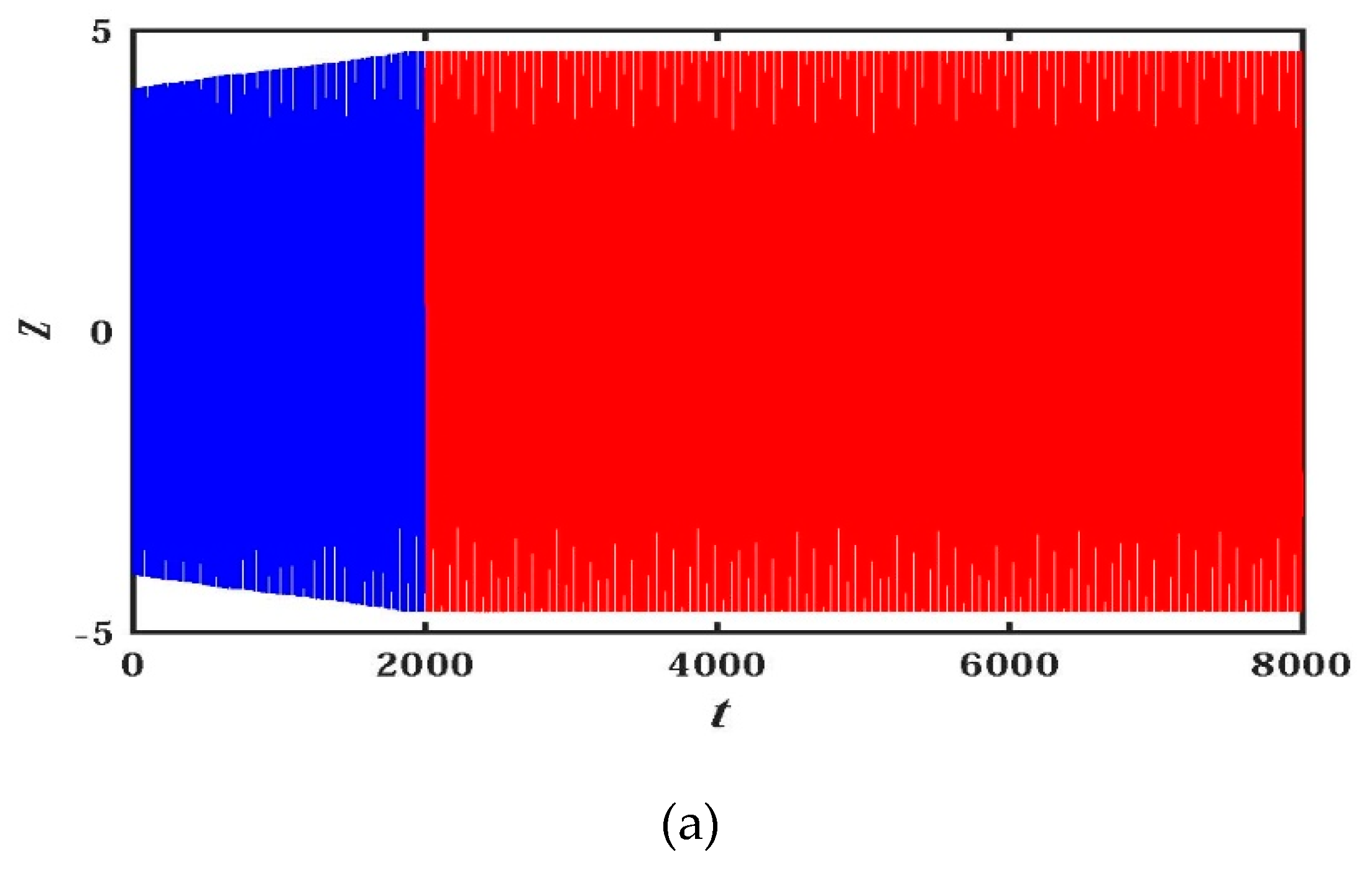
2.4. Analysis of Transient Chaos
3. Entropy Analysis for Memristive Chaotic Systems
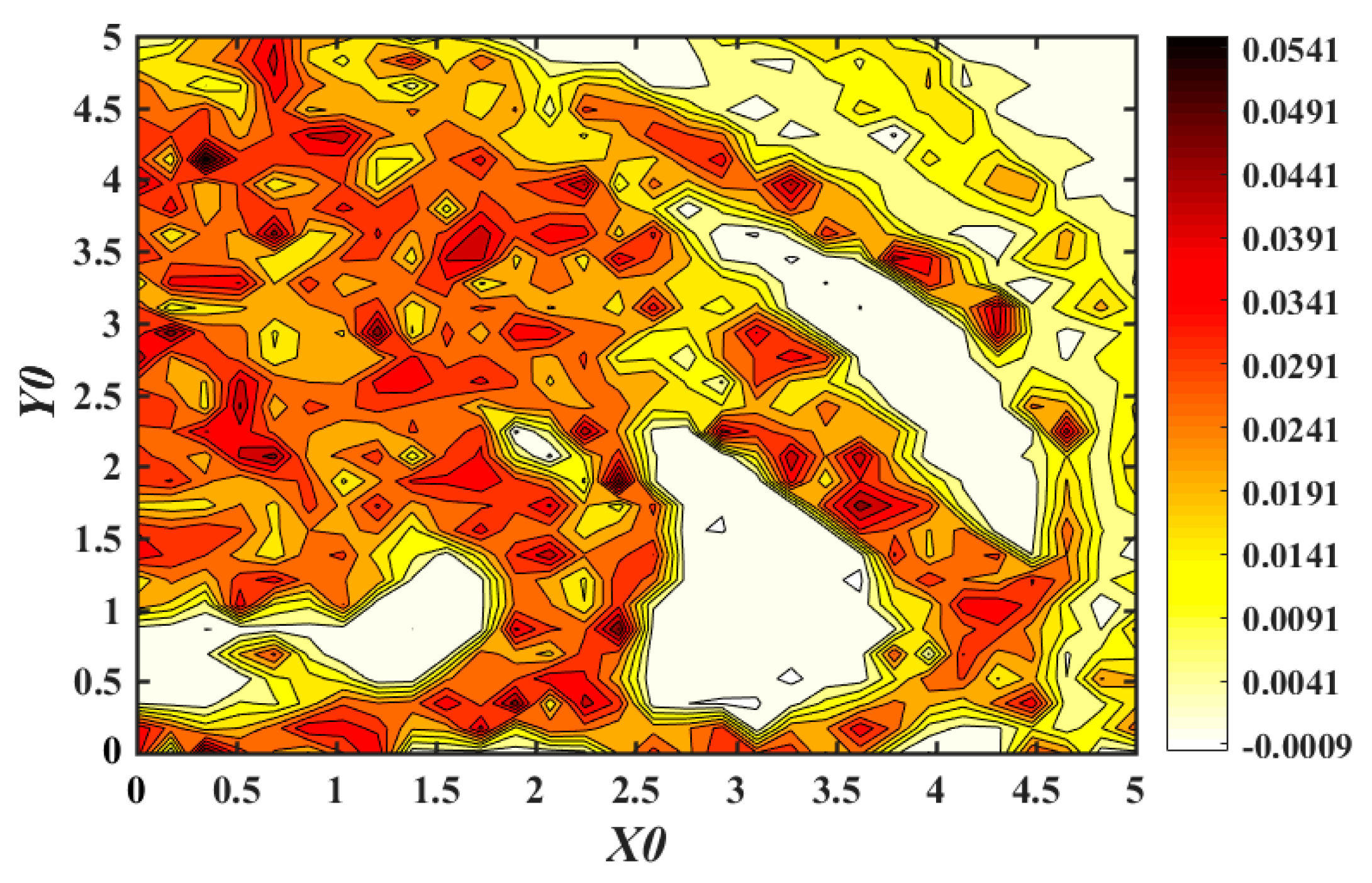
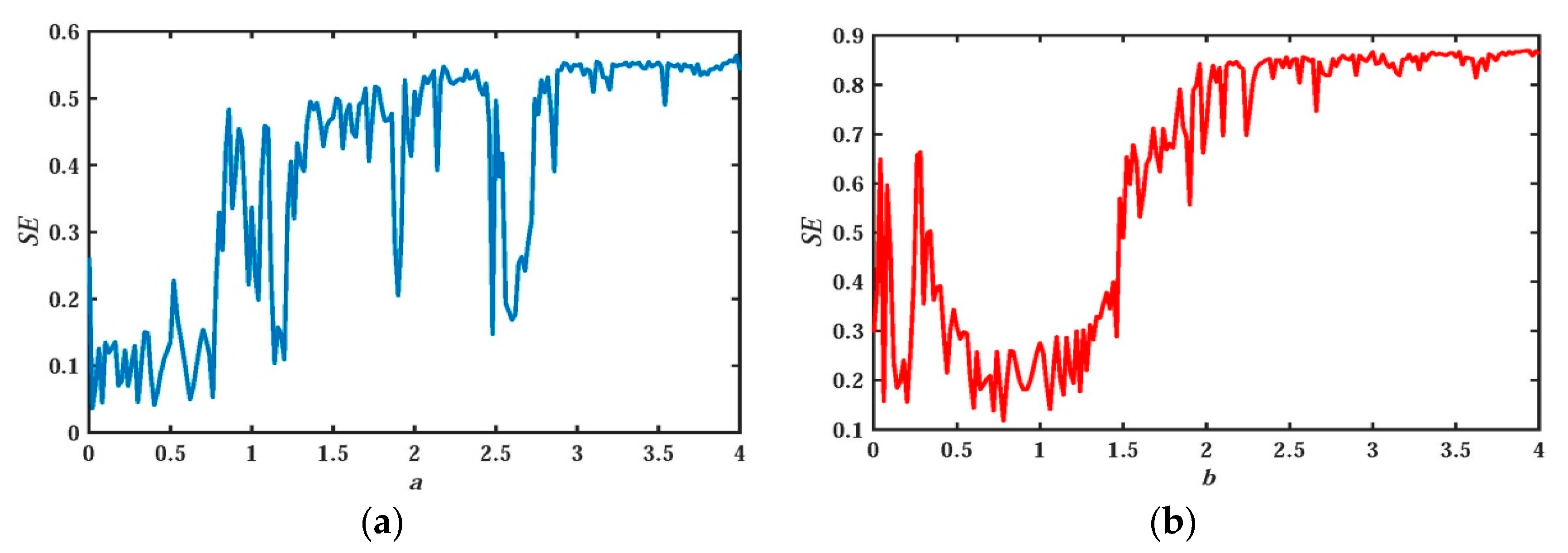
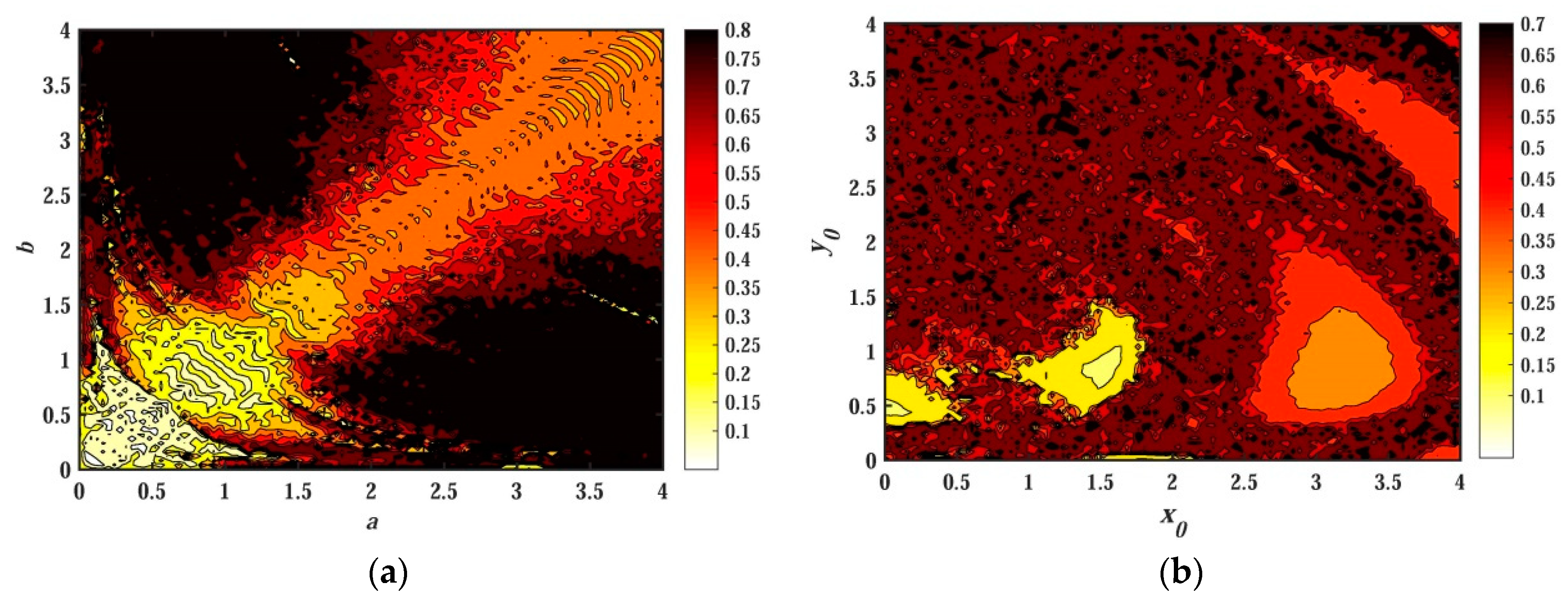
3.1. SE Analysis Depending on Parameters
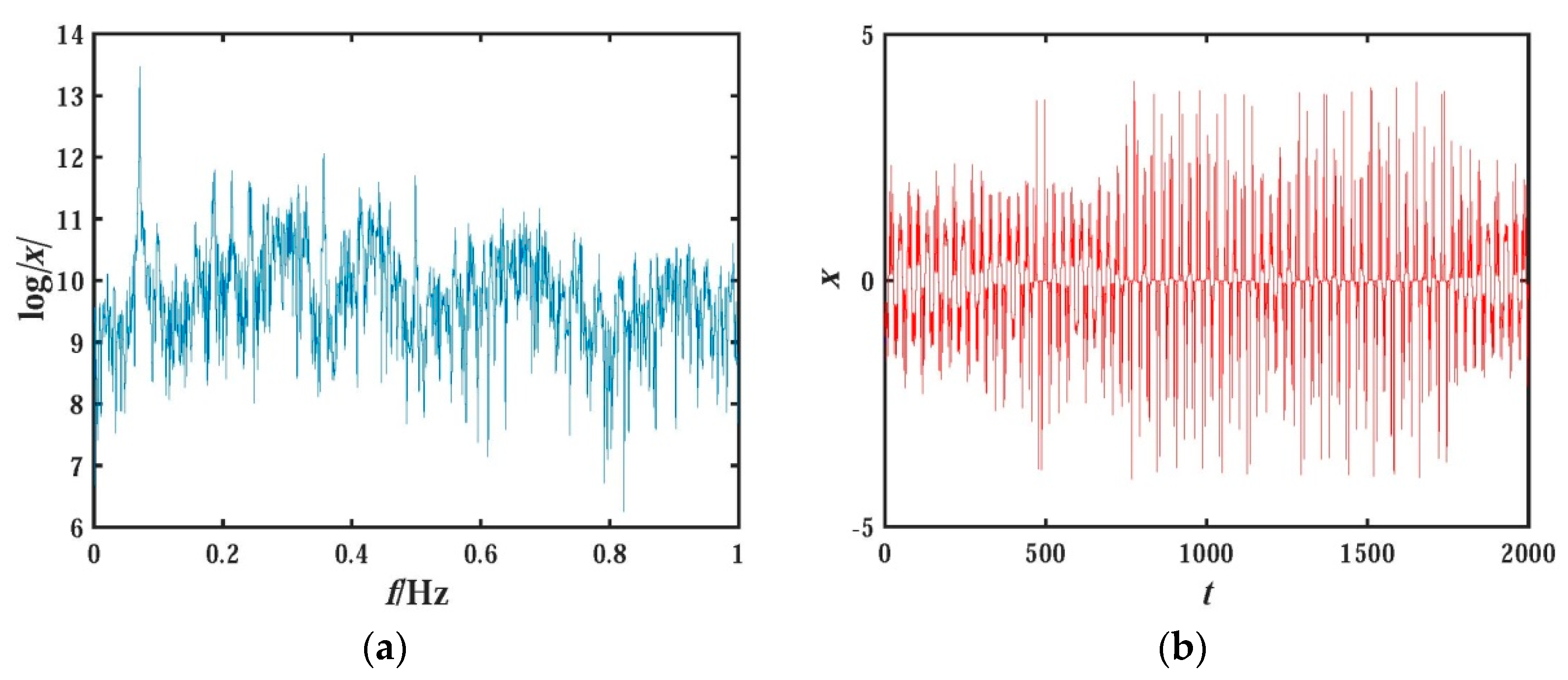
3.2. Entropy Analysis of Chaotic Behavior
4. Circuitry Realization of Memristor-Based Chaotic System
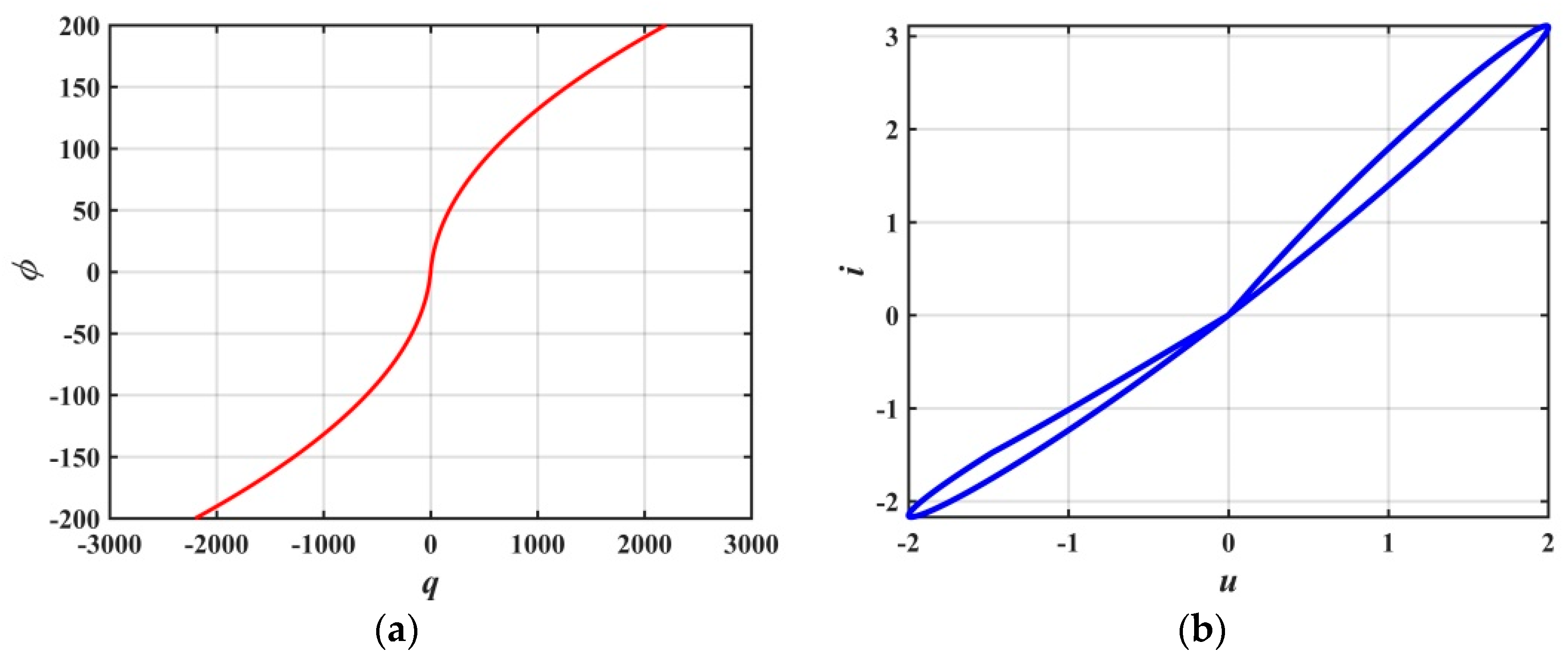
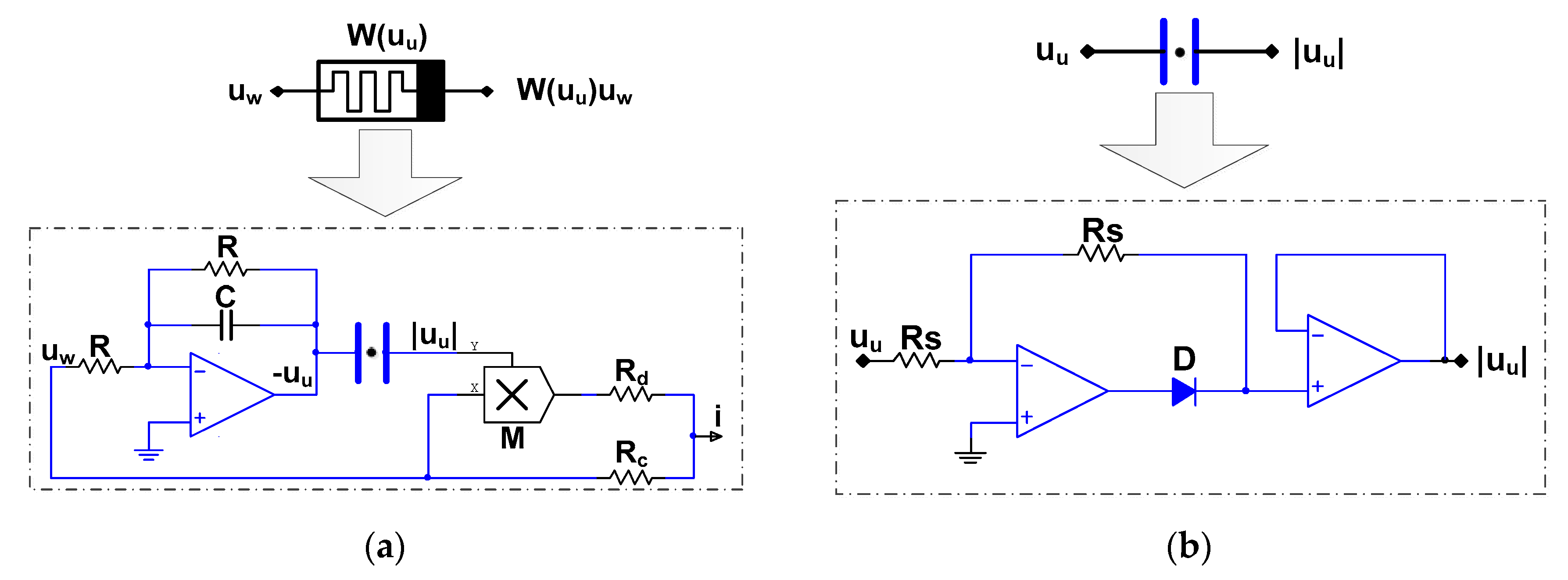
4.1. Equivalent Circuit implementation for Memristor
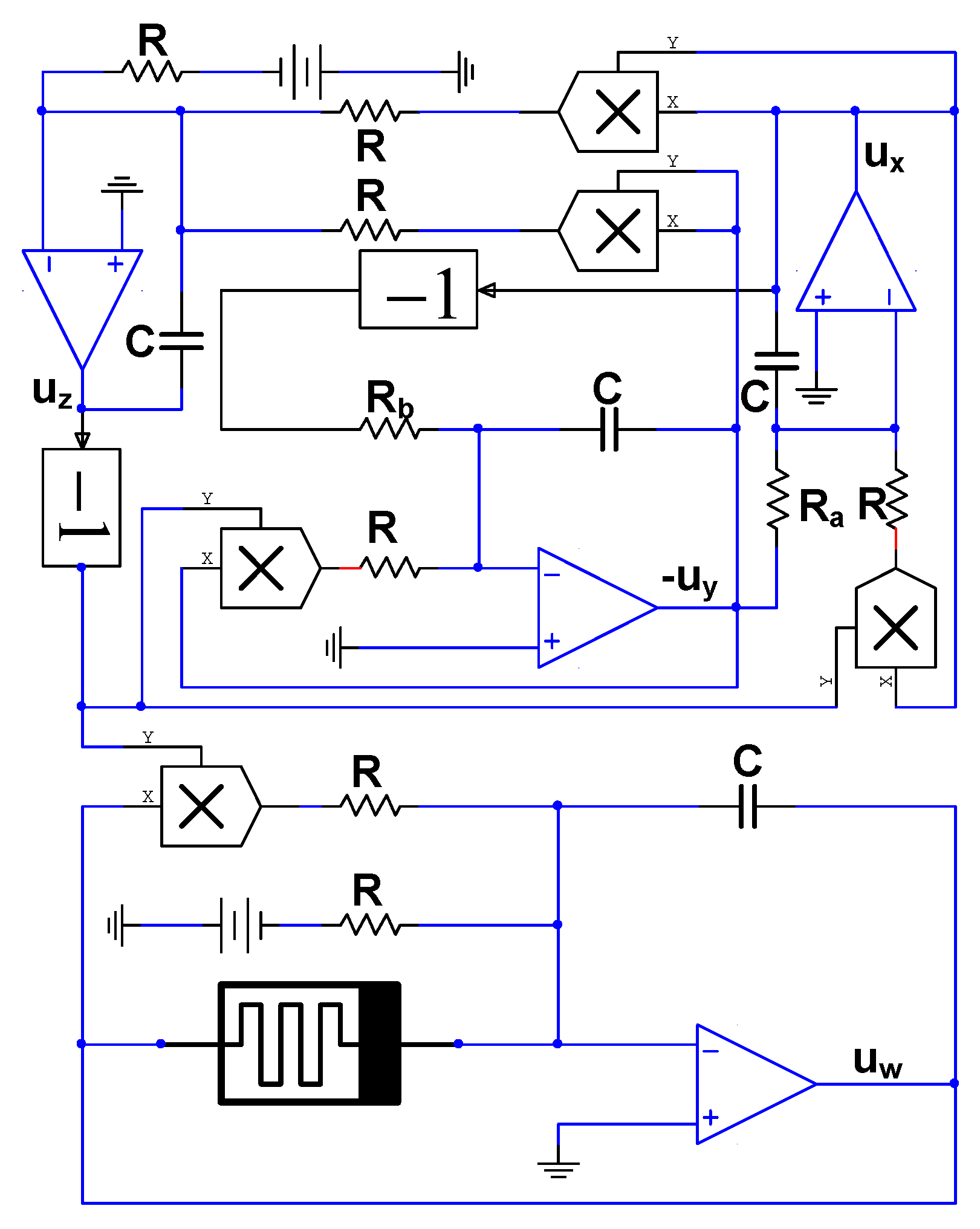
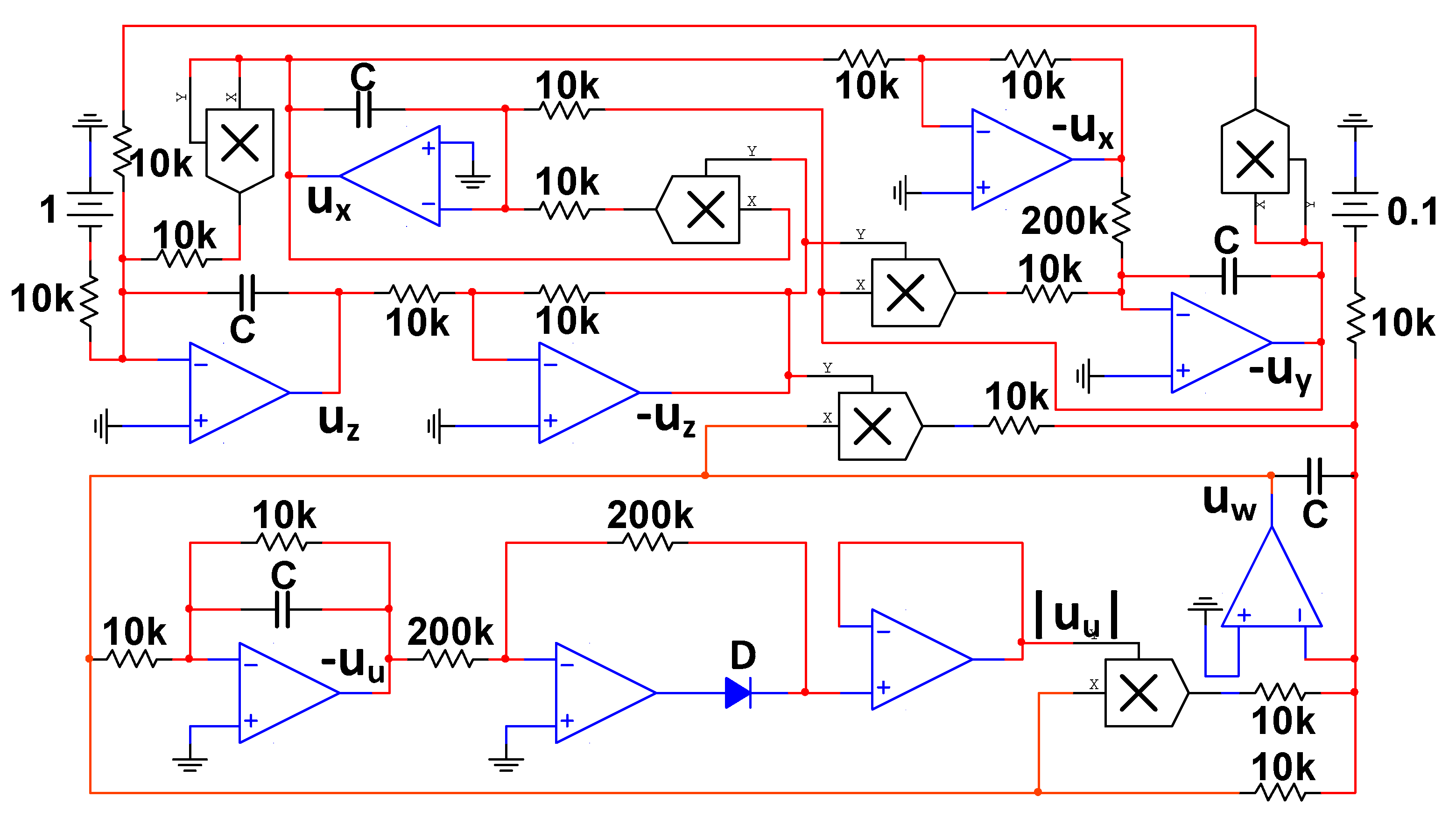
4.2. Circuit of Memristive Chaotic System
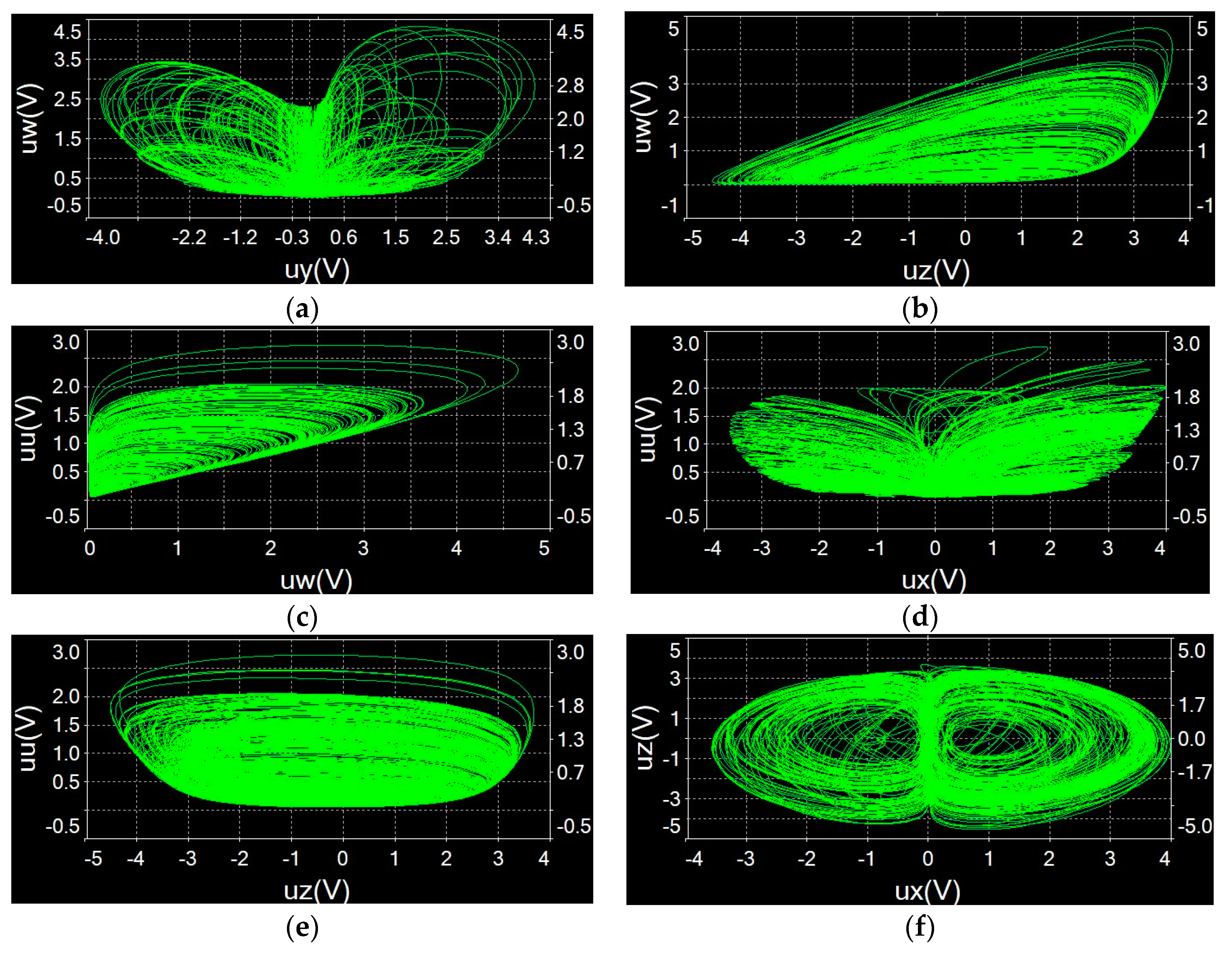
4.3. Circuit simulation of Memristive Chaotic System
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Lu, J.G. Chaotic dynamics of the fractional-order Lü system and its synchronization. Phys. Lett. A 2006, 354, 305–311. [Google Scholar] [CrossRef]
- Lü, J.; Chen, G.; Zhang, S. Dynamical analysis of a new chaotic attractor. Int. J. Bifurc. Chaos 2002, 12, 1001–1015. [Google Scholar] [CrossRef]
- Rössler, O.E. An equation for continuous chaos. Phys. Lett. A 1976, 57, 397–398. [Google Scholar] [CrossRef]
- Ueta, T.; Chen, G. Bifurcation analysis of chen’s equation. Int. J. Bifurc. Chaos 2000, 10, 1917–1931. [Google Scholar] [CrossRef]
- Liu, C.; Liu, T.; Liu, L.; Liu, K. A new chaotic attractor. Chaos Solitons Fractals 2004, 22, 1031–1038. [Google Scholar] [CrossRef]
- Leonov, G.A.; Kuznetsov, N.V.; Vagaitsev, V.I. Localization of hidden Chuaʼs attractors. Phys. Lett. A 2011, 375, 2230–2233. [Google Scholar] [CrossRef]
- Liu, L.; Du, C.; Zhang, X.; Li, J.; Shi, S. Adaptive Synchronization Strategy between Two Autonomous Dissipative Chaotic Systems Using Fractional-Order Mittag–Leffler Stability. Entropy 2019, 21, 383. [Google Scholar] [CrossRef]
- Wang, C.; Ding, Q. A New Two-Dimensional Map with Hidden Attractors. Entropy 2018, 20, 322. [Google Scholar] [CrossRef]
- Fan, C.; Xie, Z.; Ding, Q. A Novel Algorithm to Improve Digital Chaotic Sequence Complexity through CCEMD and PE. Entropy 2018, 20, 295. [Google Scholar] [CrossRef]
- Stewart, I.I. Mathematics. The Lorenz attractor exists. Nature 2000, 406, 948–949. [Google Scholar] [CrossRef] [PubMed]
- Lilian, H.; Fang, X.; Linyu, W. Circuit implementation and control of a new fractional-order hyperchaotic system. Acta Physica Sinica 2011, 60, 67–75. [Google Scholar]
- Khan, A.; Tyagi, A. Analysis and hyper-chaos control of a new 4-D hyper-chaotic system by using optimal and adaptive control design. Int. J. Dyn. Control 2016, 5, 1147–1155. [Google Scholar] [CrossRef]
- Zhou, C.; Yang, C.; Xu, D.; Chen, C.-Y. Dynamic Analysis and Finite-Time Synchronization of a New Hyperchaotic System With Coexisting Attractors. IEEE Access 2019, 7, 52896–52902. [Google Scholar] [CrossRef]
- Zhang, C.; Yu, S. On constructing complex grid multi-wing hyperchaotic system: Theoretical design and circuit implementation. Int. J. Circuit Theory Appl. 2013, 41, 221–237. [Google Scholar] [CrossRef]
- Hu, X.; Liu, C.; Liu, L.; Yao, Y.; Zheng, G. Multi-scroll hidden attractors and multi-wing hidden attractors in a 5-dimensional memristive system. Chin. Phys. B 2017, 26. [Google Scholar] [CrossRef]
- Ahmad, W.M. Generation and control of multi-scroll chaotic attractors in fractional order systems. Chaos Solitons Fractals 2005, 25, 727–735. [Google Scholar] [CrossRef]
- Pano-Azucena, A.D.; de Jesus Rangel-Magdaleno, J.; Tlelo-Cuautle, E.; de Jesus Quintas-Valles, A. Arduino-based chaotic secure communication system using multi-directional multi-scroll chaotic oscillators. Nonlinear Dyn. 2016, 87, 2203–2217. [Google Scholar] [CrossRef]
- Dudkowski, D.; Jafari, S.; Kapitaniak, T.; Kuznetsov, N.V.; Leonov, G.A.; Prasad, A. Hidden attractors in dynamical systems. Phys. Rep. 2016, 637, 1–50. [Google Scholar] [CrossRef]
- Liu, L.; Du, C.; Zhang, X.; Li, J.; Shi, S. Dynamics and Entropy Analysis for a New 4-D Hyperchaotic System with Coexisting Hidden Attractors. Entropy 2019, 21, 287. [Google Scholar] [CrossRef]
- Wang, X.; Chen, G. A chaotic system with only one stable equilibrium. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 1264–1272. [Google Scholar] [CrossRef]
- Wei, Z.; Zhang, W.; Wang, Z.; Yao, M. Hidden attractors and dynamical behaviors in an extended Rikitake system. Int. J. Bifurc. Chaos 2015, 25, 1550028. [Google Scholar] [CrossRef]
- Kapitaniak, T.; Mohammadi, S.; Mekhilef, S.; Alsaadi, F.; Hayat, T.; Pham, V.-T. A New Chaotic System with Stable Equilibrium: Entropy Analysis, Parameter Estimation, and Circuit Design. Entropy 2018, 20, 670. [Google Scholar] [CrossRef]
- Jafari, S.; Sprott, J.C. Simple chaotic flows with a line equilibrium. Chaos Solitons Fractals 2013, 57, 79–84. [Google Scholar] [CrossRef]
- Kingni, S.T.; Pham, V.-T.; Jafari, S.; Woafo, P. A chaotic system with an infinite number of equilibrium points located on a line and on a hyperbola and its fractional-order form. Chaos Solitons Fractals 2017, 99, 209–218. [Google Scholar] [CrossRef]
- Vaidyanathan, S.; Volos, C. Analysis and adaptive control of a novel 3-D conservative no-equilibrium chaotic system. Arch. Control. Sci. 2015, 25, 333–353. [Google Scholar] [CrossRef]
- Vaidyanathan, S.; Pham, V.T.; Volos, C.K. A 5-D hyperchaotic Rikitake dynamo system with hidden attractors. Eur. Phys. J. Spec. Top. 2015, 224, 1575–1592. [Google Scholar] [CrossRef]
- Leonov, G.A.; Kuznetsov, N.V.; Kiseleva, M.A.; Solovyeva, E.P.; Zaretskiy, A.M. Hidden oscillations in mathematical model of drilling system actuated by induction motor with a wound rotor. Nonlinear Dyn. 2014, 77, 277–288. [Google Scholar] [CrossRef]
- Scheffer, M.; Carpenter, S.; Foley, J.A.; Folke, C.; Walker, B. Catastrophic shifts in ecosystems. Nature 2001, 413, 591–596. [Google Scholar] [CrossRef]
- Rietkerk, M.; Dekker, S.C.; de Ruiter, P.C.; van de Koppel, J. Self-organized patchiness and catastrophic shifts in ecosystems. Science 2004, 305, 1926–1929. [Google Scholar] [CrossRef]
- Chua, L.O. Memristor-The missing circuit element. IEEE Trans. Circuit Theory 1971, 18, 507–519. [Google Scholar] [CrossRef]
- Herbert Ho-Ching, I.U.; Fitch, A. Development of Memristor Based Circuits; Chua, L.O., Ed.; World Scientific: Singapore, 2012; Volume 82, p. 132. [Google Scholar]
- Strukov, D.B.; Snider, G.S.; Stewart, D.R.; Williams, R.S. The missing memristor found. Nature 2008, 453, 80–83. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; Sun, M.; Bao, B.; Wu, H.; Xu, Q.; Wang, J. Controlling extreme multistability of memristor emulator-based dynamical circuit in flux–charge domain. Nonlinear Dyn. 2017, 91, 1395–1412. [Google Scholar] [CrossRef]
- Valsa, J.; Biolek, D.; Biolek, Z. An analogue model of the memristor. Int. J. Numer. Modell. Electron. Netw. Devices Fields 2011, 24, 400–408. [Google Scholar] [CrossRef]
- Itoh, M.; Chua, L.O. Memristor Oscillators. Int. J. Bifurc. Chaos 2011, 18, 3183–3206. [Google Scholar] [CrossRef]
- Muthuswamy, B. Implementing Memristor Based Chaotic Circuits. Int. J. Bifurc. Chaos 2010, 20, 1335–1350. [Google Scholar] [CrossRef]
- Rajagopal, K.; Arun, S.; Karthikeyan, A.; Duraisamy, P.; Srinivasan, A. A hyperchaotic memristor system with exponential and discontinuous memductance function. AEU Int. J. Electron. Commun. 2018, 95, 249–255. [Google Scholar] [CrossRef]
- Rajagopal, K.; Li, C.; Nazarimehr, F.; Karthikeyan, A.; Duraisamy, P.; Jafari, S. Chaotic Dynamics of Modified Wien Bridge Oscillator with Fractional Order Memristor. Radioengineering 2019, 27, 165–174. [Google Scholar] [CrossRef]
- Song, Y.; Yuan, F.; Li, Y. Coexisting Attractors and Multistability in a Simple Memristive Wien-Bridge Chaotic Circuit. Entropy 2019, 21, 678. [Google Scholar] [CrossRef]
- Prousalis, D.A.; Volos, C.K.; Stouboulos, I.N.; Kyprianidis, I.M. Hyperchaotic memristive system with hidden attractors and its adaptive control scheme. Nonlinear Dyn. 2017, 90, 1681–1694. [Google Scholar] [CrossRef]
- Bao, H.; Wang, N.; Bao, B.; Chen, M.; Jin, P.; Wang, G. Initial condition-dependent dynamics and transient period in memristor-based hypogenetic jerk system with four line equilibria. Commun. Nonlinear Sci. Numer. Simul. 2018, 57, 264–275. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, C.; Zhou, L. Generating hyperchaotic multi-wing attractor in a 4D memristive circuit. Nonlinear Dyn. 2016, 85, 2653–2663. [Google Scholar] [CrossRef]
- Li, Q.; Hu, S.; Tang, S.; Zeng, G. Hyperchaos and horseshoe in a 4D memristive system with a line of equilibria and its implementation. Int. J. Circuit Theory Appl. 2014, 42, 1172–1188. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Physica D 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Holmes, P. Poincaré, celestial mechanics, dynamical-systems theory and “chaos”. Phys. Rep. 1990, 193, 137–163. [Google Scholar] [CrossRef]
- Lauritzen, B. Semiclassical Poincare map for integrable systems. Chaos 1992, 2, 409–412. [Google Scholar] [CrossRef]
- Kuznetsov, A.P.; Kuznetsov, S.P.; Mosekilde, E.; Stankevich, N.V. Co-existing hidden attractors in a radio-physical oscillator system. J. Phys. A Math. Theor. 2015, 48. [Google Scholar] [CrossRef]
- Sprott, J.C. A Proposed Standard for the Publication of New Chaotic Systems. Int. J. Bifurc. Chaos 2012, 21, 2391–2394. [Google Scholar] [CrossRef]
- Wang, G.; Lai, Y.C.; Grebogi, C. Transient chaos—A resolution of breakdown of quantum-classical correspondence in optomechanics. Sci. Rep. 2016, 6, 35381. [Google Scholar] [CrossRef]
- Dadras, S.; Momeni, H.R.; Qi, G. Analysis of a new 3D smooth autonomous system with different wing chaotic attractors and transient chaos. Nonlinear Dyn. 2010, 62, 391–405. [Google Scholar] [CrossRef]
- Bao, B.C.; Bao, H.; Wang, N.; Chen, M.; Xu, Q. Hidden extreme multistability in memristive hyperchaotic system. Chaos Solitons Fractals 2017, 94, 102–111. [Google Scholar] [CrossRef]
- Abedi, M.; Moghaddam, M.M.; Fallah, D. A Poincare map based analysis of stroke patients’ walking after a rehabilitation by a robot. Math. Biosci. 2018, 299, 73–84. [Google Scholar] [CrossRef] [PubMed]
- Wang, N.; Zhang, G.; Bao, H. Bursting oscillations and coexisting attractors in a simple memristor-capacitor-based chaotic circuit. Nonlinear Dyn. 2019, 97, 1477–1494. [Google Scholar] [CrossRef]
- Mou, J.; Sun, K.; Wang, H.; Ruan, J. Characteristic Analysis of Fractional-Order 4D Hyperchaotic Memristive Circuit. Math. Prob. Eng. 2017, 2313768. [Google Scholar] [CrossRef]
- He, S.B.; Sun, K.H.; Wang, H.H. Complexity Analysis and DSP Implementation of the Fractional-Order Lorenz Hyperchaotic System. Entropy 2015, 17, 8299–8311. [Google Scholar] [CrossRef]
- Munoz-Pacheco, J.M.; Zambrano-Serrano, E.; Volos, C.; Jafari, S.; Kengne, J.; Rajagopal, K. A New Fractional-Order Chaotic System with Different Families of Hidden and Self-Excited Attractors. Entropy 2018, 20, 564. [Google Scholar] [CrossRef]
- Peng, D.; Sun, K.; He, S.; Zhang, L.; Alamodi, A.O.A. Numerical analysis of a simplest fractional-order hyperchaotic system. Theor. Appl. Mech. Lett. 2019, 9, 220–228. [Google Scholar] [CrossRef]
- Peng, D.; Sun, K.H.; Alamodi, A.O.A. Dynamics analysis of fractional-order permanent magnet synchronous motor and its DSP implementation. Int. J. Mod. Phys. B 2019, 33, 1950031. [Google Scholar] [CrossRef]
- Ran, J.; Li, Y.; Wang, C. Chaos and Complexity Analysis of a Discrete Permanent-Magnet Synchronous Motor System. Complexity 2018, 7961214. [Google Scholar] [CrossRef]
- Wang, M.J.; Liao, X.H.; Deng, Y.; Li, Z.J.; Zeng, Y.C.; Ma, M.L. Bursting, Dynamics, and Circuit Implementation of a New Fractional-Order Chaotic System With Coexisting Hidden Attractors. J. Comput. Nonlinear Dyn. 2019, 14, 071002. [Google Scholar] [CrossRef]
- Ye, X.; Wang, X.; Mou, J.; Yan, X.; Xian, Y. Characteristic analysis of the fractional-order hyperchaotic memristive circuit based on the Wien bridge oscillator. Eur. Phys. J. Plus 2018, 133, 516. [Google Scholar] [CrossRef]
- Ye, X.; Wang, X.; Zhao, H.; Gao, H.; Zhang, M. Extreme multistability in a new hyperchaotic meminductive circuit and its circuit implementation. Eur. Phys. J. Plus 2019, 134, 206. [Google Scholar] [CrossRef]
- Zhang, S.; Zeng, Y.; Li, Z. One to four-wing chaotic attractors coined from a novel 3D fractional-order chaotic system with complex dynamics. Chin. J. Phys. 2018, 56, 793–806. [Google Scholar] [CrossRef]
- Zhang, S.; Zeng, Y.; Li, Z.; Zhou, C. Hidden Extreme Multistability, Antimonotonicity and Offset Boosting Control in a Novel Fractional-Order Hyperchaotic System Without Equilibrium. Int. J. Bifurcation Chaos 2018, 28, 1850167. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Z. Hidden extreme multistability in a novel 4D fractional-order chaotic system. Int. J. Non Linear Mech. 2019, 111, 14–27. [Google Scholar] [CrossRef]
- Zhou, C.; Li, Z.; Xie, F. Coexisting attractors, crisis route to chaos in a novel 4D fractional-order system and variable-order circuit implementation. Eur. Phys. J. Plus 2019, 134, 73. [Google Scholar] [CrossRef]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Du, C.; Liang, L.; Zhang, X. A High Spectral Entropy (SE) Memristive Hidden Chaotic System with Multi-Type Quasi-Periodic and its Circuit. Entropy 2019, 21, 1026. https://doi.org/10.3390/e21101026
Liu L, Du C, Liang L, Zhang X. A High Spectral Entropy (SE) Memristive Hidden Chaotic System with Multi-Type Quasi-Periodic and its Circuit. Entropy. 2019; 21(10):1026. https://doi.org/10.3390/e21101026
Chicago/Turabian StyleLiu, Licai, Chuanhong Du, Lixiu Liang, and Xiefu Zhang. 2019. "A High Spectral Entropy (SE) Memristive Hidden Chaotic System with Multi-Type Quasi-Periodic and its Circuit" Entropy 21, no. 10: 1026. https://doi.org/10.3390/e21101026
APA StyleLiu, L., Du, C., Liang, L., & Zhang, X. (2019). A High Spectral Entropy (SE) Memristive Hidden Chaotic System with Multi-Type Quasi-Periodic and its Circuit. Entropy, 21(10), 1026. https://doi.org/10.3390/e21101026




