Multiscale Entropy of Cardiac and Postural Control Reflects a Flexible Adaptation to a Cognitive Task
Abstract
1. Introduction
2. Materials and Methods
2.1. Population
2.2. Protocol
2.3. Recordings of RR Interval Time Series
2.4. Recordings of Center of Pressure Time Series
2.5. Cognitive Tasks
2.6. Analysis of RR Interval Time Series: Classic Indices
2.7. Analysis of Center of Pressure Time Series: Classic Indices
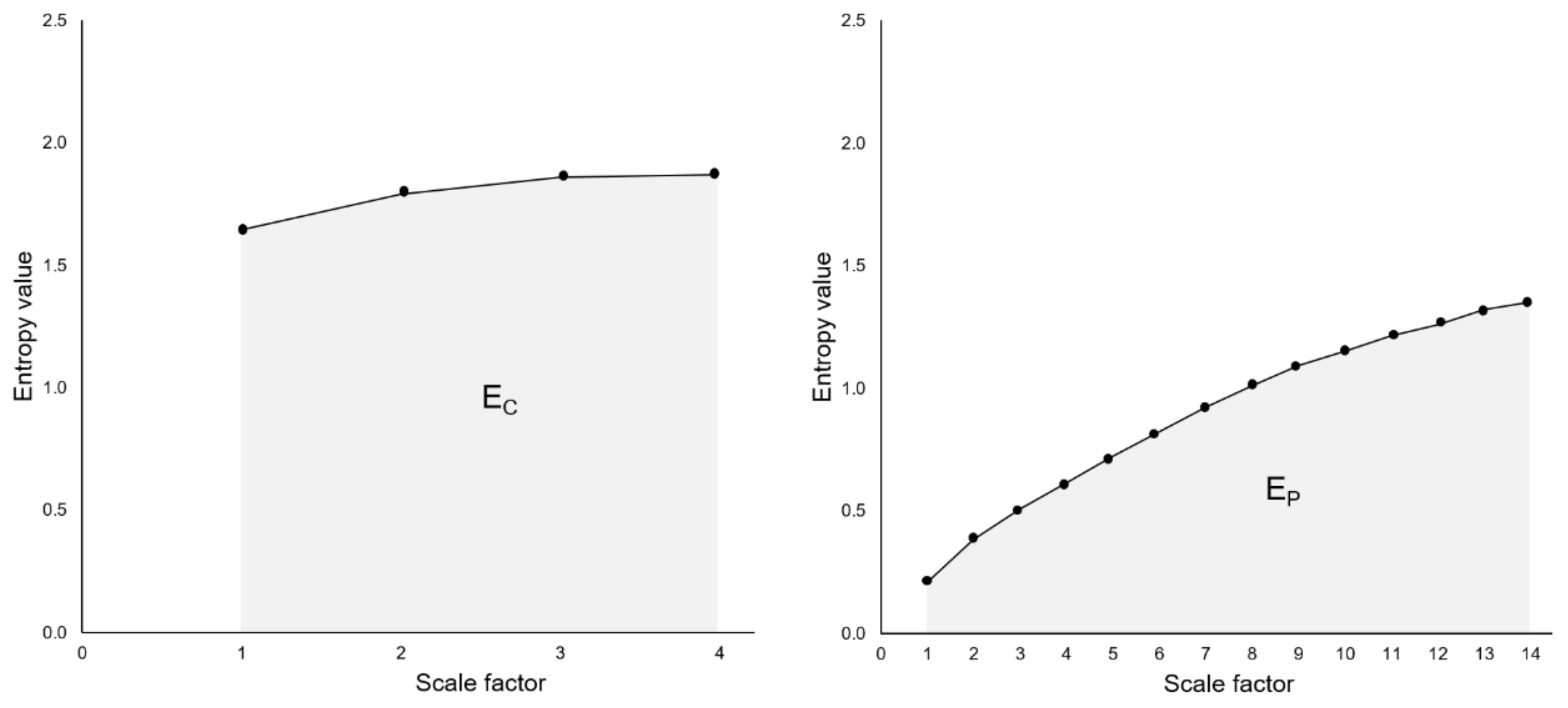
2.8. Analysis of Complexity: Entropy Indices
- At each scale factor of , the number of matched vector pairs and is calculated for all coarse-grained series, with corresponding to the sequence length considered. In the present study, .
- The RCMSE at a scale factor of is provided as follows, with corresponding to the tolerance for matches. In the present study, of the standard deviation of the initial time series [30].
2.9. Statistical Analyses
3. Results
3.1. Classic Indices in Temporal and Frequency Domains
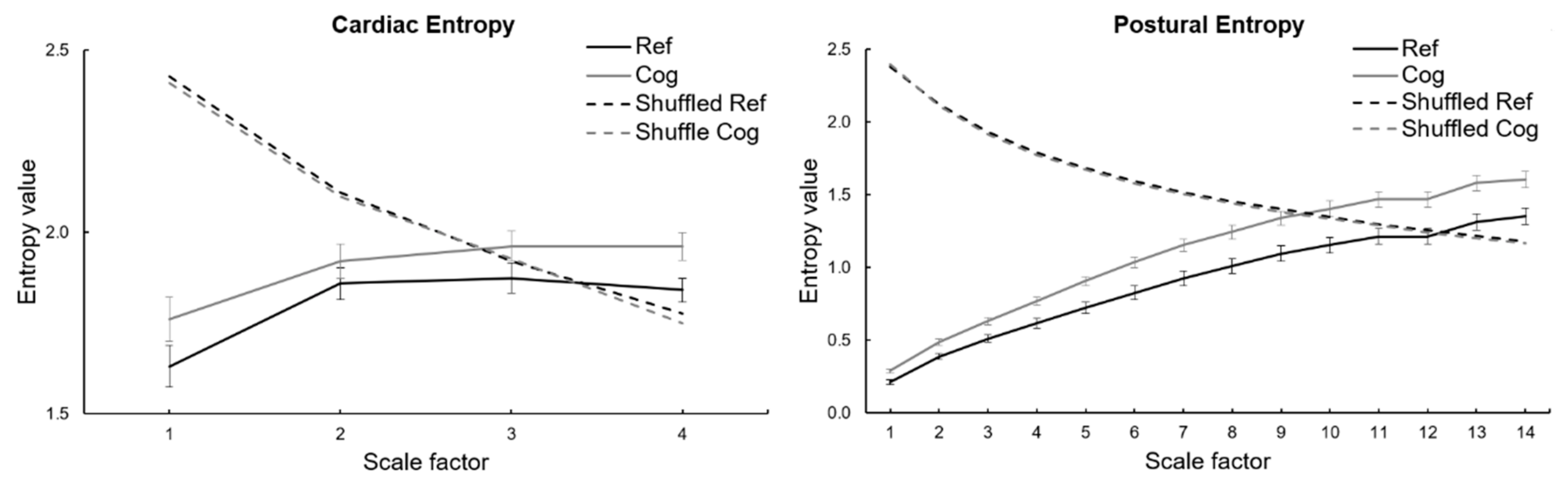
3.2. Entropy Indices
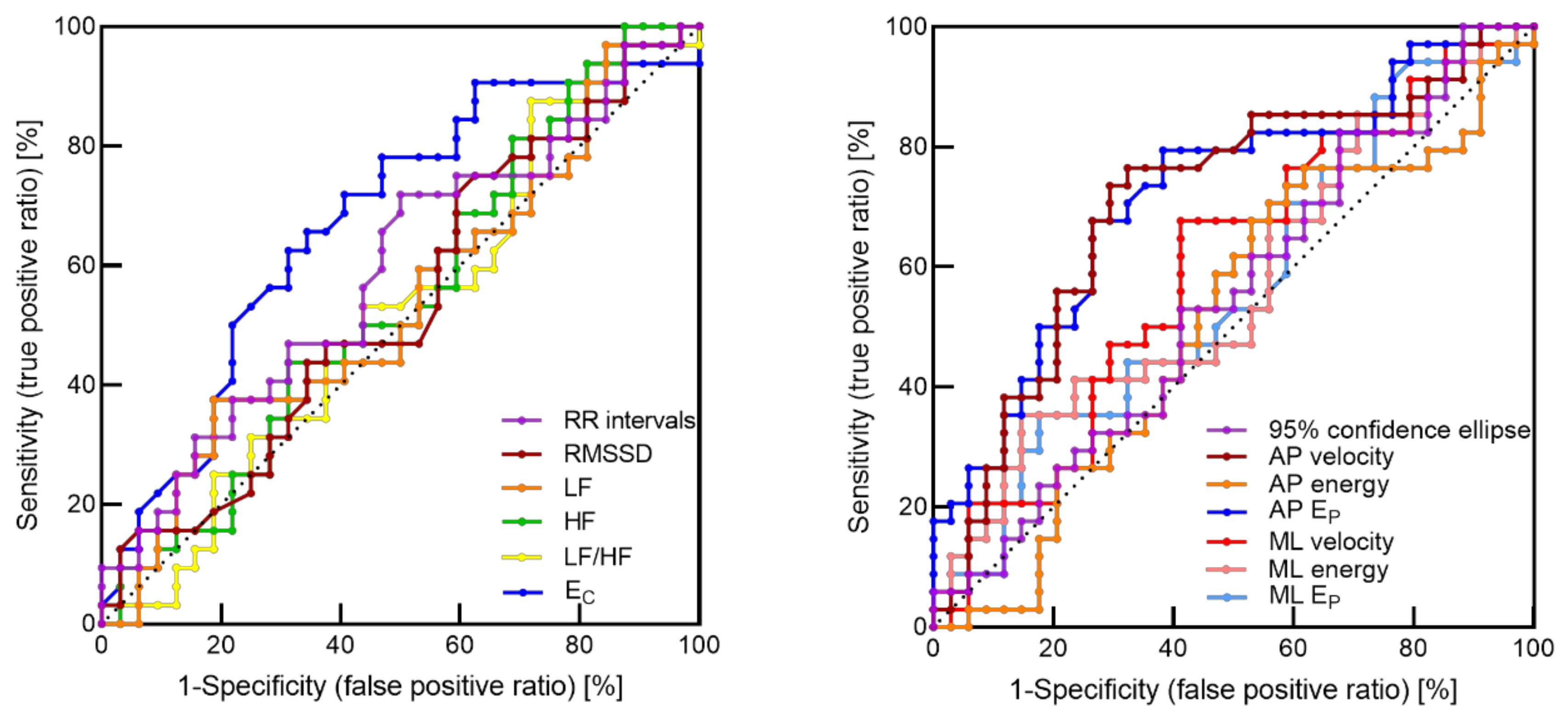
3.3. ROC Curves Analysis
4. Discussion
5. Conclusions
6. Limitations
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Costa, M.; Goldberger, A.L.; Peng, C.-K. Multiscale entropy analysis of biological signals. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2005, 71, 021906. [Google Scholar] [CrossRef] [PubMed]
- Costa, M.; Goldberger, A.L.; Peng, C.-K. Multiscale entropy analysis of complex physiologic time series. Phys. Rev. Lett. 2002, 89, 68102. [Google Scholar] [CrossRef] [PubMed]
- Kang, H.G.; Costa, M.D.; Priplata, A.A.; Starobinets, O.V.; Goldberger, A.L.; Peng, C.-K.; Kiely, D.K.; Cupples, L.A.; Lipsitz, L.A. Frailty and the degradation of complex balance dynamics during a dual-task protocol. J. Gerontol. A Biol. Sci. Med. Sci. 2009, 64, 1304–1311. [Google Scholar] [CrossRef] [PubMed]
- Wayne, P.M.; Gow, B.J.; Costa, M.D.; Peng, C.-K.; Lipsitz, L.A.; Hausdorff, J.M.; Davis, R.B.; Walsh, J.N.; Lough, M.; Novak, V.; et al. Complexity-Based Measures Inform Effects of Tai Chi Training on Standing Postural Control: Cross-Sectional and Randomized Trial Studies. PLoS ONE 2014, 9, e114731. [Google Scholar] [CrossRef] [PubMed]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef] [PubMed]
- Costa, M.; Priplata, A.A.; Lipsitz, L.A.; Wu, Z.; Huang, N.E.; Goldberger, A.L.; Peng, C.-K. Noise and poise: Enhancement of postural complexity in the elderly with a stochastic-resonance-based therapy. Europhys. Lett. 2007, 77, 68008. [Google Scholar] [CrossRef] [PubMed]
- Wayne, P.M.; Manor, B.; Novak, V.; Costa, M.D.; Hausdorff, J.M.; Goldberger, A.L.; Ahn, A.C.; Yeh, G.Y.; Peng, C.-K.; Lough, M.; et al. A systems biology approach to studying Tai Chi, physiological complexity and healthy aging: design and rationale of a pragmatic randomized controlled trial. Contemp. Clin. Trials 2013, 34, 21–34. [Google Scholar] [CrossRef]
- Manor, B.; Costa, M.D.; Hu, K.; Newton, E.; Starobinets, O.; Kang, H.G.; Peng, C.K.; Novak, V.; Lipsitz, L.A. Physiological complexity and system adaptability: Evidence from postural control dynamics of older adults. J. Appl. Physiol. 2010, 109, 1786–1791. [Google Scholar] [CrossRef]
- Manor, B.; Lipsitz, L.A.; Wayne, P.M.; Peng, C.-K.; Li, L. Complexity-based measures inform Tai Chi’s impact on standing postural control in older adults with peripheral neuropathy. BMC Complement. Altern. Med. 2013, 13, 87. [Google Scholar] [CrossRef]
- Busa, M.A.; Jones, S.L.; Hamill, J.; van Emmerik, R.E.A. Multiscale entropy identifies differences in complexity in postural control in women with multiple sclerosis. Gait Posture 2016, 45, 7–11. [Google Scholar] [CrossRef]
- Gruber, A.H.; Busa, M.A.; Gorton Iii, G.E.; Van Emmerik, R.E.A.; Masso, P.D.; Hamill, J. Time-to-contact and multiscale entropy identify differences in postural control in adolescent idiopathic scoliosis. Gait Posture 2011, 34, 13–18. [Google Scholar] [CrossRef] [PubMed]
- Tsai, C.-H.; Ma, H.-P.; Lin, Y.-T.; Hung, C.-S.; Hsieh, M.-C.; Chang, T.-Y.; Kuo, P.-H.; Lin, C.; Lo, M.-T.; Hsu, H.-H.; et al. Heart Rhythm Complexity Impairment in Patients with Pulmonary Hypertension. Sci. Rep. 2019, 9, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Yang, Z.; Meng, F.; Huang, L.; Qu, W.; Hao, H.; Zhang, J.; Li, L. Chronic vagus nerve stimulation reverses heart rhythm complexity in patients with drug-resistant epilepsy: An assessment with multiscale entropy analysis. Epilepsy Behav. 2018, 83, 168–174. [Google Scholar] [CrossRef] [PubMed]
- Silva, L.E.V.; Lataro, R.M.; Castania, J.A.; da Silva, C.A.A.; Valencia, J.F.; Murta, L.O.; Salgado, H.C.; Fazan, R.; Porta, A. Multiscale entropy analysis of heart rate variability in heart failure, hypertensive, and sinoaortic-denervated rats: classical and refined approaches. Am. J. Physiol. Regul. Integr. Comp. Physiol. 2016, 311, R150–R156. [Google Scholar] [CrossRef]
- Silva, L.E.V.; Lataro, R.M.; Castania, J.A.; Silva, C.A.A.; Salgado, H.C.; Fazan, R.; Porta, A. Nonlinearities of heart rate variability in animal models of impaired cardiac control: contribution of different time scales. J. Appl. Physiol. 2017, 123, 344–351. [Google Scholar] [CrossRef]
- Silva, L.E.V.; Silva, C.A.A.; Salgado, H.C.; Fazan, R. The role of sympathetic and vagal cardiac control on complexity of heart rate dynamics. Am. J. Physiol. Heart Circ. Physiol. 2017, 312, H469–H477. [Google Scholar] [CrossRef]
- Marwaha, P.; Sunkaria, R.K. Exploring total cardiac variability in healthy and pathophysiological subjects using improved refined multiscale entropy. Med. Biol. Eng. Comput. 2017, 55, 191–205. [Google Scholar] [CrossRef]
- O’Keeffe, C.; Taboada, L.P.; Feerick, N.; Gallagher, L.; Lynch, T.; Reilly, R.B. Complexity based measures of postural stability provide novel evidence of functional decline in fragile X premutation carriers. J. Neuroeng. Rehabil. 2019, 16, 87. [Google Scholar] [CrossRef]
- Jiang, B.C.; Yang, W.-H.; Shieh, J.-S.; Fan, J.S.-Z.; Peng, C.-K. Entropy-based method for COP data analysis. Theor. Issues Ergon. Sci. 2013, 14, 227–246. [Google Scholar] [CrossRef]
- Miyake, A.; Friedman, N.P.; Emerson, M.J.; Witzki, A.H.; Howerter, A.; Wager, T.D. The Unity and Diversity of Executive Functions and Their Contributions to Complex “Frontal Lobe” Tasks: A Latent Variable Analysis. Cogn. Psychol. 2000, 41, 49–100. [Google Scholar] [CrossRef]
- Vendrell, P.; Junqué, C.; Pujol, J.; Jurado, M.A.; Molet, J.; Grafman, J. The role of prefrontal regions in the Stroop task. Neuropsychologia 1995, 33, 341–352. [Google Scholar] [CrossRef]
- Stroop, J.R. Studies of interference in serial verbal reactions. J. Exp. Psychol. 1935, 18, 643–662. [Google Scholar] [CrossRef]
- Burgess, P.W.; Shallice, T. The Hayling and Brixton Tests; Thames Valley Test Company: Bury St Edmunds, UK, 1997. [Google Scholar]
- Gronwall, D.M. Paced auditory serial-addition task: a measure of recovery from concussion. Percept. Mot. Skills 1977, 44, 367–373. [Google Scholar] [CrossRef] [PubMed]
- Stokholm, J.; Jørgensen, K.; Vogel, A. Performances on five verbal fluency tests in a healthy, elderly Danish sample. Neuropsychol. Dev. Cogn. B Aging. Neuropsychol. Cogn. 2013, 20, 22–33. [Google Scholar] [CrossRef] [PubMed]
- Camm, A.J.; Malik, M.; Bigger, J.T.; Breithardt, G.; Cerutti, S.; Cohen, R.J.; Lombardi, F. Heart rate variability. Standards of measurement, physiological interpretation, and clinical use. Task Force of the European Society of Cardiology and the North American Society of Pacing and Electrophysiology. Eur. Heart J. 1996, 17, 354–381. [Google Scholar]
- Wu, S.-D.; Wu, C.-W.; Lin, S.-G.; Lee, K.-Y.; Peng, C.-K. Analysis of complex time series using refined composite multiscale entropy. Phys. Lett. A 2014, 378, 1369–1374. [Google Scholar] [CrossRef]
- Humeau-Heurtier, A. The Multiscale Entropy Algorithm and Its Variants: A Review. Entropy 2015, 17, 3110–3123. [Google Scholar] [CrossRef]
- Wu, S.-D.; Wu, C.-W.; Lin, S.-G.; Wang, C.-C.; Lee, K.-Y. Time Series Analysis Using Composite Multiscale Entropy. Entropy 2013, 15, 1069–1084. [Google Scholar] [CrossRef]
- Castiglioni, P.; Coruzzi, P.; Bini, M.; Parati, G.; Faini, A. Multiscale Sample Entropy of Cardiovascular Signals: Does the Choice between Fixed- or Varying-Tolerance among Scales Influence Its Evaluation and Interpretation? Entropy 2017, 19, 590. [Google Scholar] [CrossRef]
- Gow, B.J.; Peng, C.-K.; Wayne, P.M.; Ahn, A.C. Multiscale Entropy Analysis of Center-of-Pressure Dynamics in Human Postural Control: Methodological Considerations. Entropy 2015, 17, 7926–7947. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Metz, C.E. Basic principles of ROC analysis. Semin. Nucl. Med. 1978, 8, 283–298. [Google Scholar] [CrossRef]
- Hanley, J.A.; McNeil, B.J. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology 1982, 143, 29–36. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Habtemariam, D.; Iloputaife, I.; Lipsitz, L.A.; Manor, B. The Complexity of Standing Postural Sway Associates with Future Falls in Community-Dwelling Older Adults: The MOBILIZE Boston Study. Sci. Rep. 2017, 7, 2924. [Google Scholar] [CrossRef] [PubMed]
- Błaszczyk, J.W.; Klonowski, W. Postural stability and fractal dynamics. Acta Neurobiol. Exp. 2001, 61, 105–112. [Google Scholar]
- Benarroch, E.E. The central autonomic network: functional organization, dysfunction, and perspective. Mayo Clin. Proc. 1993, 68, 988–1001. [Google Scholar] [CrossRef]
- Thayer, J.F.; Ahs, F.; Fredrikson, M.; Sollers, J.J.; Wager, T.D. A meta-analysis of heart rate variability and neuroimaging studies: implications for heart rate variability as a marker of stress and health. Neurosci. Biobehav. Rev. 2012, 36, 747–756. [Google Scholar] [CrossRef]
- Thome, J.; Densmore, M.; Frewen, P.A.; McKinnon, M.C.; Théberge, J.; Nicholson, A.A.; Koenig, J.; Thayer, J.F.; Lanius, R.A. Desynchronization of autonomic response and central autonomic network connectivity in posttraumatic stress disorder. Hum. Brain Mapp. 2017, 38, 27–40. [Google Scholar] [CrossRef]
- Beissner, F.; Meissner, K.; Bär, K.-J.; Napadow, V. The autonomic brain: an activation likelihood estimation meta-analysis for central processing of autonomic function. J. Neurosci. 2013, 33, 10503–10511. [Google Scholar] [CrossRef]
- Thayer, J.F.; Lane, R.D. Claude Bernard and the heart-brain connection: further elaboration of a model of neurovisceral integration. Neurosci. Biobehav. Rev. 2009, 33, 81–88. [Google Scholar] [CrossRef]
- Allen, B.; Jennings, J.R.; Gianaros, P.J.; Thayer, J.F.; Manuck, S.B. Resting high-frequency heart rate variability is related to resting brain perfusion. Psychophysiology 2015, 52, 277–287. [Google Scholar] [CrossRef] [PubMed]
- Gianaros, P.J.; Wager, T.D. Brain-Body Pathways Linking Psychological Stress and Physical Health. Curr. Dir. Psychol. Sci. 2015, 24, 313–321. [Google Scholar] [CrossRef] [PubMed]
- Sakaki, M.; Yoo, H.J.; Nga, L.; Lee, T.-H.; Thayer, J.F.; Mather, M. Heart rate variability is associated with amygdala functional connectivity with MPFC across younger and older adults. Neuroimage 2016, 139, 44–52. [Google Scholar] [CrossRef] [PubMed]
- Lane, R.D.; McRae, K.; Reiman, E.M.; Chen, K.; Ahern, G.L.; Thayer, J.F. Neural correlates of heart rate variability during emotion. Neuroimage 2009, 44, 213–222. [Google Scholar] [CrossRef]
- Lipsitz, L.A. Dynamics of stability: The physiologic basis of functional health and frailty. J. Gerontol. A Biol. Sci. Med. Sci. 2002, 57, B115–B125. [Google Scholar] [CrossRef]
- Delignieres, D.; Marmelat, V. Fractal fluctuations and complexity: current debates and future challenges. Crit. Rev. Biomed. Eng. 2012, 40, 485–500. [Google Scholar] [CrossRef]
- Hoshikawa, Y.; Yamamoto, Y. Effects of Stroop color-word conflict test on the autonomic nervous system responses. Am. J. Physiol. 1997, 272, H1113–H1121. [Google Scholar] [CrossRef]
- Francis, D.P.; Willson, K.; Georgiadou, P.; Wensel, R.; Davies, L.C.; Coats, A.; Piepoli, M. Physiological basis of fractal complexity properties of heart rate variability in man. J. Physiol. 2002, 542, 619–629. [Google Scholar] [CrossRef]
- Castiglioni, P. Commentary: Decomposition of Heart Rate Variability Spectrum into a Power-Law Function and a Residual Spectrum. Front. Cardiovasc. Med. 2018, 5, 94. [Google Scholar] [CrossRef]
- Chen, M.-S.; Jiang, B.C. Resistance training exercise program for intervention to enhance gait function in elderly chronically ill patients: Multivariate multiscale entropy for center of pressure signal analysis. Comput. Math. Methods Med. 2014, 2014, 471356. [Google Scholar] [CrossRef]
- Almurad, Z.M.H.; Roume, C.; Blain, H.; Delignières, D. Complexity Matching: Restoring the Complexity of Locomotion in Older People Through Arm-in-Arm Walking. Front. Physiol. 2018, 9, 1766. [Google Scholar] [CrossRef] [PubMed]
- Young, H.; Benton, D. We should be using nonlinear indices when relating heart-rate dynamics to cognition and mood. Sci. Rep. 2015, 5, 16619. [Google Scholar] [CrossRef] [PubMed]

| Heart Rate Dynamics | Ref | Cog |
|---|---|---|
| RR intervals (ms) | 952 ± 120 | 915 ± 131 ** |
| RMSSD (ms) | 58 ± 36 | 52 ± 30 |
| LFs (ms2) | 2243 ± 2058 | 1894 ± 1602 |
| HFs (ms2) | 1459 ± 1448 | 1150 ± 1196 |
| LFs/HFs | 2.96 ± 3.09 | 2.82 ± 2.62 |
| EC | 5.45 ± 0.60 | 5.75 ± 0.69 * |
| Postural Dynamics | Ref | Cog |
| 95% confidence ellipse (mm2) | 217.5 ± 148.5 | 184.7 ± 103.5 |
| AP velocity (mm·s−1) | 4.4 ± 1.1 | 5.1 ± 1.2 *** |
| AP energy (mm2) | 10.29 ± 19.1 | 9.04 ± 5.5 |
| AP EP | 11.81 ± 3.07 | 14.45 ± 3.27 *** |
| ML velocity (mm·s−1) | 4.9 ± 1.6 | 5.3 ± 1.5 * |
| ML energy (mm2) | 6.42 ± 3.59 | 8.00 ± 5.54 |
| ML EP | 13.99 ± 2.76 | 14.72 ± 3.03 |
| Heart Rate Dynamics | J | AUC |
|---|---|---|
| RR intervals | 0.22 | 0.59 |
| RMSSD | 0.13 | 0.54 |
| LFs | 0.19 | 0.54 |
| HFs | 0.13 | 0.54 |
| LFs/HFs | 0.16 | 0.52 |
| EC | 0.31 | 0.67 |
| Postural Dynamics | J | AUC |
| 95% confidence ellipse (mm2) | 0.15 | 0.55 |
| AP velocity | 0.44 | 0.71 |
| AP energy | 0.15 | 0.51 |
| AP EP | 0.41 | 0.72 |
| ML velocity | 0.27 | 0.60 |
| ML energy | 0.21 | 0.67 |
| ML EP | 0.18 | 0.56 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blons, E.; Arsac, L.M.; Gilfriche, P.; Deschodt-Arsac, V. Multiscale Entropy of Cardiac and Postural Control Reflects a Flexible Adaptation to a Cognitive Task. Entropy 2019, 21, 1024. https://doi.org/10.3390/e21101024
Blons E, Arsac LM, Gilfriche P, Deschodt-Arsac V. Multiscale Entropy of Cardiac and Postural Control Reflects a Flexible Adaptation to a Cognitive Task. Entropy. 2019; 21(10):1024. https://doi.org/10.3390/e21101024
Chicago/Turabian StyleBlons, Estelle, Laurent M. Arsac, Pierre Gilfriche, and Veronique Deschodt-Arsac. 2019. "Multiscale Entropy of Cardiac and Postural Control Reflects a Flexible Adaptation to a Cognitive Task" Entropy 21, no. 10: 1024. https://doi.org/10.3390/e21101024
APA StyleBlons, E., Arsac, L. M., Gilfriche, P., & Deschodt-Arsac, V. (2019). Multiscale Entropy of Cardiac and Postural Control Reflects a Flexible Adaptation to a Cognitive Task. Entropy, 21(10), 1024. https://doi.org/10.3390/e21101024





